MetaTrader 5で隠れマルコフモデルを統合する

はじめに

金融時系列の基本的な特徴のひとつに「記憶」があることはよく知られています。時系列分析の文脈では、メモリはデータ内の依存構造を指し、過去の値が現在および将来の値に影響を与えます。メモリ構造を理解することは、時系列に適切なモデルを選択するのに役立ちます。この記事では、異なる種類の記憶について説明します 隠れマルコフモード（HMM）（英語）の形をとるタイプです。HMMの基礎を探り、Pythonのhmmlearnモジュールを使用してHMMを構築する方法を実演します。最後に、PythonとMQL5によるコードを紹介し、MetaTrader 5プログラムで使用するためのHMMの書き出しを可能にします。

隠れマルコフモデルを理解する

隠れマルコフモデルは、時系列データをモデル化するために使用される強力な統計的ツールであり、モデル化されるシステムは観測不可能な（隠れた）状態によって特徴付けられます。HMMの基本的な前提は、ある時刻にある状態にある確率は、その前のタイムスロットにおけるプロセスの状態に依存するということです。この依存関係はHMMの記憶を表しています。

金融時系列では、その時系列が上昇トレンドにあるか、下降トレンドにあるか、あるいは特定の範囲内で振動しているかを表す。金融指標を使ったことがある人なら誰でも、金融時系列に内在するノイズによって引き起こされるウィップソー効果に精通しています。HMMは、このような誤ったシグナルをフィルタリングし、根本的なトレンドをより明確に理解するために採用することができます。

HMMを構築するには、プロセスを定義する振る舞いの全体性を捕らえる観測が必要です。このデータのサンプルは、適切なHMMのパラメータを学習するために使用されます。このデータセットは、モデル化されるプロセスのさまざまな特徴で構成されます。例えば、ある金融資産の終値を研究する場合、終値に関連する他の側面、例えば、理想的には、私たちが興味を持っている隠れた状態を定義するのに役立つ様々な指標も含めることができます。

モデルパラメータの学習プロセスは、モデル化される系列が常に2つ以上の状態のいずれかにあるという仮定の下でおこなわれます。状態は単純に0からS-1と表示されます。これらの状態に対して、プロセスがある状態から別の状態に切り替わる可能性を捕らえる確率のセットを割り当てなければなりません。これらの確率は通常、遷移行列と呼ばれます。最初の観測は、それぞれの可能な状態にあるための特別な初期確率のセットを持っています。観測が特定の状態にある場合、その状態に関連する特定の分布に従うことが期待されます。

したがって、HMMは4つの特性によって完全に定義されます。

• 想定する状態の数
• 最初の観測がいずれかの状態である初期確率
• 確率の遷移行列
• 各状態の確率密度関数
  

最初にあるのは、観測と想定される状態数です。目の前のデータセットに適合するHMMのパラメータを見つけたいのです。これは、最尤推定と呼ばれる統計的手法を用いて尤度を観測することによっておこなわれます。この文脈では、最尤推定は、データサンプルに対応する可能性が最も高いモデル特性を探索するプロセスです。これは、各サンプルが特定の時間に特定の状態にある可能性を計算することによって達成されます。これはフォワードとバックワードアルゴリズムを使用しておこなわれ、それぞれ時間的に前方と後方にすべてのサンプルをトラバースします。

前進アルゴリズム

後続のサンプルの尤度を計算する前に、データセットの最初の観測から始めます。最初のサンプルでは、初期状態確率を使用します。この時点では、候補HMMの試行パラメータと考えられます。モデル化されるプロセスについて何もわかっていない場合、すべての初期状態確率を1/Sに設定することはまったく問題ありません。ベイズの定理を適用すると、次のような一般式が成り立ちます。

ここで、lkは、時刻tのサンプルが状態iにある可能性であり、pは、時刻tまでのサンプルが与えられたとき、時刻tに状態iにある確率です。Oは個々のサンプルで、データセットの1行です。

最初のサンプルの尤度は、P(A)= P(A|B)P(B)という条件付き確率規則に従って計算されます。したがって、最初のサンプルについて、状態iにあることの尤度は、状態iにあることの初期状態確率に最初のサンプルの確率密度関数を乗算することによって計算されます。

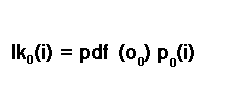
これも候補HMMの試行パラメータです。文献的には、放出確率と呼ばれることもあります。放出確率については後ほど詳しく説明します。とりあえず、現段階ではもうひとつのトライアルパラメータであることを意識してください。自分たちがどのような状態にあるのか確信が持てないことを忘れてはなりません。私たちは、ありとあらゆる状態のどれかにいる可能性を考慮しなければなりません。この結果、最終的な初期尤度は、すべての可能な状態のすべての尤度の合計となります。

 

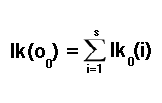
後続の観測の尤度を計算するには、前のタイムスロットで可能な状態のいずれかから特定の状態に遷移する可能性を考慮しなければなりません。ここで、遷移確率が効果を発揮します。これは、この時点でのもう 1 つの試行パラメータです。現在のタイムスロットの確率を計算した上で、次のタイムスロットで特定の状態に到達する確率は、現在わかっている状態確率と対応する遷移確率を掛け合わせることで推定されます。

これは、移行確率や移行行列について話す良い機会です。

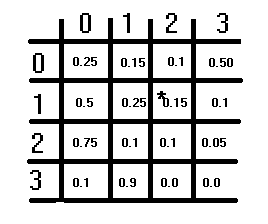
上の図は、仮想的な遷移行列を示しています。S×Sの構造を持ち、Sは想定される状態の数です。各要素は確率を表し、各行の確率の合計は1になるはずです。この条件は列には適用されません。ある状態から別の状態への切り替えに対応する遷移確率を求めるには、まず行を参照し、次に列を参照します。切り替え元の状態は行インデックスに対応し、切り替え先の状態は列インデックスに対応します。これらのインデックスの値が、対応する移行確率です。行列の対角線は、状態が変化しない確率を表しています。

選択したデータ標本の残りの観測の尤度を計算する作業に戻ると、状態確率に遷移確率を掛けていました。しかし、全体像を把握するためには、あらゆる可能性のある状態のどれかに移行する可能性を考慮しなければなりません。次の式に従って、すべての可能性を足し算します。

            

これで、データセットの各サンプルについての個別尤度の計算は終了です。これらの個々の尤度は、乗算によって結合され、データセット全体の尤度を得ることができます。先ほど説明した計算は、この方法が時間的前方再帰であることから、フォワードアルゴリズムと呼ばれています。これは、次のセクションで説明するバックワードアルゴリズムとは対照的です。

バックワードアルゴリズム

最後のデータサンプルから最初のデータ サンプルまで、時間を遡って個々の尤度を計算することもできます。まず、最後のデータサンプルの全状態の尤度を1に設定します。各データサンプルについて、特定の状態にある場合、どの状態にも遷移できると考え、後続のサンプルセットの尤度を計算します。これは、各状態の尤度の加重和を計算することによっておこないます。つまり、その状態にある確率に、サンプルが同じ状態にある確率密度関数を掛けたものです。この計算結果は、現在の状態から次の状態に移行する確率を加重係数として用いて調整されます。これはすべて、以下の式に集約されています。

確率密度関数

フォワードアルゴリズムとバックワードアルゴリズムの議論の中で、HMMのパラメータとして確率密度関数(pdf)について言及がありました。そこで疑問が生じます。どのような配分を想定しているのでしょうか。前述したように、HMMのpdfパラメータは通常、放出確率と呼ばれます。モデル化されるデータが離散値またはカテゴリ値で構成される場合、それらは確率と呼ばれます。連続変数を扱うときはpdfを使用します。

このテキストでは、多変量正規分布に従う連続変数のデータセットをモデル化するHMMを示します。実際、後ほど紹介するPythonモジュールには、モデル化されるデータのさまざまな分布に対応するHMMの実装があります。その延長線上で、仮定された分布のパラメータはHMMのパラメータの1つになります。多変量正規分布の場合、そのパラメータは平均と共分散です。

バウム＝ウェルチアルゴリズム

バウム＝ウェルチアルゴリズムは期待値最大化手法であり、HMMの候補に対してさまざまなパラメータを試行し、最適なものを導き出すために使用されます。この最適化手順で最大化される値は、サンプルのデータセット全体の尤度です。バウム＝ウェルチアルゴリズムは効率的で信頼できることで知られていますが、欠点もあります。その欠点は、非凸であることです。最適化に関する非凸関数とは、多数の局所的極小値または極大値を持つ関数のことです。

つまり、収束が達成されても、パラメータ空間の大域的な最大値や最小値が見つかっていない可能性があります。この関数は基本的に最適点に収束することは保証されていません。この欠点を軽減する最善の方法は、パラメータ空間内の他のパラメータに比べて大きな尤度を持つパラメータを試行することです。そのためには、最適化プロセスを開始するための最適な初期パラメータ空間を見つけるために、数多くのランダムなパラメータ値を試行しなければなりません。

状態確率の計算

最適なHMMとそのパラメータが得られたら、それを使用して未見のデータサンプルの状態確率を計算することができます。このような計算の結果は、各状態ごとに1つずつ、各状態にある確率を示す確率の集合となります。フォワードアルゴリズムからの個々の尤度とバックワードアルゴリズムからの尤度が掛け合わされ、特定の状態の尤度が得られます。ベイズの法則によると、ある観測が特定の状態にある確率は、次のように計算されます。

ビタビアルゴリズムによる状態確率の計算

状態確率と同様に、ビタビアルゴリズムを使用することで、観測がどのような状態にあるのかを推測することもできます。計算は最初の観測から始まり、その状態確率は初期状態確率に放出確率を掛けたものを用いて計算されます。

2番目から最後までの各観測について、各状態確率は、前の状態確率、対応する遷移確率、およびその放出確率を用いて計算されます。最も確率の高い状態が、最も確率の高い状態となります。

ここまで隠れマルコフモデルのすべての構成要素を見てきました。ここでは、その実用的な実装について掘り下げていきます。hmmlearnパッケージで提供されているPythonベースのHMMの実装を見ることから始めます。MQL5のコードに切り替える前に、hmmlearnのガウスHMM実装の使用について説明し、hmmlearnを使用してPythonで学習したモデルをMetaTrader 5アプリケーションに統合する方法を示します。

Pythonのhmmlearnパッケージ

Pythonのhmmlearnライブラリは隠れマルコフモデルを扱うためのツールを提供します。HMMを訓練するためのツールはhmm名前空間にあります。hmmの中では、異なる分布のプロセスを扱うための特別なクラスがいくつか宣言されています。すなわち：

• MultinomialHMM：観測が離散的で多項分布に従うHMMをモデル化する
• GMMHMM：観測がガウス分布の混合から生成されるHMMをモデル化する
• PoissonHMM：観測がポアソン分布に従うと仮定されたHMMをモデル化する
• 最後に、多変量ガウス（正規）分布に従う傾向のあるデータセットを扱うGaussianHMMクラスがある。このクラスでデモをおこない、その結果のモデルをMetaTrader 5とリンクさせる。

パッケージをインストールするには、以下のコマンドを使用します。

pip install hmmlearn

パッケージをインストールしたら、以下の importステートメントを使用して GaussianHMMクラスをインポートできます。

from hmmlearn.hmm import GaussianHMM

あるいは、上記のすべてのクラスとその他の便利なユーティリティを含むhmmモジュールをインポートすることもできます。このメソッドを使用する場合は、クラス名の前にhmmをつけなければなりません。

from hmmlearn import hmm

GaussianHMMオブジェクトはいくつかのパラメータで初期化できます：

model = GaussianHMM(n_components=3, covariance_type='diag', n_iter=100, tol=0.01)

ここで

• n_components：モデルの状態数
• covariance_type：使用する共分散パラメータの種類（'spherical'、'diag'、'full'、'tied'）。使用される共分散タイプは、データセットの特徴に関係します。モデル化されるデータセットの特徴や変数が、相関している可能性がなく、同じような分散を持っている場合は、球形の共分散を選ぶべきです。そうでなければ、変数が対照的な分散を持つ場合、対角共分散型を選択するのが最良の選択です。変数に相関がある場合は、完全共分散型か同値共分散型のどちらかを選ぶべきです。完全共分散を選択すると、最も柔軟性が高くなるが、計算コストが高くなります。これは、モデル化されるプロセスに関する仮定の数を制限する最も安全な選択です。タイド共分散は、各州が同じような共分散構造を共有しているという付加的な仮定を立てる。完全な共分散に比べれば少し効率的です。
• n_iter：訓練中の最大反復回数
• tol：収束のしきい値

モデルを指定するすべてのパラメータを調べるには、hmmlearnライブラリのドキュメントを参照してください。この文書では、さまざまなパラメータとその使用法について詳しく説明しています。hmmlearnライブラリの公式サイト、またはPythonのヘルプユーティリティから、ライブラリのインストール時に同梱されているドキュメントにアクセスしてください。

help(GaussianHMM)

モデルを訓練するには、fit()メソッドを呼び出します。入力として少なくとも1つの2次元配列を必要とします。

model.fit(data)

学習が完了したら、predict()か decode()を呼び出すことで、データセットの隠れた状態を得ることができます。どちらも、モデルの訓練に使われたデータセットと同じ数の特徴を持つ2次元配列を想定しています。predict()メソッドは計算された隠れ状態の配列を返し、decode()はタプルで囲まれた隠れ状態の配列と対数尤度を返します。

score_samples()を呼び出すと、入力として与えられたデータセットに対する対数尤度と状態確率が返されます。この場合も、モデルの訓練に使用したデータと同じ特徴数を持つデータでなければなりません。

隠れマルコフモデルの書き出し

MetaTrader5で使用するためにhmmlearnパッケージを使用してPythonで訓練されたモデルを書き出すには、2つのカスタムコンポーネントを実装する必要があります。

• Pythonコンポーネント：このコンポーネントは、訓練済みモデルのパラメータをMetaTraderアプリケーションから読み取り可能な形式で保存する役割を果たします。MetaTrader 5アプリケーションで解析可能なファイル形式にモデルパラメータをエクスポートします。
• MQL5コンポーネント：MQL5コンポーネントは、MQL5で書かれたコードで構成されています。このコンポーネントは、Pythonコンポーネントによって書き出されたHMMパラメータを読み込む機能を含むべきです。さらに、指定されたHMMに基づいてデータセットの隠れ状態と状態確率を計算するために、フォワード、バックワード、ビタビアルゴリズムを実装する必要があります。
  

これらのコンポーネントを実装するには、PythonとMQL5の両方で、データのシリアライズ形式、ファイルの入出力操作、アルゴリズムの実装を慎重に検討する必要があります。学習済みモデルを正確に転送し、MetaTrader 5で推論タスクを実行するには、PythonとMQL5の実装間の互換性を確保することが不可欠です。

hmmlearnパッケージは、pickleモジュールを使用して学習済みHMMを保存する機能を提供します。問題は、Python以外でpickledファイルを扱うのが簡単ではないということです。より良い選択肢はjson形式を使用することでしょう。HMMパラメータは、MQL5コードを使用して読み取ることができる構造化JSONファイルに書き込まれます。この機能は以下のPython関数に実装されています。

def hmm2json(hmm_model, filename):
    """
    function save a GaussianHMM model to json format 
    readable from MQL5 code.
    param: hmm_model should an instance of GaussianHMM
    param: string. filename or path to file where HMM 
    parameters will be written to
    """
    if hmm_model.__class__.__name__ != 'GaussianHMM':
        raise TypeError(f'invalid type supplied')
    if len(filename) < 1 or not isinstance(filename,str):
        raise TypeError(f'invalid filename supplied')
    jm  = {
            "numstates":hmm_model.n_components,
            "numvars":hmm_model.n_features,
            "algorithm":str(hmm_model.algorithm),
            "implementation":str(hmm_model.implementation), 
            "initprobs":hmm_model.startprob_.tolist(),
            "means":hmm_model.means_.tolist(),
            "transitions":hmm_model.transmat_.tolist(),
            "covars":hmm_model.covars_.tolist()
          }
    with open(filename,'w') as file:
        json.dump(jm,file,indent=None,separators=(',', ':')) 
    return 

この関数は、GaussianHMMクラスのインスタンスとファイル名を入力として受け取り、HMMパラメータをMQL5コードで読み込める構造化形式でJSONファイルに書き出します。

MQL5のコードでは、JSON形式で保存されたHMMモデルを読み込む機能は、hmmlearn.mqhで囲まれています。このファイルにはHMMクラスの定義が含まれています。

//+------------------------------------------------------------------+
//|                                                     hmmlearn.mqh |
//|                                  Copyright 2024, MetaQuotes Ltd. |
//|                                             https://www.mql5.com |
//+------------------------------------------------------------------+
#property copyright "Copyright 2024, MetaQuotes Ltd."
#property link      "https://www.mql5.com"
#include<Math\Alglib\dataanalysis.mqh>
#include<Math\Stat\Uniform.mqh>
#include<Math\Stat\Math.mqh>
#include<JAson.mqh>
#include<Files/FileTxt.mqh>
#include<np.mqh>

//+------------------------------------------------------------------+
//|Markov model estimation method                                    |
//+------------------------------------------------------------------+
enum ENUM_HMM_METHOD
  {
   MODE_LOG=0,
   MODE_SCALING
  };
//+------------------------------------------------------------------+
//| state sequence decoding algorithm                                |
//+------------------------------------------------------------------+
enum ENUM_DECODE_METHOD
  {
   MODE_VITERBI=0,
   MODE_MAP
  };
//+------------------------------------------------------------------+
//| Hidden Markov Model class                                        |
//+------------------------------------------------------------------+
class HMM
  {
private:
   ulong m_samples ;       // Number of cases in dataset
   ulong m_vars ;        // Number of variables in each case
   ulong m_states ;      // Number of states
   vector            m_initprobs;   // vector of probability that first case is in each state
   matrix            m_transition;  // probability matrix
   matrix m_means ;                 //state means
   matrix m_covars[] ;              // covariances
   matrix densities ;              // probability densities
   matrix alpha ;       // result of forward algorithm
   matrix beta ;        // result of backward algorithm
   matrix m_stateprobs ; // probabilities of state
   double likelihood ;  //  log likelihood
   matrix            trial_transition;
   bool              trained;
   double            m_mincovar;
   ENUM_HMM_METHOD   m_hmm_mode;
   ENUM_DECODE_METHOD m_decode_mode;
   //+------------------------------------------------------------------+
   //| normalize array so sum(exp(a)) == 1                              |
   //+------------------------------------------------------------------+
   matrix            log_normalize(matrix &in)
     {
      matrix out;
      if(in.Cols()==1)
         out = matrix::Zeros(in.Rows(), in.Cols());
      else
         out = logsumexp(in);
      return in-out;
     }
   //+------------------------------------------------------------------+
   //| log of the sum of exponentials of input elements                 |
   //+------------------------------------------------------------------+
   matrix            logsumexp(matrix &in)
     {
      matrix out;

      vector amax = in.Max(1);

      for(ulong i = 0; i<amax.Size(); i++)
         if(fpclassify(MathAbs(amax[i])) == FP_INFINITE)
            amax[i] = 0.0;

      matrix ama(amax.Size(),in.Cols());
      for(ulong i=0; i<ama.Cols();i++)
         ama.Col(amax,i);

      matrix tmp = exp(in - ama);

      vector s = tmp.Sum(1);

      out.Init(s.Size(),in.Cols());
      for(ulong i=0; i<out.Cols();i++)
         out.Col(log(s),i);

      out+=ama;

      return out;
     }

   //+------------------------------------------------------------------+
   //| normarlize vector                                                |
   //+------------------------------------------------------------------+
   vector            normalize_vector(vector &in)
     {
      double sum = in.Sum();
      return in/sum;
     }
   //+------------------------------------------------------------------+
   //|  normalize matrix                                                |
   //+------------------------------------------------------------------+
   matrix            normalize_matrix(matrix &in)
     {
      vector sum = in.Sum(1);

      for(ulong i = 0; i<sum.Size(); i++)
         if(sum[i] == 0.0)
            sum[i] = 1.0;

      matrix n;
      n.Init(sum.Size(), in.Cols());
      for(ulong i =0; i<n.Cols(); i++)
         n.Col(sum,i);

      return in/n;
     }
   //+------------------------------------------------------------------+
   //|   Set up model from JSON object                                  |
   //+------------------------------------------------------------------+
   bool              fromJSON(CJAVal &jsonmodel)
     {

      if(jsonmodel["implementation"].ToStr() == "log")
         m_hmm_mode = MODE_LOG;
      else
         m_hmm_mode = MODE_SCALING;

      if(jsonmodel["algorithm"].ToStr() == "Viterbi")
         m_decode_mode = MODE_VITERBI;
      else
         m_decode_mode = MODE_MAP;

      m_states = (ulong)jsonmodel["numstates"].ToInt();
      m_vars = (ulong)jsonmodel["numvars"].ToInt();


      if(!m_initprobs.Resize(m_states) || !m_means.Resize(m_states,m_vars) ||
         !m_transition.Resize(m_states,m_states) || ArrayResize(m_covars,int(m_states))!=int(m_states))
        {
         Print(__FUNCTION__, " error ", GetLastError());
         return false;
        }

      for(uint i = 0; i<m_covars.Size(); i++)
        {
         if(!m_covars[i].Resize(m_vars,m_vars))
           {
            Print(__FUNCTION__, " error ", GetLastError());
            return false;
           }

         for(int k = 0; k<int(m_covars[i].Rows()); k++)
            for(int j = 0; j<int(m_covars[i].Cols()); j++)
               m_covars[i][k][j] = jsonmodel["covars"][i][k][j].ToDbl();
        }

      for(int i =0; i<int(m_initprobs.Size()); i++)
        {
         m_initprobs[i] = jsonmodel["initprobs"][i].ToDbl();
        }

      for(int i=0; i<int(m_states); i++)
        {
         for(int j = 0; j<int(m_vars); j++)
            m_means[i][j] = jsonmodel["means"][i][j].ToDbl();
        }

      for(int i=0; i<int(m_states); i++)
        {
         for(int j = 0; j<int(m_states); j++)
            m_transition[i][j] = jsonmodel["transitions"][i][j].ToDbl();
        }

      return true;
     }

   //+------------------------------------------------------------------+
   //|  Multivariate Normal Density function                            |
   //+------------------------------------------------------------------+
   double            mv_normal(ulong nv,vector &x, vector &mean, matrix &in_covar)
     {
      matrix cv_chol;
      vector vc = x-mean;

      if(!in_covar.Cholesky(cv_chol))
        {
         matrix ncov = in_covar+(m_mincovar*matrix::Eye(nv,nv));
         if(!ncov.Cholesky(cv_chol))
           {
            Print(__FUNCTION__,": covars matrix might not be symmetric positive-definite, error ", GetLastError());
            return EMPTY_VALUE;
           }
        }

      double cv_log_det = 2.0 * (MathLog(cv_chol.Diag())).Sum();
      vector cv_sol = cv_chol.Solve(vc);

      return -0.5*((nv*log(2.0 * M_PI)) + (pow(cv_sol,2.0)).Sum() + cv_log_det);

     }


   //+------------------------------------------------------------------+
   //|logadd exp                                                        |
   //+------------------------------------------------------------------+
   double            logaddexp(double a, double b)
     {
      return a==-DBL_MIN?b:b==-DBL_MIN?a:MathMax(a,b)+log1p(exp(-1.0*MathAbs(b-a)));
     }
   //+------------------------------------------------------------------+
   //| scaled trans calculation                                         |
   //+------------------------------------------------------------------+
   matrix            compute_scaling_xi_sum(matrix &trans, matrix &dens,matrix &alf, matrix &bta)
     {
      matrix logdens = exp(dens).Transpose();

      ulong ns = logdens.Rows();
      ulong nc = logdens.Cols();

      matrix out;
      out.Resize(nc,nc);
      out.Fill(0.0);

      for(ulong t =0; t<ns-1; t++)
        {
         for(ulong i = 0; i<nc; i++)
           {
            for(ulong j = 0; j<nc; j++)
              {
               out[i][j] += alf[t][i] * trans[i][j] * logdens[t+1][j]*bta[t+1][j];
              }
           }
        }
      return out;
     }
   //+------------------------------------------------------------------+
   //| log trans calculation                                            |
   //+------------------------------------------------------------------+
   matrix            compute_log_xi_sum(matrix &trans, matrix &dens,matrix &alf, matrix &bta)
     {
      matrix logtrans = log(trans);
      matrix logdens = dens.Transpose();

      ulong ns = logdens.Rows();
      ulong nc = logdens.Cols();

      vector row = alf.Row(ns-1);
      double logprob = (log(exp(row-row[row.ArgMax()]).Sum()) + row[row.ArgMax()]);

      matrix out;
      out.Init(nc,nc);

      out.Fill(-DBL_MIN);

      for(ulong t = 0 ; t<ns-1; t++)
        {
         for(ulong i =0; i<nc; i++)
           {
            for(ulong j =0; j<nc; j++)
              {
               double vl = alf[t][i] + logtrans[i][j]+ logdens[t+1][j]+bta[t+1][j] - logprob;
               out[i][j] = logaddexp(out[i][j], vl);
              }
           }
        }

      return out;

     }
   //+------------------------------------------------------------------+
   //| forward scaling                                                  |
   //+------------------------------------------------------------------+
   double            forwardscaling(vector &startp, matrix &trans, matrix &dens,matrix &out, vector&outt)
     {
      double minsum = 1.e-300;
      vector gstartp = startp;
      matrix gtrans = trans;
      matrix gdens = exp(dens).Transpose();

      ulong ns = gdens.Rows();
      ulong nc = gdens.Cols();

      if(out.Cols()!=nc || out.Rows()!=ns)
         out.Resize(ns,nc);

      if(outt.Size()!=ns)
         outt.Resize(ns);

      out.Fill(0.0);

      double logprob = 0.0;

      for(ulong i = 0; i<nc; i++)
         out[0][i] = gstartp[i]*gdens[0][i];

      double sum  = (out.Row(0)).Sum();

      if(sum<minsum)
         Print("WARNING: forward pass failed with underflow consider using log implementation ");

      double scale = outt[0] = 1.0/sum;
      logprob -= log(scale);

      for(ulong i=0; i<nc; i++)
         out[0][i] *=scale;

      for(ulong t =1; t<ns; t++)
        {
         for(ulong j=0; j<nc; j++)
           {
            for(ulong i=0; i<nc; i++)
              {
               out[t][j]+=out[t-1][i] * gtrans[i][j];
              }
            out[t][j]*=gdens[t][j];
           }
         sum = (out.Row(t)).Sum();
         if(sum<minsum)
            Print("WARNING: forward pass failed with underflow consider using log implementation ");

         scale = outt[t] = 1.0/sum;
         logprob -= log(scale);
         for(ulong j = 0; j<nc; j++)
            out[t][j] *= scale;

        }
      return logprob;
     }
   //+------------------------------------------------------------------+
   //|backward scaling                                                  |
   //+------------------------------------------------------------------+
   matrix            backwardscaling(vector &startp, matrix &trans, matrix &dens,vector &scaling)
     {
      vector gstartp = startp;
      vector scaled = scaling;
      matrix gtrans = trans;
      matrix gdens =  exp(dens).Transpose();

      ulong ns = gdens.Rows();
      ulong nc = gdens.Cols();

      matrix out;
      out.Init(ns,nc);

      out.Fill(0.0);
      for(ulong i = 0; i<nc; i++)
         out[ns-1][i] = scaling[ns-1];

      for(long t = long(ns-2); t>=0; t--)
        {
         for(ulong i=0; i<nc; i++)
           {
            for(ulong j =0; j<nc; j++)
              {
               out[t][i]+=(gtrans[i][j]*gdens[t+1][j]*out[t+1][j]);
              }
            out[t][i]*=scaling[t];
           }
        }
      return out;
     }
   //+------------------------------------------------------------------+
   //| forward log                                                      |
   //+------------------------------------------------------------------+
   double            forwardlog(vector &startp, matrix &trans, matrix &dens,matrix &out)
     {
      vector logstartp = log(startp);
      matrix logtrans = log(trans);
      matrix logdens = dens.Transpose();

      ulong ns = logdens.Rows();
      ulong nc = logdens.Cols();

      if(out.Cols()!=nc || out.Rows()!=ns)
         out.Resize(ns,nc);

      vector buf;
      buf.Init(nc);

      for(ulong i =0; i<nc; i++)
         out[0][i] = logstartp[i] + logdens[0][i];

      for(ulong t =1; t<ns; t++)
        {
         for(ulong j =0; j<nc; j++)
           {
            for(ulong i =0; i<nc; i++)
              {
               buf[i] = out[t-1][i] + logtrans[i][j];
              }
            out[t][j] = logdens[t][j] + (log(exp(buf-buf[buf.ArgMax()]).Sum()) + buf[buf.ArgMax()]);
           }
        }

      vector row = out.Row(ns-1);

      return (log(exp(row-row[row.ArgMax()]).Sum()) + row[row.ArgMax()]);
     }
   //+------------------------------------------------------------------+
   //|  backwardlog                                                     |
   //+------------------------------------------------------------------+
   matrix            backwardlog(vector &startp, matrix &trans, matrix &dens)
     {
      vector logstartp = log(startp);
      matrix logtrans = log(trans);
      matrix logdens = dens.Transpose();

      ulong ns = logdens.Rows();
      ulong nc = logdens.Cols();

      matrix out;
      out.Init(ns,nc);

      vector buf;
      buf.Init(nc);

      for(ulong i =0; i<nc; i++)
         out[ns-1][i] = 0.0;

      for(long t = long(ns-2); t>=0; t--)
        {
         for(long i =0; i<long(nc); i++)
           {
            for(long j =0; j<long(nc); j++)
              {
               buf[j] = logdens[t+1][j] + out[t+1][j] + logtrans[i][j];
              }
            out[t][i] = (log(exp(buf-buf[buf.ArgMax()]).Sum()) + buf[buf.ArgMax()]);
           }
        }
      return out;
     }
   //+------------------------------------------------------------------+
   //| compute posterior state probabilities scaling                    |
   //+------------------------------------------------------------------+
   matrix            compute_posteriors_scaling(matrix &alf, matrix &bta)
     {
      return normalize_matrix(alf*bta);
     }
   //+------------------------------------------------------------------+
   //| compute posterior state probabilities log                        |
   //+------------------------------------------------------------------+
   matrix            compute_posteriors_log(matrix &alf, matrix &bta)
     {
      return exp(log_normalize(alf+bta));
     }
   //+------------------------------------------------------------------+
   //|calculate the probability of a state                              |
   //+------------------------------------------------------------------+
   double            compute_posteriors(matrix &data, matrix &result, ENUM_HMM_METHOD use_log=MODE_LOG)
     {
      matrix alfa,bt,dens;
      double logp=0.0;
      dens = find_densities(m_vars,m_states,data,m_means,m_covars);
      if(use_log == MODE_LOG)
        {
         logp = forwardlog(m_initprobs,m_transition,dens,alfa);
         bt = backwardlog(m_initprobs,m_transition,dens);
         result = compute_posteriors_log(alfa,bt);
        }
      else
        {
         vector scaling_factors;
         logp = forwardscaling(m_initprobs,m_transition,dens,alfa,scaling_factors);
         bt = backwardscaling(m_initprobs,m_transition,dens,scaling_factors);
         result = compute_posteriors_scaling(alfa,bt);
        }
      return logp;
     }
   //+------------------------------------------------------------------+
   //| map  implementation                                              |
   //+------------------------------------------------------------------+
   double            map(matrix &data,vector &out, ENUM_HMM_METHOD use_log=MODE_LOG)
     {
      matrix posteriors;
      double lp = compute_posteriors(data,posteriors,use_log);
      lp = (posteriors.Max(1)).Sum();
      out = posteriors.ArgMax(1);
      return lp;
     }
   //+------------------------------------------------------------------+
   //| viterbi implementation                                           |
   //+------------------------------------------------------------------+
   double            viterbi(vector &startp, matrix &trans, matrix &dens, vector &out)
     {
      vector logstartp = log(startp);
      matrix logtrans = log(trans);
      matrix logdens = dens.Transpose();

      double logprob = 0;
      ulong ns = logdens.Rows();
      ulong nc = logdens.Cols();

      if(out.Size()<ns)
         out.Resize(ns);

      matrix vit(ns,nc);
      for(ulong i = 0; i<nc; i++)
         vit[0][i] = logstartp[i] + logdens[0][i];

      for(ulong t = 1; t<ns; t++)
        {
         for(ulong i =0; i<nc; i++)
           {
            double max = -DBL_MIN;
            for(ulong j = 0; j<nc; j++)
              {
               max = MathMax(max,vit[t-1][j]+logtrans[j][i]);
              }
            vit[t][i] = max+logdens[t][i];
           }
        }
      out[ns-1] = (double)(vit.Row(ns-1)).ArgMax();
      double prev = out[ns-1];
      logprob = vit[ns-1][long(prev)];
      for(long t = long(ns-2); t>=0; t--)
        {
         for(ulong i =0; i<nc; i++)
           {
            prev = ((vit[t][i]+logtrans[i][long(prev)])>=-DBL_MIN && i>=0)?double(i):double(0);
           }
         out[t] = prev;
        }
      return logprob;
     }
   //+------------------------------------------------------------------+
   //| Calculate the probability density function                       |
   //+------------------------------------------------------------------+
   matrix              find_densities(ulong variables,ulong states,matrix &mdata,matrix &the_means, matrix &covs[])
     {
      matrix out;
      out.Resize(states,mdata.Rows());

      for(ulong state=0 ; state<states ; state++)
        {
         for(ulong i=0 ; i<mdata.Rows() ; i++)
            out[state][i] = mv_normal(variables, mdata.Row(i), the_means.Row(state), covs[state]) ;
        }

      return out;
     }
   //+------------------------------------------------------------------+
   //| Forward algorithm                                                |
   //+------------------------------------------------------------------+

   double            forward(matrix &_transitions)
     {
      double sum, denom, log_likelihood;

      denom = 0.0 ;
      for(ulong i=0 ; i<m_states ; i++)
        {
         alpha[0][i] = m_initprobs[i] * densities[i][0] ;
         denom += alpha[0][i] ;
        }

      log_likelihood = log(denom) ;
      for(ulong i=0 ; i<m_states ; i++)
         alpha[0][i] /= denom ;


      for(ulong t=1 ; t<m_samples ; t++)
        {
         denom = 0.0 ;
         for(ulong i=0 ; i<m_states ; i++)
           {
            ulong trans_ptr = i;
            sum = 0.0 ;
            for(ulong j=0 ; j<m_states ; j++)
              {
               sum += alpha[t-1][j] * _transitions.Flat(trans_ptr);
               trans_ptr += m_states ;
              }
            alpha[t][i] = sum * densities[i][t] ;
            denom += alpha[t][i] ;
           }
         log_likelihood += log(denom) ;
         for(ulong i=0 ; i<m_states ; i++)
            alpha[t][i] /= denom ;
        }

      return log_likelihood ;

     }
   //+------------------------------------------------------------------+
   //| Backward algorithm                                               |
   //+------------------------------------------------------------------+
   double            backward(void)
     {
      double sum, denom, log_likelihood ;

      denom = 0.0 ;
      for(ulong i=0 ; i<m_states ; i++)
        {
         beta[(m_samples-1)][i] = 1.0 ;
         denom += beta[(m_samples-1)][i] ;
        }

      log_likelihood = log(denom) ;
      for(ulong i=0 ; i<m_states ; i++)
         beta[(m_samples-1)][i] /= denom ;

      for(long t=long(m_samples-2) ; t>=0 ; t--)
        {
         denom = 0.0 ;
         for(ulong i=0 ; i<m_states ; i++)
           {
            sum = 0.0 ;
            for(ulong j=0 ; j<m_states ; j++)
               sum += m_transition[i][j] * densities[j][t+1] * beta[(t+1)][j] ;
            beta[t][i] = sum ;
            denom += beta[t][i] ;
           }
         log_likelihood += log(denom) ;
         for(ulong i=0 ; i<m_states ; i++)
            beta[t][i] /= denom ;
        }

      sum = 0.0 ;
      for(ulong i=0 ; i<m_states ; i++)
         sum += m_initprobs[i] * densities[i][0] * beta[0][i] ;

      return log(sum) + log_likelihood ;
     }

public:
   //+------------------------------------------------------------------+
   //| constructor                                                      |
   //+------------------------------------------------------------------+

                     HMM(void)
     {
      trained =false;

      m_hmm_mode = MODE_LOG;
      m_decode_mode = MODE_VITERBI;
      m_mincovar = 1.e-7;
     }
   //+------------------------------------------------------------------+
   //| desctructor                                                      |
   //+------------------------------------------------------------------+

                    ~HMM(void)
     {

     }

   //+------------------------------------------------------------------+
   //| Load model data from regular file                                |
   //+------------------------------------------------------------------+
   bool               load(string file_name)
     {
      trained = false;
      CFileTxt modelFile;
      CJAVal js;
      ResetLastError();

      if(modelFile.Open(file_name,FILE_READ|FILE_COMMON,0)==INVALID_HANDLE)
        {
         Print(__FUNCTION__," failed to open file ",file_name," .Error - ",::GetLastError());
         return false;
        }
      else
        {
         if(!js.Deserialize(modelFile.ReadString()))
           {
            Print("failed to read from ",file_name,".Error -",::GetLastError());
            return false;
           }
         trained = fromJSON(js);
        }
      return trained;
     }
   //+------------------------------------------------------------------+
   //|Predict the state given arbitrary input variables                 |
   //+------------------------------------------------------------------+

   matrix            predict_state_probs(matrix &inputs)
     {
      ResetLastError();

      if(!trained)
        {
         Print(__FUNCTION__, " Call fit() to estimate the model parameters");
         matrix::Zeros(1, m_states);
        }

      if(inputs.Rows()<2 || inputs.Cols()<m_vars)
        {
         Print(__FUNCTION__, " invalid matrix size ");
         matrix::Zeros(1, m_states);
        }

      matrix probs;
      compute_posteriors(inputs,probs,m_hmm_mode);

      return probs;
     }
   //+------------------------------------------------------------------+
   //|Predict the state sequence of arbitrary input variables           |
   //+------------------------------------------------------------------+
   vector            predict_state_sequence(matrix &inputs, ENUM_DECODE_METHOD decoder=WRONG_VALUE)
     {
      ResetLastError();

      if(!trained)
        {
         Print(__FUNCTION__, " Call fit() to estimate the model parameters");
         matrix::Zeros(1, m_states);
        }

      if(inputs.Rows()<2 || inputs.Cols()<m_vars)
        {
         Print(__FUNCTION__, " invalid matrix size ");
         vector::Zeros(1);
        }

      vector seq = vector::Zeros(inputs.Rows());
      ENUM_DECODE_METHOD decm;
      if(decoder!=WRONG_VALUE)
         decm = decoder;
      else
         decm = m_decode_mode;

      switch(decm)
        {
         case MODE_VITERBI:
           {
            matrix d = find_densities(m_vars,m_states,inputs,m_means,m_covars);
            viterbi(m_initprobs,m_transition,d,seq);
            break;
           }
         case MODE_MAP:
           {
            map(inputs,seq,m_hmm_mode);
            break;
           }
        }

      return seq;
     }
   //+------------------------------------------------------------------+
   //| get the loglikelihood of the model                             |
   //+------------------------------------------------------------------+

   double            get_likelihood(matrix &data)
     {
      ResetLastError();

      if(!trained)
        {
         Print(__FUNCTION__," invalid call ");
         return EMPTY_VALUE;
        }

      matrix dens = find_densities(m_vars,m_states,data,m_means,m_covars);
      matrix alfa;
      vector sc;

      switch(m_hmm_mode)
        {
         case MODE_LOG:
            likelihood = forwardlog(m_initprobs,m_transition,dens,alfa);
            break;
         case MODE_SCALING:
            likelihood = forwardscaling(m_initprobs,m_transition,dens,alfa,sc);
            break;
        }

      return likelihood;
     }
   //+------------------------------------------------------------------+
   //| get the initial state probabilities of the model          |
   //+------------------------------------------------------------------+

   vector            get_init_probs(void)
     {
      if(!trained)
        {
         Print(__FUNCTION__," invalid call ");
         return vector::Zeros(1);
        }
      return m_initprobs;
     }
   //+------------------------------------------------------------------+
   //| get the probability transition matrix                            |
   //+------------------------------------------------------------------+

   matrix            get_transition_matrix(void)
     {
      if(!trained)
        {
         Print(__FUNCTION__," invalid call ");
         return matrix::Zeros(1,1);
        }
      return m_transition;
     }
   //+------------------------------------------------------------------+
   //|get the state means matrix                                        |
   //+------------------------------------------------------------------+

   matrix            get_means(void)
     {
      if(!trained)
        {
         Print(__FUNCTION__," invalid call ");
         return matrix::Zeros(1,1);
        }
      return m_means;
     }

   //+------------------------------------------------------------------+
   //| get the covariance matrix for a particular state                 |
   //+------------------------------------------------------------------+

   matrix            get_covar_matrix_for_state_at(ulong state_index)
     {
      if(!trained || state_index>m_states)
        {
         Print(__FUNCTION__," invalid call ");
         return matrix::Zeros(1,1);
        }
      return m_covars[state_index];
     }
   //+------------------------------------------------------------------+
   //|  get the number of features for the model                |
   //+------------------------------------------------------------------+
   ulong             get_num_features(void)
     {
      return m_vars;
     }
  };


//+------------------------------------------------------------------+

HMMクラスのインスタンスを作成したら、ファイル名を指定して load()メソッドを呼び出します。

//---declare object
   HMM hmm;
//--load exampleHMM model from json file
   if(!hmm.load("exampleHMM.json"))
     {
      Print("error loading model");
      return;
     }

モデルパラメータの読み込みに成功すれば、このメソッドはtrueを返します。

モデルが読み込まれると、特定の観測集合に対する隠れた状態と状態確率を得ることができます。しかし、本文で前述したすべてのアルゴリズムの実装が若干異なることに注意することが重要です。このコードでは、生の尤度の代わりに、数値の安定性を確保するために生の値の対数を使用しています。したがって、尤度の代わりに対数尤度を用います。これはまた、掛け算が求められるところでは、値の対数を扱っているため、足し算を使わなければならないことを意味します。

HMMメソッドget_likelihood()は、読み込まれたモデルパラメータに基づいて、観測の集合の対数尤度を返します。これはフォワードアルゴリズムを使用して計算されます。predict_state_probs()メソッドは、入力として与えられた各観測の状態確率を計算します。このメソッドは、各行が観測の状態確率を表す行列を返します。

一方、predict_state_sequence()メソッドは、入力として与えられた各サンプルの状態を表すベクトルを返します。デフォルトでは、ビタビアルゴリズムを使用して、最も確率の高い状態シーケンスを計算します。しかし、GaussianHMMのdecode()メソッドの動作を模倣した、単純なmapテクニックを選択することも可能です。

HMMクラスは、読みこまれたモデルのパラメータを抽出するためのゲッターメソッドを提供します。

• get_means()：確率密度を決定するために使用された平均の行列を返す
• get_covar_matrix_for_state_at()：特定の状態に関する完全な共分散行列を取得する
• get_transition_matrix()：遷移確率を行列として返す
• get_init_probs()：モデルの初期状態確率のベクトルを返す
• get_num_features()：モデルの入力として期待される変数の数をunsigned longで返すこれは、predict_state_probs()、predict_state_sequence()、get_likelihood()の入力として提供される行列は、この数の列と少なくとも2つの行を持つべきであることを意味します。

saveHMM.pyスクリプトはランダムなデータセットに基づいてHMMを学習します。最終的なモデルパラメータをjsonファイルに保存する関数hmm2json()の定義も含まれています。データは10行5列で構成されています。GaussianHMMクラスのインスタンスが作成され、ランダムなデータでHMMが訓練されます。モードフィッティング後、hmm2json()が呼び出され、モデルパラメータをjsonファイルに保存します。そして、対数尤度、隠れ状態、状態確率が出力されます。

# Copyright 2024, MetaQuotes Ltd.
# https://www.mql5.com
from hmmlearn import hmm
import numpy as np
import pandas as pd
import json 


assumed_states = 2 #number of states of process
maxhmm_iters = 10000 #maximum number of iterations for optimization procedure

def hmm2json(hmm_model, filename):
    """
    function save a GaussianHMM model to json format 
    readable from MQL5 code.
    param: hmm_model should an instance of GaussianHMM
    param: string. filename or path to file where HMM 
    parameters will be written to
    """
    if hmm_model.__class__.__name__ != 'GaussianHMM':
        raise TypeError(f'invalid type supplied')
    if len(filename) < 1 or not isinstance(filename,str):
        raise TypeError(f'invalid filename supplied')
    jm  = {
            "numstates":hmm_model.n_components,
            "numvars":hmm_model.n_features,
            "algorithm":str(hmm_model.algorithm),
            "implementation":str(hmm_model.implementation), 
            "initprobs":hmm_model.startprob_.tolist(),
            "means":hmm_model.means_.tolist(),
            "transitions":hmm_model.transmat_.tolist(),
            "covars":hmm_model.covars_.tolist()
          }
    with open(filename,'w') as file:
        json.dump(jm,file,indent=None,separators=(',', ':')) 
    return 
#dataset to train model on    
dataset = np.array([[0.56807844,0.67179966,0.13639585,0.15092627,0.17708295],
                   [0.62290044,0.15188847,0.91947761,0.29483647,0.34073613],
                   [0.47687505,0.06388765,0.20589139,0.16474974,0.64383775],
                   [0.25606858,0.50927144,0.49009671,0.0284832,0.37357852],
                   [0.95855305,0.93687549,0.88496015,0.48772751,0.10256193],
                   [0.36752403,0.5283874 ,0.52245909,0.77968798,0.88154157],
                   [0.35161822,0.50672902,0.7722671,0.56911901,0.98874104],
                   [0.20354888,0.82106204,0.60828044,0.13380222,0.4181293,],
                   [0.43461371,0.60170739,0.56270993,0.46426138,0.53733481],
                   [0.51646574,0.54536398,0.03818231,0.32574409,0.95260478]])  
#instantiate an HMM and train on dataset
model = hmm.GaussianHMM(assumed_states,n_iter=maxhmm_iters,covariance_type='full',random_state=125, verbose=True).fit(dataset)  
#save the model to the common folder of Metatrader 5 install
hmm2json(model,r'C:\Users\Zwelithini\AppData\Roaming\MetaQuotes\Terminal\Common\Files\exampleHMM.json')
#get the state probabilities and log likelihood
result = model.score_samples(dataset)
print("log_likelihood " ,result[0]) #print the loglikelihood
print("state sequence ", model.decode(dataset)[1]) #print the state sequence of dataset
print("state probs ", result[1]) #print the state probabilities 

対応するMetaTrader 5スクリプトtestHMM.mq5は、saveHMM.pyによって作成されたjsonファイルを読み込むように設計されています。saveHMM.pyが出力する対数尤度、隠れ状態、状態確率を再現することです。

//+------------------------------------------------------------------+
//|                                                      TestHMM.mq5 |
//|                                  Copyright 2024, MetaQuotes Ltd. |
//|                                             https://www.mql5.com |
//+------------------------------------------------------------------+
#property copyright "Copyright 2024, MetaQuotes Ltd."
#property link      "https://www.mql5.com"
#property version   "1.00"
#include<hmmlearn.mqh>
//+------------------------------------------------------------------+
//| Script program start function                                    |
//+------------------------------------------------------------------+
void OnStart()
  {
//--- random dataset equal to that used in corresponding python script saveHMM.py
   matrix dataset =
     {
        {0.56807844,0.67179966,0.13639585,0.15092627,0.17708295},
        {0.62290044,0.15188847,0.91947761,0.29483647,0.34073613},
        {0.47687505,0.06388765,0.20589139,0.16474974,0.64383775},
        {0.25606858,0.50927144,0.49009671,0.0284832,0.37357852},
        {0.95855305,0.93687549,0.88496015,0.48772751,0.10256193},
        {0.36752403,0.5283874,0.52245909,0.77968798,0.88154157},
        {0.35161822,0.50672902,0.7722671,0.56911901,0.98874104},
        {0.20354888,0.82106204,0.60828044,0.13380222,0.4181293},
        {0.43461371,0.60170739,0.56270993,0.46426138,0.53733481},
        {0.51646574,0.54536398,0.03818231,0.32574409,0.95260478}
     };
//---declare object
   HMM hmm;
//--load exampleHMM model from json file
   if(!hmm.load("exampleHMM.json"))
     {
      Print("error loading model");
      return;
     }
//--get the log likelihood of the model
   double lk = hmm.get_likelihood(dataset);
   Print("LL ", lk);
//-- get the state probabilities for a dataset
   matrix probs = hmm.predict_state_probs(dataset);
   Print("state probs ", probs);
//---get the hidden states for the provided dataset
   vector stateseq = hmm.predict_state_sequence(dataset);
   Print("state seq ", stateseq);
  }
//+------------------------------------------------------------------+

両方のスクリプトを実行した結果を以下に示します。

saveHMM.pyの出力

KO      0       15:29:18.866    saveHMM (DEX 600 UP Index,M5)   log_likelihood  47.90226114316213
IJ      0       15:29:18.866    saveHMM (DEX 600 UP Index,M5)   state sequence  [0 1 1 1 1 0 0 1 0 0]
ED      0       15:29:18.866    saveHMM (DEX 600 UP Index,M5)   state probs  [[1.00000000e+000 1.32203104e-033]
RM      0       15:29:18.867    saveHMM (DEX 600 UP Index,M5)    [0.00000000e+000 1.00000000e+000]
JR      0       15:29:18.867    saveHMM (DEX 600 UP Index,M5)    [0.00000000e+000 1.00000000e+000]
RH      0       15:29:18.867    saveHMM (DEX 600 UP Index,M5)    [0.00000000e+000 1.00000000e+000]
JM      0       15:29:18.867    saveHMM (DEX 600 UP Index,M5)    [0.00000000e+000 1.00000000e+000]
LS      0       15:29:18.867    saveHMM (DEX 600 UP Index,M5)    [1.00000000e+000 5.32945369e-123]
EH      0       15:29:18.867    saveHMM (DEX 600 UP Index,M5)    [1.00000000e+000 8.00195599e-030]
RN      0       15:29:18.867    saveHMM (DEX 600 UP Index,M5)    [0.00000000e+000 1.00000000e+000]
HS      0       15:29:18.867    saveHMM (DEX 600 UP Index,M5)    [1.00000000e+000 1.04574121e-027]
RD      0       15:29:18.867    saveHMM (DEX 600 UP Index,M5)    [9.99999902e-001 9.75116254e-008]]

保存されたJSONファイルの内容

{"numstates":2,"numvars":5,"algorithm":"viterbi","implementation":"log","initprobs":[1.0,8.297061845628157e-28],"means":[[0.44766002665812865,0.5707974904960126,0.406402863181157,0.4579477485782787,0.7074610252191268],[0.5035892002511225,0.4965970189510691,0.6217412486192438,0.22191983002481444,0.375768737249644]],"transitions":[[0.4999999756220927,0.5000000243779074],[0.39999999999999913,0.6000000000000008]],"covars":[[[0.009010166768420797,0.0059122234200326374,-0.018865453701221935,-0.014521967883281419,-0.015149047353550696],[0.0059122234200326374,0.0055414217505728725,-0.0062874071503534424,-0.007643976931274206,-0.016093347935464856],[-0.018865453701221935,-0.0062874071503534424,0.0780495488091017,0.044115693492388836,0.031892068460887116],[-0.014521967883281419,-0.007643976931274206,0.044115693492388836,0.04753113728071052,0.045326684356283],[-0.015149047353550696,-0.016093347935464856,0.031892068460887116,0.045326684356283,0.0979523557527634]],[[0.07664631322010616,0.01605057520615223,0.042602194598462206,0.043095659393111246,-0.02756159799208612],[0.01605057520615223,0.12306893856632573,0.03943267795353822,0.019117932498522734,-0.04009804834113386],[0.042602194598462206,0.03943267795353822,0.07167474799610704,0.030420143149584727,-0.03682040884824712],[0.043095659393111246,0.019117932498522734,0.030420143149584727,0.026884283954788642,-0.01676189860422705],[-0.02756159799208612,-0.04009804834113386,-0.03682040884824712,-0.01676189860422705,0.03190589647162701]]]}

testHMM.mq5の出力

HD      0       15:30:51.727    TestHMM (DEX 600 UP Index,M5)   LL 47.90226114316213
EO      0       15:30:51.727    TestHMM (DEX 600 UP Index,M5)   state probs [[1,1.322031040402482e-33]
KP      0       15:30:51.727    TestHMM (DEX 600 UP Index,M5)    [0,1]
KO      0       15:30:51.727    TestHMM (DEX 600 UP Index,M5)    [0,1]
KF      0       15:30:51.727    TestHMM (DEX 600 UP Index,M5)    [0,1]
KM      0       15:30:51.727    TestHMM (DEX 600 UP Index,M5)    [0,1]
EJ      0       15:30:51.727    TestHMM (DEX 600 UP Index,M5)    [1,5.329453688054051e-123]
IP      0       15:30:51.727    TestHMM (DEX 600 UP Index,M5)    [1,8.00195599043147e-30]
KG      0       15:30:51.727    TestHMM (DEX 600 UP Index,M5)    [0,1]
ES      0       15:30:51.727    TestHMM (DEX 600 UP Index,M5)    [1,1.045741207369424e-27]
RQ      0       15:30:51.727    TestHMM (DEX 600 UP Index,M5)    [0.999999902488374,9.751162535898832e-08]]
QH      0       15:30:51.727    TestHMM (DEX 600 UP Index,M5)   state seq [0,1,1,1,1,0,0,1,0,0]

結論

HMMは逐次データをモデル化し分析するための強力な統計ツールです。観測された系列を動かしている根底にある隠れた状態を捕らえることができるため、金融データのような時系列を含むタスクで重宝されます。HMMはその長所にもかかわらず、限界がないわけではありません。これらは一次マルコフ仮定に依存しており、複雑な依存関係に対しては単純すぎる可能性があります。特に大きな状態空間に対する学習と推論の計算負荷と、過剰適合の可能性は大きな課題です。さらに、最適な状態数の選択とモデルパラメータの初期化には慎重な検討が必要で、性能に影響を与える可能性があります。それにもかかわらず、HMMはシーケンスモデリングにおける基礎的な手法であり続け、多くの実用的なアプリケーションに頑健なフレームワークを提供しています。HMMの進化と、より柔軟なモデルを組み合わせたハイブリッドアプローチにより、その有用性は進化し続けています。実務家にとって、HMMの能力と限界の両方を理解することは、自動売買開発においてHMMの可能性を効果的に活用するために不可欠です。

この記事で説明されているすべてのコードを以下に添付します。各ソースコードファイルを表に示す。

ファイル	詳細
Mql5\Python\script\saveHMM.py	隠れマルコフモデルの訓練と保存を示し、hmm2json()関数の定義が含まれています
Mql5\include\hmmlearn.mqh	Pythonで学習したHMMをMQL5で使用するために読み込むためのHMMクラスの定義が含まれています
Mql5\script\testHMM.mq5	保存されたHMMのロード方法を示すMT5スクリプト