在MetaTrader 5中集成隐马尔可夫模型

MetaTrader 5 — 积分 | 6 十二月 2024, 11:23

779

Francis Dube

概述

众所周知，金融时间序列的一个基本特征就是它们具有记忆性。在时间序列分析的情境中，记忆性指的是数据内部的依赖结构，即过去值会影响当前值和未来值。了解记忆结构有助于为时间序列选择合适的模型。在本文中，我们讨论了一种不同类型的记忆：以隐马尔可夫模型（HMM）的形式存在的记忆。我们将探讨隐马尔可夫模型的基本原理，并演示如何使用Python的hmmlearn模块构建隐马尔可夫模型。最后，我们将展示Python和MQL5的代码，这些代码能够将隐马尔可夫模型导出，以便在MetaTrader 5程序中使用。

理解HMM

HMM是一种强大的统计工具，用于对时间序列数据进行建模，其中被建模的系统以不可观察（隐藏）的状态为特征。HMM的一个基本前提是，在特定时间处于给定状态的概率取决于该过程在前一个时间点的状态。这种依赖性代表了HMM的记忆。

在金融时间序列的背景下，这些状态可能代表一个序列是处于上升趋势、下降趋势，还是在特定范围内振荡。任何使用过金融指标的人都熟悉金融时间序列中固有噪声所引起的反复无常效应（即“锯齿效应”或“振荡效应”）。HMM可以用来过滤掉这些虚假信号，从而更清晰地了解潜在的趋势。

为了构建HMM，我们需要能够捕捉定义该过程全部行为的观测值。这组数据被用来学习匹配HMM的参数。这个数据集将由建模过程的各种特征组成。例如，如果我们研究的是金融资产的收盘价，我们还可以包括与收盘价相关的其他方面，如各种理论上有助于定义我们感兴趣的隐藏状态的指标。

学习模型参数的过程是在假设被建模的序列将始终处于两个或更多状态之一的条件下进行的。这些状态简单地被标记为0到S-1（S为状态总数）。对于这些状态，我们必须分配一组概率，这些概率能够捕捉过程从一个状态切换到另一个状态的可能性。这些概率通常被称为转移矩阵。对第一个观测值有特殊的设定，有关它处于每个可能状态的初始概率。如果观测值处于特定状态，则期望它遵循与该状态相关的特定分布。

HMM完全由以下四个属性定义：

假设的状态数量
第一个观测值处于任何一个状态的初始概率
概率转移矩阵
每个状态的概率密度函数

在开始时，我们有观测值和假设的状态数量。我们想要找到与当前数据集相匹配的HMM参数。这通过使用一种称为最大似然估计的统计技术观测似然度来完成。在上下文中，最大似然估计是寻找最可能与我们的数据样本相对应的模型属性的过程。它是通过计算每个样本在特定时间处于特定状态的可能性来实现的。这是使用正向算法和反向算法完成的，这两个算法分别沿着时间顺序向前和向后遍历所有样本。

正向算法

我们在计算后续样本的似然度之前，从数据集中的第一个观测值开始。对于第一个样本，我们使用初始状态概率，这些概率在此时被视为候选HMM的试验参数。如果对所建模的过程一无所知，将所有初始状态概率设置为1/S是完全可以接受的，其中S表示假设状态的总数。应用贝叶斯定理，我们得到以下通用方程：

贝叶斯定理

其中，“lk”表示在时间“t”时样本处于状态“i”的似然度，而“p”表示在给定直到时间“t”的样本条件下，在时间“t”时处于状态“i”的概率。“O”是数据集中的单个样本，即数据集的一行。

第一个样本的似然度是根据条件概率规则 P(A) = P(A|B)P(B) 来计算的。因此，对于第一个样本，保持状态i的似然度是通过将保持状态i的初始状态概率与第一个样本的概率密度函数相乘来计算的。

初始似然公式

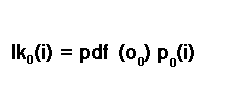
这是HMM候选者的另一个试验参数。在文献中，它有时被称为发射概率。我们将在后文中更详细地讨论发射概率。目前，只需知道在这个阶段它是另一个试验参数。我们必须牢记，我们并不确定自己处于哪个状态。我们必须考虑到自己可能处于所有可能状态中的任何一个状态的可能性。这使得最终的初始似然是所有可能状态的似然之和。

所有可能状态的初始可能性

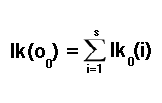
为了计算后续观测的似然度，我们必须考虑到从上一个时间段的任何一个可能状态过渡到特定状态的可能性。这时，转移概率就发挥了作用，这也是当前阶段的另一个试验参数。在已知当前时间段的概率的情况下，到达下一个时间段特定状态的概率是通过将当前已知的状态概率与相应的转移概率相乘来估计的。

现在非常适合谈论转移概率或转移矩阵。

转移状态概率

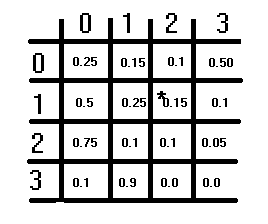
上述图示展示了一个假设的转移矩阵。它具有S×S的结构，其中S是假设的状态数量。每个元素代表一个概率，且每一行的概率之和应为1。这一条件不适用于列。要获取从一个状态转换到另一个状态的相应转移概率，您首先需要参考行，然后参考列。当前正在转换出的状态对应于行索引，而正在转换到的状态对应于列索引。这些索引处的值即为相应的转移概率。矩阵的对角线表示状态不发生变化的概率。

在继续计算我们选定数据样本中其余观测值的似然度时，我们之前是将一个状态概率与转移概率相乘。然而，为了获得完整的图像，我们必须考虑转移到所有可能状态中的任何一个的可能性。我们按照以下方程，将所有可能性相加来实现这一点：

后续样本的似然度公式

这样就完成了我们数据集中每个样本的个体似然度的计算。这些个体似然度可以通过乘法组合起来，以获得整个数据集的似然度。上面描述的计算过程被称为正向算法，这是因为它采用了时间上的前向递归方法。这与我们将在下一节中讨论的反向算法形成对比。

反向算法

同样，我们也可以从最后一个数据样本开始，逆向计算每个样本的个体似然度，直到第一个数据样本。我们从最后一个数据样本开始，将所有状态的似然度都设为1。对于每个数据样本，如果我们处于某个特定状态，我们会计算后续样本集的似然度，同时考虑到我们可以转移到任何一个状态。这是通过计算每个状态似然度的加权和来实现的：即处于该状态的概率乘以样本处于同一状态的概率密度函数。然后，我们使用从当前状态转移到下一个状态的概率作为加权因子来调整这个计算结果。所有这些都被包含在以下公式中：

返向似然度公式

概率密度函数

在讨论正向算法和返向算法时，提到了概率密度函数（pdf）作为HMM的参数。这时一个问题出现了：我们假设的是哪种分布？如前所述，HMM的概率密度函数参数通常被称为发射概率。当被建模的数据由离散值或分类值组成时，这些参数被称为概率。在处理连续变量时，我们使用概率密度函数。

本文中，我们展示了用于建模连续变量数据集的HMM，这些数据集遵循多元正态分布。当然，也可以使用其他分布；事实上，稍后将介绍的Python模块包含了为不同数据分布建模的HMM的实现。由此，所假设分布的参数成为HMM的一个参数。在多元正态分布的情况下，其参数是均值和协方差。

鲍姆-韦尔奇（Baum-Welch）算法

Baum-Welch算法是一种期望最大化技术，用于为候选HMM试验不同的参数，以找到最优模型。在此优化过程中，被最大化的值是整个样本数据集的似然度。Baum-Welch算法以其高效和可靠而闻名，但它也存在缺陷。一个明显的缺点是它的非凸性。与优化相关的非凸函数是具有多个局部最小值或最大值的函数。

这意味着当算法收敛时，可能并未找到参数空间的全局最大值或最小值。该函数基本上无法保证在最优点收敛。缓解这一缺陷的最优方法是试验那些与参数空间中其他参数相比具有较大似然度的参数。为此，我们需要试验大量的随机参数值，以找到开始优化过程的最优初始参数空间。

计算状态概率

一旦我们有了最优的HMM及其参数，就可以使用它来计算未见数据样本的状态概率。这种计算的结果是一组概率，每个状态一个，表示处于每个状态的概率。正向算法中的个体似然度与反向算法中的似然度相乘，得出特定状态的似然度。根据贝叶斯规则，观测值处于特定状态的概率计算如下：

状态概率公式

使用维特比（Viterbi）算法计算状态概率

除了状态概率之外，我们还可以使用Viterbi算法来推断观测值可能所处的状态。计算从第一个观测值开始，其状态概率是通过初始状态概率乘以发射概率来计算的。

对于从第二个到最后一个观测值，每个状态的概率都是根据前一个状态的概率、相应的转移概率以及它的发射概率来计算的。最可能的状态将是概率最高的那个。

我们已经了解了HMM的所有组成部分。现在，我们将深入探讨其实际应用。我们从基于Python的HMM的实现开始，这个实现是在hmmlearn包中提供的。在讨论使用hmmlearn包的高斯HMM实现之前，我们将切换到MQL5代码，演示如何将hmmlearn在Python中训练的模型集成到MetaTrader 5应用程序中。

Python的hmmlearn包

Python中的hmmlearn库提供了用于处理HMM的工具。用于训练HMM的工具位于以`hmm`命名的文件中。在`hmm`中，定义了几个特殊类，用于处理不同分布的过程。即：

MultinomialHMM：该模型用于处理观察值为离散且遵循多项式分布的HMM
GMMHMM：该模型用于处理观察值由高斯分布混合生成的HMM
PoissonHMM：该模型假设观察值遵循泊松分布的HMM
最后，我们有GaussianHMM类，它用于处理倾向于遵循多元高斯（正态）分布的数据集。这是我们将要演示的类，并且我们会将其生成的模型与MetaTrader 5进行连接。

要安装这个包，您可以使用以下命令：

pip install hmmlearn

安装完成后，您可以使用以下语句来导入`GaussianHMM` 类：

from hmmlearn.hmm import GaussianHMM

或者，您也可以导入包含上述所有类以及其他有用工具的`hmm`模块。如果采用这种方法，那么类名前需要加上`hmm`前缀，如下所示：

from hmmlearn import hmm

您可以使用多个参数来初始化一个GaussianHMM对象：

model = GaussianHMM(n_components=3, covariance_type='diag', n_iter=100, tol=0.01)

其中：

"n_components"：模型中的状态数量
"covariance_type"：要使用的协方差参数的类型（'spherical'、'diag'、'full'、'tied'）。所使用的协方差类型与数据集的特征相关。如果数据集中被建模的特征或变量具有相似的方差且不可能相关，则应选择球形协方差。否则，如果变量的方差差异较大，那么最优选择是对角协方差类型。如果变量之间存在相关性，则应选择全协方差或绑定协方差类型。全协方差提供了最大的灵活性，但也可能导致计算成本高昂。这是最安全的选择，因为它对正在建模的过程所做的假设最少。绑定协方差做出了额外的假设，即状态共享相似的协方差结构。相对于全协方差，它更加高效一些。
"n_iter"：训练期间要执行的最大迭代次数
"tol"：收敛阈值

要探索指定模型的所有参数，您可以参考hmmlearn库的文档。该文档提供了关于各种参数及其用法的详细信息。您可以在线访问hmmlearn库的官方网站或通过该库安装包中的文档，利用Python内置的help工具来访问这些文档。

help(GaussianHMM)

为了训练模型，我们调用“fit()”方法。该方法要求至少有一个二维数组作为输入。

model.fit(data)

训练完成后，我们可以通过调用“predict()”或“decode()”来获取数据集的隐藏状态。这两个方法都要求输入一个二维数组，该数组的特征数量应与用于训练模型的数据集相同。“predict()”方法返回一个包含计算出的隐藏状态的数组，而“decode()”方法则返回一个元组，其中包含隐藏状态数组和对应的对数似然度。

调用“score_samples()”方法也会返回对数似然度，以及为提供的输入数据集计算出的状态概率。同样，数据应具有与用于训练模型的数据相同的特征数量。

导出HMM

将使用Python的hmmlearn包的训练模型导出，以便在MetaTrader 5中使用，需要实现两个自定义组件：

Python组件：此组件负责将训练好的模型参数保存为MetaTrader应用程序可读取的格式。这需要将模型参数导出为一种MetaTrader 5应用程序可以解析的文件格式。
MQL5组件：MQL5组件包含用MQL5编写的代码。此组件应包含读取Python组件导出的HMM参数的功能。此外，它还需要实现正向算法、反向算法和Viterbi算法，以便根据指定的HMM计算数据集的隐藏状态和状态概率。

实现这些组件需要仔细考虑数据序列化格式、文件输入输出操作以及在Python和MQL5中的算法实现。确保Python和MQL5实现之间的兼容性对于在MetaTrader 5中正确传输训练模型和执行推导任务至关重要。

hmmlearn包提供了使用pickle模块保存训练好的HMM的能力。但问题是，pickle文件在Python之外不易使用。因此，一个更好的选择是使用json格式。HMM的参数将被写入一个结构化的JSON文件，该文件可以使用MQL5代码读取。这一功能会通过下面的Python函数实现。

def hmm2json(hmm_model, filename):
    """
    function save a GaussianHMM model to json format 
    readable from MQL5 code.
    param: hmm_model should an instance of GaussianHMM
    param: string. filename or path to file where HMM 
    parameters will be written to
    """
    if hmm_model.__class__.__name__ != 'GaussianHMM':
        raise TypeError(f'invalid type supplied')
    if len(filename) < 1 or not isinstance(filename,str):
        raise TypeError(f'invalid filename supplied')
    jm  = {
            "numstates":hmm_model.n_components,
            "numvars":hmm_model.n_features,
            "algorithm":str(hmm_model.algorithm),
            "implementation":str(hmm_model.implementation), 
            "initprobs":hmm_model.startprob_.tolist(),
            "means":hmm_model.means_.tolist(),
            "transitions":hmm_model.transmat_.tolist(),
            "covars":hmm_model.covars_.tolist()
          }
    with open(filename,'w') as file:
        json.dump(jm,file,indent=None,separators=(',', ':')) 
    return

该函数接受一个GaussianHMM类的实例和一个文件名作为输入，并将HMM参数以结构化格式写入一个JSON文件中，该文件可以使用MQL5代码读取。

在MQL5代码中，用于读取保存在JSON格式中的HMM模型的功能被封装在hmmlearn.mqh文件中。该文件包含了HMM类的定义。

//+------------------------------------------------------------------+
//|                                                     hmmlearn.mqh |
//|                                  Copyright 2024, MetaQuotes Ltd. |
//|                                             https://www.mql5.com |
//+------------------------------------------------------------------+
#property copyright "Copyright 2024, MetaQuotes Ltd."
#property link      "https://www.mql5.com"
#include<Math\Alglib\dataanalysis.mqh>
#include<Math\Stat\Uniform.mqh>
#include<Math\Stat\Math.mqh>
#include<JAson.mqh>
#include<Files/FileTxt.mqh>
#include<np.mqh>

//+------------------------------------------------------------------+
//|Markov model estimation method                                    |
//+------------------------------------------------------------------+
enum ENUM_HMM_METHOD
  {
   MODE_LOG=0,
   MODE_SCALING
  };
//+------------------------------------------------------------------+
//| state sequence decoding algorithm                                |
//+------------------------------------------------------------------+
enum ENUM_DECODE_METHOD
  {
   MODE_VITERBI=0,
   MODE_MAP
  };
//+------------------------------------------------------------------+
//| Hidden Markov Model class                                        |
//+------------------------------------------------------------------+
class HMM
  {
private:
   ulong m_samples ;       // Number of cases in dataset
   ulong m_vars ;        // Number of variables in each case
   ulong m_states ;      // Number of states
   vector            m_initprobs;   // vector of probability that first case is in each state
   matrix            m_transition;  // probability matrix
   matrix m_means ;                 //state means
   matrix m_covars[] ;              // covariances
   matrix densities ;              // probability densities
   matrix alpha ;       // result of forward algorithm
   matrix beta ;        // result of backward algorithm
   matrix m_stateprobs ; // probabilities of state
   double likelihood ;  //  log likelihood
   matrix            trial_transition;
   bool              trained;
   double            m_mincovar;
   ENUM_HMM_METHOD   m_hmm_mode;
   ENUM_DECODE_METHOD m_decode_mode;
   //+------------------------------------------------------------------+
   //| normalize array so sum(exp(a)) == 1                              |
   //+------------------------------------------------------------------+
   matrix            log_normalize(matrix &in)
     {
      matrix out;
      if(in.Cols()==1)
         out = matrix::Zeros(in.Rows(), in.Cols());
      else
         out = logsumexp(in);
      return in-out;
     }
   //+------------------------------------------------------------------+
   //| log of the sum of exponentials of input elements                 |
   //+------------------------------------------------------------------+
   matrix            logsumexp(matrix &in)
     {
      matrix out;

      vector amax = in.Max(1);

      for(ulong i = 0; i<amax.Size(); i++)
         if(fpclassify(MathAbs(amax[i])) == FP_INFINITE)
            amax[i] = 0.0;

      matrix ama(amax.Size(),in.Cols());
      for(ulong i=0; i<ama.Cols();i++)
         ama.Col(amax,i);

      matrix tmp = exp(in - ama);

      vector s = tmp.Sum(1);

      out.Init(s.Size(),in.Cols());
      for(ulong i=0; i<out.Cols();i++)
         out.Col(log(s),i);

      out+=ama;

      return out;
     }

   //+------------------------------------------------------------------+
   //| normarlize vector                                                |
   //+------------------------------------------------------------------+
   vector            normalize_vector(vector &in)
     {
      double sum = in.Sum();
      return in/sum;
     }
   //+------------------------------------------------------------------+
   //|  normalize matrix                                                |
   //+------------------------------------------------------------------+
   matrix            normalize_matrix(matrix &in)
     {
      vector sum = in.Sum(1);

      for(ulong i = 0; i<sum.Size(); i++)
         if(sum[i] == 0.0)
            sum[i] = 1.0;

      matrix n;
      n.Init(sum.Size(), in.Cols());
      for(ulong i =0; i<n.Cols(); i++)
         n.Col(sum,i);

      return in/n;
     }
   //+------------------------------------------------------------------+
   //|   Set up model from JSON object                                  |
   //+------------------------------------------------------------------+
   bool              fromJSON(CJAVal &jsonmodel)
     {

      if(jsonmodel["implementation"].ToStr() == "log")
         m_hmm_mode = MODE_LOG;
      else
         m_hmm_mode = MODE_SCALING;

      if(jsonmodel["algorithm"].ToStr() == "Viterbi")
         m_decode_mode = MODE_VITERBI;
      else
         m_decode_mode = MODE_MAP;

      m_states = (ulong)jsonmodel["numstates"].ToInt();
      m_vars = (ulong)jsonmodel["numvars"].ToInt();


      if(!m_initprobs.Resize(m_states) || !m_means.Resize(m_states,m_vars) ||
         !m_transition.Resize(m_states,m_states) || ArrayResize(m_covars,int(m_states))!=int(m_states))
        {
         Print(__FUNCTION__, " error ", GetLastError());
         return false;
        }

      for(uint i = 0; i<m_covars.Size(); i++)
        {
         if(!m_covars[i].Resize(m_vars,m_vars))
           {
            Print(__FUNCTION__, " error ", GetLastError());
            return false;
           }

         for(int k = 0; k<int(m_covars[i].Rows()); k++)
            for(int j = 0; j<int(m_covars[i].Cols()); j++)
               m_covars[i][k][j] = jsonmodel["covars"][i][k][j].ToDbl();
        }

      for(int i =0; i<int(m_initprobs.Size()); i++)
        {
         m_initprobs[i] = jsonmodel["initprobs"][i].ToDbl();
        }

      for(int i=0; i<int(m_states); i++)
        {
         for(int j = 0; j<int(m_vars); j++)
            m_means[i][j] = jsonmodel["means"][i][j].ToDbl();
        }

      for(int i=0; i<int(m_states); i++)
        {
         for(int j = 0; j<int(m_states); j++)
            m_transition[i][j] = jsonmodel["transitions"][i][j].ToDbl();
        }

      return true;
     }

   //+------------------------------------------------------------------+
   //|  Multivariate Normal Density function                            |
   //+------------------------------------------------------------------+
   double            mv_normal(ulong nv,vector &x, vector &mean, matrix &in_covar)
     {
      matrix cv_chol;
      vector vc = x-mean;

      if(!in_covar.Cholesky(cv_chol))
        {
         matrix ncov = in_covar+(m_mincovar*matrix::Eye(nv,nv));
         if(!ncov.Cholesky(cv_chol))
           {
            Print(__FUNCTION__,": covars matrix might not be symmetric positive-definite, error ", GetLastError());
            return EMPTY_VALUE;
           }
        }

      double cv_log_det = 2.0 * (MathLog(cv_chol.Diag())).Sum();
      vector cv_sol = cv_chol.Solve(vc);

      return -0.5*((nv*log(2.0 * M_PI)) + (pow(cv_sol,2.0)).Sum() + cv_log_det);

     }


   //+------------------------------------------------------------------+
   //|logadd exp                                                        |
   //+------------------------------------------------------------------+
   double            logaddexp(double a, double b)
     {
      return a==-DBL_MIN?b:b==-DBL_MIN?a:MathMax(a,b)+log1p(exp(-1.0*MathAbs(b-a)));
     }
   //+------------------------------------------------------------------+
   //| scaled trans calculation                                         |
   //+------------------------------------------------------------------+
   matrix            compute_scaling_xi_sum(matrix &trans, matrix &dens,matrix &alf, matrix &bta)
     {
      matrix logdens = exp(dens).Transpose();

      ulong ns = logdens.Rows();
      ulong nc = logdens.Cols();

      matrix out;
      out.Resize(nc,nc);
      out.Fill(0.0);

      for(ulong t =0; t<ns-1; t++)
        {
         for(ulong i = 0; i<nc; i++)
           {
            for(ulong j = 0; j<nc; j++)
              {
               out[i][j] += alf[t][i] * trans[i][j] * logdens[t+1][j]*bta[t+1][j];
              }
           }
        }
      return out;
     }
   //+------------------------------------------------------------------+
   //| log trans calculation                                            |
   //+------------------------------------------------------------------+
   matrix            compute_log_xi_sum(matrix &trans, matrix &dens,matrix &alf, matrix &bta)
     {
      matrix logtrans = log(trans);
      matrix logdens = dens.Transpose();

      ulong ns = logdens.Rows();
      ulong nc = logdens.Cols();

      vector row = alf.Row(ns-1);
      double logprob = (log(exp(row-row[row.ArgMax()]).Sum()) + row[row.ArgMax()]);

      matrix out;
      out.Init(nc,nc);

      out.Fill(-DBL_MIN);

      for(ulong t = 0 ; t<ns-1; t++)
        {
         for(ulong i =0; i<nc; i++)
           {
            for(ulong j =0; j<nc; j++)
              {
               double vl = alf[t][i] + logtrans[i][j]+ logdens[t+1][j]+bta[t+1][j] - logprob;
               out[i][j] = logaddexp(out[i][j], vl);
              }
           }
        }

      return out;

     }
   //+------------------------------------------------------------------+
   //| forward scaling                                                  |
   //+------------------------------------------------------------------+
   double            forwardscaling(vector &startp, matrix &trans, matrix &dens,matrix &out, vector&outt)
     {
      double minsum = 1.e-300;
      vector gstartp = startp;
      matrix gtrans = trans;
      matrix gdens = exp(dens).Transpose();

      ulong ns = gdens.Rows();
      ulong nc = gdens.Cols();

      if(out.Cols()!=nc || out.Rows()!=ns)
         out.Resize(ns,nc);

      if(outt.Size()!=ns)
         outt.Resize(ns);

      out.Fill(0.0);

      double logprob = 0.0;

      for(ulong i = 0; i<nc; i++)
         out[0][i] = gstartp[i]*gdens[0][i];

      double sum  = (out.Row(0)).Sum();

      if(sum<minsum)
         Print("WARNING: forward pass failed with underflow consider using log implementation ");

      double scale = outt[0] = 1.0/sum;
      logprob -= log(scale);

      for(ulong i=0; i<nc; i++)
         out[0][i] *=scale;

      for(ulong t =1; t<ns; t++)
        {
         for(ulong j=0; j<nc; j++)
           {
            for(ulong i=0; i<nc; i++)
              {
               out[t][j]+=out[t-1][i] * gtrans[i][j];
              }
            out[t][j]*=gdens[t][j];
           }
         sum = (out.Row(t)).Sum();
         if(sum<minsum)
            Print("WARNING: forward pass failed with underflow consider using log implementation ");

         scale = outt[t] = 1.0/sum;
         logprob -= log(scale);
         for(ulong j = 0; j<nc; j++)
            out[t][j] *= scale;

        }
      return logprob;
     }
   //+------------------------------------------------------------------+
   //|backward scaling                                                  |
   //+------------------------------------------------------------------+
   matrix            backwardscaling(vector &startp, matrix &trans, matrix &dens,vector &scaling)
     {
      vector gstartp = startp;
      vector scaled = scaling;
      matrix gtrans = trans;
      matrix gdens =  exp(dens).Transpose();

      ulong ns = gdens.Rows();
      ulong nc = gdens.Cols();

      matrix out;
      out.Init(ns,nc);

      out.Fill(0.0);
      for(ulong i = 0; i<nc; i++)
         out[ns-1][i] = scaling[ns-1];

      for(long t = long(ns-2); t>=0; t--)
        {
         for(ulong i=0; i<nc; i++)
           {
            for(ulong j =0; j<nc; j++)
              {
               out[t][i]+=(gtrans[i][j]*gdens[t+1][j]*out[t+1][j]);
              }
            out[t][i]*=scaling[t];
           }
        }
      return out;
     }
   //+------------------------------------------------------------------+
   //| forward log                                                      |
   //+------------------------------------------------------------------+
   double            forwardlog(vector &startp, matrix &trans, matrix &dens,matrix &out)
     {
      vector logstartp = log(startp);
      matrix logtrans = log(trans);
      matrix logdens = dens.Transpose();

      ulong ns = logdens.Rows();
      ulong nc = logdens.Cols();

      if(out.Cols()!=nc || out.Rows()!=ns)
         out.Resize(ns,nc);

      vector buf;
      buf.Init(nc);

      for(ulong i =0; i<nc; i++)
         out[0][i] = logstartp[i] + logdens[0][i];

      for(ulong t =1; t<ns; t++)
        {
         for(ulong j =0; j<nc; j++)
           {
            for(ulong i =0; i<nc; i++)
              {
               buf[i] = out[t-1][i] + logtrans[i][j];
              }
            out[t][j] = logdens[t][j] + (log(exp(buf-buf[buf.ArgMax()]).Sum()) + buf[buf.ArgMax()]);
           }
        }

      vector row = out.Row(ns-1);

      return (log(exp(row-row[row.ArgMax()]).Sum()) + row[row.ArgMax()]);
     }
   //+------------------------------------------------------------------+
   //|  backwardlog                                                     |
   //+------------------------------------------------------------------+
   matrix            backwardlog(vector &startp, matrix &trans, matrix &dens)
     {
      vector logstartp = log(startp);
      matrix logtrans = log(trans);
      matrix logdens = dens.Transpose();

      ulong ns = logdens.Rows();
      ulong nc = logdens.Cols();

      matrix out;
      out.Init(ns,nc);

      vector buf;
      buf.Init(nc);

      for(ulong i =0; i<nc; i++)
         out[ns-1][i] = 0.0;

      for(long t = long(ns-2); t>=0; t--)
        {
         for(long i =0; i<long(nc); i++)
           {
            for(long j =0; j<long(nc); j++)
              {
               buf[j] = logdens[t+1][j] + out[t+1][j] + logtrans[i][j];
              }
            out[t][i] = (log(exp(buf-buf[buf.ArgMax()]).Sum()) + buf[buf.ArgMax()]);
           }
        }
      return out;
     }
   //+------------------------------------------------------------------+
   //| compute posterior state probabilities scaling                    |
   //+------------------------------------------------------------------+
   matrix            compute_posteriors_scaling(matrix &alf, matrix &bta)
     {
      return normalize_matrix(alf*bta);
     }
   //+------------------------------------------------------------------+
   //| compute posterior state probabilities log                        |
   //+------------------------------------------------------------------+
   matrix            compute_posteriors_log(matrix &alf, matrix &bta)
     {
      return exp(log_normalize(alf+bta));
     }
   //+------------------------------------------------------------------+
   //|calculate the probability of a state                              |
   //+------------------------------------------------------------------+
   double            compute_posteriors(matrix &data, matrix &result, ENUM_HMM_METHOD use_log=MODE_LOG)
     {
      matrix alfa,bt,dens;
      double logp=0.0;
      dens = find_densities(m_vars,m_states,data,m_means,m_covars);
      if(use_log == MODE_LOG)
        {
         logp = forwardlog(m_initprobs,m_transition,dens,alfa);
         bt = backwardlog(m_initprobs,m_transition,dens);
         result = compute_posteriors_log(alfa,bt);
        }
      else
        {
         vector scaling_factors;
         logp = forwardscaling(m_initprobs,m_transition,dens,alfa,scaling_factors);
         bt = backwardscaling(m_initprobs,m_transition,dens,scaling_factors);
         result = compute_posteriors_scaling(alfa,bt);
        }
      return logp;
     }
   //+------------------------------------------------------------------+
   //| map  implementation                                              |
   //+------------------------------------------------------------------+
   double            map(matrix &data,vector &out, ENUM_HMM_METHOD use_log=MODE_LOG)
     {
      matrix posteriors;
      double lp = compute_posteriors(data,posteriors,use_log);
      lp = (posteriors.Max(1)).Sum();
      out = posteriors.ArgMax(1);
      return lp;
     }
   //+------------------------------------------------------------------+
   //| viterbi implementation                                           |
   //+------------------------------------------------------------------+
   double            viterbi(vector &startp, matrix &trans, matrix &dens, vector &out)
     {
      vector logstartp = log(startp);
      matrix logtrans = log(trans);
      matrix logdens = dens.Transpose();

      double logprob = 0;
      ulong ns = logdens.Rows();
      ulong nc = logdens.Cols();

      if(out.Size()<ns)
         out.Resize(ns);

      matrix vit(ns,nc);
      for(ulong i = 0; i<nc; i++)
         vit[0][i] = logstartp[i] + logdens[0][i];

      for(ulong t = 1; t<ns; t++)
        {
         for(ulong i =0; i<nc; i++)
           {
            double max = -DBL_MIN;
            for(ulong j = 0; j<nc; j++)
              {
               max = MathMax(max,vit[t-1][j]+logtrans[j][i]);
              }
            vit[t][i] = max+logdens[t][i];
           }
        }
      out[ns-1] = (double)(vit.Row(ns-1)).ArgMax();
      double prev = out[ns-1];
      logprob = vit[ns-1][long(prev)];
      for(long t = long(ns-2); t>=0; t--)
        {
         for(ulong i =0; i<nc; i++)
           {
            prev = ((vit[t][i]+logtrans[i][long(prev)])>=-DBL_MIN && i>=0)?double(i):double(0);
           }
         out[t] = prev;
        }
      return logprob;
     }
   //+------------------------------------------------------------------+
   //| Calculate the probability density function                       |
   //+------------------------------------------------------------------+
   matrix              find_densities(ulong variables,ulong states,matrix &mdata,matrix &the_means, matrix &covs[])
     {
      matrix out;
      out.Resize(states,mdata.Rows());

      for(ulong state=0 ; state<states ; state++)
        {
         for(ulong i=0 ; i<mdata.Rows() ; i++)
            out[state][i] = mv_normal(variables, mdata.Row(i), the_means.Row(state), covs[state]) ;
        }

      return out;
     }
   //+------------------------------------------------------------------+
   //| Forward algorithm                                                |
   //+------------------------------------------------------------------+

   double            forward(matrix &_transitions)
     {
      double sum, denom, log_likelihood;

      denom = 0.0 ;
      for(ulong i=0 ; i<m_states ; i++)
        {
         alpha[0][i] = m_initprobs[i] * densities[i][0] ;
         denom += alpha[0][i] ;
        }

      log_likelihood = log(denom) ;
      for(ulong i=0 ; i<m_states ; i++)
         alpha[0][i] /= denom ;


      for(ulong t=1 ; t<m_samples ; t++)
        {
         denom = 0.0 ;
         for(ulong i=0 ; i<m_states ; i++)
           {
            ulong trans_ptr = i;
            sum = 0.0 ;
            for(ulong j=0 ; j<m_states ; j++)
              {
               sum += alpha[t-1][j] * _transitions.Flat(trans_ptr);
               trans_ptr += m_states ;
              }
            alpha[t][i] = sum * densities[i][t] ;
            denom += alpha[t][i] ;
           }
         log_likelihood += log(denom) ;
         for(ulong i=0 ; i<m_states ; i++)
            alpha[t][i] /= denom ;
        }

      return log_likelihood ;

     }
   //+------------------------------------------------------------------+
   //| Backward algorithm                                               |
   //+------------------------------------------------------------------+
   double            backward(void)
     {
      double sum, denom, log_likelihood ;

      denom = 0.0 ;
      for(ulong i=0 ; i<m_states ; i++)
        {
         beta[(m_samples-1)][i] = 1.0 ;
         denom += beta[(m_samples-1)][i] ;
        }

      log_likelihood = log(denom) ;
      for(ulong i=0 ; i<m_states ; i++)
         beta[(m_samples-1)][i] /= denom ;

      for(long t=long(m_samples-2) ; t>=0 ; t--)
        {
         denom = 0.0 ;
         for(ulong i=0 ; i<m_states ; i++)
           {
            sum = 0.0 ;
            for(ulong j=0 ; j<m_states ; j++)
               sum += m_transition[i][j] * densities[j][t+1] * beta[(t+1)][j] ;
            beta[t][i] = sum ;
            denom += beta[t][i] ;
           }
         log_likelihood += log(denom) ;
         for(ulong i=0 ; i<m_states ; i++)
            beta[t][i] /= denom ;
        }

      sum = 0.0 ;
      for(ulong i=0 ; i<m_states ; i++)
         sum += m_initprobs[i] * densities[i][0] * beta[0][i] ;

      return log(sum) + log_likelihood ;
     }

public:
   //+------------------------------------------------------------------+
   //| constructor                                                      |
   //+------------------------------------------------------------------+

                     HMM(void)
     {
      trained =false;

      m_hmm_mode = MODE_LOG;
      m_decode_mode = MODE_VITERBI;
      m_mincovar = 1.e-7;
     }
   //+------------------------------------------------------------------+
   //| desctructor                                                      |
   //+------------------------------------------------------------------+

                    ~HMM(void)
     {

     }

   //+------------------------------------------------------------------+
   //| Load model data from regular file                                |
   //+------------------------------------------------------------------+
   bool               load(string file_name)
     {
      trained = false;
      CFileTxt modelFile;
      CJAVal js;
      ResetLastError();

      if(modelFile.Open(file_name,FILE_READ|FILE_COMMON,0)==INVALID_HANDLE)
        {
         Print(__FUNCTION__," failed to open file ",file_name," .Error - ",::GetLastError());
         return false;
        }
      else
        {
         if(!js.Deserialize(modelFile.ReadString()))
           {
            Print("failed to read from ",file_name,".Error -",::GetLastError());
            return false;
           }
         trained = fromJSON(js);
        }
      return trained;
     }
   //+------------------------------------------------------------------+
   //|Predict the state given arbitrary input variables                 |
   //+------------------------------------------------------------------+

   matrix            predict_state_probs(matrix &inputs)
     {
      ResetLastError();

      if(!trained)
        {
         Print(__FUNCTION__, " Call fit() to estimate the model parameters");
         matrix::Zeros(1, m_states);
        }

      if(inputs.Rows()<2 || inputs.Cols()<m_vars)
        {
         Print(__FUNCTION__, " invalid matrix size ");
         matrix::Zeros(1, m_states);
        }

      matrix probs;
      compute_posteriors(inputs,probs,m_hmm_mode);

      return probs;
     }
   //+------------------------------------------------------------------+
   //|Predict the state sequence of arbitrary input variables           |
   //+------------------------------------------------------------------+
   vector            predict_state_sequence(matrix &inputs, ENUM_DECODE_METHOD decoder=WRONG_VALUE)
     {
      ResetLastError();

      if(!trained)
        {
         Print(__FUNCTION__, " Call fit() to estimate the model parameters");
         matrix::Zeros(1, m_states);
        }

      if(inputs.Rows()<2 || inputs.Cols()<m_vars)
        {
         Print(__FUNCTION__, " invalid matrix size ");
         vector::Zeros(1);
        }

      vector seq = vector::Zeros(inputs.Rows());
      ENUM_DECODE_METHOD decm;
      if(decoder!=WRONG_VALUE)
         decm = decoder;
      else
         decm = m_decode_mode;

      switch(decm)
        {
         case MODE_VITERBI:
           {
            matrix d = find_densities(m_vars,m_states,inputs,m_means,m_covars);
            viterbi(m_initprobs,m_transition,d,seq);
            break;
           }
         case MODE_MAP:
           {
            map(inputs,seq,m_hmm_mode);
            break;
           }
        }

      return seq;
     }
   //+------------------------------------------------------------------+
   //| get the loglikelihood of the model                             |
   //+------------------------------------------------------------------+

   double            get_likelihood(matrix &data)
     {
      ResetLastError();

      if(!trained)
        {
         Print(__FUNCTION__," invalid call ");
         return EMPTY_VALUE;
        }

      matrix dens = find_densities(m_vars,m_states,data,m_means,m_covars);
      matrix alfa;
      vector sc;

      switch(m_hmm_mode)
        {
         case MODE_LOG:
            likelihood = forwardlog(m_initprobs,m_transition,dens,alfa);
            break;
         case MODE_SCALING:
            likelihood = forwardscaling(m_initprobs,m_transition,dens,alfa,sc);
            break;
        }

      return likelihood;
     }
   //+------------------------------------------------------------------+
   //| get the initial state probabilities of the model          |
   //+------------------------------------------------------------------+

   vector            get_init_probs(void)
     {
      if(!trained)
        {
         Print(__FUNCTION__," invalid call ");
         return vector::Zeros(1);
        }
      return m_initprobs;
     }
   //+------------------------------------------------------------------+
   //| get the probability transition matrix                            |
   //+------------------------------------------------------------------+

   matrix            get_transition_matrix(void)
     {
      if(!trained)
        {
         Print(__FUNCTION__," invalid call ");
         return matrix::Zeros(1,1);
        }
      return m_transition;
     }
   //+------------------------------------------------------------------+
   //|get the state means matrix                                        |
   //+------------------------------------------------------------------+

   matrix            get_means(void)
     {
      if(!trained)
        {
         Print(__FUNCTION__," invalid call ");
         return matrix::Zeros(1,1);
        }
      return m_means;
     }

   //+------------------------------------------------------------------+
   //| get the covariance matrix for a particular state                 |
   //+------------------------------------------------------------------+

   matrix            get_covar_matrix_for_state_at(ulong state_index)
     {
      if(!trained || state_index>m_states)
        {
         Print(__FUNCTION__," invalid call ");
         return matrix::Zeros(1,1);
        }
      return m_covars[state_index];
     }
   //+------------------------------------------------------------------+
   //|  get the number of features for the model                |
   //+------------------------------------------------------------------+
   ulong             get_num_features(void)
     {
      return m_vars;
     }
  };


//+------------------------------------------------------------------+

创建HMM类的实例后，我们将使用特定的文件名调用“load()”方法。

//---declare object
   HMM hmm;
//--load exampleHMM model from json file
   if(!hmm.load("exampleHMM.json"))
     {
      Print("error loading model");
      return;
     }

如果模型参数成功读取，该方法将返回true。

一旦模型被加载，我们就可以针对特定的一组观测值获取隐藏状态和状态概率。但是，重要的是要注意，前文中描述的所有算法的实现都略有不同。代码不使用原始似然度，而是使用原始值的对数来确保数值稳定性。因此，我们使用的是对数似然度而不是似然度。这也意味着，在需要进行乘法运算的地方，我们都要使用加法运算，因为我们处理的是值的对数。

HMM方法`get_likelihood()`基于加载的模型参数返回一组观测值的对数似然度。它使用正向算法计算得到。通过"predict_state_probs()"方法计算每个给定输入观测值的状态概率。该方法返回一个矩阵，其中每一行代表一个观测值的状态概率。

另一方面，“predict_state_sequence()”方法返回一个向量，该向量表示作为输入提供的每个样本的状态。默认情况下，它使用Viterbi算法来计算最可能的状态序列。但是，也可以选择简单的“映射”技术，以模仿GaussianHMM的“decode()”方法的行为。

“HMM”类提供了用于提取加载模型参数的getter方法：

“get_means()”：返回用于确定概率密度的均值矩阵
“get_covar_matrix_for_state_at()”：获取特定状态的完整协方差矩阵
“get_transition_matrix()”：返回作为矩阵的转移概率
“get_init_probs()”：返回一个向量，表示模型的初始状态概率
“get_num_features()”：返回一个无符号长整型值，表示模型要求的输入变量的数量。这意味着，对于提供给“predict_state_probs()”、“predict_state_sequence()”和“get_likelihood()”作为输入的任何矩阵，它应具有此数量的列和至少2行。

saveHMM.py脚本基于一个随机数据集训练HMM。它包含了一个名为"hmm2json()" 的函数定义，该函数负责将最终的模型参数保存到一个json文件中。相关数据由10行和5列组成。下面创建一个GaussianHMM类的实例，并用随机数据训练这个HMM。在模型拟合之后，调用hmm2json()函数将模型参数保存到一个json文件中。之后，将对数似然度、隐藏状态和状态概率打印好。

# Copyright 2024, MetaQuotes Ltd.
# https://www.mql5.com
from hmmlearn import hmm
import numpy as np
import pandas as pd
import json 


assumed_states = 2 #number of states of process
maxhmm_iters = 10000 #maximum number of iterations for optimization procedure

def hmm2json(hmm_model, filename):
    """
    function save a GaussianHMM model to json format 
    readable from MQL5 code.
    param: hmm_model should an instance of GaussianHMM
    param: string. filename or path to file where HMM 
    parameters will be written to
    """
    if hmm_model.__class__.__name__ != 'GaussianHMM':
        raise TypeError(f'invalid type supplied')
    if len(filename) < 1 or not isinstance(filename,str):
        raise TypeError(f'invalid filename supplied')
    jm  = {
            "numstates":hmm_model.n_components,
            "numvars":hmm_model.n_features,
            "algorithm":str(hmm_model.algorithm),
            "implementation":str(hmm_model.implementation), 
            "initprobs":hmm_model.startprob_.tolist(),
            "means":hmm_model.means_.tolist(),
            "transitions":hmm_model.transmat_.tolist(),
            "covars":hmm_model.covars_.tolist()
          }
    with open(filename,'w') as file:
        json.dump(jm,file,indent=None,separators=(',', ':')) 
    return 
#dataset to train model on    
dataset = np.array([[0.56807844,0.67179966,0.13639585,0.15092627,0.17708295],
                   [0.62290044,0.15188847,0.91947761,0.29483647,0.34073613],
                   [0.47687505,0.06388765,0.20589139,0.16474974,0.64383775],
                   [0.25606858,0.50927144,0.49009671,0.0284832,0.37357852],
                   [0.95855305,0.93687549,0.88496015,0.48772751,0.10256193],
                   [0.36752403,0.5283874 ,0.52245909,0.77968798,0.88154157],
                   [0.35161822,0.50672902,0.7722671,0.56911901,0.98874104],
                   [0.20354888,0.82106204,0.60828044,0.13380222,0.4181293,],
                   [0.43461371,0.60170739,0.56270993,0.46426138,0.53733481],
                   [0.51646574,0.54536398,0.03818231,0.32574409,0.95260478]])  
#instantiate an HMM and train on dataset
model = hmm.GaussianHMM(assumed_states,n_iter=maxhmm_iters,covariance_type='full',random_state=125, verbose=True).fit(dataset)  
#save the model to the common folder of Metatrader 5 install
hmm2json(model,r'C:\Users\Zwelithini\AppData\Roaming\MetaQuotes\Terminal\Common\Files\exampleHMM.json')
#get the state probabilities and log likelihood
result = model.score_samples(dataset)
print("log_likelihood " ,result[0]) #print the loglikelihood
print("state sequence ", model.decode(dataset)[1]) #print the state sequence of dataset
print("state probs ", result[1]) #print the state probabilities

对应MetaTrader 5脚本testHMM.mq5是为了加载由saveHMM.py创建的json文件而设计的。其理念是复制saveHMM.py输出的对数似然度、隐藏状态和状态概率。

//+------------------------------------------------------------------+
//|                                                      TestHMM.mq5 |
//|                                  Copyright 2024, MetaQuotes Ltd. |
//|                                             https://www.mql5.com |
//+------------------------------------------------------------------+
#property copyright "Copyright 2024, MetaQuotes Ltd."
#property link      "https://www.mql5.com"
#property version   "1.00"
#include<hmmlearn.mqh>
//+------------------------------------------------------------------+
//| Script program start function                                    |
//+------------------------------------------------------------------+
void OnStart()
  {
//--- random dataset equal to that used in corresponding python script saveHMM.py
   matrix dataset =
     {
        {0.56807844,0.67179966,0.13639585,0.15092627,0.17708295},
        {0.62290044,0.15188847,0.91947761,0.29483647,0.34073613},
        {0.47687505,0.06388765,0.20589139,0.16474974,0.64383775},
        {0.25606858,0.50927144,0.49009671,0.0284832,0.37357852},
        {0.95855305,0.93687549,0.88496015,0.48772751,0.10256193},
        {0.36752403,0.5283874,0.52245909,0.77968798,0.88154157},
        {0.35161822,0.50672902,0.7722671,0.56911901,0.98874104},
        {0.20354888,0.82106204,0.60828044,0.13380222,0.4181293},
        {0.43461371,0.60170739,0.56270993,0.46426138,0.53733481},
        {0.51646574,0.54536398,0.03818231,0.32574409,0.95260478}
     };
//---declare object
   HMM hmm;
//--load exampleHMM model from json file
   if(!hmm.load("exampleHMM.json"))
     {
      Print("error loading model");
      return;
     }
//--get the log likelihood of the model
   double lk = hmm.get_likelihood(dataset);
   Print("LL ", lk);
//-- get the state probabilities for a dataset
   matrix probs = hmm.predict_state_probs(dataset);
   Print("state probs ", probs);
//---get the hidden states for the provided dataset
   vector stateseq = hmm.predict_state_sequence(dataset);
   Print("state seq ", stateseq);
  }
//+------------------------------------------------------------------+

运行这两个脚本的结果如下所示。

来自saveHMM.py的输出。

KO      0       15:29:18.866    saveHMM (DEX 600 UP Index,M5)   log_likelihood  47.90226114316213
IJ      0       15:29:18.866    saveHMM (DEX 600 UP Index,M5)   state sequence  [0 1 1 1 1 0 0 1 0 0]
ED      0       15:29:18.866    saveHMM (DEX 600 UP Index,M5)   state probs  [[1.00000000e+000 1.32203104e-033]
RM      0       15:29:18.867    saveHMM (DEX 600 UP Index,M5)    [0.00000000e+000 1.00000000e+000]
JR      0       15:29:18.867    saveHMM (DEX 600 UP Index,M5)    [0.00000000e+000 1.00000000e+000]
RH      0       15:29:18.867    saveHMM (DEX 600 UP Index,M5)    [0.00000000e+000 1.00000000e+000]
JM      0       15:29:18.867    saveHMM (DEX 600 UP Index,M5)    [0.00000000e+000 1.00000000e+000]
LS      0       15:29:18.867    saveHMM (DEX 600 UP Index,M5)    [1.00000000e+000 5.32945369e-123]
EH      0       15:29:18.867    saveHMM (DEX 600 UP Index,M5)    [1.00000000e+000 8.00195599e-030]
RN      0       15:29:18.867    saveHMM (DEX 600 UP Index,M5)    [0.00000000e+000 1.00000000e+000]
HS      0       15:29:18.867    saveHMM (DEX 600 UP Index,M5)    [1.00000000e+000 1.04574121e-027]
RD      0       15:29:18.867    saveHMM (DEX 600 UP Index,M5)    [9.99999902e-001 9.75116254e-008]]

保存的JSON文件内容。

{"numstates":2,"numvars":5,"algorithm":"viterbi","implementation":"log","initprobs":[1.0,8.297061845628157e-28],"means":[[0.44766002665812865,0.5707974904960126,0.406402863181157,0.4579477485782787,0.7074610252191268],[0.5035892002511225,0.4965970189510691,0.6217412486192438,0.22191983002481444,0.375768737249644]],"transitions":[[0.4999999756220927,0.5000000243779074],[0.39999999999999913,0.6000000000000008]],"covars":[[[0.009010166768420797,0.0059122234200326374,-0.018865453701221935,-0.014521967883281419,-0.015149047353550696],[0.0059122234200326374,0.0055414217505728725,-0.0062874071503534424,-0.007643976931274206,-0.016093347935464856],[-0.018865453701221935,-0.0062874071503534424,0.0780495488091017,0.044115693492388836,0.031892068460887116],[-0.014521967883281419,-0.007643976931274206,0.044115693492388836,0.04753113728071052,0.045326684356283],[-0.015149047353550696,-0.016093347935464856,0.031892068460887116,0.045326684356283,0.0979523557527634]],[[0.07664631322010616,0.01605057520615223,0.042602194598462206,0.043095659393111246,-0.02756159799208612],[0.01605057520615223,0.12306893856632573,0.03943267795353822,0.019117932498522734,-0.04009804834113386],[0.042602194598462206,0.03943267795353822,0.07167474799610704,0.030420143149584727,-0.03682040884824712],[0.043095659393111246,0.019117932498522734,0.030420143149584727,0.026884283954788642,-0.01676189860422705],[-0.02756159799208612,-0.04009804834113386,-0.03682040884824712,-0.01676189860422705,0.03190589647162701]]]}

testHMM.mq5的输出。

HD      0       15:30:51.727    TestHMM (DEX 600 UP Index,M5)   LL 47.90226114316213
EO      0       15:30:51.727    TestHMM (DEX 600 UP Index,M5)   state probs [[1,1.322031040402482e-33]
KP      0       15:30:51.727    TestHMM (DEX 600 UP Index,M5)    [0,1]
KO      0       15:30:51.727    TestHMM (DEX 600 UP Index,M5)    [0,1]
KF      0       15:30:51.727    TestHMM (DEX 600 UP Index,M5)    [0,1]
KM      0       15:30:51.727    TestHMM (DEX 600 UP Index,M5)    [0,1]
EJ      0       15:30:51.727    TestHMM (DEX 600 UP Index,M5)    [1,5.329453688054051e-123]
IP      0       15:30:51.727    TestHMM (DEX 600 UP Index,M5)    [1,8.00195599043147e-30]
KG      0       15:30:51.727    TestHMM (DEX 600 UP Index,M5)    [0,1]
ES      0       15:30:51.727    TestHMM (DEX 600 UP Index,M5)    [1,1.045741207369424e-27]
RQ      0       15:30:51.727    TestHMM (DEX 600 UP Index,M5)    [0.999999902488374,9.751162535898832e-08]]
QH      0       15:30:51.727    TestHMM (DEX 600 UP Index,M5)   state seq [0,1,1,1,1,0,0,1,0,0]

结论

HMM是建模和分析序列数据的强大统计工具。它们能够捕捉驱动观测序列的潜在隐藏状态，这使得它们在涉及时间序列（如金融数据）的任务中非常有价值。尽管它们具有诸多优点，但HMM也存在局限性。它们依赖于一阶马尔可夫假设，这对于复杂的依赖关系来说可能过于简单。特别是在大型状态空间中进行训练和推理的计算需求，以及过拟合的潜在风险，都是重大的挑战。此外，选择最优状态数量和初始化模型参数需要仔细考虑，并可能影响性能。尽管如此，HMM仍然是序列建模中的基础方法，为许多实际应用提供了一个稳定的框架。随着技术的不断进步以及将HMM与更灵活的模型相结合的混合方法的出现，其可用性也在不断扩大。对于从业者来说，了解HMM的能力和局限性对于在自动交易开发中有效利用其潜力至关重要。

本文描述的所有代码均附于下文。每行源代码文件都在表格中做了说明。

文件	说明
Mql5\Python\script\saveHMM.py	演示了如何训练并保存HMM，并包含了hmm2json()函数的定义
Mql5\include\hmmlearn.mqh	该文件包含了HMM类的定义，使得在Python中训练的HMM能够被导入并在MQL5中使用。
Mql5\script\testHMM.mq5	MT5脚本演示如何加载保存的HMM