Реализация обобщенного показателя Херста и теста коэффициента дисперсии в MQL5

Введение

В статье "Вычисление коэффициента Херста" была рассмотрена концепция фрактального анализа и ее применение к финансовым рынкам. В ней автор описал метод нормированного размаха (rescaled range method, R/S) для вычисления коэффициента Херста. В этой статье мы применим другой подход и покажем реализацию обобщенной экспоненты Херста (Generalized Hurst Exponent, GHE) для классификации рядов. Мы сосредоточимся на использовании GHE для выявления форекс-символов, которые имеют тенденцию к возврату к значению, в надежде использовать это поведение.

Для начала кратко обсудим основы GHE и то, чем он отличается от исходного коэффициента Херста. Мы опишем статистический тест, который можно использовать для подтверждения результатов анализа GHE, называемый тестом коэффициента дисперсии (VRT). Далее мы перейдем к применению GHE для определения потенциальных форекс-символов для торговли с возвратом к среднему. Также мы представим индикатор для генерации сигналов на вход и выход и протестируем его в составе советника.

Обобщенный показатель Херста

Коэффициент Херста измеряет масштабирующие свойства временных рядов. Свойства масштабирования — это фундаментальные характеристики, которые описывают, как система ведет себя при изменении ее размера или масштаба времени. В контексте данных временных рядов свойства масштабирования дают представление о взаимосвязи между различными временными масштабами и закономерностями, присутствующими в данных. Для стационарного ряда изменения последующих значений с течением времени происходят более постепенно по сравнению с тем, что происходило бы при геометрическом случайном блуждании. Чтобы количественно оценить это поведение математически, мы анализируем скорость диффузии в ряду. Дисперсия служит показателем, выражающим степень отклонения других значений от первого в ряду.

В приведенной выше формуле K представляет собой произвольную задержку, с которой проводится анализ. Чтобы получить лучшее представление о характере ряда, нам придется оценить дисперсию и при других задержках. Таким образом, K может быть присвоено любое положительное целое значение меньше длины ряда. Максимальная применяемая задержка является дискреционной. Важно иметь это в виду. Таким образом, коэффициент Херста связан с масштабным поведением дисперсии при разных задержках. При использовании степенного закона он определяется следующим образом:

GHE представляет собой обобщение оригинала, в котором цифра 2 заменяет переменную, обычно обозначаемую как q. Тем самым приведенные выше формулы принимают следующий вид:

и

GHE расширяет первоначальный коэффициент Херста, анализируя, как различные статистические характеристики изменений между последовательными точками временного ряда изменяются в зависимости от порядков моментов (orders of moments). С математической точки зрения моменты (moments) — это статистические меры, которые описывают форму и характеристики распределения. Момент q-го порядка — это особый тип момента, где q — параметр, определяющий порядок. GHE подчеркивает различные характеристики временного ряда для каждого значения q. В частности, когда q=1, результат отображает масштабные свойства абсолютного отклонения. При этом q=2 является наиболее важным при исследовании зависимости на больших расстояниях.

Реализация GHE в MQL5

В этом разделе мы рассмотрим реализацию GHE в MQL5. После этого мы проверим его, проанализировав случайные выборки искусственно сгенерированных временных рядов. Наша реализация содержится в файле GHE.mqh. Файл начинается с включения VectorMatrixTools.mqh, который содержит определения различных функций для инициализации распространенных типов векторов и матриц. Содержимое этого файла показано ниже.

//+------------------------------------------------------------------+
//|                                            VectorMatrixTools.mqh |
//|                                  Copyright 2023, MetaQuotes Ltd. |
//|                                             https://www.mql5.com |
//+------------------------------------------------------------------+
#property copyright "Copyright 2023, MetaQuotes Ltd."
#property link      "https://www.mql5.com"
//+------------------------------------------------------------------+
//|Vector arange initialization                                      |
//+------------------------------------------------------------------+
template<typename T>
void arange(vector<T> &vec,T value=0.0,T step=1.0)
  {
   for(ulong i=0; i<vec.Size(); i++,value+=step)
      vec[i]=value;
  }
//+------------------------------------------------------------------+
//| Vector sliced initialization                                     |
//+------------------------------------------------------------------+
template<typename T>
void slice(vector<T> &vec,const vector<T> &toCopyfrom,ulong start=0,ulong stop=ULONG_MAX, ulong step=1)
  {
   start = (start>=toCopyfrom.Size())?toCopyfrom.Size()-1:start;
   stop  = (stop>=toCopyfrom.Size())?toCopyfrom.Size()-1:stop;
   step  = (step==0)?1:step;

   ulong numerator = (stop>=start)?stop-start:start-stop;
   ulong size = (numerator/step)+1;
   if(!vec.Resize(size))
     {
      Print(__FUNCTION__ " invalid slicing parameters for vector initialization");
      return;
     }

   if(stop>start)
     {
      for(ulong i =start, k = 0; i<toCopyfrom.Size() && k<vec.Size() && i<=stop; i+=step, k++)
         vec[k] = toCopyfrom[i];
     }
   else
     {
      for(long i = long(start), k = 0; i>-1 && k<long(vec.Size()) && i>=long(stop); i-=long(step), k++)
         vec[k] = toCopyfrom[i];
     }
  }
//+------------------------------------------------------------------+
//| Vector sliced initialization  using array                        |
//+------------------------------------------------------------------+
template<typename T>
void assign(vector<T> &vec,const T &toCopyfrom[],ulong start=0,ulong stop=ULONG_MAX, ulong step=1)
  {
   start = (start>=toCopyfrom.Size())?toCopyfrom.Size()-1:start;
   stop  = (stop>=toCopyfrom.Size())?toCopyfrom.Size()-1:stop;
   step  = (step==0)?1:step;

   ulong numerator = (stop>=start)?stop-start:start-stop;
   ulong size = (numerator/step)+1;

   if(size != vec.Size() &&  !vec.Resize(size))
     {
      Print(__FUNCTION__ " invalid slicing parameters for vector initialization");
      return;
     }

   if(stop>start)
     {
      for(ulong i =start, k = 0; i<ulong(toCopyfrom.Size()) && k<vec.Size() && i<=stop; i+=step, k++)
         vec[k] = toCopyfrom[i];
     }
   else
     {
      for(long i = long(start), k = 0; i>-1 && k<long(vec.Size()) && i>=long(stop); i-=long(step), k++)
         vec[k] = toCopyfrom[i];
     }
  }
//+------------------------------------------------------------------+
//| Matrix initialization                                            |
//+------------------------------------------------------------------+
template<typename T>
void rangetrend(matrix<T> &mat,T value=0.0,T step=1.0)
  {
   ulong r = mat.Rows();

   vector col1(r,arange,value,step);

   vector col2 = vector::Ones(r);

   if(!mat.Resize(r,2) || !mat.Col(col1,0) || !mat.Col(col2,1))
     {
      Print(__FUNCTION__ " matrix initialization error: ", GetLastError());
      return;
     }

  }
//+-------------------------------------------------------------------------------------+
//| ols design Matrix initialization with constant and first column from specified array|
//+-------------------------------------------------------------------------------------+
template<typename T>
void olsdmatrix(matrix<T> &mat,const T &toCopyfrom[],ulong start=0,ulong stop=ULONG_MAX, ulong step=1)
  {
   vector col0(1,assign,toCopyfrom,start,stop,step);

   ulong r = col0.Size();

   if(!r)
     {
      Print(__FUNCTION__," failed to initialize first column ");
      return;
     }

   vector col1 = vector::Ones(r);

   if(!mat.Resize(r,2) || !mat.Col(col0,0) || !mat.Col(col1,1))
     {
      Print(__FUNCTION__ " matrix initialization error: ", GetLastError());
      return;
     }

  }
//+------------------------------------------------------------------+
//|vector to array                                                   |
//+------------------------------------------------------------------+
bool vecToArray(const vector &in, double &out[])
  {
//---
   if(in.Size()<1)
     {
      Print(__FUNCTION__," Empty vector");
      return false;
     }
//---
   if(ulong(out.Size())!=in.Size() && ArrayResize(out,int(in.Size()))!=int(in.Size()))
     {
      Print(__FUNCTION__," resize error ", GetLastError());
      return false;
     }
//---
   for(uint i = 0; i<out.Size(); i++)
      out[i]=in[i];
//---
   return true;
//---
  }
//+------------------------------------------------------------------+
//| difference a vector                                               |
//+------------------------------------------------------------------+
vector difference(const vector &in)
  {
//---
   if(in.Size()<1)
     {
      Print(__FUNCTION__," Empty vector");
      return vector::Zeros(1);
     }
//---
   vector yy,zz;
//---
   yy.Init(in.Size()-1,slice,in,1,in.Size()-1,1);
//---
   zz.Init(in.Size()-1,slice,in,0,in.Size()-2,1);
//---
   return yy-zz;
  }
//+------------------------------------------------------------------+

 GHE.mqh содержит определение функции gen_hurst() и ее перегрузку. Одна функция предоставляет данные для анализа в векторе, а другая ожидает их в массиве. Функция также принимает целое число q и необязательные целочисленные параметры lower и upper со значениями по умолчанию. Это тот же самый «q», который упоминался в описании GHE в предыдущем разделе. Последние два параметра являются необязательными, lower и upper вместе определяют диапазон задержек, при которых будет проводиться анализ, аналогичный диапазону значений К в формулах выше.  

//+--------------------------------------------------------------------------+
//|overloaded gen_hurst() function that works with series contained in vector|
//+--------------------------------------------------------------------------+
double general_hurst(vector &data, int q, int lower=0,int upper=0)
  {
   double series[];

   if(!vecToArray(data,series))
      return EMPTY_VALUE;
   else
      return general_hurst(series,q,lower,upper);
  }

При возникновении ошибки функция вернет эквивалент встроенной константы EMPTY_VALUE, а также вывод полезного строкового сообщения на вкладке "Эксперты". Внутри gen_hurst() процедура начинается с проверки переданных аргументов. Необходимо убедиться, что они соответствуют следующим условиям:

• q не может быть меньше 1.
• lower не может быть меньше 2, а также не может быть больше или равно upper.
• При этом аргумент upper не может быть больше половины размера анализируемого ряда данных. Если какое-либо из этих условий не выполнено, функция немедленно сообщит об ошибке.

if(data.Size()<100)
     {
      Print("data array is of insufficient length");
      return EMPTY_VALUE;
     }

   if(lower>=upper || lower<2 ||  upper>int(floor(0.5*data.Size())))
     {
      Print("Invalid input for lower and/or upper");
      return EMPTY_VALUE;
     }

   if(q<=0)
     {
      Print("Invalid input for q");
      return EMPTY_VALUE;
     }

   uint len = data.Size();

   int k =0;

   matrix H,mcord,lmcord;
   vector n_vector,dv,vv,Y,ddVd,VVVd,XP,XY,PddVd,PVVVd,Px_vector,Sqx,pt;
   double dv_array[],vv_array[],mx,SSxx,my,SSxy,cc1,cc2,N;

   if(!H.Resize(ulong(upper-lower),1))
     {
      Print(__LINE__," ",__FUNCTION__," ",GetLastError());
      return EMPTY_VALUE;
     }

   for(int i=lower; i<upper; i++)
     {
      vector x_vector(ulong(i),arange,1.0,1.0);

      if(!mcord.Resize(ulong(i),1))
        {
         Print(__LINE__," ",__FUNCTION__," ",GetLastError());
         return EMPTY_VALUE;
        }

      mcord.Fill(0.0);

Внутренняя работа функции начинается с цикла for от lower к upper. Для каждого i создается вектор x_vector с элементами i при использовании функции arange. Затем она изменяет размер матрицы mcord, чтобы в ней были строки i и один столбец.

 for(int j=1; j<i+1; j++)
        {
         if(!diff_array(j,data,dv,Y))
            return EMPTY_VALUE;

Внутренний цикл начинается с использования вспомогательной функции diff_array() для вычисления различий в массиве данных и сохранения их в векторах dv и Y.

 N = double(Y.Size());

         vector X(ulong(N),arange,1.0,1.0);

         mx = X.Sum()/N;

         XP = MathPow(X,2.0);

         SSxx = XP.Sum() - N*pow(mx,2.0);

         my = Y.Sum()/N;

         XY = X*Y;

         SSxy = XY.Sum() - N*mx*my;

         cc1 = SSxy/SSxx;

         cc2 = my - cc1*mx;

         ddVd = dv - cc1;

         VVVd = Y - cc1*X - cc2;

         PddVd = MathAbs(ddVd);

         PddVd = pow(PddVd,q);

         PVVVd = MathAbs(VVVd);

         PVVVd = pow(PVVVd,q);

         mcord[j-1][0] = PddVd.Mean()/PVVVd.Mean();
        }

Здесь рассчитывается дисперсия при определенной задержке. Результаты сохраняются в матрице mcord.

 Px_vector = MathLog10(x_vector);

      mx = Px_vector.Mean();

      Sqx = MathPow(Px_vector,2.0);

      SSxx = Sqx.Sum() - i*pow(mx,2.0);

      lmcord = log10(mcord);

      my = lmcord.Mean();

      pt = Px_vector*lmcord.Col(0);

      SSxy = pt.Sum() - i*mx*my;

      H[k][0]= SSxy/SSxx;

      k++;

За пределами внутреннего цикла, на последнем этапе внешнего цикла, обновляются основные значения матрицы H. Наконец, функция возвращает среднее значение матрицы H, деленное на q.

 return H.Mean()/double(q);

Для тестирования нашей функции GHE было подготовлено приложение GHE.ex5, реализованное в виде советника. Это позволяет визуализировать случайные ряды с заранее заданными характеристиками и наблюдать, как работает GHE. Полная интерактивность позволяет регулировать все параметры GHE, а также длину серии в определенных пределах. Интересной особенностью является возможность регистрировать преобразование ряда перед применением GHE, чтобы проверить, есть ли какие-либо преимущества от предварительной обработки данных таким способом.

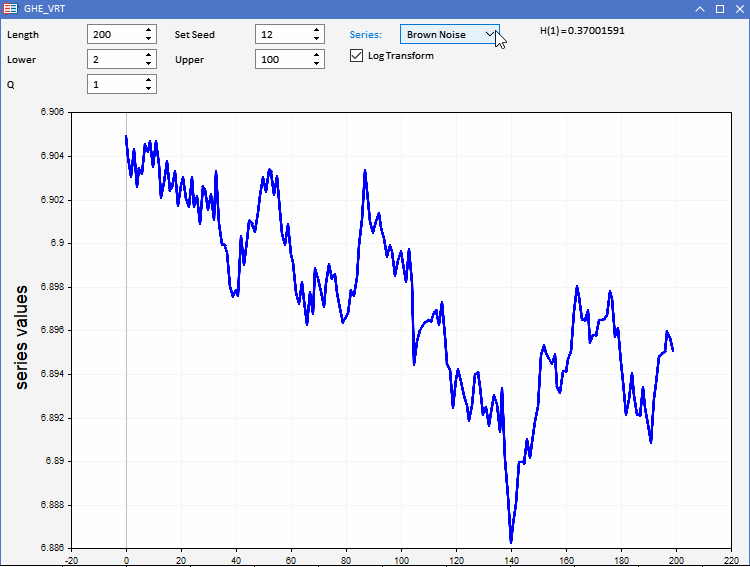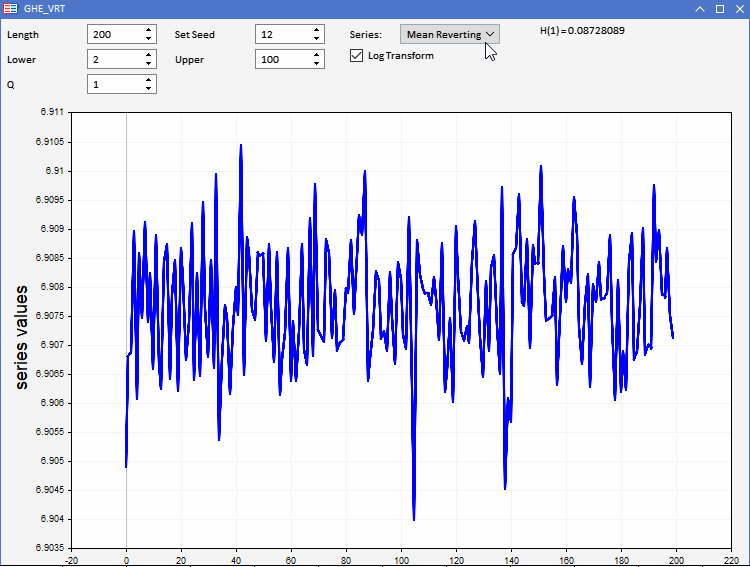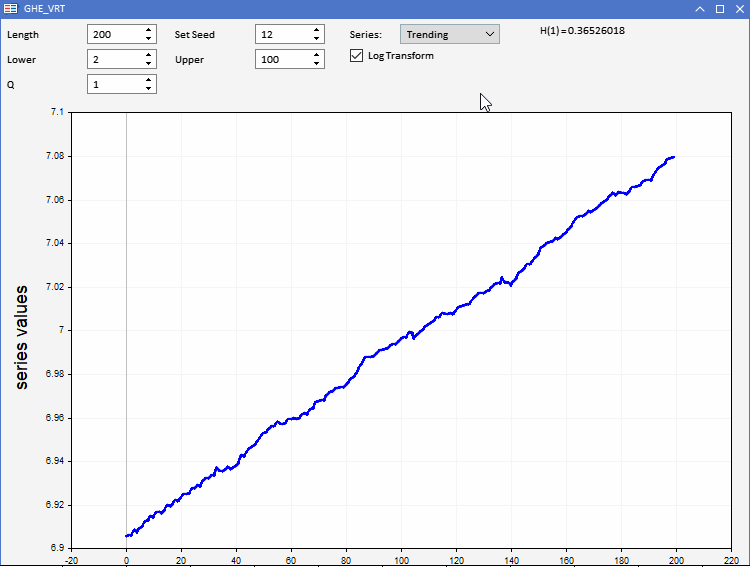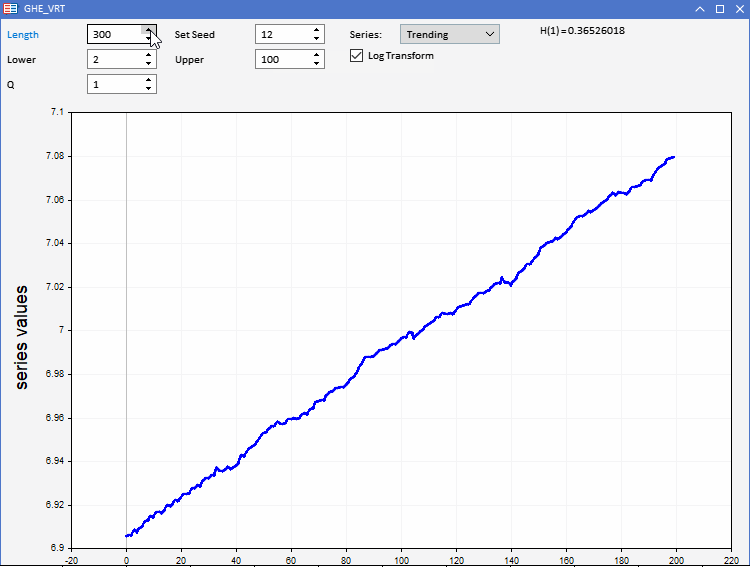
Мы знаем, что когда дело доходит до реальных приложений, наборы данных страдают от чрезмерного шума. Поскольку GHE дает оценку, чувствительную к размеру выборки, нам необходимо проверить значимость результата. Это можно сделать, проведя тест гипотезы, называемый тестом коэффициента дисперсии (VR).

Тест коэффициента дисперсии

Тест коэффициента дисперсии — это статистический тест, используемый для оценки случайности временного ряда путем проверки того, увеличивается ли дисперсия ряда пропорционально длине временного интервала. Тест основан на идее, что если проверяемый ряд следует случайному блужданию, дисперсия изменений ряда в течение заданного интервала времени должна увеличиваться линейно с длиной интервала. Если дисперсия увеличивается более медленными темпами, это может указывать на серийную корреляцию в изменениях ряда с предположением, что ряд предсказуем. Коэффициент дисперсии позволяет убедиться в том, что:

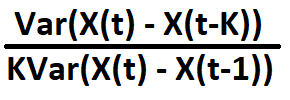
равен 1, где:
- X() - интересующий временной ряд.
- K - произвольная задержка.
- Var() - дисперсия.

Нулевая гипотеза теста состоит в том, что временной ряд следует случайному блужданию, и, следовательно, коэффициент дисперсии должен быть равен 1. Коэффициент дисперсии, значительно отличающийся от 1, может привести к отклонению нулевой гипотезы, предполагая наличие некоторой формы предсказуемости или серийной корреляции во временном ряду.

Реализация теста коэффициента дисперсии

Тест VR реализован как класс CVarianceRatio, определенный в VRT.mqh. Существует два метода, которые можно вызвать для проведения VR-теста Vrt(): один работает с векторами, а другой — с массивами. Параметры метода описаны ниже:

• lags определяет количество периодов или задержек, используемых при вычислении дисперсии. В контексте того, как мы хотим использовать тест VR для оценки значимости нашей оценки GHE, мы можем установить lags либо на соответствующее значение параметра gen_hurst() - lower или upper. Значение не может быть меньше 2. 
• trend — это перечисление, позволяющее указать тип случайного блуждания, которое мы хотим проверить. Только две опции имеют эффект - TREND_CONST_ONLY и TREND_NONE.
• debiased указывает, следует ли использовать смещенную версию теста, которая применима только в том случае, если overlap равно true. При true функция использует метод коррекции смещения для корректировки оценки коэффициента дисперсии, стремясь к более точному представлению истинной взаимосвязи между дисперсиями. Это особенно полезно при работе с небольшими сериями выборок.
  
• overlap указывает, использовать ли все перекрывающиеся блоки. При false длина ряда минус единица должна быть кратна значению lags. Если это условие не выполняется, некоторые значения в конце входного ряда будут отброшены.
• robust выбирает, следует ли учитывать гетероскедастичность (true) или только гомоскедастичность (false). В статистическом анализе процесс, который является гетероскедастическим, имеет непостоянную дисперсию, тогда как гомоскедастический ряд характеризуется постоянной дисперсией. 
  

Метод Vrt() возвращает true при успешном выполнении, после чего можно вызвать любой из методов получения для получения всех аспектов результата теста.

//+------------------------------------------------------------------+
//| CVarianceRatio  class                                            |
//| Variance ratio hypthesis test for a random walk                  |
//+------------------------------------------------------------------+
class CVarianceRatio
  {
private:
   double            m_pvalue;     //pvalue
   double            m_statistic;  //test statistic
   double            m_variance;   //variance
   double            m_vr;         //variance ratio
   vector            m_critvalues; //critical values

public:
                     CVarianceRatio(void);
                    ~CVarianceRatio(void);

   bool              Vrt(const double &in_data[], ulong lags, ENUM_TREND trend = TREND_CONST_ONLY, bool debiased=true, bool robust=true, bool overlap = true);
   bool              Vrt(const vector &in_vect, ulong lags, ENUM_TREND trend = TREND_CONST_ONLY, bool debiased=true, bool robust=true, bool overlap = true);

   double            Pvalue(void) { return m_pvalue;}
   double            Statistic(void) { return m_statistic;}
   double            Variance(void) { return m_variance;}
   double            VRatio(void) { return m_vr;}
   vector            CritValues(void) { return m_critvalues;}
  };

Внутри Vrt(), если overlap имеет значение false, мы проверяем, делится ли длина входной серии на lags. Если нет, мы обрезаем конец ряда и выдаем предупреждение о длине данных. Затем мы переназначаем nobs в зависимости от обновленной длины серии. Вычисляем mu, условие тренда. Здесь мы вычисляем различия соседних элементов в ряду и сохраняем их в delta_y. При использвании delta_y дисперсия вычисляется и сохраняется в переменной sigma2_1. Если перекрытия нет, мы вычисляем дисперсию для непересекающихся блоков. В противном случае мы вычисляем дисперсию для перекрывающихся блоков. Если debiased и overlap включены, корректируем дисперсии. Здесь m_varianced рассчитывается в зависимости от overlap и robust. Наконец, рассчитываются коэффициент дисперсии, тестовая статистика и значение p.

//+------------------------------------------------------------------+
//| main method for computing Variance ratio test                    |
//+------------------------------------------------------------------+
bool CVarianceRatio::Vrt(const vector &in_vect,ulong lags,ENUM_TREND trend=1,bool debiased=true,bool robust=true,bool overlap=true)
  {
   ulong nobs = in_vect.Size();

   vector y = vector::Zeros(2),delta_y;

   double mu;

   ulong nq = nobs - 1;

   if(in_vect.Size()<1)
     {
      Print(__FUNCTION__, "Invalid input, no data supplied");
      return false;
     }

   if(lags<2 || lags>=in_vect.Size())
     {
      Print(__FUNCTION__," Invalid input for lags");
      return false;
     }

   if(!overlap)
     {
      if(nq % lags != 0)
        {
         ulong extra = nq%lags;
         if(!y.Init(5,slice,in_vect,0,in_vect.Size()-extra-1))
           {
            Print(__FUNCTION__," ",__LINE__);
            return false;
           }
         Print("Warning:Invalid length for input data, size is not exact multiple of lags");
        }
     }
   else
      y.Copy(in_vect);

   nobs = y.Size();

   if(trend == TREND_NONE)
      mu = 0;
   else
      mu = (y[y.Size()-1] - y[0])/double(nobs - 1);

   delta_y = difference(y);

   nq = delta_y.Size();

   vector mudiff = delta_y - mu;

   vector mudiff_sq = MathPow(mudiff,2.0);

   double sigma2_1 = mudiff_sq.Sum()/double(nq);

   double sigma2_q;

   vector delta_y_q;

   if(!overlap)
     {
      vector y1,y2;
      if(!y1.Init(3,slice,y,lags,y.Size()-1,lags) ||
         !y2.Init(3,slice,y,0,y.Size()-lags-1,lags))
        {
         Print(__FUNCTION__," ",__LINE__);
         return false;
        }

      delta_y_q = y1-y2;

      vector delta_d = delta_y_q - double(lags) * mu;

      vector delta_d_sqr = MathPow(delta_d,2.0);

      sigma2_q = delta_d_sqr.Sum()/double(nq);
     }
   else
     {
      vector y1,y2;
      if(!y1.Init(3,slice,y,lags,y.Size()-1) ||
         !y2.Init(3,slice,y,0,y.Size()-lags-1))
        {
         Print(__FUNCTION__," ",__LINE__);
         return false;
        }

      delta_y_q = y1-y2;

      vector delta_d = delta_y_q - double(lags) * mu;

      vector delta_d_sqr = MathPow(delta_d,2.0);

      sigma2_q = delta_d_sqr.Sum()/double(nq*lags);
     }


   if(debiased && overlap)
     {
      sigma2_1 *= double(nq)/double(nq-1);
      double mm = (1.0-(double(lags)/double(nq)));
      double m = double(lags*(nq - lags+1));// * (1.0-double(lags/nq));
      sigma2_q *= double(nq*lags)/(m*mm);
     }

   if(!overlap)
      m_variance = 2.0 * (lags-1);
   else
      if(!robust)
         m_variance = double((2 * (2 * lags - 1) * (lags - 1)) / (3 * lags));
      else
        {
         vector z2, o, p;
         z2=MathPow((delta_y-mu),2.0);
         double scale = pow(z2.Sum(),2.0);
         double theta = 0;
         double delta;
         for(ulong k = 1; k<lags; k++)
           {
            if(!o.Init(3,slice,z2,k,z2.Size()-1) ||
               !p.Init(3,slice,z2,0,z2.Size()-k-1))
              {
               Print(__FUNCTION__," ",__LINE__);
               return false;
              }
            o*=double(nq);
            p/=scale;
            delta = o.Dot(p);
            theta+=4.0*pow((1.0-double(k)/double(lags)),2.0)*delta;
           }
         m_variance = theta;
        }
   m_vr = sigma2_q/sigma2_1;

   m_statistic = sqrt(nq) * (m_vr - 1)/sqrt(m_variance);

   double abs_stat = MathAbs(m_statistic);

   m_pvalue = 2 - 2*CNormalDistr::NormalCDF(abs_stat);

   return true;
  }

Чтобы протестировать класс, мы модифицируем приложение GHE.ex5, используемое для демонстрации функции gen_hurst(), потому что GHE определяется диапазоном задержек, на которых сосредоточен анализ. Мы можем откалибровать VRT, чтобы проверить значимость результатов GHE в том же диапазоне задержек. Мы должны получить достаточную информацию, запустив VRT с минимальной и максимальной задержкой. В GHE.ex5 коэффициент дисперсии на lower отображается первым перед коэффициентом дисперсии на задержке upper.
Коэффициент дисперсии со значительным расхождением является показателем предсказуемости данных. Коэффициенты дисперсии, близкие к 1, позволяют предположить, что ряд близок к случайному блужданию. Протестировав различные комбинации параметров, мы заметили, что на результаты GHE и VRT влияет размер выборки.

Для серий длиной менее 1000 оба метода иногда давали неожиданные результаты.

Кроме того, были случаи, когда результаты GHE значительно отличались при сравнении тестов с использованием необработанных и логарифмически преобразованных значений.

Теперь, когда мы знакомы с VRT и GHE, мы можем применить их к нашей стратегии возврата к среднему значению. Если известно, что ценовой ряд возвращается к среднему значению, мы можем приблизительно оценить, что будет делать цена, основываясь на ее текущем отклонении от среднего значения. В основу нашей стратегии будет положен анализ характеристик ценового ряда за определенный период времени. Используя этот анализ, мы формируем модель, которая оценивает точки, в которых цена может вернуться назад после слишком далекого отклонения от нормы. Нам нужен какой-то способ измерить и количественно оценить это отклонение, чтобы генерировать сигналы на вход и выход.

Z-счет

Z-счет (z-score) измеряет количество стандартных отклонений цены от ее среднего значения. При нормализации цен z-счет колеблется около нуля. Давайте посмотрим, как выглядит график z-счета при его реализации в качестве индикатора. Полный код показан ниже.

//+------------------------------------------------------------------+
//|                                                       Zscore.mq5 |
//|                                  Copyright 2023, MetaQuotes Ltd. |
//|                                             https://www.mql5.com |
//+------------------------------------------------------------------+
#property copyright "Copyright 2023, MetaQuotes Ltd."
#property link      "https://www.mql5.com"
#property version   "1.00"
#include<VectorMatrixTools.mqh>
#property indicator_separate_window
#property indicator_buffers 1
#property indicator_plots   1
//--- plot Zscore
#property indicator_label1  "Zscore"
#property indicator_type1   DRAW_LINE
#property indicator_color1  clrBlue
#property indicator_style1  STYLE_SOLID
#property indicator_width1  1
//--- input parameters
input int      z_period = 10;
//--- indicator buffers
double         ZscoreBuffer[];
vector vct;
//+------------------------------------------------------------------+
//| Custom indicator initialization function                         |
//+------------------------------------------------------------------+
int OnInit()
  {
//--- indicator buffers mapping
   SetIndexBuffer(0,ZscoreBuffer,INDICATOR_DATA);
//----
   PlotIndexSetDouble(0,PLOT_EMPTY_VALUE,0);
//---
   PlotIndexSetInteger(0,PLOT_DRAW_BEGIN,z_period-1);
//---
   return(INIT_SUCCEEDED);
  }
//+------------------------------------------------------------------+
//| Custom indicator iteration function                              |
//+------------------------------------------------------------------+
int OnCalculate(const int rates_total,
                const int prev_calculated,
                const datetime &time[],
                const double &open[],
                const double &high[],
                const double &low[],
                const double &close[],
                const long &tick_volume[],
                const long &volume[],
                const int &spread[])
  {
//---
   if(rates_total<z_period)
     {
      Print("Insufficient history");
      return -1;
     }
//---
   int limit;
   if(prev_calculated<=0)
      limit = z_period - 1;
   else
      limit = prev_calculated - 1;
//---
   for(int i = limit; i<rates_total; i++)
     {
      vct.Init(ulong(z_period),assign,close,ulong(i-(z_period-1)),i,1);
      if(vct.Size()==ulong(z_period))
         ZscoreBuffer[i] = (close[i] - vct.Mean())/vct.Std();
      else
         ZscoreBuffer[i]=0.0;
     }

//--- return value of prev_calculated for next call
   return(rates_total);
  }
//+------------------------------------------------------------------+

Из этого графика видно, что значения индикатора теперь выглядят более нормально распределенными.

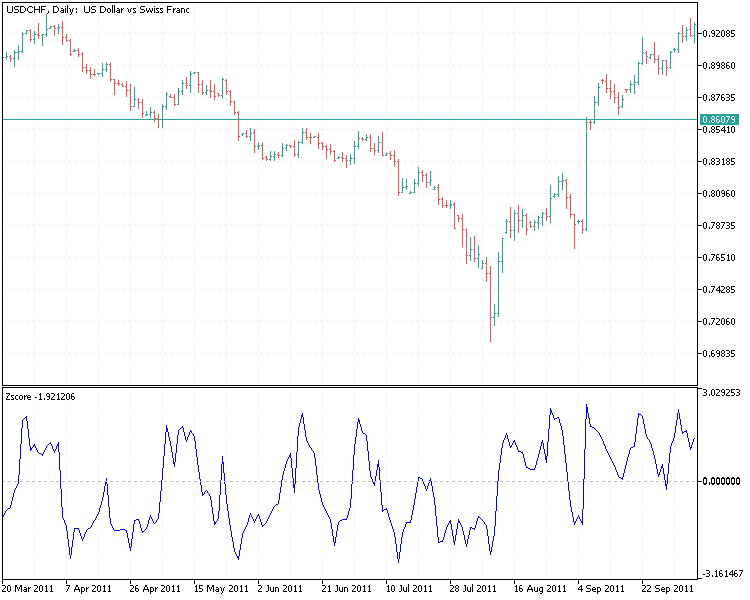
Торговые сигналы генерируются, когда z-показатель значительно отклоняется от 0 и превышает некоторый исторически сложившийся порог. Сильно отрицательный z-счет указывает на подходящее время для открытия длинной позиции, тогда как сильно положительный указывает на подходящее время для открытия короткой позиции. Это означает, что нам нужны два порога для сигналов на покупку и продажу. Один отрицательный (на покупку) и один положительный (на продажу). Один из вариантов — получить новый набор пороговых значений, которые будут работать в определенной позиции (длинной или короткой). В случае короткой позиции мы можем закрыть нашу позицию, когда z-счет возвращается к 0. Аналогично, мы закрываем длинную позицию, когда z-счет приближается к 0 от экстремального уровня, на котором была совершена покупка.

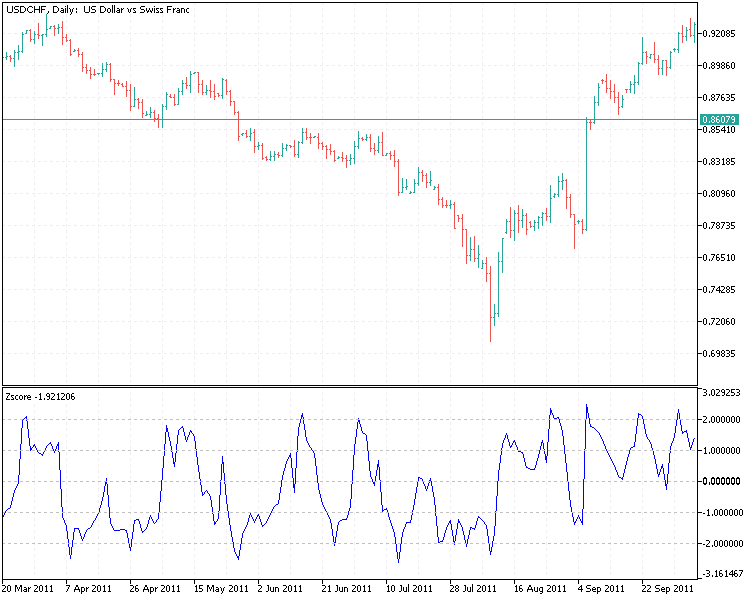
Теперь у нас есть входы и выходы, определенные с помощью индикатора Zscore.ex5. Давайте объединим все это в советнике. Ниже представлен фрагмент.

//+------------------------------------------------------------------+
//|                                                MeanReversion.mq5 |
//|                                  Copyright 2024, MetaQuotes Ltd. |
//|                                             https://www.mql5.com |
//+------------------------------------------------------------------+
#property copyright "Copyright 2024, MetaQuotes Ltd."
#property link      "https://www.mql5.com"
#property version   "1.00"
#resource "\\Indicators\\Zscore.ex5"
#include<ExpertTools.mqh>
//---Input parameters
input int  PeriodLength  = 10;
input double LotsSize = 0.01;
input double  LongOpenLevel = -2.0;
input double  ShortOpenLevel = 2.0;
input double  LongCloseLevel = -0.5;
input double  ShortCloseLevel = 0.5;
input ulong  SlippagePoints = 10;
input ulong  MagicNumber    = 123456;
//---
 int indi_handle;
//---
 double zscore[2];
//+------------------------------------------------------------------+
//| Expert initialization function                                   |
//+------------------------------------------------------------------+
int OnInit()
  {
//---
   if(PeriodLength<2)
    {
     Print("Invalid parameter value for PeriodLength");
     return INIT_FAILED;
    }
//---
   if(!InitializeIndicator())
    return INIT_FAILED;
//---        
   return(INIT_SUCCEEDED);
  }
//+------------------------------------------------------------------+
//| Expert deinitialization function                                 |
//+------------------------------------------------------------------+
void OnDeinit(const int reason)
  {
//---
   
  }
//+------------------------------------------------------------------+
//| Expert tick function                                             |
//+------------------------------------------------------------------+
void OnTick()
  {
//---    
      int signal = GetSignal();
//---      
      if(SumMarketOrders(MagicNumber,_Symbol,-1))
       {
        if(signal==0)
         CloseAll(MagicNumber,_Symbol,-1);
        return; 
       }
      else
        OpenPosition(signal);
//---   
  }
//+------------------------------------------------------------------+
//+------------------------------------------------------------------+
//| Initialize indicator                                             |
//+------------------------------------------------------------------+
bool InitializeIndicator(void)
{
 indi_handle = INVALID_HANDLE;
//---
 int try = 10;
//---
 while(indi_handle == INVALID_HANDLE && try>0)
  {
   indi_handle = (indi_handle==INVALID_HANDLE)?iCustom(NULL,PERIOD_CURRENT,"::Indicators\\Zscore.ex5",PeriodLength):indi_handle;
   try--;
  }
//---
 if(try<0)
  {
   Print("Failed to initialize Zscore indicator ");
   return false;
  }
//---
 return true;
}
//+------------------------------------------------------------------+
//|Get the signal to trade or close                                  |
//+------------------------------------------------------------------+
int GetSignal(const int sig_shift=1)
{
//---
 if( CopyBuffer(indi_handle,int(0),sig_shift,int(2),zscore)<2)
   {
    Print(__FUNCTION__," Error copying from indicator buffers: ", GetLastError());
    return INT_MIN;
   } 
//---   
 if(zscore[1]<LongOpenLevel && zscore[0]>LongOpenLevel)
     return (1);
//---   
 if(zscore[1]>ShortOpenLevel && zscore[0]<ShortOpenLevel)
     return (-1);          
//---   
 if((zscore[1]>LongCloseLevel && zscore[0]<LongCloseLevel) ||
    (zscore[1]<ShortCloseLevel && zscore[0]>ShortCloseLevel))
     return (0);
//---
 return INT_MIN;
//--- 
}
//+------------------------------------------------------------------+
//|  Go long or short                                                |
//+------------------------------------------------------------------+
bool OpenPosition(const int sig)
{

 long pid;
//--- 
 if(LastOrderOpenTime(pid,NULL,MagicNumber)>=iTime(NULL,0,0))
   return false;
//---   
 if(sig==1)
   return SendOrder(_Symbol,0,ORDER_TYPE_BUY,LotsSize,SlippagePoints,0,0,NULL,MagicNumber);
 else
  if(sig==-1)
    return SendOrder(_Symbol,0,ORDER_TYPE_SELL,LotsSize,SlippagePoints,0,0,NULL,MagicNumber); 
//--- 
  return false;                   
}

Код очень простой. Здесь не определены уровни стоп-лосса или тейк-профита. Наша цель — сначала оптимизировать советник, чтобы получить оптимальный период для индикатора Zscore, а также оптимальные пороги входа и выхода. Мы проведем оптимизацию данных за несколько лет и проверим оптимальные параметры на выборке, но прежде сделаем небольшое отступление, чтобы представить еще один интересный инструмент. В книге "Алгоритмический трейдинг: выигрышные стратегии и их обоснование" (Algorithmic Trading: Winning Strategies And Their Rationale) автор Эрнест Чен (Ernest Chan) описывает интересный инструмент для разработки стратегий возврата к среднему, который называется "период полураспада возврата к среднему" (half life of mean reversion).

Период полураспада возврата к среднему

Период полураспада возврата к среднему представляет собой время, необходимое для того, чтобы отклонение от среднего уменьшилось вдвое. В контексте цены актива период полураспада возврата к среднему показывает, насколько быстро цена имеет тенденцию возвращаться к своему историческому среднему значению после отклонения от него. Это мера скорости, с которой происходит процесс возврата к среднему значению. Математически период полураспада можно связать со скоростью возврата к среднему уравнению:

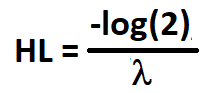
где:
- HL - период полураспада.
- log() - натуральный логарифм.
- lambda - скорость возврата к среднему значению.

С практической точки зрения, более короткий период полураспада предполагает более быстрый процесс возврата к среднему значению, тогда как более длительный период полураспада предполагает более медленный процесс возврата к среднему значению. Концепция периода полураспада может использоваться для точной настройки параметров торговых стратегий, возвращающихся к среднему значению, помогая оптимизировать точки входа и выхода на основе исторических данных и наблюдаемой скорости возврата к среднему значению. Период полураспада возврата к среднему значению выводится из математического представления процесса возврата к среднему значению, обычно моделируемого как процесс Орнштейна-Уленбека. Процесс Орнштейна-Уленбека представляет собой стохастическое дифференциальное уравнение, которое описывает версию поведения возврата к среднему значению с непрерывным временем.

Как отмечает Чен, можно определить, является ли возвращение к среднему подходящей стратегией, рассчитав период полураспада возврата к среднему. Во-первых, если лямбда положительна, то возврат к среднему значению вообще не следует применять. Даже если лямбда отрицательна и очень близка к нулю, применение возврата к среднему значению не рекомендуется, поскольку это указывает на то, что период полураспада будет долгим. Возвращение к среднему значению следует использовать только в том случае, если период полураспада достаточно короткий.

Период полураспада возврата к среднему реализован как функция в MeanReversionUtilities.mqh, код приведен ниже. Он рассчитывается путем регрессии ценового ряда на ряд различий между последующими значениями. Лямбда равна бета-параметру регрессионной модели, а период полураспада вычисляется путем деления -log(2) на лямбда.

//+------------------------------------------------------------------+
//|Calculate Half life of Mean reversion                             |
//+------------------------------------------------------------------+
double mean_reversion_half_life(vector &data, double &lambda)
  {
//---
   vector yy,zz;
   matrix xx;
//---
   OLS ols_reg;
//---
   yy.Init(data.Size()-1,slice,data,1,data.Size()-1,1);
//---
   zz.Init(data.Size()-1,slice,data,0,data.Size()-2,1);
//---
   if(!xx.Init(zz.Size(),2) || !xx.Col(zz,0) || !xx.Col(vector::Ones(zz.Size()),1) || !ols_reg.Fit(yy-zz,xx))
     {
      Print(__FUNCTION__," Error in calculating half life of mean reversion ", GetLastError());
      return 0;
     }
//---
   vector params = ols_reg.ModelParameters();
   lambda = params[0];
//---
   return (-log(2)/lambda);
//---
  }

Мы будем использовать его вместе с GHE и VRT для тестирования выборки цен за выбранный период лет для нескольких форекс-символов. Мы будем использовать результаты тестирования, чтобы выбрать подходящий символ, к которому будет применен созданный нами ранее советник. Он будет оптимизирован на том же периоде в годах и окончательно протестирован на выборке. Сценарий ниже принимает список символов-кандидатов, которые будут проверены с использованием GHE, VRT и периода полураспада.

//+------------------------------------------------------------------+
//|                                                 SymbolTester.mq5 |
//|                                  Copyright 2024, MetaQuotes Ltd. |
//|                                             https://www.mql5.com |
//+------------------------------------------------------------------+
#property copyright "Copyright 2024, MetaQuotes Ltd."
#property link      "https://www.mql5.com"
#property version   "1.00"
#property script_show_inputs
#include<MeanReversionUtilities.mqh>
#include<GHE.mqh>
#include<VRT.mqh>

//--- input parameters
input string   Symbols = "EURUSD,GBPUSD,USDCHF,USDJPY";//Comma separated list of symbols to test
input ENUM_TIMEFRAMES TimeFrame = PERIOD_D1;
input datetime StartDate=D'2020.01.02 00:00:01';
input datetime StopDate=D'2015.01.18 00:00:01';
input int Q_parameter = 2;
input int MinimumLag = 2;
input int MaximumLag = 100;
input bool ApplyLogTransformation = true;
//---
CVarianceRatio vrt;
double ghe,hl,lb,vlower,vupper;
double prices[];
//+------------------------------------------------------------------+
//| Script program start function                                    |
//+------------------------------------------------------------------+
void OnStart()
  {
//---Check Size input value
   if(StartDate<=StopDate)
     {
      Print("Invalid input for StartDater or StopDate");
      return;
     }
//---array for symbols
   string symbols[];
//---process list of symbols from user input
   int num_symbols = StringSplit(Symbols,StringGetCharacter(",",0),symbols);
//---incase list contains ending comma
   if(symbols[num_symbols-1]=="")
      num_symbols--;
//---in case there are less than two symbols specified
   if(num_symbols<1)
     {
      Print("Invalid input. Please list at least one symbol");
      return;
     }
//---loop through all paired combinations from list
   for(uint i=0; i<symbols.Size(); i++)
     {

      //--- get prices for the pair of symbols
      if(CopyClose(symbols[i],TimeFrame,StartDate,StopDate,prices)<1)
        {
         Print("Failed to copy close prices ", ::GetLastError());
         return;
        }
      //---
      if(ApplyLogTransformation && !MathLog(prices))
        {
         Print("Mathlog error ", GetLastError());
         return;
        }
      //---
      if(!vrt.Vrt(prices,MinimumLag))
         return;
      //---
      vlower = vrt.VRatio();
      //---
      if(!vrt.Vrt(prices,MaximumLag))
         return;
      //---
      vupper = vrt.VRatio();
      //---
      ghe = general_hurst(prices,Q_parameter,MinimumLag,MaximumLag);
      //---
      hl = mean_reversion_half_life(prices,lb);
      //--- output the results
      Print(symbols[i], " GHE:  ", DoubleToString(ghe)," | Vrt: ",DoubleToString(vlower)," ** ",DoubleToString(vupper)," | HalfLife ",DoubleToString(hl)," | Lambda: ",DoubleToString(lb));
     }
  }
//+------------------------------------------------------------------+

Запуск скрипта дает следующие результаты:

19:31:03.143    SymbolTester (USDCHF,D1)        EURUSD GHE:  0.44755644 | Vrt: 0.97454284 ** 0.61945905 | HalfLife 85.60548208 | Lambda: -0.00809700
19:31:03.326    SymbolTester (USDCHF,D1)        GBPUSD GHE:  0.46304381 | Vrt: 1.01218672 ** 0.82086185 | HalfLife 201.38001205 | Lambda: -0.00344199
19:31:03.509    SymbolTester (USDCHF,D1)        USDCHF GHE:  0.42689382 | Vrt: 1.02233286 ** 0.47888803 | HalfLife 28.90550869 | Lambda: -0.02397976
19:31:03.694    SymbolTester (USDCHF,D1)        USDJPY GHE:  0.49198795 | Vrt: 0.99875744 ** 1.06103587 | HalfLife 132.66433924 | Lambda: -0.00522482

Символ USDCHF имеет наиболее многообещающие результаты тестирования за выбранный период времени. Итак, мы оптимизируем параметры советника, торгуя на USDCHF. Интересно было бы выбрать период Zscore для оптимизации и посмотреть, отличается ли он от рассчитанного периода полураспада.

Здесь мы можем видеть оптимальный период Zscore. Он очень близок к рассчитанному периоду полураспада возврата к среднему. Это обнадеживает. Конечно, потребуется более обширное тестирование, чтобы определить полезность периода полураспада.

Наконец, мы тестируем советник вне выборки с оптимальными параметрами.

Результаты оставляют желают лучшего. Вероятно, это связано с тем, что рынок находится в постоянном движении, поэтому характеристики, наблюдавшиеся за период оптимизации советника, больше не применимы. Нам нужны более динамичные пороги входа и выхода, которые учитывают изменения в базовой динамике рынка.

Мы можем использовать полученные здесь знания как основу для дальнейшего развития. Одним из возможных направлений является применение описанных здесь инструментов для реализации стратегии парной торговли. Вместо одной ценовой пары, индикатор Zscore может основываться на спреде двух коинтегрированных или коррелирующих инструментов.

Заключение

В этой статье мы продемонстрировали реализацию обобщенной экспоненты Херста в MQL5 и показали, как ее можно использовать для определения характеристик ценового ряда. Мы также рассмотрели применение теста коэффициента дисперсии, а также период полураспада возврата к среднему значению. Следующая таблица представляет собой описание всех файлов, прикрепленных к статье.

Файл	Описание
Mql5\include\ExpertTools.mqh	Содержит определения функций для проведения торговых операций, используемых в советнике MeanReversion.
Mql5\include\GHE.mqh	Содержит определение функции, реализующей обобщенную экспоненту Херста.
Mql5\include\OLS.mqh	Содержит определение класса OLS, реализующего обычную регрессию наименьших квадратов.
Mql5\include\VRT.mqh	Содержит определение класса CVarianceRatio, который инкапсулирует тест коэффициента дисперсии.
Mql5\include\VectorMatrixTools.mqh	Имеет различные определения функций для быстрой инициализации общих векторов и матриц.
Mql5\include\TestUtilities.mqh	Имеет ряд объявлений, используемых в определении класса OLS.
Mql5\include\MeanReversionUtilities.mqh	Содержит различные определения функций, включая определение периода полураспада возврата к среднему значению.
Mql5\Indicators\Zscore.mq5	Индикатор, используемый в советнике MeanReversion
Mql5\scripts\SymbolTester.mq5	Скрипт, который можно использовать для проверки символов на возврат к среднему значению
Mql5\Experts\GHE.ex5	Советник для изучения и экспериментирования с инструментами GHE и VRT.
Mql5\scripts\MeanReversion.mq5	Советник демонстрирует простую стратегию возврата к среднему значению