MQL5における一般化ハースト指数と分散比検定の実装

はじめに

「ハースト指数の計算」稿では、フラクタル解析の概念と、それが金融市場にどのように応用できるかを紹介しました。その論文の中で著者は、ハースト指数を推定するための再スケールレンジ法(R/S)について述べています。この記事では、系列の性質を分類するための一般化ハースト指数(GHE)の実装を実証することで、異なるアプローチを取ります。GHEを使用して、平均回帰傾向を示すFX銘柄を特定することに焦点を当て、この挙動を利用することを期待しています。

はじめに、GHEの基礎と、元のハースト指数との違いについて簡単に説明します。それに関連して、分散比検定(VRT)と呼ばれる、GHE分析の結果を肯定するために使用できる統計検定について説明します。そこから、平均回帰取引のためのFX銘柄候補の特定におけるGHEの応用に移ります。ここでは、エントリシグナルとエグジットシグナルを生成する指標を紹介します。最終的に、これを基本的なEAで試します。

一般化ハースト指数について

ハースト指数（英語）は時系列のスケーリング特性を測定します。スケーリング特性とは、システムのサイズや時間スケールが変化したときに、システムがどのように振る舞うかを説明する基本的な特性です。時系列データの場合、スケーリング特性は、異なる時間スケールとデータ中に存在するパターンとの関係についての洞察を提供します。定常系列では、幾何学的ランダムウォークに比べ、その後の値の時間的変化はより緩やかに起こります。この挙動を数学的に定量化するために、系列の拡散速度を分析します。分散は、他の値が系列の最初の値から乖離する割合を表す指標となります。

上記の式において、Kは分析がおこなわれる任意のラグを表します。系列の性質をよりよく把握するためには、他のラグにおける分散も評価する必要があります。つまり、Kには系列の長さより小さい任意の正の整数を割り当てることができます。最大ラグ適用は任意です。このことを肝に銘じておくことが重要です。したがって、ハーストは、異なるラグにおける分散のスケーリング挙動と関連しています。累乗則を用いると、次のように定義されます。

GHEは元のハースト指数を一般化したもので、2が変数（通常qと表記）に置き換えられています。これにより、上記の式は次のように変更されます。

および

GHEは、時系列の連続するポイント間の変化の異なる統計的特徴が、異なる次数のモーメントによってどのように変化するかを分析することによって、元のハーストを拡張したものです。数学用語では、モーメントとは分布の形や特徴を表す統計的尺度です。q次モーメントは特定のタイプのモーメントで、qは次数を決定するパラメータです。GHEはqの値ごとに時系列の異なる特徴を強調します。具体的には、q=1のとき、結果は絶対偏差のスケーリング特性を示します。一方、q=2は長距離依存性を調べる際に最も重要です。

MQL5におけるGHEの実装

このセクションでは、MQL5におけるGHEの実装について説明します。その後、人工的に生成した時系列のランダムサンプルを分析することでテストします。実装はGHE.mqhファイルに含まれています。このファイルには、一般的なベクトルや行列を初期化するためのさまざまな関数の定義を含むVectorMatrixTools.mqhが含まれています。このファイルの内容を以下に示します。

//+------------------------------------------------------------------+
//|                                            VectorMatrixTools.mqh |
//|                                  Copyright 2023, MetaQuotes Ltd. |
//|                                             https://www.mql5.com |
//+------------------------------------------------------------------+
#property copyright "Copyright 2023, MetaQuotes Ltd."
#property link      "https://www.mql5.com"
//+------------------------------------------------------------------+
//|Vector arange initialization                                      |
//+------------------------------------------------------------------+
template<typename T>
void arange(vector<T> &vec,T value=0.0,T step=1.0)
  {
   for(ulong i=0; i<vec.Size(); i++,value+=step)
      vec[i]=value;
  }
//+------------------------------------------------------------------+
//| Vector sliced initialization                                     |
//+------------------------------------------------------------------+
template<typename T>
void slice(vector<T> &vec,const vector<T> &toCopyfrom,ulong start=0,ulong stop=ULONG_MAX, ulong step=1)
  {
   start = (start>=toCopyfrom.Size())?toCopyfrom.Size()-1:start;
   stop  = (stop>=toCopyfrom.Size())?toCopyfrom.Size()-1:stop;
   step  = (step==0)?1:step;

   ulong numerator = (stop>=start)?stop-start:start-stop;
   ulong size = (numerator/step)+1;
   if(!vec.Resize(size))
     {
      Print(__FUNCTION__ " invalid slicing parameters for vector initialization");
      return;
     }

   if(stop>start)
     {
      for(ulong i =start, k = 0; i<toCopyfrom.Size() && k<vec.Size() && i<=stop; i+=step, k++)
         vec[k] = toCopyfrom[i];
     }
   else
     {
      for(long i = long(start), k = 0; i>-1 && k<long(vec.Size()) && i>=long(stop); i-=long(step), k++)
         vec[k] = toCopyfrom[i];
     }
  }
//+------------------------------------------------------------------+
//| Vector sliced initialization  using array                        |
//+------------------------------------------------------------------+
template<typename T>
void assign(vector<T> &vec,const T &toCopyfrom[],ulong start=0,ulong stop=ULONG_MAX, ulong step=1)
  {
   start = (start>=toCopyfrom.Size())?toCopyfrom.Size()-1:start;
   stop  = (stop>=toCopyfrom.Size())?toCopyfrom.Size()-1:stop;
   step  = (step==0)?1:step;

   ulong numerator = (stop>=start)?stop-start:start-stop;
   ulong size = (numerator/step)+1;

   if(size != vec.Size() &&  !vec.Resize(size))
     {
      Print(__FUNCTION__ " invalid slicing parameters for vector initialization");
      return;
     }

   if(stop>start)
     {
      for(ulong i =start, k = 0; i<ulong(toCopyfrom.Size()) && k<vec.Size() && i<=stop; i+=step, k++)
         vec[k] = toCopyfrom[i];
     }
   else
     {
      for(long i = long(start), k = 0; i>-1 && k<long(vec.Size()) && i>=long(stop); i-=long(step), k++)
         vec[k] = toCopyfrom[i];
     }
  }
//+------------------------------------------------------------------+
//| Matrix initialization                                            |
//+------------------------------------------------------------------+
template<typename T>
void rangetrend(matrix<T> &mat,T value=0.0,T step=1.0)
  {
   ulong r = mat.Rows();

   vector col1(r,arange,value,step);

   vector col2 = vector::Ones(r);

   if(!mat.Resize(r,2) || !mat.Col(col1,0) || !mat.Col(col2,1))
     {
      Print(__FUNCTION__ " matrix initialization error: ", GetLastError());
      return;
     }

  }
//+-------------------------------------------------------------------------------------+
//| ols design Matrix initialization with constant and first column from specified array|
//+-------------------------------------------------------------------------------------+
template<typename T>
void olsdmatrix(matrix<T> &mat,const T &toCopyfrom[],ulong start=0,ulong stop=ULONG_MAX, ulong step=1)
  {
   vector col0(1,assign,toCopyfrom,start,stop,step);

   ulong r = col0.Size();

   if(!r)
     {
      Print(__FUNCTION__," failed to initialize first column ");
      return;
     }

   vector col1 = vector::Ones(r);

   if(!mat.Resize(r,2) || !mat.Col(col0,0) || !mat.Col(col1,1))
     {
      Print(__FUNCTION__ " matrix initialization error: ", GetLastError());
      return;
     }

  }
//+------------------------------------------------------------------+
//|vector to array                                                   |
//+------------------------------------------------------------------+
bool vecToArray(const vector &in, double &out[])
  {
//---
   if(in.Size()<1)
     {
      Print(__FUNCTION__," Empty vector");
      return false;
     }
//---
   if(ulong(out.Size())!=in.Size() && ArrayResize(out,int(in.Size()))!=int(in.Size()))
     {
      Print(__FUNCTION__," resize error ", GetLastError());
      return false;
     }
//---
   for(uint i = 0; i<out.Size(); i++)
      out[i]=in[i];
//---
   return true;
//---
  }
//+------------------------------------------------------------------+
//| difference a vector                                               |
//+------------------------------------------------------------------+
vector difference(const vector &in)
  {
//---
   if(in.Size()<1)
     {
      Print(__FUNCTION__," Empty vector");
      return vector::Zeros(1);
     }
//---
   vector yy,zz;
//---
   yy.Init(in.Size()-1,slice,in,1,in.Size()-1,1);
//---
   zz.Init(in.Size()-1,slice,in,0,in.Size()-2,1);
//---
   return yy-zz;
  }
//+------------------------------------------------------------------+

 GHE.mqhには、gen_hurst()関数とそのオーバーロードの定義が含まれています。一方はベクトルで、もう一方は配列で分析対象データを供給します。この関数はまた、整数qと、オプションの整数パラメータlowerとupper（デフォルト値）を取ります。これは前節のGHEの説明で述べたqと同じです。最後の2つのパラメータはオプションであり、lowerとupperは、上記の式におけるK値の範囲と同様に、分析が実施されるラグの範囲を定義します。 

//+--------------------------------------------------------------------------+
//|overloaded gen_hurst() function that works with series contained in vector|
//+--------------------------------------------------------------------------+
double general_hurst(vector &data, int q, int lower=0,int upper=0)
  {
   double series[];

   if(!vecToArray(data,series))
      return EMPTY_VALUE;
   else
      return general_hurst(series,q,lower,upper);
  }

エラーが発生した場合、この関数は内蔵の定数EMPTY_VALUEに相当するものを、端末の[エクスパート]タブに出力される有用な文字列メッセージとともに返します。gen_hurst()内で、ルーチンは渡された引数の確認から始まります。以下の条件に適合していることを確認してください。

• qが1より小さくなることはありません。
• lowerに2より小さい値を設定することはできず、またupperよりも大きいか等しい値を設定することもできません。 
• 一方、upper引数には、分析対象のデータ系列の半分以上のサイズを指定することはできません。これらの条件のいずれかが満たされない場合、この関数は直ちにエラーをフラグします。

if(data.Size()<100)
     {
      Print("data array is of insufficient length");
      return EMPTY_VALUE;
     }

   if(lower>=upper || lower<2 ||  upper>int(floor(0.5*data.Size())))
     {
      Print("Invalid input for lower and/or upper");
      return EMPTY_VALUE;
     }

   if(q<=0)
     {
      Print("Invalid input for q");
      return EMPTY_VALUE;
     }

   uint len = data.Size();

   int k =0;

   matrix H,mcord,lmcord;
   vector n_vector,dv,vv,Y,ddVd,VVVd,XP,XY,PddVd,PVVVd,Px_vector,Sqx,pt;
   double dv_array[],vv_array[],mx,SSxx,my,SSxy,cc1,cc2,N;

   if(!H.Resize(ulong(upper-lower),1))
     {
      Print(__LINE__," ",__FUNCTION__," ",GetLastError());
      return EMPTY_VALUE;
     }

   for(int i=lower; i<upper; i++)
     {
      vector x_vector(ulong(i),arange,1.0,1.0);

      if(!mcord.Resize(ulong(i),1))
        {
         Print(__LINE__," ",__FUNCTION__," ",GetLastError());
         return EMPTY_VALUE;
        }

      mcord.Fill(0.0);

この関数の内部動作は、lowerからupperまでのforループから始まり、各iに対してarange関数を使用してi個の要素を持つベクトルx_vectorを作成します。そして、行列mcordをi行1列になるようにリサイズします。

 for(int j=1; j<i+1; j++)
        {
         if(!diff_array(j,data,dv,Y))
            return EMPTY_VALUE;

内部ループは、まずヘルパー関数diff_array()を使用してdata配列の差分を計算し、ベクターdvとYに格納します。

 N = double(Y.Size());

         vector X(ulong(N),arange,1.0,1.0);

         mx = X.Sum()/N;

         XP = MathPow(X,2.0);

         SSxx = XP.Sum() - N*pow(mx,2.0);

         my = Y.Sum()/N;

         XY = X*Y;

         SSxy = XY.Sum() - N*mx*my;

         cc1 = SSxy/SSxx;

         cc2 = my - cc1*mx;

         ddVd = dv - cc1;

         VVVd = Y - cc1*X - cc2;

         PddVd = MathAbs(ddVd);

         PddVd = pow(PddVd,q);

         PVVVd = MathAbs(VVVd);

         PVVVd = pow(PVVVd,q);

         mcord[j-1][0] = PddVd.Mean()/PVVVd.Mean();
        }

ここで特定のラグにおける分散が計算されます。その結果は行列mcordに格納されます。

 Px_vector = MathLog10(x_vector);

      mx = Px_vector.Mean();

      Sqx = MathPow(Px_vector,2.0);

      SSxx = Sqx.Sum() - i*pow(mx,2.0);

      lmcord = log10(mcord);

      my = lmcord.Mean();

      pt = Px_vector*lmcord.Col(0);

      SSxy = pt.Sum() - i*mx*my;

      H[k][0]= SSxy/SSxx;

      k++;

内側ループの外側では、外側ループの最後のレグで、メインのH行列の値が更新されます。最後に、この関数はH行列の平均をqで割って返します。

 return H.Mean()/double(q);

GHE機能をテストするために、EAとして実装されたアプリケーションGHE.ex5を用意しました。これにより、あらかじめ定義された特性を持つランダムな系列を視覚化し、GHEがどのように機能するかを観察することができます。完全な双方向性により、GHEの全パラメータと系列の長さを制限内で調整することができます。興味深い機能は、GHEを適用する前に、この方法でデータを前処理するメリットがあるかどうかをテストするために系列を対数変換するものです。

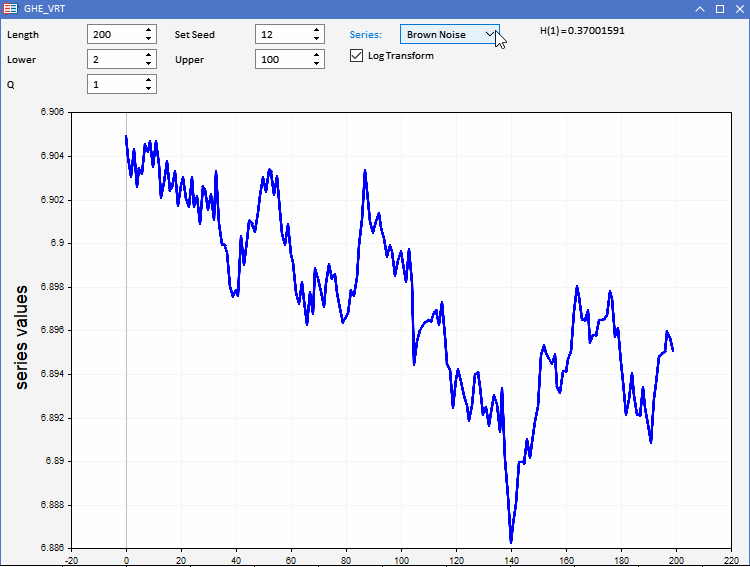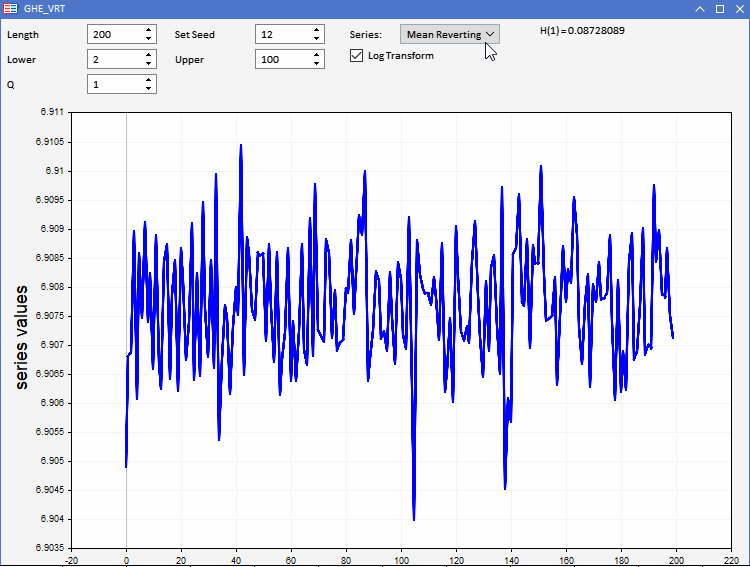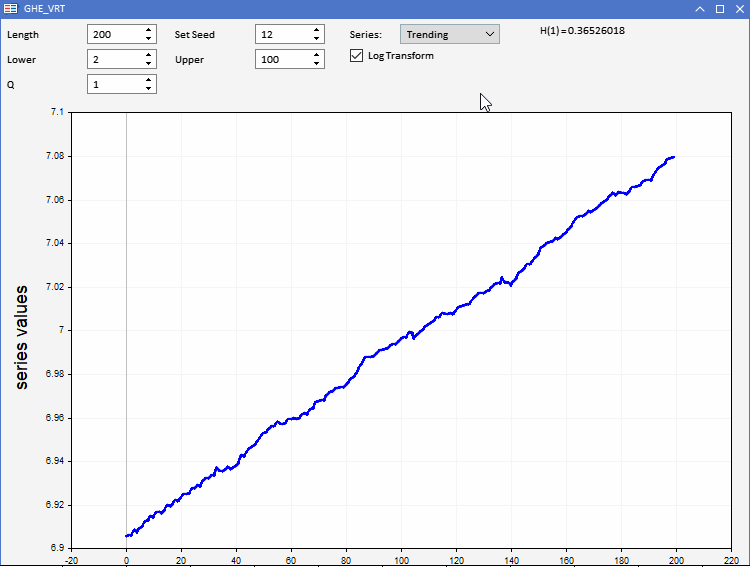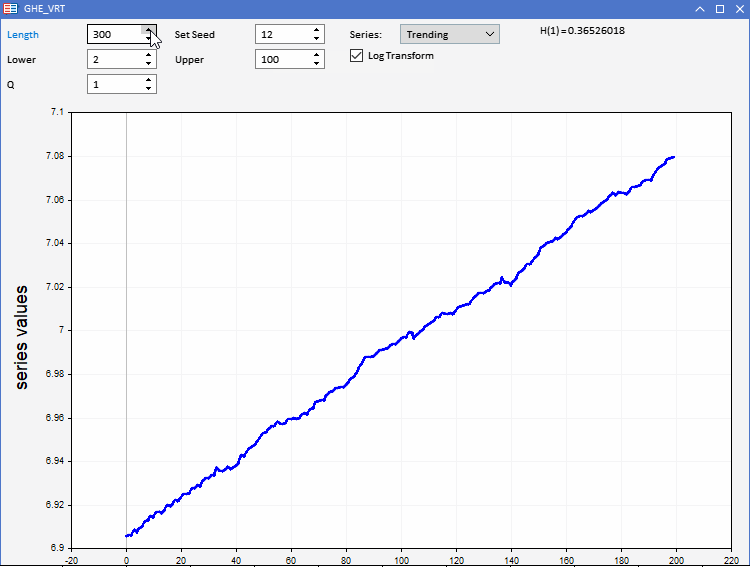
実世界での応用となると、データセットが過剰なノイズに悩まされることは誰もが知っています。GHEはサンプルサイズに敏感な推定値を出すので、結果の有意性を検証する必要があります。これは、分散比(VR)検定と呼ばれる仮説検定を実施することによっておこなうことができます。

分散比検定

分散比検定は、時系列の分散が時間間隔の長さに比例して増加するかどうかを調べることによって、時系列のランダム性を評価するために使用される統計的検定です。この検定は、検定対象の系列がランダムウォークに従うならば、ある時間間隔における系列の変化の分散は、その間隔の長さとともに線形に増加するはずだという考えに基づいています。分散の増加速度が遅い場合は、系列の変化における系列相関を示している可能性があり、系列が予測可能であることを示唆しています。分散比は、以下のようなテストです。

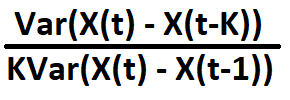
は1に等しいです。ここで、
-X()：関心のある時系列
-K：任意のラグ
-Var()：分散

検定の帰無仮説は、時系列がランダムウォークに従うというもので、したがって分散比は1に等しいはずです。分散比が1と有意に異なる場合、帰無仮説が棄却される可能性があり、時系列に何らかの予測可能性や系列相関が存在することを示唆します。

分散比検定の実装

VR検定はVRT.mqhで定義されているCVarianceRatioクラスとして実装されています。VR検定Vrt()を実施するために呼び出すことができるメソッドは2つあり、1つはベクトルを扱い、もう1つは配列を扱います。メソッドのパラメータを以下に記します。

• GHE推定値の有意性を評価するためにVR検定をどのように使用する文脈では、lagsをgen_hurst()の対応するlowerまたはupperパラメータのいずれかに設定することができます。この値を2未満に設定することはできません。 
• trendは、テストしたいランダムウォークのタイプを指定できる列挙です。TREND_CONST_ONLYとTREND_NONEの2つのオプションだけが効果を持ちます。
• debiasedは、overlapがtrueの場合にのみ適用され、debiasedバージョンのテストを使用するかどうかを示します。trueに設定すると、この関数は分散比の推定値を調整するためにバイアス補正技術を採用し、分散間の真の関係をより正確に表現することを目指します。これは主に、サンプル数の少ない系列を扱う場合に有効です。
  
• overlapは、重なっているブロックをすべて使用するかどうかを示します。falseの場合、系列の長さから1を引いた値は、lagsの正確な倍数でなければなりません。  この条件が満たされない場合、入力系列の末尾のいくつかの値は破棄されます。
• robustは、不均一分散性(true)または均一分散性(false)のどちらを考慮するかを選択します。統計分析では、不均一分散的な過程は分散が一定でないのに対し、均一分散的な系列は分散が一定です。 
  

Vrt()メソッドは、実行に成功するとtrueを返し、その後、ゲッターメソッドのいずれかを呼び出すことで、テスト結果のあらゆる側面を取得することができます。

//+------------------------------------------------------------------+
//| CVarianceRatio  class                                            |
//| Variance ratio hypthesis test for a random walk                  |
//+------------------------------------------------------------------+
class CVarianceRatio
  {
private:
   double            m_pvalue;     //pvalue
   double            m_statistic;  //test statistic
   double            m_variance;   //variance
   double            m_vr;         //variance ratio
   vector            m_critvalues; //critical values

public:
                     CVarianceRatio(void);
                    ~CVarianceRatio(void);

   bool              Vrt(const double &in_data[], ulong lags, ENUM_TREND trend = TREND_CONST_ONLY, bool debiased=true, bool robust=true, bool overlap = true);
   bool              Vrt(const vector &in_vect, ulong lags, ENUM_TREND trend = TREND_CONST_ONLY, bool debiased=true, bool robust=true, bool overlap = true);

   double            Pvalue(void) { return m_pvalue;}
   double            Statistic(void) { return m_statistic;}
   double            Variance(void) { return m_variance;}
   double            VRatio(void) { return m_vr;}
   vector            CritValues(void) { return m_critvalues;}
  };

Vrt()の内部では、overlapがfalseの場合、入力系列の長さがlagsで割り切れるかどうかを確認します。そうでない場合は、系列の最後を切り捨て、データ長に関する警告を出します。そして、更新された系列の長さに基づいてnobsを再割り当て、トレンド項であるmuを計算します。ここでは、系列の隣接する要素の差分を計算し、delta_yに保存します。delta_yを使用して分散が計算され、変数sigma2_1に保存されます。重なっていない場合は、重なっていないブロックの分散を計算します。そうでない場合は、重なっているブロックの分散を計算します。deviasedがoverlapとともに有効になっていれば、分散を調整します。ここでm_variancedはoverlapとrobustに応じて計算されます。最後に、分散比、検定統計量、p値を計算します。

//+------------------------------------------------------------------+
//| main method for computing Variance ratio test                    |
//+------------------------------------------------------------------+
bool CVarianceRatio::Vrt(const vector &in_vect,ulong lags,ENUM_TREND trend=1,bool debiased=true,bool robust=true,bool overlap=true)
  {
   ulong nobs = in_vect.Size();

   vector y = vector::Zeros(2),delta_y;

   double mu;

   ulong nq = nobs - 1;

   if(in_vect.Size()<1)
     {
      Print(__FUNCTION__, "Invalid input, no data supplied");
      return false;
     }

   if(lags<2 || lags>=in_vect.Size())
     {
      Print(__FUNCTION__," Invalid input for lags");
      return false;
     }

   if(!overlap)
     {
      if(nq % lags != 0)
        {
         ulong extra = nq%lags;
         if(!y.Init(5,slice,in_vect,0,in_vect.Size()-extra-1))
           {
            Print(__FUNCTION__," ",__LINE__);
            return false;
           }
         Print("Warning:Invalid length for input data, size is not exact multiple of lags");
        }
     }
   else
      y.Copy(in_vect);

   nobs = y.Size();

   if(trend == TREND_NONE)
      mu = 0;
   else
      mu = (y[y.Size()-1] - y[0])/double(nobs - 1);

   delta_y = difference(y);

   nq = delta_y.Size();

   vector mudiff = delta_y - mu;

   vector mudiff_sq = MathPow(mudiff,2.0);

   double sigma2_1 = mudiff_sq.Sum()/double(nq);

   double sigma2_q;

   vector delta_y_q;

   if(!overlap)
     {
      vector y1,y2;
      if(!y1.Init(3,slice,y,lags,y.Size()-1,lags) ||
         !y2.Init(3,slice,y,0,y.Size()-lags-1,lags))
        {
         Print(__FUNCTION__," ",__LINE__);
         return false;
        }

      delta_y_q = y1-y2;

      vector delta_d = delta_y_q - double(lags) * mu;

      vector delta_d_sqr = MathPow(delta_d,2.0);

      sigma2_q = delta_d_sqr.Sum()/double(nq);
     }
   else
     {
      vector y1,y2;
      if(!y1.Init(3,slice,y,lags,y.Size()-1) ||
         !y2.Init(3,slice,y,0,y.Size()-lags-1))
        {
         Print(__FUNCTION__," ",__LINE__);
         return false;
        }

      delta_y_q = y1-y2;

      vector delta_d = delta_y_q - double(lags) * mu;

      vector delta_d_sqr = MathPow(delta_d,2.0);

      sigma2_q = delta_d_sqr.Sum()/double(nq*lags);
     }


   if(debiased && overlap)
     {
      sigma2_1 *= double(nq)/double(nq-1);
      double mm = (1.0-(double(lags)/double(nq)));
      double m = double(lags*(nq - lags+1));// * (1.0-double(lags/nq));
      sigma2_q *= double(nq*lags)/(m*mm);
     }

   if(!overlap)
      m_variance = 2.0 * (lags-1);
   else
      if(!robust)
         m_variance = double((2 * (2 * lags - 1) * (lags - 1)) / (3 * lags));
      else
        {
         vector z2, o, p;
         z2=MathPow((delta_y-mu),2.0);
         double scale = pow(z2.Sum(),2.0);
         double theta = 0;
         double delta;
         for(ulong k = 1; k<lags; k++)
           {
            if(!o.Init(3,slice,z2,k,z2.Size()-1) ||
               !p.Init(3,slice,z2,0,z2.Size()-k-1))
              {
               Print(__FUNCTION__," ",__LINE__);
               return false;
              }
            o*=double(nq);
            p/=scale;
            delta = o.Dot(p);
            theta+=4.0*pow((1.0-double(k)/double(lags)),2.0)*delta;
           }
         m_variance = theta;
        }
   m_vr = sigma2_q/sigma2_1;

   m_statistic = sqrt(nq) * (m_vr - 1)/sqrt(m_variance);

   double abs_stat = MathAbs(m_statistic);

   m_pvalue = 2 - 2*CNormalDistr::NormalCDF(abs_stat);

   return true;
  }

クラスをテストするために、gen_hurst()関数のデモに使用したアプリケーションGHE.ex5を修正します。GHEは、分析が集中するラグ幅によって定義されるからです。VRTを較正することで、同じラグ幅でGHEの結果の有意性を検証することができます。最小と最大のラグでVRTを実行すれば、十分な情報が得られるはずです。GHE.ex5では、lowerラグでの分散比がupperラグでの分散比より先に表示されます。
有意に乖離する分散比は、データの予測可能性を示していることを忘れないでください。1に近い分散比は、この系列がランダムウォークからそれほど離れていないことを示唆します。アプリケーションを操作し、パラメータの様々な組み合わせをテストすることで、GHEとVRTの両方の結果がサンプルサイズに影響されることに気づきます。

系列の長さが1000未満の場合は、どちらも予期せぬ結果を出すことがありました。

また、生の値と対数変換した値でテストを比較した場合、GHEの結果が大きく異なる場合がありました。

VRTとGHEを理解したところで、これらを平均回帰戦略に適用してみましょう。ある価格系列が平均回帰していることが分かっている場合、平均からの現在の乖離に基づいて価格がどうなるかを大まかに推定することができます。私たちの戦略の基本は、一定期間における価格系列の特徴を分析することにあります。この分析を使用して、価格が標準から大きく乖離した後にスナップバックする可能性のあるポイントを推定するモデルを構築します。エントリシグナルとエグジットシグナルを生成するために、この乖離を測定し定量化する方法が必要です。

Z得点

Z得点は、価格のその平均からの標準偏差を測定します。価格を正規化することで、z得点はゼロ付近で推移します。z得点のプロットがどのように見えるか、指標として実装して見てみましょう。完全なコードを以下に示します。

//+------------------------------------------------------------------+
//|                                                       Zscore.mq5 |
//|                                  Copyright 2023, MetaQuotes Ltd. |
//|                                             https://www.mql5.com |
//+------------------------------------------------------------------+
#property copyright "Copyright 2023, MetaQuotes Ltd."
#property link      "https://www.mql5.com"
#property version   "1.00"
#include<VectorMatrixTools.mqh>
#property indicator_separate_window
#property indicator_buffers 1
#property indicator_plots   1
//--- plot Zscore
#property indicator_label1  "Zscore"
#property indicator_type1   DRAW_LINE
#property indicator_color1  clrBlue
#property indicator_style1  STYLE_SOLID
#property indicator_width1  1
//--- input parameters
input int      z_period = 10;
//--- indicator buffers
double         ZscoreBuffer[];
vector vct;
//+------------------------------------------------------------------+
//| Custom indicator initialization function                         |
//+------------------------------------------------------------------+
int OnInit()
  {
//--- indicator buffers mapping
   SetIndexBuffer(0,ZscoreBuffer,INDICATOR_DATA);
//----
   PlotIndexSetDouble(0,PLOT_EMPTY_VALUE,0);
//---
   PlotIndexSetInteger(0,PLOT_DRAW_BEGIN,z_period-1);
//---
   return(INIT_SUCCEEDED);
  }
//+------------------------------------------------------------------+
//| Custom indicator iteration function                              |
//+------------------------------------------------------------------+
int OnCalculate(const int rates_total,
                const int prev_calculated,
                const datetime &time[],
                const double &open[],
                const double &high[],
                const double &low[],
                const double &close[],
                const long &tick_volume[],
                const long &volume[],
                const int &spread[])
  {
//---
   if(rates_total<z_period)
     {
      Print("Insufficient history");
      return -1;
     }
//---
   int limit;
   if(prev_calculated<=0)
      limit = z_period - 1;
   else
      limit = prev_calculated - 1;
//---
   for(int i = limit; i<rates_total; i++)
     {
      vct.Init(ulong(z_period),assign,close,ulong(i-(z_period-1)),i,1);
      if(vct.Size()==ulong(z_period))
         ZscoreBuffer[i] = (close[i] - vct.Mean())/vct.Std();
      else
         ZscoreBuffer[i]=0.0;
     }

//--- return value of prev_calculated for next call
   return(rates_total);
  }
//+------------------------------------------------------------------+

このプロットから、指標値がより正規分布していることがわかります。

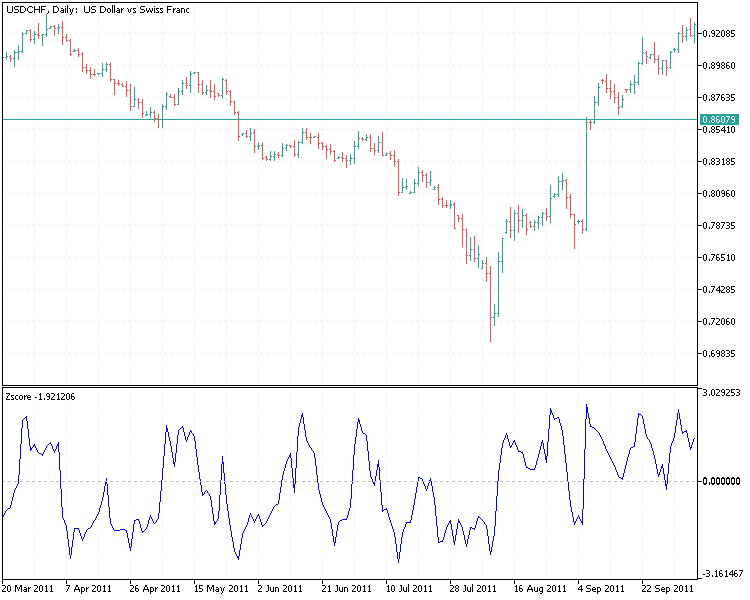
z得点が0から大きく乖離し、履歴的に導き出された閾値を超えたときに売買シグナルが発生します。z得点が極端にマイナスであればロング、その逆であればショートのタイミングです。つまり、売買シグナルには2つの閾値が必要です。負（買い）と正（売り）です。エントリが完了したら、次は存在の確認です。1つの選択肢は、特定のポジション（ロングまたはショート）にいるときに機能する、別の閾値のセットを導き出すことです。ショートの場合、z得点が0に戻ったらポジションを閉じます。同様に、z得点が買いの極端なレベルから0に向かって上昇したら、ロングポジションを決済します。

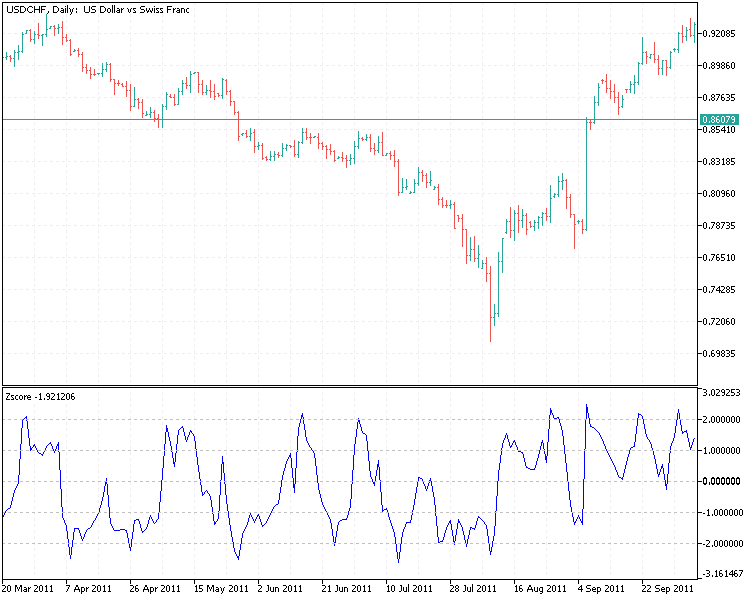
これで指標Zscore.ex5を使用したエントリとエグジットが定義できました。これをEAにまとめてみましょう。コードを以下に示します。

//+------------------------------------------------------------------+
//|                                                MeanReversion.mq5 |
//|                                  Copyright 2024, MetaQuotes Ltd. |
//|                                             https://www.mql5.com |
//+------------------------------------------------------------------+
#property copyright "Copyright 2024, MetaQuotes Ltd."
#property link      "https://www.mql5.com"
#property version   "1.00"
#resource "\\Indicators\\Zscore.ex5"
#include<ExpertTools.mqh>
//---Input parameters
input int  PeriodLength  = 10;
input double LotsSize = 0.01;
input double  LongOpenLevel = -2.0;
input double  ShortOpenLevel = 2.0;
input double  LongCloseLevel = -0.5;
input double  ShortCloseLevel = 0.5;
input ulong  SlippagePoints = 10;
input ulong  MagicNumber    = 123456;
//---
 int indi_handle;
//---
 double zscore[2];
//+------------------------------------------------------------------+
//| Expert initialization function                                   |
//+------------------------------------------------------------------+
int OnInit()
  {
//---
   if(PeriodLength<2)
    {
     Print("Invalid parameter value for PeriodLength");
     return INIT_FAILED;
    }
//---
   if(!InitializeIndicator())
    return INIT_FAILED;
//---        
   return(INIT_SUCCEEDED);
  }
//+------------------------------------------------------------------+
//| Expert deinitialization function                                 |
//+------------------------------------------------------------------+
void OnDeinit(const int reason)
  {
//---
   
  }
//+------------------------------------------------------------------+
//| Expert tick function                                             |
//+------------------------------------------------------------------+
void OnTick()
  {
//---    
      int signal = GetSignal();
//---      
      if(SumMarketOrders(MagicNumber,_Symbol,-1))
       {
        if(signal==0)
         CloseAll(MagicNumber,_Symbol,-1);
        return; 
       }
      else
        OpenPosition(signal);
//---   
  }
//+------------------------------------------------------------------+
//+------------------------------------------------------------------+
//| Initialize indicator                                             |
//+------------------------------------------------------------------+
bool InitializeIndicator(void)
{
 indi_handle = INVALID_HANDLE;
//---
 int try = 10;
//---
 while(indi_handle == INVALID_HANDLE && try>0)
  {
   indi_handle = (indi_handle==INVALID_HANDLE)?iCustom(NULL,PERIOD_CURRENT,"::Indicators\\Zscore.ex5",PeriodLength):indi_handle;
   try--;
  }
//---
 if(try<0)
  {
   Print("Failed to initialize Zscore indicator ");
   return false;
  }
//---
 return true;
}
//+------------------------------------------------------------------+
//|Get the signal to trade or close                                  |
//+------------------------------------------------------------------+
int GetSignal(const int sig_shift=1)
{
//---
 if( CopyBuffer(indi_handle,int(0),sig_shift,int(2),zscore)<2)
   {
    Print(__FUNCTION__," Error copying from indicator buffers: ", GetLastError());
    return INT_MIN;
   } 
//---   
 if(zscore[1]<LongOpenLevel && zscore[0]>LongOpenLevel)
     return (1);
//---   
 if(zscore[1]>ShortOpenLevel && zscore[0]<ShortOpenLevel)
     return (-1);          
//---   
 if((zscore[1]>LongCloseLevel && zscore[0]<LongCloseLevel) ||
    (zscore[1]<ShortCloseLevel && zscore[0]>ShortCloseLevel))
     return (0);
//---
 return INT_MIN;
//--- 
}
//+------------------------------------------------------------------+
//|  Go long or short                                                |
//+------------------------------------------------------------------+
bool OpenPosition(const int sig)
{

 long pid;
//--- 
 if(LastOrderOpenTime(pid,NULL,MagicNumber)>=iTime(NULL,0,0))
   return false;
//---   
 if(sig==1)
   return SendOrder(_Symbol,0,ORDER_TYPE_BUY,LotsSize,SlippagePoints,0,0,NULL,MagicNumber);
 else
  if(sig==-1)
    return SendOrder(_Symbol,0,ORDER_TYPE_SELL,LotsSize,SlippagePoints,0,0,NULL,MagicNumber); 
//--- 
  return false;                   
}

非常に基本的なもので、損切りや利食いのレベルは定義されていません。ここでの目標は、まずEAを最適化して、Zscore指標の最適な期間と、最適なエントリとエグジットの閾値を得ることです。数年分のデータで最適化し、サンプルなしで最適なパラメータをテストする予定ですが、その前に少し回り道をして、もう1つ興味深いツールを紹介しましょう。『Algorithmic Trading:Winning Strategies And Their Rationale』で、著者のErnest Chanは、「平均回帰の半減期」と呼ばれる、平均回帰戦略を開発するための興味深いツールについて述べています。

平均回帰の半減期

平均回帰の半減期は、平均からの乖離が半分になるまでの時間を表します。資産価格の文脈では、平均回帰の半減期は、価格が過去の平均から乖離した後、どの程度の速さでその平均に回帰する傾向を示します。これは、平均回帰プロセスの発生速度を示す指標です。数学的には、半減期は式によって平均回帰の速さと関連づけることができます。

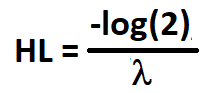
ここで、
-HL：半減期
-log()：自然対数
-λ：平均回帰の速度

実際的には、半減期が短いほど平均回帰が早く、半減期が長いほど平均回帰が遅いことを意味します。半減期の概念は、平均回帰取引戦略のパラメータを微調整するために使用することができ、過去のデータと観測された平均回帰のスピードに基づいて、エントリポイントとエグジットポイントを最適化するのに役立ちます。平均回帰の半減期は、平均回帰過程の数学的表現から導かれ、一般的には オルンシュタイン＝ウーレンベック過程 としてモデル化されます。オルンシュタイン＝ウーレンベック過程 過程は、平均回帰行動の連続時間バージョンを記述する確率微分方程式です。

Chanによれば、平均回帰の半減期を計算することで、平均回帰が適切な戦略かどうかを判断することができます。まず、λが正であれば、平均回帰はまったく適用されるべきではありません。λが負でゼロに非常に近い場合でも、平均回帰を適用することは、半減期が長くなることを示すため、推奨されません。平均回帰は、半減期がそれなりに短い場合にのみ採用すべきです。

平均回帰の半減期はMeanReversionUtilities.mqhで関数として実装されています。これは、物価の系列を、その後の物価の差の系列に対して回帰することによって計算されます。λは回帰モデルのβパラメータに等しく、半減期は-log(2)をλで割ることによって計算されます。

//+------------------------------------------------------------------+
//|Calculate Half life of Mean reversion                             |
//+------------------------------------------------------------------+
double mean_reversion_half_life(vector &data, double &lambda)
  {
//---
   vector yy,zz;
   matrix xx;
//---
   OLS ols_reg;
//---
   yy.Init(data.Size()-1,slice,data,1,data.Size()-1,1);
//---
   zz.Init(data.Size()-1,slice,data,0,data.Size()-2,1);
//---
   if(!xx.Init(zz.Size(),2) || !xx.Col(zz,0) || !xx.Col(vector::Ones(zz.Size()),1) || !ols_reg.Fit(yy-zz,xx))
     {
      Print(__FUNCTION__," Error in calculating half life of mean reversion ", GetLastError());
      return 0;
     }
//---
   vector params = ols_reg.ModelParameters();
   lambda = params[0];
//---
   return (-log(2)/lambda);
//---
  }

GHEおよびVRTと併用して、いくつかのFX銘柄について、選択した数年間の価格サンプルをテストします。テスト結果を使用して、先ほど構築したEAを適用する適切な銘柄を選択します。同じ年数で最適化され、最終的にはサンプルなしでテストされます。  以下のスクリプトは、GHE、VRT、半減期を用いてテストされる候補銘柄のリストを受毛取ります。

//+------------------------------------------------------------------+
//|                                                 SymbolTester.mq5 |
//|                                  Copyright 2024, MetaQuotes Ltd. |
//|                                             https://www.mql5.com |
//+------------------------------------------------------------------+
#property copyright "Copyright 2024, MetaQuotes Ltd."
#property link      "https://www.mql5.com"
#property version   "1.00"
#property script_show_inputs
#include<MeanReversionUtilities.mqh>
#include<GHE.mqh>
#include<VRT.mqh>

//--- input parameters
input string   Symbols = "EURUSD,GBPUSD,USDCHF,USDJPY";//Comma separated list of symbols to test
input ENUM_TIMEFRAMES TimeFrame = PERIOD_D1;
input datetime StartDate=D'2020.01.02 00:00:01';
input datetime StopDate=D'2015.01.18 00:00:01';
input int Q_parameter = 2;
input int MinimumLag = 2;
input int MaximumLag = 100;
input bool ApplyLogTransformation = true;
//---
CVarianceRatio vrt;
double ghe,hl,lb,vlower,vupper;
double prices[];
//+------------------------------------------------------------------+
//| Script program start function                                    |
//+------------------------------------------------------------------+
void OnStart()
  {
//---Check Size input value
   if(StartDate<=StopDate)
     {
      Print("Invalid input for StartDater or StopDate");
      return;
     }
//---array for symbols
   string symbols[];
//---process list of symbols from user input
   int num_symbols = StringSplit(Symbols,StringGetCharacter(",",0),symbols);
//---incase list contains ending comma
   if(symbols[num_symbols-1]=="")
      num_symbols--;
//---in case there are less than two symbols specified
   if(num_symbols<1)
     {
      Print("Invalid input. Please list at least one symbol");
      return;
     }
//---loop through all paired combinations from list
   for(uint i=0; i<symbols.Size(); i++)
     {

      //--- get prices for the pair of symbols
      if(CopyClose(symbols[i],TimeFrame,StartDate,StopDate,prices)<1)
        {
         Print("Failed to copy close prices ", ::GetLastError());
         return;
        }
      //---
      if(ApplyLogTransformation && !MathLog(prices))
        {
         Print("Mathlog error ", GetLastError());
         return;
        }
      //---
      if(!vrt.Vrt(prices,MinimumLag))
         return;
      //---
      vlower = vrt.VRatio();
      //---
      if(!vrt.Vrt(prices,MaximumLag))
         return;
      //---
      vupper = vrt.VRatio();
      //---
      ghe = general_hurst(prices,Q_parameter,MinimumLag,MaximumLag);
      //---
      hl = mean_reversion_half_life(prices,lb);
      //--- output the results
      Print(symbols[i], " GHE:  ", DoubleToString(ghe)," | Vrt: ",DoubleToString(vlower)," ** ",DoubleToString(vupper)," | HalfLife ",DoubleToString(hl)," | Lambda: ",DoubleToString(lb));
     }
  }
//+------------------------------------------------------------------+

スクリプトを実行すると、次のような結果が得られます。

19:31:03.143    SymbolTester (USDCHF,D1)        EURUSD GHE:  0.44755644 | Vrt: 0.97454284 ** 0.61945905 | HalfLife 85.60548208 | Lambda: -0.00809700
19:31:03.326    SymbolTester (USDCHF,D1)        GBPUSD GHE:  0.46304381 | Vrt: 1.01218672 ** 0.82086185 | HalfLife 201.38001205 | Lambda: -0.00344199
19:31:03.509    SymbolTester (USDCHF,D1)        USDCHF GHE:  0.42689382 | Vrt: 1.02233286 ** 0.47888803 | HalfLife 28.90550869 | Lambda: -0.02397976
19:31:03.694    SymbolTester (USDCHF,D1)        USDJPY GHE:  0.49198795 | Vrt: 0.99875744 ** 1.06103587 | HalfLife 132.66433924 | Lambda: -0.00522482

USDCHFの銘柄は、選択した日付期間において最も有望なテスト結果を示しています。そこで、USDCHFを取引するEAのパラメータを最適化します。興味深いのは、最適化のためにZ得点の期間を選択し、それが計算された半減期と異なるかどうかを確認することでしょう。

ここでは、最適なZ得点の期間を見ることができ、それは平均回帰の計算された半減期に非常に近いです。これは心強いです。もちろん、半減期の有用性を判断するには、より広範な検査が必要でしょう。

最後に、最適なパラメータを用いてEAをサンプル外でテストします。

結果は思わしくありません。おそらく、市場が絶えず流動的であるため、EAが最適化された期間に観察された特性がもはや当てはまらないためでしょう。根本的な市場ダイナミクスの変化を考慮した、よりダイナミックな参入と撤退の閾値が必要です。

ここで学んだことは、さらなる発展のための基礎とすることができます。ペア取引戦略を実行するために、ここで説明したツールを応用するのも1つの方法です。Z得点指標は単一の価格系列に基づく代わりに、2つの共和分または相関のある商品のスプレッドに基づくことができます。

結論

この記事では、MQL5における一般化ハースト指数の実装を示し、価格系列の特性を決定するためにそれをどのように使用できるかを示しました。  また、分散比検定の適用や平均回帰の半減期についても調べました。  以下の表は、記事に添付されたすべてのファイルの説明です。

ファイル	詳細
Mql5\include\ExpertTools.mqh	MeanReversion EAで使用される取引操作をおこなうための関数定義を含む
Mql5\include\GHE.mqh	一般化ハースト指数を実装する関数の定義を含む
Mql5\include\OLS.mqh	通常の最小二乗回帰を実装するOLSクラスの定義を含む
Mql5\include\VRT.mqh	分散比検定をカプセル化するCVarianceRatioクラスの定義を含む
Mql5\include\VectorMatrixTools.mqh	一般的なベクトルや行列を素早く初期化するためのさまざまな関数定義を含む
Mql5\include\TestUtilities.mqh	OLSクラス定義で使用される多くの宣言を含む
Mql5\include\MeanReversionUtilities.mqh	様々な関数定義を含む（平均回帰の半減期の実装を含む）
Mql5\Indicators\Zscore.mq5	MeanReversion EAで使用される指標
Mql5\scripts\SymbolTester.mq5	銘柄の平均回帰テストに使用できるスクリプト
Mql5\Experts\GHE.ex5	GHEとVRTツールの探求と実験に使用できるEAアプリ
Mql5\scripts\MeanReversion.mq5	EAによるシンプルな平均回帰戦略の実演