Aplicamos el coeficiente generalizado de Hurst y la prueba del coeficiente de varianza en MQL5

Introducción

En el artículo "Cálculo del coeficiente de Hurst" se analiza el concepto de análisis fractal y su aplicación a los mercados financieros. En él, el autor describe el método del alcance normalizado (rescaled range method, R/S) para calcular el coeficiente de Hurst. En este artículo, adoptaremos un enfoque diferente y mostraremos la aplicación del coeficiente generalizado de Hurst (GHE) para la clasificación de series. Nos centramos en usar el GHE para identificar los símbolos de divisas que tienden a regresar a su valor, con la esperanza de explotar este comportamiento.

En primer lugar, analizaremos brevemente los fundamentos del GHE y en qué se diferencia del coeficiente de Hurst original. Asimismo, describiremos una prueba estadística que puede utilizarse para validar los resultados del análisis de GHE, denominada prueba del coeficiente de varianza (VRT). A continuación, pasaremos a la aplicación del GHE para identificar posibles símbolos de divisas para las operaciones de reversión a la media. También presentaremos un indicador para generar señales de entrada y salida y lo probaremos como parte del asesor.

Coeficiente generalizado de Hurst

El coeficiente de Hurst mide las propiedades de escala de las series temporales. Las propiedades de escala son características fundamentales que describen cómo se comporta un sistema al cambiar su tamaño o su escala temporal. En el contexto de los datos de series temporales, las propiedades de escalado permiten comprender la relación entre las distintas escalas temporales y los patrones presentes en los datos. Para una serie estacionaria, los cambios en los valores posteriores a lo largo del tiempo serán más graduales en comparación con lo que ocurriría con un paseo aleatorio geométrico. Para cuantificar matemáticamente este comportamiento, analizaremos la tasa de difusión en la serie. La varianza servirá como índice que expresa el grado de desviación de otros valores con respecto al primero de una serie.

En la fórmula anterior, K representa el retraso arbitrario al que se realiza el análisis. Para hacernos una mejor idea de la naturaleza de la serie, deberemos estimar también la varianza en otros retrasos. Así, podremos asignar a K cualquier valor entero positivo inferior a la longitud de la serie. El retraso máximo aplicado será discrecional. Será importante tener esto en cuenta. De este modo, el coeficiente de Hurst estará relacionado con el comportamiento escalar de la varianza a diferentes retrasos. Al utilizar la ley de potencia, el coeficiente se definirá del siguiente modo:

El GHE es una generalización del original, en la que el número 2 sustituye a la variable q. Así pues, las fórmulas anteriores adoptarán la siguiente forma:

y

El GHE amplía el coeficiente de Hurst original analizando cómo varían diversas características estadísticas de los cambios entre los puntos sucesivos de una serie temporal en función de los órdenes de momentos (orders of moments). En términos matemáticos, los momentos son medidas estadísticas que describen la forma y las características de una distribución. Un momento de orden q-ésimo es un tipo especial de momento, donde q será el parámetro que define el orden. El GHE hace hincapié en las diferentes características de las series temporales para cada valor q. En particular, cuando q=1, el resultado mostrará las propiedades de escala de la desviación absoluta. Así, q=2 será el más importante cuando se investiga la dependencia a grandes distancias.

Implementación de GHE en MQL5

En esta sección, analizaremos la implementación de GHE en MQL5. A continuación, lo pondremos a prueba analizando muestras aleatorias de series temporales generadas artificialmente. Nuestra implementación estará contenida en el archivo GHE.mqh. El archivo comienza incluyendo VectorMatrixTools.mqh, que contiene las definiciones de varias funciones para inicializar tipos comunes de vectores y matrices. Más abajo se muestra el contenido de este archivo.

//+------------------------------------------------------------------+
//|                                            VectorMatrixTools.mqh |
//|                                  Copyright 2023, MetaQuotes Ltd. |
//|                                             https://www.mql5.com |
//+------------------------------------------------------------------+
#property copyright "Copyright 2023, MetaQuotes Ltd."
#property link      "https://www.mql5.com"
//+------------------------------------------------------------------+
//|Vector arange initialization                                      |
//+------------------------------------------------------------------+
template<typename T>
void arange(vector<T> &vec,T value=0.0,T step=1.0)
  {
   for(ulong i=0; i<vec.Size(); i++,value+=step)
      vec[i]=value;
  }
//+------------------------------------------------------------------+
//| Vector sliced initialization                                     |
//+------------------------------------------------------------------+
template<typename T>
void slice(vector<T> &vec,const vector<T> &toCopyfrom,ulong start=0,ulong stop=ULONG_MAX, ulong step=1)
  {
   start = (start>=toCopyfrom.Size())?toCopyfrom.Size()-1:start;
   stop  = (stop>=toCopyfrom.Size())?toCopyfrom.Size()-1:stop;
   step  = (step==0)?1:step;

   ulong numerator = (stop>=start)?stop-start:start-stop;
   ulong size = (numerator/step)+1;
   if(!vec.Resize(size))
     {
      Print(__FUNCTION__ " invalid slicing parameters for vector initialization");
      return;
     }

   if(stop>start)
     {
      for(ulong i =start, k = 0; i<toCopyfrom.Size() && k<vec.Size() && i<=stop; i+=step, k++)
         vec[k] = toCopyfrom[i];
     }
   else
     {
      for(long i = long(start), k = 0; i>-1 && k<long(vec.Size()) && i>=long(stop); i-=long(step), k++)
         vec[k] = toCopyfrom[i];
     }
  }
//+------------------------------------------------------------------+
//| Vector sliced initialization  using array                        |
//+------------------------------------------------------------------+
template<typename T>
void assign(vector<T> &vec,const T &toCopyfrom[],ulong start=0,ulong stop=ULONG_MAX, ulong step=1)
  {
   start = (start>=toCopyfrom.Size())?toCopyfrom.Size()-1:start;
   stop  = (stop>=toCopyfrom.Size())?toCopyfrom.Size()-1:stop;
   step  = (step==0)?1:step;

   ulong numerator = (stop>=start)?stop-start:start-stop;
   ulong size = (numerator/step)+1;

   if(size != vec.Size() &&  !vec.Resize(size))
     {
      Print(__FUNCTION__ " invalid slicing parameters for vector initialization");
      return;
     }

   if(stop>start)
     {
      for(ulong i =start, k = 0; i<ulong(toCopyfrom.Size()) && k<vec.Size() && i<=stop; i+=step, k++)
         vec[k] = toCopyfrom[i];
     }
   else
     {
      for(long i = long(start), k = 0; i>-1 && k<long(vec.Size()) && i>=long(stop); i-=long(step), k++)
         vec[k] = toCopyfrom[i];
     }
  }
//+------------------------------------------------------------------+
//| Matrix initialization                                            |
//+------------------------------------------------------------------+
template<typename T>
void rangetrend(matrix<T> &mat,T value=0.0,T step=1.0)
  {
   ulong r = mat.Rows();

   vector col1(r,arange,value,step);

   vector col2 = vector::Ones(r);

   if(!mat.Resize(r,2) || !mat.Col(col1,0) || !mat.Col(col2,1))
     {
      Print(__FUNCTION__ " matrix initialization error: ", GetLastError());
      return;
     }

  }
//+-------------------------------------------------------------------------------------+
//| ols design Matrix initialization with constant and first column from specified array|
//+-------------------------------------------------------------------------------------+
template<typename T>
void olsdmatrix(matrix<T> &mat,const T &toCopyfrom[],ulong start=0,ulong stop=ULONG_MAX, ulong step=1)
  {
   vector col0(1,assign,toCopyfrom,start,stop,step);

   ulong r = col0.Size();

   if(!r)
     {
      Print(__FUNCTION__," failed to initialize first column ");
      return;
     }

   vector col1 = vector::Ones(r);

   if(!mat.Resize(r,2) || !mat.Col(col0,0) || !mat.Col(col1,1))
     {
      Print(__FUNCTION__ " matrix initialization error: ", GetLastError());
      return;
     }

  }
//+------------------------------------------------------------------+
//|vector to array                                                   |
//+------------------------------------------------------------------+
bool vecToArray(const vector &in, double &out[])
  {
//---
   if(in.Size()<1)
     {
      Print(__FUNCTION__," Empty vector");
      return false;
     }
//---
   if(ulong(out.Size())!=in.Size() && ArrayResize(out,int(in.Size()))!=int(in.Size()))
     {
      Print(__FUNCTION__," resize error ", GetLastError());
      return false;
     }
//---
   for(uint i = 0; i<out.Size(); i++)
      out[i]=in[i];
//---
   return true;
//---
  }
//+------------------------------------------------------------------+
//| difference a vector                                               |
//+------------------------------------------------------------------+
vector difference(const vector &in)
  {
//---
   if(in.Size()<1)
     {
      Print(__FUNCTION__," Empty vector");
      return vector::Zeros(1);
     }
//---
   vector yy,zz;
//---
   yy.Init(in.Size()-1,slice,in,1,in.Size()-1,1);
//---
   zz.Init(in.Size()-1,slice,in,0,in.Size()-2,1);
//---
   return yy-zz;
  }
//+------------------------------------------------------------------+

 GHE.mqh contiene la definición de gen_hurst() y su sobrecarga. Una función ofrecerá los datos a analizar en un vector, mientras que la otra los esperará en un array. La función también aceptará el entero q y los parámetros opcionales enteros lower y upper con valores por defecto. Se trata de la misma "q" mencionada en la descripción del GHE en el apartado anterior. Los dos últimos parámetros son opcionales, lower y upper definirán conjuntamente el intervalo de retrasos al que se realizará el análisis, similar al intervalo de valores de K en las fórmulas anteriores.  

//+--------------------------------------------------------------------------+
//|overloaded gen_hurst() function that works with series contained in vector|
//+--------------------------------------------------------------------------+
double general_hurst(vector &data, int q, int lower=0,int upper=0)
  {
   double series[];

   if(!vecToArray(data,series))
      return EMPTY_VALUE;
   else
      return general_hurst(series,q,lower,upper);
  }

Si se produce un error, la función retornará el equivalente de la constante EMPTY_VALUE incorporada y mostrará un mensaje de cadena útil en la pestaña Expertos. Dentro de gen_hurst(), el procedimiento comenzará comprobando los argumentos transmitidos. Deberemos garantizar que cumplen las siguientes condiciones:

• q no puede ser inferior a 1.
• lower no puede ser inferior a 2, ni mayor o igual que upper.
• El argumento superior no podrá ser superior a la mitad del tamaño de la serie de datos analizada. Si alguna de estas condiciones no se cumple, la función informará inmediatamente sobre un error.

if(data.Size()<100)
     {
      Print("data array is of insufficient length");
      return EMPTY_VALUE;
     }

   if(lower>=upper || lower<2 ||  upper>int(floor(0.5*data.Size())))
     {
      Print("Invalid input for lower and/or upper");
      return EMPTY_VALUE;
     }

   if(q<=0)
     {
      Print("Invalid input for q");
      return EMPTY_VALUE;
     }

   uint len = data.Size();

   int k =0;

   matrix H,mcord,lmcord;
   vector n_vector,dv,vv,Y,ddVd,VVVd,XP,XY,PddVd,PVVVd,Px_vector,Sqx,pt;
   double dv_array[],vv_array[],mx,SSxx,my,SSxy,cc1,cc2,N;

   if(!H.Resize(ulong(upper-lower),1))
     {
      Print(__LINE__," ",__FUNCTION__," ",GetLastError());
      return EMPTY_VALUE;
     }

   for(int i=lower; i<upper; i++)
     {
      vector x_vector(ulong(i),arange,1.0,1.0);

      if(!mcord.Resize(ulong(i),1))
        {
         Print(__LINE__," ",__FUNCTION__," ",GetLastError());
         return EMPTY_VALUE;
        }

      mcord.Fill(0.0);

El funcionamiento interno de la función comenzará con un ciclo for de lower a upper. Para cada i, se creará un vector x_vector con los elementos de i utilizando la función arange. A continuación, se redimensionará la matriz mcord para que tenga filas i y una columna.

 for(int j=1; j<i+1; j++)
        {
         if(!diff_array(j,data,dv,Y))
            return EMPTY_VALUE;

El ciclo interno comenzará utilizando la función auxiliar diff_array() para calcular las diferencias en el array de datos y almacenarlas en los vectores dv e Y.

 N = double(Y.Size());

         vector X(ulong(N),arange,1.0,1.0);

         mx = X.Sum()/N;

         XP = MathPow(X,2.0);

         SSxx = XP.Sum() - N*pow(mx,2.0);

         my = Y.Sum()/N;

         XY = X*Y;

         SSxy = XY.Sum() - N*mx*my;

         cc1 = SSxy/SSxx;

         cc2 = my - cc1*mx;

         ddVd = dv - cc1;

         VVVd = Y - cc1*X - cc2;

         PddVd = MathAbs(ddVd);

         PddVd = pow(PddVd,q);

         PVVVd = MathAbs(VVVd);

         PVVVd = pow(PVVVd,q);

         mcord[j-1][0] = PddVd.Mean()/PVVVd.Mean();
        }

Aquí se calculará la varianza con un determinado retraso. Los resultados se almacenarán en la matriz mcord.

 Px_vector = MathLog10(x_vector);

      mx = Px_vector.Mean();

      Sqx = MathPow(Px_vector,2.0);

      SSxx = Sqx.Sum() - i*pow(mx,2.0);

      lmcord = log10(mcord);

      my = lmcord.Mean();

      pt = Px_vector*lmcord.Col(0);

      SSxy = pt.Sum() - i*mx*my;

      H[k][0]= SSxy/SSxx;

      k++;

Más allá del ciclo interno, el último paso del ciclo externo actualizará los valores principales de la matriz H. Por último, la función retornará el valor medio de la matriz H dividido por q. Por último, la función devolverá el valor medio de la matriz H dividido por q.

 return H.Mean()/double(q);

Para probar nuestra función GHE, hemos preparado una aplicación GHE.ex5, implementada como asesor. Esto nos permitirá visualizar series aleatorias con características predefinidas y observar cómo funciona el GHE. La interactividad total nos permitirá ajustar todos los parámetros del GHE, así como la longitud de la serie dentro de ciertos límites. Una característica interesante es la posibilidad de registrar la transformación de las filas antes de aplicar GHE para ver si existe algún beneficio al preprocesar los datos de esta forma.

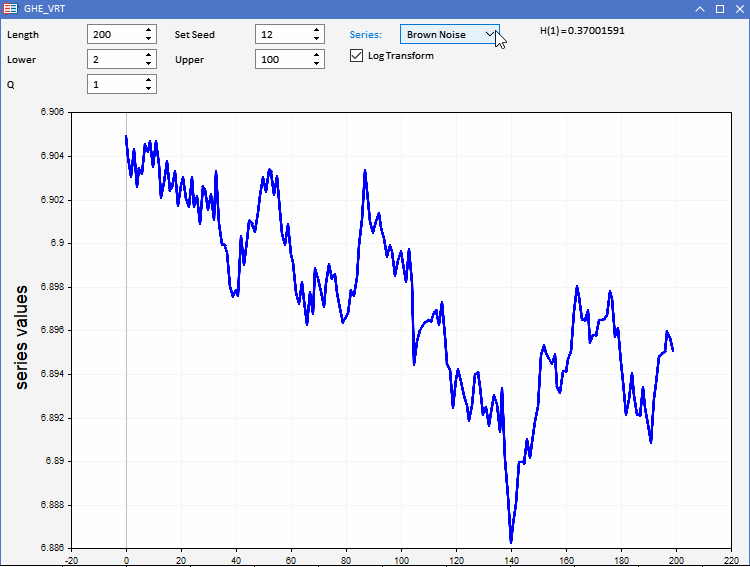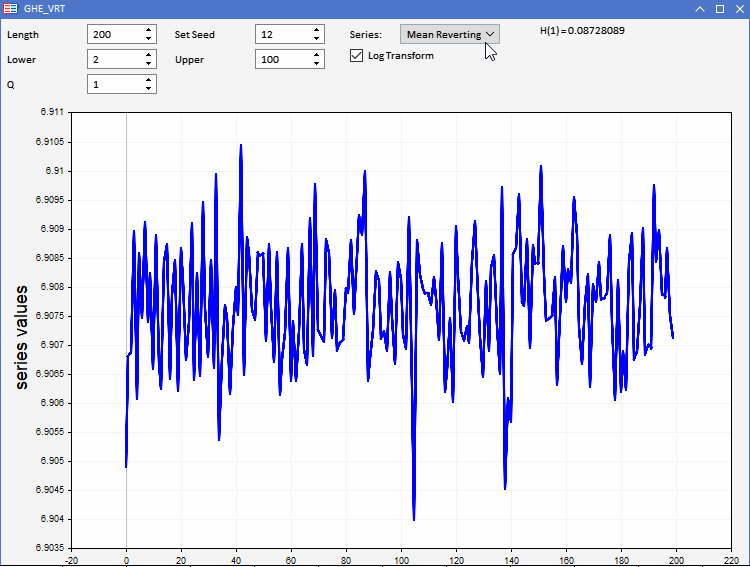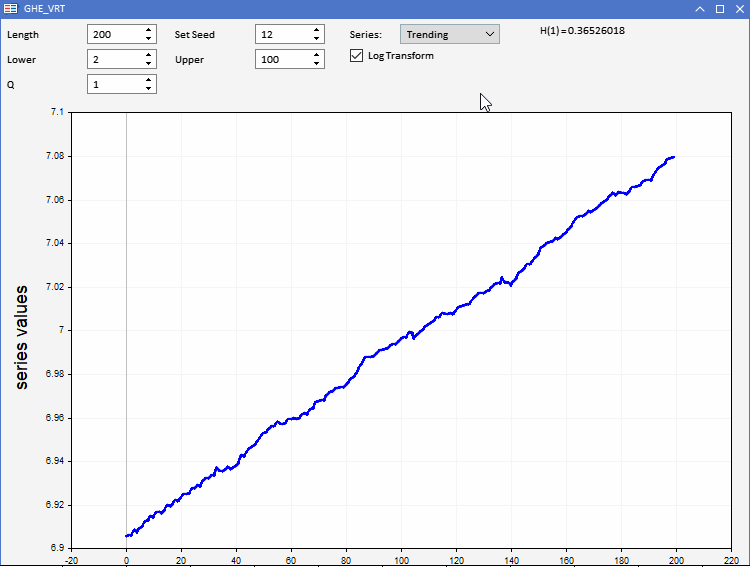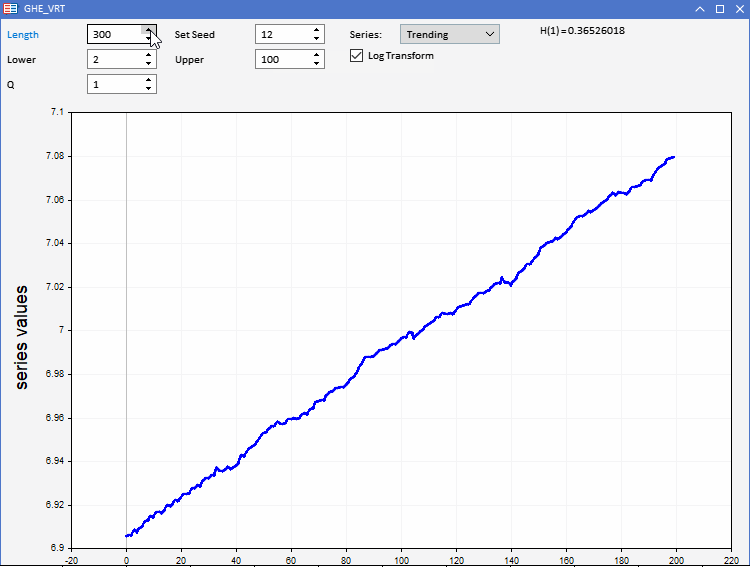
Ya sabemos que, cuando se trata de aplicaciones del mundo real, los conjuntos de datos sufren un exceso de ruido. Como el GHE ofrece una estimación sensible al tamaño de la muestra, deberemos comprobar cómo de significativo es el resultado. Esto puede lograrse realizando una prueba de hipótesis denominada prueba del coeficiente de varianza (RV).

Prueba del coeficiente de varianza

La prueba del coeficiente de varianza es un test estadístico utilizado para evaluar la aleatoriedad de una serie temporal comprobando si la varianza de la serie aumenta en proporción a la longitud del intervalo temporal. La prueba se basa en la idea de que si la serie objeto de la prueba sigue un camino aleatorio, la varianza de los cambios en la serie durante un intervalo de tiempo dado debería aumentar linealmente con la longitud del intervalo. Si la varianza aumenta a un ritmo menor, esto puede indicar la correlación serial en los cambios de la serie con la suposición de que la serie es predecible. El coeficiente de varianza asegura que:

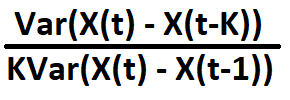
es igual a 1, donde:
- X() - serie temporal de interés.
- K - retraso arbitrario.
- Var() - varianza.

La hipótesis nula de la prueba es que la serie temporal seguirá un camino aleatorio y, por tanto, el coeficiente de varianza debería ser igual a 1. Un coeficiente de varianza sustancialmente distinto de 1 podría llevar a rechazar la hipótesis nula, sugiriendo alguna forma de predictibilidad o correlación serial en las series temporales.

Aplicación de la prueba del coeficiente de varianza

La prueba VR se implementará como la clase CVarianceRatio definida en VRT.mqh. Hay dos métodos que se pueden llamar para realizar la prueba VR Vrt(): uno funciona con vectores y el otro con arrays. A continuación, describiremos los parámetros del método:

• lags definirá el número de periodos o retrasos utilizados en el cálculo de la varianza. En el contexto de cómo queremos utilizar la prueba VR para evaluar la significación de nuestra valoración GHE, podemos establecer lags en el valor correspondiente de gen_hurst(), inferior o superior. El valor no puede ser inferior a 2. 
• trend es una enumeración que nos permitirá especificar el tipo de paseo aleatorio que queremos probar. Solo dos opciones tendrán efecto, TREND_CONST_ONLY y TREND_NONE.
• debiased especificará si vamos a utilizar una versión desplazada de la prueba, que solo será aplicable si overlap es igual a true. La función true utilizará un método de corrección del desplazamiento para ajustar la estimación de la relación de la varianza, con el objetivo de obtener una representación más exacta de la verdadera relación entre varianzas. Esto resultará especialmente útil al trata con series de muestras pequeñas.
  
• overlap especificará si debemos utilizar todos los bloques solapados. Si es igual a false, la longitud de la fila menos uno deberá ser múltiplo del valor lags. Si no se cumple esta condición, se descartarán algunos valores al final de la serie de entrada.
• robust elegirá si considerar la heterocedasticidad (true) o solo la homocedasticidad (false). En análisis estadístico, un proceso heterocedástico tiene una varianza no constante, mientras que una serie homocedástica se caracteriza por una varianza constante. 
  

El método Vrt() retornará true en caso de éxito, tras lo cual podremos llamar a cualquiera de los métodos get para recuperar todos los aspectos del resultado de la prueba.

//+------------------------------------------------------------------+
//| CVarianceRatio  class                                            |
//| Variance ratio hypthesis test for a random walk                  |
//+------------------------------------------------------------------+
class CVarianceRatio
  {
private:
   double            m_pvalue;     //pvalue
   double            m_statistic;  //test statistic
   double            m_variance;   //variance
   double            m_vr;         //variance ratio
   vector            m_critvalues; //critical values

public:
                     CVarianceRatio(void);
                    ~CVarianceRatio(void);

   bool              Vrt(const double &in_data[], ulong lags, ENUM_TREND trend = TREND_CONST_ONLY, bool debiased=true, bool robust=true, bool overlap = true);
   bool              Vrt(const vector &in_vect, ulong lags, ENUM_TREND trend = TREND_CONST_ONLY, bool debiased=true, bool robust=true, bool overlap = true);

   double            Pvalue(void) { return m_pvalue;}
   double            Statistic(void) { return m_statistic;}
   double            Variance(void) { return m_variance;}
   double            VRatio(void) { return m_vr;}
   vector            CritValues(void) { return m_critvalues;}
  };

Dentro de Vrt(), si el solapamiento es igual a false, comprobaremos si la longitud de la serie de entrada es divisible por los retrasos. Si no, recortaremos el final de la fila y mostraremos un aviso sobre la longitud de los datos. A continuación, reasignaremos los nobs en función de la longitud actualizada de la serie. Y calcularemos mu, la condición de la tendencia. Aquí calcularemos las diferencias de los elementos vecinos de la fila y las almacenaremos en delta_y. Al utilizar delta_y, la varianza se calculará y se almacenará en la variable sigma2_1. Si no hay solapamiento, calcularemos la varianza de los bloques no solapados. En caso contrario, calcularemos la varianza de los bloques solapados. Si están activados debiased y overlap, corregiremos la desviación. Aquí m_varianced se calculará según la overlap y robust. Por último, calcularemos el coeficiente de varianza, la estadística de prueba y el valor p.

//+------------------------------------------------------------------+
//| main method for computing Variance ratio test                    |
//+------------------------------------------------------------------+
bool CVarianceRatio::Vrt(const vector &in_vect,ulong lags,ENUM_TREND trend=1,bool debiased=true,bool robust=true,bool overlap=true)
  {
   ulong nobs = in_vect.Size();

   vector y = vector::Zeros(2),delta_y;

   double mu;

   ulong nq = nobs - 1;

   if(in_vect.Size()<1)
     {
      Print(__FUNCTION__, "Invalid input, no data supplied");
      return false;
     }

   if(lags<2 || lags>=in_vect.Size())
     {
      Print(__FUNCTION__," Invalid input for lags");
      return false;
     }

   if(!overlap)
     {
      if(nq % lags != 0)
        {
         ulong extra = nq%lags;
         if(!y.Init(5,slice,in_vect,0,in_vect.Size()-extra-1))
           {
            Print(__FUNCTION__," ",__LINE__);
            return false;
           }
         Print("Warning:Invalid length for input data, size is not exact multiple of lags");
        }
     }
   else
      y.Copy(in_vect);

   nobs = y.Size();

   if(trend == TREND_NONE)
      mu = 0;
   else
      mu = (y[y.Size()-1] - y[0])/double(nobs - 1);

   delta_y = difference(y);

   nq = delta_y.Size();

   vector mudiff = delta_y - mu;

   vector mudiff_sq = MathPow(mudiff,2.0);

   double sigma2_1 = mudiff_sq.Sum()/double(nq);

   double sigma2_q;

   vector delta_y_q;

   if(!overlap)
     {
      vector y1,y2;
      if(!y1.Init(3,slice,y,lags,y.Size()-1,lags) ||
         !y2.Init(3,slice,y,0,y.Size()-lags-1,lags))
        {
         Print(__FUNCTION__," ",__LINE__);
         return false;
        }

      delta_y_q = y1-y2;

      vector delta_d = delta_y_q - double(lags) * mu;

      vector delta_d_sqr = MathPow(delta_d,2.0);

      sigma2_q = delta_d_sqr.Sum()/double(nq);
     }
   else
     {
      vector y1,y2;
      if(!y1.Init(3,slice,y,lags,y.Size()-1) ||
         !y2.Init(3,slice,y,0,y.Size()-lags-1))
        {
         Print(__FUNCTION__," ",__LINE__);
         return false;
        }

      delta_y_q = y1-y2;

      vector delta_d = delta_y_q - double(lags) * mu;

      vector delta_d_sqr = MathPow(delta_d,2.0);

      sigma2_q = delta_d_sqr.Sum()/double(nq*lags);
     }


   if(debiased && overlap)
     {
      sigma2_1 *= double(nq)/double(nq-1);
      double mm = (1.0-(double(lags)/double(nq)));
      double m = double(lags*(nq - lags+1));// * (1.0-double(lags/nq));
      sigma2_q *= double(nq*lags)/(m*mm);
     }

   if(!overlap)
      m_variance = 2.0 * (lags-1);
   else
      if(!robust)
         m_variance = double((2 * (2 * lags - 1) * (lags - 1)) / (3 * lags));
      else
        {
         vector z2, o, p;
         z2=MathPow((delta_y-mu),2.0);
         double scale = pow(z2.Sum(),2.0);
         double theta = 0;
         double delta;
         for(ulong k = 1; k<lags; k++)
           {
            if(!o.Init(3,slice,z2,k,z2.Size()-1) ||
               !p.Init(3,slice,z2,0,z2.Size()-k-1))
              {
               Print(__FUNCTION__," ",__LINE__);
               return false;
              }
            o*=double(nq);
            p/=scale;
            delta = o.Dot(p);
            theta+=4.0*pow((1.0-double(k)/double(lags)),2.0)*delta;
           }
         m_variance = theta;
        }
   m_vr = sigma2_q/sigma2_1;

   m_statistic = sqrt(nq) * (m_vr - 1)/sqrt(m_variance);

   double abs_stat = MathAbs(m_statistic);

   m_pvalue = 2 - 2*CNormalDistr::NormalCDF(abs_stat);

   return true;
  }

Para probar la clase, modificaremos la aplicación GHE.ex5 utilizada para mostrar la función gen_hurst(), ya que GHE se define por el intervalo de retrasos en el que se centra el análisis. Podemos calibrar la VRT para comprobar la significación de los resultados de GHE en el mismo intervalo de retrasos. Tendremos que obtener información suficiente ejecutando VRT con retraso mínimo y máximo. En GHE.ex5, el coeficiente de dispersión en la parte inferior se mostrará primero antes que el coeficiente de dispersión en la parte superior del retraso.
El coeficiente de varianza con diferencia significativa será un indicador de la previsibilidad de los datos. Los coeficientes de varianza cercanos a 1 sugieren que la serie se aproximará al paseo aleatorio. Al probar distintas combinaciones de parámetros, podremos observar que los resultados de GHE y VRT se ven afectados por el tamaño de la muestra.

Para series de longitud inferior a 1 000, ambos métodos daban a veces resultados inesperados.

Además, había casos en los que los resultados de GHE diferían significativamente al comparar las pruebas que utilizaban valores brutos y valores transformados logarítmicamente.

Ahora que ya conocemos el VRT y el GHE, podemos aplicarlos a nuestra estrategia de reversión a la media. Si sabemos que la serie de precios regresa a la media, podremos estimar aproximadamente lo que hará el precio basándonos en su desviación actual respecto a la media. Nuestra estrategia se basará en el análisis de las características de las series de precios a lo largo de un periodo temporal. Usando este análisis, formaremos un modelo que estimará los puntos en los que el precio puede retroceder tras desviarse demasiado de la norma. Para generar las señales de entrada y salida, necesitaremos alguna forma de medir y cuantificar esta desviación.

Puntación Z

La puntuación z mide el número de desviaciones estándar de un precio con respecto a su media. Al normalizar los precios, la puntuación z fluctuará en torno a cero. Veamos qué aspecto tiene el gráfico de puntuación z cuando se implementa como indicador. A continuación mostraremos el código completo.

//+------------------------------------------------------------------+
//|                                                       Zscore.mq5 |
//|                                  Copyright 2023, MetaQuotes Ltd. |
//|                                             https://www.mql5.com |
//+------------------------------------------------------------------+
#property copyright "Copyright 2023, MetaQuotes Ltd."
#property link      "https://www.mql5.com"
#property version   "1.00"
#include<VectorMatrixTools.mqh>
#property indicator_separate_window
#property indicator_buffers 1
#property indicator_plots   1
//--- plot Zscore
#property indicator_label1  "Zscore"
#property indicator_type1   DRAW_LINE
#property indicator_color1  clrBlue
#property indicator_style1  STYLE_SOLID
#property indicator_width1  1
//--- input parameters
input int      z_period = 10;
//--- indicator buffers
double         ZscoreBuffer[];
vector vct;
//+------------------------------------------------------------------+
//| Custom indicator initialization function                         |
//+------------------------------------------------------------------+
int OnInit()
  {
//--- indicator buffers mapping
   SetIndexBuffer(0,ZscoreBuffer,INDICATOR_DATA);
//----
   PlotIndexSetDouble(0,PLOT_EMPTY_VALUE,0);
//---
   PlotIndexSetInteger(0,PLOT_DRAW_BEGIN,z_period-1);
//---
   return(INIT_SUCCEEDED);
  }
//+------------------------------------------------------------------+
//| Custom indicator iteration function                              |
//+------------------------------------------------------------------+
int OnCalculate(const int rates_total,
                const int prev_calculated,
                const datetime &time[],
                const double &open[],
                const double &high[],
                const double &low[],
                const double &close[],
                const long &tick_volume[],
                const long &volume[],
                const int &spread[])
  {
//---
   if(rates_total<z_period)
     {
      Print("Insufficient history");
      return -1;
     }
//---
   int limit;
   if(prev_calculated<=0)
      limit = z_period - 1;
   else
      limit = prev_calculated - 1;
//---
   for(int i = limit; i<rates_total; i++)
     {
      vct.Init(ulong(z_period),assign,close,ulong(i-(z_period-1)),i,1);
      if(vct.Size()==ulong(z_period))
         ZscoreBuffer[i] = (close[i] - vct.Mean())/vct.Std();
      else
         ZscoreBuffer[i]=0.0;
     }

//--- return value of prev_calculated for next call
   return(rates_total);
  }
//+------------------------------------------------------------------+

En este gráfico podemos ver que los valores de los indicadores tienen ahora una distribución más normal.

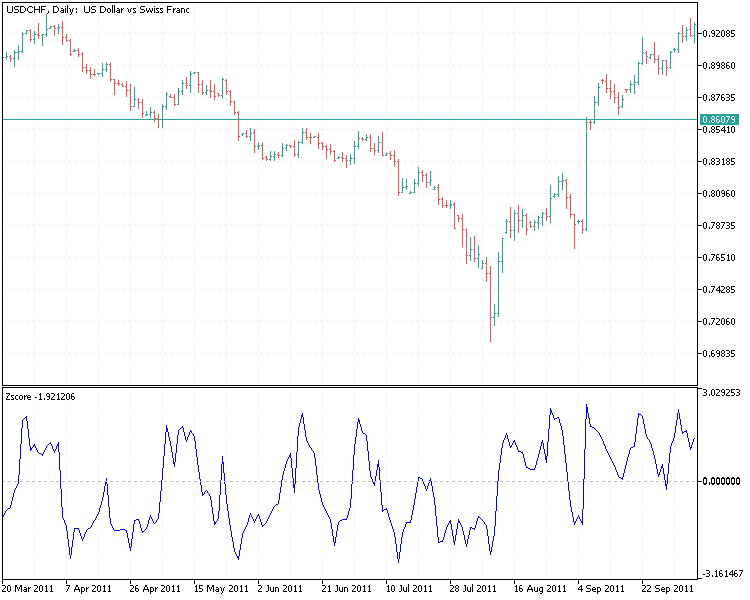
Las señales comerciales se generarán cuando la puntuación z se desvíe significativamente de 0 y supere algún umbral histórico. Una puntuación z fuertemente negativa indicará un buen momento para una posición larga, mientras que una puntuación z fuertemente positiva indicará un buen momento para una posición corta. Y esto significa que necesitaremos dos umbrales para las señales de compra y venta. Uno negativo (para comprar) y otro positivo (para vender). Una opción sería obtener un nuevo conjunto de umbrales que funcionen para una posición concreta (larga o corta). En el caso de una posición corta, podremos cerrar nuestra posición cuando la puntuación z regrese a 0. Del mismo modo, cerraremos una posición larga cuando la puntuación z se acerca a 0 desde el nivel extremo en el que se ha realizado la compra.

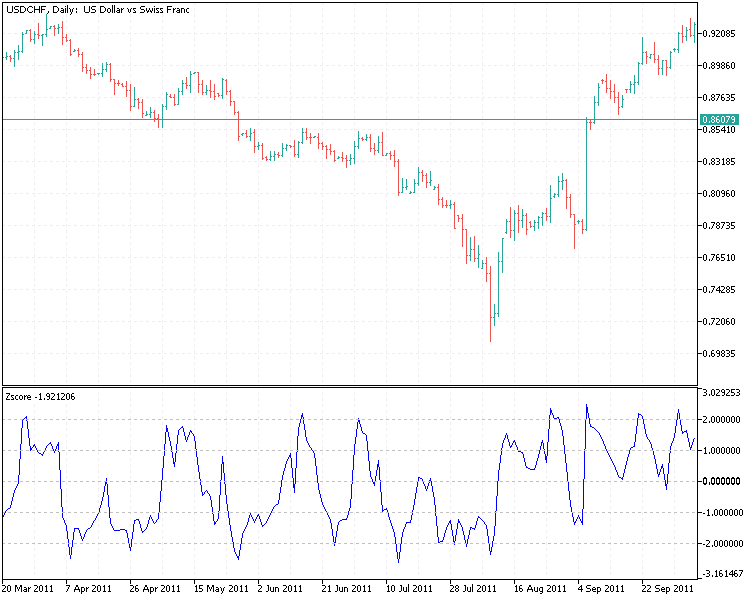
Ahora tenemos las entradas y salidas definidas con el indicador Zscore.ex5. Recopilémoslo todo en un asesor. A continuación, mostraremos un fragmento.

//+------------------------------------------------------------------+
//|                                                MeanReversion.mq5 |
//|                                  Copyright 2024, MetaQuotes Ltd. |
//|                                             https://www.mql5.com |
//+------------------------------------------------------------------+
#property copyright "Copyright 2024, MetaQuotes Ltd."
#property link      "https://www.mql5.com"
#property version   "1.00"
#resource "\\Indicators\\Zscore.ex5"
#include<ExpertTools.mqh>
//---Input parameters
input int  PeriodLength  = 10;
input double LotsSize = 0.01;
input double  LongOpenLevel = -2.0;
input double  ShortOpenLevel = 2.0;
input double  LongCloseLevel = -0.5;
input double  ShortCloseLevel = 0.5;
input ulong  SlippagePoints = 10;
input ulong  MagicNumber    = 123456;
//---
 int indi_handle;
//---
 double zscore[2];
//+------------------------------------------------------------------+
//| Expert initialization function                                   |
//+------------------------------------------------------------------+
int OnInit()
  {
//---
   if(PeriodLength<2)
    {
     Print("Invalid parameter value for PeriodLength");
     return INIT_FAILED;
    }
//---
   if(!InitializeIndicator())
    return INIT_FAILED;
//---        
   return(INIT_SUCCEEDED);
  }
//+------------------------------------------------------------------+
//| Expert deinitialization function                                 |
//+------------------------------------------------------------------+
void OnDeinit(const int reason)
  {
//---
   
  }
//+------------------------------------------------------------------+
//| Expert tick function                                             |
//+------------------------------------------------------------------+
void OnTick()
  {
//---    
      int signal = GetSignal();
//---      
      if(SumMarketOrders(MagicNumber,_Symbol,-1))
       {
        if(signal==0)
         CloseAll(MagicNumber,_Symbol,-1);
        return; 
       }
      else
        OpenPosition(signal);
//---   
  }
//+------------------------------------------------------------------+
//+------------------------------------------------------------------+
//| Initialize indicator                                             |
//+------------------------------------------------------------------+
bool InitializeIndicator(void)
{
 indi_handle = INVALID_HANDLE;
//---
 int try = 10;
//---
 while(indi_handle == INVALID_HANDLE && try>0)
  {
   indi_handle = (indi_handle==INVALID_HANDLE)?iCustom(NULL,PERIOD_CURRENT,"::Indicators\\Zscore.ex5",PeriodLength):indi_handle;
   try--;
  }
//---
 if(try<0)
  {
   Print("Failed to initialize Zscore indicator ");
   return false;
  }
//---
 return true;
}
//+------------------------------------------------------------------+
//|Get the signal to trade or close                                  |
//+------------------------------------------------------------------+
int GetSignal(const int sig_shift=1)
{
//---
 if( CopyBuffer(indi_handle,int(0),sig_shift,int(2),zscore)<2)
   {
    Print(__FUNCTION__," Error copying from indicator buffers: ", GetLastError());
    return INT_MIN;
   } 
//---   
 if(zscore[1]<LongOpenLevel && zscore[0]>LongOpenLevel)
     return (1);
//---   
 if(zscore[1]>ShortOpenLevel && zscore[0]<ShortOpenLevel)
     return (-1);          
//---   
 if((zscore[1]>LongCloseLevel && zscore[0]<LongCloseLevel) ||
    (zscore[1]<ShortCloseLevel && zscore[0]>ShortCloseLevel))
     return (0);
//---
 return INT_MIN;
//--- 
}
//+------------------------------------------------------------------+
//|  Go long or short                                                |
//+------------------------------------------------------------------+
bool OpenPosition(const int sig)
{

 long pid;
//--- 
 if(LastOrderOpenTime(pid,NULL,MagicNumber)>=iTime(NULL,0,0))
   return false;
//---   
 if(sig==1)
   return SendOrder(_Symbol,0,ORDER_TYPE_BUY,LotsSize,SlippagePoints,0,0,NULL,MagicNumber);
 else
  if(sig==-1)
    return SendOrder(_Symbol,0,ORDER_TYPE_SELL,LotsSize,SlippagePoints,0,0,NULL,MagicNumber); 
//--- 
  return false;                   
}

El código es muy sencillo. Aquí no definiremos niveles de stop loss o take profit. Nuestro objetivo será optimizar primero el asesor para obtener el periodo óptimo para el indicador Zscore, así como los umbrales óptimos de entrada y salida. Asimismo, optimizaremos los datos a lo largo de varios años y probaremos los parámetros óptimos en una muestra, pero antes haremos una pequeña digresión para presentar otra herramienta interesante. En el libro "Trading algorítmico: Estrategias ganadoras y su fundamento" (Algorithmic Trading: Winning Strategies And Their Rationale), de Ernest Chan, se describe una interesante herramienta para desarrollar estrategias de reversión a la media denominada semivida de reversión a la media (half life of mean reversion).

Semivida de reversión a la media

La semivida de la regresión a la media es el tiempo que tarda en reducirse a la mitad la desviación con respecto a la media. En el contexto del precio de un activo, la semivida de retorno a la media indica la rapidez con la que el precio tiende a volver a su media histórica tras desviarse de ella. Es una medida de la velocidad a la que se produce el proceso de regreso a la media. Matemáticamente, la semivida puede relacionarse con la tasa de retorno a la ecuación media:

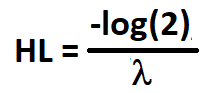
donde:
- HL - semivida.
- log() - logaritmo natural.
- lambda - velocidad de retorno al valor medio.

Desde un punto de vista práctico, una semivida más corta implicará un proceso de retorno a la media más rápido, mientras que una semivida más larga implicará un proceso de retorno a la media más lento. El concepto de semivida puede usarse para afinar los parámetros de las estrategias comerciales con reversión a la media, ayudando a optimizar los puntos de entrada y salida usando como base los datos históricos y la tasa de reversión a la media observada. La semivida de retorno a la media se derivará de la representación matemática del proceso de retorno a la media, normalmente modelizado como el proceso Ornstein-Uhlenbeck. El proceso Ornstein-Uhlenbeck es una ecuación diferencial estocástica que describe una versión del comportamiento de reversión a la media con tiempo continuo.

Como señala Chan, podemos determinar si la reversión a la media es una estrategia adecuada calculando la semivida de la reversión a la media. En primer lugar, si la lambda es positiva, no deberemos aplicar en absoluto la reversión a la media. Incluso si la lambda es negativa y muy cercana a cero, no se recomienda aplicar un retorno al valor medio porque indica que la semivida será larga. El retorno a la media solo debe usarse si la semivida es suficientemente corta.

La semivida del retorno a la media se implementará como una función en MeanReversionUtilities.mqh, mostramos el código a continuación. Se calculará haciendo una regresión de una serie de precios sobre una serie de diferencias entre valores sucesivos. Lambda será igual al parámetro beta del modelo de regresión, y la semivida se calculará dividiendo -log(2) por lambda.

//+------------------------------------------------------------------+
//|Calculate Half life of Mean reversion                             |
//+------------------------------------------------------------------+
double mean_reversion_half_life(vector &data, double &lambda)
  {
//---
   vector yy,zz;
   matrix xx;
//---
   OLS ols_reg;
//---
   yy.Init(data.Size()-1,slice,data,1,data.Size()-1,1);
//---
   zz.Init(data.Size()-1,slice,data,0,data.Size()-2,1);
//---
   if(!xx.Init(zz.Size(),2) || !xx.Col(zz,0) || !xx.Col(vector::Ones(zz.Size()),1) || !ols_reg.Fit(yy-zz,xx))
     {
      Print(__FUNCTION__," Error in calculating half life of mean reversion ", GetLastError());
      return 0;
     }
//---
   vector params = ols_reg.ModelParameters();
   lambda = params[0];
//---
   return (-log(2)/lambda);
//---
  }

Lo usaremos junto con GHE y VRT para probar una muestra de precios durante un periodo seleccionado de años para varios símbolos de divisas. Usaremos los resultados de la prueba para seleccionar el símbolo correspondiente al que se aplicará el asesor que hemos creado anteriormente. Lo optimizaremos durante el mismo periodo de años y finalmente lo probaremos en la muestra. El script que mostramos a continuación tomará una lista de símbolos candidatos para probarlos usando GHE, VRT y la semivida.

//+------------------------------------------------------------------+
//|                                                 SymbolTester.mq5 |
//|                                  Copyright 2024, MetaQuotes Ltd. |
//|                                             https://www.mql5.com |
//+------------------------------------------------------------------+
#property copyright "Copyright 2024, MetaQuotes Ltd."
#property link      "https://www.mql5.com"
#property version   "1.00"
#property script_show_inputs
#include<MeanReversionUtilities.mqh>
#include<GHE.mqh>
#include<VRT.mqh>

//--- input parameters
input string   Symbols = "EURUSD,GBPUSD,USDCHF,USDJPY";//Comma separated list of symbols to test
input ENUM_TIMEFRAMES TimeFrame = PERIOD_D1;
input datetime StartDate=D'2020.01.02 00:00:01';
input datetime StopDate=D'2015.01.18 00:00:01';
input int Q_parameter = 2;
input int MinimumLag = 2;
input int MaximumLag = 100;
input bool ApplyLogTransformation = true;
//---
CVarianceRatio vrt;
double ghe,hl,lb,vlower,vupper;
double prices[];
//+------------------------------------------------------------------+
//| Script program start function                                    |
//+------------------------------------------------------------------+
void OnStart()
  {
//---Check Size input value
   if(StartDate<=StopDate)
     {
      Print("Invalid input for StartDater or StopDate");
      return;
     }
//---array for symbols
   string symbols[];
//---process list of symbols from user input
   int num_symbols = StringSplit(Symbols,StringGetCharacter(",",0),symbols);
//---incase list contains ending comma
   if(symbols[num_symbols-1]=="")
      num_symbols--;
//---in case there are less than two symbols specified
   if(num_symbols<1)
     {
      Print("Invalid input. Please list at least one symbol");
      return;
     }
//---loop through all paired combinations from list
   for(uint i=0; i<symbols.Size(); i++)
     {

      //--- get prices for the pair of symbols
      if(CopyClose(symbols[i],TimeFrame,StartDate,StopDate,prices)<1)
        {
         Print("Failed to copy close prices ", ::GetLastError());
         return;
        }
      //---
      if(ApplyLogTransformation && !MathLog(prices))
        {
         Print("Mathlog error ", GetLastError());
         return;
        }
      //---
      if(!vrt.Vrt(prices,MinimumLag))
         return;
      //---
      vlower = vrt.VRatio();
      //---
      if(!vrt.Vrt(prices,MaximumLag))
         return;
      //---
      vupper = vrt.VRatio();
      //---
      ghe = general_hurst(prices,Q_parameter,MinimumLag,MaximumLag);
      //---
      hl = mean_reversion_half_life(prices,lb);
      //--- output the results
      Print(symbols[i], " GHE:  ", DoubleToString(ghe)," | Vrt: ",DoubleToString(vlower)," ** ",DoubleToString(vupper)," | HalfLife ",DoubleToString(hl)," | Lambda: ",DoubleToString(lb));
     }
  }
//+------------------------------------------------------------------+

La ejecución del script producirá los siguientes resultados:

19:31:03.143    SymbolTester (USDCHF,D1)        EURUSD GHE:  0.44755644 | Vrt: 0.97454284 ** 0.61945905 | HalfLife 85.60548208 | Lambda: -0.00809700
19:31:03.326    SymbolTester (USDCHF,D1)        GBPUSD GHE:  0.46304381 | Vrt: 1.01218672 ** 0.82086185 | HalfLife 201.38001205 | Lambda: -0.00344199
19:31:03.509    SymbolTester (USDCHF,D1)        USDCHF GHE:  0.42689382 | Vrt: 1.02233286 ** 0.47888803 | HalfLife 28.90550869 | Lambda: -0.02397976
19:31:03.694    SymbolTester (USDCHF,D1)        USDJPY GHE:  0.49198795 | Vrt: 0.99875744 ** 1.06103587 | HalfLife 132.66433924 | Lambda: -0.00522482

El símbolo USDCHF presenta los resultados más prometedores para el periodo de tiempo seleccionado. Por ello, optimizaremos los parámetros del asesor comerciando en USDCHF. Sería interesante seleccionar el periodo Zscore para la optimización y ver si difiere de la semivida calculada.

Aquí podemos ver el periodo óptimo de Zscore. Se aproxima mucho a la semivida de retorno calculada. Y eso es alentador. Obviamente, serían necesarias pruebas más exhaustivas para determinar la utilidad de la semivida.

Por último, probaremos el asesor fuera de muestra con parámetros óptimos.

Los resultados dejan mucho que desear. Esto se debe probablemente a que el mercado está en constante movimiento, por lo que las características observadas durante el periodo de optimización del asesor ya no son aplicables. Necesitaremos umbrales de entrada y salida más dinámicos que tengan en cuenta los cambios en la dinámica subyacente del mercado.

Podemos usar los conocimientos adquiridos aquí como base para futuros desarrollos. Un posible rumbo a tomar sería utilizar las herramientas aquí descritas para aplicar una estrategia comercial por pares. En lugar de un único par de precios, el indicador Zscore podría basarse en el spread de dos instrumentos cointegrados o correlacionados.

Conclusión

En este artículo, hemos mostrado la implementación del coeficiente de Hurst generalizado en MQL5 y cómo se puede utilizar para determinar las características de una serie de precios. También hemos analizado la aplicación de la prueba del coeficiente de varianza, así como la semivida del retorno a la media. La siguiente tabla es una descripción de todos los archivos adjuntos al artículo.

Archivo	Descripción
Mql5\include\ExpertTools.mqh	Contiene las definiciones de las funciones para las operaciones comerciales utilizadas en el asesor MeanReversion.
Mql5\include\GHE.mqh	Contiene la definición de la función que implementa el coeficiente de Hurst generalizado.
Mql5\include\OLS.mqh	Contiene la definición de la clase OLS que implementa la regresión por mínimos cuadrados ordinarios.
Mql5\include\VRT.mqh	Contiene la definición de la clase CVarianceRatio, que encapsula la prueba de coeficiente de varianza.
Mql5\include\VectorMatrixTools.mqh	Tiene varias definiciones de funciones para la inicialización rápida de vectores y matrices comunes.
Mql5\include\TestUtilities.mqh	Contiene una serie de declaraciones usadas en la definición de la clase OLS.
Mql5\include\MeanReversionUtilities.mqh	Contiene varias definiciones de funciones, incluida la definición de la semivida del retorno a la media.
Mql5\Indicators\Zscore.mq5	Indicador utilizado en el asesor MeanReversion
Mql5\scripts\SymbolTester.mq5	Secuencia de comandos que se puede utilizar para comprobar los símbolos para ver si vuelven al valor medio
Mql5\Experts\GHE.ex5	Asesor para aprender y experimentar con las herramientas GHE y VRT.
Mql5\scripts\MeanReversion.mq5	Asesor que muestra una estrategia simple de regreso al valor medio