MetaTrader 5 / Статистика и анализ
English 中文 Español Deutsch 日本語 Português
preview
Машинное обучение и Data Science (Часть 10): Гребневая регрессия

Машинное обучение и Data Science (Часть 10): Гребневая регрессия

MetaTrader 5 — Статистика и анализ | 31 марта 2023, 15:45
1 989 0
Omega J Msigwa
Omega J Msigwa

Введение 

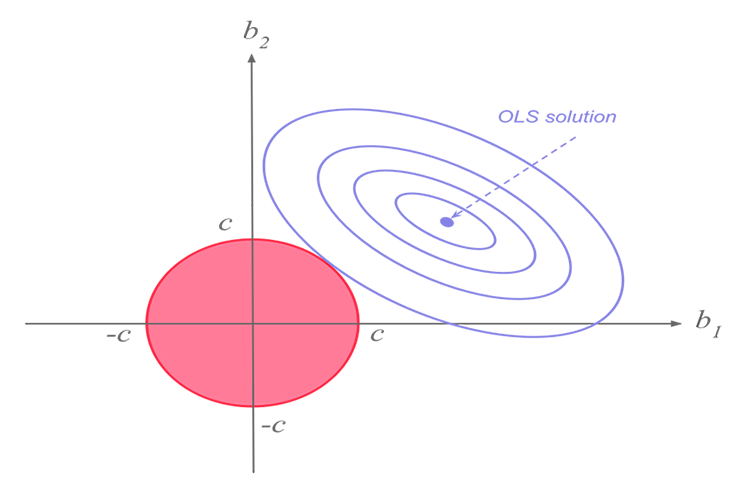
Ридж-регрессия (гребневая регрессия) — это метод оценки коэффициентов моделей множественной регрессии, когда независимые переменные сильно коррелированы. Метод обеспечивает повышенную эффективность в задачах оценки параметров за счет допустимой степени смещения. Подобно регрессии Лассо (оператор наименьшего абсолютного сжатия и выбора) вводит штрафной коэффициент, накладывая ограничение, но в отличие от нее принимает квадрат, а не величину коэффициентов. Данный метод регрессионного анализа выполняет как выбор переменных, так и регуляризацию для повышения точности прогнозирования и интерпретируемости результирующих статистических данных. Хотя гребневая оценка и смещена, она имеет достаточно низкую дисперсию. Использование коэффициента позволяет выбрать наилучшее подмножество, также с ними связывают так называемую мягкую пороговую обработку. Кроме того, как и при стандартной линейной регрессии, оценки коэффициентов не обязательно должны быть уникальными, если ковариаты коллинеарны.

Теперь, чтобы понять, зачем нам нужны такие модели, давайте в первую очередь разберемся в терминах смещения и дисперсии.


Смещение 

Это это неспособность машинного обучения уловить истинную связь между независимой переменной и переменной отклика

Что это значит для модели?

  • Модель с низким смещением делает меньше предположений о форме целевой функции.
  • При высоком смещении модель делает больше предположений и может фиксировать отношения в обучающем наборе данных.

    Дисперсия

    Дисперсия показывает, насколько случайная величина отличается от ожидаемого значения.
    Способы уменьшения высокого смещения:
    • Увеличение входных параметров, поскольку модель недостаточно подогнана
    • Уменьшение срока регуляризации
    • Использование более сложных моделей, например, включающих полиномиальные функции

    Способы уменьшения высокой дисперсии:

    • Уменьшение входных параметров, поскольку при большой дисперсии происходит подгонка
    • Использование не слишком сложной модели
    • Увеличение обучающей выборки
    • Увеличение срока регуляризации


    Компромисс смещения и дисперсии

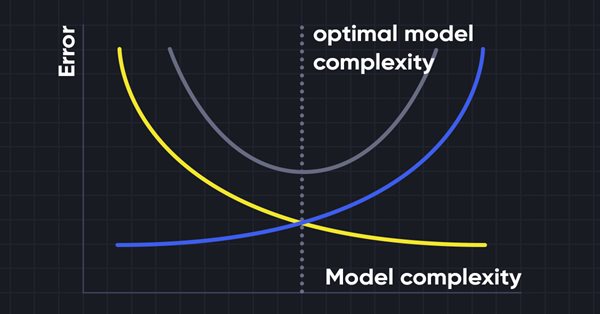
    При построении модели машинного обучения очень важно позаботиться о смещении и дисперсии, чтобы избежать переобучения модели. Если модель очень простая и с меньшим количеством параметров, она, как правило, имеет большее смещение, но небольшую дисперсию, тогда как сложные модели часто имеют низкое смещение, но высокое значение дисперсии. Поэтому необходимо найти баланс между ошибками смещения и дисперсии. Поиск такого баланса называют компромиссом между смещением и дисперсией.


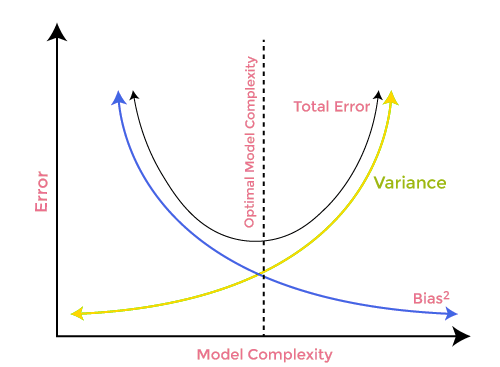
    При этом для точных прогнозов модели алгоритмам требуется более низкое смещение и более низкая дисперсия, но это практически невозможно, поскольку смещение и дисперсия отрицательно связаны друг с другом.

    Если мы увеличим смещение, дисперсия уменьшится, и наоборот.


    Гребневая регрессия

    Ридж-регрессия и лассо-регрессия выполняют схожую функцию, но у них есть существенное различие, которое мы увидим позже, когда углубимся в математику и попытаемся выяснить, как работает каждый алгоритм.

    Идея гребневой регрессии

    При работе со множеством линейно коррелированых измерений, с уверенностью можно сказать, что метод наименьших квадратов прекрасно отобразит взаимосвязь между независимой и целевой переменной.

    Взгляните на приведенный ниже пример зависимости между размером мыши и весом.


    Но что, если в нашем наборе данных только два измерения, а остальные используются в качестве набора данных для тестирования. Подгонка модели с методом наименьших квадратов приведет к идеальной подгонке, которая даст нулевую сумму квадратов остатков.


    Теперь протестируем эту модель на новом наборе данных:



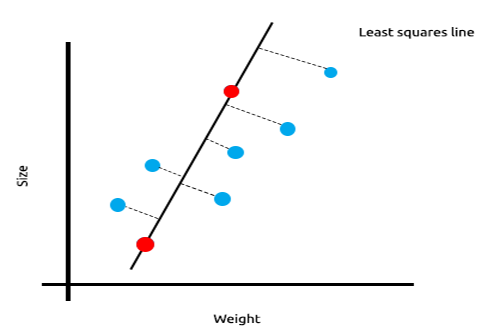
    Сумма квадратов ошибок на обучающих данных равна нулю, но сумма квадратов остатков для тестовых данных получилась большой, это означает, что наша модель имеет высокую дисперсию. На языке машинного обучения это означает, что модель подогнали под обучающие данные.

    Основная идея гребневой и лассо-регрессии состоит в том, чтобы найти модель, которая не подогнана под обучающие данные.


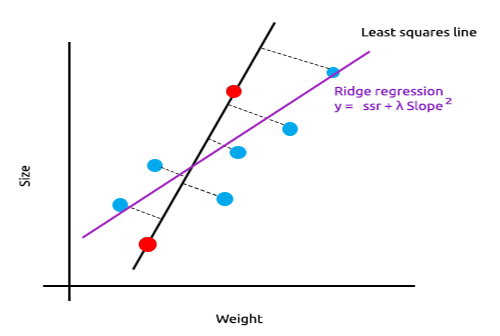
    В гребневой регрессии вводится небольшое смещение, в результате чего мы получаем значительное снижение дисперсии. Поскольку ридж-регрессия внесла небольшое смещение, модель теперь плохо подогнана, а результаты на обучающей выборке и на тестовых данных позволяют оценить модель как надежную в долгосрочной перспективе.

    Когда использовать эти регуляризованные модели

    Возможно, метод наименьших квадратов/модель линейной регрессии тоже могут работать хорошо, зачем использовать эти модели L1Norm и L2Norm?

    Чтобы понять это, давайте посмотрим, как многомерная линейная регрессия работает с обученным набором данных.


    Для демонстрации подхода я подготовил набор из данных осцилляторов и индикатора объемов по инструменту EURUSD:

    Даже не глядя на корреляционную матрицу, каждый, кто знаком с этими индикаторами, точно знает, что они не подходят для задач регрессии. Ниже приведена корреляционная матрица

        ArrayPrint(matrix_utils.csv_header);
    Print(Matrix.CorrCoef(false));

    Результат:

    CS      0       06:29:41.493    TestEA (EURUSD,H1)      "Stochastic" "Rsi"        "Volume"     "Bears"      "Bulls"      "EURUSD"    
CS      0       06:29:41.493    TestEA (EURUSD,H1)      [[1,0.680705511991766,0.02399740959375265,0.6910892641498844,0.7291018045506749,0.1490856367010467]
CS      0       06:29:41.493    TestEA (EURUSD,H1)       [0.680705511991766,1,0.07620207894739518,0.8184961346648213,0.8258569040865805,0.1567269000583347]
CS      0       06:29:41.493    TestEA (EURUSD,H1)       [0.02399740959375265,0.07620207894739518,1,0.3752014290536041,-0.1289026185114097,-0.1024017077869821]
CS      0       06:29:41.493    TestEA (EURUSD,H1)       [0.6910892641498844,0.8184961346648213,0.3752014290536041,1,0.7826404088603456,0.07283638913665436]
CS      0       06:29:41.493    TestEA (EURUSD,H1)       [0.7291018045506749,0.8258569040865805,-0.1289026185114097,0.7826404088603456,1,0.08392530400705019]
CS      0       06:29:41.493    TestEA (EURUSD,H1)       [0.1490856367010467,0.1567269000583347,-0.1024017077869821,0.07283638913665436,0.08392530400705019,1]]
    Как видите, корреляция составляет менее 20% для столбца EURUSD по сравнению со всеми индикаторами. Стохастик и RSI немногим лучше коррелируют, чем другие, но все равно со значением примерно 14% и 15% соответственно. Давайте создадим модель линейной регрессии, начав со стохастика, а затем продолжим добавлять независимые переменные/показатели других индикаторов.

    Таблица результатов:

    Независимые переменные Оценка R2 (точность)
      Стохастик     1.2 %
      Стохастик и RSI     1.8 %
      Стохастик, RSI и Volume     2.8 %
      Стохастик, RSI, Volume, Сила медведей и Сила быков
    (Все независимые переменные)    		     4.9%

    Какой вывод можно сделать из этой таблицы. По мере увеличения количества независимых переменных точность обученной линейной модели всегда увеличивается независимо от того, что это за переменные. Корреляция для независимых переменных, которые я использовал в этом примере, очень низкая, поэтому мы получаем небольшое улучшение точности каждый раз при добавлении новой независимой переменной. Но ситуация может быть иной, если переменные коррелируют примерно на 30%-40%. Если подать модели слишком много независимых переменных, на этапе обучения модель даже может достичь точности в 90%.

    Увеличение независимых переменных увеличивает дисперсию. Очевидно эта модель будет работать хуже на новой выборке, поскольку эта модель переобучена. Именно для борьбы с такими ситуациями и были разработаны ридж- и лассо-регрессии. Как мы сказали ранее, они добавляют небольшой сдвиг чтобы добиться значительного снижения дисперсии.


    Теория ридж-регрессии

    Сама по себе гребневая регрессия (ридж) представляет собой метод оценки коэффициентов модели линейной регрессии, когда независимые переменные сильно коррелированы.

    Гребневая регрессия была разработана как возможное решение проблемы неточности оценок наименьших квадратов, когда модели линейной регрессии имеют некоторую мультиколлинеарность (сильно коррелированы), путем создания ридж-регрессионной оценки (RR). Это получается благодаря более точным параметрам гребня, поскольку его дисперсия и смещение часто меньше, чем у оценок методом наименьших квадратов.

    Ридж-оценка

    По аналогии с обычной оценкой по методу наименьших квадратов, простая ридж-оценка задается выражением 

    Где y — матрица независимых переменных, X — матрица дизайна, I — единичная матрица, λ — параметр гребня, равный или больше нуля.

    Напишем все это в коде:

    CRidgeregression::CRidgeregression(matrix &_matrix)
 {
    
    n = _matrix.Rows();
    k = _matrix.Cols();
    
    pre_processing.Standardization(_matrix);
    m_dataset.Copy(_matrix);
    
    matrix_utils.XandYSplitMatrices(_matrix,XMatrix,yVector);
    
    YMatrix = matrix_utils.VectorToMatrix(yVector);
    
//---

    Id_matrix.Resize(k,k);
    
    Id_matrix.Identity();

 }

    В конструкторе функций выполняются три важные вещи. Во-первых, это стандартизация данных. Как и многомерный градиентный спуск и многие другие методы машинного обучения, гребневая регрессия работает со стандартизированном набором данных. Во-вторых, данные разбиваются на матрицы x и y, а также создается матрица идентичности.

    Внутри функции L2Norm:

    vector CRidgeregression::L2Norm(double lambda)
 {    
   matrix design = matrix_utils.DesignMatrix(XMatrix);
   
   matrix XT = design.Transpose();
   
   matrix XTX = XT.MatMul(design);
   
   matrix lamdaxI = lambda * Id_matrix;
   
   //Print("LambdaxI \n",lamdaxI);
   
   //Print("XTX\n",XTX);
   
   matrix sum_matrix = XTX + lamdaxI;
   
   matrix Inverse_sum = sum_matrix.Inv();
   
   matrix XTy = XT.MatMul(YMatrix);
   
   Betas = Inverse_sum.MatMul(XTy);
 
   #ifdef DEBUG_MODE
      Print("Betas\n",Betas);
   #endif 
   
  return(matrix_utils.MatrixToVector(Betas));
 }

    Эта функция находит коэффициенты с использованием гребневой регрессии точно так же, как показано в формуле выше.

    Чтобы проверить, как все это работает, давайте воспользуемся другим набором данных NASDAQ_DATA.csv, с которым читатель этой серии статей уже знаком.

    int OnInit()
  {
//---
    matrix Matrix = matrix_utils.ReadCsv("NASDAQ_DATA.csv",","); 
   
    pre_processing.Standardization(Matrix);
    Linear_reg = new  CLinearRegression(Matrix);
    
    ridge_reg = new CRidgeregression(Matrix);
    
    ridge_reg.L2Norm(0.3);
 }    

    Я установил случайное значение штрафа 0,3 для гребневой регрессии, чтобы посмотреть, что из этого получится. Запустим функцию и посмотрим, какие из этого получатся коэффициенты:

    CS 0 10:27:41.338 TestEA (EURUSD,H1) [[5.015577002384403e-16]

    CS 0 10:27:41.338 TestEA (EURUSD,H1) [0.6013523727380532]

    CS 0 10:27:41.338 TestEA (EURUSD,H1) [0.3381524618200134]

    CS 0 10:27:41.338 TestEA (EURUSD,H1) [0.2119467984461254]]

    Давайте также запустим модель линейной регрессии для того же набора данных и посмотрим на полученные коэффициенты. Поскольку метод наименьших квадратов не стандартизирует выборку, мы также стандартизируем ее, прежде чем передавать данные в модель.

        matrix Matrix = matrix_utils.ReadCsv("NASDAQ_DATA.csv",","); 
   
    pre_processing.Standardization(Matrix);
    Linear_reg = new  CLinearRegression(Matrix);

    Выводимая информация:

    CS 0 10:27:41.338 TestEA (EURUSD,H1) Betas

    CS 0 10:27:41.338 TestEA (EURUSD,H1) [[-4.143037461930866e-14]

    CS 0 10:27:41.338 TestEA (EURUSD,H1) [0.6034777119810752]

    CS 0 10:27:41.338 TestEA (EURUSD,H1) [0.3363532376334173]

    CS 0 10:27:41.338 TestEA (EURUSD,H1) [0.21126507562567]]

    Коэффициенты выглядят немного иначе, поэтому я думаю, что наша функция работает. Давайте обучим и протестируем каждую из моделей, а затем построим соответствующие графики, чтобы увидеть еще больше.

    Поскольку гребневая регрессия сама по себе не является моделью, а является лишь оценкой коэффициентов, которые затем необходимо использовать с моделью линейной регрессии, я внес некоторые изменения в класс линейной регрессии, который мы обсуждали в Части 3. 

    Модель обучается в конструкторе класса линейной регрессии. В этой части коэффициенты сохраняются, чтобы остальные функции могли их использовать. Я добавил новый конструктор, который позволяет передавать коэффициенты в модель. Благодаря этому от нас понадобится минимум усилий в следующий раз, когда мы будем использовать другие оценки, чтобы получить коэффициенты для использования в нашей регрессионной модели.

    class CLinearRegression
  {
   public: 
                        CLinearRegression(matrix &Matrix_); //Least squares estimator
                        CLinearRegression(matrix<double> &Matrix_, double Lr, uint iters = 1000); //Lr by Gradient descent
                        CLinearRegression(matrix &Matrix_, vector &coeff_vector);
                        
                       ~CLinearRegression(void);


    Гребневая и линейная регрессии

        Print("----> Ridge regression");
    
    ridge_reg = new CRidgeregression(Matrix);
    vector coeff = ridge_reg.L2Norm(0.3);
    
    Linear_reg = new CLinearRegression(Matrix,coeff); //passing the coefficients made by ridge regression
                                                      // to the Linear regression model
    double acc =0;
    
    vector ridge_predictions = Linear_reg.LRModelPred(Matrix,acc); //making the predictions and storing them to a vector
    
    delete(Linear_reg); //deleting that instance
    
    Print("----> Linear Regression");
   
    pre_processing.Standardization(Matrix);
     
    Linear_reg = new CLinearRegression(Matrix); //new Linear reg instance that gets coefficients by least squares
    
    vector linear_pred = Linear_reg.LRModelPred(Matrix,acc);

    Результат

    CS 0 11:35:52.153 TestEA (EURUSD,H1) ----> Ridge regression

    CS 0 11:35:52.153 TestEA (EURUSD,H1) Betas

    CS 0 11:35:52.153 TestEA (EURUSD,H1) [[-4.142058558619502e-14]

    CS 0 11:35:52.153 TestEA (EURUSD,H1) [0.601352372738047]

    CS 0 11:35:52.153 TestEA (EURUSD,H1) [0.3381524618200102]

    CS 0 11:35:52.153 TestEA (EURUSD,H1) [0.2119467984461223]]

    CS 0 11:35:52.154 TestEA (EURUSD,H1) R squared 0.982949 Adjusted R 0.982926

    CS 0 11:35:52.154 TestEA (EURUSD,H1) ----> Linear Regression

    CS 0 11:35:52.154 TestEA (EURUSD,H1) Betas

    CS 0 11:35:52.154 TestEA (EURUSD,H1) [[5.014846059117108e-16]

    CS 0 11:35:52.154 TestEA (EURUSD,H1) [0.6034777119810601]

    CS 0 11:35:52.154 TestEA (EURUSD,H1) [0.3363532376334217]

    CS 0 11:35:52.154 TestEA (EURUSD,H1) [0.2112650756256718]]

    CS 0 11:35:52.154 TestEA (EURUSD,H1) R squared 0.982933 Adjusted R 0.982910

    Показатели моделей немного различаются, если использовать все данные для обучения.

    Мы сохранили результаты и нанесли их на графике по одной и той же оси:

    Гребневая и линейная регрессии

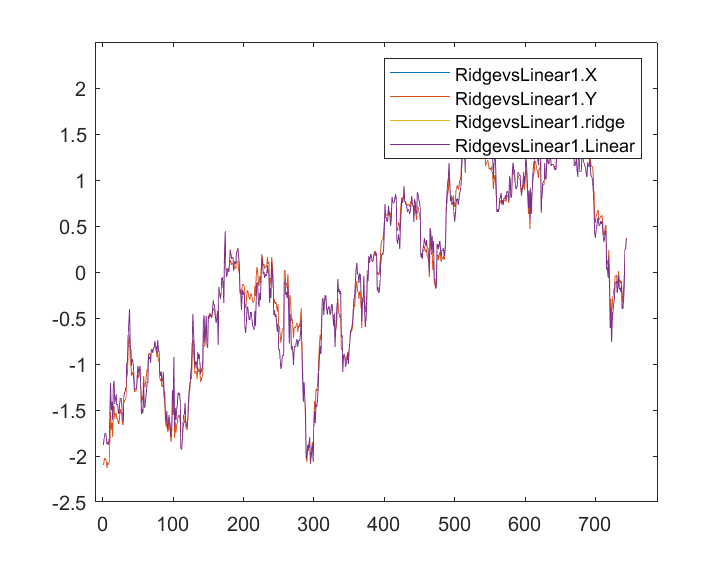
    Я почти не вижу разницы между линейной моделью и предиктором, отмеченным синим цветом, я вижу только разницу между двумя моделями, и гребневая регрессия не очень хорошо подходит для набора данных, это хорошая новость. Давайте обучим и протестируем обе модели по отдельности.

        matrix_utils.TrainTestSplitMatrices(Matrix,TrainMatrix,TestMatrix);
    
    Print("----> Ridge regression | Train ");
    
    ridge_reg = new CRidgeregression(TrainMatrix);
    vector coeff = ridge_reg.L2Norm(0.3);
    
    Linear_reg = new CLinearRegression(TrainMatrix,coeff); //passing the coefficients made by ridge regression
                                                      // to the Linear regression model
    Linear_reg.LRModelPred(TrainMatrix,acc);
    
    printf("Accuracy %.5f ",acc);
    
    Print("----> Ridge regression | Test");
    
    vector ridge_predictions = Linear_reg.LRModelPred(TestMatrix,acc); //making the predictions and storing them to a vector
    
    printf("Accuracy %.5f ",acc);
    
    delete(Linear_reg); //deleting that instance
    
    Print("\n----> Linear Regression | Train ");
     
    Linear_reg = new CLinearRegression(TrainMatrix); //new Linear reg instance that gets coefficients by least squares
    
    Linear_reg.LRModelPred(TrainMatrix,acc);
    
    printf("Accuracy %.5f ",acc);
    
    Print("----> Linear Regression | Test ");
    
    vector linear_pred = Linear_reg.LRModelPred(TestMatrix,acc); 
    
    printf("Accuracy %.5f ",acc);
    

    Выводимая информация:

    CS 0 13:27:40.744 TestEA (EURUSD,H1) ----> Ridge regression | Train 

    CS 0 13:27:40.744 TestEA (EURUSD,H1) Accuracy 0.97580 

    CS 0 13:27:40.744 TestEA (EURUSD,H1) ----> Ridge regression | Test

    CS 0 13:27:40.744 TestEA (EURUSD,H1) Accuracy 0.78620 

    CS 0 13:27:40.744 TestEA (EURUSD,H1)

    CS 0 13:27:40.744 TestEA (EURUSD,H1) ----> Linear Regression | Train 

    CS 0 13:27:40.744 TestEA (EURUSD,H1) Accuracy 0.97580 

    CS 0 13:27:40.744 TestEA (EURUSD,H1) ----> Linear Regression | Test 

    CS 0 13:27:40.744 TestEA (EURUSD,H1) Accuracy 0.78540 

    Похоже, что обе модели имели примерно одинаковую точность при обучении, но показали небольшую разницу в наборе данных для тестирования, что неплохо, учитывая, используемый гребневой регрессией штраф для наказания независимых переменных 0,3 достаточно мал. Нам еще предстоит определить, как выбрать правильное наказание.

    Когда я установил значение лямбда равным 10, точность обучения гребневой регрессии упала до 0,95760 от 0,97580, в то время как точность тестирования выросла с 0,78540 до 0,80050, что конечно, небольшая прибавка.


    Выбор правильного значения штрафа (лямбда)

    Чтобы найти правильные значения лямбда, мы воспользуемся методом LEAVE ONE OUT CROSS VALIDATION (LOOCV). Это метод поиска оптимальных параметров некоторых моделей в машинном обучении. Для этого метод проходит по всему набору данных, исключая некую выборку из набора данных. Затем обучает модель на оставшейся части набора данных, который равен n-1. Затем использует одну выборку, которая была исключена для тестирования, проходит по всему набору данных до n-й выборки и измеряет потери для всех значений на каждой итерации. Далее метод находит, где была функция минимальных потерь при определенных значениях лямбда. И кто дает наименьшую ошибку, тот и является лучшим параметром.

    Давайте импортируем класс перекрестной проверки, чтобы найти оптимальное значение лямбда.

    #include <MALE5\cross_validation.mqh>
CCrossValidation *cross_validation;

    Ниже приведен код для LOOCV для ридж-регрессии:

    double CCrossValidation::LeaveOneOut(double init, double step, double finale)
 {
    matrix XMatrix;
    vector yVector;
    
    matrix_utils.XandYSplitMatrices(Matrix,XMatrix,yVector);
 
    matrix train = Matrix; vector test = {};
    
    int size = int(finale/step);
    vector validation_output(ulong(size));
    vector lambda_vector(ulong(size));
    
    vector forecast(n); 
    vector actual = yVector;
    
    double lambda = init;
    
     for (int i=0; i<size; i++)
       {
         lambda += step;
         
          for (ulong j=0; j<n; j++)
            {               
               train.Copy(Matrix);
               ZeroMemory(test);
               
               test = XMatrix.Row(j);
               
               matrix_utils.MatrixRemoveRow(train,j);
               
               vector coeff = {};
               double acc =0;
               
                switch(selected_model)
                  {
                   case  RIDGE_REGRESSION:

                        ridge_regression = new CRidgeregression(train);
                        coeff = ridge_regression.L2Norm(lambda); //ridge regression
                        
                        Linear_reg = new CLinearRegression(train,coeff);   

                        forecast[j] =  Linear_reg.LRModelPred(test);  
                        
                        //---
                        
                        delete (Linear_reg); 
                        delete (ridge_regression);
                        
                     break; 
                  }
            }
          
          validation_output[i] = forecast.Loss(actual,LOSS_MSE)/double(n); 
          
          lambda_vector[i] = lambda;
          
          #ifdef DEBUG_MODE
             printf("%.5f LOOCV mse %.5f",lambda_vector[i],validation_output[i]);
          #endif           
       }

//---

      #ifdef  DEBUG_MODE
         matrix store_matrix(size,2);
         
         store_matrix.Col(validation_output,0);
         store_matrix.Col(lambda_vector,1); 
         
         string name = EnumToString(selected_model)+"\\LOOCV.csv";
         
         string header[2] = {"Validation output","lambda"};
         matrix_utils.WriteCsv(name,store_matrix,header);
      #endif 
      
    return(lambda_vector[validation_output.ArgMin()]);
 }

    Давайте воплотим все это в жизнь:

    int OnInit()
  {    
    matrix Matrix = matrix_utils.ReadCsv("NASDAQ_DATA.csv",",");  
    
    ridge_reg = new CRidgeregression(Matrix);
    
    cross_validation = new CCrossValidation(Matrix,RIDGE_REGRESSION);
    
    double best_lambda = cross_validation.LeaveOneOut(0,1,10);
    
    Print("Best lambda ",best_lambda);

    Выводимая информация:

    CS      0       10:12:51.346    ridge_test (EURUSD,H1)  1.00000 LOOCV mse 0.00020
CS      0       10:12:51.465    ridge_test (EURUSD,H1)  2.00000 LOOCV mse 0.00020
CS      0       10:12:51.576    ridge_test (EURUSD,H1)  3.00000 LOOCV mse 0.00020
CS      0       10:12:51.684    ridge_test (EURUSD,H1)  4.00000 LOOCV mse 0.00020
CS      0       10:12:51.788    ridge_test (EURUSD,H1)  5.00000 LOOCV mse 0.00020
CS      0       10:12:51.888    ridge_test (EURUSD,H1)  6.00000 LOOCV mse 0.00020
CS      0       10:12:51.987    ridge_test (EURUSD,H1)  7.00000 LOOCV mse 0.00021
CS      0       10:12:52.090    ridge_test (EURUSD,H1)  8.00000 LOOCV mse 0.00021
CS      0       10:12:52.201    ridge_test (EURUSD,H1)  9.00000 LOOCV mse 0.00021
CS      0       10:12:52.317    ridge_test (EURUSD,H1)  10.00000 LOOCV mse 0.00021
CS      0       10:12:52.319    ridge_test (EURUSD,H1)  Best lambda 1.0

    Если в коде все правильно, наилучшее значение лямбда равно единице при поиске от 1 до 10. Получается, значение лямбда для этой модели несколько меньше, поэтому я решил запустить цикл от 0 до 10, размер шага был установлен на 0,01 (всего 1000 итераций), это заняло около 5 минут, но мне удалось получить значение 0,09 как наилучшее значение лямбда. Ниже приведен график:

    LOOCV

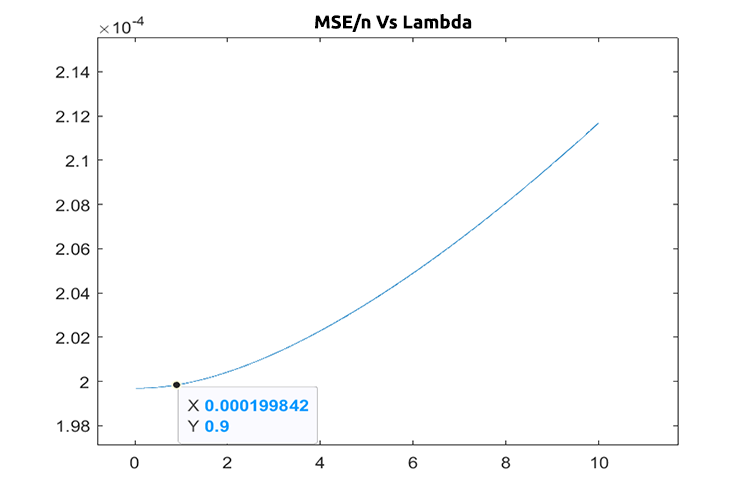
    Круто, теперь все в порядке с ридж-регрессией.


    Преимущества гребневой регрессии

    • Давайте посмотрим, какие же преимущества дает использование оценки гребневой регрессии
    •  Защищает модель от переобучения
    •  Снижает сложность модели
    •  Хорошо работает, как линейная регрессия в наборе данных с множеством переменных
    •  Не использует несмещенные оценки

    Недостатки гребневой регрессии

    •  Включает все предикторы в конечной модели
    •  Не может выбирать параметры
    •  Сводит коэффициенты к нулю
    •  Меняет дисперсию на смещение


    Заключительные мысли

    Гребневая регрессия может помочь избежать переобучения регрессионной модели при использовании множества переменных, но по-прежнему важно вручную удалять нежелательные переменные из модели. Например, из нашего набора NASDAQ_DATA мы могли бы удалить столбец RSI, потому что все мы знаем, что оно не коррелирует с нашей целевой переменной. Вот и все, что касается этой статьи. Вообзе эта тема очень обширная, и не могу сейчас охватить всего.

    Следите за развитием темы по ридж-регрессии в моем репозитории GitHub https://github.com/MegaJoctan/MALE5

    Имя файла Описание
    cross_validation.mqh  Как и кросс-валидация sklearn, файл содержит техники валидации LOOCV
    Linear regression.mqh  Этот файл содержит метод наименьших квадратов/модель линейной регрессии
     matrix_utils.mqh  Эта функция служебного класса содержит дополнительные функции матричных операций
     Preprocessing.mqh         Как и sklearn.preprocessing, класс содержит функции для контроля и масштабирования наборов данных
     Ridge Regression.mqh  Этот файл содержит модель гребневой регрессии и соответствующие функции.
     ridge_test.mq5  Это скрипт, который используется для тестирования всего, что мы обсуждали в этой статье.
     prepare_dataset.mq5  Этот скрипт создает набор данных для используемых индикаторов осцилляторов. Данные сохраняются в файл Oscillators.csv
     NASDAQ_DATA.csv  Этот CSV-файл содержит набор данных, который мы использовали в этой статье.

    Перевод с английского произведен MetaQuotes Ltd.
    Оригинальная статья: https://www.mql5.com/en/articles/11735

    Прикрепленные файлы |
    Загрузить ZIP
    MQL5.zip (142.77 KB)
    Предупреждение: все права на данные материалы принадлежат MetaQuotes Ltd. Полная или частичная перепечатка запрещена.

    Другие статьи автора

    Перейти к обсуждению на форуме трейдеров
    Измерение информативности индикатора Измерение информативности индикатора
    Машинное обучение стало популярным методом разработки стратегий. В трейдинге традиционно больше внимания уделяется максимизации прибыльности и точности прогнозов. При этом обработка данных, используемых для построения прогностических моделей, остается на периферии. В этой статье мы рассматриваем использование концепции энтропии для оценки пригодности индикаторов при построении прогностических моделей, как описано в книге Тимоти Мастерса "Тестирование и настройка систем рыночной торговли" (Testing and Tuning Market Trading Systems by Timothy Masters).
    Как выбрать торгового советника: Двадцать явных признаков плохого робота Как выбрать торгового советника: Двадцать явных признаков плохого робота
    В этой статье мы попытаемся ответить на вопрос, как выбрать подходящего торгового советника. Какие из них лучше всего подходят для нашего портфеля и как мы можем отсеять большую часть торговых роботов, доступных на рынке? В статье представлены двадцать явных признаков некачественного советника. Статья поможет вам принимать более обоснованные решения и создать коллекцию прибыльных торговых советников.
    Разработка торговой системы на основе индикатора Gator Oscillator Разработка торговой системы на основе индикатора Gator Oscillator
    Представляю вашему вниманию новую статью из серии, в которой мы учимся строить торговые системы на основе самых популярных индикаторов. На этот раз мы поговорим об индикаторе Gator Oscillator и создадим торговую систему по простым стратегиям.
    Популяционные алгоритмы оптимизации: Электромагнитный алгоритм (ElectroMagnetism-like algorithm, ЕМ) Популяционные алгоритмы оптимизации: Электромагнитный алгоритм (ElectroMagnetism-like algorithm, ЕМ)
    Статья описывает принципы, методы и возможности применения Электромагнитного алгоритма EM в различных задачах оптимизации. EM-алгоритм является эффективным инструментом оптимизации, способным работать с большими объемами данных и многомерными функциями.