Datenwissenschaft und maschinelles Lernen (Teil 10): Ridge-Regression
587
0
Einführung
Die Ridge-Regression ist eine Methode zur Schätzung der Koeffizienten von Mehrfach-Regressionsmodellen in Szenarien, in denen die unabhängigen Variablen stark korreliert sind. Die Methode bietet eine verbesserte Effizienz bei Parameterschätzungsproblemen im Austausch für ein tolerierbares Maß an Verzerrungen. Lasso (Least absolute shrinkage and selection operator) ist eine Regressionsanalysemethode, die sowohl eine Variablenauswahl als auch eine Regularisierung durchführt, um die Vorhersagegenauigkeit und die Interpretierbarkeit des resultierenden statistischen Modells zu verbessern. Lasso wurde ursprünglich für lineare Regressionsmodelle formuliert. Dieser einfache Fall verrät eine Menge über den Schätzer. Dazu gehören die Beziehung zur Ridge-Regression und zur Auswahl der besten Teilmengen sowie die Verbindungen zwischen Lasso-Koeffizientenschätzungen und dem so genannten Soft Thresholding. Sie zeigt auch, dass (wie bei der linearen Standardregression) die Koeffizientenschätzungen nicht eindeutig sein müssen, wenn die Kovariaten kollinear sind.
Um nun zu verstehen, warum wir solche Modelle überhaupt brauchen, müssen wir die Begriffe Bias und Varianz verstehen.
Bias
ist die Unfähigkeit des maschinellen Lernens, die wahre Beziehung zwischen der unabhängigen und der Antwortvariablen zu erfassenWas bedeutet das für das Modell?
- Kleines Bias: Das Modell mit einem geringen Bias macht weniger Annahmen über die Form der Zielfunktion
- Hohes Bias: Das Modell mit einem hohen Bias macht mehr Annahmen und kann Beziehungen innerhalb des Trainingsdatensatzes erfassen
Varianz
Die Varianz gibt an, wie stark sich eine Zufallsvariable von ihrem Erwartungswert unterscheidet.Wege zur Verringerung eines hohen Bias.
- Erhöhen der Eingabemerkmale, wenn das Modell nicht ausreichend angepasst ist.
- Verringern des Regularisierungsterms
- Verwenden komplexerer Merkmale, wie z. B. einige polynomiale Merkmale
Wege zur Verringerung einer hohen Varianz.
- Reduzieren der Eingabemerkmale; die Anzahl der Parameter, da das Modell nicht ausreichend angepasst ist
- Verwenden von nicht so komplexen Modellen
- Vergrößern der Trainingsdaten
- Erhöhen des Regularisierungsterms
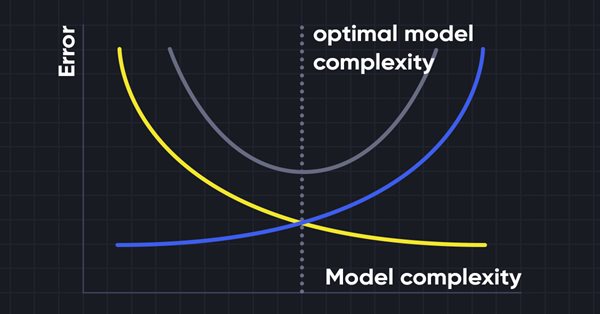
Bias-Varianz-Abgleich
Bei der Erstellung des maschinellen Lernmodells ist es sehr wichtig, auf Bias und Varianz zu achten, um eine Überanpassung des Modells zu vermeiden. Wenn das Modell sehr einfach und mit weniger Parametern ist, neigt es dazu, eine hohes Bias, aber eine geringere Varianz zu haben, während komplexe Modelle oft eine geringes Bias, aber eine hohe Varianz aufweisen. Daher ist es erforderlich, ein Gleichgewicht zwischen Bias und Varianzfehlern herzustellen.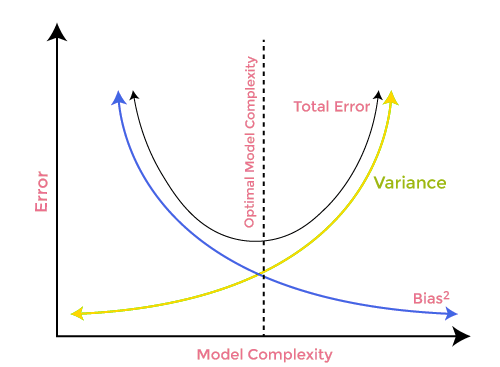
Für genaue Vorhersagen des Modells benötigen die Algorithmen ein geringeres Bias und eine geringere Varianz, was jedoch praktisch unmöglich ist, da Bias und Varianz in einem negativen Verhältnis zueinander stehen.
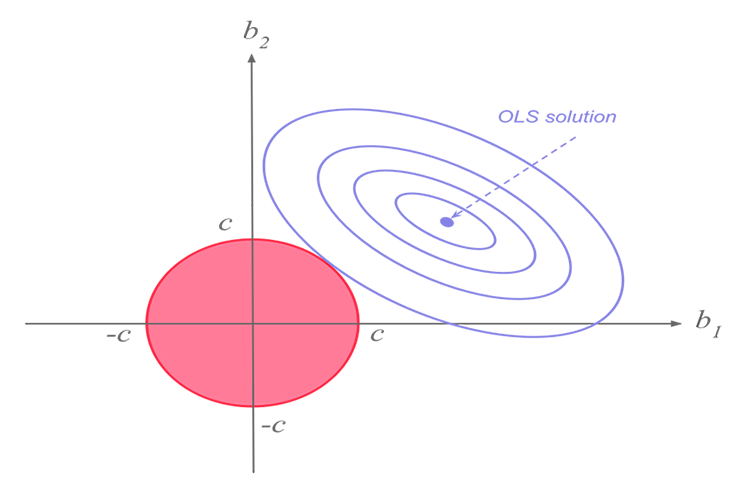
Ridge-Regression
Ridge- und Lasso-Regression haben beide dasselbe Ziel, weisen jedoch einen wesentlichen Unterschied auf, den wir später sehen werden, wenn wir in die Mathematik eintauchen und versuchen herauszufinden, wie die einzelnen Algorithmen funktionieren.Die Idee hinter der Ridge-Regression.
Bei einer Vielzahl von Messungen, die linear korreliert sind, können wir davon ausgehen, dass die kleinsten Quadrate die Beziehung zwischen der unabhängigen Variablen und der Zielvariablen sehr gut wiedergeben werden.
Sehen Sie sich das folgende Beispiel an, in dem die Größe der Mäuse gegen das Gewicht der Mäuse aufgetragen ist.
Nun wollen wir dieses Modell an einem neuen Datensatz testen;
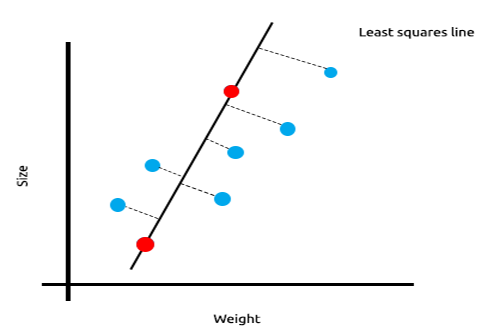
Die Summe der quadrierten Fehler für die Trainingsdaten ist Null, aber die Summe der quadrierten Residuen für die Testdaten ist groß, was bedeutet, dass unser Modell eine hohe Varianz hat.
Die Hauptidee hinter der Ridge- und Lasso-Regression ist es, das Modell zu finden, das nicht so gut zu den Trainingsdaten passt. Im Fachjargon des maschinellen Lernens sagt man, dass dieses Modell an die Trainingsdaten überangepasst ist.
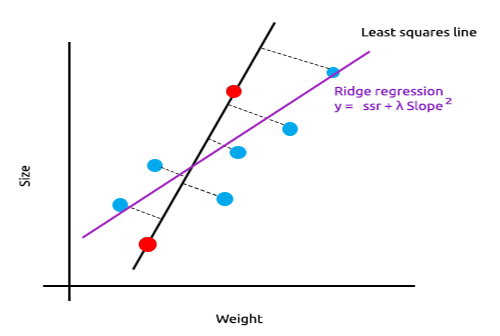
Bei der Ridge-Regression wird eine kleines Bias in die neue Linie eingebracht, was zu einem deutlichen Rückgang der Varianz führt. Da die Ridge-Regression eine kleines Bias eingeführt hat, passt das Modell nun nicht mehr so gut zu den Trainings- und Testdaten, sodass wir langfristig ein zuverlässiges Modell erhalten.
Wann sind diese regularisierten Modelle zu verwenden?
Man kann sich fragen, wenn die Methode der kleinsten Quadrate bzw. das lineare Regressionsmodell so gut funktioniert, warum dann diese L1norm- und L2Norm-Modelle verwenden?
Um dies zu verstehen, sehen wir uns an, wie eine multivariable lineare Regression auf dem trainierten Datensatz abschneidet
Um den Punkt, den ich zu machen versuche, gut zu illustrieren, habe ich den Datensatz voller Oszillatoren und den Volumenindikator für EURUSD vorbereitet;
Ohne auch nur einen Blick auf die Korrelationsmatrix zu werfen, weiß jeder, der mit diesen Indikatoren vertraut ist, mit Sicherheit, dass diese Indikatoren für Regressionsprobleme nicht geeignet sind. Nachstehend ist die Korrelationsmatrix aufgeführt
ArrayPrint(matrix_utils.csv_header); Print(Matrix.CorrCoef(false));
Ergebnis:
CS 0 06:29:41.493 TestEA (EURUSD,H1) "Stochastic" "Rsi" "Volume" "Bears" "Bulls" "EURUSD" CS 0 06:29:41.493 TestEA (EURUSD,H1) [[1,0.680705511991766,0.02399740959375265,0.6910892641498844,0.7291018045506749,0.1490856367010467] CS 0 06:29:41.493 TestEA (EURUSD,H1) [0.680705511991766,1,0.07620207894739518,0.8184961346648213,0.8258569040865805,0.1567269000583347] CS 0 06:29:41.493 TestEA (EURUSD,H1) [0.02399740959375265,0.07620207894739518,1,0.3752014290536041,-0.1289026185114097,-0.1024017077869821] CS 0 06:29:41.493 TestEA (EURUSD,H1) [0.6910892641498844,0.8184961346648213,0.3752014290536041,1,0.7826404088603456,0.07283638913665436] CS 0 06:29:41.493 TestEA (EURUSD,H1) [0.7291018045506749,0.8258569040865805,-0.1289026185114097,0.7826404088603456,1,0.08392530400705019] CS 0 06:29:41.493 TestEA (EURUSD,H1) [0.1490856367010467,0.1567269000583347,-0.1024017077869821,0.07283638913665436,0.08392530400705019,1]]Der Stochastik-Indikator und der RSI scheinen am besten mit den anderen Indikatoren korreliert zu sein, aber nur zu etwa 14 bzw. 15 Prozent. Wir erstellen ein lineares Regressionsmodell, das nur mit dem stochastischen Indikator beginnt, und fügen dann die unabhängigen Variablen bzw. die Werte anderer Indikatoren hinzu.
Tabelle der Ergebnisse:
| Unabhängige Variablen | R2 Score(Genauigkeit) |
|---|---|
| Stochastic | 1.2 % |
| Stochastik und RSI | 1.8 % |
| Stochastik, RSI und Volumen | 2.8 % |
| Stochastic, RSI, Volumen, Bears Power und Bulls Power (Alle unabhängigen Variablen) | 4.9% |
Die Korrelation für die unabhängigen Variablen, die ich in diesem Beispiel verwendet habe, ist sehr gering, weshalb Sie jedes Mal, wenn eine neue unabhängige Variable hinzugefügt wird, eine leichte Verbesserung der Genauigkeit sehen. Das ist jedoch nicht der Fall, wenn die Variablen zu jeweils 30 % bis 40 % korreliert sind. Wir können beobachten, dass unser Modell in der Trainingsphase eine Genauigkeit von 90 % erreicht, wenn wir ihm zu viele dieser unabhängigen Variablen geben.
Um dieses Problem zu lösen, wurden sowohl die Ridge- als auch die Lasso-Regression eingeführt. Wie bereits erwähnt, führt das Hinzufügen einer Art von Bias zu einem deutlichen Rückgang der Varianz.
Theorie der Ridge-Regression
Die Ridge-Regression selbst ist eine Methode zur Schätzung der Koeffizienten eines linearen Regressionsmodells, wenn die unabhängigen Variablen stark korreliert sind.
Die Ridge-Regression wurde als mögliche Lösung für die Ungenauigkeit der Schätzer der kleinsten Quadrate entwickelt, wenn die linearen Regressionsmodelle einige multikollineare (hoch korrelierte) Merkmale aufweisen, indem ein Ridge-Regressionsschätzer (RR) erstellt wurde. Dies führt zu präziseren Ridge-Parametern, da die Varianz und das Bias oft geringer sind als bei den Schätzern der kleinsten Quadrate.
Ridge-Schätzer
Analog zum gewöhnlichen Schätzer der kleinsten Quadrate ist der einfache Ridge-Schätzer gegeben durch
wobei y die Matrix der unabhängigen Variablen ist, X die Entwurfsmatrix, I die Identitätsmatrix und der Ridge-Parameter λ ist größer oder gleich Null ist.
Lassen Sie uns dafür einen Code schreiben:
CRidgeregression::CRidgeregression(matrix &_matrix) { n = _matrix.Rows(); k = _matrix.Cols(); pre_processing.Standardization(_matrix); m_dataset.Copy(_matrix); matrix_utils.XandYSplitMatrices(_matrix,XMatrix,yVector); YMatrix = matrix_utils.VectorToMatrix(yVector); //--- Id_matrix.Resize(k,k); Id_matrix.Identity(); }
Im Funktionskonstruktor werden drei wichtige Dinge erledigt: Erstens die Standardisierung der Daten. Genau wie der multivariable Gradientenabstieg und viele andere maschinelle Lerntechniken arbeitet die Ridge-Regression mit einem standardisierten Datensatz. Anschließend werden die Daten in x- und y-Matrizen aufgeteilt, und schließlich wird die Identitätsmatrix erstellt.
Innerhalb der L2Norm-Funktion:
vector CRidgeregression::L2Norm(double lambda) { matrix design = matrix_utils.DesignMatrix(XMatrix); matrix XT = design.Transpose(); matrix XTX = XT.MatMul(design); matrix lamdaxI = lambda * Id_matrix; //Print("LambdaxI \n",lamdaxI); //Print("XTX\n",XTX); matrix sum_matrix = XTX + lamdaxI; matrix Inverse_sum = sum_matrix.Inv(); matrix XTy = XT.MatMul(YMatrix); Betas = Inverse_sum.MatMul(XTy); #ifdef DEBUG_MODE Print("Betas\n",Betas); #endif return(matrix_utils.MatrixToVector(Betas)); }
Diese Funktion tut alles, was in der obigen Formel zur Ermittlung der Koeffizienten mit Hilfe der Ridge-Regression beschrieben ist.
Um zu sehen, wie das funktioniert, verwenden wir einen anderen Datensatz NASDAQ_DATA.csv, den die Leser dieser Artikelserie bereits kennen.
int OnInit() { //--- matrix Matrix = matrix_utils.ReadCsv("NASDAQ_DATA.csv",","); pre_processing.Standardization(Matrix); Linear_reg = new CLinearRegression(Matrix); ridge_reg = new CRidgeregression(Matrix); ridge_reg.L2Norm(0.3); }
Ich habe für die Ridge-Regression einen zufälligen Strafwert von 0,3 festgelegt, damit wir sehen können, was dabei herauskommt. Nun ist es an der Zeit, die Funktion auszuführen und zu sehen, welche Koeffizienten dabei herauskommen;
CS 0 10:27:41.338 TestEA (EURUSD,H1) [[5.015577002384403e-16]
CS 0 10:27:41.338 TestEA (EURUSD,H1) [0.6013523727380532]
CS 0 10:27:41.338 TestEA (EURUSD,H1) [0.3381524618200134]
CS 0 10:27:41.338 TestEA (EURUSD,H1) [0.2119467984461254]]
Da die Methode der kleinsten Quadrate den Datensatz nicht standardisiert, sollten wir ihn ebenfalls standardisieren, bevor wir die Daten in das Modell eingeben.
matrix Matrix = matrix_utils.ReadCsv("NASDAQ_DATA.csv",","); pre_processing.Standardization(Matrix); Linear_reg = new CLinearRegression(Matrix);
Ausgabe:
CS 0 10:27:41.338 TestEA (EURUSD,H1) Betas
CS 0 10:27:41.338 TestEA (EURUSD,H1) [[-4.143037461930866e-14]
CS 0 10:27:41.338 TestEA (EURUSD,H1) [0.6034777119810752]
CS 0 10:27:41.338 TestEA (EURUSD,H1) [0.3363532376334173]
CS 0 10:27:41.338 TestEA (EURUSD,H1) [0.21126507562567]]
Die Koeffizienten sehen etwas anders aus, sodass ich davon ausgehe, dass unsere Funktion funktioniert. Lassen Sie uns jedes der Modelle trainieren und testen und dann schließlich ihre jeweiligen Graphen darstellen, um mehr zu verstehen.
Da die Ridge-Regression selbst kein Modell ist, sondern ein Schätzer für die Koeffizienten, die dann mit dem linearen Regressionsmodell verwendet werden müssen, habe ich einige Änderungen an der Klasse der linearen Regression vorgenommen, die wir in Teil 3 besprochen haben.
Im Konstruktor der Klasse Lineare Regression wird das Modell trainiert. Es ist ein Bereich, in dem die Koeffizienten dann gespeichert werden, um vom Rest der Funktionen verwendet zu werden. Ich habe einen neuen Konstruktor hinzugefügt, der es erlaubt, die Koeffizienten an das Modell zu übergeben, Dies wird uns helfen, den minimalen Aufwand zu betreiben, wenn wir das nächste Mal andere Schätzer verwenden, um die Koeffizienten zu erhalten, die wir für unser Regressionsmodell verwenden wollen.
class CLinearRegression { public: CLinearRegression(matrix &Matrix_); //Least squares estimator CLinearRegression(matrix<double> &Matrix_, double Lr, uint iters = 1000); //Lr by Gradient descent CLinearRegression(matrix &Matrix_, vector &coeff_vector); ~CLinearRegression(void);
Ridge vs. Lineare Regression
Print("----> Ridge regression"); ridge_reg = new CRidgeregression(Matrix); vector coeff = ridge_reg.L2Norm(0.3); Linear_reg = new CLinearRegression(Matrix,coeff); //passing the coefficients made by ridge regression // to the Linear regression model double acc =0; vector ridge_predictions = Linear_reg.LRModelPred(Matrix,acc); //making the predictions and storing them to a vector delete(Linear_reg); //deleting that instance Print("----> Linear Regression"); pre_processing.Standardization(Matrix); Linear_reg = new CLinearRegression(Matrix); //new Linear reg instance that gets coefficients by least squares vector linear_pred = Linear_reg.LRModelPred(Matrix,acc);
Ausgaben:
CS 0 11:35:52.153 TestEA (EURUSD,H1) ----> Ridge regression
CS 0 11:35:52.153 TestEA (EURUSD,H1) Betas
CS 0 11:35:52.153 TestEA (EURUSD,H1) [[-4.142058558619502e-14]
CS 0 11:35:52.153 TestEA (EURUSD,H1) [0.601352372738047]
CS 0 11:35:52.153 TestEA (EURUSD,H1) [0.3381524618200102]
CS 0 11:35:52.153 TestEA (EURUSD,H1) [0.2119467984461223]]
CS 0 11:35:52.154 TestEA (EURUSD,H1) R squared 0.982949 Adjusted R 0.982926
CS 0 11:35:52.154 TestEA (EURUSD,H1) ----> Linear Regression
CS 0 11:35:52.154 TestEA (EURUSD,H1) Betas
CS 0 11:35:52.154 TestEA (EURUSD,H1) [[5.014846059117108e-16]
CS 0 11:35:52.154 TestEA (EURUSD,H1) [0.6034777119810601]
CS 0 11:35:52.154 TestEA (EURUSD,H1) [0.3363532376334217]
CS 0 11:35:52.154 TestEA (EURUSD,H1) [0.2112650756256718]]
CS 0 11:35:52.154 TestEA (EURUSD,H1) R squared 0.982933 Adjusted R 0.982910
Die Modelle haben eine etwas andere Leistung, wenn Sie alle Daten als Trainingsdaten verwenden.
Wenn die Ausgaben gespeichert und auf der gleichen Achse aufgetragen wurden, ist dies unsere Grafik;
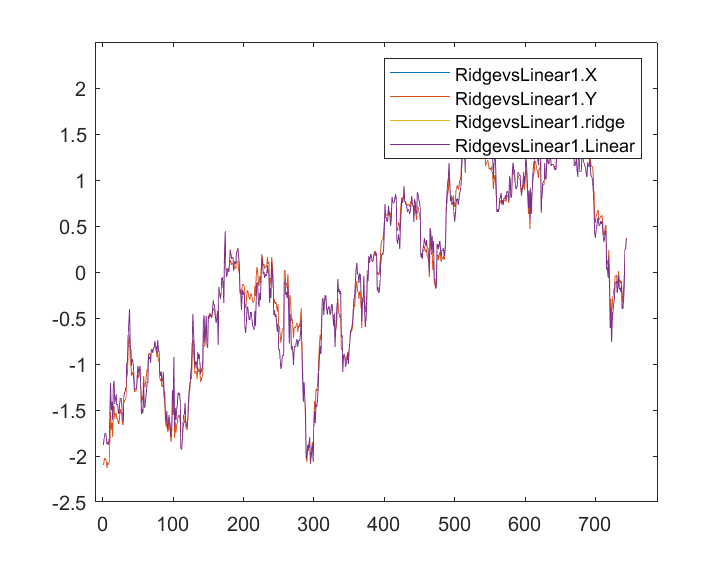
Ich kann kaum einen Unterschied zwischen dem linearen Modell und dem blau markierten Prädiktor erkennen, ich kann nur den Unterschied zwischen den beiden Modellen sehen, und die Ridge-Regression passt nicht gut zum Datensatz, das ist eine gute Nachricht. Lassen Sie uns die beiden Modelle nacheinander trainieren und testen.
matrix_utils.TrainTestSplitMatrices(Matrix,TrainMatrix,TestMatrix); Print("----> Ridge regression | Train "); ridge_reg = new CRidgeregression(TrainMatrix); vector coeff = ridge_reg.L2Norm(0.3); Linear_reg = new CLinearRegression(TrainMatrix,coeff); //passing the coefficients made by ridge regression // to the Linear regression model Linear_reg.LRModelPred(TrainMatrix,acc); printf("Accuracy %.5f ",acc); Print("----> Ridge regression | Test"); vector ridge_predictions = Linear_reg.LRModelPred(TestMatrix,acc); //making the predictions and storing them to a vector printf("Accuracy %.5f ",acc); delete(Linear_reg); //deleting that instance Print("\n----> Linear Regression | Train "); Linear_reg = new CLinearRegression(TrainMatrix); //new Linear reg instance that gets coefficients by least squares Linear_reg.LRModelPred(TrainMatrix,acc); printf("Accuracy %.5f ",acc); Print("----> Linear Regression | Test "); vector linear_pred = Linear_reg.LRModelPred(TestMatrix,acc); printf("Accuracy %.5f ",acc);
Ausgabe:
CS 0 13:27:40.744 TestEA (EURUSD,H1) ----> Ridge regression | Train
CS 0 13:27:40.744 TestEA (EURUSD,H1) Accuracy 0.97580
CS 0 13:27:40.744 TestEA (EURUSD,H1) ----> Ridge regression | Test
CS 0 13:27:40.744 TestEA (EURUSD,H1) Accuracy 0.78620
CS 0 13:27:40.744 TestEA (EURUSD,H1)
CS 0 13:27:40.744 TestEA (EURUSD,H1) ----> Linear Regression | Train
CS 0 13:27:40.744 TestEA (EURUSD,H1) Accuracy 0.97580
CS 0 13:27:40.744 TestEA (EURUSD,H1) ----> Linear Regression | Test
CS 0 13:27:40.744 TestEA (EURUSD,H1) Accuracy 0.78540
Es scheint, dass beide Modelle ungefähr die gleiche Genauigkeit im Training hatten, aber einen leichten Unterschied im Testdatensatz, nicht schlecht, wenn man bedenkt, dass die Strafe, die die Ridge-Regression verwendet, um die unabhängigen Variablen zu bestrafen, mit 0,3 gering ist und wir noch herausfinden müssen, wie wir die richtige Strafe wählen.
Wenn ich den Lambda-Wert auf 10 setze, sinkt die Trainingsgenauigkeit der Ridge-Regression von 0.95760 auf 0.97580, während die Testgenauigkeit von 0.78540 auf 0.80050 steigt, was natürlich eine kleine Steigerung darstellt.
Die Wahl des richtigen Strafwertes (Lambda)
Um die richtigen Lambda-Werte zu finden, müssen wir die Technik der LEAVE ONE OUT CROSS VALIDATION (LOOCV) verwenden. Für diejenigen, die damit nicht vertraut sind, ist dies die Technik, um die optimalen Parameter einiger Modelle in ML zu finden. Die Art und Weise, wie dies erreicht wird, besteht darin, dass der gesamte Datensatz durchlaufen wird, wobei ich eine Probe aus dem Datensatz auslasse, dann das Modell mit dem Rest des Datensatzes trainiert wird, der n-1 ist, und dann die eine Probe, die ausgelassen wurde, als Testprobe verwendet wird, Es geht durch den gesamten Datensatz bis zur n-ten Stichprobe, misst schließlich den Verlust für alle Werte in jeder Iteration und findet schließlich heraus, wo die minimale Verlustfunktion bei bestimmten Lambda-Werten liegt, d.h. diejenige, die den geringsten Fehler erzeugt, ist der beste Parameter, weitere Informationen finden Sie hier.
Wir importieren die Klasse der Kreuzvalidierung, die uns helfen soll, den optimalen Wert des Lambdas zu finden.
#include <MALE5\cross_validation.mqh>
CCrossValidation *cross_validation; Nachstehend finden Sie den Code von LOOCV für die Ridge-Regression;
double CCrossValidation::LeaveOneOut(double init, double step, double finale) { matrix XMatrix; vector yVector; matrix_utils.XandYSplitMatrices(Matrix,XMatrix,yVector); matrix train = Matrix; vector test = {}; int size = int(finale/step); vector validation_output(ulong(size)); vector lambda_vector(ulong(size)); vector forecast(n); vector actual = yVector; double lambda = init; for (int i=0; i<size; i++) { lambda += step; for (ulong j=0; j<n; j++) { train.Copy(Matrix); ZeroMemory(test); test = XMatrix.Row(j); matrix_utils.MatrixRemoveRow(train,j); vector coeff = {}; double acc =0; switch(selected_model) { case RIDGE_REGRESSION: ridge_regression = new CRidgeregression(train); coeff = ridge_regression.L2Norm(lambda); //ridge regression Linear_reg = new CLinearRegression(train,coeff); forecast[j] = Linear_reg.LRModelPred(test); //--- delete (Linear_reg); delete (ridge_regression); break; } } validation_output[i] = forecast.Loss(actual,LOSS_MSE)/double(n); lambda_vector[i] = lambda; #ifdef DEBUG_MODE printf("%.5f LOOCV mse %.5f",lambda_vector[i],validation_output[i]); #endif } //--- #ifdef DEBUG_MODE matrix store_matrix(size,2); store_matrix.Col(validation_output,0); store_matrix.Col(lambda_vector,1); string name = EnumToString(selected_model)+"\\LOOCV.csv"; string header[2] = {"Validation output","lambda"}; matrix_utils.WriteCsv(name,store_matrix,header); #endif return(lambda_vector[validation_output.ArgMin()]); }
Lassen Sie uns das in die Tat umsetzen;
int OnInit() { matrix Matrix = matrix_utils.ReadCsv("NASDAQ_DATA.csv",","); ridge_reg = new CRidgeregression(Matrix); cross_validation = new CCrossValidation(Matrix,RIDGE_REGRESSION); double best_lambda = cross_validation.LeaveOneOut(0,1,10); Print("Best lambda ",best_lambda);
Ausgabe:
CS 0 10:12:51.346 ridge_test (EURUSD,H1) 1.00000 LOOCV mse 0.00020 CS 0 10:12:51.465 ridge_test (EURUSD,H1) 2.00000 LOOCV mse 0.00020 CS 0 10:12:51.576 ridge_test (EURUSD,H1) 3.00000 LOOCV mse 0.00020 CS 0 10:12:51.684 ridge_test (EURUSD,H1) 4.00000 LOOCV mse 0.00020 CS 0 10:12:51.788 ridge_test (EURUSD,H1) 5.00000 LOOCV mse 0.00020 CS 0 10:12:51.888 ridge_test (EURUSD,H1) 6.00000 LOOCV mse 0.00020 CS 0 10:12:51.987 ridge_test (EURUSD,H1) 7.00000 LOOCV mse 0.00021 CS 0 10:12:52.090 ridge_test (EURUSD,H1) 8.00000 LOOCV mse 0.00021 CS 0 10:12:52.201 ridge_test (EURUSD,H1) 9.00000 LOOCV mse 0.00021 CS 0 10:12:52.317 ridge_test (EURUSD,H1) 10.00000 LOOCV mse 0.00021 CS 0 10:12:52.319 ridge_test (EURUSD,H1) Best lambda 1.0
Unter der Annahme, dass es keine Fehler im Code gibt, ist der beste Wert von lambda eins, wenn die Suche von 1 bis 10 ging. Dies sagt uns, dass der Wert von Lambda für dieses Modell etwas kleiner ist, also beschloss ich, die Schleife von 0 bis 10 laufen zu lassen, wobei die Schrittweite auf 0,01 gesetzt wurde (insgesamt 1000 Iterationen), es dauerte etwa 5 Minuten, aber ich war in der Lage, den Wert von 0,09 als den besten Wert von Lambda zu erhalten, unten ist die Darstellung;
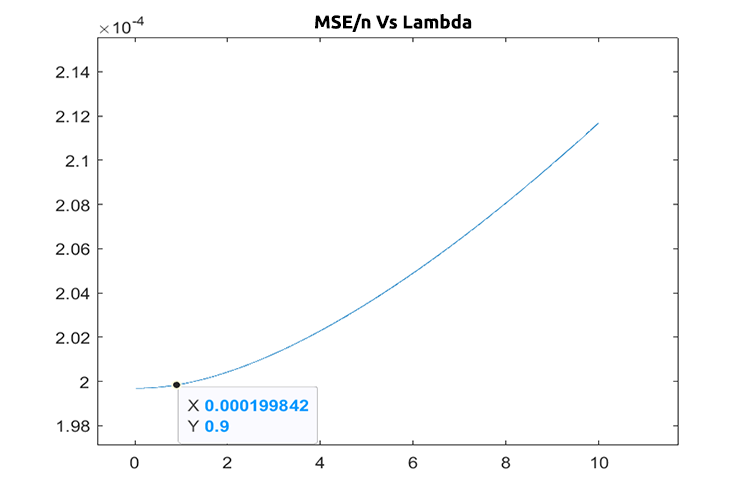
Cool, jetzt ist alles in Ordnung mit dem Ridge-Regressionsteil.
Vorteile der Ridge-Regression
- Einige Vorteile der Verwendung eines Ridge-Regressionsschätzers
- Sie schützt das Modell vor Überanpassung
- Die Modellkomplexität wird reduziert
- Sie schneidet besser ab als die lineare Regression im multivariablen Datensatz
- Sie braucht keine unverzerrten Schätzer
Nachteile der Ridge-Regression
- Es werden alle Prädiktoren in das endgültige Modell aufgenommen
- Sie ist nicht in der Lage, eine Merkmalsauswahl durchzuführen.
- Sie schrumpft die Koeffizienten gegen Null
- Sie tauscht Varianz gegen Verzerrung
Abschließende Überlegungen
Die Ridge-Regression kann helfen, eine Überanpassung des Regressionsmodells in Fällen zu vermeiden, in denen es multivariable Variablen gibt, aber es ist immer noch entscheidend, unerwünschte Variablen selbst manuell aus dem Modell zu vermeiden/zu entfernen. Aus unseren NASDAQ_DATA hätten wir die RSI-Spalte entfernen können, weil wir wahrscheinlich alle wissen, dass sie nicht mit unserer Zielvariablen korreliert.
Verfolgen Sie die Entwicklung der Ridge Regression auf meinem GitHub Repo > https://github.com/MegaJoctan/MALE5
| Dateiname | Beschreibung |
|---|---|
| cross_validation.mqh | Ebenso wie Kreuzvalidierung sklearn enthält diese Datei Validierungstechniken wie LOOCV |
| Linear regression.mqh | Diese Datei enthält die Methode der kleinsten Quadrate / das lineare Regressionsmodell |
| matrix_utils.mqh | Diese Funktion der Utility-Klasse enthält zusätzliche Funktionen für Matrixoperationen |
| Preprocessing.mqh | Ebenso wie sklearn.preprocessing enthält diese Klasse Funktionen, die zur Bearbeitung und Skalierung von Datensätzen verwendet werden können. |
| Ridge Regression.mqh | Diese Datei enthält das Ridge-Regressionsmodell und die zugehörigen Funktionen |
| ridge_test.mq5 | Dieses Skript wird verwendet, um alles zu testen, was wir in diesem Artikel besprochen haben |
| prepare_dataset.mq5 | Dieses Skript erstellt einen Datensatz für die Oszillator-Indikatoren, die wir zuvor besprochen haben. Diese Daten werden in der Datei Oscillators.csv gespeichert |
| NASDAQ_DATA.csv | Diese csv-Datei enthält den Datensatz, den wir in diesem Artikel verwendet haben |
Übersetzt aus dem Englischen von MetaQuotes Ltd.
Originalartikel: https://www.mql5.com/en/articles/11735
Erstellen eines EA, der automatisch funktioniert (Teil 08): OnTradeTransaktion
MQL5 Kochbuch — Datenbank für makroökonomische Ereignisse
Neuronale Netze leicht gemacht (Teil 34): Vollständig parametrisierte Quantilfunktion
Testen und Optimieren von Strategien für binäre Optionen in MetaTrader 5
- Freie Handelsapplikationen
- Über 8.000 Signale zum Kopieren
- Wirtschaftsnachrichten für die Lage an den Finanzmärkte
Sie stimmen der Website-Richtlinie und den Nutzungsbedingungen zu.