Análise de ciclos usando o algoritmo de Goertzel

Introdução

O algoritmo de Goertzel é uma técnica de processamento digital de sinais conhecida por sua eficiência na detecção de componentes de frequência específicos. Sua precisão, capacidade em tempo real e eficiência computacional o tornam adequado para a análise de séries temporais financeiras. Neste artigo, examinaremos e demonstraremos maneiras práticas de como o método pode ser usado para analisar ciclos dominantes para possível desenvolvimento de estratégias. Vamos dar uma olhada na implementação do algoritmo em MQL5 e apresentar um exemplo de como usar o código para identificar ciclos em cotações de preços.

O algoritmo de Goertzel

O algoritmo de Goertzel, que recebe seu nome de Gerald Goertzel, é utilizado para calcular termos individuais da Transformada Discreta de Fourier (DFT) de maneira eficiente. Essa técnica foi introduzida inicialmente em 1958 e desde então tem sido aplicada em diversas áreas, incluindo engenharia, matemática e física. A principal aplicação do algoritmo de Goertzel é identificar componentes de frequência específicos dentro de um sinal digital, tornando-o altamente valioso em cenários onde apenas alguns componentes de frequência são importantes. Comparado à Transformada Rápida de Fourier (FFT), ele requer menos cálculos ao detectar um número limitado de componentes de frequência, tornando-o eficiente computacionalmente.

É representado pela fórmula:

Onde:

• X é a magnitude acumulada na frequência k
• cos() é a função cosseno
• π é a constante matemática pi (aproximadamente 3.14159)
• k é o índice do bin de frequência de interesse (variando de 0 a N - 1, onde N é o número total de amostras)
• N é o comprimento do sinal de entrada
• X[k-1] e X[k-2] são os valores calculados anteriormente de X para a frequência k
• x[n] é a amostra n-ésima do sinal de entrada

Para calcular os componentes real e imaginário usando o algoritmo de Goertzel, precisamos iterar pelas amostras do sinal de entrada e realizar os cálculos a seguir:

Vamos inicializar as variáveis:

• N - o número de amostras no sinal de entrada.
• k - o índice da faixa de frequência de interesse (0 <= k < N).
• omega - a frequência correspondente à faixa de frequência desejada (2 * pi * k / N).
• coeff - o coeficiente usado no cálculo (2 * cos(omega)).
• s_prev - o valor anterior da variável state.
• s_prev2 - o valor antes do valor anterior da variável state.
• s - o valor atual da variável state.

Vamos percorrer cada amostra no sinal de entrada:

• Atualizar o valor atual da variável "state" (s) usando a fórmula:

  
  

onde x[n] é a amostra de entrada atual.

Atualizar os valores anteriores da variável "state":

Após iterar por todas as amostras, os valores finais das variáveis "state" (S, Sprev, Sprev2) representam os componentes real e imaginário da DFT no bin de frequência desejado (k).

O componente real é dado por:

O componente imaginário é dado por:

As frequências que podem ser detectadas pela DFT variam de 1/N a (N/2)/N, onde N representa o número de pontos de dados na série ou, no nosso caso, o número de barras de preços em análise. Ao analisar cotações de preços, pode ser limitante apenas observar bandas de frequência restritas ao espaçamento de 1/N. Esta é a razão pela qual pessoas como J. Ehlers propuseram a técnica de Análise Espectral de Entropia Máxima (Maximum Entropy Spectral Analysis, MESA) para superar essa limitação.

O algoritmo de Goertzel pode ser usado como uma alternativa ao MESA de Ehler, o que, de acordo com um artigo de pesquisa escrito por D. Meyers, é capaz de obter melhores resultados (em termos de resolução espectral) em certas condições. Uma dessas condições está relacionada à quantidade de ruído contido no sinal. Segundo Meyers, o algoritmo de Goertzel é capaz de superar a técnica MESA, especialmente ao lidar com sinais ruidosos, o que é um problema comum com séries temporais financeiras. Leitores interessados podem ler o artigo técnico disponível em formato PDF.

A classe CGoertzel

A classe CGoertzel é uma implementação simples do algoritmo de Goertzel que permite amostrar uma variedade de frequências em um conjunto de dados.

//+------------------------------------------------------------------+
//| CGoertze class implementing Goertzel algorithm                   |
//+------------------------------------------------------------------+
class CGoertzel
  {
private:
   uint              m_minPeriod;
   uint              m_maxPeriod;
public:
   //constructor
                     CGoertzel(void)
     {
      m_minPeriod=m_maxPeriod=0;
     }
   //destructor
                    ~CGoertzel(void)
     {
     }
   //get methods
   uint              GetMinPeriodLength(void) {   return m_minPeriod;}
   uint              GetMaxPerodLength(void) {   return m_maxPeriod;}
   //set methods
   bool              SetMinMaxPeriodLength(const uint min_wavePeriod, const uint max_wavePeriod);
   // goertzel dft transform methods
   bool              Dft(const double &in_data[],complex &out[]);
   bool              Dft(const double &in_data[], double &out_real[], double &out_imaginary[]);
   bool              Dft(const uint min_wavePeriod,const uint max_wavePeriod,const double &in_data[],complex &out[]);
   bool              Dft(const uint min_wavePeriod,const uint max_wavePeriod,const double &in_data[], double &out_real[], double &out_imaginary[]);
  };

Como o algoritmo de Goertzel amostra apenas um número limitado de frequências de cada vez, precisamos definir a faixa de frequência de nosso interesse. Na classe, a faixa de frequência é definida em termos do período mínimo e máximo das frequências.

Existem duas maneiras de definir esses valores: usando o SetMinMaxPeriodLength(), os períodos mínimo e máximo podem ser especificados.

//+------------------------------------------------------------------+
//| Set the Minimum and maximum periods of selected frequency band   |
//+------------------------------------------------------------------+
bool CGoertzel::SetMinMaxPeriodLength(const uint min_wavePeriod,const uint max_wavePeriod)
  {
   if(min_wavePeriod<2 || min_wavePeriod>=max_wavePeriod)
     {
      Print("Critical error min_wavePeriod cannot be less than max_wavePeriod or less than 2");
      return false;
     }

   m_minPeriod=min_wavePeriod;
   m_maxPeriod=max_wavePeriod;

   return true;
  }

Além disso, a faixa de frequência pode ser definida ao chamar uma das duas sobrecargas do método Dft.

//+-----------------------------------------------------------------------------------+
//| Calculate the frequency domain representation of input array as complex array     |
//+-----------------------------------------------------------------------------------+
bool CGoertzel::Dft(const uint min_wavePeriod,const uint max_wavePeriod,const double &in_data[],complex &out[])
  {
   if(!SetMinMaxPeriodLength(min_wavePeriod,max_wavePeriod))
      return(false);

   return Dft(in_data,out);
  }
//+------------------------------------------------------------------------------------+
//| Calculate the frequency domain representation of input array as two separate arrays|
//+------------------------------------------------------------------------------------+
bool CGoertzel::Dft(const uint min_wavePeriod,const uint max_wavePeriod,const double &in_data[], double &out_real[], double &out_imaginary[])
  {
   if(!SetMinMaxPeriodLength(min_wavePeriod,max_wavePeriod))
      return(false);

   return Dft(in_data,out_real,out_imaginary);

  }

Dependendo da versão do método Dft usada, os componentes real e imaginário da DFT são gerados em arrays separados ou em um único array de tipo complexo.

//+-----------------------------------------------------------------------------------+
//| Calculate the frequency domain representation of input array as complex array     |
//+-----------------------------------------------------------------------------------+
bool CGoertzel::Dft(const double &in_data[],complex &out[])
  {
   uint minsize=(3*m_maxPeriod);
   uint fullsize=in_data.Size();

   if(fullsize<minsize)
     {
      Print("Sample size too small in relation to the largest period cycle parameter");
      return false;
     }

   if(m_minPeriod>=m_maxPeriod || m_minPeriod<2)
     {
      Print("Critical error: Invalid input parameters :- max_period should be larger than min_period and min_period cannot be less than 2");
      return false;
     }

   if(out.Size()!=m_maxPeriod)
      ArrayResize(out,m_maxPeriod);
   
   double v0,v1,v2,freq,coeff,real,imag;


   for(uint i=0; i<m_maxPeriod; i++)
     {
      if(i<m_minPeriod)
        {
         out[i].imag=out[i].real=0.0;
         continue;
        }

      v0=v1=v2=0.0;
      freq=MathPow(i,-1);
      coeff=2.0*MathCos(2.0*M_PI*freq);
      for(uint k=minsize-1; k>0; k--)
        {
         v0=coeff*v1-v2+in_data[k];
         v2=v1;
         v1=v0;
        }

      real=v1-v2*0.5*coeff;

      imag=v2*MathSin(2*M_PI*freq);

      out[i].real=real;
      out[i].imag=imag;

     }

   return true;
  }
//+------------------------------------------------------------------------------------+
//| Calculate the frequency domain representation of input array as two separate arrays|
//+------------------------------------------------------------------------------------+
bool CGoertzel::Dft(const double &in_data[],double &out_real[],double &out_imaginary[])
  {
   uint minsize=(3*m_maxPeriod);
   uint fullsize=in_data.Size();

   if(fullsize<minsize)
     {
      Print("Sample size too small in relation to the largest period cycle parameter");
      return false;
     }

   if(m_minPeriod>=m_maxPeriod || m_minPeriod<2)
     {
      Print("Critical error: Invalid input parameters :- max_period should be larger than min_period and min_period cannot be less than 2");
      return false;
     }

   if(out_real.Size()!=m_maxPeriod)
      ArrayResize(out_real,m_maxPeriod);

   if(out_imaginary.Size()!=m_maxPeriod)
      ArrayResize(out_imaginary,m_maxPeriod);

   double v0,v1,v2,freq,coeff,real,imag;


   for(uint i=0; i<m_maxPeriod; i++)
     {
      if(i<m_minPeriod)
        {
         out_real[i]=out_imaginary[i]=0.0;
         continue;
        }

      v0=v1=v2=0.0;
      freq=MathPow(i,-1);
      coeff=2.0*MathCos(2.0*M_PI*freq);
      for(uint k=minsize-1; k>0; k--)
        {
         v0=coeff*v1-v2+in_data[k];
         v2=v1;
         v1=v0;
        }

      real=v1-v2*0.5*coeff;

      imag=v2*MathSin(2*M_PI*freq);

      out_real[i]=real;
      out_imaginary[i]=imag;

     }

   return true;
  }

Pré-processamento

Os dados nem sempre podem ser simplesmente inseridos no algoritmo de Goertzel e transformados no domínio de frequência. Dependendo da natureza da amostra de dados, algumas etapas de pré-processamento podem ser necessárias. O algoritmo de Goertzel é um subconjunto da DFT e, portanto, as transformações necessárias antes de realizar uma Transformada Rápida de Fourier também se aplicam aqui. Isso é especialmente verdadeiro para dados que não são periódicos. Tais séries precisam ser tratadas com uma função de janela apropriada, que ajustará adequadamente as extremidades da série, minimizando a possibilidade de vazamento espectral. A maioria das aplicações do algoritmo de Goertzel na literatura geralmente emprega um algoritmo de achatamento no ponto final. A implementação dessa técnica é dada pela fórmula:

onde "a" é o primeiro valor de preço na série a ser analisada, "b" é o último, "flat(i)" é a série que será passada para o algoritmo de Goertzel.

Antes de realizar o processamento de janela dos dados, é aconselhável remover quaisquer tendências óbvias e valores atípicos. Os dados brutos devem ser desprovidos de tendência, mas apenas quando necessário. A remoção de tendência não justificada pode introduzir distorções que serão refletidas na representação da amostra no domínio da frequência. A remoção de tendência é um tópico amplo, com diversos métodos disponíveis. Cada um deles possui vantagens e desvantagens próprias. É importante que os profissionais se empenhem em uma investigação cuidadosa para determinar o método mais apropriado a ser utilizado. Neste artigo, utilizaremos um método simples de mínimos quadrados, adequado para remover a tendência das cotações de preços. Abaixo está um trecho.

//+------------------------------------------------------------------+
//|               helper method for detrending data                  |
//+------------------------------------------------------------------+
void CGoertzelCycle::detrend(const double &in_data[], double &out_data[])
  {
   uint i ;
   double xmean, ymean, x, y, xy, xx ;
   xmean=ymean=x=y=xx=xy=0.0;

   xmean=0.5*double(in_data.Size()-1);

   if(out_data.Size()!=in_data.Size())
      ArrayResize(out_data,in_data.Size());


   for(i=0; i<out_data.Size(); i++)
     {
      x = double(i) - xmean ;
      y = in_data[i] - ymean ;
      xx += x * x ;
      xy += x * y ;
     }

   m_slope=xy/xx;
   m_pivot=xmean;

   for(i=0; i<out_data.Size(); i++)
      out_data[i]=in_data[i]-(double(i)-xmean)*m_slope;
  }

Classe CGoertzelCycle

O arquivo de inclusão GoertzelCycle.mqh conterá a classe CGoertzelCycle usada para realizar análise de ciclos em conjuntos de dados com o algoritmo de Goertzel.

//+------------------------------------------------------------------+
//|   CGoertzelCycle class for cycle using the Goertzel Algorithm    |
//+------------------------------------------------------------------+
class CGoertzelCycle
  {
private:
   CGoertzel*m_ga;
   double            m_pivot;
   double            m_slope;
   bool              m_detrend;
   bool              m_squaredamp;
   bool              m_flatten;
   uint              m_cycles;
   uint              m_maxper,m_minper;
   double            m_amplitude[];
   double            m_peaks[];
   double            m_cycle[];
   double            m_phase[];
   uint              m_peaks_index[];
   double            m_detrended[];
   double            m_flattened[];
   double            m_raw[];


   void              detrend(const double &in_data[], double &out_data[]);
   double            wavepoint(bool use_cycle_strength,uint max_cycles);
   bool              spectrum(const double &in_data[],int shift=-1);
   uint              cyclepeaks(bool use_cycle_strength);

public :
                     CGoertzelCycle(void);
                     CGoertzelCycle(bool detrend,bool squared_amp,bool apply_window, uint min_period,uint max_period);
                    ~CGoertzelCycle(void);


   bool              GetSpectrum(const double &in_data[],double &out_amplitude[]);
   bool              GetSpectrum(bool detrend,bool squared_amp,bool apply_window, uint min_period,uint max_period,const double &in_data[],double &out_amplitude[]);
   uint              GetDominantCycles(bool use_cycle_strength,const double &in_data[],double &out_cycles[]);
   uint              GetDominantCycles(bool use_cycle_strenght,bool detrend,bool squared_amp,bool apply_window, uint min_period,uint max_period,const double &in_data[],double &out_cycles[]);
   void              CalculateDominantCycles(uint prev,uint total,bool use_cycle_strength,const double &in_data[], double &out_signal[]);
   void              CalculateWave(uint prev,uint total,uint max_cycles, bool use_cycle_strength,const double &in_data[], double &out_signal[]);
  };

Ela possui dois construtores. O construtor parametrizado permite a inicialização de uma instância com configurações personalizadas.

//+------------------------------------------------------------------+
//|                     Default Constructor                          |
//+------------------------------------------------------------------+
CGoertzelCycle::CGoertzelCycle(void)
  {
   m_pivot=m_slope=0.0;
   m_maxper=m_minper=m_cycles=0;
   m_detrend=m_squaredamp=m_flatten=false;
   m_ga=new CGoertzel();
  }
//+------------------------------------------------------------------+
//|                      Parametric Constructor                      |
//+------------------------------------------------------------------+
CGoertzelCycle::CGoertzelCycle(bool detrend,bool squared_amp,bool apply_window, uint min_period,uint max_period)
  {
   m_pivot=m_slope=0.0;
   m_cycles=0;
   m_maxper=max_period;
   m_minper=min_period;
   m_detrend=detrend;
   m_squaredamp=squared_amp;
   m_flatten=apply_window;
   m_ga=new CGoertzel();

   if(m_maxper)
     {
      ArrayResize(m_amplitude,m_maxper);
      ArrayResize(m_phase,m_maxper);
      ArrayResize(m_cycle,m_maxper);
      ArrayResize(m_peaks,m_maxper);
      ArrayResize(m_peaks_index,m_maxper);
     }

  }

Os parâmetros de entrada são fornecidos abaixo:

• detrend - parâmetro de entrada lógico que indica a necessidade de remoção de tendência.
• apply_window - parâmetro lógico que determina se deve ser aplicada uma função de janela.
• min_period - período mais curto ou a frequência mais alta permitida pelo algoritmo de Goertzel. O valor não pode ser menor que 2.
• max_period - período mais longo a ser considerado na análise. Este valor representa a frequência com o período mais longo e não pode ser menor ou igual ao min_period.
• squard_amp - como o valor da amplitude deve ser representado. Caso seja false, a amplitude será calculada como a raiz quadrada.

A classe possui 6 métodos acessíveis que devem ser do interesse dos usuários.

//+-------------------------------------------------------------------+
//|          public method to access the amplitude values             |
//+-------------------------------------------------------------------+
bool CGoertzelCycle::GetSpectrum(const double &in_data[],double &out_amplitude[])
  {
   if(spectrum(in_data))
     {
      ArrayCopy(out_amplitude,m_amplitude);
      return true;
     }
   return false;
  }

GetSpectrum() requer 2 arrays de entrada, sendo o primeiro deles in_data a série bruta a ser analisada. O segundo array é onde os valores de amplitude serão gerados. Os parâmetros usados para a transformação devem ter sido especificados ao inicializar uma instância usando o construtor parametrizado.

//+------------------------------------------------------------------+
//|         public method to access the amplitude values             |
//+------------------------------------------------------------------+
bool CGoertzelCycle::GetSpectrum(bool detrend,bool squared_amp,bool apply_window,uint min_period,uint max_period,const double &in_data[],double &out_amplitude[])
  {
   m_pivot=m_slope=0.0;
   m_cycles=0;
   m_maxper=max_period;
   m_minper=min_period;
   m_detrend=detrend;
   m_squaredamp=squared_amp;
   m_flatten=apply_window;

   if(m_maxper)
     {
      ArrayResize(m_amplitude,m_maxper);
      ArrayResize(m_phase,m_maxper);
      ArrayResize(m_cycle,m_maxper);
      ArrayResize(m_peaks,m_maxper);
      ArrayResize(m_peaks_index,m_maxper);
     }

   if(spectrum(in_data))
     {
      ArrayCopy(out_amplitude,m_amplitude);
      return true;
     }
   return false;

  }

O outro método sobrecarregado GetSpectrum() leva parâmetros adicionais idênticos aos do construtor parametrizado. Ambos retornam true em caso de sucesso e false em caso de falha. Quaisquer dados de erro serão registrados no diário do terminal.

//+----------------------------------------------------------------------------+
//|public method to get the dominant cycle periods arranged in descending order|
//+----------------------------------------------------------------------------+
uint CGoertzelCycle::GetDominantCycles(bool use_cycle_strength,const double &in_data[],double &out_cycles[])
  {
   if(!spectrum(in_data))
     {
      ArrayInitialize(out_cycles,0.0);
      return(0);
     }

   cyclepeaks(use_cycle_strength);

   if(out_cycles.Size()!=m_cycles)
      ArrayResize(out_cycles,m_cycles);

   for(uint i=0; i<m_cycles; i++)
      out_cycles[i]=m_cycle[m_peaks_index[i]];

   return m_cycles;

  }
//+----------------------------------------------------------------------------+
//|public method to get the dominant cycle periods arranged in descending order|
//+----------------------------------------------------------------------------+
uint CGoertzelCycle::GetDominantCycles(bool use_cycle_strength,bool detrend,bool squared_amp,bool apply_window,uint min_period,uint max_period,const double &in_data[],double &out_cycles[])
  {
   m_pivot=m_slope=0.0;
   m_cycles=0;
   m_maxper=max_period;
   m_minper=min_period;
   m_detrend=detrend;
   m_squaredamp=squared_amp;
   m_flatten=apply_window;

   if(m_maxper)
     {
      ArrayResize(m_amplitude,m_maxper);
      ArrayResize(m_phase,m_maxper);
      ArrayResize(m_cycle,m_maxper);
      ArrayResize(m_peaks,m_maxper);
      ArrayResize(m_peaks_index,m_maxper);
     }

   return(GetDominantCycles(use_cycle_strength,in_data,out_cycles));

  }

O método GetDominantCycle() é sobrecarregado de maneira semelhante ao GetSpectrum(). Além dos 2 arrays, um parâmetro booleano use_cycle_strength precisa ser especificado. Isso indica os critérios para determinar o ciclo dominante. Definir como false significa que as frequências com as maiores amplitudes são usadas, enquanto a alternativa determina o ciclo dominante calculando a força do ciclo dada pela fórmula:

Os ciclos dominantes são gerados no último dos arrays de entrada, com valores dispostos em ordem decrescente.

//+-----------------------------------------------------------------------+
//|method used to access calculated dominant cycles , for use in indcators|
//+-----------------------------------------------------------------------+
void CGoertzelCycle::CalculateDominantCycles(uint prev,uint total,bool use_cycle_strength,const double &in_data[], double &out_signal[])
  {

   uint limit =0;
   bool indexOut=ArrayGetAsSeries(out_signal);
   bool indexIn=ArrayGetAsSeries(in_data);

   if(prev<=0)
     {
      uint firstindex=0;
      if(indexOut)
        {
         limit=total-(m_maxper*3);
         firstindex=limit+1;
        }
      else
        {
         limit=m_maxper*3;
         firstindex=limit-1;
        }
      out_signal[firstindex]=0;
     }
   else
     {
      limit=(indexOut)?total-prev:prev;
     }

   uint found_cycles=0;
   if(indexOut)
     {
      for(int ibar=(int)limit; ibar>=0; ibar--)
        {
         spectrum(in_data,(indexIn)?ibar:total-ibar-1);
         out_signal[ibar]=(cyclepeaks(use_cycle_strength))?m_cycle[m_peaks_index[0]]:0.0;
        }
     }
   else
     {
      for(int ibar=(int)limit; ibar<(int)total; ibar++)
        {
         spectrum(in_data,(indexIn)?total-ibar-1:ibar);
         out_signal[ibar]=(cyclepeaks(use_cycle_strength))?m_cycle[m_peaks_index[0]]:0.0;
        }
     }


  }

Os métodos prefixados com Calculate devem idealmente ser usados em indicadores. CalculateDominantCycles() gera ciclos dominantes para uma barra correspondente. prev deve ser definido como o número de valores de indicador previamente calculados. Total deve ser o número de barras disponíveis no gráfico. in_data é onde você passaria as cotações de preço e out_signal deve ser um dos buffers do indicador.

//+-----------------------------------------------------------------------+
//|method used to access newly formed wave form, for use in indcators     |
//+-----------------------------------------------------------------------+
void CGoertzelCycle::CalculateWave(uint prev,uint total,uint max_cycles,bool use_cycle_strength,const double &in_data[], double &out_signal[])
  {
   uint limit =0;
   bool indexOut=ArrayGetAsSeries(out_signal);
   bool indexIn=ArrayGetAsSeries(in_data);

   if(prev<=0)
     {
      uint firstindex=0;
      if(indexOut)
        {
         limit=total-(m_maxper*3);
         firstindex=limit+1;
        }
      else
        {
         limit=m_maxper*3;
         firstindex=limit-1;
        }
      out_signal[firstindex]=0;
     }
   else
     {
      limit=(indexOut)?total-prev:prev;
     }

   uint found_cycles=0;
   if(indexOut)
     {
      for(int ibar=(int)limit; ibar>=0; ibar--)
        {
         spectrum(in_data,(indexIn)?ibar:total-ibar-1);
         out_signal[ibar]=out_signal[ibar+1]+wavepoint(use_cycle_strength,max_cycles);
        }
     }
   else
     {
      for(int ibar=(int)limit; ibar<(int)total; ibar++)
        {
         spectrum(in_data,(indexIn)?total-ibar-1:ibar);
         out_signal[ibar]=out_signal[ibar-1]+wavepoint(use_cycle_strength,max_cycles);
        }
     }

  }
//+------------------------------------------------------------------+

O método CalculateWave() tem a maioria de seus parâmetros em comum com o CalculateDominantCycles(). Ele gera um valor filtrado calculado a partir dos componentes de frequência dominante revelados pelo algoritmo de Goertzel. O número máximo de componentes de frequência é definido pelo parâmetro max_cycles.

Construção da forma de onda

Para demonstrar tanto o uso da classe quanto as possíveis aplicações do Goertzel no desenvolvimento de estratégias, apresentaremos dois indicadores. Ele chama essa estratégia de Sistema Adaptativo de 10 Ciclos Goertzel DFT. Detalhes exatos sobre a estratégia estão disponíveis no documento. Em resumo, a estratégia utiliza o Goertzel para extrair os dez principais ciclos dominantes de uma janela móvel de dados de preço e, em seguida, usa esses ciclos para construir uma nova curva de preço. Supostamente, essa curva representa o comportamento do preço com o ruído filtrado. Parâmetros-chave dessa estratégia são os períodos mínimos e máximos das frequências a serem amostradas, juntamente com o número máximo de componentes de frequência a serem usados para construir o sinal filtrado.

//--- input parameters
input bool     Detrend=true;
input bool     EndFlatten=true; 
input bool     SquaredAmp=true;
input bool     UseCycleStrength=false;
input uint     Maxper=72;
input uint     Minper=5;
input uint     MaxCycles=10;
input double   pntup=0.5;//Percent increase threshold
input double   pntdn=0.5;//Percent decrease threshold
//--- indicator buffers

O indicador utiliza dois limiares para acionar sinais longos e curtos, dependendo da magnitude de um movimento em relação a um pico ou vale recente. No código, as variáveis de entrada pntup e pntdn representam porcentagens.

//+------------------------------------------------------------------+
//|                                            NCycleGoertzelDft.mq5 |
//|                                  Copyright 2023, MetaQuotes Ltd. |
//|                                             https://www.mql5.com |
//+------------------------------------------------------------------+
#property copyright "Copyright 2023, MetaQuotes Ltd."
#property link      "https://www.mql5.com"
#property version   "1.00"
#include<GoertzelCycle.mqh>
#property indicator_separate_window
#property indicator_buffers 5
#property indicator_plots   5 
//--- plot Wave
#property indicator_label1  "Wave"
#property indicator_type1   DRAW_LINE
#property indicator_color1  clrBlack
#property indicator_style1  STYLE_SOLID
#property indicator_width1  1
//--- plot Up
#property indicator_label2  "Peak"
#property indicator_type2   DRAW_NONE
//--- plot Dwn
#property indicator_label3  "Trough"
#property indicator_type3   DRAW_NONE
//--- plot Up
#property indicator_label4  "Long"
#property indicator_type4   DRAW_LINE
#property indicator_color4  clrBlue
#property indicator_style4  STYLE_SOLID
#property indicator_width4  2
//--- plot Dwn
#property indicator_label5  "Short"
#property indicator_type5   DRAW_LINE
#property indicator_color5  clrRed
#property indicator_style5  STYLE_SOLID
#property indicator_width5  2
//--- input parameters
input bool     Detrend=true;
input bool     EndFlatten=true; 
input bool     SquaredAmp=true;
input bool     UseCycleStrength=false;
input uint     Maxper=72;
input uint     Minper=5;
input uint     MaxCycles=10;
input double   pntup=0.5;//Percent increase threshold
input double   pntdn=0.5;//Percent decrease threshold
//--- indicator buffers

double  Wave[],Peak[],Trough[],Long[],Short[];
CGoertzelCycle *Gc;
//+------------------------------------------------------------------+
//| Custom indicator initialization function                         |
//+------------------------------------------------------------------+
int OnInit()
  {
//--- indicator buffers mapping
   SetIndexBuffer(0,Wave,INDICATOR_DATA);
   SetIndexBuffer(1,Peak,INDICATOR_DATA);
   SetIndexBuffer(2,Trough,INDICATOR_DATA);
   SetIndexBuffer(3,Long,INDICATOR_DATA);
   SetIndexBuffer(4,Short,INDICATOR_DATA);
//---   
   IndicatorSetInteger(INDICATOR_DIGITS,5);
//---   
   PlotIndexSetDouble(0,PLOT_EMPTY_VALUE,0.0);
   PlotIndexSetDouble(1,PLOT_EMPTY_VALUE,0.0);
   PlotIndexSetDouble(2,PLOT_EMPTY_VALUE,0.0);
   PlotIndexSetDouble(3,PLOT_EMPTY_VALUE,0.0);
   PlotIndexSetDouble(4,PLOT_EMPTY_VALUE,0.0);
//---
   Gc=new CGoertzelCycle(Detrend,SquaredAmp,EndFlatten,Minper,Maxper);
   
   if(Gc==NULL)
    {
     Print("Invalid Goertzel object");
     return(INIT_FAILED);
    }  
//---     
   return(INIT_SUCCEEDED);
  }
//+------------------------------------------------------------------+
//| Indicator DeInitialization function                              |
//+------------------------------------------------------------------+
void OnDeinit (const int reason)
 {
  if(CheckPointer(Gc)==POINTER_DYNAMIC)
      delete Gc;
 }  
//+------------------------------------------------------------------+
//| Custom indicator iteration function                              |
//+------------------------------------------------------------------+
int OnCalculate(const int rates_total,
                const int prev_calculated,
                const int begin,
                const double &price[])
  {
   int lim=0;
   
   if(prev_calculated<=0)
      lim=(int)(Maxper*3)+2;
   else 
      lim=prev_calculated;
   
   
//---
    Gc.CalculateWave(prev_calculated,rates_total,MaxCycles,UseCycleStrength,price,Wave);
//---
   for(int i=lim;i<rates_total-1;i++)
      {
       Peak[i]=Trough[i]=0.0;   
       
       if(Wave[i]>Wave[i+1] && Wave[i]>Wave[i-1])
         Peak[i]=Wave[i];
       else 
         if(Wave[i]<Wave[i+1] && Wave[i]<Wave[i-1])
           Trough[i]=Wave[i];
         
       if(i<int(Maxper*3*2)) 
          {
           continue;
          } 
          
       double lp,lt;
          lp=lt=0;  
               
       if(i==int(Maxper*3*2))
         {
          lp=getlastPeakTrough(i,Peak);
          lt=getlastPeakTrough(i,Trough);
          if(Wave[i]>Wave[i-1] && lt)
            {
             Long[i]=Wave[i];
             Short[i]=0.0;
            } 
          else
            if(Wave[i]<Wave[i-1] && lp)
              {
               Short[i]=Wave[i];
               Long[i]=0.0;
              } 
         }
       else
         {
         
           Long[i]=(Long[i-1]!=0)?Wave[i]:Long[i-1];
           Short[i]=(Short[i-1]!=0)?Wave[i]:Short[i-1];
          
          if(Short[i-1]!=0 && Wave[i]>Wave[i-1])
           {
            lt=getlastPeakTrough(i,Trough);
            if(lt && (Wave[i]-lt)/lt > pntup/100 )
              {
               Long[i]=Wave[i];
               Short[i]=0.0;
              }
            else
              {
               Short[i]=Wave[i];
               Long[i]=0.0;
              }    
           }
          else
           if(Long[i-1]!=0 && Wave[i]<Wave[i-1])
           {
            lp=getlastPeakTrough(i,Peak);
            if(lp && (lp-Wave[i])/lp > pntdn/100 )
              {
                Short[i]=Wave[i];
                Long[i]=0.0;
              }
             else
              {
                Long[i]=Wave[i];
                Short[i]=0.0;
              }    
           }
         }  
      
      }
//--- return value of prev_calculated for next call
   return(rates_total);
  }
//+------------------------------------------------------------------+
//| helper function that returns either last peak or trough          |
//+------------------------------------------------------------------+
double getlastPeakTrough(int shift, double &buffer[])
  {
   uint j;
   double value=0.0;
   for(j=shift-1;j>(Maxper*3)+2;j--)
     {
      if(buffer[j]==0.0)
         continue;
      else
         return(buffer[j]);
     }
   return(value);
  }
//+-----------------------------------------------------------------------------------------------++
        

O sinal é calculado usando a fórmula:

onde: a é a amplitude, phi é a fase, f é a frequência, B é o número de barras passadas amostradas, representando os dados de onde os componentes de frequência são extraídos, equivalente ao tamanho da janela móvel. Esse valor é igual a três vezes o ciclo de período máximo considerado. O código do indicador é mostrado acima. Wave point é o valor da curva no índice correspondente.

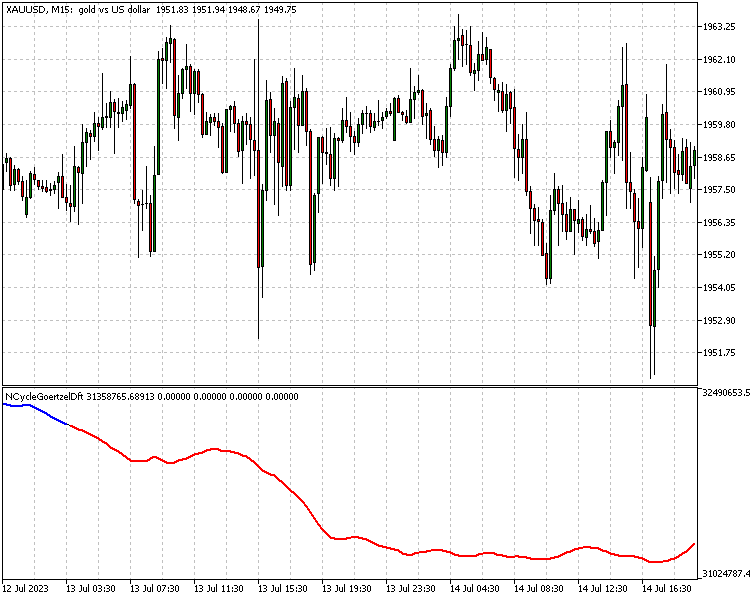
Mais detalhes sobre as regras de negociação estão disponíveis no artigo técnico, se houver interesse.

Indicadores adaptativos

Outra maneira de aplicar o Goertzel no desenvolvimento de estratégias é usá-lo para tornar indicadores adaptativos. O artigo Teoria Avançada Adaptativa e Implementação em MQL5 detalha esse método usando as técnicas famosas de J. Ehlers. Podemos fazer o mesmo usando o Goertzel. Abaixo está uma implementação de uma versão adaptativa do indicador de força relativa.

//+------------------------------------------------------------------+
//|                                                AdaptiveGARSI.mq5 |
//|                                  Copyright 2023, MetaQuotes Ltd. |
//|                                             https://www.mql5.com |
//+------------------------------------------------------------------+
#property copyright "Copyright 2023, MetaQuotes Ltd."
#property link      "https://www.mql5.com"
#property version   "1.00"
#property indicator_separate_window
#include<GoertzelCycle.mqh>
#property indicator_buffers 2
#property indicator_plots   1
//--- plot RSi
#property indicator_label1  "RSi"
#property indicator_type1   DRAW_LINE
#property indicator_color1  clrRed
#property indicator_style1  STYLE_SOLID
#property indicator_width1  1
//---
#property indicator_level1        70
#property indicator_level2        50
#property indicator_level3        30
//---
input bool     Detrend=true;
input bool     EndFlatten=true; 
input bool     SquaredAmp=true;
input bool     UseCycleStrength=false;
input uint     Maxper=72;
input uint     Minper=5;
//--- indicator buffers
double         RSiBuffer[];
double         DomPeriodBuffer[];

CGoertzelCycle *Gc;
//+------------------------------------------------------------------+
//| Custom indicator initialization function                         |
//+------------------------------------------------------------------+
int OnInit()
  {
//--- indicator buffers mapping
   SetIndexBuffer(0,RSiBuffer,INDICATOR_DATA);
   SetIndexBuffer(1,DomPeriodBuffer,INDICATOR_CALCULATIONS);
//---
   Gc=new CGoertzelCycle(Detrend,SquaredAmp,EndFlatten,Minper,Maxper);
//---   
   if(Gc==NULL)
    {
     Print("Invalid Goertzel object");
     return(INIT_FAILED);
    }  
//---    
   return(INIT_SUCCEEDED);
  }
//+------------------------------------------------------------------+
//| Indicator DeInitialization function                              |
//+------------------------------------------------------------------+
void OnDeinit (const int reason)
 {
  if(CheckPointer(Gc)==POINTER_DYNAMIC)
      delete Gc;
 }    
//+------------------------------------------------------------------+
//| Custom indicator iteration function                              |
//+------------------------------------------------------------------+
int OnCalculate(const int rates_total,
                const int prev_calculated,
                const datetime &time[],
                const double &open[],
                const double &high[],
                const double &low[],
                const double &close[],
                const long &tick_volume[],
                const long &volume[],
                const int &spread[])
  {
//---
   uint lim=0;
//---
   Gc.CalculateDominantCycles(prev_calculated,rates_total,UseCycleStrength,close,DomPeriodBuffer);
//---
   if(prev_calculated<=0)
       lim=int(Maxper*3)+int(DomPeriodBuffer[(Maxper*3)-1]) - 1;
   else
       lim=prev_calculated; 
       
//---
   double cu,cd;
   for(int i =int(lim);i<rates_total;i++)
    {
      cd=0.0;
      cu=0.0;
      double p=DomPeriodBuffer[i];
      int j=0;
      for(j=0;j<int(p);j++)
        {
         if(close[i-j]-close[i-j-1]>0)cu=cu+(close[i-j]-close[i-j-1]);
         if(close[i-j]-close[i-j-1]<0)cd=cd+(close[i-j-1]-close[i-j]);
        }
      if(cu+cd!=0)
         RSiBuffer[i]=100*cu/(cu+cd);
      else 
         RSiBuffer[i]=0.0;
    
    }        
//--- return value of prev_calculated for next call
   return(rates_total);
  }
//+------------------------------------------------------------------+

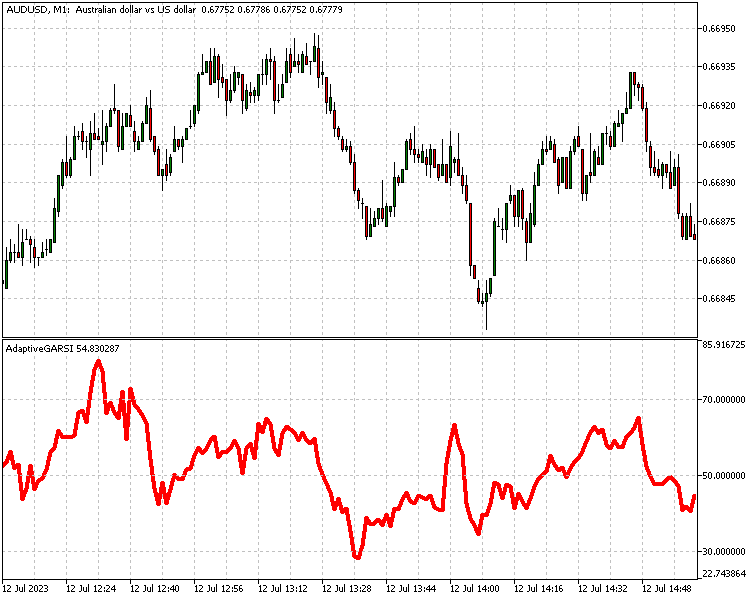
Considerações finais

As capacidades do algoritmo de Goertzel foram claramente demonstradas, juntamente com utilitários de código úteis para sua aplicação. O desafio está em como aplicar efetivamente essa técnica a dados financeiros e extrair sinais significativos. O GA claramente está em desvantagem em relação à técnica MESA, pois só é capaz de resolver uma frequência de cada vez. Sua aplicação prática também destaca a fraqueza na detecção de ciclos nos mercados financeiros, pois é difícil medir um ciclo predominante e determinar com precisão quando ele terminará. Enfrentar essas dificuldades requer uma combinação de conhecimento do domínio, técnicas robustas de pré-processamento de dados, estratégias de gerenciamento de risco e monitoramento contínuo e adaptação às mudanças nas dinâmicas do mercado.

O arquivo zip anexado contém todo o código-fonte descrito no artigo.

Nome do arquivo	Descrição
Mql5/include/Goertzel.mqh	Arquivo de inclusão para a classe CGoertzel, que implementa o algoritmo de Goertzel.
Mql5/include/ GoertzelCycle.mqh	Arquivo de inclusão para a classe CGoertzelCycle, usada para análise de ciclos com o algoritmo de Goertzel.
Mql5/indicators/ NCycleGoertzelDft.mq5	Indicador que implementa parcialmente a estratégia de D. Meyers, utilizando o algoritmo de Goertzel.
Mql5/indicators/ AdaptiveGARSI.mq5	Implementação de uma versão adaptativa do indicador RSI com análise retrospectiva dinâmica, calculada pelo algoritmo de Goertzel.