Cycle analysis using the Goertzel algorithm
6 007
0
Introduction
The Goertzel algorithm is a digital signal processing technique known for its efficiency in detecting particular frequency components. Its precision, real-time abilities, and computational efficiency make it suitable for financial time series analysis. In this article we will examine and demonstrate practical ways in which the method can be used to analyze dominant cycles for possible strategy development. We will take a look at the implementation of the algorithm in MQL5 and present an example of how to use the code to identify cycles in price quotes.
The Goertzel algorithm
The Goertzel algorithm, which derives its name from Gerald Goertzel, is utilized to calculate individual terms of the Discrete Fourier Transform (DFT) in an efficient manner. This technique was initially introduced in 1958 and has since been applied in various areas, including engineering, mathematics, and physics.The Goertzel algorithm's primary application is to identify specific frequency components within a digital signal, making it highly valuable in scenarios where only a few frequency components are important. Compared to the Fast Fourier Transform (FFT), it requires fewer computations when detecting a limited number of frequency components, rendering it computationally efficient.
It is represented by the formula:
Where:
- X is the accumulated magnitude at frequency k
- cos() is the cosine function
- π is the mathematical constant pi (approximately 3.14159)
- k is the index of the frequency bin you are interested in (ranging from 0 to N - 1, where N is the total number of samples)
- N is the length of the input signal
- X[k-1] and X[k-2] are the previously calculated values of X for frequency at k
- x[n] is the nth sample of the input signal
To calculate the real and imaginary components using the Goertzel algorithm, we need to iterate through the input signal samples and perform the following calculations:
- N : Number of samples in the input signal.
- k : Index of the frequency bin of interest (0 <= k < N).
- omega : frequency corresponding to the desired frequency bin (2 * pi * k / N).
- coeff : Coefficient used in the calculation (2 * cos(omega)).
- s_prev : Previous value of the "state" variable.
- s_prev2 : Value before the previous value of the "state" variable.
- s : Current value of the "state" variable.
-
Update the current value of the "state" variable ( s ) using the formula:
where x[n] is the current input sample.
Update the previous values of the "state" variable:
After iterating through all the samples, the final values of the "state" variables (S, Sprev, Sprev2) represent the real and imaginary components of the DFT at the desired frequency bin (k).
The real component is given by:
The imaginary component is given by:
Frequencies that can be detected by the DFT range from 1/N to (N/2)/N, where N represents the number of data points in the series or in our case the number of price bars under analysis. When analyzing price quotes it can be limiting to only be able to observe frequency bands confined to the 1/N spacing. This is the reason why the likes of J.Ehlers proposed the Maximum Entropy Spectral Analysis (MESA) technique to overcome this constraint.
The goertzel algorithm can be used as an alternative to Ehler's MESA, which according to a research paper written by D. Meyers, is able to achieve better results (in terms of spectral resolution), in certain conditions. One of these conditions just happens to relate to the amount of noise contained in the signal. According to Meyers the goertzel algorithm is able to outperform the MESA technique particularly when dealing with noisy signals, which is a common problem with financial time series. Interested readers can read the whitepaper available in pdf format.
The CGoertzel class
The CGoertzel class is a simple implementation of the goertzel algorithm that enables sampling a range of frequencies on a dataset.
//+------------------------------------------------------------------+ //| CGoertze class implementing Goertzel algorithm | //+------------------------------------------------------------------+ class CGoertzel { private: uint m_minPeriod; uint m_maxPeriod; public: //constructor CGoertzel(void) { m_minPeriod=m_maxPeriod=0; } //destructor ~CGoertzel(void) { } //get methods uint GetMinPeriodLength(void) { return m_minPeriod;} uint GetMaxPerodLength(void) { return m_maxPeriod;} //set methods bool SetMinMaxPeriodLength(const uint min_wavePeriod, const uint max_wavePeriod); // goertzel dft transform methods bool Dft(const double &in_data[],complex &out[]); bool Dft(const double &in_data[], double &out_real[], double &out_imaginary[]); bool Dft(const uint min_wavePeriod,const uint max_wavePeriod,const double &in_data[],complex &out[]); bool Dft(const uint min_wavePeriod,const uint max_wavePeriod,const double &in_data[], double &out_real[], double &out_imaginary[]); };
Since the goertzel only samples a limited number frequencies at a time, we have to set the frequency band we are interested in. In the class the frequency band is set in terms of the minimum and maximum period of the frequencies.
There are two ways to set these values: Using the SetMinMaxPeriodLength(), the minimum and maximum periods can be specified.
//+------------------------------------------------------------------+ //| Set the Minimum and maximum periods of selected frequency band | //+------------------------------------------------------------------+ bool CGoertzel::SetMinMaxPeriodLength(const uint min_wavePeriod,const uint max_wavePeriod) { if(min_wavePeriod<2 || min_wavePeriod>=max_wavePeriod) { Print("Critical error min_wavePeriod cannot be less than max_wavePeriod or less than 2"); return false; } m_minPeriod=min_wavePeriod; m_maxPeriod=max_wavePeriod; return true; }
Also the frequency band can be set when calling one of two overloads of the Dft method.
//+-----------------------------------------------------------------------------------+ //| Calculate the frequency domain representation of input array as complex array | //+-----------------------------------------------------------------------------------+ bool CGoertzel::Dft(const uint min_wavePeriod,const uint max_wavePeriod,const double &in_data[],complex &out[]) { if(!SetMinMaxPeriodLength(min_wavePeriod,max_wavePeriod)) return(false); return Dft(in_data,out); } //+------------------------------------------------------------------------------------+ //| Calculate the frequency domain representation of input array as two separate arrays| //+------------------------------------------------------------------------------------+ bool CGoertzel::Dft(const uint min_wavePeriod,const uint max_wavePeriod,const double &in_data[], double &out_real[], double &out_imaginary[]) { if(!SetMinMaxPeriodLength(min_wavePeriod,max_wavePeriod)) return(false); return Dft(in_data,out_real,out_imaginary); }
Depending on the version of the Dft method used the real and imaginary components of the dft are output either in separate arrays or a single array of typle complex.
//+-----------------------------------------------------------------------------------+ //| Calculate the frequency domain representation of input array as complex array | //+-----------------------------------------------------------------------------------+ bool CGoertzel::Dft(const double &in_data[],complex &out[]) { uint minsize=(3*m_maxPeriod); uint fullsize=in_data.Size(); if(fullsize<minsize) { Print("Sample size too small in relation to the largest period cycle parameter"); return false; } if(m_minPeriod>=m_maxPeriod || m_minPeriod<2) { Print("Critical error: Invalid input parameters :- max_period should be larger than min_period and min_period cannot be less than 2"); return false; } if(out.Size()!=m_maxPeriod) ArrayResize(out,m_maxPeriod); double v0,v1,v2,freq,coeff,real,imag; for(uint i=0; i<m_maxPeriod; i++) { if(i<m_minPeriod) { out[i].imag=out[i].real=0.0; continue; } v0=v1=v2=0.0; freq=MathPow(i,-1); coeff=2.0*MathCos(2.0*M_PI*freq); for(uint k=minsize-1; k>0; k--) { v0=coeff*v1-v2+in_data[k]; v2=v1; v1=v0; } real=v1-v2*0.5*coeff; imag=v2*MathSin(2*M_PI*freq); out[i].real=real; out[i].imag=imag; } return true; } //+------------------------------------------------------------------------------------+ //| Calculate the frequency domain representation of input array as two separate arrays| //+------------------------------------------------------------------------------------+ bool CGoertzel::Dft(const double &in_data[],double &out_real[],double &out_imaginary[]) { uint minsize=(3*m_maxPeriod); uint fullsize=in_data.Size(); if(fullsize<minsize) { Print("Sample size too small in relation to the largest period cycle parameter"); return false; } if(m_minPeriod>=m_maxPeriod || m_minPeriod<2) { Print("Critical error: Invalid input parameters :- max_period should be larger than min_period and min_period cannot be less than 2"); return false; } if(out_real.Size()!=m_maxPeriod) ArrayResize(out_real,m_maxPeriod); if(out_imaginary.Size()!=m_maxPeriod) ArrayResize(out_imaginary,m_maxPeriod); double v0,v1,v2,freq,coeff,real,imag; for(uint i=0; i<m_maxPeriod; i++) { if(i<m_minPeriod) { out_real[i]=out_imaginary[i]=0.0; continue; } v0=v1=v2=0.0; freq=MathPow(i,-1); coeff=2.0*MathCos(2.0*M_PI*freq); for(uint k=minsize-1; k>0; k--) { v0=coeff*v1-v2+in_data[k]; v2=v1; v1=v0; } real=v1-v2*0.5*coeff; imag=v2*MathSin(2*M_PI*freq); out_real[i]=real; out_imaginary[i]=imag; } return true; }
Preprocessing
Data cannot always be simply plugged into the goertzel algorithm and transformed into the frequency domain. Depending on the nature of the data sample, a few preprocessing steps may be necessary. The goertzel algorithm is a subset of the dft and therefore transformations required before performing a fast fourier transform also apply here. This is especially true for data that is not periodic. Such series need to be treated with an appropriate windowing fucntion. Which will adequately taper the ends of the series minimizing the possibility of spectral leakage. Most applications of the goertzel in literature usuallly employ an end point flattening algorithm. Implementation of this technique is given by the formula:
where a is the first price value in series to be analyzed, b is the last , flat(i) is the series that will passed to the goertzel algorithm.
Prior to windowing the data it is good practice to remove any obvious trends and outliers. The raw data should be detrended, but only if it necessary.Unwarranted detrending can induce distortions that will be carried onto the frequency domain representation of the sample. Detrending is a vast topic and there are numerous types of detrending that can be adopted. Each one has its own advantages and disadvantages. Practitioners should make the effort to thoroughly investigate the most appropriate method to apply. For the sake of this article we will use a simple least squares fit to detrend price quotes . The code is shown below.
//+------------------------------------------------------------------+ //| helper method for detrending data | //+------------------------------------------------------------------+ void CGoertzelCycle::detrend(const double &in_data[], double &out_data[]) { uint i ; double xmean, ymean, x, y, xy, xx ; xmean=ymean=x=y=xx=xy=0.0; xmean=0.5*double(in_data.Size()-1); if(out_data.Size()!=in_data.Size()) ArrayResize(out_data,in_data.Size()); for(i=0; i<out_data.Size(); i++) { x = double(i) - xmean ; y = in_data[i] - ymean ; xx += x * x ; xy += x * y ; } m_slope=xy/xx; m_pivot=xmean; for(i=0; i<out_data.Size(); i++) out_data[i]=in_data[i]-(double(i)-xmean)*m_slope; }
CGoertzelCycle class
The include file GoertzelCycle.mqh will contain the CGoertzelCycle class used to conduct cycle analysis of data sets with the goertzel algorithm.
//+------------------------------------------------------------------+ //| CGoertzelCycle class for cycle using the Goertzel Algorithm | //+------------------------------------------------------------------+ class CGoertzelCycle { private: CGoertzel*m_ga; double m_pivot; double m_slope; bool m_detrend; bool m_squaredamp; bool m_flatten; uint m_cycles; uint m_maxper,m_minper; double m_amplitude[]; double m_peaks[]; double m_cycle[]; double m_phase[]; uint m_peaks_index[]; double m_detrended[]; double m_flattened[]; double m_raw[]; void detrend(const double &in_data[], double &out_data[]); double wavepoint(bool use_cycle_strength,uint max_cycles); bool spectrum(const double &in_data[],int shift=-1); uint cyclepeaks(bool use_cycle_strength); public : CGoertzelCycle(void); CGoertzelCycle(bool detrend,bool squared_amp,bool apply_window, uint min_period,uint max_period); ~CGoertzelCycle(void); bool GetSpectrum(const double &in_data[],double &out_amplitude[]); bool GetSpectrum(bool detrend,bool squared_amp,bool apply_window, uint min_period,uint max_period,const double &in_data[],double &out_amplitude[]); uint GetDominantCycles(bool use_cycle_strength,const double &in_data[],double &out_cycles[]); uint GetDominantCycles(bool use_cycle_strenght,bool detrend,bool squared_amp,bool apply_window, uint min_period,uint max_period,const double &in_data[],double &out_cycles[]); void CalculateDominantCycles(uint prev,uint total,bool use_cycle_strength,const double &in_data[], double &out_signal[]); void CalculateWave(uint prev,uint total,uint max_cycles, bool use_cycle_strength,const double &in_data[], double &out_signal[]); };
It has two constructors. The parametized constructor allows initilization of an instance with custom settings.
//+------------------------------------------------------------------+ //| Default Constructor | //+------------------------------------------------------------------+ CGoertzelCycle::CGoertzelCycle(void) { m_pivot=m_slope=0.0; m_maxper=m_minper=m_cycles=0; m_detrend=m_squaredamp=m_flatten=false; m_ga=new CGoertzel(); } //+------------------------------------------------------------------+ //| Parametric Constructor | //+------------------------------------------------------------------+ CGoertzelCycle::CGoertzelCycle(bool detrend,bool squared_amp,bool apply_window, uint min_period,uint max_period) { m_pivot=m_slope=0.0; m_cycles=0; m_maxper=max_period; m_minper=min_period; m_detrend=detrend; m_squaredamp=squared_amp; m_flatten=apply_window; m_ga=new CGoertzel(); if(m_maxper) { ArrayResize(m_amplitude,m_maxper); ArrayResize(m_phase,m_maxper); ArrayResize(m_cycle,m_maxper); ArrayResize(m_peaks,m_maxper); ArrayResize(m_peaks_index,m_maxper); } }
The input parameters are given below:
- detrend - a boolean input indicating the need for trend removal.
- apply_window - another boolean parameter specifying whether a windowing function should be applied or not.
- min_period - this parameter defines the shortest period or the highest frequency that will be resolved by the goertzel algorithm.Please note that this value cannot be set below 2.
- max_period - the longest period that will considered during analysis.This value represents the frequency with the longest period, it cannot be less than or equal to min_period.
- squard_amp - indicates how the amplitude value should be presented. Selecting false will have the amplitude calculated as the square root.
The class has 6 accessible methods that should be of interest to users.
//+-------------------------------------------------------------------+ //| public method to access the amplitude values | //+-------------------------------------------------------------------+ bool CGoertzelCycle::GetSpectrum(const double &in_data[],double &out_amplitude[]) { if(spectrum(in_data)) { ArrayCopy(out_amplitude,m_amplitude); return true; } return false; }
GetSpectrum() requires 2 input arrays, the first of which in_data is the raw series to be analyzed. The second array is where the amplitude values will be output. The parameters used to do the transform should have been specified by initializing an instance using the parametized constructor.
//+------------------------------------------------------------------+ //| public method to access the amplitude values | //+------------------------------------------------------------------+ bool CGoertzelCycle::GetSpectrum(bool detrend,bool squared_amp,bool apply_window,uint min_period,uint max_period,const double &in_data[],double &out_amplitude[]) { m_pivot=m_slope=0.0; m_cycles=0; m_maxper=max_period; m_minper=min_period; m_detrend=detrend; m_squaredamp=squared_amp; m_flatten=apply_window; if(m_maxper) { ArrayResize(m_amplitude,m_maxper); ArrayResize(m_phase,m_maxper); ArrayResize(m_cycle,m_maxper); ArrayResize(m_peaks,m_maxper); ArrayResize(m_peaks_index,m_maxper); } if(spectrum(in_data)) { ArrayCopy(out_amplitude,m_amplitude); return true; } return false; }
The other overloaded GetSpectrum() method takes additional parameters identical to those of the parametized constructor. Both return true on success and false on failure.Any error data will be written to the terminal's journal.
//+----------------------------------------------------------------------------+ //|public method to get the dominant cycle periods arranged in descending order| //+----------------------------------------------------------------------------+ uint CGoertzelCycle::GetDominantCycles(bool use_cycle_strength,const double &in_data[],double &out_cycles[]) { if(!spectrum(in_data)) { ArrayInitialize(out_cycles,0.0); return(0); } cyclepeaks(use_cycle_strength); if(out_cycles.Size()!=m_cycles) ArrayResize(out_cycles,m_cycles); for(uint i=0; i<m_cycles; i++) out_cycles[i]=m_cycle[m_peaks_index[i]]; return m_cycles; } //+----------------------------------------------------------------------------+ //|public method to get the dominant cycle periods arranged in descending order| //+----------------------------------------------------------------------------+ uint CGoertzelCycle::GetDominantCycles(bool use_cycle_strength,bool detrend,bool squared_amp,bool apply_window,uint min_period,uint max_period,const double &in_data[],double &out_cycles[]) { m_pivot=m_slope=0.0; m_cycles=0; m_maxper=max_period; m_minper=min_period; m_detrend=detrend; m_squaredamp=squared_amp; m_flatten=apply_window; if(m_maxper) { ArrayResize(m_amplitude,m_maxper); ArrayResize(m_phase,m_maxper); ArrayResize(m_cycle,m_maxper); ArrayResize(m_peaks,m_maxper); ArrayResize(m_peaks_index,m_maxper); } return(GetDominantCycles(use_cycle_strength,in_data,out_cycles)); }
The GetDominantCycle() method is similarly overloaded like GetSpectrum(). Beyond the 2 arrays, a boolean parameter use_cycle_strength needs to be specified. It indicates the criteria for determining the dominant cycle.Setting to false means the frequencies with the largest amplitudes are used, whilst the alternative determines the dominant cycle by calculating the cycle strength given by the formula :
The dominant cycles are output to the last of the input arrays with values arranged in descending order.
//+-----------------------------------------------------------------------+ //|method used to access calculated dominant cycles , for use in indcators| //+-----------------------------------------------------------------------+ void CGoertzelCycle::CalculateDominantCycles(uint prev,uint total,bool use_cycle_strength,const double &in_data[], double &out_signal[]) { uint limit =0; bool indexOut=ArrayGetAsSeries(out_signal); bool indexIn=ArrayGetAsSeries(in_data); if(prev<=0) { uint firstindex=0; if(indexOut) { limit=total-(m_maxper*3); firstindex=limit+1; } else { limit=m_maxper*3; firstindex=limit-1; } out_signal[firstindex]=0; } else { limit=(indexOut)?total-prev:prev; } uint found_cycles=0; if(indexOut) { for(int ibar=(int)limit; ibar>=0; ibar--) { spectrum(in_data,(indexIn)?ibar:total-ibar-1); out_signal[ibar]=(cyclepeaks(use_cycle_strength))?m_cycle[m_peaks_index[0]]:0.0; } } else { for(int ibar=(int)limit; ibar<(int)total; ibar++) { spectrum(in_data,(indexIn)?total-ibar-1:ibar); out_signal[ibar]=(cyclepeaks(use_cycle_strength))?m_cycle[m_peaks_index[0]]:0.0; } } }
The methods prefixed with Calculate should idealy be used in indicators. CalculateDominantCycles() outputs dominant cycles for a corresponding bar. prev should be set to the number of prevously calculated indicator values.Total should be the number of available bars on the chart. in_data is where one would pass in the price quotes and out_signal should be one of the indicator buffers.
//+-----------------------------------------------------------------------+ //|method used to access newly formed wave form, for use in indcators | //+-----------------------------------------------------------------------+ void CGoertzelCycle::CalculateWave(uint prev,uint total,uint max_cycles,bool use_cycle_strength,const double &in_data[], double &out_signal[]) { uint limit =0; bool indexOut=ArrayGetAsSeries(out_signal); bool indexIn=ArrayGetAsSeries(in_data); if(prev<=0) { uint firstindex=0; if(indexOut) { limit=total-(m_maxper*3); firstindex=limit+1; } else { limit=m_maxper*3; firstindex=limit-1; } out_signal[firstindex]=0; } else { limit=(indexOut)?total-prev:prev; } uint found_cycles=0; if(indexOut) { for(int ibar=(int)limit; ibar>=0; ibar--) { spectrum(in_data,(indexIn)?ibar:total-ibar-1); out_signal[ibar]=out_signal[ibar+1]+wavepoint(use_cycle_strength,max_cycles); } } else { for(int ibar=(int)limit; ibar<(int)total; ibar++) { spectrum(in_data,(indexIn)?total-ibar-1:ibar); out_signal[ibar]=out_signal[ibar-1]+wavepoint(use_cycle_strength,max_cycles); } } } //+------------------------------------------------------------------+
CalculateWave() has most of its parameters incommon with CalculateDominantCycles(). It outputs a filtered value calculated from the dominant frequency components revealed by the goertzel algorithm. The maximum number of frequency components is set by the max_cycles parameter.
Waveform construction
To demonstrate both the use of the class as well as the possible applications of the goertzel in strategy development. We will present two indicators. The first is an implementation of a strategy presented in a white paper written by Dennis Meyers. He calls this strategy the Adaptive 10 Cycle Goertzel DFT System. Exact details about the strategy are available in the document. In brief the strategy uses the goertzel to extract the top ten dominant cycles from a moving window of price data , then uses these cycles to construct a new price curve. Which supposedly represents the behaviour of the price with the noise filtered out. Key parameters of this strategy are the minimum and maximum periods of frequencies to be sampled. Along with the maximum number of frequency components to be used to construct the filtered signal.
//--- input parameters input bool Detrend=true; input bool EndFlatten=true; input bool SquaredAmp=true; input bool UseCycleStrength=false; input uint Maxper=72; input uint Minper=5; input uint MaxCycles=10; input double pntup=0.5;//Percent increase threshold input double pntdn=0.5;//Percent decrease threshold //--- indicator buffers
The indicator uses two thresholds to trigger long and short signals depending on the magnitude of a move relative to either a recent peak or trough. In the code, input variables pntup and pntdn represent percentages.
//+------------------------------------------------------------------+ //| NCycleGoertzelDft.mq5 | //| Copyright 2023, MetaQuotes Ltd. | //| https://www.mql5.com | //+------------------------------------------------------------------+ #property copyright "Copyright 2023, MetaQuotes Ltd." #property link "https://www.mql5.com" #property version "1.00" #include<GoertzelCycle.mqh> #property indicator_separate_window #property indicator_buffers 5 #property indicator_plots 5 //--- plot Wave #property indicator_label1 "Wave" #property indicator_type1 DRAW_LINE #property indicator_color1 clrBlack #property indicator_style1 STYLE_SOLID #property indicator_width1 1 //--- plot Up #property indicator_label2 "Peak" #property indicator_type2 DRAW_NONE //--- plot Dwn #property indicator_label3 "Trough" #property indicator_type3 DRAW_NONE //--- plot Up #property indicator_label4 "Long" #property indicator_type4 DRAW_LINE #property indicator_color4 clrBlue #property indicator_style4 STYLE_SOLID #property indicator_width4 2 //--- plot Dwn #property indicator_label5 "Short" #property indicator_type5 DRAW_LINE #property indicator_color5 clrRed #property indicator_style5 STYLE_SOLID #property indicator_width5 2 //--- input parameters input bool Detrend=true; input bool EndFlatten=true; input bool SquaredAmp=true; input bool UseCycleStrength=false; input uint Maxper=72; input uint Minper=5; input uint MaxCycles=10; input double pntup=0.5;//Percent increase threshold input double pntdn=0.5;//Percent decrease threshold //--- indicator buffers double Wave[],Peak[],Trough[],Long[],Short[]; CGoertzelCycle *Gc; //+------------------------------------------------------------------+ //| Custom indicator initialization function | //+------------------------------------------------------------------+ int OnInit() { //--- indicator buffers mapping SetIndexBuffer(0,Wave,INDICATOR_DATA); SetIndexBuffer(1,Peak,INDICATOR_DATA); SetIndexBuffer(2,Trough,INDICATOR_DATA); SetIndexBuffer(3,Long,INDICATOR_DATA); SetIndexBuffer(4,Short,INDICATOR_DATA); //--- IndicatorSetInteger(INDICATOR_DIGITS,5); //--- PlotIndexSetDouble(0,PLOT_EMPTY_VALUE,0.0); PlotIndexSetDouble(1,PLOT_EMPTY_VALUE,0.0); PlotIndexSetDouble(2,PLOT_EMPTY_VALUE,0.0); PlotIndexSetDouble(3,PLOT_EMPTY_VALUE,0.0); PlotIndexSetDouble(4,PLOT_EMPTY_VALUE,0.0); //--- Gc=new CGoertzelCycle(Detrend,SquaredAmp,EndFlatten,Minper,Maxper); if(Gc==NULL) { Print("Invalid Goertzel object"); return(INIT_FAILED); } //--- return(INIT_SUCCEEDED); } //+------------------------------------------------------------------+ //| Indicator DeInitialization function | //+------------------------------------------------------------------+ void OnDeinit (const int reason) { if(CheckPointer(Gc)==POINTER_DYNAMIC) delete Gc; } //+------------------------------------------------------------------+ //| Custom indicator iteration function | //+------------------------------------------------------------------+ int OnCalculate(const int rates_total, const int prev_calculated, const int begin, const double &price[]) { int lim=0; if(prev_calculated<=0) lim=(int)(Maxper*3)+2; else lim=prev_calculated; //--- Gc.CalculateWave(prev_calculated,rates_total,MaxCycles,UseCycleStrength,price,Wave); //--- for(int i=lim;i<rates_total-1;i++) { Peak[i]=Trough[i]=0.0; if(Wave[i]>Wave[i+1] && Wave[i]>Wave[i-1]) Peak[i]=Wave[i]; else if(Wave[i]<Wave[i+1] && Wave[i]<Wave[i-1]) Trough[i]=Wave[i]; if(i<int(Maxper*3*2)) { continue; } double lp,lt; lp=lt=0; if(i==int(Maxper*3*2)) { lp=getlastPeakTrough(i,Peak); lt=getlastPeakTrough(i,Trough); if(Wave[i]>Wave[i-1] && lt) { Long[i]=Wave[i]; Short[i]=0.0; } else if(Wave[i]<Wave[i-1] && lp) { Short[i]=Wave[i]; Long[i]=0.0; } } else { Long[i]=(Long[i-1]!=0)?Wave[i]:Long[i-1]; Short[i]=(Short[i-1]!=0)?Wave[i]:Short[i-1]; if(Short[i-1]!=0 && Wave[i]>Wave[i-1]) { lt=getlastPeakTrough(i,Trough); if(lt && (Wave[i]-lt)/lt > pntup/100 ) { Long[i]=Wave[i]; Short[i]=0.0; } else { Short[i]=Wave[i]; Long[i]=0.0; } } else if(Long[i-1]!=0 && Wave[i]<Wave[i-1]) { lp=getlastPeakTrough(i,Peak); if(lp && (lp-Wave[i])/lp > pntdn/100 ) { Short[i]=Wave[i]; Long[i]=0.0; } else { Long[i]=Wave[i]; Short[i]=0.0; } } } } //--- return value of prev_calculated for next call return(rates_total); } //+------------------------------------------------------------------+ //| helper function that returns either last peak or trough | //+------------------------------------------------------------------+ double getlastPeakTrough(int shift, double &buffer[]) { uint j; double value=0.0; for(j=shift-1;j>(Maxper*3)+2;j--) { if(buffer[j]==0.0) continue; else return(buffer[j]); } return(value); } //+-----------------------------------------------------------------------------------------------++
The signal is calculated using the formula:
where : - a is the amplitude - phi is the phase - f is the frequency - B are the number of the past bars sampled representing the data where frequency components are extracted from, equivalent to the moving window size. This value is equal to three times the maximum period cycle considered. The code for the indicator is shown above. Wave point is the value of the curve at the corresponding index.
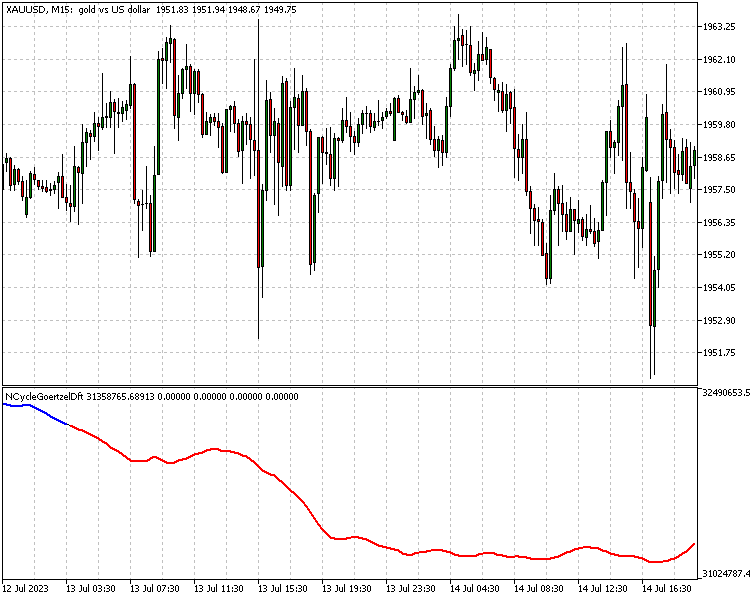
More details of the trade rules are given in the white paper if interested.
Adaptive indicators
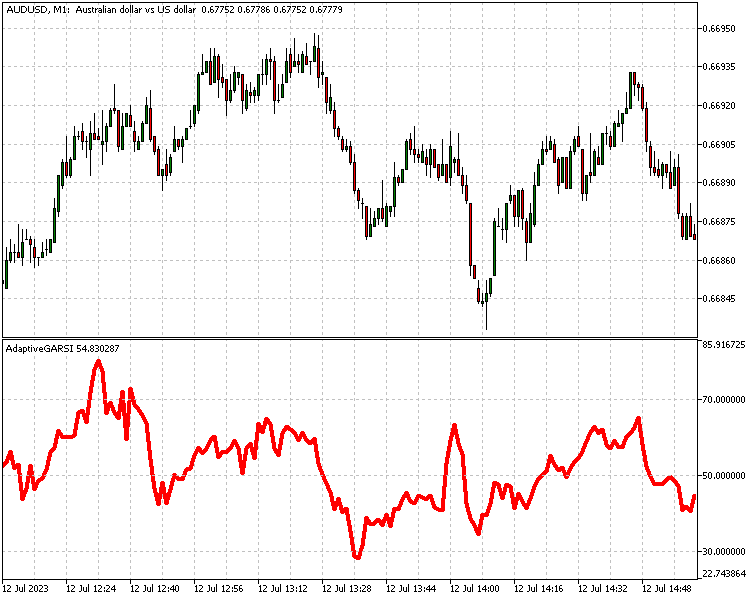
Another way to apply the goertzel for strategy developement is to use it to make indicators adaptive. The article Advanced Adaptive Theory and Implementation in Mql5 , details this method using J.Ehlers' famous techniques. We can do the same using the goertzel. Below is an implementation of an adaptive version of the relative strength indicator .
//+------------------------------------------------------------------+ //| AdaptiveGARSI.mq5 | //| Copyright 2023, MetaQuotes Ltd. | //| https://www.mql5.com | //+------------------------------------------------------------------+ #property copyright "Copyright 2023, MetaQuotes Ltd." #property link "https://www.mql5.com" #property version "1.00" #property indicator_separate_window #include<GoertzelCycle.mqh> #property indicator_buffers 2 #property indicator_plots 1 //--- plot RSi #property indicator_label1 "RSi" #property indicator_type1 DRAW_LINE #property indicator_color1 clrRed #property indicator_style1 STYLE_SOLID #property indicator_width1 1 //--- #property indicator_level1 70 #property indicator_level2 50 #property indicator_level3 30 //--- input bool Detrend=true; input bool EndFlatten=true; input bool SquaredAmp=true; input bool UseCycleStrength=false; input uint Maxper=72; input uint Minper=5; //--- indicator buffers double RSiBuffer[]; double DomPeriodBuffer[]; CGoertzelCycle *Gc; //+------------------------------------------------------------------+ //| Custom indicator initialization function | //+------------------------------------------------------------------+ int OnInit() { //--- indicator buffers mapping SetIndexBuffer(0,RSiBuffer,INDICATOR_DATA); SetIndexBuffer(1,DomPeriodBuffer,INDICATOR_CALCULATIONS); //--- Gc=new CGoertzelCycle(Detrend,SquaredAmp,EndFlatten,Minper,Maxper); //--- if(Gc==NULL) { Print("Invalid Goertzel object"); return(INIT_FAILED); } //--- return(INIT_SUCCEEDED); } //+------------------------------------------------------------------+ //| Indicator DeInitialization function | //+------------------------------------------------------------------+ void OnDeinit (const int reason) { if(CheckPointer(Gc)==POINTER_DYNAMIC) delete Gc; } //+------------------------------------------------------------------+ //| Custom indicator iteration function | //+------------------------------------------------------------------+ int OnCalculate(const int rates_total, const int prev_calculated, const datetime &time[], const double &open[], const double &high[], const double &low[], const double &close[], const long &tick_volume[], const long &volume[], const int &spread[]) { //--- uint lim=0; //--- Gc.CalculateDominantCycles(prev_calculated,rates_total,UseCycleStrength,close,DomPeriodBuffer); //--- if(prev_calculated<=0) lim=int(Maxper*3)+int(DomPeriodBuffer[(Maxper*3)-1]) - 1; else lim=prev_calculated; //--- double cu,cd; for(int i =int(lim);i<rates_total;i++) { cd=0.0; cu=0.0; double p=DomPeriodBuffer[i]; int j=0; for(j=0;j<int(p);j++) { if(close[i-j]-close[i-j-1]>0)cu=cu+(close[i-j]-close[i-j-1]); if(close[i-j]-close[i-j-1]<0)cd=cd+(close[i-j-1]-close[i-j]); } if(cu+cd!=0) RSiBuffer[i]=100*cu/(cu+cd); else RSiBuffer[i]=0.0; } //--- return value of prev_calculated for next call return(rates_total); } //+------------------------------------------------------------------+
Conclusion
The capabilities of the Goertzel algorithm have clearly been demostrated along with useful code utilities for its application. The challenge is how to effectively apply this technique to financial data and extract meaningful signals. The GA is clearly at a disadvantage, relative to the MESA technique, as it is only able to resolve for one frequency at a time. Its practical application also highlights the weakness of cycle detection in financial markets, as it is difficult to measure a prevailing cycle and accurately determine when it will end. Addressing these difficulties requires a combination of domain knowledge, robust data preprocessing techniques, risk management strategies, and continuous monitoring and adaptation to changing market dynamics.
The attached zip file contains all the source code described in the article.
| FileName | Description |
|---|---|
| Mql5/include/Goertzel.mqh | include file for CGoertzel class implementing the goertzel algorithm |
| Mql5/include/ GoertzelCycle.mqh | include file for CGoertzelCycle class for cycle analyis using the goertzel algorithm |
| Mql5/indicators/ NCycleGoertzelDft.mq5 | Indicator that partly implements a strategy developed by D. Meyers that uses the goertzel algorithm |
| Mql5/indicators/ AdaptiveGARSI.mq5 | Implementation of an adaptive version of the Relative strength indicator with dynamic lookback calculated by the goertzel algorithm |
Category Theory in MQL5 (Part 14): Functors with Linear-Orders
Developing a Replay System — Market simulation (Part 03): Adjusting the settings (I)
Category Theory in MQL5 (Part 15) : Functors with Graphs
Understanding functions in MQL5 with applications
- Free trading apps
- Over 8,000 signals for copying
- Economic news for exploring financial markets
You agree to website policy and terms of use