Анализ циклов с использованием алгоритма Гёрцеля

Введение

Алгоритм Гёрцеля — это метод цифровой обработки сигналов, известный своей эффективностью в обнаружении определенных частотных составляющих. Его точность, возможности работы в режиме реального времени и вычислительная эффективность делают его подходящим для анализа финансовых временных рядов. В этой статье мы рассмотрим практические способы использования метода для анализа доминирующих циклов при разработке стратегии. Мы рассмотрим реализацию алгоритма на MQL5 и приведем пример использования кода для определения циклов в котировках.

Алгоритм Гёрцеля

Алгоритм Гёрцеля, предложенный Джеральдом Гёрцелем, используется для эффективного расчета отдельных членов дискретного преобразования Фурье (ДПФ). Метод был представлен в 1958 году и с тех пор применяется в различных областях, включая инженерное дело, математику и физику. Основное применение алгоритма Герцеля — идентифицировать определенные частотные компоненты в цифровом сигнале, что делает его очень ценным в сценариях, где важны лишь некоторые частотные составляющие. По сравнению с быстрым преобразованием Фурье (БПФ), он требует меньше вычислений при обнаружении ограниченного числа частотных составляющих, что делает его вычислительно эффективным.

Он представлен формулой:

где:

• X - накопленная величина на частоте k
• cos() - функция косинуса
• π - математическая константа пи (приблизительно 3,14159)
• k - индекс интересующего нас интервала частоты (в диапазоне от 0 до N — 1, где N — общее количество выборок)
• N - длина входного сигнала
• X[k-1] и X[k-2] - ранее рассчитанные значения X для частоты на k
• x[n] - n-я выборка входного сигнала

Чтобы вычислить действительные и мнимые компоненты с помощью алгоритма Гёрцеля, нам необходимо перебрать выборки входного сигнала и выполнить следующие вычисления:

Проинициализируем переменные:

• N - количество выборок во входном сигнале.
• k - индекс интересующего нас интервала частоты (0 <= k < N).
• omega - частота, соответствующая желаемому интервалу частоты (2 * pi * k / N).
• coeff - коэффициент, используемый в расчете (2 * cos(omega)).
• s_prev - предыдущее значение переменной state.
• s_prev2 - значение перед предыдущим значением переменной state.
• s - текущее значение переменной state.

Переберем каждую выборку входного сигнала:

• Обновим текущее значение переменной state (s), используя формулу:

  
  

где x[n] — текущая входная выборка.

Обновим предыдущие значения переменной state:

После перебора всех выборок окончательные значения переменных state (S, Sprev, Sprev2) представляют действительные и мнимые компоненты ДПФ в необходимом интервале частоты (k).

Реальный компонент определяется следующим образом:

Мнимый компонент определяется как:

Частоты, которые могут быть обнаружены с помощью ДПФ, варьируются от 1/N до (N/2)/N, где N - количество точек данных в серии или, в нашем случае, количество анализируемых ценовых баров. При анализе ценовых котировок мы можем иметь возможность наблюдать только диапазоны частот, ограниченные интервалом 1/N. Именно по этой причине Джон Элерс предложил метод спектрального анализа максимальной энтропии (Maximum Entropy Spectral Analysis, MESA), чтобы преодолеть это ограничение.

Алгоритм Гёрцеля можно использовать как альтернативу MESA Элера, который, согласно исследовательской работе Д. Мейерса, в определенных условиях способен достигать лучших результатов (с точки зрения спектрального разрешения). Одно из этих условий связано с количеством шума, содержащегося в сигнале. По словам Мейерса, алгоритм Гёрцеля способен превзойти метод MESA, особенно при работе с зашумленными сигналами, что является распространенной проблемой финансовых временных рядов. Заинтересованные читатели могут прочитать документацию в pdf-формате (на английском).

Класс CGoertzel

Класс CGoertzel — это простая реализация алгоритма Гёрцеля, которая позволяет осуществлять выборку диапазона частот в наборе данных.

//+------------------------------------------------------------------+
//| CGoertze class implementing Goertzel algorithm                   |
//+------------------------------------------------------------------+
class CGoertzel
  {
private:
   uint              m_minPeriod;
   uint              m_maxPeriod;
public:
   //constructor
                     CGoertzel(void)
     {
      m_minPeriod=m_maxPeriod=0;
     }
   //destructor
                    ~CGoertzel(void)
     {
     }
   //get methods
   uint              GetMinPeriodLength(void) {   return m_minPeriod;}
   uint              GetMaxPerodLength(void) {   return m_maxPeriod;}
   //set methods
   bool              SetMinMaxPeriodLength(const uint min_wavePeriod, const uint max_wavePeriod);
   // goertzel dft transform methods
   bool              Dft(const double &in_data[],complex &out[]);
   bool              Dft(const double &in_data[], double &out_real[], double &out_imaginary[]);
   bool              Dft(const uint min_wavePeriod,const uint max_wavePeriod,const double &in_data[],complex &out[]);
   bool              Dft(const uint min_wavePeriod,const uint max_wavePeriod,const double &in_data[], double &out_real[], double &out_imaginary[]);
  };

Поскольку Гёрцель производит выборку только ограниченного числа частот за раз, нам необходимо установить интересующую нас полосу частот. В классе полоса частот задается исходя из минимального и максимального периода частот.

Есть два способа установить эти значения: используя SetMinMaxPeriodLength(), можно указать минимальный и максимальный периоды.

//+------------------------------------------------------------------+
//| Set the Minimum and maximum periods of selected frequency band   |
//+------------------------------------------------------------------+
bool CGoertzel::SetMinMaxPeriodLength(const uint min_wavePeriod,const uint max_wavePeriod)
  {
   if(min_wavePeriod<2 || min_wavePeriod>=max_wavePeriod)
     {
      Print("Critical error min_wavePeriod cannot be less than max_wavePeriod or less than 2");
      return false;
     }

   m_minPeriod=min_wavePeriod;
   m_maxPeriod=max_wavePeriod;

   return true;
  }

Также полосу частот можно задать при вызове одной из двух перегрузок метода ДПФ.

//+-----------------------------------------------------------------------------------+
//| Calculate the frequency domain representation of input array as complex array     |
//+-----------------------------------------------------------------------------------+
bool CGoertzel::Dft(const uint min_wavePeriod,const uint max_wavePeriod,const double &in_data[],complex &out[])
  {
   if(!SetMinMaxPeriodLength(min_wavePeriod,max_wavePeriod))
      return(false);

   return Dft(in_data,out);
  }
//+------------------------------------------------------------------------------------+
//| Calculate the frequency domain representation of input array as two separate arrays|
//+------------------------------------------------------------------------------------+
bool CGoertzel::Dft(const uint min_wavePeriod,const uint max_wavePeriod,const double &in_data[], double &out_real[], double &out_imaginary[])
  {
   if(!SetMinMaxPeriodLength(min_wavePeriod,max_wavePeriod))
      return(false);

   return Dft(in_data,out_real,out_imaginary);

  }

В зависимости от используемой версии метода ДПФ действительная и мнимая компоненты ДПФ выводятся либо в отдельные массивы, либо в один массив типового комплекса.

//+-----------------------------------------------------------------------------------+
//| Calculate the frequency domain representation of input array as complex array     |
//+-----------------------------------------------------------------------------------+
bool CGoertzel::Dft(const double &in_data[],complex &out[])
  {
   uint minsize=(3*m_maxPeriod);
   uint fullsize=in_data.Size();

   if(fullsize<minsize)
     {
      Print("Sample size too small in relation to the largest period cycle parameter");
      return false;
     }

   if(m_minPeriod>=m_maxPeriod || m_minPeriod<2)
     {
      Print("Critical error: Invalid input parameters :- max_period should be larger than min_period and min_period cannot be less than 2");
      return false;
     }

   if(out.Size()!=m_maxPeriod)
      ArrayResize(out,m_maxPeriod);
   
   double v0,v1,v2,freq,coeff,real,imag;


   for(uint i=0; i<m_maxPeriod; i++)
     {
      if(i<m_minPeriod)
        {
         out[i].imag=out[i].real=0.0;
         continue;
        }

      v0=v1=v2=0.0;
      freq=MathPow(i,-1);
      coeff=2.0*MathCos(2.0*M_PI*freq);
      for(uint k=minsize-1; k>0; k--)
        {
         v0=coeff*v1-v2+in_data[k];
         v2=v1;
         v1=v0;
        }

      real=v1-v2*0.5*coeff;

      imag=v2*MathSin(2*M_PI*freq);

      out[i].real=real;
      out[i].imag=imag;

     }

   return true;
  }
//+------------------------------------------------------------------------------------+
//| Calculate the frequency domain representation of input array as two separate arrays|
//+------------------------------------------------------------------------------------+
bool CGoertzel::Dft(const double &in_data[],double &out_real[],double &out_imaginary[])
  {
   uint minsize=(3*m_maxPeriod);
   uint fullsize=in_data.Size();

   if(fullsize<minsize)
     {
      Print("Sample size too small in relation to the largest period cycle parameter");
      return false;
     }

   if(m_minPeriod>=m_maxPeriod || m_minPeriod<2)
     {
      Print("Critical error: Invalid input parameters :- max_period should be larger than min_period and min_period cannot be less than 2");
      return false;
     }

   if(out_real.Size()!=m_maxPeriod)
      ArrayResize(out_real,m_maxPeriod);

   if(out_imaginary.Size()!=m_maxPeriod)
      ArrayResize(out_imaginary,m_maxPeriod);

   double v0,v1,v2,freq,coeff,real,imag;


   for(uint i=0; i<m_maxPeriod; i++)
     {
      if(i<m_minPeriod)
        {
         out_real[i]=out_imaginary[i]=0.0;
         continue;
        }

      v0=v1=v2=0.0;
      freq=MathPow(i,-1);
      coeff=2.0*MathCos(2.0*M_PI*freq);
      for(uint k=minsize-1; k>0; k--)
        {
         v0=coeff*v1-v2+in_data[k];
         v2=v1;
         v1=v0;
        }

      real=v1-v2*0.5*coeff;

      imag=v2*MathSin(2*M_PI*freq);

      out_real[i]=real;
      out_imaginary[i]=imag;

     }

   return true;
  }

Предварительная обработка

Данные не всегда могут быть просто включены в алгоритм Гёрцеля и преобразованы в частотную область. В зависимости от характера выборки данных может потребоваться несколько этапов предварительной обработки. Алгоритм Гёрцеля является подмножеством ДПФ, поэтому здесь также применимы преобразования, необходимые перед выполнением быстрого преобразования Фурье. Это особенно верно для данных, которые не являются периодическими. Такие серии необходимо обрабатывать с помощью соответствующей оконной функции. Это позволит адекватно сужать концы серии, сводя к минимуму возможность утечки спектра. В исследованиях алгоритма Гёрцеля обычно используется алгоритм сглаживания конечной точки. Реализация этого приема отображается формулой:

где а— первое значение цены в серии, подлежащее анализу,b — последнее, Flat(i) — это ряд, который будет передан в алгоритм Гёрцеля.

Перед оконной обработкой данных рекомендуется удалить любые очевидные тренды и выбросы. Из необработанных данных следует удалить тренд, но только в случае необходимости. Необоснованное удаление тренда может вызвать искажения, которые будут перенесены в представление выборки в частотной области. Удаление тренда — это обширная тема, и существует множество типов удаления тренда. Каждый из них имеет свои преимущества и недостатки. Специалистам следует приложить усилия для тщательного изучения наиболее подходящего метода для применения. В этой статье мы будем использовать простой метод наименьших квадратов, подходящий для удаления тренда ценовых котировок. Ниже представлен фрагмент.

//+------------------------------------------------------------------+
//|               helper method for detrending data                  |
//+------------------------------------------------------------------+
void CGoertzelCycle::detrend(const double &in_data[], double &out_data[])
  {
   uint i ;
   double xmean, ymean, x, y, xy, xx ;
   xmean=ymean=x=y=xx=xy=0.0;

   xmean=0.5*double(in_data.Size()-1);

   if(out_data.Size()!=in_data.Size())
      ArrayResize(out_data,in_data.Size());


   for(i=0; i<out_data.Size(); i++)
     {
      x = double(i) - xmean ;
      y = in_data[i] - ymean ;
      xx += x * x ;
      xy += x * y ;
     }

   m_slope=xy/xx;
   m_pivot=xmean;

   for(i=0; i<out_data.Size(); i++)
      out_data[i]=in_data[i]-(double(i)-xmean)*m_slope;
  }

Класс CGoertzelCycle

Включаемый файл GoertzelCycle.mqh будет содержать класс CGoertzelCycle, используемый для проведения циклического анализа наборов данных с помощью алгоритма Гёрцеля.

//+------------------------------------------------------------------+
//|   CGoertzelCycle class for cycle using the Goertzel Algorithm    |
//+------------------------------------------------------------------+
class CGoertzelCycle
  {
private:
   CGoertzel*m_ga;
   double            m_pivot;
   double            m_slope;
   bool              m_detrend;
   bool              m_squaredamp;
   bool              m_flatten;
   uint              m_cycles;
   uint              m_maxper,m_minper;
   double            m_amplitude[];
   double            m_peaks[];
   double            m_cycle[];
   double            m_phase[];
   uint              m_peaks_index[];
   double            m_detrended[];
   double            m_flattened[];
   double            m_raw[];


   void              detrend(const double &in_data[], double &out_data[]);
   double            wavepoint(bool use_cycle_strength,uint max_cycles);
   bool              spectrum(const double &in_data[],int shift=-1);
   uint              cyclepeaks(bool use_cycle_strength);

public :
                     CGoertzelCycle(void);
                     CGoertzelCycle(bool detrend,bool squared_amp,bool apply_window, uint min_period,uint max_period);
                    ~CGoertzelCycle(void);


   bool              GetSpectrum(const double &in_data[],double &out_amplitude[]);
   bool              GetSpectrum(bool detrend,bool squared_amp,bool apply_window, uint min_period,uint max_period,const double &in_data[],double &out_amplitude[]);
   uint              GetDominantCycles(bool use_cycle_strength,const double &in_data[],double &out_cycles[]);
   uint              GetDominantCycles(bool use_cycle_strenght,bool detrend,bool squared_amp,bool apply_window, uint min_period,uint max_period,const double &in_data[],double &out_cycles[]);
   void              CalculateDominantCycles(uint prev,uint total,bool use_cycle_strength,const double &in_data[], double &out_signal[]);
   void              CalculateWave(uint prev,uint total,uint max_cycles, bool use_cycle_strength,const double &in_data[], double &out_signal[]);
  };

Класс имеет два конструктора. Параметризованный конструктор позволяет инициализировать экземпляр с пользовательскими настройками.

//+------------------------------------------------------------------+
//|                     Default Constructor                          |
//+------------------------------------------------------------------+
CGoertzelCycle::CGoertzelCycle(void)
  {
   m_pivot=m_slope=0.0;
   m_maxper=m_minper=m_cycles=0;
   m_detrend=m_squaredamp=m_flatten=false;
   m_ga=new CGoertzel();
  }
//+------------------------------------------------------------------+
//|                      Parametric Constructor                      |
//+------------------------------------------------------------------+
CGoertzelCycle::CGoertzelCycle(bool detrend,bool squared_amp,bool apply_window, uint min_period,uint max_period)
  {
   m_pivot=m_slope=0.0;
   m_cycles=0;
   m_maxper=max_period;
   m_minper=min_period;
   m_detrend=detrend;
   m_squaredamp=squared_amp;
   m_flatten=apply_window;
   m_ga=new CGoertzel();

   if(m_maxper)
     {
      ArrayResize(m_amplitude,m_maxper);
      ArrayResize(m_phase,m_maxper);
      ArrayResize(m_cycle,m_maxper);
      ArrayResize(m_peaks,m_maxper);
      ArrayResize(m_peaks_index,m_maxper);
     }

  }

Входные параметры приведены ниже:

• detrend - логический входной параметр, указывающий на необходимость удаления тренда.
• apply_window - логический параметр, определяющий, следует ли применять оконную функцию.
• min_period - самый короткий период или самая высокая частота, которая будет разрешена алгоритмом Гёрцеля. Значение не может быть ниже 2.
• max_period - самый длинный период, который будет учитываться при анализе. Это значение представляет частоту с самым длинным периодом, оно не может быть меньше или равно min_period.
• squard_amp - как должно быть представлено значение амплитуды. При false амплитуда будет рассчитываться как квадратный корень.

Класс имеет шесть доступных методов, которые будут интересны пользователям.

//+-------------------------------------------------------------------+
//|          public method to access the amplitude values             |
//+-------------------------------------------------------------------+
bool CGoertzelCycle::GetSpectrum(const double &in_data[],double &out_amplitude[])
  {
   if(spectrum(in_data))
     {
      ArrayCopy(out_amplitude,m_amplitude);
      return true;
     }
   return false;
  }

GetSpectrum() требует два входных массива, первый из которых in_data — это необработанный ряд для анализа. Во втором массиве будут выводиться значения амплитуды. Параметры, используемые для преобразования, должны были быть указаны путем инициализации экземпляра с помощью параметризованного конструктора.

//+------------------------------------------------------------------+
//|         public method to access the amplitude values             |
//+------------------------------------------------------------------+
bool CGoertzelCycle::GetSpectrum(bool detrend,bool squared_amp,bool apply_window,uint min_period,uint max_period,const double &in_data[],double &out_amplitude[])
  {
   m_pivot=m_slope=0.0;
   m_cycles=0;
   m_maxper=max_period;
   m_minper=min_period;
   m_detrend=detrend;
   m_squaredamp=squared_amp;
   m_flatten=apply_window;

   if(m_maxper)
     {
      ArrayResize(m_amplitude,m_maxper);
      ArrayResize(m_phase,m_maxper);
      ArrayResize(m_cycle,m_maxper);
      ArrayResize(m_peaks,m_maxper);
      ArrayResize(m_peaks_index,m_maxper);
     }

   if(spectrum(in_data))
     {
      ArrayCopy(out_amplitude,m_amplitude);
      return true;
     }
   return false;

  }

Другой перегруженный метод GetSpectrum() принимает дополнительные параметры, идентичные параметрам параметризованного конструктора. Оба возвращают true в случае успеха и false в случае неудачи. Любые данные об ошибках будут записаны в журнал терминала.

//+----------------------------------------------------------------------------+
//|public method to get the dominant cycle periods arranged in descending order|
//+----------------------------------------------------------------------------+
uint CGoertzelCycle::GetDominantCycles(bool use_cycle_strength,const double &in_data[],double &out_cycles[])
  {
   if(!spectrum(in_data))
     {
      ArrayInitialize(out_cycles,0.0);
      return(0);
     }

   cyclepeaks(use_cycle_strength);

   if(out_cycles.Size()!=m_cycles)
      ArrayResize(out_cycles,m_cycles);

   for(uint i=0; i<m_cycles; i++)
      out_cycles[i]=m_cycle[m_peaks_index[i]];

   return m_cycles;

  }
//+----------------------------------------------------------------------------+
//|public method to get the dominant cycle periods arranged in descending order|
//+----------------------------------------------------------------------------+
uint CGoertzelCycle::GetDominantCycles(bool use_cycle_strength,bool detrend,bool squared_amp,bool apply_window,uint min_period,uint max_period,const double &in_data[],double &out_cycles[])
  {
   m_pivot=m_slope=0.0;
   m_cycles=0;
   m_maxper=max_period;
   m_minper=min_period;
   m_detrend=detrend;
   m_squaredamp=squared_amp;
   m_flatten=apply_window;

   if(m_maxper)
     {
      ArrayResize(m_amplitude,m_maxper);
      ArrayResize(m_phase,m_maxper);
      ArrayResize(m_cycle,m_maxper);
      ArrayResize(m_peaks,m_maxper);
      ArrayResize(m_peaks_index,m_maxper);
     }

   return(GetDominantCycles(use_cycle_strength,in_data,out_cycles));

  }

Метод GetDominantCycle() перегружен аналогично GetSpectrum(). Помимо двух массивов, необходимо указать логический параметр use_cycle_strength. Он указывает критерии определения доминирующего цикла. При false используются частоты с наибольшими амплитудами. В противном случае доминирующий цикл определяется путем расчета силы цикла, определяемой по формуле:

Доминирующие циклы выводятся в последний из входных массивов со значениями, расположенными в порядке убывания.

//+-----------------------------------------------------------------------+
//|method used to access calculated dominant cycles , for use in indcators|
//+-----------------------------------------------------------------------+
void CGoertzelCycle::CalculateDominantCycles(uint prev,uint total,bool use_cycle_strength,const double &in_data[], double &out_signal[])
  {

   uint limit =0;
   bool indexOut=ArrayGetAsSeries(out_signal);
   bool indexIn=ArrayGetAsSeries(in_data);

   if(prev<=0)
     {
      uint firstindex=0;
      if(indexOut)
        {
         limit=total-(m_maxper*3);
         firstindex=limit+1;
        }
      else
        {
         limit=m_maxper*3;
         firstindex=limit-1;
        }
      out_signal[firstindex]=0;
     }
   else
     {
      limit=(indexOut)?total-prev:prev;
     }

   uint found_cycles=0;
   if(indexOut)
     {
      for(int ibar=(int)limit; ibar>=0; ibar--)
        {
         spectrum(in_data,(indexIn)?ibar:total-ibar-1);
         out_signal[ibar]=(cyclepeaks(use_cycle_strength))?m_cycle[m_peaks_index[0]]:0.0;
        }
     }
   else
     {
      for(int ibar=(int)limit; ibar<(int)total; ibar++)
        {
         spectrum(in_data,(indexIn)?total-ibar-1:ibar);
         out_signal[ibar]=(cyclepeaks(use_cycle_strength))?m_cycle[m_peaks_index[0]]:0.0;
        }
     }


  }

Методы с префиксом Calculate в идеале следует использовать в индикаторах. CalculateDominantCycles() выводит доминирующие циклы для соответствующего бара. В prev должно быть установлено количество ранее рассчитанных значений индикатора. Total должно быть количеством доступных баров на графике. in_data — это место, куда можно передать ценовые котировки, а out_signal должен быть одним из индикаторных буферов.

//+-----------------------------------------------------------------------+
//|method used to access newly formed wave form, for use in indcators     |
//+-----------------------------------------------------------------------+
void CGoertzelCycle::CalculateWave(uint prev,uint total,uint max_cycles,bool use_cycle_strength,const double &in_data[], double &out_signal[])
  {
   uint limit =0;
   bool indexOut=ArrayGetAsSeries(out_signal);
   bool indexIn=ArrayGetAsSeries(in_data);

   if(prev<=0)
     {
      uint firstindex=0;
      if(indexOut)
        {
         limit=total-(m_maxper*3);
         firstindex=limit+1;
        }
      else
        {
         limit=m_maxper*3;
         firstindex=limit-1;
        }
      out_signal[firstindex]=0;
     }
   else
     {
      limit=(indexOut)?total-prev:prev;
     }

   uint found_cycles=0;
   if(indexOut)
     {
      for(int ibar=(int)limit; ibar>=0; ibar--)
        {
         spectrum(in_data,(indexIn)?ibar:total-ibar-1);
         out_signal[ibar]=out_signal[ibar+1]+wavepoint(use_cycle_strength,max_cycles);
        }
     }
   else
     {
      for(int ibar=(int)limit; ibar<(int)total; ibar++)
        {
         spectrum(in_data,(indexIn)?total-ibar-1:ibar);
         out_signal[ibar]=out_signal[ibar-1]+wavepoint(use_cycle_strength,max_cycles);
        }
     }

  }
//+------------------------------------------------------------------+

CalculateWave() имеет большинство параметров, общих с CalculateDominantCycles(). Он выводит отфильтрованное значение, рассчитанное на основе доминирующих частотных составляющих, выявленных алгоритмом Гёрцеля. Максимальное количество частотных составляющих задается параметром max_cycles.

Построение графика

Чтобы продемонстрировать использование класса и возможные применения Гёрцеля при разработке стратегии, представим два индикатора. Первый – это реализация стратегии, представленной в работе Денниса Мейерса (на английском). Он называет эту стратегию адаптивной 10-цикловой системой ДПФ Гёрцеля (Adaptive 10 Cycle Goertzel DFT System). С деталями можно ознакомиться по ссылке. Если говорить коротко, стратегия использует алгоритм Гёрцеля для извлечения десяти основных доминирующих циклов из скользящего окна ценовых данных, а затем использует эти циклы для построения новой ценовой кривой. Это предположительно отражает поведение цены при отфильтрованном шуме. Ключевыми параметрами этой стратегии являются минимальный и максимальный периоды частот, подлежащих выборке, наряду с максимальным количеством частотных составляющих, которые будут использоваться для построения отфильтрованного сигнала.

//--- input parameters
input bool     Detrend=true;
input bool     EndFlatten=true; 
input bool     SquaredAmp=true;
input bool     UseCycleStrength=false;
input uint     Maxper=72;
input uint     Minper=5;
input uint     MaxCycles=10;
input double   pntup=0.5;//Percent increase threshold
input double   pntdn=0.5;//Percent decrease threshold
//--- indicator buffers

Индикатор использует два порога для запуска сигналов длинной и короткой позиции в зависимости от величины движения относительно недавнего пика или минимума. В коде входные переменные pntup и pntdn представляют собой проценты.

//+------------------------------------------------------------------+
//|                                            NCycleGoertzelDft.mq5 |
//|                                  Copyright 2023, MetaQuotes Ltd. |
//|                                             https://www.mql5.com |
//+------------------------------------------------------------------+
#property copyright "Copyright 2023, MetaQuotes Ltd."
#property link      "https://www.mql5.com"
#property version   "1.00"
#include<GoertzelCycle.mqh>
#property indicator_separate_window
#property indicator_buffers 5
#property indicator_plots   5 
//--- plot Wave
#property indicator_label1  "Wave"
#property indicator_type1   DRAW_LINE
#property indicator_color1  clrBlack
#property indicator_style1  STYLE_SOLID
#property indicator_width1  1
//--- plot Up
#property indicator_label2  "Peak"
#property indicator_type2   DRAW_NONE
//--- plot Dwn
#property indicator_label3  "Trough"
#property indicator_type3   DRAW_NONE
//--- plot Up
#property indicator_label4  "Long"
#property indicator_type4   DRAW_LINE
#property indicator_color4  clrBlue
#property indicator_style4  STYLE_SOLID
#property indicator_width4  2
//--- plot Dwn
#property indicator_label5  "Short"
#property indicator_type5   DRAW_LINE
#property indicator_color5  clrRed
#property indicator_style5  STYLE_SOLID
#property indicator_width5  2
//--- input parameters
input bool     Detrend=true;
input bool     EndFlatten=true; 
input bool     SquaredAmp=true;
input bool     UseCycleStrength=false;
input uint     Maxper=72;
input uint     Minper=5;
input uint     MaxCycles=10;
input double   pntup=0.5;//Percent increase threshold
input double   pntdn=0.5;//Percent decrease threshold
//--- indicator buffers

double  Wave[],Peak[],Trough[],Long[],Short[];
CGoertzelCycle *Gc;
//+------------------------------------------------------------------+
//| Custom indicator initialization function                         |
//+------------------------------------------------------------------+
int OnInit()
  {
//--- indicator buffers mapping
   SetIndexBuffer(0,Wave,INDICATOR_DATA);
   SetIndexBuffer(1,Peak,INDICATOR_DATA);
   SetIndexBuffer(2,Trough,INDICATOR_DATA);
   SetIndexBuffer(3,Long,INDICATOR_DATA);
   SetIndexBuffer(4,Short,INDICATOR_DATA);
//---   
   IndicatorSetInteger(INDICATOR_DIGITS,5);
//---   
   PlotIndexSetDouble(0,PLOT_EMPTY_VALUE,0.0);
   PlotIndexSetDouble(1,PLOT_EMPTY_VALUE,0.0);
   PlotIndexSetDouble(2,PLOT_EMPTY_VALUE,0.0);
   PlotIndexSetDouble(3,PLOT_EMPTY_VALUE,0.0);
   PlotIndexSetDouble(4,PLOT_EMPTY_VALUE,0.0);
//---
   Gc=new CGoertzelCycle(Detrend,SquaredAmp,EndFlatten,Minper,Maxper);
   
   if(Gc==NULL)
    {
     Print("Invalid Goertzel object");
     return(INIT_FAILED);
    }  
//---     
   return(INIT_SUCCEEDED);
  }
//+------------------------------------------------------------------+
//| Indicator DeInitialization function                              |
//+------------------------------------------------------------------+
void OnDeinit (const int reason)
 {
  if(CheckPointer(Gc)==POINTER_DYNAMIC)
      delete Gc;
 }  
//+------------------------------------------------------------------+
//| Custom indicator iteration function                              |
//+------------------------------------------------------------------+
int OnCalculate(const int rates_total,
                const int prev_calculated,
                const int begin,
                const double &price[])
  {
   int lim=0;
   
   if(prev_calculated<=0)
      lim=(int)(Maxper*3)+2;
   else 
      lim=prev_calculated;
   
   
//---
    Gc.CalculateWave(prev_calculated,rates_total,MaxCycles,UseCycleStrength,price,Wave);
//---
   for(int i=lim;i<rates_total-1;i++)
      {
       Peak[i]=Trough[i]=0.0;   
       
       if(Wave[i]>Wave[i+1] && Wave[i]>Wave[i-1])
         Peak[i]=Wave[i];
       else 
         if(Wave[i]<Wave[i+1] && Wave[i]<Wave[i-1])
           Trough[i]=Wave[i];
         
       if(i<int(Maxper*3*2)) 
          {
           continue;
          } 
          
       double lp,lt;
          lp=lt=0;  
               
       if(i==int(Maxper*3*2))
         {
          lp=getlastPeakTrough(i,Peak);
          lt=getlastPeakTrough(i,Trough);
          if(Wave[i]>Wave[i-1] && lt)
            {
             Long[i]=Wave[i];
             Short[i]=0.0;
            } 
          else
            if(Wave[i]<Wave[i-1] && lp)
              {
               Short[i]=Wave[i];
               Long[i]=0.0;
              } 
         }
       else
         {
         
           Long[i]=(Long[i-1]!=0)?Wave[i]:Long[i-1];
           Short[i]=(Short[i-1]!=0)?Wave[i]:Short[i-1];
          
          if(Short[i-1]!=0 && Wave[i]>Wave[i-1])
           {
            lt=getlastPeakTrough(i,Trough);
            if(lt && (Wave[i]-lt)/lt > pntup/100 )
              {
               Long[i]=Wave[i];
               Short[i]=0.0;
              }
            else
              {
               Short[i]=Wave[i];
               Long[i]=0.0;
              }    
           }
          else
           if(Long[i-1]!=0 && Wave[i]<Wave[i-1])
           {
            lp=getlastPeakTrough(i,Peak);
            if(lp && (lp-Wave[i])/lp > pntdn/100 )
              {
                Short[i]=Wave[i];
                Long[i]=0.0;
              }
             else
              {
                Long[i]=Wave[i];
                Short[i]=0.0;
              }    
           }
         }  
      
      }
//--- return value of prev_calculated for next call
   return(rates_total);
  }
//+------------------------------------------------------------------+
//| helper function that returns either last peak or trough          |
//+------------------------------------------------------------------+
double getlastPeakTrough(int shift, double &buffer[])
  {
   uint j;
   double value=0.0;
   for(j=shift-1;j>(Maxper*3)+2;j--)
     {
      if(buffer[j]==0.0)
         continue;
      else
         return(buffer[j]);
     }
   return(value);
  }
//+-----------------------------------------------------------------------------------------------++
        

Сигнал рассчитывается по формуле:

где: a - амплитуда, phi - фаза, f - частота, B - количество последних выбранных баров, представляющих данные, из которых извлекаются частотные компоненты, что эквивалентно размеру скользящего окна. Это значение равно трехкратному максимальному периоду рассматриваемого цикла. Код индикатора показан выше. Волновая точка – это значение кривой по соответствующему индексу.

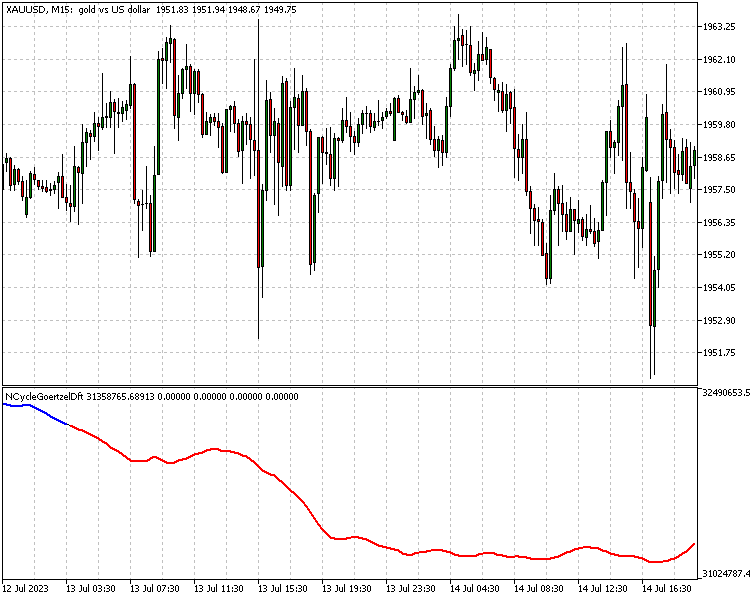
Более подробная информация о торговых правилах приведена в работе Мейерса.

Адаптивные индикаторы

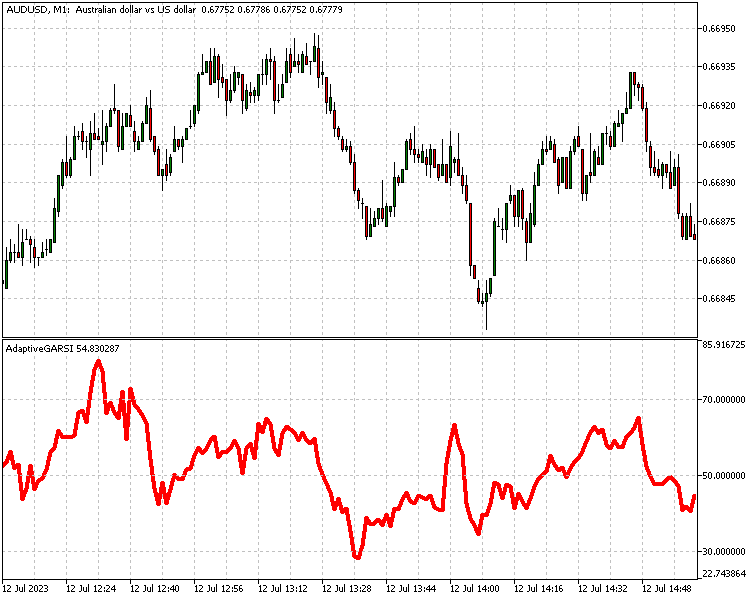
Еще один способ применить метод Гёрцеля для разработки стратегии — сделать индикаторы адаптивными с его помощью. Статья "Теория адаптивных индикаторов и ее реализация в MQL5" подробно описывает этот метод с использованием методик Джона Элерса. Мы можем сделать то же самое, используя алгоритм Гёрцеля. Ниже представлена реализация адаптивной версии индикатора относительной силы (RSI).

//+------------------------------------------------------------------+
//|                                                AdaptiveGARSI.mq5 |
//|                                  Copyright 2023, MetaQuotes Ltd. |
//|                                             https://www.mql5.com |
//+------------------------------------------------------------------+
#property copyright "Copyright 2023, MetaQuotes Ltd."
#property link      "https://www.mql5.com"
#property version   "1.00"
#property indicator_separate_window
#include<GoertzelCycle.mqh>
#property indicator_buffers 2
#property indicator_plots   1
//--- plot RSi
#property indicator_label1  "RSi"
#property indicator_type1   DRAW_LINE
#property indicator_color1  clrRed
#property indicator_style1  STYLE_SOLID
#property indicator_width1  1
//---
#property indicator_level1        70
#property indicator_level2        50
#property indicator_level3        30
//---
input bool     Detrend=true;
input bool     EndFlatten=true; 
input bool     SquaredAmp=true;
input bool     UseCycleStrength=false;
input uint     Maxper=72;
input uint     Minper=5;
//--- indicator buffers
double         RSiBuffer[];
double         DomPeriodBuffer[];

CGoertzelCycle *Gc;
//+------------------------------------------------------------------+
//| Custom indicator initialization function                         |
//+------------------------------------------------------------------+
int OnInit()
  {
//--- indicator buffers mapping
   SetIndexBuffer(0,RSiBuffer,INDICATOR_DATA);
   SetIndexBuffer(1,DomPeriodBuffer,INDICATOR_CALCULATIONS);
//---
   Gc=new CGoertzelCycle(Detrend,SquaredAmp,EndFlatten,Minper,Maxper);
//---   
   if(Gc==NULL)
    {
     Print("Invalid Goertzel object");
     return(INIT_FAILED);
    }  
//---    
   return(INIT_SUCCEEDED);
  }
//+------------------------------------------------------------------+
//| Indicator DeInitialization function                              |
//+------------------------------------------------------------------+
void OnDeinit (const int reason)
 {
  if(CheckPointer(Gc)==POINTER_DYNAMIC)
      delete Gc;
 }    
//+------------------------------------------------------------------+
//| Custom indicator iteration function                              |
//+------------------------------------------------------------------+
int OnCalculate(const int rates_total,
                const int prev_calculated,
                const datetime &time[],
                const double &open[],
                const double &high[],
                const double &low[],
                const double &close[],
                const long &tick_volume[],
                const long &volume[],
                const int &spread[])
  {
//---
   uint lim=0;
//---
   Gc.CalculateDominantCycles(prev_calculated,rates_total,UseCycleStrength,close,DomPeriodBuffer);
//---
   if(prev_calculated<=0)
       lim=int(Maxper*3)+int(DomPeriodBuffer[(Maxper*3)-1]) - 1;
   else
       lim=prev_calculated; 
       
//---
   double cu,cd;
   for(int i =int(lim);i<rates_total;i++)
    {
      cd=0.0;
      cu=0.0;
      double p=DomPeriodBuffer[i];
      int j=0;
      for(j=0;j<int(p);j++)
        {
         if(close[i-j]-close[i-j-1]>0)cu=cu+(close[i-j]-close[i-j-1]);
         if(close[i-j]-close[i-j-1]<0)cd=cd+(close[i-j-1]-close[i-j]);
        }
      if(cu+cd!=0)
         RSiBuffer[i]=100*cu/(cu+cd);
      else 
         RSiBuffer[i]=0.0;
    
    }        
//--- return value of prev_calculated for next call
   return(rates_total);
  }
//+------------------------------------------------------------------+

Заключение

В статье были наглядно продемонстрированы возможности алгоритма Гёрцеля и полезные утилиты для его применения. Задача состоит в том, как эффективно применить этот метод к финансовым данным и извлечь значимые сигналы. Алгоритм явно находится в невыгодном положении по сравнению с MESA, поскольку он способен определять только одну частоту за раз. Его практическое применение также подчеркивает слабость обнаружения циклов на финансовых рынках, поскольку трудно измерить преобладающий цикл и точно определить, когда он закончится. Решение этих трудностей требует сочетания знаний предметной области, надежных методов предварительной обработки данных, стратегий управления рисками, а также постоянного мониторинга и адаптации к меняющейся динамике рынка.

Прикрепленный zip-файл содержит весь исходный код, описанный в статье.

Имя файла	Описание
Mql5/include/Goertzel.mqh	Включаемый файл для класса CGoertzel, реализующего алгоритм Гёрцеля
Mql5/include/ GoertzelCycle.mqh	Включаемый файл для класса CGoertzelCycle для анализа циклов с использованием алгоритма Гёрцеля
Mql5/indicators/ NCycleGoertzelDft.mq5	Индикатор, частично реализующий стратегию Д. Мейерса, использующую алгоритм Гёрцеля.
Mql5/indicators/ AdaptiveGARSI.mq5	Реализация адаптивной версии индикатора RSI с динамическим ретроспективным анализом, рассчитанного по алгоритму Гёрцеля.