Análisis de ciclos usando el algoritmo de Goertzel

Introducción

El algoritmo de Goertzel es una técnica de tratamiento digital de señales conocida por su eficacia para detectar determinados componentes de frecuencia. Su precisión, su capacidad de operar en tiempo real y su eficiencia computacional lo hacen adecuado para analizar series temporales financieras. En este artículo, veremos algunas formas prácticas de utilizar el método para analizar los ciclos dominantes en el desarrollo de estrategias. Consideraremos la implementación del algoritmo en MQL5 y ofreceremos un ejemplo de uso del código para definir ciclos en las cotizaciones.

El algoritmo de Goertzel

El algoritmo de Goertzel, propuesto por Gerald Goertzel, se usa para calcular eficazmente los términos individuales de la transformada discreta de Fourier (DFT). El método se introdujo en 1958 y desde entonces se ha aplicado en diversos campos, tales como la ingeniería, las matemáticas y la física. La principal aplicación del algoritmo de Hertzel consiste en identificar determinados componentes de frecuencia en una señal digital, lo cual lo hace muy valioso en escenarios en los que solo son importantes determinados componentes de frecuencia. En comparación con la transformada rápida de Fourier (FFT), requiere menos cálculos para detectar un número limitado de componentes de frecuencia, cosa que lo hace eficiente desde el punto de vista computacional.

El algoritmo se representa mediante la fórmula:

donde:

• X - valor acumulado en la frecuencia k
• cos() - función de coseno
• π - constante matemática pi (aproximadamente 3,14159)
• k - índice del intervalo de frecuencias de interés (en el rango de 0 a N - 1, donde N es el número total de muestras)
• N - longitud de la señal de entrada
• X[k-1] y X[k-2] - valores de X calculados previamente para la frecuencia en k
• x[n] - n-ésima muestra de la señal de entrada

Para calcular los componentes real e imaginario usando el algoritmo de Goertzel, necesitaremos iterar las muestras de la señal de entrada y realizar los siguientes cálculos:

Inicializamos las variables:

• N - número de muestras en la señal de entrada.
• k - índice del intervalo de frecuencias de interés (0 <= k < N).
• omega - frecuencia correspondiente al intervalo de frecuencia necesario (2 * pi * k / N).
• coeff - coeficiente usado en el cálculo (2 * cos(omega)).
• s_prev - valor anterior de la variable state.
• s_prev2 - valor previo al valor anterior de la variable state.
• s - valor actual de la variable state.

Vamos a iterar cada muestra de la señal de entrada:

• Actualizaremos el valor actual de la variable state (s) utilizando la fórmula:

  
  

donde x[n] es la muestra de entrada actual.

Ahora actualizaremos los valores anteriores de la variable state:

Tras enumerar todas las muestras, los valores finales de las variables state (S,Sprev,Sprev2) representarán los componentes real e imaginario de la DPF en el intervalo de frecuencia deseado (k).

El componente real se definirá de la forma siguiente:

El componente imaginario se definirá como:

Las frecuencias que pueden detectarse mediante la DFT oscilan entre 1/N y (N/2)/N, siendo N el número de puntos de datos en la serie o, en nuestro caso, el número de barras de precios analizadas. Al analizar las cotizaciones de precios, es posible que solo podamos observar rangos de frecuencia limitados al intervalo 1/N. Debido a ello, John Ehlers propuso el método de Análisis Espectral de Entropía Máxima (MESA) para superar esta limitación.

El algoritmo de Goertzel puede usarse como alternativa al MESA de Ehler, que, según un trabajo de investigación de D. Meyers, es capaz de obtener mejores resultados (en términos de resolución espectral) en determinadas condiciones. Una de estas condiciones tiene que ver con la cantidad de ruido contenido en la señal. Según Meyers, el algoritmo de Goertzel es capaz de superar al método MESA, especialmente cuando hablamos de señales llenas de ruido, un problema habitual en las series temporales financieras. Si le resulta de interés, el lector podrá leer la documentación en formato pdf (en inglés).

La clase CGoertzel

La clase CGoertzel es una implementación sencilla del algoritmo de Goertzel que permite muestrear un rango de frecuencias en un conjunto de datos.

//+------------------------------------------------------------------+
//| CGoertze class implementing Goertzel algorithm                   |
//+------------------------------------------------------------------+
class CGoertzel
  {
private:
   uint              m_minPeriod;
   uint              m_maxPeriod;
public:
   //constructor
                     CGoertzel(void)
     {
      m_minPeriod=m_maxPeriod=0;
     }
   //destructor
                    ~CGoertzel(void)
     {
     }
   //get methods
   uint              GetMinPeriodLength(void) {   return m_minPeriod;}
   uint              GetMaxPerodLength(void) {   return m_maxPeriod;}
   //set methods
   bool              SetMinMaxPeriodLength(const uint min_wavePeriod, const uint max_wavePeriod);
   // goertzel dft transform methods
   bool              Dft(const double &in_data[],complex &out[]);
   bool              Dft(const double &in_data[], double &out_real[], double &out_imaginary[]);
   bool              Dft(const uint min_wavePeriod,const uint max_wavePeriod,const double &in_data[],complex &out[]);
   bool              Dft(const uint min_wavePeriod,const uint max_wavePeriod,const double &in_data[], double &out_real[], double &out_imaginary[]);
  };

Como Goertzel solo muestrea un número limitado de frecuencias a la vez, deberemos establecer la banda de frecuencias de interés. En una clase, la anchura de la banda se especifica según el periodo de frecuencia mínimo y máximo.

Existen dos formas de establecer estos valores: utilizando SetMinMaxPeriodLength(), podemos especificar los periodos mínimo y máximo.

//+------------------------------------------------------------------+
//| Set the Minimum and maximum periods of selected frequency band   |
//+------------------------------------------------------------------+
bool CGoertzel::SetMinMaxPeriodLength(const uint min_wavePeriod,const uint max_wavePeriod)
  {
   if(min_wavePeriod<2 || min_wavePeriod>=max_wavePeriod)
     {
      Print("Critical error min_wavePeriod cannot be less than max_wavePeriod or less than 2");
      return false;
     }

   m_minPeriod=min_wavePeriod;
   m_maxPeriod=max_wavePeriod;

   return true;
  }

La anchura de la banda también puede especificarse llamando a una de las dos sobrecargas del método DFT.

//+-----------------------------------------------------------------------------------+
//| Calculate the frequency domain representation of input array as complex array     |
//+-----------------------------------------------------------------------------------+
bool CGoertzel::Dft(const uint min_wavePeriod,const uint max_wavePeriod,const double &in_data[],complex &out[])
  {
   if(!SetMinMaxPeriodLength(min_wavePeriod,max_wavePeriod))
      return(false);

   return Dft(in_data,out);
  }
//+------------------------------------------------------------------------------------+
//| Calculate the frequency domain representation of input array as two separate arrays|
//+------------------------------------------------------------------------------------+
bool CGoertzel::Dft(const uint min_wavePeriod,const uint max_wavePeriod,const double &in_data[], double &out_real[], double &out_imaginary[])
  {
   if(!SetMinMaxPeriodLength(min_wavePeriod,max_wavePeriod))
      return(false);

   return Dft(in_data,out_real,out_imaginary);

  }

Dependiendo de la versión del método DFT utilizado, los componentes reales e imaginarios de la DFT se muestran en arrays aparte o en un único array de tipo complejo.

//+-----------------------------------------------------------------------------------+
//| Calculate the frequency domain representation of input array as complex array     |
//+-----------------------------------------------------------------------------------+
bool CGoertzel::Dft(const double &in_data[],complex &out[])
  {
   uint minsize=(3*m_maxPeriod);
   uint fullsize=in_data.Size();

   if(fullsize<minsize)
     {
      Print("Sample size too small in relation to the largest period cycle parameter");
      return false;
     }

   if(m_minPeriod>=m_maxPeriod || m_minPeriod<2)
     {
      Print("Critical error: Invalid input parameters :- max_period should be larger than min_period and min_period cannot be less than 2");
      return false;
     }

   if(out.Size()!=m_maxPeriod)
      ArrayResize(out,m_maxPeriod);
   
   double v0,v1,v2,freq,coeff,real,imag;


   for(uint i=0; i<m_maxPeriod; i++)
     {
      if(i<m_minPeriod)
        {
         out[i].imag=out[i].real=0.0;
         continue;
        }

      v0=v1=v2=0.0;
      freq=MathPow(i,-1);
      coeff=2.0*MathCos(2.0*M_PI*freq);
      for(uint k=minsize-1; k>0; k--)
        {
         v0=coeff*v1-v2+in_data[k];
         v2=v1;
         v1=v0;
        }

      real=v1-v2*0.5*coeff;

      imag=v2*MathSin(2*M_PI*freq);

      out[i].real=real;
      out[i].imag=imag;

     }

   return true;
  }
//+------------------------------------------------------------------------------------+
//| Calculate the frequency domain representation of input array as two separate arrays|
//+------------------------------------------------------------------------------------+
bool CGoertzel::Dft(const double &in_data[],double &out_real[],double &out_imaginary[])
  {
   uint minsize=(3*m_maxPeriod);
   uint fullsize=in_data.Size();

   if(fullsize<minsize)
     {
      Print("Sample size too small in relation to the largest period cycle parameter");
      return false;
     }

   if(m_minPeriod>=m_maxPeriod || m_minPeriod<2)
     {
      Print("Critical error: Invalid input parameters :- max_period should be larger than min_period and min_period cannot be less than 2");
      return false;
     }

   if(out_real.Size()!=m_maxPeriod)
      ArrayResize(out_real,m_maxPeriod);

   if(out_imaginary.Size()!=m_maxPeriod)
      ArrayResize(out_imaginary,m_maxPeriod);

   double v0,v1,v2,freq,coeff,real,imag;


   for(uint i=0; i<m_maxPeriod; i++)
     {
      if(i<m_minPeriod)
        {
         out_real[i]=out_imaginary[i]=0.0;
         continue;
        }

      v0=v1=v2=0.0;
      freq=MathPow(i,-1);
      coeff=2.0*MathCos(2.0*M_PI*freq);
      for(uint k=minsize-1; k>0; k--)
        {
         v0=coeff*v1-v2+in_data[k];
         v2=v1;
         v1=v0;
        }

      real=v1-v2*0.5*coeff;

      imag=v2*MathSin(2*M_PI*freq);

      out_real[i]=real;
      out_imaginary[i]=imag;

     }

   return true;
  }

Pre-procesamiento

Los datos no siempre pueden introducirse sin más en el algoritmo de Goertzel y transformarse en el dominio de la frecuencia. Dependiendo de la naturaleza de la muestra de datos, podrían ser necesarios varios pasos de pre-procesamiento. El algoritmo de Goertzel es un subconjunto de la DPF, por lo que aquí también se pueden aplicar las transformaciones necesarias antes de realizar la transformada rápida de Fourier. Esto resulta especialmente cierto para los datos que no son periódicos. Estas series deben tratarse con la función de ventana correspondiente. Esto permitirá estrechar adecuadamente los extremos de la serie, minimizando así la posibilidad de fugas de espectro. En los estudios del algoritmo de Goertzel, se suele usar un algoritmo de aplanamiento del punto final. La aplicación de esta técnica se muestra mediante la fórmula:

donde a es el primer valor de precio de la serie a analizar,b es el último, y Flat(i) es la serie que se transmitirá al algoritmo de Goertzel.

Resulta recomendable eliminar las tendencias y los valores atípicos evidentes antes de aplicar la ventana a los datos. Las tendencias deberán eliminarse de los datos de origen, pero solo si es necesario. La eliminación injustificada de una tendencia puede causar distorsiones que se trasladarán a la representación de la muestra en el dominio de la frecuencia. Este es un tema amplio: existen muchos tipos de eliminación de tendencias, con sus propias ventajas e inconvenientes. Los profesionales deben poner interés y esforzarse al examinar el método más adecuado para su posterior aplicación. En este artículo, usaremos un sencillo método de mínimos cuadrados adecuado para eliminar la tendencia de las cotizaciones de precios. A continuación, le mostramos un extracto.

//+------------------------------------------------------------------+
//|               helper method for detrending data                  |
//+------------------------------------------------------------------+
void CGoertzelCycle::detrend(const double &in_data[], double &out_data[])
  {
   uint i ;
   double xmean, ymean, x, y, xy, xx ;
   xmean=ymean=x=y=xx=xy=0.0;

   xmean=0.5*double(in_data.Size()-1);

   if(out_data.Size()!=in_data.Size())
      ArrayResize(out_data,in_data.Size());


   for(i=0; i<out_data.Size(); i++)
     {
      x = double(i) - xmean ;
      y = in_data[i] - ymean ;
      xx += x * x ;
      xy += x * y ;
     }

   m_slope=xy/xx;
   m_pivot=xmean;

   for(i=0; i<out_data.Size(); i++)
      out_data[i]=in_data[i]-(double(i)-xmean)*m_slope;
  }

La clase CGoertzelCycle

El archivo de inclusión GoertzelCycle.mqh contendrá la clase CGoertzelCycle usada para realizar análisis cíclicos de conjuntos de datos utilizando el algoritmo de Goertzel.

//+------------------------------------------------------------------+
//|   CGoertzelCycle class for cycle using the Goertzel Algorithm    |
//+------------------------------------------------------------------+
class CGoertzelCycle
  {
private:
   CGoertzel*m_ga;
   double            m_pivot;
   double            m_slope;
   bool              m_detrend;
   bool              m_squaredamp;
   bool              m_flatten;
   uint              m_cycles;
   uint              m_maxper,m_minper;
   double            m_amplitude[];
   double            m_peaks[];
   double            m_cycle[];
   double            m_phase[];
   uint              m_peaks_index[];
   double            m_detrended[];
   double            m_flattened[];
   double            m_raw[];


   void              detrend(const double &in_data[], double &out_data[]);
   double            wavepoint(bool use_cycle_strength,uint max_cycles);
   bool              spectrum(const double &in_data[],int shift=-1);
   uint              cyclepeaks(bool use_cycle_strength);

public :
                     CGoertzelCycle(void);
                     CGoertzelCycle(bool detrend,bool squared_amp,bool apply_window, uint min_period,uint max_period);
                    ~CGoertzelCycle(void);


   bool              GetSpectrum(const double &in_data[],double &out_amplitude[]);
   bool              GetSpectrum(bool detrend,bool squared_amp,bool apply_window, uint min_period,uint max_period,const double &in_data[],double &out_amplitude[]);
   uint              GetDominantCycles(bool use_cycle_strength,const double &in_data[],double &out_cycles[]);
   uint              GetDominantCycles(bool use_cycle_strenght,bool detrend,bool squared_amp,bool apply_window, uint min_period,uint max_period,const double &in_data[],double &out_cycles[]);
   void              CalculateDominantCycles(uint prev,uint total,bool use_cycle_strength,const double &in_data[], double &out_signal[]);
   void              CalculateWave(uint prev,uint total,uint max_cycles, bool use_cycle_strength,const double &in_data[], double &out_signal[]);
  };

La clase tiene dos constructores. El constructor parametrizado permite inicializar un ejemplar con ajustes personalizados.

//+------------------------------------------------------------------+
//|                     Default Constructor                          |
//+------------------------------------------------------------------+
CGoertzelCycle::CGoertzelCycle(void)
  {
   m_pivot=m_slope=0.0;
   m_maxper=m_minper=m_cycles=0;
   m_detrend=m_squaredamp=m_flatten=false;
   m_ga=new CGoertzel();
  }
//+------------------------------------------------------------------+
//|                      Parametric Constructor                      |
//+------------------------------------------------------------------+
CGoertzelCycle::CGoertzelCycle(bool detrend,bool squared_amp,bool apply_window, uint min_period,uint max_period)
  {
   m_pivot=m_slope=0.0;
   m_cycles=0;
   m_maxper=max_period;
   m_minper=min_period;
   m_detrend=detrend;
   m_squaredamp=squared_amp;
   m_flatten=apply_window;
   m_ga=new CGoertzel();

   if(m_maxper)
     {
      ArrayResize(m_amplitude,m_maxper);
      ArrayResize(m_phase,m_maxper);
      ArrayResize(m_cycle,m_maxper);
      ArrayResize(m_peaks,m_maxper);
      ArrayResize(m_peaks_index,m_maxper);
     }

  }

Los parámetros de entrada serán los siguientes:

• detrend - parámetro de entrada lógico que indica la necesidad de eliminar la tendencia.
• apply_window - parámetro booleano que determina si se debe aplicar la función de ventana.
• min_period - periodo más corto o la frecuencia más alta que permitirá el algoritmo Goertzel. El valor no puede ser inferior a 2.
• max_period - periodo más largo que se tendrá en cuenta en el análisis. Este valor representará la frecuencia con el periodo más largo, y no puede ser menor o igual que min_period.
• squard_amp - cómo debe representarse el valor de amplitud. La amplitud se calculará como la raíz cuadrada.

La clase tendrá seis métodos disponibles que serán de interés para los usuarios.

//+-------------------------------------------------------------------+
//|          public method to access the amplitude values             |
//+-------------------------------------------------------------------+
bool CGoertzelCycle::GetSpectrum(const double &in_data[],double &out_amplitude[])
  {
   if(spectrum(in_data))
     {
      ArrayCopy(out_amplitude,m_amplitude);
      return true;
     }
   return false;
  }

GetSpectrum() requiere dos arrays de entrada, el primero de los cuales, in_data, será la serie sin procesar que se va a analizar. El segundo array mostrará los valores de amplitud. Los parámetros usados para la conversión deberán haberse especificado inicializando el ejemplar usando un constructor parametrizado.

//+------------------------------------------------------------------+
//|         public method to access the amplitude values             |
//+------------------------------------------------------------------+
bool CGoertzelCycle::GetSpectrum(bool detrend,bool squared_amp,bool apply_window,uint min_period,uint max_period,const double &in_data[],double &out_amplitude[])
  {
   m_pivot=m_slope=0.0;
   m_cycles=0;
   m_maxper=max_period;
   m_minper=min_period;
   m_detrend=detrend;
   m_squaredamp=squared_amp;
   m_flatten=apply_window;

   if(m_maxper)
     {
      ArrayResize(m_amplitude,m_maxper);
      ArrayResize(m_phase,m_maxper);
      ArrayResize(m_cycle,m_maxper);
      ArrayResize(m_peaks,m_maxper);
      ArrayResize(m_peaks_index,m_maxper);
     }

   if(spectrum(in_data))
     {
      ArrayCopy(out_amplitude,m_amplitude);
      return true;
     }
   return false;

  }

Otro método sobrecargado GetSpectrum() aceptará parámetros adicionales idénticos a los del constructor parametrizado. Ambos retornarán true si todo se ha realizado correctamente y false si no. Cualquier dato sobre errores se anotará en el registro del terminal.

//+----------------------------------------------------------------------------+
//|public method to get the dominant cycle periods arranged in descending order|
//+----------------------------------------------------------------------------+
uint CGoertzelCycle::GetDominantCycles(bool use_cycle_strength,const double &in_data[],double &out_cycles[])
  {
   if(!spectrum(in_data))
     {
      ArrayInitialize(out_cycles,0.0);
      return(0);
     }

   cyclepeaks(use_cycle_strength);

   if(out_cycles.Size()!=m_cycles)
      ArrayResize(out_cycles,m_cycles);

   for(uint i=0; i<m_cycles; i++)
      out_cycles[i]=m_cycle[m_peaks_index[i]];

   return m_cycles;

  }
//+----------------------------------------------------------------------------+
//|public method to get the dominant cycle periods arranged in descending order|
//+----------------------------------------------------------------------------+
uint CGoertzelCycle::GetDominantCycles(bool use_cycle_strength,bool detrend,bool squared_amp,bool apply_window,uint min_period,uint max_period,const double &in_data[],double &out_cycles[])
  {
   m_pivot=m_slope=0.0;
   m_cycles=0;
   m_maxper=max_period;
   m_minper=min_period;
   m_detrend=detrend;
   m_squaredamp=squared_amp;
   m_flatten=apply_window;

   if(m_maxper)
     {
      ArrayResize(m_amplitude,m_maxper);
      ArrayResize(m_phase,m_maxper);
      ArrayResize(m_cycle,m_maxper);
      ArrayResize(m_peaks,m_maxper);
      ArrayResize(m_peaks_index,m_maxper);
     }

   return(GetDominantCycles(use_cycle_strength,in_data,out_cycles));

  }

El método GetDominantCycle() se sobrecargará de forma similar a GetSpectrum(). Además de los dos arrays, deberá especificarse el parámetro lógico use_cycle_strength. Este indica los criterios para determinar el ciclo dominante. Se usarán las frecuencias con las amplitudes más altas. De lo contrario, el ciclo dominante se determinará calculando la potencia del ciclo, determinada mediante la fórmula:

Los ciclos dominantes se enviarán al último de los arrays de entrada con los valores ordenados de forma descendente.

//+-----------------------------------------------------------------------+
//|method used to access calculated dominant cycles , for use in indcators|
//+-----------------------------------------------------------------------+
void CGoertzelCycle::CalculateDominantCycles(uint prev,uint total,bool use_cycle_strength,const double &in_data[], double &out_signal[])
  {

   uint limit =0;
   bool indexOut=ArrayGetAsSeries(out_signal);
   bool indexIn=ArrayGetAsSeries(in_data);

   if(prev<=0)
     {
      uint firstindex=0;
      if(indexOut)
        {
         limit=total-(m_maxper*3);
         firstindex=limit+1;
        }
      else
        {
         limit=m_maxper*3;
         firstindex=limit-1;
        }
      out_signal[firstindex]=0;
     }
   else
     {
      limit=(indexOut)?total-prev:prev;
     }

   uint found_cycles=0;
   if(indexOut)
     {
      for(int ibar=(int)limit; ibar>=0; ibar--)
        {
         spectrum(in_data,(indexIn)?ibar:total-ibar-1);
         out_signal[ibar]=(cyclepeaks(use_cycle_strength))?m_cycle[m_peaks_index[0]]:0.0;
        }
     }
   else
     {
      for(int ibar=(int)limit; ibar<(int)total; ibar++)
        {
         spectrum(in_data,(indexIn)?total-ibar-1:ibar);
         out_signal[ibar]=(cyclepeaks(use_cycle_strength))?m_cycle[m_peaks_index[0]]:0.0;
        }
     }


  }

De una forma ideal, los métodos con el prefijo Calculate deberían utilizarse en los indicadores. CalculateDominantCycles() muestra los ciclos dominantes de la barra correspondiente. prev debe definirse como el número de valores de indicador calculados previamente. Total deberá ser el número de barras disponibles en el gráfico. in_data será el lugar a donde se pueden transmitir las cotizaciones de precios, mientras que out_signal deberá ser uno de los búferes de indicador.

//+-----------------------------------------------------------------------+
//|method used to access newly formed wave form, for use in indcators     |
//+-----------------------------------------------------------------------+
void CGoertzelCycle::CalculateWave(uint prev,uint total,uint max_cycles,bool use_cycle_strength,const double &in_data[], double &out_signal[])
  {
   uint limit =0;
   bool indexOut=ArrayGetAsSeries(out_signal);
   bool indexIn=ArrayGetAsSeries(in_data);

   if(prev<=0)
     {
      uint firstindex=0;
      if(indexOut)
        {
         limit=total-(m_maxper*3);
         firstindex=limit+1;
        }
      else
        {
         limit=m_maxper*3;
         firstindex=limit-1;
        }
      out_signal[firstindex]=0;
     }
   else
     {
      limit=(indexOut)?total-prev:prev;
     }

   uint found_cycles=0;
   if(indexOut)
     {
      for(int ibar=(int)limit; ibar>=0; ibar--)
        {
         spectrum(in_data,(indexIn)?ibar:total-ibar-1);
         out_signal[ibar]=out_signal[ibar+1]+wavepoint(use_cycle_strength,max_cycles);
        }
     }
   else
     {
      for(int ibar=(int)limit; ibar<(int)total; ibar++)
        {
         spectrum(in_data,(indexIn)?total-ibar-1:ibar);
         out_signal[ibar]=out_signal[ibar-1]+wavepoint(use_cycle_strength,max_cycles);
        }
     }

  }
//+------------------------------------------------------------------+

CalculateWave() tiene la mayoría de los parámetros en común con CalculateDominantCycles(), y produce un valor filtrado calculado a partir de los componentes de frecuencia dominantes identificados por el algoritmo de Goertzel. El número máximo de componentes de frecuencia se especificará usando el parámetro max_cycles.

Gráficos

Para demostrar el uso de la clase y las posibles aplicaciones de Goertzel en el desarrollo de estrategias, presentaremos dos indicadores. El primero será la aplicación de la estrategia presentada en el trabajo de Dennis Meyers (en inglés). El autor denomina esta estrategia Sistema DFT Adaptativo de 10 Ciclos de Goertzel (Adaptive 10 Cycle Goertzel DFT System). Podrá consultar los detalles en el enlace. Resumiendo, la estrategia utiliza el algoritmo de Goertzel para extraer diez grandes ciclos dominantes de una ventana deslizante de datos de precio y, a continuación, utiliza esos ciclos para construir una nueva curva de precios. Esto presumiblemente reflejará el comportamiento del precio bajo ruido filtrado. Los parámetros clave de esta estrategia son los periodos mínimo y máximo de frecuencias que deben muestrearse, junto con el número máximo de componentes de frecuencia que deben usarse para construir la señal filtrada.

//--- input parameters
input bool     Detrend=true;
input bool     EndFlatten=true; 
input bool     SquaredAmp=true;
input bool     UseCycleStrength=false;
input uint     Maxper=72;
input uint     Minper=5;
input uint     MaxCycles=10;
input double   pntup=0.5;//Percent increase threshold
input double   pntdn=0.5;//Percent decrease threshold
//--- indicator buffers

El indicador usa dos umbrales para activar las señales de posición larga y corta según la magnitud del movimiento en relación con el máximo o mínimo reciente. En el código, las variables de entrada pntup y pntdn supondrán porcentajes.

//+------------------------------------------------------------------+
//|                                            NCycleGoertzelDft.mq5 |
//|                                  Copyright 2023, MetaQuotes Ltd. |
//|                                             https://www.mql5.com |
//+------------------------------------------------------------------+
#property copyright "Copyright 2023, MetaQuotes Ltd."
#property link      "https://www.mql5.com"
#property version   "1.00"
#include<GoertzelCycle.mqh>
#property indicator_separate_window
#property indicator_buffers 5
#property indicator_plots   5 
//--- plot Wave
#property indicator_label1  "Wave"
#property indicator_type1   DRAW_LINE
#property indicator_color1  clrBlack
#property indicator_style1  STYLE_SOLID
#property indicator_width1  1
//--- plot Up
#property indicator_label2  "Peak"
#property indicator_type2   DRAW_NONE
//--- plot Dwn
#property indicator_label3  "Trough"
#property indicator_type3   DRAW_NONE
//--- plot Up
#property indicator_label4  "Long"
#property indicator_type4   DRAW_LINE
#property indicator_color4  clrBlue
#property indicator_style4  STYLE_SOLID
#property indicator_width4  2
//--- plot Dwn
#property indicator_label5  "Short"
#property indicator_type5   DRAW_LINE
#property indicator_color5  clrRed
#property indicator_style5  STYLE_SOLID
#property indicator_width5  2
//--- input parameters
input bool     Detrend=true;
input bool     EndFlatten=true; 
input bool     SquaredAmp=true;
input bool     UseCycleStrength=false;
input uint     Maxper=72;
input uint     Minper=5;
input uint     MaxCycles=10;
input double   pntup=0.5;//Percent increase threshold
input double   pntdn=0.5;//Percent decrease threshold
//--- indicator buffers

double  Wave[],Peak[],Trough[],Long[],Short[];
CGoertzelCycle *Gc;
//+------------------------------------------------------------------+
//| Custom indicator initialization function                         |
//+------------------------------------------------------------------+
int OnInit()
  {
//--- indicator buffers mapping
   SetIndexBuffer(0,Wave,INDICATOR_DATA);
   SetIndexBuffer(1,Peak,INDICATOR_DATA);
   SetIndexBuffer(2,Trough,INDICATOR_DATA);
   SetIndexBuffer(3,Long,INDICATOR_DATA);
   SetIndexBuffer(4,Short,INDICATOR_DATA);
//---   
   IndicatorSetInteger(INDICATOR_DIGITS,5);
//---   
   PlotIndexSetDouble(0,PLOT_EMPTY_VALUE,0.0);
   PlotIndexSetDouble(1,PLOT_EMPTY_VALUE,0.0);
   PlotIndexSetDouble(2,PLOT_EMPTY_VALUE,0.0);
   PlotIndexSetDouble(3,PLOT_EMPTY_VALUE,0.0);
   PlotIndexSetDouble(4,PLOT_EMPTY_VALUE,0.0);
//---
   Gc=new CGoertzelCycle(Detrend,SquaredAmp,EndFlatten,Minper,Maxper);
   
   if(Gc==NULL)
    {
     Print("Invalid Goertzel object");
     return(INIT_FAILED);
    }  
//---     
   return(INIT_SUCCEEDED);
  }
//+------------------------------------------------------------------+
//| Indicator DeInitialization function                              |
//+------------------------------------------------------------------+
void OnDeinit (const int reason)
 {
  if(CheckPointer(Gc)==POINTER_DYNAMIC)
      delete Gc;
 }  
//+------------------------------------------------------------------+
//| Custom indicator iteration function                              |
//+------------------------------------------------------------------+
int OnCalculate(const int rates_total,
                const int prev_calculated,
                const int begin,
                const double &price[])
  {
   int lim=0;
   
   if(prev_calculated<=0)
      lim=(int)(Maxper*3)+2;
   else 
      lim=prev_calculated;
   
   
//---
    Gc.CalculateWave(prev_calculated,rates_total,MaxCycles,UseCycleStrength,price,Wave);
//---
   for(int i=lim;i<rates_total-1;i++)
      {
       Peak[i]=Trough[i]=0.0;   
       
       if(Wave[i]>Wave[i+1] && Wave[i]>Wave[i-1])
         Peak[i]=Wave[i];
       else 
         if(Wave[i]<Wave[i+1] && Wave[i]<Wave[i-1])
           Trough[i]=Wave[i];
         
       if(i<int(Maxper*3*2)) 
          {
           continue;
          } 
          
       double lp,lt;
          lp=lt=0;  
               
       if(i==int(Maxper*3*2))
         {
          lp=getlastPeakTrough(i,Peak);
          lt=getlastPeakTrough(i,Trough);
          if(Wave[i]>Wave[i-1] && lt)
            {
             Long[i]=Wave[i];
             Short[i]=0.0;
            } 
          else
            if(Wave[i]<Wave[i-1] && lp)
              {
               Short[i]=Wave[i];
               Long[i]=0.0;
              } 
         }
       else
         {
         
           Long[i]=(Long[i-1]!=0)?Wave[i]:Long[i-1];
           Short[i]=(Short[i-1]!=0)?Wave[i]:Short[i-1];
          
          if(Short[i-1]!=0 && Wave[i]>Wave[i-1])
           {
            lt=getlastPeakTrough(i,Trough);
            if(lt && (Wave[i]-lt)/lt > pntup/100 )
              {
               Long[i]=Wave[i];
               Short[i]=0.0;
              }
            else
              {
               Short[i]=Wave[i];
               Long[i]=0.0;
              }    
           }
          else
           if(Long[i-1]!=0 && Wave[i]<Wave[i-1])
           {
            lp=getlastPeakTrough(i,Peak);
            if(lp && (lp-Wave[i])/lp > pntdn/100 )
              {
                Short[i]=Wave[i];
                Long[i]=0.0;
              }
             else
              {
                Long[i]=Wave[i];
                Short[i]=0.0;
              }    
           }
         }  
      
      }
//--- return value of prev_calculated for next call
   return(rates_total);
  }
//+------------------------------------------------------------------+
//| helper function that returns either last peak or trough          |
//+------------------------------------------------------------------+
double getlastPeakTrough(int shift, double &buffer[])
  {
   uint j;
   double value=0.0;
   for(j=shift-1;j>(Maxper*3)+2;j--)
     {
      if(buffer[j]==0.0)
         continue;
      else
         return(buffer[j]);
     }
   return(value);
  }
//+-----------------------------------------------------------------------------------------------++
        

La señal se calculará mediante la fórmula

donde: a es la amplitud, phi es la fase, f es la frecuencia, B es el número de últimas barras seleccionadas que representan los datos de los que se extraen los componentes de frecuencia, lo cual equivale al tamaño de la ventana deslizante. Este valor será igual a tres veces el periodo máximo del ciclo considerado. El código del indicador se muestra más arriba. El punto de la onda será el valor de la curva en el índice correspondiente.

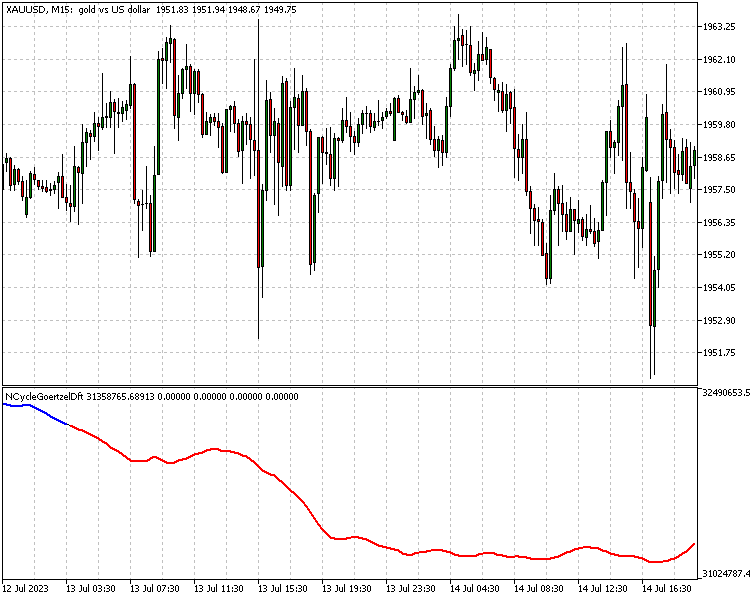
Encontrará información más detallada sobre las reglas comerciales en la obra de Meyers.

Indicadores adaptativos

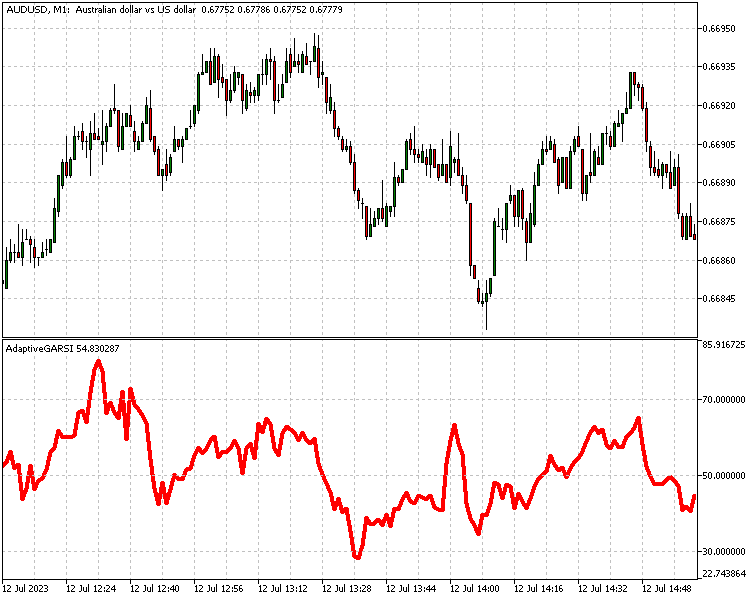
Otra forma de aplicar el método de Goertzel al desarrollo de estrategias es hacer que los indicadores se adapten a él. El artículo "Teoría de Indicadores Adaptables Avanzados e Implementación en MQL5" describe detalladamente este método utilizando los métodos de John Ehlers. Podemos hacer lo mismo usando el algoritmo de Goertzel. A continuación le mostramos la implementación de una versión adaptativa del Indicador de Fuerza Relativa (RSI).

//+------------------------------------------------------------------+
//|                                                AdaptiveGARSI.mq5 |
//|                                  Copyright 2023, MetaQuotes Ltd. |
//|                                             https://www.mql5.com |
//+------------------------------------------------------------------+
#property copyright "Copyright 2023, MetaQuotes Ltd."
#property link      "https://www.mql5.com"
#property version   "1.00"
#property indicator_separate_window
#include<GoertzelCycle.mqh>
#property indicator_buffers 2
#property indicator_plots   1
//--- plot RSi
#property indicator_label1  "RSi"
#property indicator_type1   DRAW_LINE
#property indicator_color1  clrRed
#property indicator_style1  STYLE_SOLID
#property indicator_width1  1
//---
#property indicator_level1        70
#property indicator_level2        50
#property indicator_level3        30
//---
input bool     Detrend=true;
input bool     EndFlatten=true; 
input bool     SquaredAmp=true;
input bool     UseCycleStrength=false;
input uint     Maxper=72;
input uint     Minper=5;
//--- indicator buffers
double         RSiBuffer[];
double         DomPeriodBuffer[];

CGoertzelCycle *Gc;
//+------------------------------------------------------------------+
//| Custom indicator initialization function                         |
//+------------------------------------------------------------------+
int OnInit()
  {
//--- indicator buffers mapping
   SetIndexBuffer(0,RSiBuffer,INDICATOR_DATA);
   SetIndexBuffer(1,DomPeriodBuffer,INDICATOR_CALCULATIONS);
//---
   Gc=new CGoertzelCycle(Detrend,SquaredAmp,EndFlatten,Minper,Maxper);
//---   
   if(Gc==NULL)
    {
     Print("Invalid Goertzel object");
     return(INIT_FAILED);
    }  
//---    
   return(INIT_SUCCEEDED);
  }
//+------------------------------------------------------------------+
//| Indicator DeInitialization function                              |
//+------------------------------------------------------------------+
void OnDeinit (const int reason)
 {
  if(CheckPointer(Gc)==POINTER_DYNAMIC)
      delete Gc;
 }    
//+------------------------------------------------------------------+
//| Custom indicator iteration function                              |
//+------------------------------------------------------------------+
int OnCalculate(const int rates_total,
                const int prev_calculated,
                const datetime &time[],
                const double &open[],
                const double &high[],
                const double &low[],
                const double &close[],
                const long &tick_volume[],
                const long &volume[],
                const int &spread[])
  {
//---
   uint lim=0;
//---
   Gc.CalculateDominantCycles(prev_calculated,rates_total,UseCycleStrength,close,DomPeriodBuffer);
//---
   if(prev_calculated<=0)
       lim=int(Maxper*3)+int(DomPeriodBuffer[(Maxper*3)-1]) - 1;
   else
       lim=prev_calculated; 
       
//---
   double cu,cd;
   for(int i =int(lim);i<rates_total;i++)
    {
      cd=0.0;
      cu=0.0;
      double p=DomPeriodBuffer[i];
      int j=0;
      for(j=0;j<int(p);j++)
        {
         if(close[i-j]-close[i-j-1]>0)cu=cu+(close[i-j]-close[i-j-1]);
         if(close[i-j]-close[i-j-1]<0)cd=cd+(close[i-j-1]-close[i-j]);
        }
      if(cu+cd!=0)
         RSiBuffer[i]=100*cu/(cu+cd);
      else 
         RSiBuffer[i]=0.0;
    
    }        
//--- return value of prev_calculated for next call
   return(rates_total);
  }
//+------------------------------------------------------------------+

Conclusión

El presente material ha demostrado claramente las capacidades del algoritmo de Goertzel, así como utilidades adecuadas para su aplicación. El reto consiste en aplicar eficazmente este método a los datos financieros y extraer señales significativas. El algoritmo está en clara desventaja respecto al método MESA, ya que solo es capaz de detectar una frecuencia cada vez. Su aplicación práctica también pone de relieve la debilidad de la detección de ciclos en los mercados financieros, ya que resulta difícil medir el ciclo imperante y determinar exactamente cuándo terminará. Para hacer frente a estos retos se necesitará una combinación de conocimientos especializados, técnicas sólidas de pre-procesamiento de datos, estrategias de gestión de riesgos y un seguimiento y adaptación continuos a la dinámica cambiante del mercado.

El archivo zip adjunto contiene al completo el código fuente del que hemos hablado en el artículo.

Nombre del archivo	Descripción
Mql5/include/Goertzel.mqh	Archivo de inclusión para la clase CGoertzel que implementa el algoritmo de Goertzel
Mql5/include/ GoertzelCycle.mqh	Archivo de inclusión para la clase CGoertzelCycle, sirve para analizar ciclos usando el algoritmo de Goertzel.
Mql5/indicators/ NCycleGoertzelDft.mq5	Indicador que implementa parcialmente la estrategia de D. Meyers utilizando el algoritmo de Goertzel.
Mql5/indicators/ AdaptiveGARSI.mq5	Aplicación de una versión adaptativa del indicador RSI con análisis retrospectivo dinámico calculado con la ayuda del algoritmo de Goertzel.