Métodos de conjunto para aprimorar previsões numéricas em MQL5

Introdução

O aprendizado de máquina frequentemente produz múltiplos modelos preditivos de qualidades variadas. Praticantes normalmente avaliam esses modelos e selecionam o de melhor desempenho para aplicações no mundo real. No entanto, este artigo explora uma abordagem alternativa: reaproveitar modelos aparentemente inferiores combinando suas saídas para potencialmente melhorar o desempenho preditivo geral. Examinaremos diversas técnicas para combinar previsões e demonstraremos sua implementação em puro MQL5. Finalmente, compararemos esses métodos e discutiremos sua adequação para diferentes cenários.

Para formalizar o conceito de combinar previsões de modelos, vamos introduzir algumas notações-chave. Considere um conjunto de treinamento composto por K pontos de dados, cada um representado como um par (xi,yi), onde xi é um vetor de preditores e yi é a variável resposta escalar que desejamos prever. Suponha que temos N modelos treinados, cada um capaz de fazer previsões. Quando apresentado um preditor x, o modelo n gera uma previsão denotada como f_n(x). Nosso objetivo é construir uma função de consenso f(x) que combine efetivamente essas N previsões individuais, resultando em uma previsão geral mais precisa do que qualquer modelo isolado.

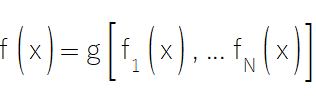
Esta função de consenso, frequentemente chamada de conjunto ou meta-modelo, tem o potencial de superar seus modelos constituintes. Nesta exploração, abordaremos diversas técnicas para construir modelos de conjunto eficazes e avaliaremos sua implementação e desempenho prático em MQL5.

Conjuntos baseados em médias das previsões

Uma das técnicas mais simples para combinar previsões numéricas é a média simples. Ao calcular a média de múltiplas previsões, geralmente é possível obter uma estimativa mais precisa e robusta do que confiar em qualquer modelo isolado. Essa abordagem é eficiente computacionalmente e fácil de implementar, tornando-se uma escolha prática para uma ampla gama de aplicações. A simplicidade da média aritmética é sua maior força. Diferentemente de métodos de conjunto mais complexos que exigem a estimação de múltiplos parâmetros, a média é inerentemente resistente ao overfitting. Overfitting ocorre quando um modelo se ajusta excessivamente às características específicas dos dados de treinamento, comprometendo sua capacidade de generalização para dados não vistos.

Ao evitar totalmente a estimação de parâmetros, a média simples contorna esse problema, garantindo desempenho consistente mesmo em conjuntos de dados pequenos ou ruidosos. Em contraste, outras técnicas de conjunto, como exploraremos adiante, frequentemente envolvem ajuste e otimização de parâmetros, o que pode introduzir certa suscetibilidade ao overfitting. Assim, embora a média possa não ter a sofisticação de métodos de conjunto avançados, sua confiabilidade e facilidade de uso a tornam uma ferramenta essencial no conjunto de técnicas de aprendizagem por conjunto.

Um princípio matemático fundamental, baseado na desigualdade de Cauchy-Schwarz, fornece a fundamentação teórica para a função que define um conjunto de médias das previsões. Essa desigualdade afirma que o quadrado da soma de N números é sempre menor ou igual a N vezes a soma de seus quadrados.

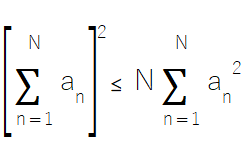
Agora, considere um vetor de preditores x usado para prever uma variável dependente y. Substituindo a na desigualdade pelos erros cometidos por um modelo ao prever y a partir de x, então a_n = f_n(x) - y. Se os somatórios no lado esquerdo dessa equação forem separados assumindo f(x) como a média das previsões. Colocando N em evidência e substituindo o termo à extrema direita da equação no lado esquerdo da desigualdade derivada de Cauchy e, em seguida, dividindo ambos os lados por N^2, chegamos à equação fundamental que embasa a média como método de conjunto:

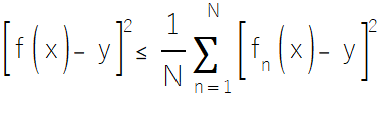
As somatórias no lado direito da equação acima representam os erros quadráticos dos modelos individuais. Somando esses erros quadráticos e dividindo pelo número de modelos componentes, obtemos o erro quadrático médio (MSE) dos modelos individuais. Enquanto isso, o lado esquerdo da equação representa o erro quadrático do modelo de consenso, que é derivado da média das previsões individuais.

Matematicamente, essa desigualdade postula que, para qualquer conjunto de preditores e alvos, o erro quadrático da previsão média nunca excederá o erro quadrático médio das previsões individuais. A igualdade só é alcançada quando os erros de previsão de todos os modelos individuais são idênticos.

Claro, esse benefício não vem sem limitações. A efetividade da média depende significativamente da natureza dos modelos componentes. Se todos os modelos tiverem poder preditivo semelhante, fazer a média das previsões costuma ser uma abordagem razoável e eficaz. No entanto, problemas podem surgir quando o poder preditivo dos modelos componentes varia muito. Nesses casos, a média pode diluir as contribuições dos modelos mais fortes enquanto supervaloriza os mais fracos, potencialmente reduzindo o desempenho preditivo geral do conjunto.

O código que implementa a média para conjuntos está encapsulado na classe CAvg, definida em ensemble.mqh. Esta classe, assim como todas as outras que implementam métodos de conjunto, depende de o usuário fornecer uma coleção de modelos previamente treinados. Esses modelos devem seguir a interface IModel, que é definida da seguinte forma:

//+------------------------------------------------------------------+
//| IModel interface defining methods for manipulation of learning   |
//| algorithms                                                       |
//+------------------------------------------------------------------+
interface IModel
  {
//train a model
   bool train(matrix &predictors,matrix&targets);
//make a prediction with a trained model
   double forecast(vector &predictors);
  };

A interface IModel especifica dois métodos:

• train(): Este método contém a lógica para treinar um modelo.
• forecast(): Este método define as operações para realizar previsões com base em novos dados de entrada.

//+------------------------------------------------------------------+
//| Compute the simple average of the predictions                    |
//+------------------------------------------------------------------+
class CAvg
  {

public:
                     CAvg(void) ;
                    ~CAvg(void) ;
   double            predict(vector &inputs, IModel* &models[]) ;

  } ;
//+------------------------------------------------------------------+
//| Constructor                                                      |
//+------------------------------------------------------------------+
CAvg::CAvg(void)
  {
  }
//+------------------------------------------------------------------+
//| Destructor                                                       |
//+------------------------------------------------------------------+
CAvg::~CAvg(void)
  {
  }
//+------------------------------------------------------------------+
//|  Make a prediction by using consensus from multiple models       |
//+------------------------------------------------------------------+
double CAvg::predict(vector &inputs, IModel* &models[])
  {
   double output = 0.0 ;

   for(uint imodel=0 ; imodel<models.Size() ; imodel++)
     {
      output +=models[imodel].forecast(inputs) ;
     }

   output /= double(models.Size()) ;
   return output;
  }

A classe CAvg inclui um método predict(), que é invocado com um vetor de dados de entrada e um array de modelos componentes previamente treinados. Este método retorna um valor escalar representando a previsão de consenso. No caso da classe CAvg, a previsão de consenso é calculada como a média das previsões obtidas do array de modelos fornecido. Ao seguir esse design, a classe CAvg garante flexibilidade e modularidade, permitindo aos usuários integrar facilmente diversos tipos de modelos em seus métodos de conjunto.

Combinações lineares irrestritas de modelos preditivos

Quando se lida com um conjunto de modelos com qualidades preditivas muito distintas, um método de conjunto que pode ser adotado é a regressão linear simples. A ideia é calcular a previsão de consenso como uma soma ponderada das previsões dos modelos componentes, incluindo um termo constante para compensar qualquer viés.

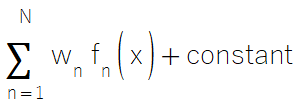
Esse método de conjunto é implementado na classe CLinReg. O construtor, destrutor e os métodos predict() têm as mesmas assinaturas dos da classe CAvg descrita anteriormente.

//+------------------------------------------------------------------+
//| Compute the linear regression of the predictions                 |
//+------------------------------------------------------------------+
class CLinReg
  {

public:

                     CLinReg(void) ;
                    ~CLinReg() ;
   bool              fit(matrix & train_vars, vector &train_targets,IModel* &models[]);

   double            predict(vector &inputs, IModel* &models[]) ;

private:
   OLS *m_linreg ;   // The linear regression object
  } ;
//+------------------------------------------------------------------+
//| Constructor                                                      |
//+------------------------------------------------------------------+
CLinReg::CLinReg(void)
  {
   m_linreg = new OLS();
  }
//+------------------------------------------------------------------+
//| Fit the consensus model from saved models                        |
//+------------------------------------------------------------------+
bool CLinReg::fit(matrix &train_vars,vector &train_targets,IModel* &models[])
  {

   matrix independent(train_vars.Rows(),models.Size()+1);

   for(ulong i=0 ; i<independent.Rows() ; i++)     // Build the design matrix
     {
      independent[i][models.Size()] = 1.0;
      vector ins = train_vars.Row(i);
      for(uint imodel=0 ; imodel<models.Size() ; imodel++)
         independent[i][imodel] = models[imodel].forecast(ins) ;

     }
   return m_linreg.Fit(train_targets,independent);
  }
//+------------------------------------------------------------------+
//|  Destructor                                                      |
//+------------------------------------------------------------------+
CLinReg::~CLinReg(void)
  {
   if(CheckPointer(m_linreg)==POINTER_DYNAMIC)
      delete m_linreg ;
  }
//+------------------------------------------------------------------+
//| Predict                                                          |
//+------------------------------------------------------------------+
double CLinReg::predict(vector &inputs, IModel* &models[])
  {
   vector args = vector::Zeros(models.Size());

   for(uint i = 0; i<models.Size(); i++)
      args[i] = models[i].forecast(inputs);

   return m_linreg.Predict(args);
  }

No entanto, a classe CLinReg introduz um método fit(), que especifica as operações para treinar o modelo de consenso.

O método fit() recebe como entrada:

• Matriz de preditores.
• Alvos vetoriais.
• Um array de modelos componentes.
  

Dentro de fit(), uma instância da classe OLS é usada para representar o modelo de regressão de consenso. A variável de matriz independent serve como matriz de design, construída a partir dos erros quadráticos das previsões feitas pelos modelos componentes individuais, acrescida de um termo constante (uma coluna de uns). Quando o método predict() da CLinReg é invocado, ele retorna o resultado de usar os erros de previsão dos modelos componentes como entradas para o modelo de regressão de consenso.

Combinar modelos como uma soma ponderada das previsões dos componentes funciona bem em cenários específicos e raros. No entanto, essa abordagem é frequentemente negligenciada em aplicações do mundo real por dois motivos principais:

• Risco de Overfitting: Os pesos no modelo de consenso são parâmetros que devem ser otimizados. Se o conjunto incluir muitos modelos componentes, o processo de otimização pode levar a um overfitting significativo, reduzindo a capacidade do modelo de generalizar para dados não vistos.
• Colinearidade: Se dois ou mais modelos produzem previsões semelhantes, a colinearidade pode causar instabilidade nas estimativas dos pesos. Esse problema surge porque os pesos para modelos com desempenho semelhante podem somar uma constante, com esses modelos se comportando de forma parecida apenas para os casos encontrados durante o treinamento.
  

No entanto, essa suposição frequentemente falha em cenários do mundo real. Quando ocorre um caso fora da amostra, modelos que antes geravam previsões semelhantes podem reagir de maneira diferente, potencialmente levando o modelo de consenso a produzir resultados extremos e não confiáveis.

Combinações lineares restritas de modelos enviesados

Usar regressão simples como base para combinar múltiplos modelos preditivos pode, às vezes, levar a um modelo instável com pesos extremos. Esse problema normalmente surge quando os coeficientes de regressão têm sinais opostos, o que é necessário para equilibrar os valores e ajustar bem os dados. Por exemplo, um coeficiente de um par de modelos correlacionados só pode ser levado a um valor positivo grande se seu correspondente for levado a um valor negativo pequeno. Para evitar esses valores extremos, podemos restringir os coeficientes de regressão para evitar valores negativos extremos. Essa abordagem também reduz os graus de liberdade no processo de otimização, tornando o modelo mais estável e menos propenso ao overfitting.

Esse método de conjunto é implementado na classe Cbiased. Ele inclui os já conhecidos métodos fit() e predict() encontrados em outras implementações de conjunto.

//+------------------------------------------------------------------+
//|Compute the optimal linear combination of the predictions         |
//|subject to the constraints that the weights are all nonnegative.  |
//|A constant term is also included.                                 |
//|This is appropriate for biased predictors                         |
//+------------------------------------------------------------------+
class Cbiased:public PowellsMethod
  {

public:

                     Cbiased(void) ;
                    ~Cbiased() ;
   bool              fit(matrix & train_vars, vector &train_targets,IModel* &models[]);
   double            predict(vector &inputs,IModel* &models[]) ;

private:
   vector m_coefs ;    // Computed coefficients here
   int biased_ncases ;
   int biased_nvars ;
   matrix biased_x ;
   vector biased_y ;
   virtual double    func(vector &p,int n=0);
  } ;
//+------------------------------------------------------------------+
//| Constructor                                                      |
//+------------------------------------------------------------------+
Cbiased::Cbiased(void)
  {
  }
//+------------------------------------------------------------------+
//| Destructor                                                       |
//+------------------------------------------------------------------+
Cbiased::~Cbiased(void)
  {
  }
//+------------------------------------------------------------------+
//| Function to be optimized                                         |
//+------------------------------------------------------------------+
double Cbiased::func(vector &p,int n = 0)
  {

   double  err, pred,diff, penalty ;
// Compute criterion
   err = 0.0 ;
   for(int i=0 ; i<biased_ncases ; i++)
     {
      pred = p[p.Size()-1] ;                    // Will cumulate prediction
      for(int j=0 ; j<biased_nvars ; j++)       // For all model outputs
         pred += biased_x[i][j] * p[j] ;        // Weight them per call
      diff = pred - biased_y[i] ;               // Predicted minus true
      err += diff * diff ;                      // Cumulate squared error
     }

   penalty = 0.0 ;
   for(int j=0 ; j<biased_nvars ; j++)
     {
      if(p[j] < 0.0)
         penalty -= 1.e30 * p[j] ;
     }

   return err + penalty ;
  }
//+------------------------------------------------------------------+
//| Fit the consensus model                                          |
//+------------------------------------------------------------------+
bool Cbiased::fit(matrix & train_vars, vector &train_targets,IModel* &models[])
  {
   biased_ncases = int(train_vars.Rows());
   biased_nvars = int(models.Size());
   biased_x = matrix::Zeros(biased_ncases,biased_nvars);

   biased_y = train_targets;

   m_coefs = vector::Zeros(biased_nvars+1);

   for(int i = 0; i<biased_ncases; i++)
     {
      vector ins = train_vars.Row(i);
      for(int j = 0; j<biased_nvars; j++)
         biased_x[i][j] = models[j].forecast(ins);
     }

   m_coefs.Fill(1.0/double(biased_nvars));
   m_coefs[m_coefs.Size()-1] = 0.0;

   int iters = Optimize(m_coefs,int(m_coefs.Size()));

   double sum = m_coefs.Sum();

   m_coefs/=sum;

   return true;
  }
//+------------------------------------------------------------------+
//| Make prediction with consensus model                             |
//+------------------------------------------------------------------+
double Cbiased::predict(vector &inputs,IModel* &models[])
  {
   double output=0.0;
   for(uint imodel=0 ; imodel<models.Size() ; imodel++)
     {
      output += m_coefs[imodel] * models[imodel].forecast(inputs);
     }
   return output;
  }

No entanto, a principal diferença em Cbiased está em como os pesos são otimizados.

A otimização dos pesos é feita usando o método de Powell para minimização de funções. Por isso, a classe Cbiased é descendente da classe PowellsMethod. A função critério é implementada no método func(), que percorre os dados de treinamento, acumulando erros quadráticos usando os pesos fornecidos. Para cada amostra no conjunto de dados:

• As previsões dos modelos componentes são ponderadas de acordo com os pesos atuais e um termo constante.
• As diferenças quadráticas entre as previsões e os valores-alvo são somadas.
  

A função critério termina verificando se algum dos pesos de teste é negativo. Se algum peso for negativo, uma penalidade é aplicada. A função retorna o erro total mais qualquer penalidade proveniente dos pesos negativos. Esse tipo de método de conjunto é mais apropriado quando se sabe que alguns modelos componentes são enviesados. Viés, neste contexto, refere-se a modelos que consistentemente produzem previsões muito altas ou muito baixas em relação aos valores-alvo, geralmente apresentando uma tendência notável. Ao restringir os pesos, Cbiased reduz efetivamente a influência de modelos enviesados, levando a uma previsão de conjunto mais equilibrada e precisa. Na próxima seção, apresentaremos um método adequado para conjuntos de modelos que apresentam pouco ou nenhum viés, onde o foco está em agregar previsões de modelos com desempenho comparável.

Combinações restritas de modelos não enviesados

Quando um conjunto de modelos componentes é conhecido por não ter viés significativo em suas previsões, não há necessidade de incluir um termo constante no modelo de consenso. Remover o termo constante ajuda a reduzir a propensão do modelo ao overfitting dos dados. Além disso, essa abordagem garante que os pesos dos modelos nunca sejam negativos, como discutido nos métodos anteriores. Além disso, uma restrição adicional é imposta aos pesos: eles devem somar um. Essa restrição oferece dois benefícios principais:

• Garantir um modelo de consenso não enviesado: Desde que os modelos componentes sejam razoavelmente não enviesados, exigir que os pesos somem um garante que o modelo de consenso também permaneça não enviesado.
• Interpolação entre previsões: A restrição de soma-um garante que a previsão de consenso é uma interpolação entre as previsões dos modelos componentes. Isso garante que a previsão final não se desvie drasticamente das previsões individuais, evitando resultados extremos que poderiam surgir de pesos extremos.
  

Isso é ilustrado pela seguinte equação:

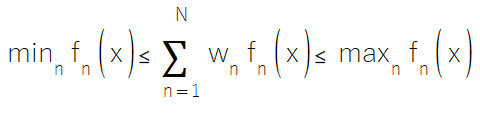
O código que implementa esse método de conjunto é em grande parte idêntico às implementações anteriores. A principal diferença com a classe CUnbiased está na função que está sendo minimizada.

//+------------------------------------------------------------------+
//|Compute the optimal linear combination of the predictions         |
//|subject to the constraints that the weights are all nonnegative   |
//|and they sum to one.  This is appropriate for unbiased predictors.|
//+------------------------------------------------------------------+
class CUnbiased:public PowellsMethod
  {

public:

                     CUnbiased(void) ;
                    ~CUnbiased() ;
   bool              fit(matrix & train_vars, vector &train_targets,IModel* &models[]);
   double            predict(vector &inputs,IModel* &models[]) ;

private:
   vector m_coefs ;    // Computed coefficients here
   int unbiased_ncases ;
   int unbiased_nvars ;
   matrix unbiased_x ;
   vector unbiased_y ;
   virtual double    func(vector &p,int n=0);
  } ;
//+------------------------------------------------------------------+
//| Constructor                                                      |
//+------------------------------------------------------------------+
CUnbiased::CUnbiased(void)
  {
  }
//+------------------------------------------------------------------+
//| Destructor                                                       |
//+------------------------------------------------------------------+
CUnbiased::~CUnbiased(void)
  {
  }
//+------------------------------------------------------------------+
//| Function to be optimized                                         |
//+------------------------------------------------------------------+
double CUnbiased::func(vector &p,int n = 0)
  {

   double sum, err, pred,diff, penalty ;

// Normalize weights to sum to one
   sum = p.Sum() ;

   if(sum < 1.e-60)    // Should almost never happen
      sum = 1.e-60 ;   // But be prepared to avoid division by zero

   vector   unbiased_work = p / sum ;

// Compute criterion
   err = 0.0 ;
   for(int i=0 ; i<unbiased_ncases ; i++)
     {
      pred = 0.0 ;                                       // Will cumulate prediction
      for(int j=0 ; j<unbiased_nvars ; j++)              // For all model outputs
         pred += unbiased_x[i][j] * unbiased_work[j] ;   // Weight them per call
      diff = pred - unbiased_y[i] ;                      // Predicted minus true
      err += diff * diff ;                               // Cumulate squared error
     }

   penalty = 0.0 ;
   for(int j=0 ; j<unbiased_nvars ; j++)
     {
      if(p[j] < 0.0)
         penalty -= 1.e30 * p[j] ;
     }

   return err + penalty ;
  }
//+------------------------------------------------------------------+
//| Fit the consensus model                                          |
//+------------------------------------------------------------------+
bool CUnbiased::fit(matrix & train_vars, vector &train_targets,IModel* &models[])
  {
   unbiased_ncases = int(train_vars.Rows());
   unbiased_nvars = int(models.Size());
   unbiased_x = matrix::Zeros(unbiased_ncases,unbiased_nvars);

   unbiased_y = train_targets;

   m_coefs = vector::Zeros(unbiased_nvars);

   for(int i = 0; i<unbiased_ncases; i++)
     {
      vector ins = train_vars.Row(i);
      for(int j = 0; j<unbiased_nvars; j++)
         unbiased_x[i][j] = models[j].forecast(ins);
     }

   m_coefs.Fill(1.0/double(unbiased_nvars));

   int iters = Optimize(m_coefs);

   double sum = m_coefs.Sum();

   m_coefs/=sum;

   return true;
  }
//+------------------------------------------------------------------+
//| Make prediction with consensus model                             |
//+------------------------------------------------------------------+
double CUnbiased::predict(vector &inputs,IModel* &models[])
  {
   double output=0.0;
   for(uint imodel=0 ; imodel<models.Size() ; imodel++)
     {
      output += m_coefs[imodel] * models[imodel].forecast(inputs);
     }
   return output;
  }

Essa função incorpora as restrições adicionais discutidas anteriormente, especificamente a não negatividade dos pesos e a exigência de que eles somem um.

Combinações ponderadas por variância de modelos preditivos

Outro método para combinar previsões de modelos componentes é baseado em pesos ótimos que são determinados pela precisão de previsão de cada modelo. Essa técnica envolve alocar pesos menores a modelos com maiores erros de previsão e pesos maiores a modelos com menores erros de previsão. Esse método é particularmente eficaz quando há variabilidade significativa na qualidade dos modelos componentes. No entanto, se os modelos forem altamente correlacionados, essa técnica pode não ser ideal, e outro método de conjunto deve ser considerado.

A ideia por trás da ponderação de acordo com a qualidade do modelo está fundamentada na teoria de que, se os modelos forem não enviesados e não correlacionados, atribuir pesos inversamente proporcionais aos erros dos modelos minimizará o erro quadrático esperado.

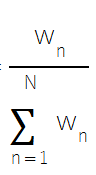
Para isso, o peso relativo de cada modelo é calculado com base no inverso de seu erro, e então os pesos são ajustados para garantir que somem um.

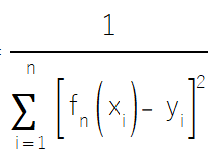
O conjunto de modelos ponderados por variância é implementado na classe CWeighted. No método fit(), para cada amostra de treinamento:

• A previsão de cada modelo componente é computada.
• E o erro quadrático de cada previsão é acumulado.
  

//+------------------------------------------------------------------+
//| Compute the variance-weighted average of the predictions         |
//+------------------------------------------------------------------+
class CWeighted
  {
public:

                     CWeighted(void) ;
                    ~CWeighted() ;
   bool              fit(matrix & train_vars, vector &train_targets,IModel* &models[]);
   double            predict(vector &inputs,IModel* &models[]) ;

private:
   vector m_coefs ;    // Computed coefficients here

  };
//+------------------------------------------------------------------+
//| Constructor                                                      |
//+------------------------------------------------------------------+
CWeighted::CWeighted(void)
  {
  }
//+------------------------------------------------------------------+
//| Destructor                                                       |
//+------------------------------------------------------------------+
CWeighted::~CWeighted(void)
  {
  }
//+------------------------------------------------------------------+
//| Fit a consensus model                                            |
//+------------------------------------------------------------------+
bool CWeighted::fit(matrix &train_vars,vector &train_targets,IModel* &models[])
  {
   m_coefs = vector::Zeros(models.Size());

   m_coefs.Fill(1.e-60);
   double diff = 0.0;
   for(ulong i = 0; i<train_vars.Rows(); i++)
     {
      vector ins = train_vars.Row(i);
      for(ulong j = 0; j<m_coefs.Size(); j++)
        {
         diff = models[j].forecast(ins) - train_targets[i];
         m_coefs[j] += (diff*diff);
        }
     }

   m_coefs=1.0/m_coefs;

   m_coefs/=m_coefs.Sum();

   return true;
  }
//+------------------------------------------------------------------+
//| Make a prediction with the consensus model                       |
//+------------------------------------------------------------------+
double CWeighted::predict(vector &inputs,IModel* &models[])
  {
   double output = 0.0;

   for(uint i = 0; i<models.Size(); i++)
      output+=m_coefs[i]*models[i].forecast(inputs);

   return output;
  }

Depois de fazer isso para todas as amostras de treinamento, o erro total de cada modelo é usado para calcular seu peso. Esses pesos são então somados e ajustados para garantir que o peso total some um. Essa abordagem garante que modelos com menores erros tenham mais influência na previsão final de conjunto, o que pode potencialmente melhorar a previsão, especialmente em cenários onde os modelos apresentam diferentes graus de precisão preditiva.

Combinações interpoladas baseadas em Redes Neurais de Regressão Geral

Os métodos de conjunto que discutimos até agora funcionam bem quando o modelo de consenso é treinado com dados limpos. No entanto, quando os dados de treinamento são ruidosos, o modelo pode sofrer com baixa generalização. Para lidar com esse problema, um método de regressão eficaz é a Rede Neural de Regressão Geral (GRNN). A grande vantagem da GRNN sobre a regressão tradicional é sua menor suscetibilidade ao overfitting. Isso ocorre porque os parâmetros das GRNNs têm impacto relativamente menor no modelo em comparação com técnicas tradicionais de regressão. Embora esse ganho em generalização venha ao custo de alguma precisão, as GRNNs podem modelar relações complexas e não lineares, proporcionando uma ferramenta útil quando os dados apresentam tais características.

As GRNNs produzem previsões que são interpolações entre os valores-alvo dos dados de treinamento. A interpolação é determinada por um peso que define o quanto um caso fora da amostra difere dos casos conhecidos na amostra. Quanto mais semelhantes forem as amostras, maior o peso relativo atribuído. Embora uma GRNN possa ser descrita como uma operação de suavização devido à sua interpolação de amostras desconhecidas para o espaço de amostras conhecidas, seus fundamentos teóricos estão baseados em estatística.

Quando apresentado a um conjunto de dados — composto por previsões dos modelos componentes e seus respectivos valores-alvo — a previsão de consenso de uma GRNN é o erro quadrático esperado mínimo, que é dado pela esperança condicional.

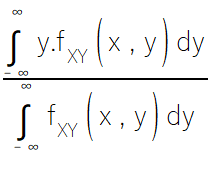
Como a densidade conjunta dos dados de treinamento normalmente é desconhecida, não podemos usar diretamente a fórmula da esperança condicional. Em vez disso, confiamos em estimativas das densidades conjuntas derivadas dos dados de treinamento, o que leva à forma da GRNN mostrada abaixo.

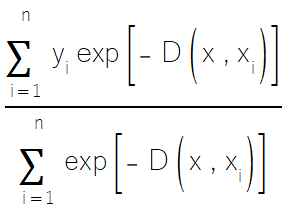
Antes de apresentar o código para o método de conjunto baseado em GRNN, precisamos primeiro discutir a implementação da GRNN. O código para a GRNN está definido em grnn.mqh, que contém a definição da classe CGrnn.

//+------------------------------------------------------------------+
//| General regression neural network                                |
//+------------------------------------------------------------------+
class CGrnn
  {
public:
                     CGrnn(void);
                     CGrnn(int num_outer, int num_inner, double start_std);
                    ~CGrnn(void);
   bool              fit(matrix &predictors,matrix &targets);
   vector            predict(vector &predictors);
   //double            get_mse(void);
private:
   bool              train(void);
   double            execute(void);
   ulong             m_inputs,m_outputs;
   int               m_inner,m_outer;
   double            m_start_std;
   ulong             m_rows,m_cols;
   bool              m_trained;
   vector            m_sigma;
   matrix            m_targets,m_preds;
  };

A implementação da GRNN para tarefas de regressão envolve vários componentes-chave. O construtor inicializa parâmetros como o número de iterações internas e externas e o desvio padrão inicial para os pesos sigma.

//+------------------------------------------------------------------+
//| Default constructor                                              |
//+------------------------------------------------------------------+
CGrnn::CGrnn(void)
  {
   m_inner = 100;
   m_outer = 10;
   m_start_std = 3.0;
  }
//+------------------------------------------------------------------+
//| Parametric constructor                                           |
//+------------------------------------------------------------------+
CGrnn::CGrnn(int num_outer,int num_inner,double start_std)
  {
   m_inner = num_inner;
   m_outer = num_outer;
   m_start_std = start_std;
  }

O método fit armazena os dados de treinamento, incluindo os preditores de entrada e os valores-alvo, e inicializa os pesos sigma. Em seguida, treina o modelo GRNN otimizando iterativamente os pesos sigma utilizando uma abordagem de recozimento simulado (simulated annealing). Durante o treinamento, os pesos sigma são perturbados e o erro de validação cruzada para os pesos perturbados é calculado. A perturbação é aceita ou rejeitada com base no erro e em um parâmetro de temperatura, com a temperatura sendo gradualmente reduzida para focar a busca.

//+------------------------------------------------------------------+
//| Fit data to a model                                              |
//+------------------------------------------------------------------+
bool CGrnn::fit(matrix &predictors,matrix &targets)
  {
   m_targets = targets;
   m_preds = predictors;
   m_trained = false;
   m_rows = m_preds.Rows();
   m_cols = m_preds.Cols();
   m_sigma = vector::Zeros(m_preds.Cols());

   if(m_targets.Rows() != m_preds.Rows())
     {
      Print(__FUNCTION__, " invalid inputs ");
      return false;
     }

   m_trained = train();

   return m_trained;
  }

O método de previsão calcula a distância entre o vetor de entrada e cada ponto de dados de treinamento, pondera os pontos de dados de treinamento com base em sua distância da entrada e computa a saída prevista como uma média ponderada dos valores alvo dos pontos de dados de treinamento. Os pesos sigma determinam a influência de cada ponto de dados de treinamento na previsão.

//+------------------------------------------------------------------+
//| Make a prediction with a trained model                           |
//+------------------------------------------------------------------+
vector CGrnn::predict(vector &predictors)
  {
   if(!m_trained)
     {
      Print(__FUNCTION__, " no trained model available for predictions ");
      return vector::Zeros(1);
     }

   if(predictors.Size() != m_cols)
     {
      Print(__FUNCTION__, " invalid inputs ");
      return vector::Zeros(1);
     }

   vector output  = vector::Zeros(m_targets.Cols());
   double diff,dist,psum=0.0;

   for(ulong i = 0; i<m_rows; i++)
     {
      dist  = 0.0;
      for(ulong j = 0; j<m_cols; j++)
        {
         diff  = predictors[j]  - m_preds[i][j];
         diff/= m_sigma[j];
         dist += (diff*diff);
        }
      dist  = exp(-dist);
      if(dist< EPS1)
         dist = EPS1;
      for(ulong k = 0; k<m_targets.Cols(); k++)
         output[k] += dist * m_targets[i][k];
      psum += dist;
     }
   output/=psum;
   return output;
  }

A validação cruzada é usada para avaliar o desempenho do modelo e otimizar os pesos sigma, enquanto o recozimento simulado serve como um algoritmo meta-heurístico de otimização para encontrar os pesos sigma ótimos. Em última análise, a GRNN realiza interpolação baseada em kernel, onde a previsão é uma interpolação ponderada entre os pontos dos dados de treinamento.

O conjunto baseado na GRNN é implementado como a classe CGenReg.

//+------------------------------------------------------------------+
//| Compute the General Regression of the predictions                |
//+------------------------------------------------------------------+
class CGenReg
  {

public:

                     CGenReg(void) ;
                    ~CGenReg(void) ;
   bool              fit(matrix & train_vars, vector &train_targets,IModel* &models[]);
   double            predict(vector &inputs,IModel* &models[]) ;

private:
   CGrnn *grnn ;       // The GRNN object
   vector m_work ;     // Work vector nmodels long
   vector            m_targs;
   matrix            m_vars;
  } ;

A classe CGenReg utiliza um objeto CGrnn para modelar relações complexas entre as previsões dos modelos individuais e os valores-alvo reais. No método fit, ela primeiro armazena os dados de treinamento, incluindo os valores-alvo (train_targets) e as variáveis de entrada (train_vars). Em seguida, reúne as previsões individuais de cada modelo, criando uma matriz (preds) onde cada linha representa uma amostra de treinamento e cada coluna guarda a previsão do modelo correspondente no conjunto. O objeto CGrnn é treinado usando a matriz de previsões individuais (preds) como entrada e os valores-alvo reais (targ) como saída.

//+------------------------------------------------------------------+
//| Fit consensus model                                              |
//+------------------------------------------------------------------+
bool CGenReg::fit(matrix & train_vars, vector &train_targets,IModel* &models[])
  {
   m_targs = train_targets;
   m_vars = train_vars;

   m_work = vector::Zeros(models.Size());

   matrix targ = matrix::Zeros(train_targets.Size(),1);

   if(!targ.Col(train_targets,0))
     {
      Print(__FUNCSIG__, " error adding column ", GetLastError());
      return false;
     }

   matrix preds(m_vars.Rows(),models.Size());
   for(ulong i = 0; i<m_vars.Rows(); i++)
     {
      vector ins = m_vars.Row(i);
      for(uint j = 0; j< models.Size(); j++)
        {
         preds[i][j] = models[j].forecast(ins);
        }
     }

   return grnn.fit(preds,targ);
  }

No método predict, a classe reúne as previsões de cada modelo para uma nova entrada (inputs) e as armazena em um vetor de trabalho (m_work). O CGrnn treinado é então usado para prever a saída final com base nessas previsões individuais. O método retorna o primeiro elemento do vetor de saída previsto como a previsão final.

//+------------------------------------------------------------------+
//| Make a prediction                                                |
//+------------------------------------------------------------------+
double CGenReg::predict(vector &inputs,IModel* &models[])
  {
   vector output;
   for(uint i = 0; i<models.Size(); i++)
      m_work[i] = models[i].forecast(inputs);
   output = grnn.predict(m_work);
   return output[0];
  }

Conclusão: Comparando métodos de conjunto

Vários métodos de conjunto foram apresentados, com seus pontos fortes e fracos discutidos brevemente. Para concluir este artigo, investigaremos como esses métodos se comparam quando aplicados a dados reais. Essa comparação é implementada como um script MetaTrader 5 chamado Ensemble_Demo.mq5.

O script gera vários grupos sintéticos de conjuntos de dados. O primeiro grupo consiste em conjuntos de dados usados para treinar modelos de referência. Modelos treinados com esses dados são distinguidos como bons modelos, e os próprios dados são considerados limpos. Um segundo grupo de conjuntos de dados é gerado para treinar modelos ruins, considerados inferiores aos bons modelos treinados com dados limpos.

O último grupo de conjuntos de dados é usado para treinar modelos considerados enviesados. Esses modelos são enviesados em relação aos bons modelos mencionados anteriormente. Um subconjunto de dados de cada grupo é combinado para simular dados ruidosos.

O script permite aos usuários especificar quantos modelos bons, ruins e enviesados serão treinados. O usuário também tem controle sobre o número de amostras que compõem os dados de treinamento, permitindo uma avaliação de como o tamanho da amostra afeta o desempenho dos métodos de conjunto. Por fim, os usuários podem optar por treinar um modelo de conjunto usando os dados limpos definindo o parâmetro TrainCombinedModelsOnCleanData como verdadeiro, ou treiná-lo com dados ruidosos definindo-o como falso.

Os modelos são redes neurais feed-forward implementadas pela classe FFNN em mlffnn.mqh.

//+------------------------------------------------------------------+
//| Class for a basic feed-forward neural network                    |
//+------------------------------------------------------------------+
class FFNN
  {
protected:

   bool              m_trained;             // flag noting if neural net successfully trained
   matrix            m_weights[];           // layer weights
   matrix            m_outputs[];           // hidden layer outputs
   matrix            m_result;              // training result
   uint              m_epochs;              // number of epochs
   ulong             m_num_inputs;          // number of input variables for nn
   ulong             m_layers;              // number of layers of neural net
   ulong             m_hidden_layers;       // number of hidden layers
   ulong             m_hidden_layer_size[]; // node config for layers
   double            m_learn_rate;          // learning rate
   ENUM_ACTIVATION_FUNCTION m_act_fn;       // activation function
   //+------------------------------------------------------------------+
   //| Initialize the neural network structure                          |
   //+------------------------------------------------------------------+

   virtual bool      create(void)
     {
      if(m_layers - m_hidden_layers != 1)
        {
         Print(__FUNCTION__,"  Network structure misconfiguration ");
         return false;
        }

      for(ulong i = 0; i<m_layers; i++)
        {
         if(i==0)
           {
            if(!m_weights[i].Init(m_num_inputs+1,m_hidden_layer_size[i]))
              {
               Print(__FUNCTION__," ",__LINE__," ", GetLastError());
               return false;
              }
           }
         else
            if(i == m_layers-1)
              {
               if(!m_weights[i].Init(m_hidden_layer_size[i-1]+1,1))
                 {
                  Print(__FUNCTION__," ",__LINE__," ", GetLastError());
                  return false;
                 }
              }
            else
              {
               if(!m_weights[i].Init(m_hidden_layer_size[i-1]+1,m_hidden_layer_size[i]))
                 {
                  Print(__FUNCTION__," ",__LINE__," ", GetLastError());
                  return false;
                 }
              }
        }

      return true;
     }
   //+------------------------------------------------------------------+
   //| Calculate output  from all layers                                |
   //+------------------------------------------------------------------+

   virtual matrix    calculate(matrix &data)
     {
      if(data.Cols() != m_weights[0].Rows()-1)
        {
         Print(__FUNCTION__," input data not compatible with network structure ");
         return matrix::Zeros(0,0);
        }

      matrix temp = data;

      for(ulong i = 0; i<m_hidden_layers; i++)
        {
         if(!temp.Resize(temp.Rows(), m_weights[i].Rows()) ||
            !temp.Col(vector::Ones(temp.Rows()), m_weights[i].Rows() - 1))
           {
            Print(__FUNCTION__," ",__LINE__," ", GetLastError());
            matrix::Zeros(0,0);
           }

         m_outputs[i]=temp.MatMul(m_weights[i]);

         if(!m_outputs[i].Activation(temp, m_act_fn))
           {
            Print(__FUNCTION__," ",__LINE__," ", GetLastError());
            return matrix::Zeros(0,0);
           }

        }

      if(!temp.Resize(temp.Rows(), m_weights[m_hidden_layers].Rows()) ||
         !temp.Col(vector::Ones(temp.Rows()), m_weights[m_hidden_layers].Rows() - 1))
        {
         Print(__FUNCTION__," ",__LINE__," ", GetLastError());
         return matrix::Zeros(0,0);
        }

      return temp.MatMul(m_weights[m_hidden_layers]);
     }
   //+------------------------------------------------------------------+
   //|  Backpropagation method                                          |
   //+------------------------------------------------------------------+

   virtual bool      backprop(matrix &data, matrix& targets, matrix &result)
     {
      if(targets.Rows() != result.Rows() ||
         targets.Cols() != result.Cols())
        {
         Print(__FUNCTION__," invalid function parameters ");
         return false;
        }
      matrix loss = (targets - result) * 2;
      matrix gradient = loss.MatMul(m_weights[m_hidden_layers].Transpose());
      matrix temp;

      for(long i = long(m_hidden_layers-1); i>-1; i--)
        {
         if(!m_outputs[i].Activation(temp, m_act_fn))
           {
            Print(__FUNCTION__," ",__LINE__," ", GetLastError());
            return false;
           }

         if(!temp.Resize(temp.Rows(), m_weights[i+1].Rows()) ||
            !temp.Col(vector::Ones(temp.Rows()), m_weights[i+1].Rows() - 1))
           {
            Print(__FUNCTION__," ",__LINE__," ", GetLastError());
            return false;
           }

         m_weights[i+1] = m_weights[i+1] + temp.Transpose().MatMul(loss) * m_learn_rate;

         if(!m_outputs[i].Derivative(temp, m_act_fn))
           {
            Print(__FUNCTION__," ",__LINE__," ", GetLastError());
            return false;
           }

         if(!gradient.Resize(gradient.Rows(), gradient.Cols() - 1))
           {
            Print(__FUNCTION__," ",__LINE__," ", GetLastError());
            return false;
           }

         loss = gradient * temp;

         gradient = (i>0)?loss.MatMul(m_weights[i].Transpose()):gradient;
        }

      temp = data;
      if(!temp.Resize(temp.Rows(), m_weights[0].Rows()) ||
         !temp.Col(vector::Ones(temp.Rows()), m_weights[0].Rows() - 1))
        {
         Print(__FUNCTION__," ",__LINE__," ", GetLastError());
         return false;
        }

      m_weights[0] = m_weights[0] + temp.Transpose().MatMul(loss) * m_learn_rate;

      return true;
     }

public:
   //+------------------------------------------------------------------+
   //| Constructor                                                      |
   //+------------------------------------------------------------------+

                     FFNN(ulong &layersizes[], ulong num_layers = 3)
     {
      m_trained = false;
      m_layers = num_layers;
      m_hidden_layers = m_layers - 1;

      ArrayCopy(m_hidden_layer_size,layersizes,0,0,int(m_hidden_layers));

      ArrayResize(m_weights,int(m_layers));

      ArrayResize(m_outputs,int(m_hidden_layers));
     }
   //+------------------------------------------------------------------+
   //| Destructor                                                       |
   //+------------------------------------------------------------------+

                    ~FFNN(void)
     {
     }
   //+------------------------------------------------------------------+
   //| Neural net training method                                       |
   //+------------------------------------------------------------------+

   bool              fit(matrix &data, matrix &targets,double learning_rate, ENUM_ACTIVATION_FUNCTION act_fn, uint num_epochs)
     {
      m_learn_rate = learning_rate;
      m_act_fn = act_fn;
      m_epochs = num_epochs;
      m_num_inputs = data.Cols();
      m_trained = false;

      if(!create())
         return false;

      for(uint ep = 0; ep < m_epochs; ep++)
        {
         m_result = calculate(data);

         if(!backprop(data, targets,m_result))
            return m_trained;
        }

      m_trained = true;
      return m_trained;
     }
   //+------------------------------------------------------------------+
   //| Predict method                                                   |
   //+------------------------------------------------------------------+

   matrix            predict(matrix &data)
     {
      if(m_trained)
         return calculate(data);
      else
         return matrix::Zeros(0,0);
     }

  };
//+------------------------------------------------------------------+

A classe FFNN define um Perceptron Multicamadas (MLP), um tipo de rede neural artificial usada para tarefas de aprendizado supervisionado. Ela contém várias propriedades, como:

• m_trained, um sinalizador booleano que indica se a rede foi treinada com sucesso;
• m_weights, um array de matrizes que armazena os pesos entre cada camada;
• m_outputs, um array de matrizes que contém as saídas de cada camada oculta;
• m_result, uma matriz que guarda a saída final da rede após o treinamento;
• m_epochs, o número de épocas (iterações) de treinamento;
• m_num_inputs, o número de variáveis de entrada da rede;
• m_layers, o número total de camadas da rede, incluindo as camadas de entrada e saída;
• m_hidden_layers, o número de camadas ocultas na rede;
• m_hidden_layer_size, um array que define o número de nós em cada camada oculta;
• m_learn_rate, a taxa de aprendizado utilizada para atualização dos pesos durante o treinamento;
• m_act_fn, a função de ativação utilizada nas camadas ocultas.

A classe inclui métodos privados e públicos. Métodos privados como:

• create, que inicializa a estrutura da rede alocando memória para as matrizes de pesos e as saídas das camadas ocultas conforme a configuração especificada;
• calculate, que propaga os dados de entrada pela rede, aplicando pesos e funções de ativação para calcular a saída;
• backprop, que implementa o algoritmo de retropropagação, ajustando os pesos com base no erro entre as saídas previstas e reais.

Os métodos públicos incluem:

• FFNN (construtor), que inicializa a rede com o número de camadas e tamanhos de camadas ocultas especificados;
• ~FFNN (destrutor), que libera os recursos alocados para a rede;
• fit, que treina a rede em um conjunto de dados fornecido, ajustando os pesos por retropropagação ao longo das épocas especificadas;
• predict, que usa a rede treinada para gerar previsões para novos dados de entrada, realizando a propagação para frente.

No script, a classe CMlfn implementa a interface IModel baseada em uma instância de FFNN. A seguir, uma breve exposição sobre a execução do script em diferentes configurações.

//+------------------------------------------------------------------+
//|                                                Ensemble_Demo.mq5 |
//|                                  Copyright 2024, MetaQuotes Ltd. |
//|                                             https://www.mql5.com |
//+------------------------------------------------------------------+
#property copyright "Copyright 2024, MetaQuotes Ltd."
#property link      "https://www.mql5.com"
#property version   "1.00"
#property script_show_inputs
#include<mlffnn.mqh>
#include<ensemble.mqh>
#include<np.mqh>
//--- input parameters
input int      NumGoodModels=3;
input int      NumBiasedModels=7;
input int      NumBadModels=5;
input int      NumSamples=20;
input int      NumAttempts=1;
input double   VarParam=3.0;//variance parameter
input bool     TrainCombinedModelsOnCleanData = true;
//+------------------------------------------------------------------+
//| Clean up dynamic array pointers                                  |
//+------------------------------------------------------------------+
void cleanup(IModel* &array[])
  {
   for(uint i = 0; i<array.Size(); i++)
      if(CheckPointer(array[i])==POINTER_DYNAMIC)
         delete array[i];
  }
//+------------------------------------------------------------------+
//| IModel implementation of Multilayered iterative algo of GMDH     |
//+------------------------------------------------------------------+
class CMlfn:public IModel
  {
private:
   FFNN              *m_mlfn;
   double             m_learningrate;
   ENUM_ACTIVATION_FUNCTION    m_actfun;
   uint               m_epochs;
   ulong              m_layer[3];

public:
                     CMlfn();
                    ~CMlfn(void);
   void              setParams(double learning_rate, ENUM_ACTIVATION_FUNCTION act_fn, uint num_epochs);
   bool              train(matrix &predictors,matrix&targets);
   double            forecast(vector &predictors);
  };
//+------------------------------------------------------------------+
//| Constructor                                                      |
//+------------------------------------------------------------------+
CMlfn::CMlfn(void)
  {
   m_learningrate=0.01;
   m_actfun=AF_SOFTMAX;
   m_epochs= 100;
   m_layer[0] = 2;
   m_layer[1] = 2;
   m_layer[2] = 1;
   m_mlfn = new FFNN(m_layer);
  }
//+------------------------------------------------------------------+
//| Destructor                                                       |
//+------------------------------------------------------------------+
CMlfn::~CMlfn(void)
  {
   if(CheckPointer(m_mlfn) == POINTER_DYNAMIC)
      delete m_mlfn;
  }
//+------------------------------------------------------------------+
//| Set other hyperparameters of the model                           |
//+------------------------------------------------------------------+
void CMlfn::setParams(double learning_rate, ENUM_ACTIVATION_FUNCTION act_fn, uint num_epochs)
  {
   m_learningrate=learning_rate;
   m_actfun=act_fn;
   m_epochs= num_epochs;
  }
//+------------------------------------------------------------------+
//| Fit a model to the data                                          |
//+------------------------------------------------------------------+
bool CMlfn::train(matrix &predictors,matrix &targets)
  {
   return m_mlfn.fit(predictors,targets,m_learningrate,m_actfun,m_epochs);
  }
//+------------------------------------------------------------------+
//| Make a prediction with the trained model                         |
//+------------------------------------------------------------------+
double CMlfn::forecast(vector &predictors)
  {
   matrix preds(1,predictors.Size());

   if(!preds.Row(predictors,0))
     {
      Print(__FUNCTION__, " error inserting row ", GetLastError());
      return EMPTY_VALUE;
     }
   matrix out = m_mlfn.predict(preds);
   return out[0][0];
  }

//+------------------------------------------------------------------+
//| Script program start function                                    |
//+------------------------------------------------------------------+
void OnStart()
  {
//---
   if(NumSamples<1 || NumAttempts<1 || VarParam<0.0 || NumBadModels<1 || NumGoodModels<1 || NumBiasedModels<1)
     {
      Print(" Invalid User inputs ");
      return;
     }

   int ndone, divisor;
   double diff, std, temp;

   double computed_err_average ;
   double computed_err_unconstrained ;
   double computed_err_unbiased ;
   double computed_err_biased ;
   double computed_err_weighted ;
   double computed_err_bagged ;
   double computed_err_genreg ;

   CAvg average;
   CLinReg unconstrained;
   CUnbiased unbiased;
   Cbiased biased;
   CWeighted weighted;
   CGenReg genreg;

   vector computed_err_raw = vector::Zeros(NumBadModels+NumGoodModels+NumBiasedModels);

   std  =  sqrt(VarParam);

   divisor = 1;

   IModel* puremodels[];
   matrix xgood[],xbad[],xbiased[],test[10];

   if(ArrayResize(puremodels,NumBadModels+NumGoodModels+NumBiasedModels)<0 ||
      ArrayResize(xgood,NumBadModels+NumGoodModels+NumBiasedModels)<0 ||
      ArrayResize(xbad,NumBadModels+NumGoodModels+NumBiasedModels)<0 ||
      ArrayResize(xbiased,NumBadModels+NumGoodModels+NumBiasedModels)<0)
     {
      Print(" failed puremodels array resize ", GetLastError());
      return;
     }

   for(uint i = 0; i<puremodels.Size(); i++)
      puremodels[i] = new CMlfn();

   for(uint i = 0; i<xgood.Size(); i++)
      xgood[i] = matrix::Zeros(NumSamples,3);

   for(uint i = 0; i<xbad.Size(); i++)
      xbad[i] = matrix::Zeros(NumSamples,3);

   for(uint i = 0; i<xbiased.Size(); i++)
      xbiased[i] = matrix::Zeros(NumSamples,3);

   for(uint i = 0; i<test.Size(); i++)
      test[i] = matrix::Zeros(NumSamples,3);

   computed_err_average = 0.0 ;
   computed_err_unconstrained = 0.0 ;
   computed_err_unbiased = 0.0 ;
   computed_err_biased = 0.0 ;
   computed_err_weighted = 0.0 ;
   computed_err_bagged = 0.0 ;
   computed_err_genreg = 0.0 ;

   vector t,v;
   matrix d;

   ndone  = 1;
   for(uint i = 0; i<xgood.Size(); i++)
     {
      xgood[i].Random(0.0,1.0);
      if(!xgood[i].Col(sin(xgood[i].Col(0)) - pow(xgood[i].Col(1),2.0) + std*xgood[i].Col(2),2))
        {
         Print(" column insertion error ", GetLastError());
         cleanup(puremodels);
         return;
        }
     }
   matrix xb(xgood[0].Rows(),1);
   for(uint i = 0; i<xbad.Size(); i++)
     {
      xbad[i] = xgood[0];
      xb.Random(0.0,1.0);
      if(!xbad[i].Col(xb.Col(0),2))
        {
         Print(" column insertion error ", GetLastError());
         cleanup(puremodels);
         return;
        }
     }
   for(uint i = 0; i<xbiased.Size(); i++)
     {
      xbiased[i] = xgood[0];
      if(!xbiased[i].Col(xgood[0].Col(2)+1.0,2))
        {
         Print(" column insertion error ", GetLastError());
         cleanup(puremodels);
         return;
        }
     }
   for(uint i = 0; i<test.Size(); i++)
     {
      test[i].Random(0.0,1.0);
      if(!test[i].Col(sin(test[i].Col(0)) - pow(test[i].Col(1),2.0) + std * test[i].Col(2),2))
        {
         Print(" column insertion error ", GetLastError());
         cleanup(puremodels);
         return;
        }
     }

   for(uint imodel=0; imodel<puremodels.Size(); imodel++)
     {
      if(imodel < xgood.Size())
        {
         t=xgood[imodel].Col(2);
         d=np::sliceMatrixCols(xgood[imodel],0,2);
        }
      else
         if(imodel >= xgood.Size() && imodel<(xgood.Size()+xbiased.Size()))
           {
            t=xbiased[imodel-xgood.Size()].Col(2);
            d=np::sliceMatrixCols(xbiased[imodel-xgood.Size()],0,2);
           }
         else
           {
            t=xbad[imodel - (xgood.Size()+xbiased.Size())].Col(2);
            d=np::sliceMatrixCols(xbad[imodel - (xgood.Size()+xbiased.Size())],0,2);
           }

      matrix tt(t.Size(),1);

      if(!tt.Col(t,0) || !puremodels[imodel].train(d,tt))
        {
         Print(" failed column insertion ", GetLastError());
         cleanup(puremodels);
         return;
        }

      temp  = 0.0;

      for(uint i = 0; i<test.Size(); i++)
        {
         for(int j = 0; j<NumSamples; j++)
           {
            t  = test[i].Row(j);
            v  = np::sliceVector(t,0,2);
            diff = puremodels[imodel].forecast(v) - t[2];
            temp += diff*diff;
           }
        }
      computed_err_raw[imodel] += temp/double(test.Size()*NumSamples);
     }
//average
   matrix tdata;
   if(TrainCombinedModelsOnCleanData)
      tdata = xgood[0];
   else
     {
      tdata = matrix::Zeros(NumSamples*3,3);
      if(!np::matrixCopyRows(tdata,xgood[0],0,NumSamples) ||
         !np::matrixCopyRows(tdata,xbad[0],NumSamples,NumSamples*2) ||
         !np::matrixCopyRows(tdata,xbiased[0],NumSamples*2))
        {
         Print(" failed to create noisy dataset");
         cleanup(puremodels);
         return;
        }
     }
   temp = 0.0;
   for(uint i  = 0; i<test.Size(); i++)
     {
      for(int j = 0; j<NumSamples; j++)
        {
         t = test[i].Row(j);
         v = np::sliceVector(t,0,2);
         diff = average.predict(v,puremodels) - t[2];
         temp += diff*diff;
        }
     }
   computed_err_average += temp/double(test.Size()*NumSamples);
//unconstrained
   temp = 0.0;
   t = tdata.Col(2);
   d = np::sliceMatrixCols(tdata,0,2);
   if(!unconstrained.fit(d,t,puremodels))
     {
      Print(" failed to fit unconstrained model ");
      cleanup(puremodels);
     }

   for(uint i  = 0; i<test.Size(); i++)
     {
      for(int j = 0; j<NumSamples; j++)
        {
         t = test[i].Row(j);
         v = np::sliceVector(t,0,2);
         diff = unconstrained.predict(v,puremodels) - t[2];
         temp += diff*diff;
        }
     }
   computed_err_unconstrained += temp/double(test.Size()*NumSamples);
//unbiased
   temp = 0.0;
   t = tdata.Col(2);
   d = np::sliceMatrixCols(tdata,0,2);
   if(!unbiased.fit(d,t,puremodels))
     {
      Print(" failed to fit unbiased model ");
      cleanup(puremodels);
     }

   for(uint i  = 0; i<test.Size(); i++)
     {
      for(int j = 0; j<NumSamples; j++)
        {
         t = test[i].Row(j);
         v = np::sliceVector(t,0,2);
         diff = unbiased.predict(v,puremodels) - t[2];
         temp += diff*diff;
        }
     }
   computed_err_unbiased += temp/double(test.Size()*NumSamples);
//biased
   temp = 0.0;
   t = tdata.Col(2);
   d = np::sliceMatrixCols(tdata,0,2);
   if(!biased.fit(d,t,puremodels))
     {
      Print(" failed to fit biased model ");
      cleanup(puremodels);
     }

   for(uint i  = 0; i<test.Size(); i++)
     {
      for(int j = 0; j<NumSamples; j++)
        {
         t = test[i].Row(j);
         v = np::sliceVector(t,0,2);
         diff = biased.predict(v,puremodels) - t[2];
         temp += diff*diff;
        }
     }
   computed_err_biased += temp/double(test.Size()*NumSamples);
//weighted
   temp = 0.0;
   t = tdata.Col(2);
   d = np::sliceMatrixCols(tdata,0,2);
   if(!weighted.fit(d,t,puremodels))
     {
      Print(" failed to fit weighted model ");
      cleanup(puremodels);
     }

   for(uint i  = 0; i<test.Size(); i++)
     {
      for(int j = 0; j<NumSamples; j++)
        {
         t = test[i].Row(j);
         v = np::sliceVector(t,0,2);
         diff = weighted.predict(v,puremodels) - t[2];
         temp += diff*diff;
        }
     }
   computed_err_weighted += temp/double(test.Size()*NumSamples);
//gendreg
   temp = 0.0;
   t = tdata.Col(2);
   d = np::sliceMatrixCols(tdata,0,2);
   if(!genreg.fit(d,t,puremodels))
     {
      Print(" failed to fit generalized regression model ");
      cleanup(puremodels);
     }
   for(uint i  = 0; i<test.Size(); i++)
     {
      for(int j = 0; j<NumSamples; j++)
        {
         t = test[i].Row(j);
         v = np::sliceVector(t,0,2);
         diff = genreg.predict(v,puremodels) - t[2];
         temp += diff*diff;
        }
     }
   computed_err_genreg += temp/double(test.Size()*NumSamples);

   temp = 0.0;
   PrintFormat("\n\n\nRandom DataSet%5d    Raw errors:", ndone);
   for(uint imodel  = 0; imodel<puremodels.Size() ; imodel++)
     {
      PrintFormat("  %.8lf", computed_err_raw[imodel] / ndone) ;
      temp += computed_err_raw[imodel] / ndone ;
     }
   PrintFormat("\n       Mean raw error = %8.8lf", temp / double(puremodels.Size())) ;

   PrintFormat("\n        Average error = %8.8lf", computed_err_average / ndone) ;
   PrintFormat("\n  Unconstrained error = %8.8lf", computed_err_unconstrained / ndone) ;
   PrintFormat("\n       Unbiased error = %8.8lf", computed_err_unbiased / ndone) ;
   PrintFormat("\n         Biased error = %8.8lf", computed_err_biased / ndone) ;
   PrintFormat("\n       Weighted error = %8.8lf", computed_err_weighted / ndone) ;
   PrintFormat("\n         GenReg error = %8.8lf", computed_err_genreg / ndone) ;

   cleanup(puremodels);
  }
//+------------------------------------------------------------------+

Executar o script com os valores padrão gera o seguinte resultado.

MR      0       15:56:41.914    Ensemble_Demo (BTCUSD,D1)       Random DataSet    1    Raw errors:
KI      0       15:56:41.914    Ensemble_Demo (BTCUSD,D1)         0.38602529
HP      0       15:56:41.914    Ensemble_Demo (BTCUSD,D1)         0.36430552
CK      0       15:56:41.914    Ensemble_Demo (BTCUSD,D1)         0.36703202
OS      0       15:56:41.914    Ensemble_Demo (BTCUSD,D1)         0.51205057
EJ      0       15:56:41.914    Ensemble_Demo (BTCUSD,D1)         0.57791798
HE      0       15:56:41.914    Ensemble_Demo (BTCUSD,D1)         0.66825953
FL      0       15:56:41.914    Ensemble_Demo (BTCUSD,D1)         0.65051234
QD      0       15:56:41.914    Ensemble_Demo (BTCUSD,D1)         0.57403745
EO      0       15:56:41.914    Ensemble_Demo (BTCUSD,D1)         0.71593174
PF      0       15:56:41.914    Ensemble_Demo (BTCUSD,D1)         0.62444495
NQ      0       15:56:41.914    Ensemble_Demo (BTCUSD,D1)         0.77552594
KI      0       15:56:41.914    Ensemble_Demo (BTCUSD,D1)         0.75079339
MP      0       15:56:41.914    Ensemble_Demo (BTCUSD,D1)         0.78851743
CK      0       15:56:41.915    Ensemble_Demo (BTCUSD,D1)         0.52343272
OR      0       15:56:41.915    Ensemble_Demo (BTCUSD,D1)         0.70166082
EK      0       15:56:41.915    Ensemble_Demo (BTCUSD,D1)       
RE      0       15:56:41.915    Ensemble_Demo (BTCUSD,D1)              Mean raw error = 0.59869651
QL      0       15:56:41.915    Ensemble_Demo (BTCUSD,D1)       
DE      0       15:56:41.915    Ensemble_Demo (BTCUSD,D1)               Average error = 0.55224337
ML      0       15:56:41.915    Ensemble_Demo (BTCUSD,D1)       
QF      0       15:56:41.915    Ensemble_Demo (BTCUSD,D1)         Unconstrained error = 10.21673109
KL      0       15:56:41.915    Ensemble_Demo (BTCUSD,D1)       
RI      0       15:56:41.915    Ensemble_Demo (BTCUSD,D1)              Unbiased error = 0.55224337
GL      0       15:56:41.915    Ensemble_Demo (BTCUSD,D1)       
PH      0       15:56:41.915    Ensemble_Demo (BTCUSD,D1)                Biased error = 0.48431477
CL      0       15:56:41.915    Ensemble_Demo (BTCUSD,D1)       
HH      0       15:56:41.915    Ensemble_Demo (BTCUSD,D1)              Weighted error = 0.51507522
OM      0       15:56:41.915    Ensemble_Demo (BTCUSD,D1)       
LK      0       15:56:41.915    Ensemble_Demo (BTCUSD,D1)                GenReg error = 0.33761372
KM      0       15:57:11.108    Ensemble_Demo (BTCUSD,D1)       
GG      0       15:57:11.108    Ensemble_Demo (BTCUSD,D1)       
CQ      0       15:57:11.108    Ensemble_Demo (BTCUSD,D1)       

Se todos os parâmetros do script forem mantidos iguais aos da execução anterior, exceto que desta vez optamos por treinar o modelo de consenso em dados ruidosos.. Observamos a seguinte saída.

NL      0       15:59:51.502    Ensemble_Demo (BTCUSD,D1)       Random DataSet    1    Raw errors:
OS      0       15:59:51.502    Ensemble_Demo (BTCUSD,D1)         0.72840629
GJ      0       15:59:51.502    Ensemble_Demo (BTCUSD,D1)         0.63345953
PE      0       15:59:51.502    Ensemble_Demo (BTCUSD,D1)         0.68442450
JL      0       15:59:51.502    Ensemble_Demo (BTCUSD,D1)         0.91936106
OD      0       15:59:51.502    Ensemble_Demo (BTCUSD,D1)         0.75230667
LO      0       15:59:51.502    Ensemble_Demo (BTCUSD,D1)         0.88366446
PF      0       15:59:51.502    Ensemble_Demo (BTCUSD,D1)         0.78226316
CQ      0       15:59:51.502    Ensemble_Demo (BTCUSD,D1)         0.87140196
II      0       15:59:51.502    Ensemble_Demo (BTCUSD,D1)         0.58672356
KP      0       15:59:51.502    Ensemble_Demo (BTCUSD,D1)         1.09990815
MK      0       15:59:51.502    Ensemble_Demo (BTCUSD,D1)         0.92548778
OR      0       15:59:51.503    Ensemble_Demo (BTCUSD,D1)         1.03795716
GJ      0       15:59:51.503    Ensemble_Demo (BTCUSD,D1)         0.80684429
GE      0       15:59:51.503    Ensemble_Demo (BTCUSD,D1)         1.24041209
GL      0       15:59:51.503    Ensemble_Demo (BTCUSD,D1)         0.92169606
NF      0       15:59:51.503    Ensemble_Demo (BTCUSD,D1)       
CS      0       15:59:51.503    Ensemble_Demo (BTCUSD,D1)              Mean raw error = 0.85828778
RF      0       15:59:51.503    Ensemble_Demo (BTCUSD,D1)       
DS      0       15:59:51.503    Ensemble_Demo (BTCUSD,D1)               Average error = 0.83433599
FF      0       15:59:51.503    Ensemble_Demo (BTCUSD,D1)       
FP      0       15:59:51.503    Ensemble_Demo (BTCUSD,D1)         Unconstrained error = 23416285121251567120416768.00000000
DS      0       15:59:51.503    Ensemble_Demo (BTCUSD,D1)       
JR      0       15:59:51.503    Ensemble_Demo (BTCUSD,D1)              Unbiased error = 0.83433599
HS      0       15:59:51.503    Ensemble_Demo (BTCUSD,D1)       
PP      0       15:59:51.503    Ensemble_Demo (BTCUSD,D1)                Biased error = 0.74321307
LD      0       15:59:51.503    Ensemble_Demo (BTCUSD,D1)       
GQ      0       15:59:51.503    Ensemble_Demo (BTCUSD,D1)              Weighted error = 0.83213118
PD      0       15:59:51.503    Ensemble_Demo (BTCUSD,D1)       
FR      0       15:59:51.503    Ensemble_Demo (BTCUSD,D1)                GenReg error = 0.78697882

As principais observações desses resultados são que métodos de conjunto geralmente superam modelos individuais, pois combinar múltiplos modelos tipicamente gera melhores resultados do que confiar em apenas um. No entanto, não existe um método universalmente melhor, pois cada um tem seus pontos fortes e fracos, e a escolha ideal depende do conjunto de dados e do problema em questão.

A regressão não restrita, embora potencialmente poderosa, é altamente suscetível ao overfitting, especialmente com conjuntos de dados pequenos ou ruidosos. Por outro lado, a GRNN se destaca no tratamento de conjuntos de dados pequenos e ruidosos ao suavizar efetivamente os dados, embora possa sacrificar algum poder de ajuste para conjuntos de dados maiores e mais limpos.

Métodos de regressão linear também podem ser eficazes, mas o overfitting é uma preocupação, especialmente com conjuntos de dados pequenos ou ruidosos. A média simples e a ponderação por variância são geralmente robustas e podem ser boas opções quando o conjunto de dados é ruidoso ou quando o método ideal é incerto. Em resumo, a escolha do método de conjunto deve ser cuidadosamente considerada com base nas características específicas do conjunto de dados, sendo muitas vezes benéfico experimentar diferentes métodos e avaliar seu desempenho em um conjunto de validação para tomar uma decisão informada. Todo o código referenciado no texto está anexado.

Nome do Arquivo	Descrição
MQL5/include/mlffnn.mqh	Contém a definição da classe FFNN que implementa um perceptron multicamadas básico.
MQL5/include/grnn.mqh	Define a classe CGrnn que implementa uma rede neural de regressão generalizada utilizando recozimento simulado.
MQL5/include/OLS.mqh	Define a classe OLS, que encapsula a regressão por mínimos quadrados ordinários.
MQL5/include/ensemble.mqh	Contém a definição de seis métodos de conjunto implementados como as classes CAvg, CLinReg, Cbiased, CUnbiased, CWeighted e CGenReg.
MQL5/include/np.mqh	Contém funções utilitárias para matriz e vetor de variação.
MQL5/scripts/Ensemble_Demo.mq5	Este é um script que demonstra as classes de conjunto definidas em ensemble.mqh