Aplicando Seleção de Recursos Localizada em Python e MQL5

Introdução

Na análise do mercado financeiro, os indicadores frequentemente apresentam eficácia variável à medida que as condições subjacentes mudam. Por exemplo, a volatilidade flutuante pode tornar ineficazes indicadores que antes eram confiáveis, à medida que os regimes de mercado mudam. Essa variabilidade explica a proliferação de indicadores usados pelos traders, já que nenhum indicador único consegue ter um bom desempenho de forma consistente em todas as condições de mercado. Do ponto de vista do aprendizado de máquina, isso exige uma técnica de seleção de recursos flexível que possa se adaptar a esse comportamento dinâmico.

Muitos algoritmos de seleção de recursos comuns priorizam recursos que mostram poder preditivo em todo o espaço de características. Esses recursos geralmente são favorecidos mesmo quando seus relacionamentos com a variável-alvo são não lineares ou influenciados por outros recursos. No entanto, esse viés global pode ser problemático, pois modelos não lineares modernos podem extrair insights valiosos de recursos com forte capacidade preditiva local ou cujos relacionamentos com a variável-alvo mudam dentro de regiões específicas do espaço de características.

Neste artigo, exploramos um algoritmo de seleção de recursos introduzido no artigo 'Local Feature Selection for Data Classification' de Narges Armanfard, James P. Reilly e Majid Komeili. Esse método busca identificar recursos preditivos que muitas vezes são negligenciados por técnicas tradicionais de seleção devido à sua utilidade global limitada. Começaremos com uma visão geral do algoritmo, seguida por sua implementação em Python para criar modelos de classificação adequados para exportação para o MetaTrader 5.

Seleção de Recursos Local

O sucesso do aprendizado de máquina depende da seleção de recursos informativos que contribuam para a resolução do problema. Em classificação supervisionada, os recursos devem diferenciar efetivamente entre categorias de dados. No entanto, identificar esses recursos informativos pode ser desafiador, já que recursos não informativos podem introduzir ruído e prejudicar o desempenho do modelo. Como resultado, a seleção de recursos costuma ser uma etapa inicial crítica na construção de modelos preditivos.

Diferente dos métodos tradicionais, que buscam um único subconjunto ótimo de recursos para todos os dados, a Seleção de Recursos Local (LFS) identifica subconjuntos ideais para regiões locais específicas. Essa adaptabilidade pode ser particularmente útil para lidar com dados não estacionários. Além disso, o LFS incorpora um classificador que leva em conta os diferentes subconjuntos de recursos usados em diferentes amostras. Ele faz isso por meio de agrupamento por classe, selecionando recursos que minimizam as distâncias intra-classes enquanto maximizam as distâncias inter-classes.

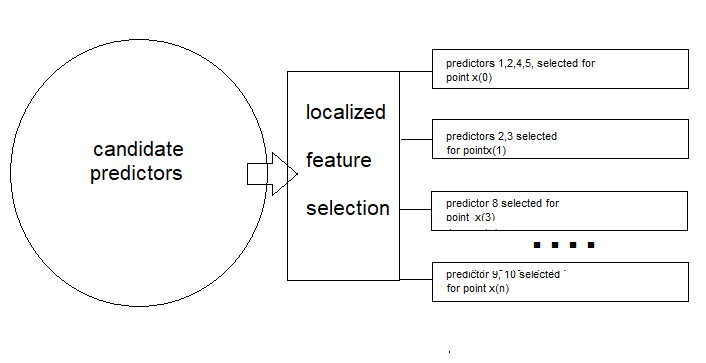
Essa abordagem identifica um subespaço de recursos localmente ótimo em regiões sobrepostas, garantindo que cada amostra seja representada em múltiplos espaços de recursos. Para entender melhor o conceito, considere um cenário em que uma empresa de telecomunicações busca prever o cancelamento de clientes — identificando clientes propensos a encerrar suas contas. A empresa coleta várias características dos clientes, incluindo:

• Tempo de permanência do cliente: há quanto tempo o cliente está com a empresa?
• Conta mensal: quanto o cliente paga por mês?
• Peso e altura do cliente.
• Número de chamadas feitas ao serviço de atendimento: com que frequência o cliente entra em contato com o suporte.

Imagine selecionar dois clientes fiéis que estão com a empresa há muitos anos. Para cada um dos recursos descritos, provavelmente haveria diferenças mínimas entre esses clientes fiéis, pois pertencem à mesma classe. Agora, compare isso com a diferença entre um cliente de longa data e outro que cancelou a assinatura pouco tempo após se inscrever. Embora peso e altura possam não diferir muito, outros preditores relevantes provavelmente apresentariam variação significativa.

O cliente fiel obviamente teria um tempo de permanência muito maior, poderia estar mais disposto a escolher um pacote de assinatura mais caro e seria mais propenso a contatar o suporte ao invés de cancelar por frustração. Enquanto isso, métricas como peso e altura permaneceriam próximas à média populacional e não contribuiriam significativamente para distinguir esses tipos de clientes.

Analisar os valores individuais dos recursos em pares usando a distância euclidiana revela que os preditores mais relevantes terão a maior distância inter-classes entre os clientes, enquanto os menos relevantes apresentarão a menor distância inter-classes. Isso torna clara a seleção de preditores eficazes: priorizamos pares com baixa distância intra-classe e alta distância inter-classe.

Embora essa abordagem pareça eficaz, ela não leva em conta as variações locais dentro dos dados. Para lidar com isso, devemos considerar como o poder preditivo pode variar entre diferentes domínios de recursos. Imagine um conjunto de dados com duas classes, onde uma delas é dividida em dois subconjuntos distintos. Um gráfico de dispersão de dois recursos desse conjunto de dados ilustra que o primeiro subconjunto pode estar bem separado da Classe 1 usando a variável x1, mas não x2. Por outro lado, o segundo subconjunto pode estar bem separado usando x2, mas não x1.

Se considerarmos apenas a separação inter-classes, o algoritmo poderia selecionar erroneamente tanto x1 quanto x2, mesmo que apenas um seja realmente eficaz em cada subconjunto. Isso ocorre porque o algoritmo poderia priorizar a grande distância geral entre os dois subconjuntos em vez das distâncias menores e mais relevantes dentro de cada subconjunto. Para resolver isso, os autores do artigo citado introduziram um esquema de ponderação para as distâncias. Ao atribuir pesos mais altos para pares de casos que estão mais próximos e pesos mais baixos para pares mais distantes, o algoritmo pode reduzir a influência de outliers dentro de uma classe. Isso considera tanto as pertenças às classes quanto a distribuição global das distâncias.

Em resumo, o algoritmo LFS, conforme descrito no artigo citado, consiste em dois componentes principais. O primeiro é o processo de seleção de recursos, no qual um subconjunto de recursos é selecionado para cada amostra. O segundo componente envolve um mecanismo localizado que mede a similaridade de uma amostra de teste com uma classe específica, o que é usado para fins de inferência.

Seleção de Recursos

Nesta seção, descreveremos o procedimento de aprendizado empregado pelo método LFS, passo a passo, com um pouco de matemática. Começamos com a estrutura esperada dos dados de treinamento. A implementação da seleção de recursos localizada é realizada em um conjunto de dados com N amostras de treinamento, classificadas em Z rótulos de classe e acompanhadas de M recursos ou candidatos a preditores.

Os dados de treinamento podem ser representados como uma matriz X, onde as linhas correspondem às amostras e as colunas representam candidatos a preditores distintos. Assim, a matriz X possui N linhas e M colunas. Cada amostra é denotada como X(i), referindo-se à i-ésima linha da matriz. Os rótulos de classe são armazenados em um vetor coluna Y separado, com cada rótulo mapeado para uma amostra (linha) correspondente na matriz.

O objetivo final de aplicar o método LFS é determinar, para cada amostra de treinamento X(i), um vetor binário de tamanho M, F(i), que indica quais candidatos a preditores são mais relevantes para determinar o rótulo de classe correspondente. A matriz F terá as mesmas dimensões que X.

Usando a distância euclidiana, o algoritmo busca minimizar a distância média entre a amostra atual e outras amostras com o mesmo rótulo de classe, ao mesmo tempo em que maximiza a distância média entre a amostra atual e aquelas com rótulos de classe diferentes. Além disso, as distâncias devem ser ponderadas para favorecer amostras na mesma vizinhança da amostra atual, introduzindo o vetor coluna de pesos W. Como os pesos (W) e o vetor binário F(i) não estão inicialmente disponíveis, é usado um procedimento iterativo para estimar ambos os vetores ótimos W e F(i).

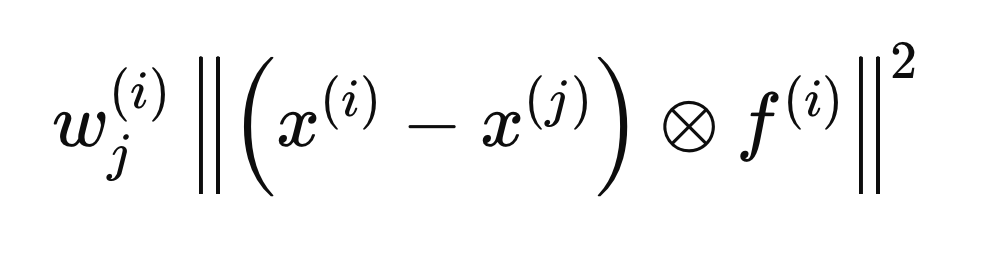
Cálculo das Distâncias Intra-Classe e Inter-Classe

Cada etapa descrita nas seções a seguir refere-se a cálculos realizados para uma única amostra, X(i), para determinar o vetor F(i) ótimo. O processo começa inicializando todas as entradas de F como zero e definindo os pesos iniciais como 1. Em seguida, calculamos as distâncias intra-classe e inter-classe em relação a X(i). A inclusão do vetor F(i) nos cálculos de distância garante que apenas as variáveis consideradas relevantes (aquelas iguais a 1) sejam consideradas. Para conveniência matemática, as distâncias euclidianas são elevadas ao quadrado, levando à seguinte equação de distância.

O círculo com um "x" dentro denota um operador de multiplicação elemento a elemento. As distâncias intra-classe e inter-classe são calculadas usando a fórmula acima, mas com diferentes elementos j (linhas) de X. A distância intra-classe é calculada usando os elementos j que compartilham o mesmo rótulo de classe que X(i),

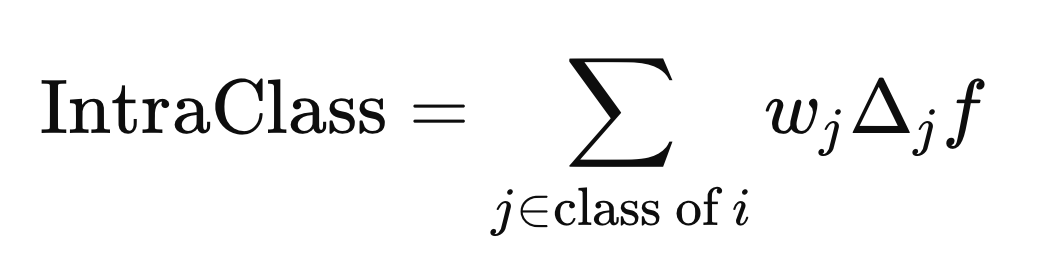
enquanto a distância inter-classe é calculada usando os elementos j com qualquer rótulo de classe diferente de Y(i).

Cálculo dos Pesos

Para a amostra X(i), calculamos um vetor de pesos (W), com tamanho N, de modo que se X(j) estiver distante de X(i), seu peso deve ser pequeno, e, inversamente, se estiver próximo, o peso deve ser maior. A ponderação não deve penalizar amostras simplesmente por terem um rótulo de classe diferente. Como F(i) ainda não é ótimo, as variáveis selecionadas para definir a base das vizinhanças ainda são desconhecidas. O artigo citado aborda esse problema calculando a média dos pesos obtidos em iterações anteriores de refinamento dos pesos.

Quando um vetor F é incluído na definição da distância entre duas amostras, ele é considerado dentro do espaço métrico definido por F(i). O cálculo dos pesos ótimos é realizado definindo distâncias em termos de um espaço métrico diferente, que chamaremos de F(z), conforme a fórmula abaixo.

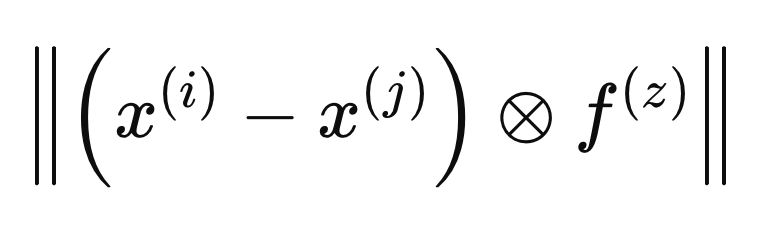
Para garantir que os pesos não penalizem amostras apenas por pertencerem a classes diferentes, calculamos a distância mínima entre X(i) e todas as outras amostras da mesma classe no espaço métrico definido por F(z).

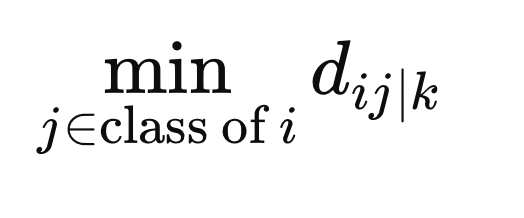
Além disso, calculamos a distância mínima de amostras com rótulo de classe diferente até X(i).

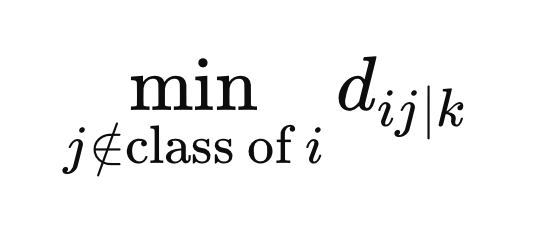
Estes são os valores finais necessários para definir os pesos. Os pesos são calculados como a média entre todos os espaços métricos, dada pelo exponencial negativo da diferença entre a distância e a distância mínima para um determinado espaço métrico, z.

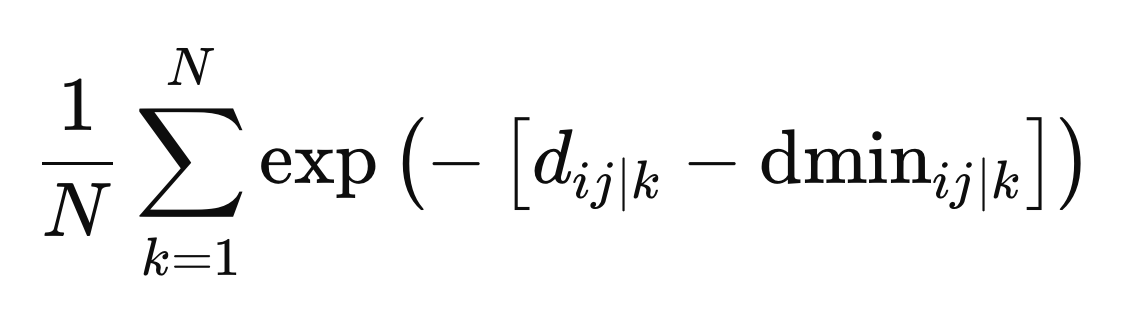
Objetivos Conflitantes

Neste ponto, já temos os pesos ótimos, o que nos permite lidar com o desafio de encontrar o equilíbrio certo entre separação inter-classe e intra-classe. Isso envolve reconciliar dois objetivos conflitantes: minimizar a separação intra-classe (tornando os pontos de dados da mesma classe o mais semelhantes possível) e maximizar a separação inter-classe (tornando as diferentes classes o mais distintas possível). Alcançar ambos os objetivos perfeitamente com o mesmo conjunto de preditores geralmente é inviável.

Uma abordagem viável é o Método da Restrição Epsilon (Epsilon-Constraint), que encontra um compromisso entre esses objetivos conflitantes. Esse método funciona resolvendo primeiro um dos problemas de otimização (geralmente o de maximização) e, em seguida, tratando o problema de minimização com a restrição adicional de que a função maximizada permaneça acima de um certo limite.

Primeiro, maximizamos a separação inter-classe e registramos o valor máximo dessa função, denotado por épsilon (ϵ), que representa a maior separação inter-classe possível. Depois, minimizamos a separação intra-classe para vários valores de um parâmetro β (variando de 0 a 1), com a restrição de que a separação inter-classe para a solução minimizada permaneça maior ou igual a βϵ.

O parâmetro β atua como um fator de compromisso, equilibrando o foco entre os dois objetivos: quando β é definido como 1, a separação inter-classe recebe prioridade total, enquanto quando β é 0, o foco se desloca inteiramente para a minimização da separação intra-classe. Quatro restrições são impostas em ambas as tarefas de otimização:

• Todos os elementos de F devem estar entre 0 e 1, inclusive.
• A soma dos elementos de um vetor F deve ser menor ou igual a um hiperparâmetro definido pelo usuário, que determina o número máximo de preditores que podem ser ativados.
• A soma dos elementos de um vetor F deve ser maior ou igual a um, garantindo que pelo menos um preditor seja ativado para cada amostra.
  

Para a minimização intra-classe, há uma restrição adicional herdada da operação de maximização inicial: o valor da função de maximização deve ser pelo menos igual ao produto de β e ϵ.

As funções e restrições envolvidas são lineares, o que indica que as tarefas de otimização são problemas de programação linear. Problemas padrão de programação linear visam maximizar uma função objetivo sujeita a restrições que especificam limites que não devem ser excedidos.

Programação linear envolve otimizar uma função objetivo linear sujeita a restrições lineares. A função objetivo, geralmente denotada por "z", é uma combinação linear de variáveis de decisão. As restrições são expressas como desigualdades ou igualdades lineares, limitando os valores das variáveis de decisão. Além das restrições definidas pelo usuário, existem restrições implícitas de não negatividade nas variáveis de decisão e nos lados direitos das desigualdades.

Embora a forma padrão assuma variáveis de decisão não negativas e desigualdades do tipo "menor ou igual", essas restrições podem ser relaxadas por meio de transformações. Multiplicando ambos os lados de uma desigualdade por -1, podemos lidar com desigualdades "maior ou igual" e lados direitos negativos. Além disso, coeficientes não positivos envolvendo variáveis de decisão podem ser transformados em positivos criando novas variáveis.

O método do ponto interior é um algoritmo eficiente para resolver problemas de programação linear, especialmente ao lidar com tarefas de otimização em larga escala. Nossa implementação em Python usará esse método para encontrar uma solução ótima de forma eficiente. Uma vez atingida a convergência, obteremos um vetor F(i) ótimo. No entanto, é importante observar que esses valores não estão no formato exigido (apenas 1s ou 0s). Isso é corrigido na etapa final do método LFS.

Testes de Beta

O problema com o vetor F(i) calculado é que ele consiste em valores reais em vez de valores binários. O objetivo do procedimento LFS é identificar as variáveis mais relevantes para cada amostra, o que é representado por uma matriz F binária, onde os valores são 0 ou 1. Um valor 0 indica que a variável correspondente é considerada irrelevante ou ignorada.

Para converter os valores reais do vetor F(i) em valores binários, utilizamos um método de Monte Carlo para encontrar o melhor equivalente binário. Isso envolve repetir o processo um número de vezes especificado pelo usuário, que é um hiperparâmetro chave do método LFS. Para cada iteração, começamos com um vetor binário onde cada candidato a preditor é inicialmente definido como 1, usando os valores contínuos de F(i) como probabilidades para cada preditor. Em seguida, verificamos se o vetor binário satisfaz as restrições do procedimento de minimização e calculamos o valor da função objetivo. O vetor binário com o menor valor da função objetivo é escolhido como o vetor F(i) final.

Pós-processamento da Seleção de Recursos

O LFS seleciona independentemente candidatos a preditores ótimos para cada amostra, o que torna impraticável relatar um único conjunto definitivo. Para lidar com isso, contamos a frequência com que cada preditor aparece nos subconjuntos ótimos. Isso permite que os usuários definam um limite e identifiquem os preditores que mais aparecem como os mais relevantes. Importante: a relevância de um preditor nesse conjunto não implica em seu valor individual; seu valor pode estar na interação com outros preditores.

Essa é uma das principais vantagens do LFS: sua capacidade de identificar preditores que podem ser individualmente insignificantes, mas valiosos quando combinados com outros. Essa etapa de pré-processamento é importante para modelos de predição modernos, que são excelentes em discernir relacionamentos complexos entre variáveis. Ao eliminar preditores irrelevantes, o LFS simplifica o processo de modelagem e melhora o desempenho do modelo.

Implementação em Python: LFSpy

Nesta seção, exploramos a aplicação prática do algoritmo LFS, focando primeiro em seu uso como técnica de seleção de recursos e discutindo brevemente suas capacidades de classificação de dados. Todas as demonstrações serão conduzidas em Python usando o pacote LFSpy, que implementa tanto a seleção de recursos quanto os aspectos de classificação do algoritmo LFS. O pacote está disponível no PyPI, onde informações detalhadas sobre ele podem ser encontradas.

Primeiramente, instale o pacote LFSpy.

pip install LFSpy

Em seguida, importe a classe LocalFeatureSelection do LFSpy.

from LFSpy import LocalFeatureSelection

Uma instância de LocalFeatureSelection pode ser criada utilizando o construtor paramétrico.

lfs = LocalFeatureSelection(alpha=8,tau=2,n_beta=20,nrrp=2000)

O construtor aceita os seguintes parâmetros opcionais:

Nome do Parâmetro	Tipo de Dado	Descrição
alpha	inteiro	Número máximo de preditores selecionados entre todos os candidatos a preditores. O valor padrão é 19.
gamma	double	Nível de tolerância que regula a razão entre amostras com rótulos de classe diferentes e aquelas com o mesmo rótulo de classe dentro de uma região local. O valor padrão é 0.2.
tau	inteiro	Número de iterações sobre todo o conjunto de dados (equivalente ao número de épocas em aprendizado de máquina tradicional). O padrão é 2, e recomenda-se manter este valor em um dígito, geralmente no máximo 5.
sigma	double	Controla a ponderação das observações com base na distância. Um valor maior que 1 reduz o peso. O valor padrão é 1.
n_beta	inteiro	Número de valores beta testados ao converter os vetores F contínuos para seus equivalentes binários.
nrrp	inteiro	Número de iterações para os testes de beta. Esse valor deve ser pelo menos 500, aumentando com o tamanho do conjunto de treinamento. O valor padrão é 2000.<br0/>
knn	inteiro	Aplica-se especificamente a tarefas de classificação. Especifica o número de vizinhos mais próximos a serem comparados para a categorização. O valor padrão é 1.

Após inicializar uma instância da classe LFSpy, usamos o método fit() com pelo menos dois parâmetros de entrada: uma matriz bidimensional de amostras de treinamento, composta por candidatos a preditores, e um array unidimensional de rótulos de classe correspondentes.

lfs.fit(xtrain,ytrain)

Após o modelo ser treinado, chamar fstar retorna a matriz de inclusão F, que consiste em valores 1s e 0s indicando os recursos selecionados. Note que essa matriz é transposta em relação à orientação das amostras de treinamento.

fstar = lfs.fstar

O método predict() é usado para classificar amostras de teste com base no modelo aprendido e retorna os rótulos de classe correspondentes aos dados de teste.

predicted_classes = lfs.predict(test_samples)

O método score() calcula a acurácia do modelo comparando os rótulos previstos com os rótulos reais. Ele retorna a fração de amostras de teste que foram corretamente classificadas.

accuracy = lfs.score(test_data,test_labels)

Exemplos de uso do LFSpy

Para a primeira demonstração prática, geramos várias milhares de variáveis aleatórias uniformemente distribuídas no intervalo [−1,1]. Essas variáveis são organizadas em uma matriz com um número específico de colunas. Em seguida, criamos um vetor de rótulos {0, 1} correspondente a cada linha, dependendo se os valores em duas colunas arbitrárias são ambos negativos ou ambos positivos. O objetivo dessa demonstração é determinar se o método LFS consegue identificar os preditores mais relevantes nesse conjunto de dados. Avaliamos os resultados somando o número de vezes que cada preditor foi selecionado (indicado por um 1) na matriz de inclusão binária F. O código que implementa este teste está mostrado abaixo.

import numpy as np
import pandas as pd
from LFSpy import LocalFeatureSelection
from timeit import default_timer as timer

#number of random numbers to generate
datalen = 500 

#number of features the dataset will have
datavars = 5

#set random number seed
rng_seed = 125
rng = np.random.default_rng(rng_seed)

#generate the numbers
data = rng.uniform(-1.0,1.0,size=datalen)

#shape our dataset
data = data.reshape([datalen//datavars,datavars])

#set up container for class labels
class_labels = np.zeros(shape=data.shape[0],dtype=np.uint8)

#set the class labels
for i in range(data.shape[0]):
    class_labels[i] = 1 if (data[i,1] > 0.0 and data[i,2] > 0.0) or (data[i,1] < 0.0 and data[i,2] < 0.0) else 0

#partition our training data
xtrain = data
ytrain = class_labels

#initialize the LFS object
lfs = LocalFeatureSelection(rr_seed=rng_seed,alpha=8,tau=2,n_beta=20,nrrp=2000)

#start timer
start = timer()

#train the model
lfs.fit(xtrain,ytrain)

#output training duration
print("Training done in ", timer()-start , " seconds. ")

#get the inclusion matrix
fstar = lfs.fstar

#add up all ones for each row of the inclusion matrix
ibins = fstar.sum(axis=1)

#calculate the percent of times a candidate was selected
original_crits = 100.0 * ibins.astype(np.float64)/np.float64(ytrain.shape[0])

#output the results
print("------------------------------> Percent of times selected <------------------------------" )
for i in range(original_crits.shape[0]):
   print( f" Variable at column {i}, selected {original_crits[i]} %")

Saída da execução de LFSdemo.py

Training done in  45.84896759999992  seconds. 
Python  ------------------------------> Percent of times selected <------------------------------
Python   Variable at column 0, selected 19.0 %
Python   Variable at column 1, selected 81.0 %
Python   Variable at column 2, selected 87.0 %
Python   Variable at column 3, selected 20.0 %
Python   Variable at column 4, selected 18.0 %

É interessante que uma das variáveis relevantes foi selecionada um pouco mais frequentemente do que a outra, apesar de ambas terem papel idêntico na predição da classe. Isso sugere que nuances sutis nos dados podem estar influenciando o processo de seleção. O que é claro é que ambas as variáveis foram consistentemente escolhidas com mais frequência do que preditores irrelevantes, indicando sua importância na determinação da classe. A execução relativamente lenta do algoritmo provavelmente se deve à sua natureza de thread única, o que pode limitar seu desempenho em conjuntos de dados maiores.

LFS para classificação de dados

Devido à natureza local do LFS, construir um classificador a partir dele requer mais esforço em comparação com métodos tradicionais de seleção de recursos com viés global. O artigo referenciado discute uma arquitetura proposta de classificador, a qual não abordaremos aqui. Leitores interessados são encorajados a consultar o artigo citado para detalhes completos. Nesta seção, focaremos na implementação.

O método predict() da classe LocalFeatureSelection avalia a similaridade de classe. Ele recebe dados de teste que seguem a mesma estrutura dos dados de treinamento e retorna os rótulos previstos com base nos padrões aprendidos pelo modelo LFS treinado. Na próxima demonstração em código, ampliaremos o script anterior para construir um modelo classificador com LFS, exportá-lo em formato JSON, carregá-lo usando um script em MQL5 e classificar um conjunto de dados fora da amostra. O código utilizado para exportar um modelo LFS está no arquivo JsonModel.py. Esse arquivo define a função lfspy2json(), que serializa o estado e os parâmetros de um modelo LocalFeatureSelection em um arquivo JSON. Isso permite que o modelo seja salvo em um formato facilmente lido e utilizado em código MQL5, facilitando a integração com o MetaTrader 5. O código completo é apresentado abaixo.

# Copyright 2024, MetaQuotes Ltd.
# https://www.mql5.com

from LFSpy import LocalFeatureSelection
import json 

MQL5_FILES_FOLDER = "MQL5\\FILES"
MQL5_COMMON_FOLDER = "FILES"

def lfspy2json(lfs_model:LocalFeatureSelection, filename:str):
    """
    function export a LFSpy model to json format 
    readable from MQL5 code.
    
    param: lfs_model should be an instance of LocalFeatureSelection
    param: filename or path to file where lfs_model
    parameters will be written to
    
    """
    if not isinstance(lfs_model,LocalFeatureSelection):
        raise TypeError(f'invalid type supplied, "lfs_model" should be an instance of LocalFeatureSelection')
    if len(filename) < 1 or not isinstance(filename,str):
        raise TypeError(f'invalid filename supplied')
    jm  = {
            "alpha":lfs_model.alpha,
            "gamma":lfs_model.gamma,
            "tau":lfs_model.tau,
            "sigma":lfs_model.sigma, 
            "n_beta":lfs_model.n_beta,
            "nrrp":lfs_model.nrrp,
            "knn":lfs_model.knn,
            "rr_seed":lfs_model.rr_seed,
            "num_observations":lfs_model.training_data.shape[1],
            "num_features":lfs_model.training_data.shape[0],
            "training_data":lfs_model.training_data.tolist(),
            "training_labels":lfs_model.training_labels.tolist(),
            "fstar":lfs_model.fstar.tolist()
          }
          
    
    with open(filename,'w') as file:
        json.dump(jm,file,indent=None,separators=(',', ':')) 
    return 

A função recebe um objeto LocalFeatureSelection e um nome de arquivo como entrada. Ela serializa os parâmetros do modelo como um objeto JSON e os salva com o nome de arquivo especificado. O módulo também define duas constantes, MQL5_FILES_FOLDER e MQL5_COMMON_FOLDER, que representam os caminhos de diretórios acessíveis em uma instalação padrão do MetaTrader 5. Essa é apenas uma parte da solução para integração com o MetaTrader 5. A outra parte é implementada em código MQL5, apresentado em lfspy.mqh. Esse arquivo de inclusão contém a definição da classe Clfspy, que facilita o carregamento de um modelo LFS salvo em formato JSON para fins de inferência. O código completo é fornecido a seguir.

//+------------------------------------------------------------------+
//|                                                        lfspy.mqh |
//|                                  Copyright 2024, MetaQuotes Ltd. |
//|                                             https://www.mql5.com |
//+------------------------------------------------------------------+
#property copyright "Copyright 2024, MetaQuotes Ltd."
#property link      "https://www.mql5.com"
#include<JAson.mqh>
#include<Files/FileTxt.mqh>
#include<np.mqh>
//+------------------------------------------------------------------+
//|structure of model parameters                                     |
//+------------------------------------------------------------------+
struct LFS_PARAMS
  {
   int               alpha;
   int               tau;
   int               n_beta;
   int               nrrp;
   int               knn;
   int               rr_seed;
   int               sigma;
   ulong             num_features;
   double            gamma;
  };
//+------------------------------------------------------------------+
//|  class encapsulates LFSpy model                                  |
//+------------------------------------------------------------------+
class Clfspy
  {
private:
   bool              loaded;
   LFS_PARAMS        model_params;
   matrix train_data,
          fstar;
   vector            train_labels;
   //+------------------------------------------------------------------+
   //|  helper function for parsing model from file                     |
   //+------------------------------------------------------------------+
   bool              fromJSON(CJAVal &jsonmodel)
     {

      model_params.alpha = (int)jsonmodel["alpha"].ToInt();
      model_params.tau = (int)jsonmodel["tau"].ToInt();
      model_params.sigma = (int)jsonmodel["sigma"].ToInt();
      model_params.n_beta = (int)jsonmodel["n_beta"].ToInt();
      model_params.nrrp = (int)jsonmodel["nrrp"].ToInt();
      model_params.knn = (int)jsonmodel["knn"].ToInt();
      model_params.rr_seed = (int)jsonmodel["rr_seed"].ToInt();
      model_params.gamma = jsonmodel["gamma"].ToDbl();

      ulong observations = (ulong)jsonmodel["num_observations"].ToInt();
      model_params.num_features = (ulong)jsonmodel["num_features"].ToInt();

      if(!train_data.Resize(model_params.num_features,observations) || !train_labels.Resize(observations) ||
         !fstar.Resize(model_params.num_features,observations))
        {
         Print(__FUNCTION__, " error ", GetLastError());
         return false;
        }


      for(int i=0; i<int(model_params.num_features); i++)
        {
         for(int j = 0; j<int(observations); j++)
           {
            if(i==0)
               train_labels[j] = jsonmodel["training_labels"][j].ToDbl();
            train_data[i][j] = jsonmodel["training_data"][i][j].ToDbl();
            fstar[i][j] = jsonmodel["fstar"][i][j].ToDbl();
           }
        }

      return true;
     }
   //+------------------------------------------------------------------+
   //| helper classification function                                   |
   //+------------------------------------------------------------------+
   matrix            classification(matrix &testing_data)
     {
      int N = int(train_labels.Size());
      int H = int(testing_data.Cols());

      matrix out(H,2);

      for(int i = 0; i<H; i++)
        {
         vector column = testing_data.Col(i);
         vector result = class_sim(column,train_data,train_labels,fstar,model_params.gamma,model_params.knn);
         if(!out.Row(result,i))
           {
            Print(__FUNCTION__, " row insertion failure ", GetLastError());
            return matrix::Zeros(1,1);
           }
        }

      return out;
     }
   //+------------------------------------------------------------------+
   //| internal feature classification function                         |
   //+------------------------------------------------------------------+
   vector            class_sim(vector &test,matrix &patterns,vector& targets, matrix &f_star, double gamma, int knn)
     {
      int N = int(targets.Size());
      int n_nt_cls_1 = (int)targets.Sum();
      int n_nt_cls_2 = N - n_nt_cls_1;
      int M = int(patterns.Rows());
      int NC1 = 0;
      int NC2 = 0;
      vector S = vector::Zeros(N);

      S.Fill(double("inf"));

      vector NoNNC1knn = vector::Zeros(N);
      vector NoNNC2knn = vector::Zeros(N);
      vector NoNNC1 = vector::Zeros(N);
      vector NoNNC2 = vector::Zeros(N);
      vector radious = vector::Zeros(N);
      double r = 0;
      int k = 0;
      for(int i = 0; i<N; i++)
        {
         vector fs = f_star.Col(i);
         matrix xpatterns = patterns * np::repeat_vector_as_rows_cols(fs,patterns.Cols(),false);
         vector testpr = test * fs;
         vector mtestpr = (-1.0 * testpr);
         matrix testprmat = np::repeat_vector_as_rows_cols(mtestpr,xpatterns.Cols(),false);
         vector dist = MathAbs(sqrt((pow(testprmat + xpatterns,2.0)).Sum(0)));
         vector min1 = dist;
         np::sort(min1);
         vector min_uniq = np::unique(min1);
         int m = -1;
         int no_nereser = 0;
         vector NN(dist.Size());
         while(no_nereser<int(knn))
           {
            m+=1;
            double a1  = min_uniq[m];
            for(ulong j = 0; j<dist.Size(); j++)
               NN[j]=(dist[j]<=a1)?1.0:0.0;
            no_nereser = (int)NN.Sum();
           }
         vector bitNN = np::bitwiseAnd(NN,targets);
         vector Not = np::bitwiseNot(targets);
         NoNNC1knn[i] = bitNN.Sum();
         bitNN = np::bitwiseAnd(NN,Not);
         NoNNC2knn[i] = bitNN.Sum();
         vector A(fs.Size());
         for(ulong v =0; v<A.Size(); v++)
            A[v] = (fs[v]==0.0)?1.0:0.0;
         vector f1(patterns.Cols());
         vector f2(patterns.Cols());
         if(A.Sum()<double(M))
           {
            for(ulong v =0; v<A.Size(); v++)
               A[v] = (A[v]==1.0)?0.0:1.0;
            matrix amask = matrix::Ones(patterns.Rows(), patterns.Cols());
            amask *= np::repeat_vector_as_rows_cols(A,patterns.Cols(),false);
            matrix patternsp = patterns*amask;
            vector testp = test*(amask.Col(0));
            vector testa = patternsp.Col(i) - testp;
            vector col = patternsp.Col(i);
            matrix colmat = np::repeat_vector_as_rows_cols(col,patternsp.Cols(),false);
            double Dist_test = MathAbs(sqrt((pow(col - testp,2.0)).Sum()));
            vector Dist_pat  = MathAbs(sqrt((pow(patternsp - colmat,2.0)).Sum(0)));
            vector eerep = Dist_pat;
            np::sort(eerep);
            int remove = 0;
            if(targets[i] == 1.0)
              {
               vector unq = np::unique(eerep);
               k = -1;
               NC1+=1;
               if(remove!=1)
                 {
                  int Next = 1;
                  while(Next == 1)
                    {
                     k+=1;
                     r = unq[k];
                     for(ulong j = 0; j<Dist_pat.Size(); j++)
                       {
                        if(Dist_pat[j] == r)
                           f1[j] = 1.0;
                        else
                           f1[j] = 0.0;
                        if(Dist_pat[j]<=r)
                           f2[j] = 1.0;
                        else
                           f2[j] = 0.0;
                       }
                     vector f2t = np::bitwiseAnd(f2,targets);
                     vector tn = np::bitwiseNot(targets);
                     vector f2tn = np::bitwiseAnd(f2,tn);
                     double nocls1clst = f2t.Sum() - 1.0;
                     double nocls2clst = f2tn.Sum();
                     if(gamma *(nocls1clst/double(n_nt_cls_1-1)) < (nocls2clst/(double(n_nt_cls_2))))
                       {
                        Next = 0 ;
                        if((k-1) == 0)
                           r = unq[k];
                        else
                           r = 0.5 * (unq[k-1] + unq[k]);
                        if(r==0.0)
                           r = pow(10.0,-6.0);
                        r = 1.0*r;
                        for(ulong j = 0; j<Dist_pat.Size(); j++)
                          {
                           if(Dist_pat[j]<=r)
                              f2[j] = 1.0;
                           else
                              f2[j] = 0.0;
                          }
                        f2t = np::bitwiseAnd(f2,targets);
                        f2tn = np::bitwiseAnd(f2,tn);
                        nocls1clst = f2t.Sum() - 1.0;
                        nocls2clst = f2tn.Sum();
                       }
                    }
                  if(Dist_test<r)
                    {
                     patternsp = patterns * np::repeat_vector_as_rows_cols(fs,patterns.Cols(),false);
                     testp = test * fs;
                     dist = MathAbs(sqrt((pow(patternsp - np::repeat_vector_as_rows_cols(testp,patternsp.Cols(),false),2.0)).Sum(0)));
                     min1 = dist;
                     np::sort(min1);
                     min_uniq = np::unique(min1);
                     m = -1;
                     no_nereser = 0;
                     while(no_nereser<int(knn))
                       {
                        m+=1;
                        double a1  = min_uniq[m];
                        for(ulong j = 0; j<dist.Size(); j++)
                           NN[j]=(dist[j]<a1)?1.0:0.0;
                        no_nereser = (int)NN.Sum();
                       }
                     bitNN = np::bitwiseAnd(NN,targets);
                     Not = np::bitwiseNot(targets);
                     NoNNC1[i] = bitNN.Sum();
                     bitNN = np::bitwiseAnd(NN,Not);
                     NoNNC2[i] = bitNN.Sum();
                     if(NoNNC1[i]>NoNNC2[i])
                        S[i] = 1.0;
                    }
                 }
              }
            if(targets[i] == 0.0)
              {
               vector unq = np::unique(eerep);
               k=-1;
               NC2+=1;
               int Next;
               if(remove!=1)
                 {
                  Next =1;
                  while(Next==1)
                    {
                     k+=1;
                     r = unq[k];
                     for(ulong j = 0; j<Dist_pat.Size(); j++)
                       {
                        if(Dist_pat[j] == r)
                           f1[j] = 1.0;
                        else
                           f1[j] = 0.0;
                        if(Dist_pat[j]<=r)
                           f2[j] = 1.0;
                        else
                           f2[j] = 0.0;
                       }
                     vector f2t = np::bitwiseAnd(f2,targets);
                     vector tn = np::bitwiseNot(targets);
                     vector f2tn = np::bitwiseAnd(f2,tn);
                     double nocls1clst = f2t.Sum() ;
                     double nocls2clst = f2tn.Sum() -1.0;
                     if(gamma *(nocls2clst/double(n_nt_cls_2-1)) < (nocls1clst/(double(n_nt_cls_1))))
                       {
                        Next = 0 ;
                        if((k-1) == 0)
                           r = unq[k];
                        else
                           r = 0.5 * (unq[k-1] + unq[k]);
                        if(r==0.0)
                           r = pow(10.0,-6.0);
                        r = 1.0*r;
                        for(ulong j = 0; j<Dist_pat.Size(); j++)
                          {
                           if(Dist_pat[j]<=r)
                              f2[j] = 1.0;
                           else
                              f2[j] = 0.0;
                          }
                        f2t = np::bitwiseAnd(f2,targets);
                        f2tn = np::bitwiseAnd(f2,tn);
                        nocls1clst = f2t.Sum();
                        nocls2clst = f2tn.Sum() -1.0;
                       }
                    }
                  if(Dist_test<r)
                    {
                     patternsp = patterns * np::repeat_vector_as_rows_cols(fs,patterns.Cols(),false);
                     testp = test * fs;
                     dist = MathAbs(sqrt((pow(patternsp - np::repeat_vector_as_rows_cols(testp,patternsp.Cols(),false),2.0)).Sum(0)));
                     min1 = dist;
                     np::sort(min1);
                     min_uniq = np::unique(min1);
                     m = -1;
                     no_nereser = 0;
                     while(no_nereser<int(knn))
                       {
                        m+=1;
                        double a1  = min_uniq[m];
                        for(ulong j = 0; j<dist.Size(); j++)
                           NN[j]=(dist[j]<a1)?1.0:0.0;
                        no_nereser = (int)NN.Sum();
                       }
                     bitNN = np::bitwiseAnd(NN,targets);
                     Not = np::bitwiseNot(targets);
                     NoNNC1[i] = bitNN.Sum();
                     bitNN = np::bitwiseAnd(NN,Not);
                     NoNNC2[i] = bitNN.Sum();
                     if(NoNNC2[i]>NoNNC1[i])
                        S[i] = 1.0;
                    }
                 }
              }
           }
         radious[i] = r;
        }
      vector q1 = vector::Zeros(N);
      vector q2 = vector::Zeros(N);
      for(int i = 0; i<N; i++)
        {
         if(NoNNC1[i] > NoNNC2knn[i])
            q1[i] = 1.0;
         if(NoNNC2[i] > NoNNC1knn[i])
            q2[i] = 1.0;
        }

      vector ntargs = np::bitwiseNot(targets);
      vector c1 = np::bitwiseAnd(q1,targets);
      vector c2 = np::bitwiseAnd(q2,ntargs);

      double sc1 = c1.Sum()/NC1;
      double sc2 = c2.Sum()/NC2;

      if(sc1==0.0 && sc2==0.0)
        {
         q1.Fill(0.0);
         q2.Fill(0.0);

         for(int i = 0; i<N; i++)
           {
            if(NoNNC1knn[i] > NoNNC2knn[i])
               q1[i] = 1.0;
            if(NoNNC2knn[i] > NoNNC1knn[i])
               q2[i] = 1.0;

            if(!targets[i])
               ntargs[i] = 1.0;
            else
               ntargs[i] = 0.0;
           }

         c1 = np::bitwiseAnd(q1,targets);
         c2 = np::bitwiseAnd(q2,ntargs);

         sc1 = c1.Sum()/NC1;
         sc2 = c2.Sum()/NC2;
        }

      vector out(2);

      out[0] = sc1;
      out[1] = sc2;

      return out;
     }
public:
   //+------------------------------------------------------------------+
   //|    constructor                                                   |
   //+------------------------------------------------------------------+
                     Clfspy(void)
     {
      loaded = false;
     }
   //+------------------------------------------------------------------+
   //|  destructor                                                      |
   //+------------------------------------------------------------------+
                    ~Clfspy(void)
     {
     }
   //+------------------------------------------------------------------+
   //|  load a LFSpy trained model from file                            |
   //+------------------------------------------------------------------+
   bool              load(const string file_name, bool FILE_IN_COMMON_DIRECTORY = false)
     {
      loaded = false;
      CFileTxt modelFile;
      CJAVal js;
      ResetLastError();
      if(modelFile.Open(file_name,FILE_IN_COMMON_DIRECTORY?FILE_READ|FILE_COMMON:FILE_READ,0)==INVALID_HANDLE)
        {
         Print(__FUNCTION__," failed to open file ",file_name," .Error - ",::GetLastError());
         return false;
        }
      else
        {
         if(!js.Deserialize(modelFile.ReadString()))
           {
            Print("failed to read from ",file_name,".Error -",::GetLastError());
            return false;
           }
         loaded = fromJSON(js);
        }
      return loaded;
     }
   //+------------------------------------------------------------------+
   //|   make a prediction based specific inputs                        |
   //+------------------------------------------------------------------+
   vector            predict(matrix &inputs)
     {
      if(!loaded)
        {
         Print(__FUNCTION__, " No model available, Load a model first before calling this method ");
         return vector::Zeros(1);
        }

      if(inputs.Cols()!=train_data.Rows())
        {
         Print(__FUNCTION__, " input matrix does np::bitwiseNot match with shape of expected model inputs (columns)");
         return vector::Zeros(1);
        }

      matrix testdata = inputs.Transpose();

      matrix probs = classification(testdata);
      vector classes = vector::Zeros(probs.Rows());

      for(ulong i = 0; i<classes.Size(); i++)
         if(probs[i][0] > probs[i][1])
            classes[i] = 1.0;

      return classes;

     }
   //+------------------------------------------------------------------+
   //| get the parameters of the loaded model                           |
   //+------------------------------------------------------------------+
   LFS_PARAMS        getmodelparams(void)
     {
      return model_params;
     }


  };
//+------------------------------------------------------------------+

Há dois métodos principais que os usuários precisam entender nesta classe:

• O método load() recebe como entrada um nome de arquivo, que deve apontar para o modelo LFS exportado.
• O método predict() recebe uma matriz com o número necessário de colunas e retorna um vetor de rótulos de classe, correspondente ao número de linhas da matriz de entrada.
  

Vamos ver como tudo isso funciona na prática. Começamos com o código Python. O arquivo LFSmodelExportDemo.py prepara conjuntos de dados de treinamento (in-sample) e teste (out-of-sample) usando números gerados aleatoriamente. Os dados de teste são salvos como um arquivo CSV. Um modelo LFS é treinado usando os dados de treinamento, então serializado e salvo em formato JSON. Testamos o modelo nos dados fora da amostra e registramos os resultados para que possamos depois compará-los com o mesmo teste feito no MetaTrader 5. O código Python é mostrado a seguir.

# Copyright 2024, MetaQuotes Ltd.
# https://www.mql5.com
# imports
import MetaTrader5 as mt5
import numpy as np
import pandas as pd
from JsonModel import lfspy2json, LocalFeatureSelection, MQL5_COMMON_FOLDER, MQL5_FILES_FOLDER
from os import path
from sklearn.metrics import accuracy_score, classification_report

#initialize MT5 terminal
if not mt5.initialize():
    print("MT5 initialization failed ")
    mt5.shutdown()
    exit() # stop the script if mt5 not initialized
  
#we want to get the path to the MT5 file sandbox
#initialize TerminalInfo instance    
terminal_info = mt5.terminal_info()

#model file name
filename = "lfsmodel.json"

#build the full path
modelfilepath = path.join(terminal_info.data_path,MQL5_FILES_FOLDER,filename)

#number of random numbers to generate
datalen = 1000

#number of features the dataset will have
datavars = 5

#set random number seed
rng_seed = 125
rng = np.random.default_rng(rng_seed)

#generate the numbers
data = rng.uniform(-1.0,1.0,size=datalen)

#shape our dataset
data = data.reshape([datalen//datavars,datavars])

#set up container for class labels
class_labels = np.zeros(shape=data.shape[0],dtype=np.uint8)

#set the class labels
for i in range(data.shape[0]):
    class_labels[i] = 1 if (data[i,1] > 0.0 and data[i,2] > 0.0) or (data[i,1] < 0.0 and data[i,2] < 0.0) else 0

#partition our data
train_size = 100
xtrain = data[:train_size,:]
ytrain = class_labels[:train_size]

#load testing data (out of sample)
test_data = data[train_size:,:]
test_labels = class_labels[train_size:]

#here we prepare the out of sample data for export using pandas
#the data will be exported in a single csv file
colnames = [ f"var_{str(col+1)}" for col in range(test_data.shape[1])]
testdata = pd.DataFrame(test_data,columns=colnames)

#the last column will be the target labels
testdata["c_labels"]=test_labels

#display first 5 samples
print("Out of sample dataframe head \n", testdata.head())
#display last 5 samples
print("Out of sample dataframe tail \n", testdata.tail())

#build the full path of the csv file
testdatafilepath=path.join(terminal_info.data_path,MQL5_FILES_FOLDER,"testdata.csv")

#try save the file
try:
    testdata.to_csv(testdatafilepath)
except Exception as e:
    print(" Error saving iris test data ")
    print(e) 
else:
    print(" test data successfully saved to csv file ")  

#initialize the LFS object
lfs = LocalFeatureSelection(rr_seed=rng_seed,alpha=8,tau=2,n_beta=20,nrrp=2000)

#train the model
lfs.fit(xtrain,ytrain)

#get the inclusion matrix
fstar = lfs.fstar

#add up all ones for each row of the inclusion matrix
bins = fstar.sum(axis=1)

#calculate the percent of times a candidate was selected
percents = 100.0 * bins.astype(np.float64)/np.float64(ytrain.shape[0])
index = np.argsort(percents)[::-1]

#output the results
print("------------------------------> Percent of times selected <------------------------------" )
for i in range(percents.shape[0]):
   print(f" Variable  {colnames[index[i]]}, selected {percents[index[i]]} %")


#conduct out of sample test of trained model
accuracy = lfs.score(test_data,test_labels)
print(f" Out of sample accuracy is {accuracy*100.0} %")


#export the model
try:
    lfspy2json(lfs,modelfilepath)
except Exception as e:
    print(" Error saving lfs model ")
    print(e)
else:
   print("lfs model saved to \n ", modelfilepath)

Em seguida, voltamos o foco para um script do MetaTrader 5, LFSmodelImportDemo.mq5. Aqui, lemos os dados fora da amostra gerados pelo script Python e carregamos o modelo treinado. O conjunto de dados fora da amostra é então testado, e os resultados são comparados com aqueles obtidos no teste em Python. O código MQL5 é apresentado abaixo.

//+------------------------------------------------------------------+
//|                                           LFSmodelImportDemo.mq5 |
//|                                  Copyright 2024, MetaQuotes Ltd. |
//|                                             https://www.mql5.com |
//+------------------------------------------------------------------+
#property copyright "Copyright 2024, MetaQuotes Ltd."
#property link      "https://www.mql5.com"
#property version   "1.00"
#property script_show_inputs
#include<lfspy.mqh>
//script inputs
input string OutOfSampleDataFile = "testdata.csv";
input bool   OutOfSampleDataInCommonFolder = false;
input string LFSModelFileName = "lfsmodel.json";
input bool   LFSModelInCommonFolder = false;
//+------------------------------------------------------------------+
//| Script program start function                                    |
//+------------------------------------------------------------------+
void OnStart()
  {
//---
   matrix testdata = np::readcsv(OutOfSampleDataFile,OutOfSampleDataInCommonFolder);
   
   if(testdata.Rows()<1)
    {
     Print(" failed to read csv file ");
     return;
    }
    
   
   vector testlabels = testdata.Col(testdata.Cols()-1);
   testdata = np::sliceMatrixCols(testdata,1,testdata.Cols()-1);
   
  
   Clfspy lfsmodel;
   
   if(!lfsmodel.load(LFSModelFileName,LFSModelInCommonFolder))
    {
     Print(" failed to load the iris lfs model ");
     return;
    }
    
   vector y_pred = lfsmodel.predict(testdata);
   
   vector check = MathAbs(testlabels-y_pred);
   
   Print("Accuracy is " , (1.0 - (check.Sum()/double(check.Size()))) * 100.0, " %");
  }
//+------------------------------------------------------------------+

Saída da execução do script Python LFSmodelExportDemo.py.

Python  Out of sample dataframe head 
Python         var_1     var_2     var_3     var_4     var_5  c_labels
Python  0  0.337773 -0.210114 -0.706754  0.940513  0.434695         1
Python  1 -0.009701 -0.119561 -0.904122 -0.409922  0.619245         1
Python  2  0.442703  0.295811  0.692888  0.618308  0.682659         1
Python  3  0.694853  0.244405 -0.414633 -0.965176  0.929655         0
Python  4  0.120284  0.247607 -0.477527 -0.993267  0.317743         0
Python  Out of sample dataframe tail 
Python          var_1     var_2     var_3     var_4     var_5  c_labels
Python  95  0.988951  0.559262 -0.959583  0.353533 -0.570316         0
Python  96  0.088504  0.250962 -0.876172  0.309089 -0.158381         0
Python  97 -0.215093 -0.267556  0.634200  0.644492  0.938260         0
Python  98  0.639926  0.526517  0.561968  0.129514  0.089443         1
Python  99 -0.772519 -0.462499  0.085293  0.423162  0.391327         0
Python  test data successfully saved to csv file 

Python  ------------------------------> Percent of times selected <------------------------------
Python   Variable  var_3, selected 87.0 %
Python   Variable  var_2, selected 81.0 %
Python   Variable  var_4, selected 20.0 %
Python   Variable  var_1, selected 19.0 %
Python   Variable  var_5, selected 18.0 %
Python   Out of sample accuracy is 92.0 %
Python  lfs model saved to 
Python    C:\Users\Zwelithini\AppData\Roaming\MetaQuotes\Terminal\FB9A56D617EDDDFE29EE54EBEFFE96C1\MQL5\FILES\lfsmodel.json

Saída da execução do script MQL5 LFSmodelImportDemo.mq5.

LFSmodelImportDemo (BTCUSD,D1)  Acurácia: 92.0 %

Comparando os resultados, podemos ver que as saídas de ambos os programas coincidem, indicando que o método de exportação do modelo funciona como esperado.

Conclusão

A Seleção de Recursos Local oferece uma abordagem inovadora para seleção de variáveis, particularmente adequada para ambientes dinâmicos como os mercados financeiros. Ao identificar recursos localmente relevantes, o LFS supera as limitações dos métodos tradicionais que dependem de um conjunto único e global de recursos. A adaptabilidade do algoritmo a padrões de dados variáveis, sua capacidade de lidar com relações não lineares e de equilibrar objetivos conflitantes o tornam uma ferramenta valiosa para construção de modelos de aprendizado de máquina. Embora o pacote LFSpy forneça uma implementação prática do LFS, há potencial para otimizar ainda mais sua eficiência computacional, especialmente para conjuntos de dados de grande escala. Em conclusão, o LFS representa uma abordagem promissora para tarefas de classificação em domínios caracterizados por dados complexos e em constante evolução.

Nome do Arquivo	Descrição
Mql5/include/np.mqh	Arquivo de inclusão contendo definições genéricas para várias funções utilitárias de matrizes e vetores.
Mql5/include/lfspy.mqh	Arquivo de inclusão contendo a definição da classe Clfspy, que oferece funcionalidade de inferência de modelo LFS em programas MetaTrader 5.
Mql5/scripts/JsonModel.py	Módulo Python local contendo a definição da função que permite exportar o modelo LFS em formato JSON.
Mql5/scripts/LFSdemo.py	Script Python demonstrando como usar a classe LocalFeatureSelection para seleção de recursos usando variáveis aleatórias.
Mql5/scripts/LFSmodelExportDemo.py	Script Python demonstrando como exportar o modelo LFS para uso no MetaTrader 5.
Mql5/scripts/LFSmodelImportDemo.mq5	Script MQL5 que mostra como carregar e utilizar um modelo LFS exportado em um programa do MetaTrader 5.