Reconhecimento de Padrões Usando Dynamic Time Warping em MQL5

Introdução

O reconhecimento de padrões sempre foi uma ferramenta valiosa para os traders. Seja identificando combinações únicas de velas ou desenhando linhas imaginárias em um gráfico, esses padrões se tornaram uma parte integral da análise técnica. Os seres humanos sempre se destacaram em encontrar e reconhecer padrões—tanto que é frequentemente dito que às vezes vemos padrões onde não existem. Portanto, seria vantajoso para nós aplicar técnicas mais objetivas ao identificar padrões potencialmente lucrativos em séries temporais financeiras. Neste artigo, discutimos a aplicação do Dynamic Time Warping (DTW) como uma técnica objetiva para encontrar padrões únicos nos dados de preços. Vamos explorar suas origens, como funciona e sua aplicação na análise de séries temporais financeiras. Além disso, apresentaremos a implementação do algoritmo em MQL5 puro e demonstraremos seu uso por meio de um exemplo prático.

Dynamic time warping

Dynamic time warping é um algoritmo sofisticado projetado para medir a semelhança entre duas sequências de dados que evoluem ao longo do tempo, mesmo quando suas velocidades ou ritmos variam Ao contrário dos métodos tradicionais, que exigem um alinhamento rígido entre os pontos de dados, o DTW oferece uma abordagem mais flexível, permitindo a distorção ou expansão do tempo para encontrar a correspondência ideal entre as sequências. Imagine duas pessoas caminhando por uma floresta em caminhos diferentes. Ambas começam no mesmo lugar e terminam no mesmo lugar, mas uma pode andar mais rápido do que a outra e fazer paradas arbitrárias por qualquer motivo. O DTW ajuda a descobrir a melhor maneira de combinar os passos de ambos, mesmo que tenham seguido caminhos diferentes. O DTW pode efetivamente lidar com diferenças de velocidade de caminhada, aceleração ou desaceleração, fornecendo uma medida de semelhança. Essa versatilidade o torna aplicável a uma ampla variedade de tipos de dados, incluindo áudio, vídeo e gráficos. Qualquer dado que possa ser transformado em um formato sequencial é um candidato potencial para a análise DTW.

O DTW foi inicialmente desenvolvido para reconhecimento de fala por Vintsyuk em 1968 e posteriormente aprimorado por pesquisadores como Sakoe e Chiba em 1978. O método ganhou popularidade em diversos campos devido à sua capacidade de comparar sequências de diferentes comprimentos ao distorcer a dimensão temporal para alinhar padrões semelhantes. O DTW desde então encontrou aplicações em áreas diversas, como bioinformática e análise de marcha. Os mercados financeiros são caracterizados por dados de séries temporais não lineares e não estacionários. Medidas tradicionais de distância, como a distância euclidiana, podem falhar ao capturar as complexidades e distorções desses dados. O DTW, no entanto, se destaca ao identificar semelhanças entre séries temporais com distorções temporais, tornando-se uma ferramenta adequada para analisar os mercados financeiros. Ao alinhar sequências com base em sua forma, e não no seu alinhamento temporal, o DTW pode descobrir padrões únicos nos dados financeiros.

Como funciona

Ao aplicar o algoritmo DTW, o objetivo é determinar se uma sequência candidata é semelhante a uma sequência de referência predefinida. A métrica final produzida pelo algoritmo indica a semelhança entre a sequência candidata e a sequência de referência—quanto menor esse valor, mais semelhantes as sequências são. Se as sequências forem iguais, esse valor seria 0. Para encontrar o alinhamento ideal entre uma sequência candidata e um conjunto de dados de referência, o algoritmo DTW segue princípios específicos. Cada ponto na sequência candidata deve corresponder a pelo menos um ponto de dados na sequência de referência, e vice-versa. O início de uma sequência deve alinhar-se com o início da outra, e o final de uma deve alinhar-se com o final da outra. Além disso, ao percorrer as sequências, os pontos correspondentes devem avançar apenas para frente. Isso garante que nenhum ponto em uma sequência possa alinhar-se com um ponto anterior na outra sequência, impedindo qualquer possibilidade de alinhamento com pontos anteriores.

O processo começa pela construção de uma matriz de distâncias que captura as distâncias par a par entre os elementos das duas sequências. Cada elemento desta matriz representa a distância entre um ponto da primeira sequência e um ponto correspondente da segunda sequência. Neste estágio, qualquer uma das medidas tradicionais de distância espacial pode ser usada. Medidas de distância espacial são métodos matemáticos usados para quantificar a distância ou dissimilaridade entre pontos de dados dentro de um espaço dado. A escolha da medida de distância depende das características específicas dos dados e da tarefa em questão. A tabela abaixo lista as medidas de distância espacial mais comuns e uma breve descrição de cada uma.

Métrica de Distância	Descrição
Distância Euclidiana	A distância euclidiana é a distância reta entre dois pontos no espaço euclidiano. É a medida de distância mais intuitiva e amplamente utilizada.
Distância de Manhattan	A distância de Manhattan, também conhecida como distância taxicab ou distância de bloco de cidade, mede a distância entre dois pontos somando as diferenças absolutas de suas coordenadas.
Distância de Minkowski	A distância de Minkowski é uma forma generalizada tanto das distâncias euclidiana quanto de Manhattan. Inclui um parâmetro que pode ser ajustado para alternar entre diferentes medidas de distância.
Distância de Chebyshev	A distância de Chebyshev, também conhecida como distância máxima ou distância de tabuleiro de xadrez, mede a diferença mais significativa entre as coordenadas de um par de pontos.
Semelhança Cosseno	A semelhança cosseno mede o cosseno do ângulo entre dois vetores não nulos, representando sua semelhança direcional em vez de magnitude.

A escolha da medida de distância espacial depende da natureza dos dados e dos requisitos específicos da tarefa. Compreender as diferenças e aplicações dessas medidas ajuda a selecionar a mais apropriada para uma análise significativa.

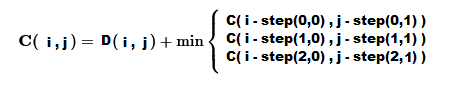
No próximo passo, a matriz de distâncias é usada para calcular a matriz de custo cumulativo, onde cada elemento representa o custo mínimo de alinhar as sequências. Este processo de alinhamento envolve transformar a sequência candidata de modo que ela se assemelhe mais à sequência de referência. A matriz de custo cumulativo quantifica o quanto os pontos individuais na sequência candidata precisam ser alterados para corresponder melhor aos valores de referência. Um custo maior indica uma transformação mais significativa, o que significa maior dissimilaridade entre as sequências. Esses valores da matriz de custo cumulativo são usados para determinar o caminho de distorção ótimo, que representa a sequência de alinhamentos que mapeiam uma série temporal para outra enquanto minimizam a distância entre elas. Essencialmente, o caminho de distorção ilustra como partes de uma sequência são esticadas ou comprimidas para se alinhar da melhor forma possível com outra sequência.

Para encontrar o caminho de distorção, imaginamos as sequências colocadas em uma grade, com uma sequência ao longo do eixo x e a outra ao longo do eixo y. Cada ponto dessa grade representa uma possível correspondência entre um elemento da primeira sequência e um elemento da segunda sequência. O caminho de distorção é o trajeto por essa grade que resulta no melhor alinhamento entre as duas sequências. O caminho começa no canto inferior esquerdo da grade, correspondente aos primeiros elementos de ambas as sequências, e termina no canto superior direito, correspondente aos últimos elementos de ambas as sequências. À medida que o caminho avança, ele pode se mover em três direções: diagonalmente, o que corresponde a elementos de ambas as sequências; horizontalmente, o que repete um elemento da primeira sequência; ou verticalmente, o que repete um elemento da segunda sequência. Esse movimento garante que o processo de alinhamento sempre avance no tempo e não pule elementos nas sequências.

O caminho de distorção é escolhido para minimizar a distância ou custo cumulativo entre os elementos alinhados das duas sequências. Para alcançar isso, os valores da matriz de distâncias são sobrepostos na grade que será usada para alinhar os pontos. O custo em cada ponto da grade é calculado adicionando a métrica de distância correspondente ao valor mínimo das distâncias cumulativas adjacentes dos pontos anteriores, seguindo as três direções possíveis (diagonal, horizontal ou vertical) que podem ser tomadas ao avançar no tempo. Como cada ponto da grade está associado à métrica de distância dos valores correspondentes das sequências, o valor mínimo representa a operação necessária para transformar a sequência candidata para corresponder à sequência de referência Se a menor distância cumulativa estiver diagonalmente ao ponto atual, ela representa uma operação de correspondência. Se a menor distância cumulativa de pontos anteriores for horizontal ao ponto atual, isso indica uma operação de inserção, onde um valor da sequência de referência é efetivamente inserido na sequência candidata. Por outro lado, se a menor distância cumulativa for vertical ao ponto atual, isso significa uma operação de exclusão, onde um valor da sequência candidata é removido. A escolha dos valores de distância cumulativa anterior considerados para encontrar o mínimo é governada por um padrão de etapas específico.

Padrões de etapas determinam os movimentos ou transições permitidos entre pontos nas sequências durante o alinhamento. Eles especificam o número de pontos em qualquer uma das direções válidas (diagonal, horizontal, vertical) consideradas ao calcular a distância cumulativa mínima. A escolha do padrão de etapas influencia significativamente o processo de alinhamento e o cálculo geral da distância. Existem vários padrões de etapas, cada um adaptado para aplicações específicas. Os profissionais também podem criar padrões de etapas personalizados, desde que sigam os princípios de movimento para frente e continuidade. Neste texto, nos concentraremos nos padrões de etapas mais comuns e genéricos, que se mostraram eficazes em diferentes domínios. Para aqueles interessados em explorar outros padrões de etapas, os artigos de Sakoe-Chiba, Rabiner-Juang e Rabiner-Myers oferecem informações detalhadas.

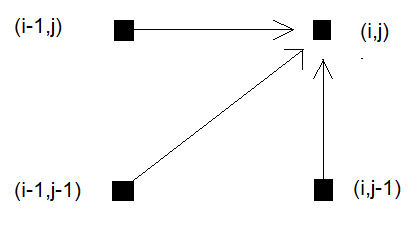
O padrão de etapas mais comumente aplicado é o padrão de etapas padrão, também conhecido como padrão simétrico ou clássico de etapas. Sua principal vantagem é que ele garante que ambas as séries temporais sejam completamente percorridas. Este padrão considera apenas os valores imediatos acima, à direita e diagonal ao ponto atual, permitindo movimentos de uma única etapa diagonal, horizontal e vertical na grade.

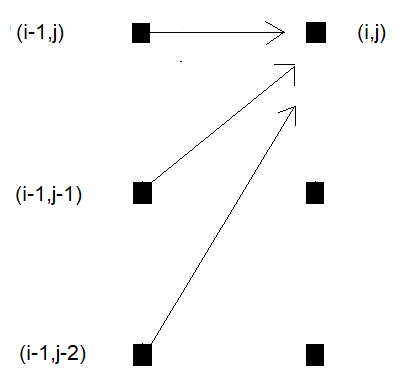
Outro padrão de etapas popular é o padrão clássico assimétrico. Semelhante ao padrão de etapas padrão, ele define transições em três direções, mas introduz um viés em direção a uma sequência. Este padrão permite que o algoritmo se mova diagonalmente, mas, se um ponto for pulado, ele favorece o avanço de uma sequência mais do que a outra. Ele é frequentemente usado juntamente com restrições adicionais que limitam os movimentos do algoritmo na grade. No caso do padrão de etapas assimétrico, uma restrição de inclinação adicional é aplicada, restringindo a acentuação ou suavidade do caminho de distorção. Essa restrição é útil quando espera-se que as sequências sejam semelhantes em comprimento e deslocamento, pois impede que uma sequência seja excessivamente esticada ou comprimida em relação à outra.

Restrições adicionais podem ser aplicadas para evitar alinhamentos que sejam tecnicamente perfeitos, mas sem sentido, o que pode resultar em um ajuste excessivo dos dados. Essas restrições garantem que o alinhamento faça sentido lógico dentro do contexto dos dados analisados, evitando o estiramento ou compressão excessivos das sequências. Essas restrições são conhecidas como restrições globais e aumentam a eficácia e a interpretabilidade do algoritmo DTW em aplicações práticas. Duas restrições globais comuns são a banda Sakoe-Chiba e o paralelogramo Itakura.

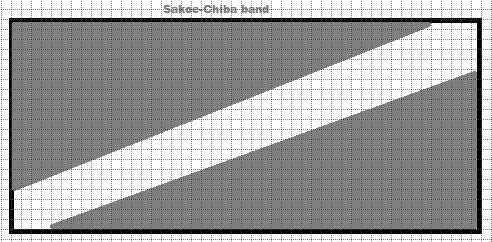
A banda Sakoe-Chiba restringe o caminho de distorção para permanecer dentro de uma faixa fixa ao redor da diagonal da matriz de alinhamento. Isso impede que o alinhamento se desvie muito do tempo ou deslocamento original, o que é útil em tarefas onde pequenas diferenças de tempo são esperadas, mas grandes desvios não.

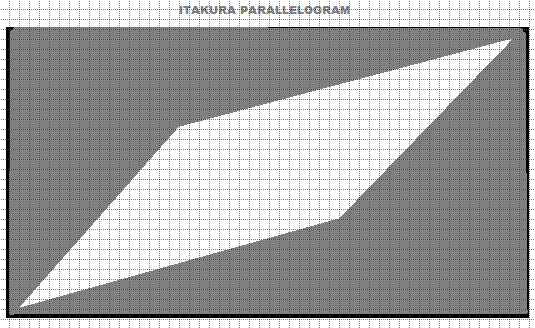
A restrição do paralelogramo Itakura define uma região em forma de paralelogramo dentro da qual o caminho de distorção deve permanecer. É mais estreito nas extremidades e mais largo no meio, o que é particularmente útil quando se espera que as sequências se alinhem mais estreitamente no início e no fim, mas permitindo alguma flexibilidade no meio. Restrições globais são essenciais para o DTW, pois controlam o processo de distorção e garantem que o alinhamento resultante seja relevante para a tarefa específica. É importante selecionar as restrições mais apropriadas com base nas características dos conjuntos de dados e nos objetivos da análise.

Uma vez que a matriz de custo cumulativo é completada, ela é usada para determinar o caminho de distorção ótimo. O algoritmo traça o caminho de volta desde o último elemento da matriz de custo cumulativo até o primeiro, identificando o caminho que minimiza o custo total de alinhamento. Este caminho representa o melhor alinhamento entre as sequências. O valor final na matriz de custo cumulativo fornece a pontuação de distância geral, que também é usada para calcular a pontuação de distância normalizada. O caminho de distorção listará os índices pareados que representam pontos alinhados em ambas as sequências. Para avaliar o procedimento de alinhamento, é comum plotar o caminho de distorção ótimo. Um resultado satisfatório deve gerar um gráfico aproximadamente diagonal. Este gráfico diagonal indica que as sequências estão bem alinhadas, com uma linha diagonal perfeitamente reta correspondendo a duas sequências idênticas. Na próxima seção, discutiremos uma implementação nativa do MQL5 do dynamic time warping.

Implementação em MQL5

A implementação do DTW em MQL5 é apresentada no arquivo de inclusão dtw.mqh. Ele não oferece uma cobertura completa ou extensiva de todos os aspectos do dynamic time warping. Mais adiante, veremos uma implementação em Python do DTW que oferece muito mais recursos. O objetivo ao criar esta biblioteca é fornecer a funcionalidade básica para calcular a pontuação de distância. A biblioteca é um fork parcial do módulo dtw-python.

O código começa definindo enumerações para padrões de etapas, várias medidas de distância e restrições globais.

//+------------------------------------------------------------------+
//|  step patterns                                                   |
//+------------------------------------------------------------------+
enum ENUM_STEP_PATTERN
  {
   STEP_SYMM1=0,//symmetric1
   STEP_SYMM2,//symmetric2
   STEP_ASYMM//asymmetric
  };

ENUM_STEP_PATTERN: Define um conjunto de enumerações que restringem os padrões de transição permitidos durante a fase de busca do caminho do algoritmo DTW. Esses padrões orientam o processo de distorção e influenciam os alinhamentos permitidos entre as séries temporais.

//+------------------------------------------------------------------+
//|  distance metric                                                 |
//+------------------------------------------------------------------+
enum ENUM_DIST_METRIC
  {
   DIST_EUCLIDEAN=0,//euclidean
   DIST_CITYBLOCK,//city block
   DIST_COSINE,//cosine
   DIST_CORRELATION,//correlation
   DIST_CHEBYSHEV,//chebyshev
   DIST_SQEUCLIDEAN//squared euclidean
  };

ENUM_DIST_METRIC: Fornece uma coleção de enumerações correspondentes às métricas de distância suportadas. Essas métricas quantificam a dissimilaridade entre os pontos de dados nas séries temporais, com opções como distância euclidiana, distância de City Block, entre outras.

//+------------------------------------------------------------------+
//|   window function                                                |
//+------------------------------------------------------------------+
enum ENUM_GLOBAL_CONSTRAINT
  {
   CONSTRAINT_NONE=0,// no constrains applied
   CONSTRAINT_SAKOECHIBA,// sakoe chiba
   CONSTRAINT_SLATEDBAND,// slated band
   CONSTRAINT_ITAKURA// itakura
  };

ENUM_GLOBAL_CONSTRAINT: Engloba diferentes restrições globais que impõem limites durante a busca do caminho. Essas restrições podem influenciar a flexibilidade da distorção e, potencialmente, melhorar a precisão do alinhamento.

//+------------------------------------------------------------------+
//| lists the transitions allowed while searching                    |
//|for the minimum-distance path                                     |
//+------------------------------------------------------------------+
class CStepPattern
  {
private:
   matrix            m_mx,m_stepsMatrix;
   ENUM_HINT         m_stephint;
public:
                     CStepPattern(matrix &mx, matrix &stepmatrix, ENUM_HINT hint=HINT_NA)
     {
      m_mx = mx;
      m_stepsMatrix = stepmatrix;
      m_stephint = hint;
     }
                    ~CStepPattern(void)
     {

     }
   matrix            getStepMatrix(void)
     {
      return m_stepsMatrix;
     }
   ulong             getNRows(void)
     {
      return m_mx.Rows();
     }
   int               getNPatterns(void)
     {
      vector vec = m_mx.Col(0);
      return (int(vec.Max()));
     }

   CStepPattern*     T(void)
     {
      ulong cols[] = {0, 2, 1, 3};

      matrix cpy = np::selectMatrixCols(m_mx,cols);
      ENUM_HINT hint = m_stephint;

      if(m_stephint == HINT_N)
         hint = HINT_M;
      else
         if(m_stephint == HINT_M)
            hint = HINT_N;

      CStepPattern* out = new CStepPattern(cpy,m_stepsMatrix,hint);

      return out;
     }

   matrix            extractPattern(vector &sn)
     {
      vector col  =  m_mx.Col(0);
      matrix out = matrix::Ones(1,1);
      for(ulong i = 0; i<m_mx.Rows(); i++)
        {
         for(ulong j = 0; j<col.Size(); j++)
           {
            if(col[j] == sn[j])
              {
               if(!out.Resize(out.Rows()+1,m_mx.Cols()-1,100))
                 {
                  Print(__FUNCTION__, " error ", GetLastError());
                  return matrix::Zeros(1,1);
                 }
               vector v = m_mx.Row(j);
               vector vv = np::sliceVector(v,1);
               if(!out.Row(vv,out.Rows()-1))
                 {
                  Print(__FUNCTION__, " error ", GetLastError());
                  return matrix::Zeros(1,1);
                 }
              }
           }
        }

      if(!np::reverseMatrixRows(out))
        {
         Print(__FUNCTION__, " Reverse Matrix failure ");
         return matrix::Zeros(1,1);
        }
      return out;
     }

   matrix            mkDIrDeltas(void)
     {
      matrix out = matrix::Zeros(1,1);
      vector col = m_mx.Col(3);
      for(ulong i = 0; i<m_mx.Rows(); i++)
        {
         for(ulong j = 0; j<col.Size(); j++)
           {
            if(col[j] == -1.0)
              {
               if(!out.Resize(out.Rows()+1,m_mx.Cols(),100))
                 {
                  Print(__FUNCTION__, " error ", GetLastError());
                  return matrix::Zeros(1,1);
                 }
               vector v = m_mx.Row(j);
               if(!out.Row(v,out.Rows()-1))
                 {
                  Print(__FUNCTION__, " error ", GetLastError());
                  return matrix::Zeros(1,1);
                 }
              }
           }
        }

      return np::sliceMatrixCols(out,1,3);
     }

   matrix             getP(void)
     {
      ulong sel[] = {0, 2, 1, 3};
      matrix s = np::selectMatrixCols(m_mx,sel);
      return s;
     }

   matrix            getMx(void)
     {
      return m_mx;
     }
  };

CStepPattern é uma classe projetada para lidar com diferentes padrões de etapas, gerenciando matrizes que definem as transições e operações permitidas. Ela fornece métodos para extrair padrões com base em sequências específicas e manipular matrizes para deltas direcionais, essenciais para os cálculos do DTW.

//+------------------------------------------------------------------+
//| Global constraints                                               |
//+------------------------------------------------------------------+
class CConstraint
  {
public:
                     CConstraint(void)
     {

     }
                    ~CConstraint(void)
     {

     }

   static matrix       noConstraint(ulong iw,ulong jw)
     {
      matrix mats[];

      np::indices(iw,jw,mats);

      for(ulong i = 0; i<mats[0].Rows(); i++)
        {
         for(ulong j = 0; j<mats[0].Cols(); j++)
           {
            long value = long(mats[0][i][j]);
            mats[0][i][j] = (double)(value|1);
            if(mats[0][i][j]==0.0)
               mats[0][i][j] = double("inf");
           }
        }

      return mats[0];
     }

   static matrix       sakoeChibaConstraint(ulong iw,ulong jw, ulong qsize, ulong refsize, ulong winsize)
     {
      matrix mats[];

      np::indices(iw,jw,mats);

      matrix abs = MathAbs(mats[1]-mats[0]);

      for(ulong i = 0; i<abs.Rows(); i++)
        {
         for(ulong j = 0; j<abs.Cols(); j++)
           {
            if(ulong(abs[i][j])<=winsize)
               abs[i][j] = (double)(1);
            else
               abs[i][j] = double("inf");
           }
        }

      return abs;
     }

   static matrix       itakuraConstraint(ulong iw,ulong jw, ulong qsize, ulong refsize)
     {
      matrix mats[];

      np::indices(iw,jw,mats);

      long a,b,c,d;

      for(ulong i = 0, k = 0; i<mats[0].Rows() && k<mats[1].Rows(); i++,k++)
        {
         for(ulong j = 0; j<mats[0].Cols(); j++)
           {
            a = long(mats[1][k][j]) < (2*long(mats[0][i][j]))?1:0;
            b = long(mats[0][i][j]) <=(2*long(mats[1][k][j]))?1:0;
            c = long(mats[0][i][j]) >=(long(qsize)-1-2*(long(refsize)-long(mats[1][k][j])))?1:0;
            d = long(mats[1][k][j]) > (long(refsize)-1-2*(long(qsize)-long(mats[0][i][j])))?1:0;
            mats[0][i][j] = double(ulong(a&b&c&d));
            if(mats[0][i][j]==0.0)
               mats[0][i][j] = double("inf");
           }
        }

      return mats[0];
     }

   static matrix       slantedBandConstraint(ulong iw,ulong jw, ulong qsize, ulong refsize,ulong winsize)
     {

      matrix mats[];

      np::indices(iw,jw,mats);

      matrix  diagj = (mats[0]*refsize/qsize);

      matrix abs = MathAbs(mats[1]-diagj);


      for(ulong i = 0; i<abs.Rows(); i++)
        {
         for(ulong j = 0; j<abs.Cols(); j++)
           {
            if(ulong(abs[i][j])<=winsize)
               abs[i][j] = (double)(1);
            else
               abs[i][j] = double("inf");
           }
        }

      return abs;

     }

  };

A classe CConstraint inclui métodos estáticos para efetuar diferentes tipos de restrições, como Sakoe-Chiba, Itakura e Slanted Band. Essas restrições ajudam a limitar o alinhamento do DTW para melhorar a eficiência computacional e a relevância, limitando o espaço de busca com base em critérios predefinidos.

• O método noConstraint(): Gera uma matriz preenchida com uns, significando a ausência de qualquer restrição.

• O método sakoeChibaConstraint(): Impõe uma restrição de Sakoe-Chiba com base no tamanho da janela e nas extensões das séries temporais.

• O método itakuraWindow(): Aplica uma restrição de Itakura usando os comprimentos das séries temporais.

• O método slantedBandConstraint(): Implementa uma restrição de Slanted Band com base no tamanho da janela e nos comprimentos das séries temporais.
  

A classe Cdtw é a classe central responsável pelos cálculos do DTW.

   //+------------------------------------------------------------------+
   //|     main interface method for dtw                                |
   //+------------------------------------------------------------------+

   bool              dtw(matrix&x, matrix&y, ENUM_DIST_METRIC dist_method,ENUM_STEP_PATTERN step_pattern=STEP_SYMM2, ENUM_GLOBAL_CONSTRAINT win_type=CONSTRAINT_NONE,ulong winsize=0)
     {
      if(y.Cols()!=x.Cols())
        {
         Print(__FUNCTION__, " invalid input parameters, size containers donot match. ");
         return false;
        }

      if(CheckPointer(m_stepPattern)==POINTER_DYNAMIC)
         delete m_stepPattern;

      switch(step_pattern)
        {
         case STEP_SYMM1:
            m_stepPattern = new CStepPattern(_symmetric1,Symmetric);
            m_stephint = HINT_NA;
            break;

         case STEP_SYMM2:
            m_stepPattern = new CStepPattern(_symmetric2,Symmetric,HINT_NM);
            m_stephint = HINT_NM;
            break;

         case STEP_ASYMM:
            m_stepPattern = new CStepPattern(_asymmetric,Asymmetric,HINT_N);
            m_stephint = HINT_N;
            break;
        }

      if(CheckPointer(m_stepPattern)==POINTER_INVALID)
        {
         Print(__FUNCTION__," failed step pointer initialization ", GetLastError());
         return false;
        }

      matrix stepsMatrix = m_stepPattern.getStepMatrix();
      m_query = x;
      m_qlen = x.Rows();
      m_ref = y;
      m_reflen = y.Rows();
      m_distMetric = dist_method;
      m_winMethod = win_type;
      m_winsize = winsize;

      if(y.Rows())
        {
         if(!m_distance.Resize(m_qlen,m_reflen))
           {
            Print(__FUNCTION__," resize error ", GetLastError());
            return false;
           }
         for(ulong i = 0; i<m_qlen; i++)
            for(ulong j =0; j<m_reflen; j++)
               m_distance[i][j]=dist(m_query.Row(i),m_ref.Row(j));
        }
      else
         m_distance = m_query;

      ulong n,m;
      n=m_distance.Rows();
      m=m_distance.Cols();
      matrix wm;
      if(m_winMethod == CONSTRAINT_NONE)
         wm = matrix::Ones(m_distance.Rows(), m_distance.Cols());
      else
        {
         switch(m_winMethod)
           {
            case CONSTRAINT_ITAKURA:
               wm = CConstraint::itakuraConstraint(n,m,m_qlen,m_reflen);
               break;
            case CONSTRAINT_SAKOECHIBA:
               wm = CConstraint::sakoeChibaConstraint(n,m,m_qlen,m_reflen,m_winsize);
               break;
            case CONSTRAINT_SLATEDBAND:
               wm = CConstraint::slantedBandConstraint(n,m,m_qlen,m_reflen,m_winsize);
               break;
            default:
               wm = CConstraint::noConstraint(n,m);
               break;
           }
        }

      if(m_winMethod!=CONSTRAINT_NONE)
        {
         for(ulong i = 0; i<wm.Rows(); i++)
            for(ulong j = 0; j<wm.Cols(); j++)
               if((i+j)>0 && wm[i][j] != 1.0)
                  m_distance[i][j] = wm[i][j];
        }


      m_costMatrix = matrix::Zeros(m_distance.Rows()+ulong(stepsMatrix.Col(0).Max()),m_distance.Cols()+ulong(stepsMatrix.Col(1).Max()));
      m_costMatrix.Fill(double("inf"));
      m_costMatrix[ulong(stepsMatrix.Col(0).Max())][ulong(stepsMatrix.Col(1).Max())] = m_distance[0][0];

      m_dirMatrix = matrix::Zeros(m_costMatrix.Rows(),m_costMatrix.Cols());
      m_dirMatrix.Fill(double(INT_MIN));
      for(ulong i = 0; i<m_dirMatrix.Cols(); i++)
         m_dirMatrix[0][i] = double(1);
      for(ulong i = 0; i<m_dirMatrix.Rows(); i++)
         m_dirMatrix[i][0] = double(2);

      if(!calCM(m_distance,stepsMatrix,m_costMatrix,m_dirMatrix))
        {
         Print(__FUNCTION__, " computeCM() failed ");
         return false;
        }

      m_jmin = m_costMatrix.Cols() - 1;

      return true;
     }

Ela fornece o método dtw() como a função principal para executar o DTW. Observe que o método é sobrecarregado para atender tanto séries temporais univariadas (vetores) quanto multivariadas (matrizes). Ele recebe duas séries temporais (representadas como matrizes ou vetores), a métrica de distância, o padrão de etapas, uma restrição global e o tamanho da janela como argumentos de entrada. Ao ser invocado, o método começa executando várias verificações sobre a validade dos dados de entrada e o padrão de etapas escolhido. Isso é seguido pelo cálculo da matriz de distâncias com base na métrica de distância selecionada. Se uma restrição global for especificada, as matrizes de custo e direção usadas durante o algoritmo DTW são preparadas conforme necessário. A função calCM() é então chamada para calcular a matriz de custo acumulado. Finalmente, a função dtw() retorna um valor booleano indicando sucesso ou falha. 

   //+------------------------------------------------------------------+
   //|    Get the optimal path: corresponding points from both series   |
   //+------------------------------------------------------------------+

   matrix            warpPath(bool openEnd=false)
     {
      matrix stmatrix = m_stepPattern.getStepMatrix();
      return backtrack(m_dirMatrix,stmatrix,openEnd,openEnd?long(m_costMatrix.Row(m_costMatrix.Rows()-1).ArgMin()):-1);
     }

O método warpPath() recupera o caminho ótimo (pontos correspondentes) identificado a partir de ambas as séries temporais com base em um argumento opcional 'openEnd' que controla a terminação do caminho (aberto ou fechado).

   //+------------------------------------------------------------------+
   //|     Get the accumulated cost matrix                              |
   //+------------------------------------------------------------------+

   matrix            costMatrix(void)
     {
      return m_costMatrix;
     }

O método costMatrix() fornece acesso à matriz de custo acumulado, uma saída chave do algoritmo DTW.

   //+------------------------------------------------------------------+
   //|       Get the cost matrix                                        |
   //+------------------------------------------------------------------+

   matrix            localCostMatrix(void)
     {
      return m_distance;
     }

O método localCostMatrix() retorna a matriz de distâncias local, representando as distâncias entre os pontos de dados nas séries temporais.

   //+------------------------------------------------------------------+
   //|        Get the direction matrix                                  |
   //+------------------------------------------------------------------+

   matrix            directionMatrix(void)
     {
      return m_dirMatrix;
     }

O método directionMatrix() concede acesso à matriz de direção, que desempenha um papel importante na orientação do processo de busca do caminho durante o DTW.

   //+------------------------------------------------------------------+
   //|  private method implementing accumulated cost calculation        |
   //+------------------------------------------------------------------+

   bool              calCM(matrix &distMatrix,matrix &stepMatrix,matrix &costMatrix,matrix &dirMatrix)
     {
      ulong max0,max1;
      max0 = ulong(stepMatrix.Col(0).Max());
      max1 = ulong(stepMatrix.Col(1).Max());
      double curCost,curd;

      for(ulong i = max0; i<costMatrix.Rows(); i++)
        {
         for(ulong j = max1; j<costMatrix.Cols(); j++)
           {
            for(ulong k = 0; k<stepMatrix.Rows(); k++)
              {
               curd = costMatrix[i-ulong(stepMatrix[k][0])][j-ulong(stepMatrix[k][1])];
               curCost = curd + distMatrix[i-max0][j-max1];
               if(curCost<costMatrix[i][j])
                 {
                  costMatrix[i][j] = curCost;
                  dirMatrix[i][j] = double(k);
                 }
              }
           }
        }
      costMatrix = np::sliceMatrix(costMatrix,max0,END,1,max1);
      dirMatrix  = np::sliceMatrix(dirMatrix,max0,END,1,max1);
      return true;

     }

O método privado calCM() calcula a matriz de custo acumulado, um componente central do algoritmo DTW. Ele utiliza a matriz de distâncias, o padrão de etapas, a matriz de custos e a matriz de direção como entrada.

   //+------------------------------------------------------------------+
   //|  distance metric calculation                                     |
   //+------------------------------------------------------------------+


   double            dist(vector &u,vector &v)
     {
      switch(m_distMetric)
        {
         case DIST_EUCLIDEAN:
            return euclidean(u,v);
         case DIST_CITYBLOCK:
            return cityblock(u,v);
         case DIST_CHEBYSHEV:
            return chebyshev(u,v);
         case DIST_CORRELATION:
            return correlation(u,v);
         case DIST_COSINE:
            return cosine(u,v);
         case DIST_SQEUCLIDEAN:
            return sqeuclidean(u,v);
         default:
            Print(__FUNCTION__, " invalid parameter ");
            return EMPTY_VALUE;
        }
     }

A função privada dist() calcula a distância entre dois pontos de dados com base em uma métrica de distância escolhida.

Testando a classe Cdtw

Nesta seção, demonstraremos as capacidades da classe Cdtw comparando sua saída com a produzida por uma implementação do DTW baseada em Python. O módulo, dtw-python, é uma das várias implementações do DTW em Python. Executaremos um script simples em Python e verificaremos se os resultados podem ser reproduzidos pela nossa implementação em MQL5. Começaremos listando o script Python.

import numpy as np
import matplotlib.pyplot as plt
import dtw

len = 10
add_noise = True
noise = np.random.uniform(size=len)if add_noise else np.zeros((len,))
arx = np.linspace(start = 1, stop = 6.28,num = len)
query = np.sin(arx) + noise
ref = np.cos(arx)

alignment =  dtw.dtw(query,ref,dist_method='cosine',step_pattern='symmetric2', window_type=None,keep_internals=True)
print( f'Accumulated Cost Matrix is {alignment.costMatrix}')
print(f'Distance is {alignment.distance}, \n normalize distance is {alignment.normalizedDistance}')
print(f'Warp Path is {alignment.index1[:]}:{alignment.index2[:]}')
plt.plot(alignment.index1,alignment.index2)
plt.show()

Este script demonstra como alinhar duas séries temporais usando o algoritmo DTW e visualizar o alinhamento. O código começa importando as bibliotecas necessárias: 'numpy' para operações numéricas, 'matplotlib.pyplot' para gráficos e 'dtw' para implementar o algoritmo DTW. O comprimento da série temporal é definido como 10, e um array arx de 10 valores igualmente espaçados entre 1 e 6.28 é criado. Uma série temporal 'query' é gerada tirando o seno de 'arx' e adicionando um ruído aleatório, enquanto a série temporal de referência (ref) é gerada tirando o cosseno de 'arx'. O alinhamento DTW é então realizado entre as séries 'query' e 'ref'. A distância entre as séries temporais é medida usando o método de distância cosseno, e um padrão de passos simétrico é aplicado ao caminho de distorção. Nenhuma restrição de janela é usada, e detalhes internos como a matriz de custos e o caminho de distorção são retidos.

O código então imprime a matriz de custos acumulada, a distância total do alinhamento, a distância normalizada e os índices do caminho de distorção entre as duas séries. Finalmente, o caminho de distorção é visualizado traçando os índices de alinhamento, mostrando como os índices das duas séries temporais se alinham, e o gráfico é exibido. Essa abordagem permite uma comparação detalhada entre duas séries temporais que podem estar fora de fase ou ter comprimentos diferentes, permitindo observar como uma série se distorce para se alinhar com a outra.

O equivalente MQL5 ao código Python descrito acima é dado abaixo.

//+------------------------------------------------------------------+
//|                                                      dtwTest.mq5 |
//|                                  Copyright 2024, MetaQuotes Ltd. |
//|                                             https://www.mql5.com |
//+------------------------------------------------------------------+
#property copyright "Copyright 2024, MetaQuotes Ltd."
#property link      "https://www.mql5.com"
#property version   "1.00"
#property script_show_inputs
#include<Math\Stat\Uniform.mqh>
#include<dtw.mqh>
//---
input ulong series_len = 10;
input bool  AddRandomNoise = false;
input ENUM_DIST_METRIC AppliedDistanceMetric = DIST_EUCLIDEAN;
input ENUM_STEP_PATTERN AppliedStepPattern = STEP_SYMM2;
input ENUM_GLOBAL_CONSTRAINT AppliedGlobalConstraint = CONSTRAINT_NONE;
input ulong GlobalConstraintWinSize = 0;
input bool WarpPathConstraint = false;
//+------------------------------------------------------------------+
//| Script program start function                                    |
//+------------------------------------------------------------------+
void OnStart()
  {
   if(series_len<10)
     {
      Alert(" Invalid input for series_len parameter. Should be >=10 ");
      return;
     }
//---
   vector arg = np::linspace(1.0,6.28,series_len);
   vector noise = vector::Zeros(series_len);

   if(AddRandomNoise)
     {
      double array[];
      if(!MathRandomUniform(0.0,1.0,int(series_len),array))
        {
         Print(__LINE__, " MathRandomUniform() failed ", GetLastError());
         return;
        }

      if(!noise.Assign(array))
        {
         Print(__LINE__, " vector assignment failure ", GetLastError());
         return;
        }
     }

   vector q = sin(arg) + noise; // candidate sequence
   vector rf =  cos(arg);       // reference sequence

   Cdtw cdtw;

   cdtw.dtw(q,rf,AppliedDistanceMetric,AppliedStepPattern,AppliedGlobalConstraint,GlobalConstraintWinSize);

   Print(" local cm ", cdtw.localCostMatrix());
   Print(" final cm ", cdtw.costMatrix());
   Print(" direction matrix \n", cdtw.directionMatrix());
   matrix path = cdtw.warpPath();
   Print(" Warp path \n", cdtw.warpPath());
   Print(" Distance metric ", cdtw.distance());
   Print(" Normalized Distance metric ", cdtw.normalizedDistance());

   vector xx = path.Col(0);
   vector yy = path.Col(1);

   CGraphic *g = np::plotXY(xx,yy,"Warp Plot", " Query ", " Reference ");

   Sleep(20000);
   g.Destroy();
   ChartRedraw();
   delete g;
  }
//+------------------------------------------------------------------+

A saída do script Python:

KQ      0       20:52:53.954    DTW (EURUSD DFX 10 Index,Daily) Accumulated Cost Matrix is [[ 0.  2.  4.  6.  8. 10. 12. 12. 12. 12.]
RD      0       20:52:53.954    DTW (EURUSD DFX 10 Index,Daily)  [ 0.  2.  4.  6.  8. 10. 12. 12. 12. 12.]
FH      0       20:52:53.954    DTW (EURUSD DFX 10 Index,Daily)  [ 0.  2.  4.  6.  8. 10. 12. 12. 12. 12.]
JL      0       20:52:53.954    DTW (EURUSD DFX 10 Index,Daily)  [ 0.  2.  4.  6.  8. 10. 12. 12. 12. 12.]
NQ      0       20:52:53.954    DTW (EURUSD DFX 10 Index,Daily)  [ 0.  2.  4.  6.  8. 10. 12. 12. 12. 12.]
GD      0       20:52:53.954    DTW (EURUSD DFX 10 Index,Daily)  [ 2.  0.  0.  0.  0.  0.  0.  2.  4.  6.]
QH      0       20:52:53.954    DTW (EURUSD DFX 10 Index,Daily)  [ 4.  0.  0.  0.  0.  0.  0.  2.  4.  6.]
KL      0       20:52:53.954    DTW (EURUSD DFX 10 Index,Daily)  [ 6.  0.  0.  0.  0.  0.  0.  2.  4.  6.]
GS      0       20:52:53.954    DTW (EURUSD DFX 10 Index,Daily)  [ 6.  2.  2.  2.  2.  2.  2.  0.  0.  0.]
PJ      0       20:52:53.954    DTW (EURUSD DFX 10 Index,Daily)  [ 6.  4.  4.  4.  4.  4.  4.  0.  0.  0.]]
LJ      0       20:52:53.954    DTW (EURUSD DFX 10 Index,Daily) Distance is 0.0, 
MM      0       20:52:53.954    DTW (EURUSD DFX 10 Index,Daily)  normalize distance is 0.0
CH      0       20:52:53.954    DTW (EURUSD DFX 10 Index,Daily) Warp Path is [0 1 2 3 4 5 5 5 5 6 7 8 8 9]:[0 0 0 0 0 1 2 3 4 5 6 7 8 9]

A saída do script MQL5:

NE      0       20:56:48.971    dtwTest (EURUSD DFX 10 Index,D1)         local cm [[0,2,2,2,2,2,2,0,0,0]
LH      0       20:56:48.971    dtwTest (EURUSD DFX 10 Index,D1)         [0,2,2,2,2,2,2,0,0,0]
FR      0       20:56:48.971    dtwTest (EURUSD DFX 10 Index,D1)         [0,2,2,2,2,2,2,0,0,0]
HE      0       20:56:48.971    dtwTest (EURUSD DFX 10 Index,D1)         [0,2,2,2,2,2,2,0,0,0]
RL      0       20:56:48.971    dtwTest (EURUSD DFX 10 Index,D1)         [0,2,2,2,2,2,2,0,0,0]
DF      0       20:56:48.971    dtwTest (EURUSD DFX 10 Index,D1)         [2,2.220446049250313e-16,0,0,2.220446049250313e-16,0,0,2,2,2]
ND      0       20:56:48.971    dtwTest (EURUSD DFX 10 Index,D1)         [2,0,0,0,0,0,0,2,2,2]
FR      0       20:56:48.971    dtwTest (EURUSD DFX 10 Index,D1)         [2,0,0,0,0,0,2.220446049250313e-16,2,2,2]
RS      0       20:56:48.971    dtwTest (EURUSD DFX 10 Index,D1)         [0,2,2,2,2,2,2,0,0,0]
OH      0       20:56:48.971    dtwTest (EURUSD DFX 10 Index,D1)         [0,2,2,2,2,2,2,0,0,0]]
ML      0       20:56:48.972    dtwTest (EURUSD DFX 10 Index,D1)         final cm [[0,2,4,6,8,10,12,12,12,12]
JR      0       20:56:48.972    dtwTest (EURUSD DFX 10 Index,D1)         [0,2,4,6,8,10,12,12,12,12]
JH      0       20:56:48.972    dtwTest (EURUSD DFX 10 Index,D1)         [0,2,4,6,8,10,12,12,12,12]
JN      0       20:56:48.972    dtwTest (EURUSD DFX 10 Index,D1)         [0,2,4,6,8,10,12,12,12,12]
JD      0       20:56:48.972    dtwTest (EURUSD DFX 10 Index,D1)         [0,2,4,6,8,10,12,12,12,12]
EI      0       20:56:48.972    dtwTest (EURUSD DFX 10 Index,D1)         [2,2.220446049250313e-16,2.220446049250313e-16,2.220446049250313e-16,4.440892098500626e-16,4.440892098500626e-16,4.440892098500626e-16,2,4,6]
CP      0       20:56:48.972    dtwTest (EURUSD DFX 10 Index,D1)         [4,2.220446049250313e-16,2.220446049250313e-16,2.220446049250313e-16,2.220446049250313e-16,2.220446049250313e-16,2.220446049250313e-16,2,4,6]
EH      0       20:56:48.972    dtwTest (EURUSD DFX 10 Index,D1)         [6,2.220446049250313e-16,2.220446049250313e-16,2.220446049250313e-16,2.220446049250313e-16,2.220446049250313e-16,4.440892098500626e-16,2,4,6]
IN      0       20:56:48.972    dtwTest (EURUSD DFX 10 Index,D1)         [6,2,2,2,2,2,2,4.440892098500626e-16,4.440892098500626e-16,4.440892098500626e-16]
HS      0       20:56:48.972    dtwTest (EURUSD DFX 10 Index,D1)         [6,4,4,4,4,4,4,4.440892098500626e-16,4.440892098500626e-16,4.440892098500626e-16]]
MO      0       20:56:48.972    dtwTest (EURUSD DFX 10 Index,D1)         direction matrix 
QK      0       20:56:48.972    dtwTest (EURUSD DFX 10 Index,D1)        [[-2147483648,1,1,1,1,1,1,1,1,1]
GN      0       20:56:48.972    dtwTest (EURUSD DFX 10 Index,D1)         [2,0,0,0,0,0,0,0,0,0]
QQ      0       20:56:48.972    dtwTest (EURUSD DFX 10 Index,D1)         [2,0,0,0,0,0,0,0,0,0]
CK      0       20:56:48.972    dtwTest (EURUSD DFX 10 Index,D1)         [2,0,0,0,0,0,0,0,0,0]
MR      0       20:56:48.972    dtwTest (EURUSD DFX 10 Index,D1)         [2,0,0,0,0,0,0,0,0,0]
OE      0       20:56:48.972    dtwTest (EURUSD DFX 10 Index,D1)         [2,0,1,1,1,1,1,1,1,1]
HO      0       20:56:48.972    dtwTest (EURUSD DFX 10 Index,D1)         [2,2,0,0,0,1,1,1,0,0]
MF      0       20:56:48.972    dtwTest (EURUSD DFX 10 Index,D1)         [2,2,0,0,0,0,0,0,0,0]
CH      0       20:56:48.972    dtwTest (EURUSD DFX 10 Index,D1)         [2,2,0,0,0,0,0,0,1,1]
LN      0       20:56:48.972    dtwTest (EURUSD DFX 10 Index,D1)         [2,2,0,0,0,0,0,2,0,0]]
PK      0       20:56:48.972    dtwTest (EURUSD DFX 10 Index,D1)         Warp path 
HM      0       20:56:48.972    dtwTest (EURUSD DFX 10 Index,D1)        [[9,9]
GJ      0       20:56:48.972    dtwTest (EURUSD DFX 10 Index,D1)         [8,8]
HS      0       20:56:48.972    dtwTest (EURUSD DFX 10 Index,D1)         [8,7]
DK      0       20:56:48.972    dtwTest (EURUSD DFX 10 Index,D1)         [7,6]
HP      0       20:56:48.972    dtwTest (EURUSD DFX 10 Index,D1)         [6,5]
QI      0       20:56:48.972    dtwTest (EURUSD DFX 10 Index,D1)         [6,4]
GQ      0       20:56:48.972    dtwTest (EURUSD DFX 10 Index,D1)         [5,3]
RN      0       20:56:48.972    dtwTest (EURUSD DFX 10 Index,D1)         [5,2]
MG      0       20:56:48.972    dtwTest (EURUSD DFX 10 Index,D1)         [5,1]
CO      0       20:56:48.972    dtwTest (EURUSD DFX 10 Index,D1)         [4,0]
LD      0       20:56:48.972    dtwTest (EURUSD DFX 10 Index,D1)         [3,0]
EL      0       20:56:48.972    dtwTest (EURUSD DFX 10 Index,D1)         [2,0]
JE      0       20:56:48.972    dtwTest (EURUSD DFX 10 Index,D1)         [1,0]
DO      0       20:56:48.972    dtwTest (EURUSD DFX 10 Index,D1)         [0,0]]
LD      0       20:56:48.972    dtwTest (EURUSD DFX 10 Index,D1)         Distance metric 4.440892098500626e-16
NR      0       20:56:48.972    dtwTest (EURUSD DFX 10 Index,D1)         Normalized Distance metric 2.2204460492503132e-17

Comparar a saída de ambos os scripts confirma que o código parece estar funcionando bem o suficiente. Portanto, podemos usá-lo para algo mais prático. Isso nos leva a como o DTW pode ser usado no desenvolvimento de estratégias.

Aplicando a distorção temporal dinâmica

O DTW pode ser utilizado no desenvolvimento automatizado de estratégias, permitindo técnicas flexíveis de reconhecimento de padrões e comparação de séries temporais financeiras. Por exemplo, o DTW permite identificar padrões recorrentes de preço, mesmo quando ocorrem em escalas diferentes ou com dinâmicas de tempo variadas. Ao alinhar esses padrões com dados históricos, torna-se possível detectar mudanças sutis e anomalias que podem preceder movimentos significativos do mercado.

No backtesting, o DTW pode ser aplicado para comparar o desempenho de diferentes estratégias em várias condições de mercado, alinhando os respectivos resultados das séries temporais. Essa abordagem ajuda a avaliar o quão bem uma estratégia se adapta às mudanças no comportamento do mercado, proporcionando uma compreensão mais profunda de sua robustez. Além disso, o DTW pode ser usado para agrupar sinais de negociação ou estados de mercado semelhantes, que podem ser analisados para identificar oportunidades de negociação de alta probabilidade. Ao reconhecer esses clusters, uma estratégia pode ser ajustada para explorar comportamentos recorrentes do mercado de forma mais eficaz.

Além disso, na otimização de estratégias algorítmicas, o DTW pode ajudar a combinar os conjuntos de parâmetros mais promissores com condições históricas de mercado que se assemelham às dinâmicas de mercado atuais. Isso permite que a estratégia se adapte mais dinamicamente às condições de mercado em evolução. Ao utilizar o DTW, estratégias automatizadas podem, assim, se tornar mais adaptativas, contextualmente conscientes e capazes de reconhecer relacionamentos temporais complexos nos dados financeiros. Embora o DTW possa ser uma ferramenta útil, ele não é uma solução mágica. Pode ser difícil de trabalhar, especialmente para usuários inexperientes.

Um dos maiores problemas com o DTW diz respeito à configuração de seus parâmetros operacionais. A combinação correta de restrições globais e locais é crucial para aproveitar ao máximo o método. O DTW é propenso a gerar correspondências espúrias, e alcançar os melhores resultados muitas vezes exige muitas tentativas e erros. Isso é demonstrado no script MQL5 abaixo.

//+------------------------------------------------------------------+
//|                                             dtwPatternSearch.mq5 |
//|                                  Copyright 2024, MetaQuotes Ltd. |
//|                                             https://www.mql5.com |
//+------------------------------------------------------------------+
#property copyright "Copyright 2024, MetaQuotes Ltd."
#property link      "https://www.mql5.com"
#property version   "1.00"
#resource "\\Indicators\\LogReturns.ex5"
#property script_show_inputs
#include<dtw.mqh>
#include<ErrorDescription.mqh>
enum ENUM_PRICE
  {
   CLOSE=0,//close price
   MEDIAN,//median price
   TYPICAL//typical price
  };

enum ENUM_TRANSFORM_TYPE
  {
   PERCENT_DIFF=0,//percent difference
   LOG_DIFF//log difference
  };
//--- input parameters
input string   Pattern = "0.0469,0.0093,0.0697,-0.0699";
input string   SymbolName="BTCUSD";
input datetime SearchStartDate=D'2024.06.01';
input datetime SearchStopDate=D'2018.04.22';
input double   NormalizedDistanceThreshold=0.01;
input ENUM_TIMEFRAMES      TimeFrame=PERIOD_D1;
input ENUM_DIST_METRIC AppliedDistanceMetric = DIST_EUCLIDEAN;
input ENUM_STEP_PATTERN AppliedStepPattern = STEP_SYMM2;
input ENUM_GLOBAL_CONSTRAINT AppliedGlobalConstraint = CONSTRAINT_NONE;
input ulong GlobalConstraintWinSize = 0;
input ENUM_PRICE AppliedPrice=CLOSE;
input ENUM_TRANSFORM_TYPE AppliedTransform=LOG_DIFF;
input int Lag = 1;
//+------------------------------------------------------------------+
//| Script program start function                                    |
//+------------------------------------------------------------------+
void OnStart()
  {
//---
   string pattern_values[];
//---
   int len = StringSplit(Pattern,StringGetCharacter(",",0),pattern_values);
   if(pattern_values[len-1]=="")
      len--;
//---
   if(len<3)
     {
      Alert("Pattern sequence is inadequately defined");
      return;
     }
//---
   vector pattern(len);
   for(ulong i = 0; i<pattern.Size(); i++)
      pattern[i]=StringToDouble(pattern_values[i]);
//---set prices handle
   int handle = INVALID_HANDLE;
   handle=iCustom(SymbolName!=""?SymbolName:NULL,TimeFrame,"::Indicators\\LogReturns.ex5",AppliedPrice,AppliedTransform,1);
   if(handle==INVALID_HANDLE)
     {
      Print("invalid handle ",ErrorDescription(GetLastError()));
      return;
     }
//---
   vector searchBuffer;
   if(!searchBuffer.CopyIndicatorBuffer(handle,0,SearchStartDate,SearchStopDate))
     {
      Print("History loading error ",ErrorDescription(GetLastError()));
      return;
     }
//---
   ulong stop = searchBuffer.Size()-pattern.Size();
   vector subv;
   Cdtw cdtw;
   ulong counter=0;
   for(ulong i = 0; i<stop; i++)
     {
      subv = np::sliceVector(searchBuffer,i,i+pattern.Size());

      if(!cdtw.dtw(subv,pattern,AppliedDistanceMetric,AppliedStepPattern,AppliedGlobalConstraint,GlobalConstraintWinSize))
        {
         Print(" dtw failed ");
         return;
        }

      if(cdtw.normalizedDistance()<NormalizedDistanceThreshold)
        {
         counter++;
         Print(" pattern found  ", datetime(SearchStopDate+(PeriodSeconds(TimeFrame)*(i+pattern.Size()-1))));
        }
     }
//---
   Print(" SearchBuffer size ", searchBuffer.Size());
   Print(" Reference pattern found ", counter, " times.");
  }
//+------------------------------------------------------------------+

O script permite que o usuário defina um padrão arbitrário feito a partir de uma sequência de retornos logarítmicos, calculados pelo indicador 'LogReturns.ex5'. O script é projetado para procurar um padrão específico nos dados de preços de um instrumento financeiro, utilizando a distorção temporal dinâmica (DTW) para comparação. Ele inclui as bibliotecas necessárias, como dtw.mqh para o algoritmo DTW e ErrorDescription.mqh para o tratamento de descrições de erro. O script define duas enumerações: ENUM_PRICE, que especifica o tipo de preço a ser usado (fechamento, mediano ou típico), e ENUM_TRANSFORM_TYPE, que determina como os dados de preços serão transformados (diferença percentual ou diferença logarítmica).

Os parâmetros de entrada permitem que o usuário especifique detalhes para a busca, incluindo o padrão a ser correspondido, o nome do símbolo (exemplo, "BTCUSD"), o intervalo de datas para a busca, um limiar para a distância normalizada, o intervalo de tempo dos dados, a métrica de distância, o padrão de etapas, a restrição global, o tamanho da janela para a restrição, o tipo de preço a ser usado, o tipo de transformação a ser aplicada e um valor de atraso. Quando o script começa, ele primeiro divide a string do padrão de entrada em um array de valores, garantindo que o padrão seja adequadamente definido com pelo menos três valores. Se o padrão for válido, ele é convertido em formato de vetor para processamento adicional. O script então tenta carregar os dados de preços utilizando a função iCustom para chamar um indicador personalizado (LogReturns.ex5) que aplica o tipo de preço selecionado e a transformação aos dados. Se o identificador retornado por iCustom for inválido, uma mensagem de erro é impressa e o script é encerrado.

Assumindo que os dados de preços sejam carregados com sucesso, eles são armazenados no vetor searchBuffer. O script então percorre o searchBuffer, dividindo-o em sub-vetores menores do mesmo tamanho que o padrão e comparando cada sub-vetor com o padrão usando o algoritmo DTW. A comparação DTW utiliza a métrica de distância especificada, o padrão de etapas e a restrição global. Para cada comparação, se a distância normalizada entre o sub-vetor e o padrão for menor que o limiar especificado, o script considera que o padrão foi encontrado naquele ponto dos dados de preços. Ele imprime uma mensagem indicando o timestamp onde o padrão foi encontrado e incrementa um contador. Finalmente, o script imprime o tamanho do searchBuffer e o número total de vezes que o padrão foi encontrado dentro do intervalo de datas especificado. Este script permite a detecção automatizada de padrões específicos nos dados de preços históricos, o que pode ser útil no desenvolvimento de estratégias de negociação baseadas em reconhecimento de padrões.

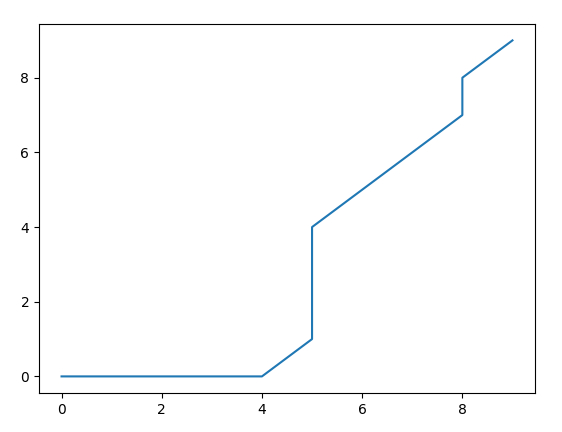
A sequência padrão descreve o padrão ilustrado abaixo.

Executar o script com diferentes restrições aplicadas produz um número variável de correspondências. Esta é a saída usando as configurações padrão.

RN      0       22:00:09.210    dtwPatternSearch (BTCUSD,D1)    Chosen Parameters
IJ      0       22:00:09.210    dtwPatternSearch (BTCUSD,D1)    Distance Threshold 0.01
CS      0       22:00:09.210    dtwPatternSearch (BTCUSD,D1)    DIST_EUCLIDEAN
ND      0       22:00:09.211    dtwPatternSearch (BTCUSD,D1)    STEP_SYMM2
CN      0       22:00:09.211    dtwPatternSearch (BTCUSD,D1)    CONSTRAINT_NONE
HG      0       22:00:09.211    dtwPatternSearch (BTCUSD,D1)     WinSize 0
OO      0       22:00:09.211    dtwPatternSearch (BTCUSD,D1)     pattern found  2018.04.25 00:00:00
NJ      0       22:00:09.221    dtwPatternSearch (BTCUSD,D1)     pattern found  2019.04.28 00:00:00
KD      0       22:00:09.222    dtwPatternSearch (BTCUSD,D1)     pattern found  2019.07.01 00:00:00
QO      0       22:00:09.230    dtwPatternSearch (BTCUSD,D1)     pattern found  2020.04.27 00:00:00
II      0       22:00:09.234    dtwPatternSearch (BTCUSD,D1)     pattern found  2020.10.26 00:00:00
PD      0       22:00:09.237    dtwPatternSearch (BTCUSD,D1)     pattern found  2021.02.06 00:00:00
RN      0       22:00:09.250    dtwPatternSearch (BTCUSD,D1)     pattern found  2024.01.29 00:00:00
DH      0       22:00:09.250    dtwPatternSearch (BTCUSD,D1)     SearchBuffer size 2197
PQ      0       22:00:09.250    dtwPatternSearch (BTCUSD,D1)     Reference pattern found 7 times.

O parâmetro NormalizedDistanceThreshold obviamente desempenha um papel significativo na determinação de se uma correspondência existe. Ainda assim, as restrições variadas podem levar a resultados consideravelmente diferentes. Não são apenas as restrições; os usuários também devem escolher a métrica de distância apropriada. Claramente, um conhecimento significativo do domínio é essencial ao empregar o algoritmo DTW.

Conclusão

A Distorsão Temporal Dinâmica oferece uma abordagem sofisticada para o reconhecimento de padrões na análise de séries temporais financeiras, mas também possui várias desvantagens que devem ser consideradas. Primeiro, o DTW é intensivo em termos computacionais, especialmente quando lidamos com séries temporais longas ou grandes conjuntos de dados. O algoritmo envolve a comparação de cada ponto em uma série temporal com cada ponto em outra, o que pode resultar em tempo de processamento significativo e uso de memória. Isso se torna particularmente problemático quando tentamos analisar dados financeiros de alta frequência ou realizar análise em tempo real. Segundo, o DTW é sensível ao ruído e aos outliers nos dados financeiros.

As séries temporais financeiras frequentemente são ruidosas devido à volatilidade do mercado, e pequenas flutuações ou anomalias podem fazer com que o algoritmo DTW produza alinhamentos enganosos. Essa sensibilidade pode levar a falsos positivos no reconhecimento de padrões, onde padrões são identificados, mas não possuem um poder preditivo significativo. Por fim, o DTW pode ter dificuldades com a interpretabilidade. Embora forneça uma medida de similaridade entre séries temporais, o caminho de distorção e a métrica de distância resultante podem ser difíceis de interpretar de maneira significativa, especialmente no contexto da análise financeira, onde informações claras e acionáveis são cruciais. Esses desafios sugerem que, embora o DTW possa ser uma ferramenta útil para o reconhecimento de padrões em séries temporais financeiras, ele deve ser aplicado com cuidado e muitas vezes em combinação com outros métodos analíticos que possam superar suas limitações.

Arquivo	Descrição
Mql5\include\np.mqh	Arquivo de cabeçalho de várias funções utilitárias de vetor e matriz
Mql5\include\dtw.mqh	Arquivo de inclusão contendo a implementação MQL5 do algoritmo de distorção temporal dinâmica
Mql5\indicators\LogReturns.mq5	Indicador de retornos logarítmicos de uma série de preços
Mql5\scripts\dwTest.mq5	Script usado para testar e demonstrar o uso da implementação MQL5 do DTW
Mql5\scripts\dtwPatternSearch.mq5	Script usado para procurar um padrão arbitrário em uma amostra de dados
Mql5\scripts\DTW.py	Um script Python que usa o módulo dtw-python para alinhar duas séries usando o algoritmo DTW