一連の取引に対するリスク評価続編

目次

• 序章
• 価格と取引システムに関する仮定
• 収率分布 - 一般的な所見
  
• 固定逆指値と指値
  
• 固定トレール注文
• 次の段階
• 統計とギャップ
  
• 統計的機械学習
• 取引システムの統計と最適化
• 添付ファイル

序章

前稿で始まったリスク推定理論の研究を続けましょう。2つの例について論理的な結論に至ります。また、確率論や数学統計の他の可能な応用について簡単に概説します。

価格と取引システムに関する仮定

前稿で考察された手法はシステムの取引結果の分析に使うことができるのでしょうか。このためには、その取引の列は、独立して同一に分布された変数の列であることが確実でなければなりませんが、残念なことに、これは実際には必ずしもそうとは言えません。

どちらの条件（独立、同一分布）も満たされない可能性があります。ラルフ·ヴィンスは“The Mathematics of Money Management”（資金管理の数学）で、これらの問題を解決する方法を概説しています。システムを必要な条件を満たすいくつかの部分（サブシステム）に分割することが提案され、2つの例が提示されます。1番目の例では、その後の取引の間に依存性を持つシステムについて論じられ、この場合、列は2つの部分に分割されます。偶数および奇数の取引は、異なるシステムから受け取られたものとして扱われます。2番目の例で考察されるのはピラミッド型のシステムです。ポジションの数量が段階的に増やされ、このような増分の各ステップは、別々のシステムと見なされます。これにより、複数のシステムが収集されます。1番目のシステムは1番目のステップで構成され、2番目のシステムは2番目のステップで構成されるなどです。

そのようなシステムの「断片」を研究したならば、それらを再構成し、それらの間の依存関係を考慮に入れた「マイクロポートフォリオ」を作成する方法を見つけなければなりません。これにはMarkowitzの現代ポートフォリオ理論と同様のものが必要です。

既にかなり複雑に見えるのですが、これで終わりではありません。 pstoplossまたはptakeprofitのいずれかで各ポジションを決済するシステムを考えてみましょう。特定の指標でのk=|ptakeprofit-penter|/|pstoploss-penter|の比は取引によって異なります。各取引の利率分布は非常に単純なものになるでしょう。ある確率での、-1とkの2つの値を持つ離散分布です。しかし、kの値は取引に特有なので、異なる取引では分布が異なります。したがって、システムを「断片」に分割しようとするとその数は取引の数と同じになり、これは明らかに無意味です。実際には、使用された kの値はすべての取引で同じである可能性が高いです（平均値、特性値）。これにより、実際の取引で使用されるシステムの簡略版で分析を実行することができます。

実際の取引システムにリスク理論を使用するためのすべての可能なオプションを要約します。

1. 取引システムをいくつかの部分に分割する。
2. システムの単純化されたアナログを研究する。
3. 分布の独立性と同一性を確認せずに一連の取引を分析する。同時に、他の分析方法を用いて得られたリスク値をわずかに調整することも可能である。
   

このシステム研究アプローチは明らかに普遍的ではなく、常に適用可能なわけでもありません。この方法をより体系的にしてみましょう。これには、価格とシステムについていくつかの前提が必要です。

1. 価格系列はランダムウォークに近い。この近さの定義を数学的に定式化することはないが、ランダムウォークと実際の価格で特定の計算を実行すると、前者の結果は後者の結果の零次近似と考えることができる。これは、価格系列から得られる確率変数の分布についての仮定がどのようになされるかの例である。
   
2. ランダムウォークで生成された気配値はシステムに送ることができる。この場合、ランダム価格は「平均して」実際の価格に近い値でなければならない。つまり、より長い時間枠でのボラティリティやティックの価格スパイクの分布は同様でなければならない。
3. システムの取引間の依存構造（実際の価格とランダムウォーク）はどちらの場合も似ているが、利率分布は大きく異なる可能性がある。たとえば、すべての利率が同じ数だけ増加すると、分布は変化（右に移動）する。しかし、利率間の相関係数は同じままである。
   
4. システムは、ランダムウォークでその取引が同じように配分され、時間的に大きく重なっている場合（2番目の取引が1番目の取引が決済される前に開かれている場合）にのみ有意に相互に依存するように構成される。
   

これらの前提をより詳細に説明しましょう。ランダムウォークは、ランダムなプロセスの広範なクラスで、離散的でも連続的でもあり得ます。どちらのタイプも解析計算に使用されますが、コンピュータ上のモデリングには最初のものだけが使用されます。これらのタイプは関連しています。離散的ランダムウォークは時間ステップがゼロになるにつれて連続的ランダムウォークとなります。また、ランダムウォークは、対称（トレンドなし、フラット）または正/負シフト（上/下降トレンド）のいずれかになります。対称ランダムウォークは、最も頻繁に考えられます。この場合、価格に関する仮定は次のようになります。

• 取引結果は指標によって予測できない。これにより、モデリングが大幅に簡素化される。システムの取引を終了する部分だけを研究する必要があることが判明する。取引がどこでどのように開かれたかは完全に無関係である。
• 平均して、利益はゼロである。これは、取引で利益を得ることを妨げるものではない。しかし、より多くの取引が開かれるほど、その結果の集計は一定の確率分布に対応する。 この分布の具体的な形式は市場エグジットアルゴリズムに依存するが、その期待値は常にゼロである。
  

実際のシステムを実際の価格でテスト（特に最適化）する際には、これらの推論を考慮する必要があります。 対称ランダムウォークでは 十分な信頼性を備えた結果が得られれないことを示す基準が必要です。これは、取引利率分配とテクニカル指標の有用性の程度に適用されます。 さらに、対称ランダムウォークからの偏差の検索は、取引システムのアイデアを検索するときにも役立ちます。例として、後で、「ギャップが常に満たされる」というステートメントを使用する可能性を考慮します。

前述の前提は取引システムに制限を課すものです。一般的に、市場エントリ/エグジットのルールにはシンプルさ、統一性、透明性が求められます。これらのルールは、取引間の関係（例えば、持分曲線を参照する）をさらに強化するものではなく、取引方法（例えば、テイクプロフィット/ストップロス比率をランダムに変更する）から既存の方法を任意に変更すべきではなく、 あまりにも頻繁にするべきではありません。これらの条件がおおよそ何を達成するかは理論的に確認するか、モンテカルロ法を使用してコンピュータ上でモデル化することができます。

収率分布 - 一般的な所見

一般的な配布形態についての所見から始めます。 確率分布関数の概念が導入されるときは通常、離散型と連続型が含意されています。 それに加えて、それらを混合することも可能であることが判明しています。つまり、P(x)=γcPc(x)+γdPd(x)の形での分布関数が可能です。ここで、γc≥0、γd≥0、γc+γd=1で、Pc(x)と Pd(x)はそれぞれ（密度を有する）分布関数および離散的（段階的）分布関数です。

一例として、シンプルなエグジット法を考察します。比率kで固定されたストップロスとテイクプロフィットのポジション保持時間をtexitで制限します。簡単に言えば、エグジットがテイクプロフィット/ストップロスに基づく取引は離散的な分布を持ち、エグジットが時刻に基づく取引は連続的な分布を持っています。 全体的な分布はそれらが混合したものです。 当然ながら、これはさらなる議論を複雑にします。 簡単化のためにtexitが十分に大きくγcを無視できるとの仮定を立てましょう。P(x)=Pd(x)と仮定します。

固定トレール注文を使用して取引を終了するのはγd=0の例です。γd≠0かつ同時にγс≠0だということも可能です。例えば、これは両方の例を組み合わせて考えることができます。この方法では、ストップロスは取引の初期段階では不動ですが、一定の条件が満たされると、トレール注文と同様に動き始めます。

上記の両方の例についてリスク理論を具体化しましょう（組み合わせた変形は考慮されません）。収率分布の特定のケースごとに最適リスク値roptを計算するためのスクリプトを以下に示します。しかし、時には他のタスクも興味深いものです。例えば、リスクが設定されており、信頼度の対応するレベル（またはオプションとしての平均収率G0の最大利用可能値）δを計算する必要があるということです。この場合、スクリプトを変更するか、異なる入力データで実行して、望ましいリスク値を達成する必要があります。

固定逆指値と指値

上記のように、分布は離散的であると考えられます。取引の収率は-1とkの2つの値をとることができ、それぞれの確率はP-1とPkです。総確率の式はP-1+Pk=1です。分布関数は-1とkの2つの点でジャンプし、大きさがP-1とPkの階段状の形をしています。分布の期待値はM=-1*P-1+k*Pkです。θ=Pkとすると、P-1=1-θ、M=(1+k)θ-1となります。したがって、ここにあるのは、パラメータk>0および0≤θ≤1によって定義される、パラメトリックな分布の系列です。 対称ランダムウォークの場合、M=0で、θ=θ0=1/(1+k)となります。

aiをn取引の収率とします。それぞれは-1またはkです。

1. 期待値の見積もりM≈Mapr=(a1+a2+...+an)/n=(1+k)nk/n-1を計算します。ここでnkは収益性のある取引の数です。Mapr≤0の場合は、不採算として取引システムを拒否します。不採算のシステムを収益性の高いシステムに変える可能性のあるリスク管理の仕組みはありません。Mapr>0の場合は、次のステップに進みます。
2. これらの取引は対称のランダムウォークを取引した結果ではないことを示す必要があります。このために、推定値Maprはゼロよりかなり大きくなければなりません（信頼性δを有する）。帰無仮説としてM=0と主張します。 検定統計量は、変数S=n(Mapr+1)/(1+k)=nkです。これは帰無仮説が満たされたとき標準二項分布 B(n,θ0)を有します。その分布関数をP(x)で表します。帰無仮説を受け入れるには、P(S)>P(nθ0)+δ/2であることを確認する必要があります。 確認できた場合は、次の手順に進みます。 そうでない場合は、取引システムを拒否します。
3. 選択された最小平均収率値G0に対して、必要な条件が満たされているかどうかを確認します。このためには、G0は、 1番目の部分 （収率の算術平均）に導入された確率変数Λのqδ分布の δ--分位数より大きくてはなりません。変数ΛはMaprと一致し、Sで表現されます。変数Sはパラメータnとθapr=nk/nを有する二項則に従って分配されると考えられます。条件が満たされる場合は、次のステップに進みます。 そうでない場合は、条件が満たされるのに必要な取引の最小値n=nminを決定します（必要な不等式が満たされる値まで固定されたθaprに対してnを徐々に増加させます）。
4. モンテカルロ法を用いて、経験分布ρoptを得ます。これを行うには、それぞれn個の取引利益を持つ多数のセットをシミュレートします。各収率は確率Pkでkに等しく、確率1-Pkで-1に等しいです。初めの部分への序論で使用された手法を使って、各セットでropt,iの値を定めます。それらは全体で確率変数ρoptの経験的分布を特定します。roptのリスクを推定するには、この分布のサンプルδ分位数を使用します。

#include <Math\Stat\Binomial.mqh>
#property script_show_inputs
input uint na=50;        // シリーズ内の取引数
input double kt=3;       // テイクプロフィットとストップロスの比
input double pk=0.5;     // 利益の確率

#define NX 300           // シリーズ内の取引の最大数（nminの検索）
#define NB 10000         // モンテカルロ法の生成サンプル数
#define NR 1000          // リスクの区間分割数
double G0=0.15;          // 最低平均収率
double D0=0.9;           // 最低の最小ゲイン
double dlt=0.05;         // 重要性レベル

void OnStart()
  {
   if (D0<=0||D0>=1) {Print("D0 must be positive and less than one"); return;}
   double m=(1+kt)*pk-1;             // 期待値
   if(m<=0) {Print("expected value must be positive"); return;}
   double s=na*pk;                   // 統計（有益な取引の平均数）
   double s0=na/(1+kt);              // 期待値ゼロでの収益性のある平均取引数
   int ner;
   double p=MathCumulativeDistributionBinomial(s,na,1/(1+kt),ner);
   if(!MathIsValidNumber(p)) {Print("MathIsValidNumber(p) error ",ner); return;}
   double p0=MathCumulativeDistributionBinomial(s0,na,1/(1+kt),ner);
   if(!MathIsValidNumber(p0)) {Print("MathIsValidNumber(p0) error ",ner); return;}
   if(p<=p0+dlt/2) {Print("expected value is close to zero"); return;}

   double q=MathQuantileBinomial(dlt,na,pk,ner),q0=na*(G0+1)/(kt+1);
   if(!MathIsValidNumber(q)) {Print("MathIsValidNumber(q) error ",ner); return;}
   if(q0>q)
     {
      Print("G0 is greater than dlt quantile of the arithmetic mean of the yield");
      uint nmin=na+1;
      for(;nmin<=NX;++nmin)
        {
         q=MathQuantileBinomial(dlt,nmin,pk,ner); q0=nmin*(G0+1)/(kt+1);
         if(!MathIsValidNumber(q)) {Print("MathIsValidNumber(q) error ",ner); return;}
         if(q0<=q) break;
        }
      if(nmin<=NX) Print("nmin = ",nmin);
      else Print("nmin is greater than ",NX);
      return;
     }
// モンテカルロ法
   MathSrand(GetTickCount());
   double a[],c[],ropt[NB],A0,A,r,g,d,cn1,cn2,stp=1.0/NR;
   uint ir;
   ArrayResize(a,na);
   ArrayResize(c,na);
   for(uint ib=0; ib<NB;++ib)
     {
      for(uint i=0; i<na;++i) if(MathRandomNonZero()<=pk) a[i]=kt; else a[i]=-1;
      A=MathMean(a); A0=a[ArrayMinimum(a)];
      if(A<G0) {ropt[ib]=0; continue;}
      if(A0>0) {ropt[ib]=1-stp; continue;}
      cn1=1;
      for(ir=1;ir<NR;++ir)
        {
         r=ir*stp;
         cn2=1; for(uint i=0; i<na;++i) cn2*=1+r*a[i];
         if(cn2<cn1) {ropt[ib]=r-stp; break;}
         cn1=cn2;
         g=(MathPow(cn2,1.0/na)-1)/r;
         if(g<G0) {ropt[ib]=r-stp; break;}
         c[0]=1+r*a[0]; for(uint i=1; i<na;++i) c[i]=c[i-1]*(1+r*a[i]);
         d=dcalc(c);
         if(d<D0) {ropt[ib]=r-stp; break;}
        }
     }
     ArraySort(ropt);
     uint nr=(uint)(dlt*NB);
     Print("ropt = ",ropt[nr]);
  }

// dcalc()関数はc1, c2, ... cN値を持つ配列を受け入れ
// 最小利得dを返す。c0==1を仮定する。
double dcalc(double &c[])
  {
   if(c[0]<=0) return 0;
   double d=c[0], mx=c[0], mn=c[0];
   for(uint i=1; i<na;++i)
     {
      if(c[i]<=0) return 0;
      if(c[i]<mn) {mn=c[i]; d=MathMin(d,mn/mx);}
      else {if(c[i]>mx) mx=mn=c[i];}
     }
   return d;
  }
//+------------------------------------------------------------------+

デフォルトの引数を使用すると、スクリプトは次のリスク値を計算します。

• ropt = 0.011

これは、各取引でリスクを負う資本の1.1％に相当します。

固定トレール注文

買取引があるとします（売取引に必要な変更は直感的です）。エントリー価格と初期ストップロスの差をΔp=penter-pstopで表します。価格がpmax-Δpの値に達すると、取引は終了します。ここでpmaxは取引が開かれてからの最大価格です。連続的な時間および線形シフトを伴うランダムウォークによってモデルをモデル化する場合、利益の分布は明示的な形で見つけることができます。それは指数分布が左に1つシフトされたものです。分布関数はより正確にP(x)=1-exp(-θ(x+1))（x≥-1）およびP(x)=0（x<-1）で表現されます。パラメータθは正のシフト（上昇トレンド）では0<θ<1、負の値（下降トレンド）ではθ>1、ゼロ（フラット）ではθ=1を満たします。期待値はM=1/θ-1で定義されます。

実際の価格はランダムウォークに近いと仮定したため、一連の取引の利率分布も同様に考慮され、パラメータθの一定の値が使用されます。これによって、連続分布の1パラメータ一族が与えられます。トレンド中のθパラメータの具体的な値は、トレンドの強さとトレール注文の比によって決まります。利用可能な取引履歴の指数分布（この場合、最尤推定を使用）のパラメトリック統計の方法を使用して計算します。さらに計算するためには、同じパラメータを持つ有限個の変数の和（および算術平均）がよく研究されたガンマ分布を持つことも重要です。

n取引の収率をaiとし、各取引がai>-1を満たす（このために、スリッページは無視される）とします。前章と同様に、さらなる行動計画を提案します。

1. 期待値の見積もりを計算します（M≈Mapr=(a1+a2+...+an)/n）。Mapr≤0の場合は、不採算として取引システムを拒否します。Mapr>0の場合は、次のステップに進みます。
2. M=0だという仮説に反論してみましょう。検定統計量は、変数S=Mapr+1です。これはガンマ分布Γ(n,1/n)を有します（M=0の場合は帰無仮説が満たされます）。その分布をP(x)で表します。次に、代替仮説を受け入れるためにはP(S)≥P(1)+δ/2不等式を満たさなければなりません。帰無仮説がうまく反論された場合は、次のステップに進み、そうでない場合は、システムを拒否します。
3. G0の必須条件を確認します。まず、パラメータθ=θaprの推定値を得る必要があります。最尤推定を用いて、θapr=1/(1+Mapr)を得ます。Λの値は左に1によってシフトされたガンマ分布Γ(n,θapr/n)によって分配されます。このガンマ分布のδ分位がG0+1以上であれば、必要条件は満たされます。満たされている場合は、先に進みます。満たされていない場合は、この条件を満たすための最小取引数を決定することが可能です。これを行うには、nの値を徐々に増やし、nminを1に設定します。これで必要条件が満たされます。

4. これは、本稿の前の章と同じ方法で実行されます。変更は、利益のランダム生成に使用される分布のみに関係します。今回は、パラメータθ=θaprを1つ左にシフトした指数分布を適用します。MQL5の統計ライブラリは、指数分布に対してわずかに異なる形のパラメータ化を使用しています。パラメータμ（期待値）はθまたはMを使用してμ=1/θまたはμ=M+1として表現されます。

#include <Math\Stat\Gamma.mqh>
#include <Math\Stat\Exponential.mqh>
#property script_show_inputs
input uint na=50;           // シリーズ内の取引数
input double tht=0.65;      // 指数分布のパラメータ 0<tht<1

#define NX 300              // シリーズ内の取引の最大数（nminの検索）
#define NB 10000            // モンテカルロ法の生成サンプル数
#define NR 1000             // リスクの区間分割数
double G0=0.15;             // 最低平均利益
double D0=0.9;              // 最低の最小ゲイン
double dlt=0.05;            // 重要性レベル

void OnStart()
  {
   if(D0<=0 || D0>=1) {Print("D0 must be positive and less than one"); return;}
   double m=1/tht-1;         // 期待値
   if(m<=0) {Print("expected value must be positive"); return;}

   int ner;   
   double p=MathCumulativeDistributionGamma(m+1,na,1.0/na,ner);
   if(!MathIsValidNumber(p)) {Print("MathIsValidNumber(p) error ",ner); return;}
   double p0=MathCumulativeDistributionGamma(1,na,1.0/na,ner);
   if(!MathIsValidNumber(p0)) {Print("MathIsValidNumber(p0) error ",ner); return;}
   if(p<=p0+dlt/2) {Print("expected value is close to zero"); return;}

   double q=MathQuantileGamma(dlt,na,1/tht/na,ner),q0=G0+1;
   if(!MathIsValidNumber(q)) {Print("MathIsValidNumber(q) error ",ner); return;}
   if(q0>q)
     {
      Print("G0 is greater than dlt quantile of the arithmetic mean of the yield");
      uint nmin=na+1;
      for(;nmin<=NX;++nmin)
        {
         q=MathQuantileGamma(dlt,nmin,1/tht/nmin,ner); q0=G0+1;
         if(!MathIsValidNumber(q)) {Print("MathIsValidNumber(q) error ",ner); return;}
         if(q0<=q) break;
        }
      if(nmin<=NX) Print("nmin = ",nmin);
      else Print("nmin is greater than ",NX);
      return;
     }    

// モンテカルロ法
   MathSrand(GetTickCount());
   double a[],c[],ropt[NB],A0,A,r,g,d,cn1,cn2,stp=1.0/NR;
   uint ir;
   ArrayResize(a,na);
   ArrayResize(c,na);
   for(uint ib=0; ib<NB;++ib)
     {
      for(uint i=0; i<na;++i)
        {
         a[i]=MathRandomExponential(m+1,ner);
         if(!MathIsValidNumber(a[i])) {Print("Error MathRandomExponential()",ner); return;}
         a[i]-=1.0;
        }
      A=MathMean(a); A0=a[ArrayMinimum(a)];
      if(A<G0) {ropt[ib]=0; continue;}
      if(A0>0) {ropt[ib]=1-stp; continue;}
      cn1=1;
      for(ir=1;ir<NR;++ir)
        {
         r=ir*stp;
         cn2=1; for(uint i=0; i<na;++i) cn2*=1+r*a[i];
         if(cn2<cn1) {ropt[ib]=r-stp; break;}
         cn1=cn2;
         g=(MathPow(cn2,1.0/na)-1)/r;
         if(g<G0) {ropt[ib]=r-stp; break;}
         c[0]=1+r*a[0]; for(uint i=1; i<na;++i) c[i]=c[i-1]*(1+r*a[i]);
         d=dcalc(c);
         if(d<D0) {ropt[ib]=r-stp; break;}
        }
     }
   ArraySort(ropt);
   uint nr=(uint)(dlt*NB);
   Print("ropt = ",ropt[nr]);
  }
// dcalc()関数はc1, c2, ... cN値を持つ配列を受け入れ
// 最小利得dを返す。c0==1を仮定する。
double dcalc(double &c[])
  {
   if(c[0]<=0) return 0;
   double d=c[0], mx=c[0], mn=c[0];
   for(uint i=1; i<na;++i)
     {
      if(c[i]<=0) return 0;
      if(c[i]<mn) {mn=c[i]; d=MathMin(d,mn/mx);}
      else {if(c[i]>mx) mx=mn=c[i];}
     }
   return d;
  }
//+------------------------------------------------------------------+

デフォルトの引数を使用すると次のリスク値が得られます。

• ropt = 0.015

これは、各取引でリスクを負う資本の1.1％に相当します。

前の部分の30取引の列は、特にトレール注文によるエグジットを持つシステムのために得られました。したがって、本手法を適用することができます。先に考察した方法と同様に、それは与えられた条件の下では列が取引に不適切であることを示しています（n, δ, G0, D0）。この結果はスリッページを除去した後でも、すべてのaiに小さな正の数を加えれば変化しないので、i=1,...,nについてai>-1が満たされます。

注: スクリプトがデフォルトの引数に対してエラー番号4を生成する場合は、ターミナルの更新が必要です。この場合、スクリプトの一部（21行目から42行目）をコメントアウトする必要があります。 この部分には、ガンマ分布に関する計算が含まれています。 それらについては、Rで次のスクリプトを使用できます。

na=50; tht=0.65; dlt=0.05; G0=0.15; nx=300
m=1/tht-1; l1=l2=l3=FALSE
l1 = m > 0
if (l1) l2 = pgamma(m+1,na,scale = 1/na) > pgamma(1,na,scale = 1/na)+dlt/2
if (l2) l3 = G0+1 <= qgamma(dlt,na,scale = 1/tht/na)

if(!l1) cat("m must be greater 0\n")

if(l1 & l3) cat("G0 and na are ok\n") else cat("na too small or G0 too big\n")

if(l1 & l2 & !l3)
{for (nmin in (na+1):(nx+1)) {if(G0+1 <= qgamma(dlt,nmin,scale = 1/tht/nmin)) break()}
 if (nmin<=nx) {cat("nmin =",nmin)} else {cat("nmin >",nx)}
}

次の段階

上記の手法は明らかに完璧とも最終的なものともみなせません。単純化のために、取引は独立しており同様に分配されているものとみなされました。しかしこれにはもっと深い研究が必要であり、そうでないことが判明するかもしれません。利益の分布が特定のパラメトリックファミリに属しているか、それに近いことが有用な場合があります。しかし、このメンバーシップについてもさらなる研究が必要とかもしれません。

ここでは分布パラメータのポイント推定値を決定し、それらの信頼区間を求めませんでした。しかし、いったんそれらが構築されると、これらのパラメータが変動とともにシステムの収益性の安定性の問題が出てくるでしょう。

もちろん、多くの可能な手法があるということは、それらを常に一貫して使用する必要があるということではありません。しかし、「乱雑さに惑わされる」よりは、それらについて知り、必要に応じて使用できるようにするほうがいいことです。

本稿の残りの部分では、確率論を適用するための他のいくつかの可能性のある方向を簡単に概説します。

統計とギャップ

ギャップとは、2つの連続するバーの終値と始値の間の大きなジャンプです。これらのバーは間にかなりの間隔を有することが要求されます。「ギャップはいつも埋められる」ということが信じられています。ギャップが埋まるということは、ギャップが発生した後、価格が最終的にギャップの前のバーの終値に戻るということです。 時にはトレーダーは、この規則性に基づいて取引システムを構築しようとします。これは可能でしょうか。

ラインの対称ランダムウォークの理論は、十分に長い時間では価格は任意の値が達し、ここの確率はほぼ1に等しいとします。つまり、これらの条件下でも、ほぼ確実に「ギャップは常に埋められます」。しかし、対称ランダムウォークでは有益なシステムは不可能であることはわかっています。ギャップベースのシステムが存在する可能性はないということでしょうか。

必ずしもそうではありません。ギャップが埋まるという事実だけでなく、ギャップがどのように埋まるかも重要です。これは、すべての特定のギャップについてを指すのではなく、それらの特定の集約を指します。すると、それらに関連する確率変数の経験的確率分布を考察することが可能です。実際の価格と対称ランダムウォークモデルとの間には違いがあるかもしれません。違いは大きく異なる可能性があります。 これは、ギャップの方向への動きの不十分さ、ランダムウォークの場合よりも閉鎖までの時間が短いことなどによって引き起こされる可能性があります。 これらの偏差の存在および重要性は、確率論および数学的統計の方法を用いて決定することができるということのみが重要です。取引システムは、これらの偏差を検証した後、その基準に基づいて構築することができます。ギャップを分類した理論のテストを試みることもできます。

ランダムウォークからの偏差を検索する最も簡単なバージョンを考えてみましょう。これは、価格が満たされるまでギャップの方向への価格の動きの尺度になります。この変数の経験的分布を価格履歴で求め、それを理論値と比較することも可能です。いくつかの適合度基準を使用して、これらの2つの分布を比較することができます。

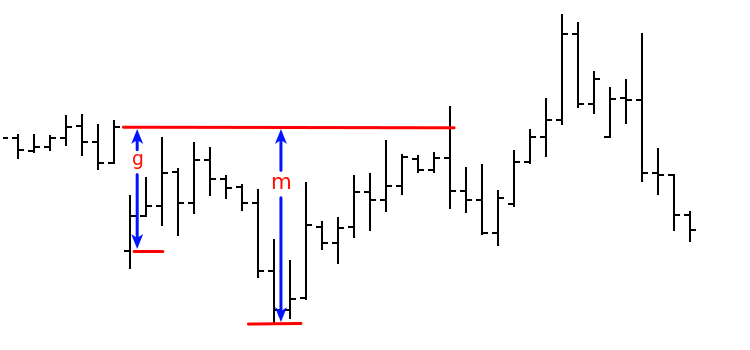
離散時間を持つ対称ランダムウォークのモデルを考えてみましょう。大きなギャップは（実際の価格でも）稀であり、ギャップの間隔でモデルを連続時間でウォークに近づけるようにします（ウィーナープロセス）。g - ギャップサイズ、 m - ギャップが埋められるまでのギャップの方向への最大移動量とします。確率変数x=m/gは関数P(x)に近い分布関数を持つことになります。ここでP(x)=1-1/x（x≥1）およびP(x)=0（x<1）です。図は導入された値を示しています。

このトピックには、より詳細で広範な研究が必要です。したがって、以下を言うだけにします。

• ギャップ研究の問題はその希少性にある。これは、パラメータに応じて（次の章で説明する方法と同様に）、関連する分布を調べようとするときに特に当てはまる。
• ギャップ分類の理論（例えばこれ）を確認するためには、ギャップからギャップが埋まるまでの価格だけでなく、その前後の価格を考察する、より複雑なモデルを構築しなければならない。これによって、考察される確率変数の数の増加がもたらされ、これは、上記したデータがないために問題を引き起こす可能性がある。
  

統計的機械学習

一例として取引システムのスキームについて考えましょう。各取引について、パラメータセットh が知られています。その値は、取引量とエグジットのアルゴリズムを一意に定義する必要があります（価格ではありません）。hの値はエントリの時点で確実に知られていなければなりません。それは何らかのテクニカル指標値などである可能性があります。機械学習については、h は一連の特徴です。

万が一のために、下記を改良します。 一般的に、取引システムは、特定の単一のシステムではなく、そのパラメトリックファミリのことです。 テストと最適化のタスクは、特定のパラメータ値を決定して修正することによって、このファミリから特定のシステムを選択します。 プレゼンテーションを複雑にしないために（このファミリのシステムの選択を定義するパラメータとhを混同しないでください）、この章では、特定のシステムを考慮し、そのファミリは考慮しません。 最適化の問題については、次の章で簡単に説明します。

hを特定の値に固定すると、市場エントリ/エグジットのための固定アルゴリズムが得られます。これは確率の分布を固定します。同じhについて、異なる収率があるかもしれないことに注意してください。固定されているのは収率分布であり、その具体的な値ではありません。

これは、利益分配法則の特徴hに対する依存性を回復させるという問題につながります。初期データは、パラメータ値の対の組としての取引履歴と、対応する収率(hi,ai)です。 このような問題は、統計的機械学習法を用いて解決されます。決定論的（非ランダム）依存を復元する問題を解決する際に、これらの方法と機械学習で使用される方法との間に根本的な違いはないことが分かります。

収率の分布が特定のファミリに属すると仮定して、問題の定式化を少し明確にしましょう。(hi,ai)対の集合が与えられます。収率分布aiは、パラメータθに依存する分布のパラメトリックファミリに属します。θ(h)の依存性を回復させることが必要です。この依存関係は、任意の関数間では求められません。初期データでは不十分です。通常は、θ(h)=θ(h,β)の関数のパラメトリックファミリの中で求められます。ここでパラメータβは(hi,ai)対の集合で決定され、ある種の最適性の要件が考慮されます。幅広い依存関係を発見するための関数族、パラメータの最適条件、およびこの最適値を検索する方法により、非常に多様な機械学習法が定義されます。

このような様々な手法から、トレーダーの視点から有意義なもの（例えば、利益の増加やドローダウンの削減など）を選択する必要があります。これは、パラメータβを選択する最適条件を選択する場合に特に重要です。この条件を変更すると、結果の依存性θ(h,β)が大きく異なる可能性があります。

与えられた収率分布のパラメトリックファミリaiに対して、リスク推定の問題は上記の2つのケースと同様に解決されたと仮定しましょう。依存関係θ=θ(h)が構築され、リスク値roptをそれぞれの与えられたθについて選択する方法も知られています。また、依存関係ropt=ropt(h)も知られています。システム構築はこれで完成したと考えることができます。

取引システムの統計と最適化

以下の最適化の単純な変形を考えてみましょう。それぞれn回の取引でシステムをN回実行します。 （平均収量が最も高い）最良の結果の中で、小さな数εN（0<ε<<1）を選択します。これらの選択された実行の中で最小の平均をmoptとし、最適なシステムがどれくらい良いかの指標と考えてます。

ここで、最適化結果を注意深く扱うべきであることを示す例として役立つシステムについて考えてみましょう。この例は、人工的ではありますが、問題の本質を見るのに十分です。利率の期待値がゼロで、パラメータにランダムな依存性があるシステムを考えてみましょう。

このシステムは、一定時刻にランダムな方向にエントリします。この方向は、同じ確率で乱数ジェネレータを使用して選択されます。ジェネレータのシード値は、各テスト実行前にパラメータの関数によって定義されます。したがって、パラメータのセットごとに同じ取引列が常に得られますが、これらのパラメータを変更すると、完全にランダムな、予測不可能な方法で列が変更されます。エグジットは一定の割合kで固定され逆指値と指値で実行されます。テスト間にはトレンドがないことにします。

明らかに、トレンドがなければ、このシステムの利率の期待値はゼロに近づきます（スプレッドが考慮された場合はわずかに負）。シリーズの取引の数をnで表します。すると、一連のn取引における利率の算術平均mは確率変数となります。これは、シリーズの収益性のある取引の数である確率変数nk によって表されます。変数nkは2項分布を有し、パラメータ 1/(1+k)およびnを有します。

Nが十分に大きいと、moptの値はm変数分布の(1-ε)分位に近くなります。この「取引システム」の無用さ（期待値がゼロのため）は明確ですが、 moptの値がかなり高くなることを示しましょう。分かりやすくするために、k=3、n=50、ε=0.1とし、mopt=2.52を得ます。

実際のテストでは、配置はすべて異り、実際の意味のあるシステムでははるかに複雑であることは明らかです。それにもかかわらず、この場合、最適化されたシステムの利点がランダムであるか否かを理解することは可能であり、必要です。

添付ファイル

番号	名称	種類	説明
1	bn.mq5	スクリプト	固定逆指値/指値でのエグジットリスクの計算
2	exp.mq5	スクリプト	固定トレール注文でのエグジットリスクの計算