Evaluación del riesgo en la secuencia de transacciones con un activo. Continuación

Índice

• Prefacio
• Suposiciones sobre los precios y sistemas de trading
• Distribución de rentabilidades. Observaciones generales
  
• Stop Loss y Take Profit fijos
  
• Trailing Stop fijo
• ¿Qué pasa a continuación?
• Estádísticas y brechas
  
• Aprendizaje automático estadístico
• Estadísticas y optimización del sistema de trading
• Archivos adjuntos

Prefacio

Continuamos estudiando nuestra teoría sobre el cálculo del riesgo que hemos empezado en la parte anterior. Vamos a llevarla a una conclusión lógica mostrando dos ejemplos. Además, esbozaremos otros posibles modos de aplicar la teoría de la probabilidad y la estadística matemática.

Suposiciones sobre los precios y sistemas de trading

¿Podemos investigar los resultados del trading de cualquier sistema usando los métodos descritos en el artículo anterior? Para eso, tenemos que estar seguros de que la secuencia de sus transacciones es una secuencia de los valores independientes y distribuidos uniformemente. Pero, por desgracia, la práctica demuestra que no siempre es así.

Pueden infringirse abmas condiciones, tanto de la independencia, como de la uniformidad de las distribuciones. Ralph Vince traza las vías para resolver estos problemas en su libro «The Mathematics of Money Management». El autor propone dividir los sistemas en varias partes, o subsistemas, para los cuales las condiciones requeridas se cumplen. Vince pone dos ejemplos. En el primer ejemplo, se trata de un sistema en el que hay una dependencia entre las transacciones consecuentes. En este caso, la secuencia se divide en dos partes: las transacciones con números pares e impares se consideran como obtenidas de diferntes sistemas. En el segundo ejemplo, se considera un sistema con pyramiding (incremento gradual de la posición). Cada paso de este incremento se considera como un sistema aparte. De esta manera, obtenemos un conjunto de varios sistemas: el primero se compone de los primeros pasos, el segundo de los segundos, etc.

Una vez investigados estos sistemas-pedacitos, tenemos que encontrar una manera de reunirlos de nuevo, es decir, hacer de ellos una «micro cartera» que considere las dependencias entre ellos. Para eso, necesitamos algo parecido a la teoría moderna del portafolio de Harry Markowitz.

Todo eso ya tiene la pinta de algo bastante complicado, pero todavía no es todo. Vamos a examinar el sistema donde la salida de cada operación se realiza por un precio fijado previamente: pstoploss o ptakeprofit. Además, la relación k=|ptakeprofit-penter|/|pstoploss-penter| se cambia de una operación a otra, dependiendo de un cierto indicador. La distribución de rentabilidades en cada transacción será muy simple: va a ser discreta, con dos valores -1 y k, aceptados con determinadas probabilidades. Pero puesto que para cada transacción el valor k es personal, la distribución para diferentes transacciones también será distinta. De esta manera, si intentamos dividir el sistema en «porciones», su número será igual al número de transacciones, y eso ya sería un contrasentido. En la práctica, al calcular el riesgo, lo más probable que k sea igual para todas las transacciones (algún valor medio, más típico). Así, para el análisis, podemos usar una versión simplificada del sistema que se utiliza en el trading real.

Sumamos todas las opciones posibles del uso de nuestra teoría del riesgo para los sistemas comerciales reales:

1. Dividimos el sistema comercial en varias partes.
2. Analizamos el análogo simplificado del sistema.
3. Analizamos la secuencia de transacciones sin comprobar la independencia y la uniformidad de las distribuciones. Además, podemos ajustar un poco el valor del riesgo obtenido usando otros métodos del análisis.
   

Es evidente que este enfoque del análisis de los sistemas no es universal y no siempre puede ser aplicado. Intentaremos hacer nuestro método más sistemático. Para eso, tendremos que hacer algunas suposiciones sobre los precios y sistemas.

1. Una serie de los precios se encuentra cerca del paseo aleatorio. No vamos a tratar de formalizar la definición de esta proximidad con una precisión matemática. Simplemente supongamos que si realizamos algunos cálculos en el paseo aleatorio y en los precios reales, los resultados de los primeros se puede considerar como la aproximación nula de los resultados de los segundos. Por ejemplo, así vamos a construir las suposiciones sobre la distribución de las variables aleatorias obtenidas desde la serie de precios.
   
2. Se puede enviar las cotizaciones producidas por el paseo aleatorio a la entrada del sistema. En este caso, los precios aleatorios «por término medio» tienen que ser próximos a los reales. Eso significa una volatilidad semejante en grandes intervalos temporales, una distribución parecida de los saltos de precios en los ticks, etc.
3. Las estructuras de la dependencia entre las transacciones del sistema en ambos casos (precios reales y paseos aleatorios) son parecidas. Pero las propias distribuciones de rentabilidades pueden diferenciarse considerablemente. Por ejemplo, si todas las rentabilidades se aumentan en el mismo número, las distribuciones se cambiarán (se desplazarán a la derecha). En este caso, los coeficientes de correlación entre las rentabilidades quedarán intactos.
   
4. El sistema está organizada de tal manera que sus transacciones en el paseo aleatorio están distribuidas uniformemente y pueden depender considerablemente entre sí sólo si se cruzan en el tiempo (la segunda se abre antes del cierre de la primera).
   

Describiremos estas suposiciones más detalladamente. El paseo aleatorio representa una amplia clase de los procesos aleatorios. Puede ser discreto o continuo. En los cálculos analíticos se usan los dos tipos, y en la modelación en el ordenador, se utiliza sólo el primero del mismo. Entre estos dos tipos hay una correlación: el paseo aleatorio con un tiempo continuo puede ser obtenido del discreto con un traspaso limitado, y cuando el paso tiende a cero en el tiempo. Este paseo aleatorio puede ser simétrico (ausencia de la tendencia, flat), o bien con un desplazamiento positivo/negativo (tendencia alcista/bajista). El paseo simétrico se considera con mayor frecuencia. En este caso, obtenemos lo siguiente de nuestra suposición sobre los precios:

• Es imposible predecir los resultados de las transacciones con ningunos indicadores. Eso nos simplifica considerablemente la modelación. Resulta que nos hace falta estudiar sólo aquélla parte del sistema que responde de la salida de las operaciones. No importa en absoluto cuándo y cómo ha ocurrido la entrada en la operación.
• En promedio, el beneficio es nulo. Eso no impide a que podamos obtener cualquier beneficio en cualquier transacción separada. Pero cuanto más transacciones cojamos, mayor totalidad de sus resultados va a corresponder a una cierta distribución de probabilidades. Un aspecto concreto de esta distribución depende del algoritmo de la salida de la operación, pero su valor esperado siempre es igual a cero.
  

Es necesario tomar en cuenta estas consecuencias durante la simulación (y sobre todo, la optimización) de los sistemas reales en los precios reales. Necesitamos unos criterios que demuestren con certeza suficiente que los resultados no han sido obtenidos en el caso del paseo aleatorio simétrico. Eso se refiere tanto a la distribuciön de rentabilidades, como al grado de la utilidad de los indicadores técnicos. Aparte de eso, la búsqueda de las desviaciones del paseo aleatorio simétrico también puede ser útil a la hora de buscar una idea para los sistemas comerciales. Más tarde, como ejemplo, veremos la posibilidad de usar lo que se llama «brechas (gaps) siempre se cierran».

Nuestran suposiciones aplican las restricciones también en los sistemas comerciales. En general, requieren una sencillez, uniformidad y transparencia respecto a las reglas de la entrada y salida en/de las transacciones. Estas reglas no deben aumentar adicionalmente la dependencia entre las transacciones (por ejemplo, dirigirse a la curva del capital), no deben cambiar ocasionalmente los modos de la salida de una transacción a otra (por ejemplo, cambiar ocasionalmente la relación beneficio/stop), las propias transacciones no deben ser demasiado frecuentes, etc. Se puede comprobar el cumpimiento aproximado de estas condiciones de una manera contemplativa, o bien por medio de una modelación en el ordenador usando el método de Monte Carlo.

Distribución de rentabilidades. Observaciones generales

Comenzaremos con la observación sobre el aspecto general de las distribuciones. Cuando introducen el concepto de la función de la distribución de probabilidades, habitualmente, hablan de los tipos discretos y continuos. Pero resulta que —aparte de estos tipos— son posibles también sus combinaciones. Es decir, son posibles las funciones de distribución representadas como P(x)=γcPc(x)+γdPd(x), donde γc≥0, γd≥0, γc+γd=1, y Pc(x) y Pd(x) —respectivamante, es la función de la distribución contínua (que tiene la densidad) y la función discreta (escalonada).

Como ejemplo, vamos a considerar un modo simple de salida: un Stop Loss y Take Profit fijos con una relación k entre ellos, con una limitación del tiempo de mantenimiento de la transacción texit. Simplificando, se puede decir que las transacciones con la slida por Take Profit/Stop Loss tienen una distribución discreta, y con la salida por el tiempo tienen una distribución continua. La distribución común será su combinación. Desde luego, eso complica los siguientes razonamientos. Hagamos una suposición más simple: supongamos que texit es bastante grande para considerar γc como un valor despreciable . Vamos a considerar que P(x)=Pd(x).

El ejemplo del caso γd=0 será la salida de la transacción con un Trailing Stop fijo. El caso cuando γd≠0 y γс≠0 al mismo tiempo también es muy posible. Por ejemplo, eso será la combinación de ambos ejemplos considerados. En este modo, el Stop Loss es inmóvil al principio de la transacción, pero apartir del momento de la ejecución de una condición, empieza a moverse como el Trailing Stop.

Vamos a concretizar nuestra teoría del riesgo para ambos ejemplos consideradeos arriba (sin analizar la versión combinada). Más abajo se muestran los scripts para calcular el valor ropt del riesgo óptimo para cada determinado caso de la distribución de rentabilidades. Pero a veces nos interesan otras tareas. Por ejemplo, el riesgo está establecido y necesitamos calcular δ que representa el nivel de certeza que le corresponde (o el valor máximo disponible de la rentabilidad media G0, como opción). En este caso, habrá que modificar el script, o bien iniciarlo con los datos de entrada diferentes, consiguiendo el valor necesario del riesgo.

Stop Loss y Take Profit fijos

Como hemos escrito más arriba, la distribución va a considerarse discreta. Las rentabilidades de las transacciones pueden adquirir dos valores: -1 y k, con probabilidades P-1 y Pk, respectivamente. Según la fórmula de la probabilidad completa P-1+Pk=1. La función de la distribución tiene una forma escalonada con dos saltos en los puntos -1 y k, el valor P-1 y Pk. El valor esperado de nuestra distribución es M=-1*P-1+k*Pk. Introducimos la denominación θ=Pk, de donde P-1=1-θ, M=(1+k)θ-1. Así, tenemos el caso con una familia paramétrica de las distribuciones que se establece con los parámetros k>0 y 0≤θ≤1. En caso del paseo aleatorio simétrico M=0, de donde θ=θ0=1/(1+k).

Que tengamos las rentabilidades ai de n transacciones, cada una de las cuales es igual o -1, o k.

1. Calculamos la estimación para el valor esperado M≈Mapr=(a1+a2+...+an)/n=(1+k)nk/n-1, donde nk es el número de las transacciones rentables. Si Mapr≤0, rechazamos el sistema comercial como no rentable. Ningunos subterfugios con la gestión del riesgo permitirán hacer un sistema rentable de un sistema no rentable. Si Mapr>0, pasamos al siguiente punto.
2. Tenemos que demostrar que las transacciones no es el resultado del trading en el paseo aleatorio simétrico. Para eso, la estimación Mapr tiene que ser bastante más grande que cero (con la certeza δ). Aceptamos la afirmación M=0 como hopótesis cero. Como estadística para la verificación, será el valor S=n(Mapr+1)/(1+k)=nk, que tendrá la distribución binomial estándar B(n,θ0) durante la ejecución de la hipótesis cero. Designamos su función de distribución a través de P(x). Para aceptar una hipótesis alternativa, tenemos que cerciorarnos de que P(S)>P(nθ0)+δ/2. Si eso se consigue, pasamos al siguiente punto. De lo contrario, rechazamos el sistema comercial.
3. Vamos a comprobar si se ejecuta la condición necesaria para el valor de la rentabilidad media mínima G0 que hemos seleccionado. Para eso, G0 no debe superar el cuantil δ qδ de la distribución de la variable aleatoria Λ, que hemos introducido en la primera parte (media aritmética de rentabilidades). El valor Λ coincide con Mapr, que se expresa a través de S. Ahora consideramos que el valor S está distribuido según la ley binomial con parámetros n y θapr=nk/n. Si la condición se cumple, pasamos al siguiente punto. Si no es así, determinamos el mínimo de transacciones n=nmin, necesario para su ejecución (aumentamosn gradualmente con θapr fijo hasta un valor con el que la desigualdad requerida se ejecuta).
4. Obtenemos la distribución empírica ρopt a través del método Monte Carlo. Para eso, modelamos un gran número de conjuntos con n rentabilidades en cada uno. Cada rentabilidad con la certeza Pk es igual a k y con la certeza 1-Pk es igual a -1. Para cada conjunto, determinamos el valor ropt,i usando el método considerado en la introducción de la primera parte. Su totalidad determina la distribución empírica de la variable aleatoria ρopt. Para estimar el riesgo ropt, usamos el cuantil δ selectivo de esta distribución.

#include <Math\Stat\Binomial.mqh>
#property script_show_inputs
input uint na=50;        // número de transacciones en la serie
input double kt=3;       // relación Take Profit/Stop Loss
input double pk=0.5;     // probabilidad del beneficio

#define NX 300           // número máximo de transacciones en la serie (para buscar nmin)
#define NB 10000         // número de muestras generadas para el método Monte Carlo
#define NR 1000          // número de intervalos de la división para el riesgo
double G0=0.15;          // rentabilidad media mínima
double D0=0.9;           // incremento mínimo más pequeño
double dlt=0.05;         // nivel de importancia

void OnStart()
  {
   if (D0<=0||D0>=1) {Print("D0 debe ser positivo y menos de uno"); return;}
   double m=(1+kt)*pk-1;             // beneficio esperado
   if(m<=0) {Print("beneficio esperado debe ser positivo"); return;}
   double s=na*pk;                   // estadística (número medio de transacciones rentables)
   double s0=na/(1+kt);              // número medio de transacciones rentables en caso del valor esperado nulo
   int ner;
   double p=MathCumulativeDistributionBinomial(s,na,1/(1+kt),ner);
   if(!MathIsValidNumber(p)) {Print("MathIsValidNumber(p) error ",ner); return;}
   double p0=MathCumulativeDistributionBinomial(s0,na,1/(1+kt),ner);
   if(!MathIsValidNumber(p0)) {Print("MathIsValidNumber(p0) error ",ner); return;}
   if(p<=p0+dlt/2) {Print("beneficio esperado cerca de cero"); return;}

   double q=MathQuantileBinomial(dlt,na,pk,ner),q0=na*(G0+1)/(kt+1);
   if(!MathIsValidNumber(q)) {Print("MathIsValidNumber(q) error ",ner); return;}
   if(q0>q)
     {
      Print("G0 supera cuantil dlt de la media aritmética de rentabilidades");
      uint nmin=na+1;
      for(;nmin<=NX;++nmin)
        {
         q=MathQuantileBinomial(dlt,nmin,pk,ner); q0=nmin*(G0+1)/(kt+1);
         if(!MathIsValidNumber(q)) {Print("MathIsValidNumber(q) error ",ner); return;}
         if(q0<=q) break;
        }
      if(nmin<=NX) Print("nmin = ",nmin);
      else Print("nmin más que ",NX);
      return;
     }
// método de Monte Carlo
   MathSrand(GetTickCount());
   double a[],c[],ropt[NB],A0,A,r,g,d,cn1,cn2,stp=1.0/NR;
   uint ir;
   ArrayResize(a,na);
   ArrayResize(c,na);
   for(uint ib=0; ib<NB;++ib)
     {
      for(uint i=0; i<na;++i) if(MathRandomNonZero()<=pk) a[i]=kt; else a[i]=-1;
      A=MathMean(a); A0=a[ArrayMinimum(a)];
      if(A<G0) {ropt[ib]=0; continue;}
      if(A0>0) {ropt[ib]=1-stp; continue;}
      cn1=1;
      for(ir=1;ir<NR;++ir)
        {
         r=ir*stp;
         cn2=1; for(uint i=0; i<na;++i) cn2*=1+r*a[i];
         if(cn2<cn1) {ropt[ib]=r-stp; break;}
         cn1=cn2;
         g=(MathPow(cn2,1.0/na)-1)/r;
         if(g<G0) {ropt[ib]=r-stp; break;}
         c[0]=1+r*a[0]; for(uint i=1; i<na;++i) c[i]=c[i-1]*(1+r*a[i]);
         d=dcalc(c);
         if(d<D0) {ropt[ib]=r-stp; break;}
        }
     }
     ArraySort(ropt);
     uint nr=(uint)(dlt*NB);
     Print("ropt = ",ropt[nr]);
  }

// la función dcalc() recibe el array de los valores c1, c2, ... cN y
// devuelve el incremento mínimo d. Supongamos que c0==1
double dcalc(double &c[])
  {
   if(c[0]<=0) return 0;
   double d=c[0], mx=c[0], mn=c[0];
   for(uint i=1; i<na;++i)
     {
      if(c[i]<=0) return 0;
      if(c[i]<mn) {mn=c[i]; d=MathMin(d,mn/mx);}
      else {if(c[i]>mx) mx=mn=c[i];}
     }
   return d;
  }
//+------------------------------------------------------------------+

Con los argumentos predefinidos, el script calcula el siguiente valor para el riesgo:

• ropt = 0.011

Eso corresponde a 1,1% del riesgo en cada transacción del capital destinado para el sistema.

Trailing Stop fijo

Vamos a considerar que trabajamos con una transacción tipo buy (los cambios necesarios para el tipo sell son evidentes). Designamos la diferencia entre el precio de entrada y el Stop Loss inicial a través de Δp=penter-pstop. La transacción será cerrada cuando el precio alcance el valor pmax-Δp, donde pmax es el precio máximo desde el momento de la entrada en la transacción. En el caso cuando la serie de los precios se modela por el paseo aleatorio con el tiempo continuo y el desplazamiento lineal, se puede encontrar la distribución de rentabilidades en forma explícita. Será la distribución exponencial desplazada a la izquierda en 1. La función de distribución será determinada más exactamente por la fórmula P(x)=1-exp(-θ(x+1)), si x≥-1 y P(x)=0, si x<-1. En caso del desplazamiento positivo (tendencia alcista) para el parámetro θ se ejecuta la desigualdad 0<θ<1, en caso del desplazamiento negativo (tendencia bajista): θ>1 y en caso del nulo (flat): θ=1. La fórmula M=1/θ-1 determina el valor esperado.

Puesto que hemos supuesto que los precios reales son próximos al paseo aleatorio, la distribución de rentabilidades de las transacciones en la serie también vamos a considerar como tal, con un valor del parámetro θ. Obtenemos una familia uno paramétrica de las distribuciones continuas. El valor concreto del parámetro θ (si hay tendencia) depende de la correlación entre la fuerza de esta tendencia y el Trailing Stop. Vamos a calcularlo usando los métodos de la estadística paramétrica para la distribución exponencial, en el historial existente de las transacciones (en este caso, usaremos el método de la estimación por máxima verosimilitud). Además, para los siguientes cálculos es importante que la suma (y la media aritmética) del número final de estas variables con el mismo parámetro tenga una distribución gamma bien estudiada.

Que tengamos ai que son las rentabilidades de n transacciones para cada una de las cuales se ejecuta ai>-1 (paraeso desatendemos el desplazamiento). Igual como en el apartado anterior, vamos a proponer un plan de siguientes acciones.

1. Calculamos la estimación para el valor esperado M≈Mapr=(a1+a2+...+an)/n. Si Mapr≤0, rechazamos el sistema comercial como no rentable. Si Mapr>0, pasamos al siguiente punto.
2. Vamos a intentar rebatir la hipótesis M=0. Como estadística para la verificación, será el valor S=Mapr+1, que tendrá (durante la ejecución de la hipótesis cero M=0) la distribución gamma Γ(n,1/n). Designamos su distribución P(x), entonces para aceptar la hipótesis alternativa, la desigualdad P(S)≥P(1)+δ/2 tiene que ser cierta. Si conseguimos rebatir la hipótesis cero, pasamos al siguiente punto, de lo contrario, rechazamos el sistema.
3. Comprobamos la condición necesaria para G0. Primero, tenemos que obtener la estimación del parámetro θ=θapr. Usando el método de la máxima verosimilitud, obtenemos θapr=1/(1+Mapr). La variable Λ será distribuida por la distribución gamma Γ(n,θapr/n) desplazada a la izquierda en 1. La condición requerida va a cumplirse si el cuantil δ de esta distribución gamma no es menos de G0+1. Si se cumple, seguimos adelante. Si no se cumple, podemos determinar el número mínimo necesario de las transacciones para el cumplimiento de esta condición. Para eso, aumentamos paso a paso el valor n, y cogemos como nmin aquél de ellos con el que la desigualdad requerida se cumple.

4. Se realiza igual como en el apartado anterior. El cambio concierne sólo a la distribución utilizada para la generación aleatoria de rentabilidades. Ahora, utilizamos la distribución exponencial con el parámetro θ=θapr desplazada a la izquierda en 1. En la libreríaMQL5 se utiliza la forma de parametrización algo diferente para la distribución exponencial, es el parámetro μ (valor esperado) que se expresa a través de θ o a través de M en forma de μ=1/θ o μ=M+1.

#include <Math\Stat\Gamma.mqh>
#include <Math\Stat\Exponential.mqh>
#property script_show_inputs
input uint na=50;           // número de transacciones en la serie
input double tht=0.65;      // parámetro de la distribución exponencial 0<tht<1

#define NX 300              // número máximo de transacciones en la serie (para buscar nmin)
#define NB 10000            // número de muestras generadas para el método Monte Carlo
#define NR 1000             // número de intervalos de la división para el riesgo
double G0=0.15;             // rentabilidad media mínima
double D0=0.9;              // incremento mínimo más pequeño
double dlt=0.05;            // nivel de importancia

void OnStart()
  {
   if(D0<=0 || D0>=1) {Print("D0 debe ser positivo y menos de uno"); return;}
   double m=1/tht-1;         // valor esperado
   if(m<=0) {Print("beneficio esperado debe ser positivo"); return;}

   int ner;   
   double p=MathCumulativeDistributionGamma(m+1,na,1.0/na,ner);
   if(!MathIsValidNumber(p)) {Print("MathIsValidNumber(p) error ",ner); return;}
   double p0=MathCumulativeDistributionGamma(1,na,1.0/na,ner);
   if(!MathIsValidNumber(p0)) {Print("MathIsValidNumber(p0) error ",ner); return;}
   if(p<=p0+dlt/2) {Print("valor esperado est”a cerca de cero"); return;}

   double q=MathQuantileGamma(dlt,na,1/tht/na,ner),q0=G0+1;
   if(!MathIsValidNumber(q)) {Print("MathIsValidNumber(q) error ",ner); return;}
   if(q0>q)
     {
      Print("G0 supera cuantil dlt de la media aritmética de rentabilidades");
      uint nmin=na+1;
      for(;nmin<=NX;++nmin)
        {
         q=MathQuantileGamma(dlt,nmin,1/tht/nmin,ner); q0=G0+1;
         if(!MathIsValidNumber(q)) {Print("MathIsValidNumber(q) error ",ner); return;}
         if(q0<=q) break;
        }
      if(nmin<=NX) Print("nmin = ",nmin);
      else Print("nmin más que ",NX);
      return;
     }    

// método de Monte Carlo
   MathSrand(GetTickCount());
   double a[],c[],ropt[NB],A0,A,r,g,d,cn1,cn2,stp=1.0/NR;
   uint ir;
   ArrayResize(a,na);
   ArrayResize(c,na);
   for(uint ib=0; ib<NB;++ib)
     {
      for(uint i=0; i<na;++i)
        {
         a[i]=MathRandomExponential(m+1,ner);
         if(!MathIsValidNumber(a[i])) {Print("Error MathRandomExponential()",ner); return;}
         a[i]-=1.0;
        }
      A=MathMean(a); A0=a[ArrayMinimum(a)];
      if(A<G0) {ropt[ib]=0; continue;}
      if(A0>0) {ropt[ib]=1-stp; continue;}
      cn1=1;
      for(ir=1;ir<NR;++ir)
        {
         r=ir*stp;
         cn2=1; for(uint i=0; i<na;++i) cn2*=1+r*a[i];
         if(cn2<cn1) {ropt[ib]=r-stp; break;}
         cn1=cn2;
         g=(MathPow(cn2,1.0/na)-1)/r;
         if(g<G0) {ropt[ib]=r-stp; break;}
         c[0]=1+r*a[0]; for(uint i=1; i<na;++i) c[i]=c[i-1]*(1+r*a[i]);
         d=dcalc(c);
         if(d<D0) {ropt[ib]=r-stp; break;}
        }
     }
   ArraySort(ropt);
   uint nr=(uint)(dlt*NB);
   Print("ropt = ",ropt[nr]);
  }
// la función dcalc() recibe el array de los valores c1, c2, ... cN y
// devuelve el incremento mínimo d. Supongamos que c0==1
double dcalc(double &c[])
  {
   if(c[0]<=0) return 0;
   double d=c[0], mx=c[0], mn=c[0];
   for(uint i=1; i<na;++i)
     {
      if(c[i]<=0) return 0;
      if(c[i]<mn) {mn=c[i]; d=MathMin(d,mn/mx);}
      else {if(c[i]>mx) mx=mn=c[i];}
     }
   return d;
  }
//+------------------------------------------------------------------+

Con los argumentos predefinidos, el script obtenemos el siguiente valor del riesgo:

• ropt = 0.015

Eso corresponde a 1,5% del riesgo en cada transacción del capital destinado para el sistema.

La secuencia considerada en la parte anterior como ejemplo de treinta transacciones fue obtenida precisamente para el sistema con la salida por el Trailing Stop. Por eso, podemos aplicar nuestro método a ella. Este método (igual como el método considerado antes) muestra que la secuencia no vale para el trading con las condiciones establecidas (n, δ, G0, D0). Este resultado no cambiará incluso si quitamos el desplazamiento, añadiendo a todos ai un pequeño número positivo de tal manera que para todos i=1,...,n se cumpla la condición ai>-1.

Nota: Si con todos los argumentos establecidos por defecto el script muestra el error con el número 4, entonces el terminal no ha superado las actualizaciones necesarias. En este caso, hay que poner comentarios en una parte del script (de la línea 21 a la línea 42). Esta parte contiene los cálculos relacionados con la distribución gamma. Para ellos, se puede usar el script en el lenguaje R que va a continuación.

na=50; tht=0.65; dlt=0.05; G0=0.15; nx=300
m=1/tht-1; l1=l2=l3=FALSE
l1 = m > 0
if (l1) l2 = pgamma(m+1,na,scale = 1/na) > pgamma(1,na,scale = 1/na)+dlt/2
if (l2) l3 = G0+1 <= qgamma(dlt,na,scale = 1/tht/na)

if(!l1) cat("m must be greater 0\n")

if(l1 & l3) cat("G0 and na are ok\n") else cat("na too small or G0 too big\n")

if(l1 & l2 & !l3)
{for (nmin in (na+1):(nx+1)) {if(G0+1 <= qgamma(dlt,nmin,scale = 1/tht/nmin)) break()}
 if (nmin<=nx) {cat("nmin =",nmin)} else {cat("nmin >",nx)}
}

¿Qué pasa a continuación?

Es obvio que no se puede considerar los métodos arriba expuestos como completos y definitivos. Para la simplicidad del estudio, hemos admitido a priori que las transacciones son independientes y están distribuidas uniformemente. Pero eso requiere un estudio más profundo y puede que no sea así. Puede ser útil que la distribución de rentabilidades pertenezca o sea próxima a una determinada familia paramétrica. Pero puede que también sea necesario estudiar esta pertenencia adicionalmente.

Nos contentábamos con las estimaciones puntuales de los parámetros de las distribuciones y no buscábamos los intervalos confiables para ellos. Pero después de su construcción, surge la pregunta sobre la estabilidad de la rentabilidad del sistema en caso de las oscilaciones de estos parámetros.

La existencia de muchos posibles métodos, desde luego, no significa que hay que usarlos constantemente y todos juntos a la vez. Pero es mejor estar interado de ellos y saber usarlos en caso de necesidad, que quedarse engañado por la casualidad.

En la parte del artículo que nos queda, marcaremos brevemente algunos otros posibles modos de aplicación de la teoría de probabilidades.

Estádísticas y brechas

Una brecha (gap) es un salto entre los precios de cierre y de apertura de dos barras sucesivas. También debe cumplirse el requerimiento que entre estas dos barras haya un intervalo considerable. Se considera que las «brechas simpre se cierran». El cierre de una brecha significa que dentro de un tiempo tras la rotura, el precio vuelve al precio de cierre de la barra precedente a la rotura. A veces algunos traders intentan construir el sistema comercial a base de esta regularidad. ¿Será posible eso?

De la teoría del paseo aleatorio simétrico en la recta, sabemos que se conseguirá cualquier valor del precio en un período de tiempo suficientemente grande, con la probabilidad casí igual a 1. Es decir, casi seguramente, el «gap siempre se cerrará» con estas condiciones también. Pero como sabemos, en caso del paseo aleatorio simétrico, es imposible obtener ningún sistema rentable. ¿Significa eso que el sistema con las brechas no tiene ningunas posibilidades para existir?

Тo tiene por qué ser así en absoluto. Es importante no sólo el propio hecho del cierre de las brechas, sino también cómo se cierran. Se tiene en cuenta el cierre no de cada brecha en concreto, sino de un conjunto de ellas; entonces, se puede considerar las distribuciones empíricas de probabilidades de las variables aleatorias relacionadas con ellas. Puede revelarse la diferencia entre los precios reales y el modelo del paseo aleatorio simétrico. Las diferencias pueden ser varias. Puede ser que el movimiento en la dirección de la ruptura no es suficiente, o el tiempo hasta el cierre es poco que para el paseo aleatorio, y muchas cosas más. Lo único que importa es que la presencia y la importancia de estas desviaciones se puede determinar a través de los métodos de la teoría de probabilidades y estadística matemática. Después de asegurarse de estas desviaciones, se puede construir sistemas comerciales en base de ellas. Además, se puede intentar comprobar la teoría que clasifica las brechas.

Vamos a considerar la variante más simple de la búsqueda de las desviaciones del paseo aleatorio. Será el valor que determina el grado de la fuerza con la que el precio se avanza en la dirección de la ruptura hasta el cierre de la brecha. Se puede obtener la distribución empírica de este valor usando el historial de precios, y compararla con la teórica. Para la comparación de estas dos distribuciones se puede usar alguna bondad de ajuste.

Vamos a considerer el modelo del paseo aleatorio simétrico con el tiempo discreto. Que las brechas grandes sean raras en él (como en los precios reales), y en los intervalos entre ellas, esté cerca del paseo con el tiempo continuo (proceso de Wiener). Introducimos las designaciones: g es el tamaño de la brecha, m es el avance máximo en dirección de la brecha hasta su cierre. Entonces, la variable aleatoria x=m/g va a tener la función de la distribució próxima a la función P(x) es tal que P(x)=1-1/x, si x≥1 y P(x)=0, si x<1. Es la imagen para mostrar la variables introducidas:

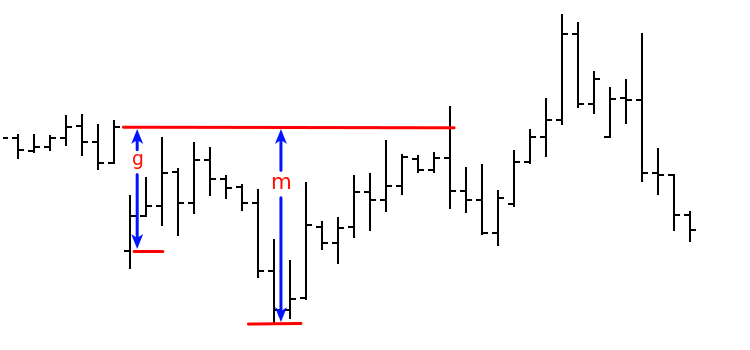
La cuestión que hemos tocado requere un estudio más profundo y detallado. Por eso, nos limitaremos con las siguientes observaciones por ahora:

• El problema del estudio de las brechas consiste en su rareza. Eso ocurre sobre todo cuando se intenta estudiar las distribuciones relacionadas con ellas dependiendo de los parámetros (parecido a lo que se escribe en el siguiente apartado).
• Para comprobar la teoría de la clasificación de las brechas (por ejemplo, aquí), será necesario construir un modelo más complejo, que toma en consideración no sólo los precios de la ruptura al cierre, sino también los anteriores y los siguientes. Eso llevará al aumento del número de las variables aleatorias consideradas. Eso, en su lugar, puede crear problemas debido a la poca cantidad de datos especificado más arriba.
  

Aprendizaje automático estadístico

Vamos a examinar la estructura esquemática del sistema comercial. Para cada transacción se sabe un conjunto de parámetros h cuyos valores deben permitir determinar explícitamente el volumen de la transacción y el algoritmo (¡no el precio!) de la salida. Se debe saber el valor h con certeza para el momento de la entrada. Pueden ser algunos valores de los indicadores técnicos, etc. En los términos del aprendizaje automático, h es un conjunto de indicios.

Por si acaso, hagamos la siguiente expresión correctiva. Habitualmente, cuando hablan de un sistema comercial, no tienen en cuenta un sistema en concreto, sino su familia paramétrica. La tarea de la simulación y optimización consiste en elegir un sistema concreto de esta familia, determinando y fijando un valor concreto del parámetro. Para no complicar lo expuesto (no confundir h con los parámetros que establecen la elección del sistema de la familia), en este capítulo estamos hablando de un sistema concreto, y no de su familia. Hablaremos brevemente del problema de la optimización en el siguiente capítulo.

Al fjar un valor h concreto, obtenemos un algoritmo fijo de la entrada/salida de la transacción. Eso nos da una distribución fija de probabilidades. Nótese que pueden haber rentabilidades diferentes con el mismo h. Se fija la distribución de rentabilidades y no su valor concreto.

De esta manera, aparece la tarea de recuperar la dependencia de la ley de la distribución de probabilidades de los indicios de h. Los datos iniciales son el historial de transacciones en forma de un conjunto de parejas desde los valores de parámetros y las rentabilidades que les corresponden (hi,ai). Estos problemas se resuelven usando los métodos del aprendizaje automático estadístico. Además, en este caso, resulta que no existe una diferencia significativa de estos métodos de los que se utilizan en el aprendizaje automático durante la solución de problemas de la recuperación de la dependencia determinada (no ocasional).

Vamos a especificar un poco el planteamiento de nuestra tarea, suponiendo la pertenencia de la distribución de rentabilidades a una cierta familia. Se establece un conjunto de parejas (hi,ai). La distribución de rentabilidades ai pertenece a un conjunto paramétrico de distribuciones que depende del parámetro θ. Se necesita recuperar la dependencia θ(h). Esta dependencia se busca entre las funciones arbitrarias: para eso, los datos iniciales no son suficientes. Normalmente, se busca entre alguna familia paramétrica de las funciones: θ(h)=θ(h,β), donde el parámetro β se determina por el conjunto de las parejas (hi,ai) tomando en cuenta los requerimientos de algún óptimo suyo. Una amplia selección de las familias de las funciones para la búsqueda de las dependencias, condiciones del óptimo para el parámetro y los métodos de la búsqueda de este valor óptimo de los valores determina una gran variedad de los métodos del aprendizaje automático.

Tenemos que elegir de esta gran variedad sobre todo los métodos que son sensatos desde el punto de vista del trader (por ejemplo, contribuyen al aumento del beneficio o reducción del drawdown). Sobre todo es importante tomar en cuenta las condiciones del óptimo para elegir el parámetro β. Cuando se cambia esta condición, la dependencia θ(h,β) obtenida como respuesta puede variar considerablemente.

Supongamos que para esta familia paramétrica de las distribuciones de rentabilidades ai hemos solucionado el problema de la estimación de los riesgos de manera parecida a dos casos considerados antes. Entonces, puesto que hemos construido la dependencia θ=θ(h) y sabemos la manera de elegir el valor del risgo ropt para cada θ establecido, también sabemos la dependencia ropt=ropt(h). Se puede considerar la construcción de nuestro sistema por concluida.

Estadísticas y optimización del sistema de tradingю

Vamos a considerar la siguiente versión simple de la optimización. Hagamos N recorridos por nuestro sistema, por n de transacciones en cada uno. Elijamos una cantidad establecida εN de ellos, donde 0<ε<<1 son los mejores (con una rentabilidad media más grande). Designamos, a través de mopt, la menor media entre estos recorridos seleccionados, y vamos a considerarla como el índice de un sistema óptimo.

Ahora, vamos a considerar un sisteba a cuyo base veremos que hay que tener con cuidado los resultados de la optimización. Aunque el ejemplo es algo artificial, pero nos permitirá distinguir el quid de la la cuestión. Vamos a considerar un sistema con el valor esperado nulo de la rentabilidad y la dependencia arbitraria de los parámetros.

Este sistema va a hacer entradas en una dirección arbitraria, en los momentos de tiempo fijos. La dirección va a elegirse a través del generador de números aleatorios con la probabilidad igual. El valor inicial para la inicialización de este generador, antes de cada recorrido de la simulación, será la función de los parámetros. De esta manera, para cada conjunto de parámetros, siempre vamos a obtener la misma secuencia de transacciones, pero con el cambio de estos parámetros, la secuencia va a cambiar de una manera absolutamente arbitraria. La salida de la transacción va a realizarse según el Stop Loss/Take Profit fijo con la relación k constante. Además, consideramos que en este intervalo de simulación no hay tendencia.

Es evidente que por falta de la tendencia, el valor esperado de las rentabilidades de este sistema será próximo a cero (un poco negativo, tomando en cuenta el spread). Designamos el número de transacciones en la serie a través de n. Entonces, la media aritmetica de las rentabilidades en la serie n de las transacciones m será una variante aleatoria. Se expresa a través de una variable aleatoria nk que representa el número de las transacciones rentables en la serie: m=(1+k)nk/n-1. El valor nk tiene la distribución binomial con los parámetros 1/(1+k) y n.

Cuando N es bastante grande, el valor mopt será próximo al cuantil (1-ε)de la distribución de la variable m. Vamos a demostrar que a pesar de la inviabilidad de este «sistema comercial» (debido al valor esperado nulo), el valor mopt será bastante elevado. Pongamos para la certeza: k=3, n=50, ε=0.1 y obtendremos mopt=2.52.

Es obvio que todo es algo diferente y más complicado para los sistemas reales y sensatos. No obstante, en este caso también se puede y se debe intentar comprender lo siguiente, ¿será casual la ventaja de un sistema optimizado?

Archivos adjuntos

№	Nombre	Tipo	Descripción
1	bn.mq5	script	cálculo del riesgo para salir con un Stop Loss y Take Profit fijos
2	exp.mq5	script	cálculo del riesgo para salir con un Trailing Stop fijo