Оценка риска в последовательности сделок с одним активом. Продолжение

Оглавление

• Предисловие
• Предположения о ценах и торговых системах
• Распределения доходностей. Общие замечания
  
• Фиксированные стоп-лосс и тейк-профит
  
• Фиксированный трейлинг-стоп
• Что дальше?
• Статистика и гэпы
  
• Статистическое машинное обучение
• Статистика и оптимизация торговой системы
• Прикреплённые файлы

Предисловие

Продолжим изучение нашей теории о вычислении риска, начатое в предыдущей части. Доведём её до логического завершения на двух примерах. Также кратко наметим другие возможные способы применения теории вероятностей и математической статистики.

Предположения о ценах и торговых системах

Можем ли мы исследовать результаты торговли любой системы методами, описанными в предыдущей статье? Для этого мы должны быть уверены, что последовательность её сделок — это последовательность независимых и одинаково распределённых величин. Но к сожалению, практика показывает, что это не всегда так.

Нарушены могут быть оба условия: и независимости, и одинаковости распределений. В своей книге “Математика управления капиталом” Ральф Винс намечает пути к решению этих проблем. Он предлагает разбивать системы на несколько частей — подсистем, для которых требуемые условия выполняются. Винс приводит два примера. В первом речь идет о системе, в которой между последующими сделками есть зависимость. В этом случае последовательность разбивается на две части — сделки с четными и нечетными номерами рассматриваются как полученные от разных систем. Во втором примере рассматривается система с пирамидингом — ступенчатым наращиванием объёма позиции. Каждый шаг такого наращивания рассматривается как отдельная система. Таким образом, мы получаем совокупность из нескольких систем: первая состоит из первых шагов, вторая из вторых и т.д.

После того, как такие системы-"кусочки" исследованы, мы должны найти способ снова собрать их вместе — сделать из них “микропортфель”, учитывающий зависимости между ними. Для этого нам нужно что-то наподобие портфельной теории Марковица.

Всё это выглядит уже достаточно сложным, но и это еще не всё. Рассмотрим систему, где выход из каждой сделки происходит по одной из заранее зафиксированных цен: pstoploss или ptakeprofit. При этом соотношение k=|ptakeprofit-penter|/|pstoploss-penter| меняется от сделки к сделке в зависимости от определенного индикатора. Распределение доходностей в каждой сделке будет очень простое — дискретное, с двумя значениями -1 и k, принимаемыми с определенными вероятностями. Но поскольку для каждой сделки значение k своё, то и распределение у разных сделок тоже будет разным. Таким образом, если мы попробуем разбить систему на “кусочки”, то их число будет равно числу сделок, а это выглядит явной бессмыслицей. На практике при расчете риска мы, скорее всего, возьмем k одинаковым для всех сделок (какое-либо среднее, наиболее характерное его значение). Таким образом, для анализа мы можем использовать упрощенную версию системы, используемой при реальной торговле.

Суммируем все возможные варианты использования нашей теории риска для реальных торговых систем:

1. Разбиваем торговую систему на несколько частей.
2. Исследуем упрощенный аналог системы.
3. Анализируем последовательность сделок без проверки на независимость и одинаковость распределений. При этом мы можем несколько скорректировать полученную величину риска, используя другие методы анализа.
   

Очевидно, что такой подход к исследованию систем не универсален и не всегда применим. Попытаемся сделать наш метод более систематичным. Для этого нам придется сделать несколько предположений о ценах и системах.

1. Ряд цен близок к случайному блужданию. Не будем пытаться математически точно формализовать определение этой близости. Лишь предположим, что если мы проводим какие-либо вычисления на случайном блуждании и на реальных ценах, то результаты первых можно рассматривать как нулевое приближение результатов вторых. Например, так будем строить предположения о распределениях случайных величин, получаемых из ценового ряда.
   
2. На вход системы можно подать котировки, порожденные случайным блужданием. При этом случайные цены "в среднем" должны быть близки к реальным. Это означает схожую волатильность на больших временных интервалах, похожее распределение скачков цен на тиках и т.д.
3. Структура зависимости между сделками системы в обоих случаях (реальные цены и случайные блуждания) близки. Сами распределения доходностей при этом могут заметно отличаться. Например, если все доходности увеличатся на одно и то же число, то распределения изменятся (сдвинутся вправо). Но при этом коэффициенты корреляции между доходностями останутся прежними.
   
4. Система устроена таким образом, что её сделки на случайном блуждании одинаково распределены и могут быть значимо зависимы между собой, только если сильно пересекаются между собой по времени (вторая открывается до закрытия первой).
   

Опишем подробнее эти предположения. Случайное блуждание — обширный класс случайных процессов. Оно может быть дискретное или непрерывное. При аналитических вычислениях применяются оба типа, а при моделировании на компьютере — только первое. Между этими типами есть связь — блуждание с непрерывным временем может быть получено из дискретного предельным переходом при стремлении шага по времени к нулю. Также блуждание может быть либо симметричным (отсутствие тренда, флэт), либо с положительным/отрицательным сдвигом (тренд вверх/вниз). Чаще всего рассматривается симметричное блуждание. В этом случае из нашего предположения о ценах получаем следующее:

• Результаты сделок невозможно предсказать никакими индикаторами. Это сильно упрощает нам моделирование. Оказывается, нам нужно изучать лишь ту часть системы, которая отвечает за выход из сделок. Когда и как произошел вход в сделку — совершенно неважно.
• Прибыль в среднем нулевая. Это не мешает тому, что в любой единичной сделке мы можем получить любую прибыль. Но чем больше мы возьмем сделок, тем больше совокупность их результатов будет соответствовать некоторому распределению вероятностей. Конкретный вид этого распределения зависит от алгоритма выхода из сделки, но его матожидание всегда равно нулю.
  

Эти следствия нужно учитывать при тестировании (и особенно оптимизации) реальных систем на реальных ценах. Нужны критерии, показывающие, что с достаточной достоверностью результаты получены не при симметричном случайном блуждании. Это касается и распределения доходностей сделок, и степени полезности технических индикаторов. Помимо этого, поиск отклонений от симметричного случайного блуждания может быть полезен и при поиске идей для торговых систем. В качестве примера позднее мы рассмотрим возможность использования того, что “гэпы всегда закрываются”.

Наши предположения накладывают ограничения и на торговые системы. В основном, они требуют простоты, однородности и прозрачности в правилах входа и выхода из сделок. Эти правила не должны дополнительно усиливать зависимость между сделками (например, обращаться к кривой капитала), не должны произвольно менять способы выхода от сделки к сделке (например, случайно менять соотношение профит/стоп), сами сделки не должны быть слишком частыми и т.д. Приближённое выполнение этих условий можно проверить либо умозрительно, либо моделированием на компьютере методом Монте-Карло.

Распределения доходностей. Общие замечания

Начнем с замечания об общем виде распределений. Когда вводят понятие функции распределения вероятностей, обычно говорят про дискретные и непрерывные виды. Но оказывается, что помимо таковых, возможны и их смеси. То есть возможны функции распределения, представимые в виде P(x)=γcPc(x)+γdPd(x), где γc≥0, γd≥0, γc+γd=1, а Pc(x) и Pd(x) — соответственно, непрерывная (имеющая плотность) и дискретная (ступенчатая) функции распределения.

В качестве примера рассмотрим простой способ выхода — фиксированные стоп-лосс и тейк-профит с отношением k между ними, дополненный ограничением по времени удержания сделки texit. Упрощая, можно сказать, что сделки с выходом по тейк-профиту/стоп-лоссу имеют дискретное распределение, а с выходом по времени — непрерывное. Общее распределение и будет их смесью. Естественно, это усложняет дальнейшие рассуждения. Сделаем упрощающее предположение: допустим, что texit достаточно велико, чтобы считать γc пренебежимо малой. Будем считать, что P(x)=Pd(x).

Примером случая γd=0 будет выход из сделки с фиксированным трейлинг-стопом. Вполне возможен и случай, когда одновременно γd≠0 и γс≠0. Например, таковым будет комбинация обоих рассмотренных примеров. При этом способе в начальный период сделки стоп-лосс неподвижен, но с момента выполнения некоторого условия он начинает передвигаться, как трейлинг-стоп.

Конкретизируем нашу теорию риска для обоих рассмотренных выше примеров (комбинированный вариант рассматривать не будем). Ниже будут приведены скрипты для вычисления величины ropt оптимального риска для каждого конкретного случая распределения доходностей. Но иногда нас интересуют другие задачи. Например, риск задан, а нам нужно вычислить δ — соответствующий ему уровень достоверности (или максимальное доступное значение средней доходности G0, как вариант). В этом случае скрипт надо будет либо изменить, либо запускать с разными входными данными, добиваясь нужного значения для риска.

Фиксированные стоп-лосс и тейк-профит

Как мы уже писали выше, распределение будем считать дискретным. Доходности сделок могут принимать два значения: -1 и k, с вероятностями P-1 и Pk, соответственно. По формуле полной вероятности P-1+Pk=1. Функция распределения имеет ступенчатую форму с двумя скачками в точках -1 и k, величиной P-1 и Pk. Матожидание нашего распределения M=-1*P-1+k*Pk. Введём обозначение θ=Pk, откуда P-1=1-θ, M=(1+k)θ-1. Таким образом, мы имеем дело с параметрическим семейством распределений, которое задается параметрами k>0 и 0≤θ≤1. В случае симметричного случайного блуждания M=0, откуда θ=θ0=1/(1+k).

Пусть у нас имеются ai — доходности n сделок, каждая из которых равна либо -1, либо k.

1. Вычислим оценку для матожидания M≈Mapr=(a1+a2+...+an)/n=(1+k)nk/n-1, где nk — количество прибыльных сделок. Если Mapr≤0, то отвергаем торговую систему как убыточную. Никакими ухищрениями с управлением риском невозможно убыточную систему сделать прибыльной. Если же Mapr>0, то переходим к следующему пункту.
2. Мы должны показать, что сделки не являются результатом торговли на симметричном случайном блуждании. Для этого оценка Mapr должна быть значимо больше нуля (с достоверностью δ). Примем в качестве нулевой гипотезы утверждение, что M=0. Статистикой для проверки будет величина S=n(Mapr+1)/(1+k)=nk, которая при выполнении нулевой гипотезы имеет стандартное биномиальное распределение B(n,θ0). Обозначим её функцию распределения через P(x). Чтобы принять альтернативную гипотезу, мы должны убедиться, что P(S)>P(nθ0)+δ/2. Если это удалось, то переходим к следующему пункту. Если нет — отвергаем торговую систему.
3. Проверим, выполняется ли необходимое условие для выбранного нами значения минимальной средней доходности G0. Для этого G0 не должно быть больше, чем δ-квантиль qδ распределения случайной величины Λ, введенной нами в первой части (среднее арифметическое доходностей). Величина Λ совпадает с Mapr, которая выражается через S. Величину теперь S считаем распределенной по биномиальному закону с параметрами n и θapr=nk/n. Если условие выполняется, переходим к следующему пункту. Если нет, то определим минимум сделок n=nmin, необходимый для его выполнения (пошагово увеличиваем n при фиксированном θapr до значения, при котором требуемое неравенство выполняется).
4. Методом Монте-Карло получаем эмпирическое распределение ρopt. Для этого моделируем большое число наборов по n доходностей сделок в каждом. Каждая доходность с вероятностью Pk равна k и с вероятностью 1-Pk равна -1. Для каждого набора определяем значение ropt,i способом, рассмотренным во введении к первой части. Их совокупность определяет эмпирическое распределение случайной величины ρopt. Для оценки риска ropt используем выборочный δ-квантиль этого распределения.

#include <Math\Stat\Binomial.mqh>
#property script_show_inputs
input uint na=50;        // число сделок в серии
input double kt=3;       // соотношение тейкпрофит/стоплосс
input double pk=0.5;     // вероятность профита

#define NX 300           // максимальное число сделок в серии (для поиска nmin)
#define NB 10000         // количество генерируемых выборок для метода Монте-Карло
#define NR 1000          // количество интервалов разбиения для риска
double G0=0.15;          // наименьшая средняя доходность
double D0=0.9;           // наименьший минимальный прирост
double dlt=0.05;         // уровень значимости

void OnStart()
  {
   if (D0<=0||D0>=1) {Print("D0 должно быть положительным и меньше единицы"); return;}
   double m=(1+kt)*pk-1;             // математическое ожидание
   if(m<=0) {Print("математическое ожидание должно быть положительным"); return;}
   double s=na*pk;                   // статистика (среднее число прибыльных сделок)
   double s0=na/(1+kt);              // среднее число прибыльных сделок при нулевом матожидании
   int ner;
   double p=MathCumulativeDistributionBinomial(s,na,1/(1+kt),ner);
   if(!MathIsValidNumber(p)) {Print("MathIsValidNumber(p) error ",ner); return;}
   double p0=MathCumulativeDistributionBinomial(s0,na,1/(1+kt),ner);
   if(!MathIsValidNumber(p0)) {Print("MathIsValidNumber(p0) error ",ner); return;}
   if(p<=p0+dlt/2) {Print("математическое ожидание близко к нулю"); return;}

   double q=MathQuantileBinomial(dlt,na,pk,ner),q0=na*(G0+1)/(kt+1);
   if(!MathIsValidNumber(q)) {Print("MathIsValidNumber(q) error ",ner); return;}
   if(q0>q)
     {
      Print("G0 больше dlt-квантиля среднего арифметического доходностей");
      uint nmin=na+1;
      for(;nmin<=NX;++nmin)
        {
         q=MathQuantileBinomial(dlt,nmin,pk,ner); q0=nmin*(G0+1)/(kt+1);
         if(!MathIsValidNumber(q)) {Print("MathIsValidNumber(q) error ",ner); return;}
         if(q0<=q) break;
        }
      if(nmin<=NX) Print("nmin = ",nmin);
      else Print("nmin более чем ",NX);
      return;
     }
// метод Монте-Карло
   MathSrand(GetTickCount());
   double a[],c[],ropt[NB],A0,A,r,g,d,cn1,cn2,stp=1.0/NR;
   uint ir;
   ArrayResize(a,na);
   ArrayResize(c,na);
   for(uint ib=0; ib<NB;++ib)
     {
      for(uint i=0; i<na;++i) if(MathRandomNonZero()<=pk) a[i]=kt; else a[i]=-1;
      A=MathMean(a); A0=a[ArrayMinimum(a)];
      if(A<G0) {ropt[ib]=0; continue;}
      if(A0>0) {ropt[ib]=1-stp; continue;}
      cn1=1;
      for(ir=1;ir<NR;++ir)
        {
         r=ir*stp;
         cn2=1; for(uint i=0; i<na;++i) cn2*=1+r*a[i];
         if(cn2<cn1) {ropt[ib]=r-stp; break;}
         cn1=cn2;
         g=(MathPow(cn2,1.0/na)-1)/r;
         if(g<G0) {ropt[ib]=r-stp; break;}
         c[0]=1+r*a[0]; for(uint i=1; i<na;++i) c[i]=c[i-1]*(1+r*a[i]);
         d=dcalc(c);
         if(d<D0) {ropt[ib]=r-stp; break;}
        }
     }
     ArraySort(ropt);
     uint nr=(uint)(dlt*NB);
     Print("ropt = ",ropt[nr]);
  }

// функция dcalc() принимает массив из значений c1, c2, ... cN и
// возвращает минимальный прирост d. Полагаем c0==1
double dcalc(double &c[])
  {
   if(c[0]<=0) return 0;
   double d=c[0], mx=c[0], mn=c[0];
   for(uint i=1; i<na;++i)
     {
      if(c[i]<=0) return 0;
      if(c[i]<mn) {mn=c[i]; d=MathMin(d,mn/mx);}
      else {if(c[i]>mx) mx=mn=c[i];}
     }
   return d;
  }
//+------------------------------------------------------------------+

При аргументах, заданных по умолчанию, скрипт рассчитывает следующее значение для риска:

• ropt = 0.011

Это соответствует 1.1% риска в каждой сделке от капитала, выделенного для системы.

Фиксированный трейлинг-стоп

Будем считать, что имеем дело со сделкой типа buy (необходимые изменения для типа sell будут очевидны). Обозначим через Δp=penter-pstop разницу между ценой входа и начальным стоп-лоссом. Сделка закроется, когда цена достигнет значения pmax-Δp, где pmax — максимальная цена с момента входа в сделку. В случае, когда ряд цен моделируется случайным блужданием с непрерывным временем и линейным сдвигом, распределение доходностей можно найти в явном виде. Это будет экспоненциальное распределение, сдвинутое влево на единицу. Более точно функция распределения будет определена формулой P(x)=1-exp(-θ(x+1)), если x≥-1 и P(x)=0, если x<-1. При положительном сдвиге (тренд вверх) для параметра θ выполняется неравенство 0<θ<1, при отрицательном (тренд вниз): θ>1 и при нулевом (флэт): θ=1. Матожидание определяется формулой M=1/θ-1.

Поскольку мы предположили, что реальные цены близки к случайному блужданию, то и распределение доходностей сделок в серии тоже будем считать таковым, с некоторым значением параметра θ. Получаем однопараметрическое семейство непрерывных распределений. Конкретное значение параметра θ при наличии тренда зависит от соотношения между силой этого тренда и трейлинг-стопом. Рассчитаем его методами параметрической статистики для экспоненциального распределения по имеющейся истории сделок (в данном случае воспользуемся методом максимального правдоподобия). Также для дальнейших вычислений важно, что сумма (и арифметическое среднее) конечного числа таких величин с одним и тем же параметром имеет хорошо изученное гамма-распределение.

Пусть у нас имеются ai — доходности n сделок, для каждой из которых выполняется ai>-1 (для этого пренебрегаем проскальзыванием). Как и в предыдущей главе, предложим план дальнейших действий.

1. Вычислим оценку для матожидания M≈Mapr=(a1+a2+...+an)/n. Если Mapr≤0, то отвергаем торговую систему как убыточную. Если же Mapr>0, то переходим к следующему пункту.
2. Попытаемся опровергнуть гипотезу M=0. Статистикой для проверки будет величина S=Mapr+1, которая имеет (при выполнении нулевой гипотезы M=0) гамма-распределение Γ(n,1/n). Обозначим её распределение P(x), тогда для принятия альтернативной гипотезы должно быть верно неравенство P(S)≥P(1)+δ/2. Если нулевую гипотезу удалось опровергнуть, то переходим к следующему пункту, а если нет — отвергаем систему.
3. Поверяем необходимое условие для G0. Для начала нам нужно получить оценку параметра θ=θapr. Используя метод максимального правдоподобия, получим θapr=1/(1+Mapr). Величина Λ будет распределена по сдвинутому влево на единицу гамма-распределению Γ(n,θapr/n). Требуемое условие будет выполняться, если δ-квантиль этого гамма-распределения не меньше G0+1. При его выполнении переходим далее. Если же оно не выполняется, то мы можем определить необходимое минимальное число сделок для выполнения этого условия. Для этого пошагово увеличиваем значение n и берем в качестве nmin то из них, при котором требуемое неравенство выполняется.

4. Выполняется так же, как и в предыдущей главе статьи. Изменение касается лишь используемого распределения для случайной генерации доходностей. Сейчас мы применяем экспоненциальное распределение с параметром θ=θapr, сдвинутое на единицу влево. В библиотеке статистики MQL5 используется немного другая форма параметризации для экспоненциального распределения — параметр μ (матожидание), который выражается через θ или через M в виде μ=1/θ или μ=M+1.

#include <Math\Stat\Gamma.mqh>
#include <Math\Stat\Exponential.mqh>
#property script_show_inputs
input uint na=50;           // число сделок в серии
input double tht=0.65;      // параметр экспоненциального распр-я 0<tht<1

#define NX 300              // максимальное число сделок в серии (для поиска nmin)
#define NB 10000            // количество генерируемых выборок для метода Монте-Карло
#define NR 1000             // количество интервалов разбиения для риска
double G0=0.15;             // наименьшая средняя доходность
double D0=0.9;              // наименьший минимальный прирост
double dlt=0.05;            // уровень значимости

void OnStart()
  {
   if(D0<=0 || D0>=1) {Print("D0 должно быть положительным и меньше единицы"); return;}
   double m=1/tht-1;         // математическое ожидание
   if(m<=0) {Print("математическое ожидание должно быть положительным"); return;}

   int ner;   
   double p=MathCumulativeDistributionGamma(m+1,na,1.0/na,ner);
   if(!MathIsValidNumber(p)) {Print("MathIsValidNumber(p) error ",ner); return;}
   double p0=MathCumulativeDistributionGamma(1,na,1.0/na,ner);
   if(!MathIsValidNumber(p0)) {Print("MathIsValidNumber(p0) error ",ner); return;}
   if(p<=p0+dlt/2) {Print("математическое ожидание близко к нулю"); return;}

   double q=MathQuantileGamma(dlt,na,1/tht/na,ner),q0=G0+1;
   if(!MathIsValidNumber(q)) {Print("MathIsValidNumber(q) error ",ner); return;}
   if(q0>q)
     {
      Print("G0 больше dlt-квантиля среднего арифметического доходностей");
      uint nmin=na+1;
      for(;nmin<=NX;++nmin)
        {
         q=MathQuantileGamma(dlt,nmin,1/tht/nmin,ner); q0=G0+1;
         if(!MathIsValidNumber(q)) {Print("MathIsValidNumber(q) error ",ner); return;}
         if(q0<=q) break;
        }
      if(nmin<=NX) Print("nmin = ",nmin);
      else Print("nmin более чем ",NX);
      return;
     }    

// метод Монте-Карло
   MathSrand(GetTickCount());
   double a[],c[],ropt[NB],A0,A,r,g,d,cn1,cn2,stp=1.0/NR;
   uint ir;
   ArrayResize(a,na);
   ArrayResize(c,na);
   for(uint ib=0; ib<NB;++ib)
     {
      for(uint i=0; i<na;++i)
        {
         a[i]=MathRandomExponential(m+1,ner);
         if(!MathIsValidNumber(a[i])) {Print("Error MathRandomExponential()",ner); return;}
         a[i]-=1.0;
        }
      A=MathMean(a); A0=a[ArrayMinimum(a)];
      if(A<G0) {ropt[ib]=0; continue;}
      if(A0>0) {ropt[ib]=1-stp; continue;}
      cn1=1;
      for(ir=1;ir<NR;++ir)
        {
         r=ir*stp;
         cn2=1; for(uint i=0; i<na;++i) cn2*=1+r*a[i];
         if(cn2<cn1) {ropt[ib]=r-stp; break;}
         cn1=cn2;
         g=(MathPow(cn2,1.0/na)-1)/r;
         if(g<G0) {ropt[ib]=r-stp; break;}
         c[0]=1+r*a[0]; for(uint i=1; i<na;++i) c[i]=c[i-1]*(1+r*a[i]);
         d=dcalc(c);
         if(d<D0) {ropt[ib]=r-stp; break;}
        }
     }
   ArraySort(ropt);
   uint nr=(uint)(dlt*NB);
   Print("ropt = ",ropt[nr]);
  }
// функция dcalc() принимает массив из значений c1, c2, ... cN и
// возвращает минимальный прирост d. Полагаем c0==1
double dcalc(double &c[])
  {
   if(c[0]<=0) return 0;
   double d=c[0], mx=c[0], mn=c[0];
   for(uint i=1; i<na;++i)
     {
      if(c[i]<=0) return 0;
      if(c[i]<mn) {mn=c[i]; d=MathMin(d,mn/mx);}
      else {if(c[i]>mx) mx=mn=c[i];}
     }
   return d;
  }
//+------------------------------------------------------------------+

При аргументах, заданных по умолчанию, получаем следующее значение риска:

• ropt = 0.015

Это соответствует 1.5% риска в каждой сделке от капитала, выделенного для системы.

Рассмотреная в предыдущей части в качестве примера последовательность из тридцати сделок была получена именно для системы с выходом по трейлинг-стопу. Поэтому наш метод можно к ней применить. Он (как и рассмотренный в прошлый раз метод) показывает, что последовательность непригодна для торговли при заданных условиях (n, δ, G0, D0). Этот результат не поменяется, даже если мы уберем проскальзывание, прибавив ко всем ai небольшое положительное число так, чтобы для всех i=1,...,n выполнялось условие ai>-1.

Примечание: Если при заданных по умолчанию аргументах скрипт выдаст ошибку с номером 4, то значит терминал не прошел необходимые обновления. В этом случае часть скрипта (с 21-й строки по 42-ю) необходимо закомментировать. В этой части находятся вычисления связанные с гамма-распределением. Для них можно воспользоваться приведённым ниже скриптом на языке R.

na=50; tht=0.65; dlt=0.05; G0=0.15; nx=300
m=1/tht-1; l1=l2=l3=FALSE
l1 = m > 0
if (l1) l2 = pgamma(m+1,na,scale = 1/na) > pgamma(1,na,scale = 1/na)+dlt/2
if (l2) l3 = G0+1 <= qgamma(dlt,na,scale = 1/tht/na)

if(!l1) cat("m must be greater 0\n")

if(l1 & l3) cat("G0 and na are ok\n") else cat("na too small or G0 too big\n")

if(l1 & l2 & !l3)
{for (nmin in (na+1):(nx+1)) {if(G0+1 <= qgamma(dlt,nmin,scale = 1/tht/nmin)) break()}
 if (nmin<=nx) {cat("nmin =",nmin)} else {cat("nmin >",nx)}
}

Что дальше?

Очевидно, что вышеприведенные методы нельзя считать полными и окончательными. Для простоты изучения мы априори приняли, что сделки независимы и распределены одинаково. Но это требует более глубокого исследования и может оказаться не так. Может оказаться полезным, чтобы распределение доходностей принадлежало или было близко к конкретному параметрическому семейству. Но и эту принадлежность тоже может понадобиться дополнительно изучить.

Мы довольствовались точечными оценками параметров распределений и не искали для них доверительных интервалов. Но после их построения встанет вопрос об устойчивости прибыльности системы при колебании этих параметров.

Множество возможных методов, конечно же, не означает, что их нужно постоянно и все сразу использовать. Но всё же лучше знать о них и уметь при необходимости использовать, чем быть "одураченным случайностью".

В оставшейся части статьи мы кратко обозначим несколько других возможных направлений для применения теории вероятностей.

Статистика и гэпы

Гэп — большой скачок между ценами закрытия и открытия двух последовательных баров. Должно также соблюдаться требование, чтоб и между самими этими барами был значительный промежуток. Считается, что “гэпы всегда закрываются”. Закрытие гэпа означает, что через некоторое время после разрыва цена возвращается к цене закрытия бара, предшествовавшего разрыву. Иногда на этой закономерности пытаются построить торговую систему. Возможно ли это?

Из теории симметричного случайного блуждания на прямой нам известно, что за достаточно большое время с вероятностью, почти равной единице, будет достигнуто любое значение цены. То есть, почти наверняка “гэп всегда закроется” и при этих условиях. Но, как мы знаем, при симметричном случайном блуждании никакая прибыльная система невозможна. Означает ли это, что система на гэпах не имеет шансов на существование?

Вовсе не обязательно. Важен не только сам факт закрытия гэпов, но и то, как именно они закрываются. Имеется в виду закрытие не каждого конкретного гэпа, а некоторой их совокупности — тогда можно рассматривать эмпирические распределения вероятностей случайных величин, связанных с ними. Может проявиться различие между реальными ценами и моделью симметричного случайного блуждания. Отличия могут быть самыми разными. Это может быть и то, что движение в направлении разрыва мало, и то, что время до закрытия меньше, чем для случайного блуждания, и многое другое. Важно лишь, что наличие и существенность этих отклонений можно определить с помощью методов теории вероятностей и математической статистики. Удостоверившись в этих отклонениях, можно на их основе строить торговые системы. Также можно попытаться проверить теорию, классифицирующую гэпы.

Рассмотрим самый простой вариант поиска отклонений от случайного блуждания. Это будет величина того, насколько сильно цена продвинется в направлении разрыва до закрытия гэпа. Можно получить эмпирическое распределение этой величины по истории цен и сравнить его с теоретическим. Для сравнения этих двух распределений можно использовать какой-либо критерий согласия.

Рассмотрим модель симметричного случайного блуждания с дискретным временем. Пусть большие гэпы в нем  редки (как и в реальных ценах), а в промежутках между ними оно близко к блужданию с непрерывным временем (винеровский процесс). Введём обозначения: g — величина гэпа, m — максимальное продвижение в сторону гэпа до его закрытия. Тогда случайная величина x=m/g будет иметь функцию распределения, близкую к функции P(x) — такой, что P(x)=1-1/x, если x≥1 и P(x)=0, если x<1. Рисунок для иллюстрации введенных нами величин:

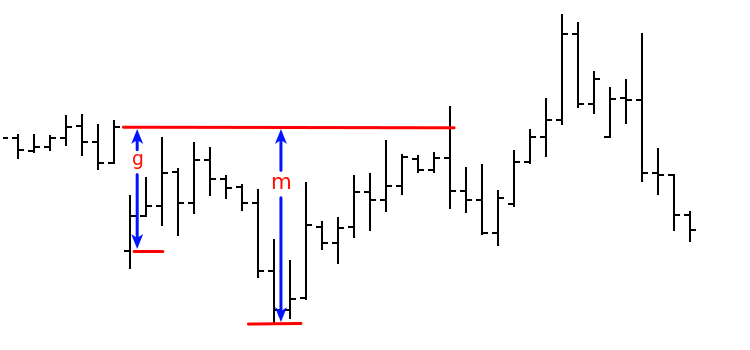
Затронутый нами вопрос требует более подробного и объёмного изучения. Поэтому ограничимся пока следующими замечаниями:

• Проблема исследований гэпов заключается в их редкости. Особенно сильно это сказывается при попытках изучать связанные с ними распределения в зависимости от параметров (наподобие того, как это будет описано в следующей главе).
• Для проверки теории классификации гэпов (например, здесь) придется строить более сложную модель, учитывающую цены не только от разрыва до закрытия, но и предыдущие и последующие. Это приведет к увеличению количества рассматриваемых случайных величин. Это, в свою очередь, может создать проблемы из-за указанного выше малого количества данных.
  

Статистическое машинное обучение

Рассмотрим схематически устройство торговой системы. Для каждой сделки известен набор параметров h, по значениям которого должны однозначно определяться объём сделки и алгоритм (не цена!) выхода. Значение h должно быть достоверно известно на момент входа. Это могут быть какие-то значения технических индикаторов и т.д. В терминах машинного обучения h — набор признаков.

На всякий случай сделаем следующее уточнение. Обычно, когда говорят про торговую систему, имеют в виду не одну конкретную систему, а их параметрическое семейство. Задача тестирования и оптимизации — выбрать конкретную систему из этого семейства, определив и зафиксировав конкретное значение параметра. Чтобы не усложнять изложение (не путать h с параметрами, задающими выбор системы из семейства), в этой главе мы говорим именно о конкретной системе, а не об их семействе. Проблемы оптимизации кратко коснёмся в следующей главе.

Зафиксировав конкретное значение h, получаем фиксированный алгоритм входа/выхода в сделку. Это даёт нам фиксированное распределение вероятностей. Обратите внимание на то, что при одном и том же h могут быть разные доходности. Фиксировано распределение доходностей, а не конкретное их значение.

Таким образом, возникает задача восстановления зависимости закона распределения доходностей от признаков h. Исходные данные — история сделок в виде набора пар из значений параметров и соответствующих им доходностей (hi,ai). Подобные задачи решаются методами статистического машинного обучения. При этом оказывается, что нет принципиального отличия этих методов от тех, что используются в машинном обучении при решении задач восстановления детерминированной (не случайной) зависимости.

Немного уточним постановку нашей задачи, предполагая принадлежность распределения доходностей к некоторому семейству. Задан набор пар (hi,ai). Распределение доходностей ai принадлежит параметрическому семейству распределений зависящему от параметра θ. Требуется восстановить зависимость θ(h). Эта зависимость ищется не среди произвольных функций — для этого исходных данных недостаточно. Обычно она ищется среди какого-либо параметрического семейства функций: θ(h)=θ(h,β), где параметр β определяется по набору пар (hi,ai) с учетом требования некоторой его оптимальности. Широкий выбор семейств функций для поиска зависимостей, условий оптимальности для параметра и методов поиска этого оптимального значения и определяет имеющееся огромное разнообразие методов машинного обучения.

Нам нужно выбирать из этого многообразия прежде всего те методы, что осмысленны с точки зрения трейдера (например, способствуют увеличению прибыли или уменьшению просадки). Особенно важно это учитывать при выборе условия оптимальности для выбора параметра β. При изменении этого условия получаемая в качестве ответа зависимость θ(h,β) может очень сильно меняться.

Предположим, что для данного параметрического семейства распределений доходностей ai мы решили задачу оценки риска аналогично двум случаям, рассмотренным выше. Тогда, поскольку мы построили зависимость θ=θ(h) и знаем, как для каждого заданного θ выбирать значение риска ropt, то нам известна и зависимость ropt=ropt(h). Можно считать построение нашей системы завершённым.

Статистика и оптимизация торговой системы.

Рассмотрим следующий простой вариант оптимизации. Сделаем N проходов нашей системы по n сделок в каждом. Выберем из них заданное небольшое количество εN, где 0<ε<<1, наилучших (с наибольшей средней доходностью). Обозначим через mopt наименьшее среднее среди этих отобранных проходов и будем считать её показателем того, насколько хороша будет оптимальная система.

Рассмотрим теперь систему, на примере которой мы увидим, что к результатам оптимизации надо относиться с осторожностью. Пример хоть и искусственный, но вполне позволит увидеть суть проблемы. Рассмотрим систему с нулевым матожиданием доходности и случайной зависимостью от параметров.

Эта система будет делать входы в случайном направлении в фиксированные моменты время. Направление будет выбираться с помощью генератора случайных чисел с равной вероятностью. Начальное значение для инициализации этого генератора перед каждым проходом тестирования будет функцией от параметров. Таким образом для каждого набора параметров мы всегда будем получать одну и ту же последовательность сделок, но при изменении этих параметров последовательность будет меняться совершенно случайным, непредсказуемым образом. Выход из сделки будет происходить по фиксированным стоплоссу/тейкпрофиту с постоянным отношением k. Также считаем, что на участке тестирования отсутствует тренд.

Очевидно, что из-за отсутствия тренда матожидание доходностей этой системы будет близким к нулевому (небольшим отрицательным — при учете спреда). Обозначим через n число сделок в серии. Тогда среднее арифметическое доходностей в серии n сделок m будет случайной величиной. Она выражается через случайную величину nk — количество прибыльных сделок в серии: m=(1+k)nk/n-1. Величина nk имеет биномиальное распределение с параметрами 1/(1+k) и n.

При достаточно большом N значение mopt будет близко к (1-ε)-квантили распределения величины m. Покажем, что несмотря на очевидную бесперспективность данной “торговой системы” (вследствие нулевого матожидания), значение mopt будет достаточно велико. Положим для определенности: k=3, n=50, ε=0.1 и получим mopt=2.52.

Очевидно, что для реальных, осмысленных систем при реальном тестировании все устроено иначе и гораздо сложнее. Тем не менее, и в этом случае можно и нужно пытаться понять — не случайно ли преимущество оптимизированной системы.

Прикреплённые файлы

№	Имя	Тип	Описание
1	bn.mq5	скрипт	вычисление риска для выхода с фиксированными стоп-лоссом и тейк-профитом
2	exp.mq5	скрипт	вычисление риска для выхода с фиксированным трейлинг-стопом