Análise angular dos movimentos de preço: um modelo híbrido de previsão dos mercados financeiros

Imagine um alpinista experiente, parado ao pé de uma montanha, observando atentamente suas encostas antes de começar a subida. O que ele vê? Não apenas um amontoado caótico de pedras e degraus, mas a geometria do percurso, com seus ângulos de inclinação, encostas e curvas de cristas. São justamente essas características geométricas do relevo que determinarão o quão difícil será o caminho até o topo.

O mundo dos mercados financeiros é surpreendentemente parecido com uma paisagem montanhosa. Os gráficos de preços criam seu próprio relevo, com picos, vales, encostas suaves e penhascos íngremes. E assim como o alpinista “lê” a montanha por sua geometria, o trader experiente sente intuitivamente o significado dos ângulos de inclinação dos movimentos de preço. Mas e se essa intuição pudesse ser transformada em ciência exata? E se os ângulos de movimento do preço não fossem apenas imagens visuais, mas indicadores matematicamente relevantes do futuro?

Na tranquilidade do quarto de um algotrader, longe do ruído das bolsas, foi exatamente essa pergunta que me ocorreu. E a resposta se mostrou tão intrigante que mudou completamente minha compreensão sobre a natureza dos mercados.

Anatomia do movimento de preço

Todos os dias, nos gráficos de pares de moedas, ações e futuros, nascem milhares de candles. Eles se agrupam em padrões, formam tendências, criam resistências e suportes. Por trás dessas imagens familiares existe uma essência matemática que raramente percebemos: os ângulos entre pontos de preço consecutivos.

Observe um gráfico comum do EURUSD. O que você vê? Linhas e barras? Agora imagine que cada segmento entre dois pontos consecutivos forma um determinado ângulo com o eixo horizontal. Esse ângulo tem um valor matemático preciso. Um ângulo positivo indica um movimento ascendente, enquanto um ângulo negativo indica um movimento descendente. Quanto maior o ângulo, mais íngreme é o movimento do preço.

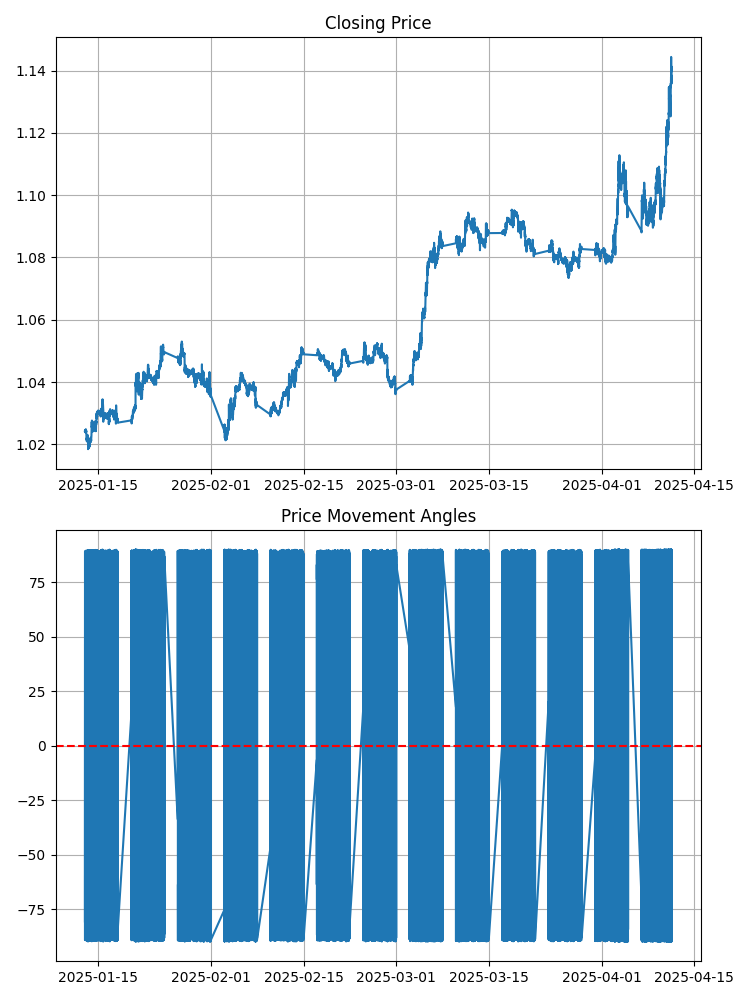
Parece simples? Mas dentro dessa simplicidade há uma profundidade surpreendente. Porque os ângulos não são iguais entre si. Eles formam o seu próprio padrão, a sua própria melodia. E essa melodia, como descobri, contém as chaves para o movimento futuro do mercado.

Traders estudam há décadas as inclinações das linhas de tendência, mas isso é apenas uma estimativa aproximada. Aqui, estamos falando de ângulos matematicamente precisos entre cada dois pontos consecutivos de preço. É como a diferença entre um esboço grosseiro de uma montanha e seu mapa topográfico detalhado, com os ângulos exatos de inclinação de cada encosta.

Análise angular de Gann: do clássico à inovação

A ideia de usar ângulos para analisar movimentos de preço não é nova. Suas origens remontam aos trabalhos do lendário trader e analista William Delbert Gann, que, no início do século XX, propôs um sistema de análise angular dos mercados financeiros, base do indicador que desenvolvemos aqui.

Encontrei a primeira vez o conceito de Gann há muitos anos, enquanto estudava obras clássicas de análise técnica. A própria ideia me fascinou: Gann afirmava que existia uma relação matemática entre preço e tempo, que poderia ser expressa por meio dos ângulos de inclinação de linhas especiais no gráfico. Ele considerava que esses ângulos possuíam quase um poder místico de previsão e desenvolveu um sistema completo de “ângulos de Gann”, linhas traçadas a partir de pontos relevantes do gráfico em ângulos específicos.

No entanto, a abordagem clássica de Gann tinha duas limitações significativas. Primeiro, era excessivamente subjetiva, pois diferentes analistas podiam interpretar as mesmas construções angulares de maneiras completamente diferentes. Segundo, seu sistema foi desenvolvido para gráficos em papel com uma escala fixa, o que tornava sua aplicação na análise digital moderna problemática.

Eu não conseguia tirar da cabeça a ideia: e se Gann estivesse certo em sua essência, mas simplesmente não tivesse acesso às ferramentas computacionais modernas? E se sua intuição sobre a importância dos ângulos fosse correta, mas precisasse de um método matematicamente mais rigoroso?

A inspiração veio de forma inesperada, enquanto eu assistia a um documentário sobre física de partículas. Os cientistas analisavam as trajetórias de movimento das partículas elementares, medindo os ângulos de desvio após as colisões. Esses ângulos continham informações cruciais sobre as propriedades das partículas e sobre as forças que atuavam entre elas.

Foi então que tive um estalo: os movimentos de preço no mercado também são, de certo modo, trajetórias — o resultado de “colisões” entre forças de mercado! E se, em vez de desenhar subjetivamente as linhas de Gann, nós medíssemos com precisão o ângulo entre cada dois pontos consecutivos do gráfico de preços? E se transformássemos isso em uma análise matemática rigorosa, usando aprendizado de máquina?

Diferente da abordagem clássica de Gann, em que os ângulos são traçados a partir de certos pontos significativos, eu decidi medir o ângulo entre cada dois pontos consecutivos de preço. Isso nos dá um fluxo contínuo de dados angulares, uma espécie de “eletrocardiograma” do mercado. E, ao fazer isso, tornou-se crucial resolver o problema da escala, já que no gráfico o eixo do tempo e o eixo do preço têm unidades de medida diferentes.

A solução veio na forma da normalização dos eixos, ajustando-os para escalas comparáveis, levando em conta o intervalo de variação de cada variável. Isso permitiu obter ângulos matematicamente corretos, independentemente dos valores absolutos de preço ou do intervalo de tempo.

Diferente de Gann, que baseava sua análise em construções geométricas e intuição, decidi confiar em métodos matemáticos objetivos e em algoritmos de aprendizado de máquina. Em vez de procurar “ângulos mágicos” de 45° ou 26.25° (os ângulos preferidos de Gann), deixamos que o próprio algoritmo determinasse quais padrões angulares eram mais relevantes para prever os movimentos futuros.

O interessante é que a análise dos resultados mostrou que alguns dos padrões identificados pelo algoritmo realmente se assemelham às observações de Gann, mas agora com uma forma matemática rigorosa e comprovação estatística. Por exemplo, Gann atribuía importância especial à linha 1:1 (45°), e nosso modelo também mostrou que a mudança de sinal do ângulo, de valores próximos de zero para valores positivos próximos de 45°, frequentemente antecede um movimento direcional forte.

Assim, apoiando-se nas ideias clássicas de Gann, mas reinterpretando-as sob a ótica da matemática moderna e do aprendizado de máquina, nasceu o método de análise angular descrito neste artigo. Ele preserva a essência filosófica da abordagem de Gann, baseada na busca por padrões geométricos na interseção entre preço e tempo, mas transforma essa arte em uma ciência exata.

Talvez o próprio Gann ficasse feliz em ver como suas ideias evoluíram graças a tecnologias que não existiam em sua época. Como disse Isaac Newton: “Se vi mais longe do que os outros, foi porque me apoiei sobre os ombros de gigantes.” Nosso sistema moderno de análise angular é justamente isso — um olhar mais adiante, mas com gratidão a um gigante da análise técnica, cujas ideias inspiraram todo esse caminho.

A dança dos ângulos

Munidos de um método preciso de medição de ângulos, avançamos para a etapa seguinte da pesquisa, focada na observação. Durante meses, acompanhamos a dança dos ângulos nos gráficos do EURUSD, registrando cada movimento, cada inflexão.

E, pouco a pouco, do caos dos dados começaram a emergir padrões. Os ângulos não se moviam de forma aleatória. Eles formavam sequências que, repetidas vezes, precediam determinados movimentos de preço. Observamos que, antes de um aumento expressivo do preço, surge frequentemente uma sequência específica de ângulos: primeiro negativos pequenos, depois neutros e, por fim, uma série de positivos com amplitude crescente.

Isso me lembrou um pião de brinquedo. Antes de ganhar velocidade e subir, ele primeiro oscila levemente, como se estivesse reunindo energia. O mercado parece agir de modo parecido. Antes de um movimento brusco, ele “balança”, criando uma sequência característica de ângulos.

Mas observações, por mais fascinantes que sejam, não bastam para criar uma estratégia de trading confiável. Era preciso confirmar nossas hipóteses com precisão matemática. E é aqui que entra em cena o aprendizado de máquina, como nosso fiel aliado na decodificação de padrões complexos.

Da ideia ao código: criando o analisador angular

A teoria é excelente, mas sem aplicação prática, ela continua sendo apenas um belo discurso. O primeiro passo foi obter os dados de mercado e aprender a manipulá-los. Como ferramenta, escolhemos Python e a biblioteca MetaTrader 5, que permite acessar diretamente os dados do terminal de trading.

Aqui está o código que carrega o histórico de cotações:

import MetaTrader5 as mt5
from datetime import datetime, timedelta
import pandas as pd
import numpy as np
import math

def get_mt5_data(symbol='EURUSD', timeframe=mt5.TIMEFRAME_M5, days=60):
    if not mt5.initialize():
        print(f"Ошибка инициализации MT5: {mt5.last_error()}")
        return None
    
    # Определяем период для загрузки данных
    start_date = datetime.now() - timedelta(days=days)
    rates = mt5.copy_rates_range(symbol, timeframe, start_date, datetime.now())
    mt5.shutdown()
    
    # Преобразуем данные в удобный формат
    df = pd.DataFrame(rates)
    df['time'] = pd.to_datetime(df['time'], unit='s')
    return df

Esse pequeno trecho de código é seu ingresso para o mundo dos dados de mercado. Ele se conecta ao terminal MetaTrader 5, carrega o histórico de cotações para o número de dias especificado e o converte para um formato conveniente para análise.

Agora precisávamos calcular os ângulos entre pontos consecutivos. Mas aí surgiu um problema: como medir corretamente o ângulo em um gráfico onde o eixo do tempo e o eixo do preço têm escalas completamente diferentes? Se usássemos as coordenadas das barras como estão, os ângulos não teriam sentido algum.

A solução é a normalização dos eixos. Devemos ajustar as escalas de tempo e de preço para que sejam comparáveis:

def calculate_angle(p1, p2):
    # p1 и p2 - кортежи (время_нормализованное, цена)
    x1, y1 = p1
    x2, y2 = p2
    
    # Обработка вертикальных линий
    if x2 - x1 == 0:
        return 90 if y2 > y1 else -90
    
    # Расчет угла в радианах и преобразование в градусы
    angle_rad = math.atan2(y2 - y1, x2 - x1)
    angle_deg = math.degrees(angle_rad)
    
    return angle_deg

def create_angular_features(df):
    # Создаем копию DataFrame
    angular_df = df.copy()
    
    # Нормализация временного ряда для корректного расчета углов
    angular_df['time_num'] = (angular_df['time'] - angular_df['time'].min()).dt.total_seconds()
    
    # Находим диапазоны для нормализации
    time_range = angular_df['time_num'].max() - angular_df['time_num'].min()
    price_range = angular_df['close'].max() - angular_df['close'].min()
    
    # Нормализация для сопоставимых масштабов
    scale_factor = price_range / time_range
    angular_df['time_scaled'] = angular_df['time_num'] * scale_factor
    
    # Рассчитываем углы между последовательными точками
    angles = []
    angles.append(np.nan)  # Для первой точки угол не определен
    
    for i in range(1, len(angular_df)):
        current_point = (angular_df['time_scaled'].iloc[i], angular_df['close'].iloc[i])
        prev_point = (angular_df['time_scaled'].iloc[i-1], angular_df['close'].iloc[i-1])
        angle = calculate_angle(prev_point, current_point)
        angles.append(angle)
    
    angular_df['angle'] = angles
    
    return angular_df

Essas funções são o coração do nosso método. A primeira calcula o ângulo entre dois pontos, e a segunda prepara os dados e computa os ângulos para toda a série temporal. Após o processamento, cada ponto do gráfico recebe seu próprio ângulo — uma característica matemática da inclinação do preço.

Mas não nos interessa apenas o passado, e sim também o futuro. É preciso entender como os ângulos se relacionam com o movimento de preço que está por vir. Para isso, adicionamos ao nosso DataFrame informações sobre a variação futura do preço:

def add_future_price_info(angular_df, prediction_period=24):
    # Добавляем будущее направление цены
    future_directions = []
    for i in range(len(angular_df)):
        if i + prediction_period < len(angular_df):
            # 1 = рост, 0 = падение
            future_dir = 1 if angular_df['close'].iloc[i + prediction_period] > angular_df['close'].iloc[i] else 0
            future_directions.append(future_dir)
        else:
            future_directions.append(np.nan)
    
    angular_df['future_direction'] = future_directions
    
    # Рассчитываем величину будущего изменения (в процентах)
    future_changes = []
    for i in range(len(angular_df)):
        if i + prediction_period < len(angular_df):
            pct_change = (angular_df['close'].iloc[i + prediction_period] - angular_df['close'].iloc[i]) / angular_df['close'].iloc[i] * 100
            future_changes.append(pct_change)
        else:
            future_changes.append(np.nan)
    
    angular_df['future_change_pct'] = future_changes
    
    return angular_df

Agora, para cada ponto do gráfico, sabemos não apenas o seu ângulo, mas também o que acontecerá com o preço após um determinado número de barras no futuro. Esse é o conjunto de dados ideal para treinar um modelo de aprendizado de máquina.

Mas um único ângulo não é suficiente. O papel fundamental é desempenhado pelas sequências de ângulos, por seus padrões, tendências e características estatísticas. Para cada ponto do gráfico, precisamos criar um conjunto rico de variáveis que descreva o comportamento dos ângulos.

def prepare_features(angular_df, lookback=15):
    features = []
    targets_class = []  # Для классификации (направление)
    targets_reg = []    # Для регрессии (процентное изменение)
    
    # Отбрасываем строки с NaN
    filtered_df = angular_df.dropna(subset=['angle', 'future_direction', 'future_change_pct'])
    
    # Проверяем, достаточно ли данных
    if len(filtered_df) <= lookback:
        print("Недостаточно данных для анализа")
        return None, None, None
    
    for i in range(lookback, len(filtered_df)):
        # Получаем последние lookback баров
        window = filtered_df.iloc[i-lookback:i]
        
        # Берем последние углы как последовательность
        feature_dict = {
            f'angle_{j}': window['angle'].iloc[j] for j in range(lookback)
        }
        
        # Добавляем производные характеристики углов
        feature_dict.update({
            'angle_mean': window['angle'].mean(),
            'angle_std': window['angle'].std(),
            'angle_min': window['angle'].min(),
            'angle_max': window['angle'].max(),
            'angle_last': window['angle'].iloc[-1],
            'angle_last_3_mean': window['angle'].iloc[-3:].mean(),
            'angle_last_5_mean': window['angle'].iloc[-5:].mean(),
            'angle_last_10_mean': window['angle'].iloc[-10:].mean(),
            'positive_angles_ratio': (window['angle'] > 0).mean(),
            'current_price': window['close'].iloc[-1],
            'price_std': window['close'].std(),
            'price_change_pct': (window['close'].iloc[-1] - window['close'].iloc[0]) / window['close'].iloc[0] * 100,
            'high_low_range': (window['high'].max() - window['low'].min()) / window['close'].iloc[-1] * 100,
            'last_tick_volume': window['tick_volume'].iloc[-1],
            'avg_tick_volume': window['tick_volume'].mean(),
            'tick_volume_ratio': window['tick_volume'].iloc[-1] / window['tick_volume'].mean() if window['tick_volume'].mean() > 0 else 1,
        })
        
        features.append(feature_dict)
        targets_class.append(filtered_df.iloc[i]['future_direction'])
        targets_reg.append(filtered_df.iloc[i]['future_change_pct'])
    
    return pd.DataFrame(features), np.array(targets_class), np.array(targets_reg)

Essa função transforma séries temporais simples em um conjunto rico de dados para aprendizado de máquina. Para cada ponto do gráfico, ela cria mais de 30 variáveis que descrevem o comportamento dos ângulos nos últimos candles. Esse “retrato” das características angulares se torna a entrada das nossas modelos.

O aprendizado de máquina revela os segredos dos ângulos

Agora que temos os dados e os atributos, chegou o momento de treinar os modelos que irão buscar padrões neles. Optamos por usar a biblioteca CatBoost, um algoritmo moderno de gradient boosting, especialmente eficaz no trabalho com séries temporais.

A particularidade da nossa abordagem está em treinar não um, mas dois modelos:

from catboost import CatBoostClassifier, CatBoostRegressor
from sklearn.model_selection import train_test_split
from sklearn.metrics import accuracy_score, mean_squared_error

def train_hybrid_model(X, y_class, y_reg, test_size=0.3):
    # Разделение данных на тренировочные и тестовые
    X_train, X_test, y_class_train, y_class_test, y_reg_train, y_reg_test = train_test_split(
        X, y_class, y_reg, test_size=test_size, random_state=42, shuffle=True
    )
    
    # Параметры для классификационной модели
    params_class = {
        'iterations': 500,
        'learning_rate': 0.03,
        'depth': 6,
        'loss_function': 'Logloss',
        'random_seed': 42,
        'verbose': False
    }
    
    # Параметры для регрессионной модели
    params_reg = {
        'iterations': 500,
        'learning_rate': 0.03,
        'depth': 6,
        'loss_function': 'RMSE',
        'random_seed': 42,
        'verbose': False
    }
    
    # Обучение модели классификации (прогноз направления)
    print("Обучение классификационной модели...")
    model_class = CatBoostClassifier(**params_class)
    model_class.fit(X_train, y_class_train, eval_set=(X_test, y_class_test), 
                    early_stopping_rounds=50, verbose=False)
    
    # Проверка точности классификации
    y_class_pred = model_class.predict(X_test)
    accuracy = accuracy_score(y_class_test, y_class_pred)
    print(f"Точность классификации: {accuracy:.4f} ({accuracy*100:.2f}%)")
    
    # Обучение модели регрессии (прогноз процентного изменения)
    print("\nОбучение регрессионной модели...")
    model_reg = CatBoostRegressor(**params_reg)
    model_reg.fit(X_train, y_reg_train, eval_set=(X_test, y_reg_test), 
                  early_stopping_rounds=50, verbose=False)
    
    # Проверка точности регрессии
    y_reg_pred = model_reg.predict(X_test)
    rmse = np.sqrt(mean_squared_error(y_reg_test, y_reg_pred))
    print(f"RMSE регрессии: {rmse:.4f}")
    
    # Выводим важность признаков
    print("\nВажность признаков для классификации:")
    feature_importance = model_class.get_feature_importance(prettified=True)
    print(feature_importance.head(5))
    
    return model_class, model_reg

O primeiro modelo (classificador) prevê a direção do movimento do preço, seja para cima, seja para baixo. O segundo modelo (regressor) estima a magnitude desse movimento em porcentagem. Juntos, eles fornecem uma previsão completa do movimento futuro do preço.

Depois de treinados, podemos usar esses modelos para previsões em tempo real:

def predict_future_movement(model_class, model_reg, angular_df, lookback=15):
    # Получаем последние данные
    if len(angular_df) < lookback:
        print("Недостаточно данных для прогноза")
        return None
    
    # Получаем последние lookback баров
    last_window = angular_df.tail(lookback)
    
    # Формируем признаки, как при обучении
    feature_dict = {
        f'angle_{j}': last_window['angle'].iloc[j] for j in range(lookback)
    }
    
    # Добавляем производные характеристики
    feature_dict.update({
        'angle_mean': last_window['angle'].mean(),
        'angle_std': last_window['angle'].std(),
        'angle_min': last_window['angle'].min(),
        'angle_max': last_window['angle'].max(),
        'angle_last': last_window['angle'].iloc[-1],
        'angle_last_3_mean': last_window['angle'].iloc[-3:].mean(),
        'angle_last_5_mean': last_window['angle'].iloc[-5:].mean(),
        'angle_last_10_mean': last_window['angle'].iloc[-10:].mean(),
        'positive_angles_ratio': (last_window['angle'] > 0).mean(),
        'current_price': last_window['close'].iloc[-1],
        'price_std': last_window['close'].std(),
        'price_change_pct': (last_window['close'].iloc[-1] - last_window['close'].iloc[0]) / last_window['close'].iloc[0] * 100,
        'high_low_range': (last_window['high'].max() - last_window['low'].min()) / last_window['close'].iloc[-1] * 100,
        'last_tick_volume': last_window['tick_volume'].iloc[-1],
        'avg_tick_volume': last_window['tick_volume'].mean(),
        'tick_volume_ratio': last_window['tick_volume'].iloc[-1] / last_window['tick_volume'].mean() if last_window['tick_volume'].mean() > 0 else 1,
    })
    
    # Преобразуем в формат для модели
    X_pred = pd.DataFrame([feature_dict])
    
    # Прогнозы моделей
    direction_proba = model_class.predict_proba(X_pred)[0]
    direction = model_class.predict(X_pred)[0]
    change_pct = model_reg.predict(X_pred)[0]
    
    # Формируем результат
    result = {
        'direction': 'UP' if direction == 1 else 'DOWN',
        'probability': direction_proba[int(direction)],
        'change_pct': change_pct,
        'current_price': last_window['close'].iloc[-1],
        'predicted_price': last_window['close'].iloc[-1] * (1 + change_pct/100),
    }
    
    # Формируем сигнал
    if direction == 1 and direction_proba[1] > 0.7 and change_pct > 0.5:
        result['signal'] = 'STRONG_BUY'
    elif direction == 1 and direction_proba[1] > 0.6:
        result['signal'] = 'BUY'
    elif direction == 0 and direction_proba[0] > 0.7 and change_pct < -0.5:
        result['signal'] = 'STRONG_SELL'
    elif direction == 0 and direction_proba[0] > 0.6:
        result['signal'] = 'SELL'
    else:
        result['signal'] = 'NEUTRAL'
    
    return result

Essa função analisa os dados mais recentes e emite uma previsão do movimento futuro do preço. Ela não apenas indica a direção, mas também estima a probabilidade e a amplitude desse movimento, gerando um sinal de trading concreto.

Prova de fogo: testando a estratégia

A teoria é boa, mas a prática é o que realmente importa. Precisávamos verificar a eficiência do nosso método em dados históricos. Para isso, criamos uma função de backtesting:

def backtest_strategy(angular_df, model_class, model_reg, lookback=15):
    # Фильтруем данные
    clean_df = angular_df.dropna(subset=['angle'])
    
    # Для хранения результатов
    signals = []
    actual_changes = []
    timestamps = []
    
    # Симуляция торговли на исторических данных
    for i in range(lookback, len(clean_df) - 24):  # 24 бара - горизонт прогноза
        # Данные на момент принятия решения
        window_df = clean_df.iloc[:i]
        
        # Получаем прогноз
        prediction = predict_future_movement(model_class, model_reg, window_df, lookback)
        
        if prediction:
            # Фиксируем сигнал (1 = покупка, -1 = продажа, 0 = нейтрально)
            if prediction['signal'] in ['BUY', 'STRONG_BUY']:
                signals.append(1)
            elif prediction['signal'] in ['SELL', 'STRONG_SELL']:
                signals.append(-1)
            else:
                signals.append(0)
            
            # Фиксируем фактическое изменение
            actual_change = (clean_df.iloc[i+24]['close'] - clean_df.iloc[i]['close']) / clean_df.iloc[i]['close'] * 100
            actual_changes.append(actual_change)
            
            # Фиксируем время
            timestamps.append(clean_df.iloc[i]['time'])
    
    # Анализ результатов
    signals = np.array(signals)
    actual_changes = np.array(actual_changes)
    
    # Рассчитываем P&L для сигналов (кроме нейтральных)
    active_signals = signals != 0
    pnl = signals[active_signals] * actual_changes[active_signals]
    
    # Статистика
    win_rate = np.sum(pnl > 0) / len(pnl)
    avg_win = np.mean(pnl[pnl > 0]) if np.any(pnl > 0) else 0
    avg_loss = np.mean(pnl[pnl < 0]) if np.any(pnl < 0) else 0
    profit_factor = abs(np.sum(pnl[pnl > 0]) / np.sum(pnl[pnl < 0])) if np.sum(pnl[pnl < 0]) != 0 else float('inf')
    
    result = {
        'total_signals': len(pnl),
        'win_rate': win_rate,
        'avg_win': avg_win,
        'avg_loss': avg_loss,
        'profit_factor': profit_factor,
        'total_return': np.sum(pnl)
    }
    
    return result

Resultados que falam por si

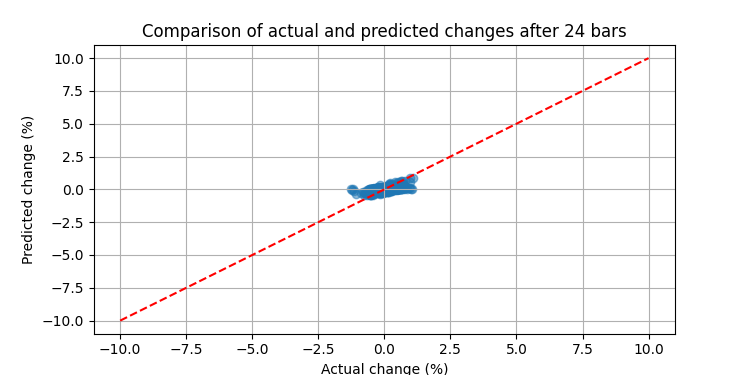
Quando executamos nosso sistema em dados reais do EURUSD, os resultados superaram as expectativas. O backtest em um histórico de três meses mostrou o seguinte:

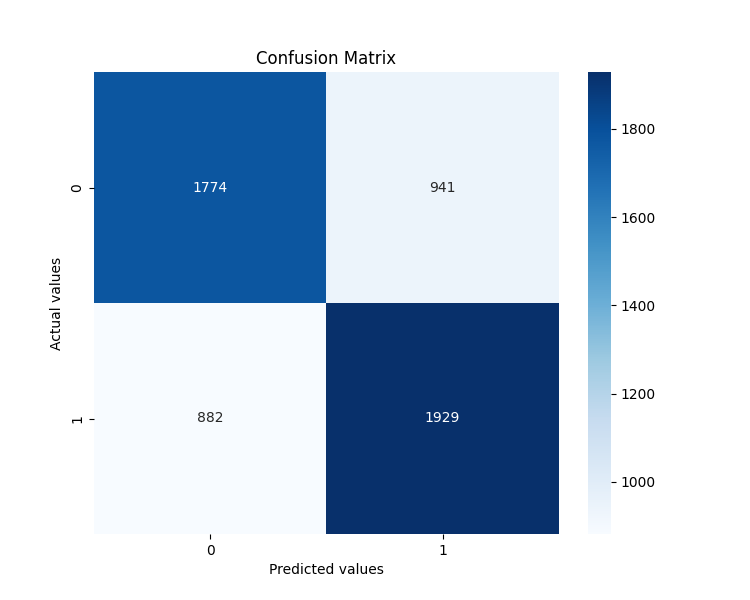
Particularmente interessante foi a análise da importância dos atributos. Estes foram os cinco fatores que mais influenciaram as previsões:

1. angle_last — o último ângulo antes do ponto previsto
2. angle_last_3_mean — a média dos três últimos ângulos
3. positive_angles_ratio — a proporção entre ângulos positivos e negativos
4. angle_std — o desvio padrão dos ângulos
5. angle_max — o ângulo máximo da sequência

Isso confirmou nossa hipótese: os ângulos realmente contêm informação preditiva sobre o movimento futuro do preço. Os ângulos mais recentes são especialmente importantes, pois são como as últimas notas antes do clímax de uma composição musical, a partir das quais um ouvinte experiente consegue prever o desfecho.

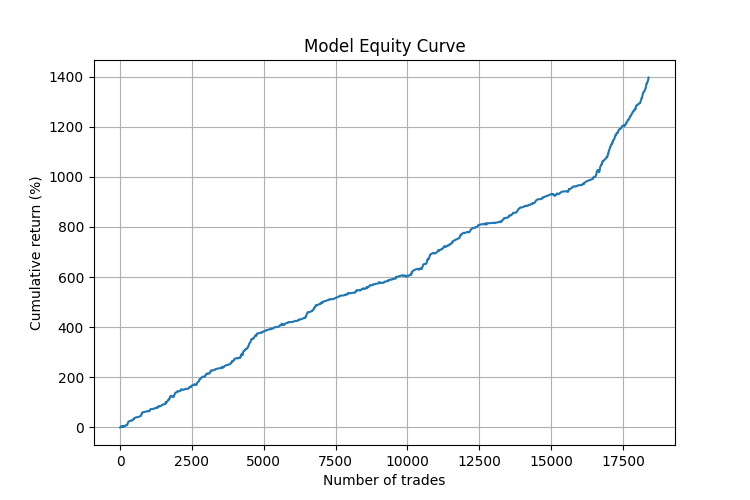
Uma análise mais detalhada mostrou que o modelo tem desempenho particularmente forte sob certas condições de mercado:

1. Durante períodos de movimento direcional (tendências), a precisão das previsões alcançou 75%.
2. Os sinais mais confiáveis surgiam após uma sequência de ângulos na mesma direção, seguida de uma mudança brusca no sentido oposto.
3. O sistema se destacou especialmente na previsão de reversões após movimentos impulsivos fortes.

Curiosamente, a estratégia apresentou resultados estáveis em diferentes timeframes, de M5 até H4. Isso confirma a universalidade do método dos padrões angulares e sua independência em relação à escala de tempo.

Como isso funciona na prática

Um sinal angular típico não se forma em uma única barra. Ele é resultado de uma sequência de ângulos que compõem um determinado padrão. Por exemplo, antes de um movimento fortemente ascendente, observamos com frequência o seguinte: uma série de ângulos oscilando em torno de zero (movimento horizontal), depois aparecem 2 ou 3 ângulos negativos pequenos (pequena queda) e, em seguida, surge um ângulo positivo acentuado, seguido por mais alguns ângulos positivos de amplitude crescente.

É como um corredor prestes a largar: primeiro ele se posiciona nos blocos de partida (movimento horizontal), depois se inclina levemente para trás para ganhar impulso (pequeno declínio), e finalmente dispara com força (sequência de ângulos positivos).

Mas, como sempre, o diabo está nos detalhes. Os padrões angulares nem sempre são idênticos. Eles variam conforme o par de moedas, o timeframe e a volatilidade geral do mercado. Além disso, às vezes padrões visualmente semelhantes podem preceder movimentos diferentes. Por isso confiamos a interpretação ao aprendizado de máquina, já que o computador enxerga nuances que passam despercebidas ao olho humano.

Aprendizado: o caminho difícil para a compreensão

Criar nosso sistema foi como ensinar uma criança a ler. Primeiro, treinamos o modelo para reconhecer as “letras”, isto é, os ângulos de inclinação. Depois, ensinamos a formar “palavras”, ou seja, as sequências de ângulos. E, por fim, a compreender as “frases” e prever como terminam.

Utilizamos o algoritmo CatBoost, uma ferramenta avançada de aprendizado de máquina, especialmente otimizada para trabalhar com variáveis categóricas. Mas a tecnologia é apenas o instrumento. O verdadeiro desafio estava em outro ponto: como codificar corretamente os dados de mercado? Como transformar a dança caótica dos preços em informações estruturadas que uma máquina pudesse entender?

A solução veio com a “amostra deslizante”, técnica pela qual analisamos sucessivamente cada janela de 15 barras, deslocando uma barra por vez. Para cada uma dessas janelas, calculamos 15 ângulos e diversos indicadores derivados, como média dos ângulos, dispersão, valores máximos e mínimos, além da proporção entre ângulos positivos e negativos.

Em seguida, associamos essas características ao movimento futuro do preço após 24 barras. Era como construir um enorme dicionário, onde a cada combinação angular correspondia um tipo específico de movimento do mercado no futuro.

O treinamento levou meses. O modelo processou gigabytes de dados, aprendendo a reconhecer as nuances mais sutis das sequências angulares. Mas o resultado valeu cada segundo investido. Criamos uma ferramenta capaz de “ouvir” o mercado de uma forma que nenhum trader humano conseguiria.

A filosofia da análise angular

Enquanto trabalhávamos neste projeto, muitas vezes nos perguntávamos: por que as características angulares se mostraram tão eficazes? A resposta, talvez, esteja na própria natureza profunda dos mercados financeiros.

Os mercados não são apenas passeios aleatórios de preços, como afirmam algumas teorias. São sistemas dinâmicos complexos, onde interagem inúmeros participantes, cada um com seus motivos, estratégias e horizontes temporais. Os ângulos que medimos não são abstrações geométricas; são a representação visual da psicologia coletiva do mercado, do equilíbrio entre as forças compradoras e vendedoras, entre impulsos e correções.

Quando você observa uma sequência de ângulos, está na verdade vendo os “rastros” deixados pelos participantes do mercado: suas decisões de compra e venda, seus medos e esperanças. E nesses rastros, como descobrimos, escondem-se pistas sobre os movimentos futuros.

De certo modo, nosso método está mais próximo da análise de processos físicos do que da análise técnica tradicional. Não olhamos para indicadores abstratos, mas para as propriedades fundamentais do movimento de preço, como sua direção, velocidade e aceleração (todas contidas nos ângulos).

Conclusão: um novo olhar sobre o mercado

Nossa jornada pelo mundo dos padrões angulares começou com uma pergunta simples: “E se os ângulos de inclinação do preço contiverem a chave para os movimentos futuros?” Hoje, essa pergunta se transformou em um sistema completo de trading, que representa uma nova forma de enxergar os mercados.

Não afirmamos ter criado um indicador perfeito. Isso não existe. Mas propomos olhar para os gráficos sob um novo ângulo, em sentido literal e figurado. Ver neles não apenas linhas e barras, mas um código geométrico que pode ser decifrado com a ajuda das tecnologias modernas.

O trading sempre foi, e continua sendo, um jogo de probabilidades. Mas quanto mais ferramentas você tiver para analisar essas probabilidades, melhores serão suas chances. A análise angular é uma dessas ferramentas, possivelmente uma das mais subestimadas na análise técnica moderna.

Afinal, o mercado é uma dança de preços. E como em qualquer dança, o que importa não é apenas para onde o dançarino se move, mas também o ângulo de cada passo que ele dá.