Determinamos la sobrecompra y la sobreventa usando la teoría del caos

Cuando el caos se convierte en patrones

Imagine que camina por el bosque durante una tormenta de nieve. Los copos de nieve parecen caóticos, con su movimiento impredecible. Pero si los observamos más de cerca, nos daremos cuenta de que se mueven a lo largo de corrientes de aire invisibles, siguiendo ciertos patrones. Al igual que estos copos de nieve, los precios en los mercados financieros bailan en una danza propia que parece aleatoria solo en apariencia.

La teoría del caos nos enseña una verdad sorprendente: existen patrones y estructuras profundas ocultas en sistemas que parecen completamente impredecibles. El meteorólogo Edward Lorenz lo descubrió cuando trabajaba con modelos meteorológicos e introdujo accidentalmente datos en su programa. Su descubrimiento, posteriormente denominado "efecto mariposa", demostró que incluso los cambios más leves en las condiciones iniciales pueden provocar resultados radicalmente distintos.

"Un sistema con un atractor extraño puede parecer completamente aleatorio, pero tiene un orden oculto" — afirma Lorenz. Y al igual que los sistemas meteorológicos tienen sus pautas invisibles, los mercados financieros siguen ciertas pautas a pesar de su aparente imprevisibilidad.

Los atractores: imanes invisibles del mercado

Imagine que lanza una pelota en una habitación. No importa lo fuerte que la lance, ni en qué dirección, acabará en el suelo. En este caso, el suelo es un atractor, un punto de atracción para la pelota.

En los mercados financieros, los atractores funcionan de forma semejante. Solo que, en lugar de la atracción física, intervienen fuerzas económicas que hacen que los precios vuelvan a ciertos niveles. Cuando una acción se vuelve demasiado cara, empiezan a dominar los vendedores; cuando se vuelve demasiado barata, dominan los compradores. Esto crea un efecto de banda elástica que tira constantemente del mercado hacia el punto de equilibrio.

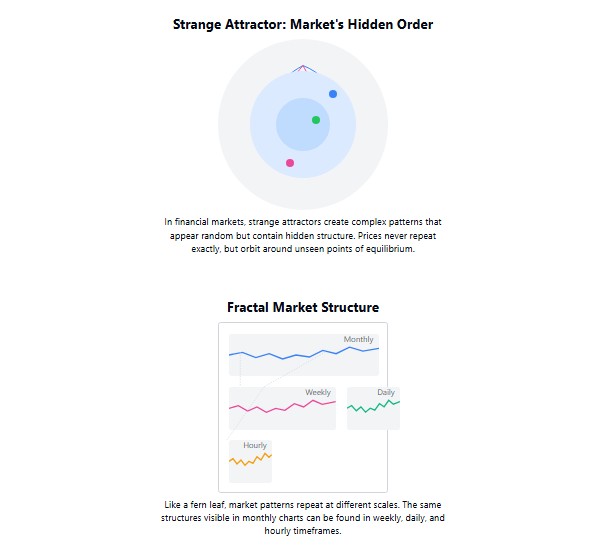
Pero a diferencia de una simple pelota, los mercados poseen lo que se denominan "atractores extraños". No son solo puntos, sino estructuras complejas hacia las que el sistema tiende, pero que nunca se repiten exactamente. Como un arroyo que desemboca en un lago: el agua siempre fluye hacia el lago, pero nunca repite exactamente el mismo camino.

Cómo entender el patrón fractal del mercado

Benoit Mandelbrot, que trabajaba para IBM en los años 60, analizó las fluctuaciones del precio del algodón durante un largo periodo, y se dio cuenta de algo sorprendente: los gráficos de precios tenían el mismo aspecto tanto si miraba los datos diarios, mensuales o anuales. Este descubrimiento llevó al desarrollo de la geometría fractal, el estudio de las formas que se repiten a diferentes escalas.

Observe una hoja de helecho: su forma general se repite en cada pequeño foliolo y, después, en partes aún más pequeñas. Los mercados funcionan de manera similar. Las pautas que se observan en el gráfico de minutos suelen repetirse en los gráficos horarios, diarios e incluso mensuales.

Esta autosimilitud no es accidental. Refleja el hecho de que los mercados no suponen solo ruido aleatorio, sino sistemas complejos con estructura interna, y comprender esta estructura nos da la clave para predecir los movimientos futuros.

Regreso a la media: el ritmo universal de la naturaleza

Hay un dicho en el mundo de las finanzas: "los árboles no crecen hasta el cielo". La historia nos muestra que, tras periodos de crecimiento o descenso extremos, los mercados tienden a regresar a su media a largo plazo.

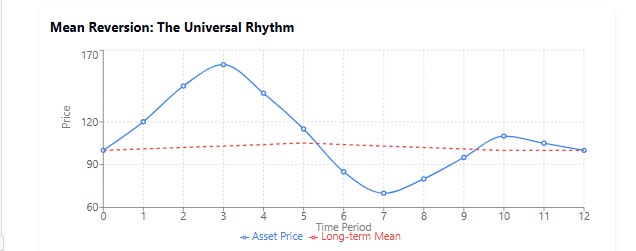
Este fenómeno puede observarse en toda la naturaleza. Imagine un péndulo: cuanto más lo desviemos, más tenderá a volver a la posición central. O piense en su temperatura corporal: cuando tiene fiebre, su cuerpo trabaja para que su temperatura regrese a los 36,6 °C normales.

Los mercados muestran este efecto constantemente. Los valores que registran rendimientos extraordinarios en un periodo suelen tener un comportamiento mediocre en el siguiente. Las empresas que crecen más rápido que el mercado durante mucho tiempo casi inevitablemente se ralentizan. Como observó el legendario inversor Peter Lynch: "El regreso a la media supone una forma de gravedad que ni siquiera una gran empresa puede superar".

Pero lo que hace revolucionario al Atractor Neuronal Sensorial es su capacidad para determinar no solo una media estática, sino el nivel dinámico hacia el que tiende el mercado en cada momento. Es como poder predecir exactamente dónde se detendrá el péndulo si la fuerza gravitatoria cambia de pronto.

La sensibilidad a las condiciones iniciales: el efecto mariposa en Wall Street

"¿Puede el batir de las alas de una mariposa en Brasil provocar un tornado en Texas?" Esta famosa pregunta de Lorenz ilustra un principio clave de la teoría del caos: la sensibilidad a las condiciones iniciales.

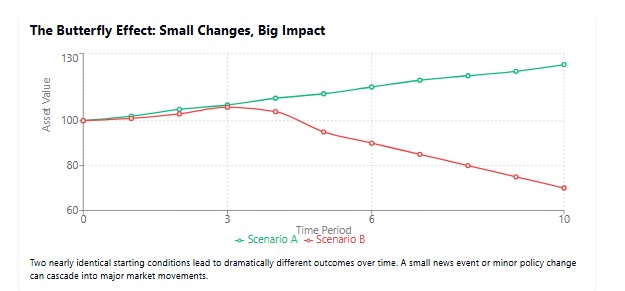
En los mercados financieros, observamos estos "efectos mariposa" todo el tiempo. El tuit de un CEO podría hundir las acciones de la empresa. Una decisión inesperada de la Reserva Federal puede desencadenar una corrección mundial. Incluso los rumores de problemas en un banco pequeño pueden provocar el pánico en todo el sector bancario, como vimos durante 2008.

Esta sensibilidad hace imposible una previsión precisa a largo plazo. Como bromeaba Niels Bohr: "predecir es muy difícil, sobre todo el futuro". Sin embargo, si comprendemos la estructura del sistema e identificamos los atractores, podremos hacer predicciones probabilísticas que supongan una ventaja.

El oscilador neuronal de atractores: domando el caos del mercado

De la teoría a la práctica: creamos el indicador

¿Ha observado alguna vez cómo el precio de un activo, como influido por una fuerza invisible, vuelve a un determinado nivel? ¿Cómo se produce una brusca corrección tras un violento repunte, o cómo comienza de pronto una recuperación tras un prolongado declive? Es como si algo invisible tirara del precio de vuelta, impidiendo que se mueva en una dirección para siempre. Precisamente esta fuerza invisible es la que atraparemos en nuestra red digital.

Mientras otros tráders siguen utilizando los indicadores del siglo pasado, usted y yo emprenderemos un viaje más profundo: la creación de un indicador que literalmente aprenderá a reconocer el ritmo oculto del mercado. Nuestra brújula en este viaje serán las redes neuronales y nuestro mapa, la teoría de los atractores.

La arquitectura de las redes neuronales: el cerebro de nuestro indicador

¿Recuerda que en las películas de hackers el protagonista crea una superinteligencia en un par de minutos de la película? En la práctica, todo es un poco más complicado, pero no tanto como para que no pueda hacerlo un tráder-programador corriente.

Nuestra red neuronal puede considerarse un rastreador experimentado que analiza las huellas en la nieve -los precios históricos- e intenta anticipar hacia dónde se dirigirá la presa (el mercado). La estructura de este rastreador es bastante sencilla: una capa de entrada que recoge los datos, una capa oculta donde se produce la "magia" del reconocimiento de patrones y una capa de salida que realiza predicciones.

Así se pone en marcha nuestro centro neurálgico:

void InitializeNetwork() {
   // Инициализация скрытого слоя
   ArrayResize(Network.hidden, HiddenNeurons);
   for(int i = 0; i < HiddenNeurons; i++) {
      ArrayResize(Network.hidden[i].weights, InputNeurons);
      // Инициализация весов случайными значениями в диапазоне [-0.5, 0.5]
      for(int j = 0; j < InputNeurons; j++) {
         Network.hidden[i].weights[j] = (MathRand() / 32767.0) - 0.5;
      }
      Network.hidden[i].bias = (MathRand() / 32767.0) - 0.5;
   }
   
   // Инициализация выходного нейрона
   ArrayResize(Network.output.weights, HiddenNeurons);
   for(int i = 0; i < HiddenNeurons; i++) {
      Network.output.weights[i] = (MathRand() / 32767.0) - 0.5;
   }
   Network.output.bias = (MathRand() / 32767.0) - 0.5;
}

Preste atención a las líneas en las que se inicializan los pesos. Es como ajustar la sensibilidad de un microscopio antes de comenzar la observación. Empezaremos con valores aleatorios y, a continuación, el proceso de aprendizaje ajustará gradualmente estos "botones de ajuste" para producir una imagen más precisa.

El entrenamiento de la red: de principiante a experto

Imagine a un niño aprendiendo a andar. Al principio se cae, da unos pasos y vuelve a caer, pero poco a poco va mejorando sus habilidades. Del mismo modo, nuestra red está aprendiendo a "caminar" usando datos históricos, ajustando constantemente sus pasos.

Una parte clave de este proceso son las pasadas directas e inversas. En las pasadas directas la red hace una predicción, mientras que en las inversas ajusta sus pesos en función del error.

double ForwardPass(double &inputs[]) {
   // Расчет выходов скрытого слоя
   for(int i = 0; i < HiddenNeurons; i++) {
      double sum = Network.hidden[i].bias;
      for(int j = 0; j < InputNeurons; j++) {
         sum += inputs[j] * Network.hidden[i].weights[j];
      }
      Network.hidden[i].output = Sigmoid(sum);
   }
   
   // Расчет выхода нейросети
   double sum = Network.output.bias;
   for(int i = 0; i < HiddenNeurons; i++) {
      sum += Network.hidden[i].output * Network.output.weights[i];
   }
   Network.output.output = Sigmoid(sum);
   
   return Network.output.output;
}

Si pudiéramos observar el funcionamiento de esta función, veríamos algo parecido a los impulsos eléctricos que recorren las neuronas del cerebro: la información pasa por una red de conexiones, transformándose y amplificándose.

La función de activación: la iluminación de las neuronas

En la versión actualizada del indicador hemos sustituido la sigmoide clásica por una tangente hiperbólica (tanh). Esta función tiene un rango de [-1, 1], lo que la hace especialmente eficaz para modelar sistemas caóticos en los que tanto los valores positivos como los negativos resultan importantes.

double Tanh(double x) {
   return (MathExp(x) - MathExp(-x)) / (MathExp(x) + MathExp(-x));
}

La tangente hiperbólica tiene una pendiente más pronunciada en el centro, lo cual permite a la red aprender más rápido y captar con mayor precisión los cambios bruscos en los datos. Esto resulta fundamental en mercados caóticos en los que las transiciones entre estados pueden producirse rápidamente.

La normalización de los datos: hablando el mismo idioma

Antes de introducir los datos en la red neuronal, debemos normalizarlos, es decir, llevarlos a una escala común. Es como traducir un texto a un idioma que el interlocutor pueda entender. Si usted habla ruso y su interlocutor solo inglés, la comunicación no funcionará.

double NormalizePrice(double price) {
   double min = ArrayMin(PriceHistory);
   double max = ArrayMax(PriceHistory);
   return (price - min) / (max - min);
}

Esta función escala todos los precios a un rango de 0 a 1, lo que resulta ideal para la entrada de nuestra función de activación sigmoidea.

El cálculo de los osciladores: la hora de la verdad

Por último, llegamos a la parte más interesante: el cálculo del valor del oscilador. ¿Cómo lo calculamos? Básicamente, compararemos el precio actual con el atractor previsto y expresaremos la desviación en un porcentaje.

// Рассчитываем значение осциллятора как отношение текущей цены к аттрактору
if(AttractorBuffer[i] > 0) {
   OscillatorBuffer[i] = (CurrentPriceBuffer[i] / AttractorBuffer[i] - 1.0) * 100.0;
} else {
   OscillatorBuffer[i] = 0; // Защита от деления на ноль
}

Esta sencilla fórmula nos indicará cuánto se ha desviado el precio actual de su nivel "natural". Si el oscilador muestra +30%, el precio estará "sobrecalentado" y podría volver pronto al atractor. Si -30%, el precio está "sobreenfriado" y podría rebotar al alza.

Adaptamos el indicador a nuestras necesidades

¿Recuerda el viejo dicho "una sola talla le viene bien a todos"? Pues esto rara vez funciona en el trading. Cada mercado, cada marco temporal tiene su propio carácter, su propio "estado de ánimo". Y nuestro indicador debe ajustarse a dichas características.

input int    InputNeurons = 10;     // Количество входных нейронов (исторические периоды)
input int    HiddenNeurons = 20;    // Количество нейронов в скрытом слое
input double LearningRate = 0.01;   // Скорость обучения
input int    TrainBars = 1000;      // Количество баров для обучения
input int    PredictionPeriod = 5;  // Период предсказания (в барах)
input bool   Smoothing = false;     // Применять сглаживание к осциллятору
input int    SmoothingPeriod = 3;   // Период сглаживания

Estos parámetros son como los controles de un amplificador de sonido caro. ¿Quiere un indicador más sensible? Aumente el número de neuronas o reduzca el periodo de predicción. ¿Hay demasiado ruido? Active el suavizado.

El periodo de predicción: mirando al futuro

El parámetro PredictionPeriod resulta especialmente interesante. Este determina lo lejos en el futuro que intentamos mirar. Si usted es un scalper que trabaja en gráficos de minutos, el valor 5 indicará una previsión para 5 minutos por delante. Si es un tráder posicional en gráficos diarios, serán 5 días.

Le recomiendo experimentar con este parámetro. Comience con valores pequeños y auméntelos gradualmente, observando el cambio en el comportamiento del indicador. Como en la ciencia real, no existen fórmulas prefabricadas, solo experiencia y experimentación.

El índice de Lyapunov: la medición de la aleatoriedad del mercado

El componente clave de nuestro indicador actualizado es el exponente de Lyapunov, una medida de la sensibilidad del sistema respecto a las condiciones iniciales. Este indicador describe matemáticamente el famoso "efecto mariposa", el fenómeno por el que pequeños cambios en las condiciones iniciales provocan diferencias significativas a largo plazo.

double CalculateLyapunovExponent(const double &close[], int bars) {
   double epsilon = 0.0001; // Малое возмущение
   double lyapunov = 0.0;
   int samples = MathMin(LyapunovPeriod, TrainBars/2);
   
   for(int i = 0; i < samples; i++) {
      int startIdx = MathRand() % (TrainBars - InputNeurons - PredictionPeriod);
      
      // Исходные входные данные
      double inputs1[];
      ArrayResize(inputs1, InputNeurons);
      for(int j = 0; j < InputNeurons; j++) {
         inputs1[j] = NormalizePrice(close[bars - TrainBars + startIdx + j]);
      }
      
      // Слегка возмущенные входные данные
      double inputs2[];
      ArrayResize(inputs2, InputNeurons);
      ArrayCopy(inputs2, inputs1);
      inputs2[MathRand() % InputNeurons] += epsilon;
      
      // Предсказания для обоих наборов данных
      double pred1 = ForwardPass(inputs1);
      double pred2 = ForwardPass(inputs2);
      
      // Расстояние между предсказаниями
      double distance = MathAbs(pred2 - pred1);
      
      // Показатель Ляпунова
      if(distance > 0) {
         lyapunov += MathLog(distance / epsilon);
      }
   }
   
   // Усредняем и нормализуем
   lyapunov = lyapunov / samples;
   
   // Ограничиваем значение для стабильности
   lyapunov = MathMax(-1.0, MathMin(1.0, lyapunov));
   
   return lyapunov;
}

El ruido fractal: añadimos estructura natural

Uno de los elementos más innovadores de nuestro indicador es la inclusión de ruido fractal generado por el algoritmo Midpoint Displacement. La geometría fractal, aplicada por primera vez a los mercados financieros por Benoit Mandelbrot, nos permite modelizar su estructura autosimilar natural.

void GenerateFractalNoise(int size) {
   ArrayResize(FractalNoiseBuffer, size);
   
   // Начальные точки
   FractalNoiseBuffer[0] = 0;
   FractalNoiseBuffer[size-1] = 0;
   
   // Рекурсивное вычисление промежуточных точек
   MidpointDisplacement(FractalNoiseBuffer, 0, size-1, 1.0, FractalDimension);
   
   // Нормализация
   double min = ArrayMin(FractalNoiseBuffer, 0, size);
   double max = ArrayMax(FractalNoiseBuffer, 0, size);
   
   for(int i = 0; i < size; i++) {
      FractalNoiseBuffer[i] = 2.0 * (FractalNoiseBuffer[i] - min) / (max - min) - 1.0;
   }
}

Cuanto mayor sea el parámetro FractalDimension, más "irregular" y caótico será el ruido, lo que permitirá modelizar con mayor precisión los mercados con alta volatilidad.

Aplicación práctica del indicador

Ahora que ya sabemos cómo funciona nuestro indicador, hablaremos de su aplicación práctica. Como cualquier oscilador, el Oscilador Neural Atractor puede usarse para identificar la sobrecompra y la sobreventa del mercado.

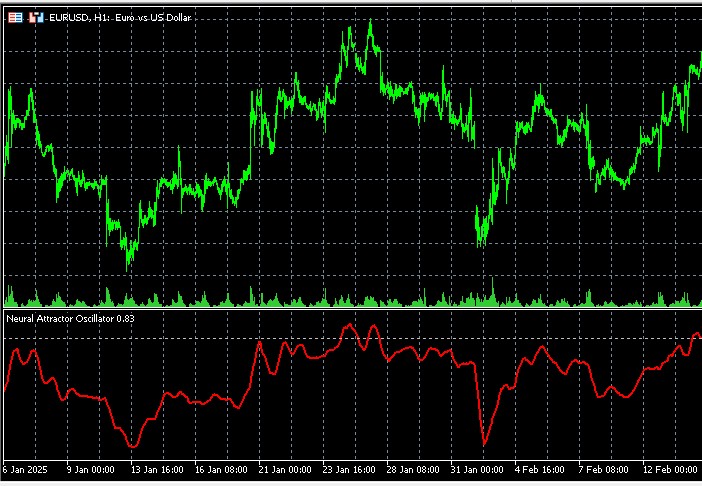
Imagine que está observando un péndulo. Si se desvía demasiado hacia la derecha, sabe que pronto empezará a moverse hacia la izquierda. Y si está demasiado a la izquierda, pronto se moverá de vuelta hacia la derecha. Nuestro indicador funciona de la misma manera, solo que en lugar de las fuerzas mecánicas que devuelven el péndulo al centro, aquí actúan las fuerzas de equilibrio del mercado.

Las señales de entrada considerando la aleatoriedad

1. Señal de compra: Cuando el oscilador cae por debajo del límite inferior del atractor (que se ajusta dinámicamente según el índice de Lyapunov) y empieza a subir, puede ser un buen momento para entrar en una posición larga. Es importante considerar el valor actual del exponente de Lyapunov: cuanto más bajo sea, más fiable será la señal.
2. Señal de venta: Cuando el oscilador supera el límite superior del atractor y comienza a caer, esto puede indicar un buen punto de entrada para una posición corta. Nuevamente, un exponente de Lyapunov bajo aumenta la fiabilidad de la señal.
3. Divergencias: una señal especialmente valiosa y muy precisa de divergencia de los picos del indicador y el precio.

Recuerde que, durante los periodos de alta aleatoriedad, incluso las señales fuertes son menos fiables (alto índice de Lyapunov), y se debería reducir el tamaño de la posición o no entrar en absoluto en el mercado.

La divergencia en el contexto de la teoría del caos

El oscilador atractor de caos ofrece una nueva visión de las divergencias clásicas. Cuando el precio forma un nuevo extremo, pero el oscilador no, esto puede indicar no solo un debilitamiento de la tendencia, sino un cambio en la estructura del atractor, el punto de equilibrio que busca el mercado.

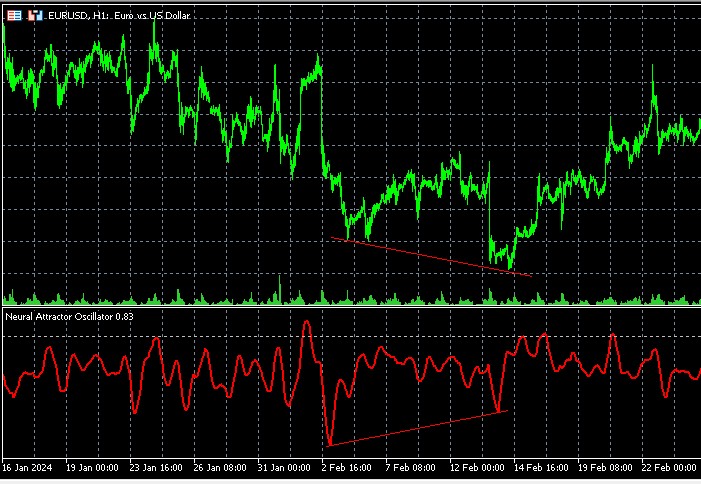
Las señales especialmente potentes surgen cuando la divergencia coincide con un cambio en el exponente de Lyapunov; por ejemplo, una transición de un valor positivo a uno negativo puede indicar la formación de una nueva tendencia estable tras un cierto periodo de caos.

La optimización de la red con impulso

En nuestro indicador actualizado, hemos aplicado la técnica de optimización del impulso, que acelera considerablemente el proceso de entrenamiento y reduce la probabilidad de quedarse atascado en mínimos locales:

// Обновление весов выходного слоя с моментом
for(int j = 0; j < HiddenNeurons; j++) {
    double delta = LearningRate * Network.output.error * Network.hidden[j].output;
    Network.output.momentum[j] = momentum * Network.output.momentum[j] + (1.0 - momentum) * delta;
    Network.output.weights[j] += Network.output.momentum[j];
}

El método del impulso funciona como la "inercia" en el mundo físico: si una red se ha estado moviendo en una dirección determinada durante mucho tiempo durante la optimización, seguirá moviéndose en esa dirección incluso cuando encuentre pequeños obstáculos (los mínimos locales). Esto resulta especialmente útil para los sistemas caóticos, en los que el panorama de la función de error puede resultar muy complejo.

Mejoras futuras

Aunque nuestro indicador ya es una herramienta potente, existen varios rumbos de desarrollo para el concepto de caos-atractor:

1. Redes neuronales recurrentes: la sustitución de nuestra red neuronal directa por una red neuronal recurrente (LSTM o GRU) puede mejorar la capacidad del modelo para captar dependencias a largo plazo en sistemas caóticos.
2. Análisis multifractal: introducción de técnicas de análisis multifractal para determinar la estructura de la volatilidad en diferentes escalas temporales.
3. Análisis de la topología de los atractores: aplicación de métodos de topología dinámica para identificar y clasificar atractores extraños en la dinámica de precios.
4. Algoritmos cuánticos: en el futuro, es posible que la computación cuántica se utilice para modelar sistemas caóticos complejos, lo que podría suponer un avance revolucionario en la predicción de los movimientos del mercado.

Y, obviamente, consideraremos crear un asesor experto para este sistema. El boceto del experto tiene este aspecto:

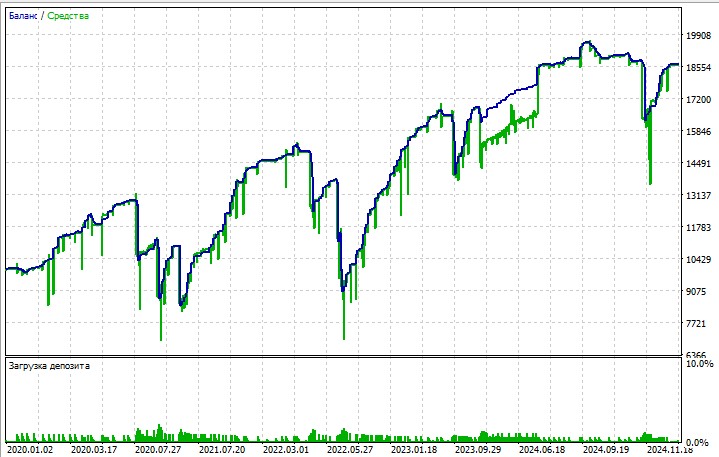
En general, el sistema funciona bastante bien: no es especialmente genial, pero tampoco es algo terrible.

Métodos de suavizado flexibles

En la versión actualizada del indicador hemos añadido la posibilidad de elegir entre distintos métodos de suavización, lo cual permite al tráder personalizar la respuesta del indicador en función de las condiciones del mercado:

void ApplySmoothing(int rates_total, int prev_calculated, int period, ENUM_MA_METHOD method) {
   int start = prev_calculated == 0 ? InputNeurons + period : prev_calculated - 1;
   
   double temp[];
   ArrayResize(temp, rates_total);
   ArrayCopy(temp, OscillatorBuffer);
   
   for(int i = start; i < rates_total; i++) {
      switch(method) {
         case MODE_SMA: // Простое скользящее среднее
            {
               double sum = 0;
               for(int j = 0; j < period; j++) {
                  sum += temp[i - j];
               }
               OscillatorBuffer[i] = sum / period;
            }
            break;
            
         case MODE_EMA: // Экспоненциальное скользящее среднее
            {
               double alpha = 2.0 / (period + 1.0);
               OscillatorBuffer[i] = temp[i] * alpha + OscillatorBuffer[i-1] * (1.0 - alpha);
            }
            break;
            
         // ... другие методы ...
      }
   }
}

Para los mercados caóticos con un exponente de Lyapunov elevado, es mejor usar la EMA, que reacciona más rápidamente a los cambios. Para mercados más predecibles con un índice de Lyapunov bajo, la SMA puede dar señales más fiables con menos falsos positivos.

Conclusión

Hoy no hemos creado un indicador técnico más, sino un sistema completo para analizar el caos del mercado. El oscilador atractor del caos combina los últimos avances de la teoría del caos, la geometría fractal y las redes neuronales para ofrecer a los tráders una herramienta con la que navegar en condiciones de mercado complejas e impredecibles.

El valor especial de este indicador reside en su capacidad no solo para generar señales comerciales, sino también para evaluar la fiabilidad de estas señales a través del índice de Lyapunov. Esto permite al tráder adaptar su estrategia al estado actual del mercado: ser agresivo cuando el sistema es predecible y cauto cuando es caótico.

En la era del trading algorítmico y la inteligencia artificial, la ventaja es para quien pueda modelar mejor la compleja naturaleza del mercado. El oscilador atractor del caos supone un paso en esta dirección y permite ver el orden donde otros solo ven aleatoriedad.

Recuerde que ni siquiera el indicador más avanzado supone una fórmula mágica para el éxito. Negociar siempre requiere disciplina, gestión del riesgo y comprensión del contexto del mercado. Pero, armado con una herramienta que le permita vislumbrar la naturaleza misma del caos del mercado, tendrá una ventaja significativa a la hora de lograr beneficios sostenibles.

Buena suerte con sus operaciones y que los atractores del caos le acompañen.