Определение перекупленности и перепроданности по теории хаоса

Когда хаос становится узором

Представьте себе прогулку по лесу во время метели. Снежинки кажутся хаотичными, их движение непредсказуемым. Но стоит посмотреть внимательнее, и вы заметите, что они движутся по невидимым потокам воздуха, следуя определенным закономерностям. Подобно этим снежинкам, цены на финансовых рынках танцуют свой собственный танец, который лишь выглядит случайным.

Теория хаоса учит нас удивительной истине: в системах, которые кажутся совершенно непредсказуемыми, скрываются глубокие узоры и структуры. Метеоролог Эдвард Лоренц обнаружил это, когда работал с моделями погоды и случайно ввел округленные данные в свою программу. Его открытие, позже названное "эффектом бабочки", показало, что даже малейшие изменения начальных условий могут привести к кардинально разным результатам.

"Система, обладающая странным аттрактором, может выглядеть совершенно случайной, но в ней есть скрытый порядок", — говорил Лоренц. И точно так же, как погодные системы имеют свои невидимые шаблоны, финансовые рынки следуют определенным закономерностям, несмотря на свою кажущуюся непредсказуемость.

Аттракторы: невидимые магниты рынка

Представьте, что вы бросаете мяч в комнате. Независимо от того, как сильно вы его бросите, или в каком направлении, в конечном итоге он окажется на полу. Пол в этом случае — это аттрактор, точка притяжения для мяча.

На финансовых рынках аттракторы работают схожим образом. Вместо физического притяжения, здесь действуют экономические силы, возвращающие цены к определенным уровням. Когда акция становится слишком дорогой, продавцы начинают преобладать; когда слишком дешевой — покупатели. Это создает эффект "резинки", постоянно тянущей рынок к точке равновесия.

Но в отличие от простого мяча, рынки обладают тем, что называется "странными аттракторами". Это не просто точки, а сложные структуры, к которым система стремится, но никогда не повторяет себя точно. Как ручей, впадающий в озеро — вода всегда течет к озеру, но никогда не повторяет точно свой путь.

Как понять фрактальный узор рынка

Бенуа Мандельброт, работая в IBM в 1960-х годах, анализировал колебания цен на хлопок за длительный период. Он заметил удивительную вещь: графики цен выглядели одинаково, независимо от того, смотрел ли он на данные за день, месяц или год. Это открытие привело к развитию фрактальной геометрии — изучения форм, которые повторяют себя на разных масштабах.

Взгляните на лист папоротника: его общая форма повторяется в каждом маленьком листочке, а затем, в еще более мелких частях. Рынки работают аналогично. Паттерны, которые вы видите на минутном графике, часто повторяются на часовом, дневном и даже месячном.

Это самоподобие не случайно. Оно отражает тот факт, что рынки — это не просто случайный шум, а сложные системы с внутренней структурой. И понимание этой структуры даёт нам ключ к предсказанию будущих движений.

Возврат к среднему: универсальный ритм природы

В мире финансов есть поговорка: "Деревья не растут до небес". История показывает нам, что после периодов экстремального роста или падения, рынки имеют тенденцию возвращаться к своему долгосрочному среднему значению.

Это явление можно наблюдать повсюду в природе. Представьте маятник: чем дальше вы его отклоняете, тем сильнее он стремится вернуться в центральное положение. Или подумайте о температуре тела: когда у вас жар, организм работает над тем, чтобы вернуть температуру к норме в 36.6°C.

На рынках этот эффект проявляется постоянно. Акции, которые показывают экстраординарную доходность в один период, часто демонстрируют посредственные результаты в следующий. Компании, которые растут быстрее рынка в течение долгого времени, почти неизбежно замедляются. Как заметил легендарный инвестор Питер Линч: "Возврат к среднему — это гравитация, которую не может преодолеть даже великая компания".

Но что делает Sensory Neural Attractor революционным, так это его способность определять не просто статичное среднее, а динамический уровень, к которому рынок стремится в данный момент. Это подобно умению предсказать, где именно маятник остановится, если сила гравитации внезапно изменится.

Чувствительность к начальным условиям: эффект бабочки на Уолл-стрит

"Может ли взмах крыльев бабочки в Бразилии вызвать торнадо в Техасе?" — этот знаменитый вопрос Лоренца иллюстрирует ключевой принцип теории хаоса: чувствительность к начальным условиям.

На финансовых рынках мы видим такие "эффекты бабочки" постоянно. Твит генерального директора может обрушить акции компании. Неожиданное решение Федеральной резервной системы может спровоцировать глобальную коррекцию. Даже слухи о проблемах у небольшого банка могут привести к панике на всём банковском секторе, как мы видели во время кризиса 2008 года.

Эта чувствительность делает точное долгосрочное прогнозирование невозможным. Как шутил Нильс Бор: "Предсказывать очень сложно, особенно будущее". Однако, понимая структуру системы и выявляя аттракторы, мы можем делать вероятностные прогнозы, которые дают преимущество.

Нейронный осциллятор аттракторов: приручая хаос рынка

От теории к практике: создание индикатора

Вы когда-нибудь замечали, как цена актива, будто под действием невидимой силы, возвращается к определенному уровню? Как после бурного ралли следует резкая коррекция, или как после затяжного падения внезапно начинается восстановление? Словно нечто невидимое притягивает цену обратно, не давая ей вечно двигаться в одном направлении. Именно эту невидимую силу мы и собираемся поймать в наш цифровой сачок.

Пока другие трейдеры продолжают использовать индикаторы прошлого века, мы с вами отправимся в более глубокое путешествие — к созданию индикатора, который буквально учится распознавать скрытый ритм рынка. Нашим компасом в этом путешествии будет нейронная сеть, а картой — теория аттракторов.

Архитектура нейронной сети: мозг нашего индикатора

Помните, как в фильмах про хакеров главный герой создаёт сверхразум за пару минут экранного времени? На практике всё несколько сложнее, но не настолько, чтобы этим не мог заниматься обычный трейдер-программист.

Нашу нейронную сеть можно представить как опытного следопыта, который анализирует следы на снегу — исторические цены — и пытается предугадать, куда направляется зверь (рынок). Структура этого следопыта довольно проста: входной слой, который собирает данные, скрытый слой, где происходит "магия" распознавания паттернов, и выходной слой, который делает предсказание.

Вот как выглядит инициализация нашего мозгового центра:

void InitializeNetwork() {
   // Инициализация скрытого слоя
   ArrayResize(Network.hidden, HiddenNeurons);
   for(int i = 0; i < HiddenNeurons; i++) {
      ArrayResize(Network.hidden[i].weights, InputNeurons);
      // Инициализация весов случайными значениями в диапазоне [-0.5, 0.5]
      for(int j = 0; j < InputNeurons; j++) {
         Network.hidden[i].weights[j] = (MathRand() / 32767.0) - 0.5;
      }
      Network.hidden[i].bias = (MathRand() / 32767.0) - 0.5;
   }
   
   // Инициализация выходного нейрона
   ArrayResize(Network.output.weights, HiddenNeurons);
   for(int i = 0; i < HiddenNeurons; i++) {
      Network.output.weights[i] = (MathRand() / 32767.0) - 0.5;
   }
   Network.output.bias = (MathRand() / 32767.0) - 0.5;
}

Обратите внимание на строчки, где происходит инициализация весов. Это как настройка чувствительности микроскопа перед исследованием. Мы начинаем со случайных значений, а затем, процесс обучения постепенно подстраивает эти "ручки настройки" для получения более точного изображения.

Обучение сети: от новичка к мастеру

Представьте ребёнка, который учится ходить. Сначала он падает, затем делает несколько шагов, снова падает, но постепенно совершенствует свои навыки. Точно так же наша сеть учится "ходить" по историческим данным, постоянно корректируя свои шаги.

Ключевая часть этого процесса — прямой и обратный проходы. В прямом проходе сеть делает предсказание, в обратном — корректирует свои веса, в зависимости от ошибки.

double ForwardPass(double &inputs[]) {
   // Расчет выходов скрытого слоя
   for(int i = 0; i < HiddenNeurons; i++) {
      double sum = Network.hidden[i].bias;
      for(int j = 0; j < InputNeurons; j++) {
         sum += inputs[j] * Network.hidden[i].weights[j];
      }
      Network.hidden[i].output = Sigmoid(sum);
   }
   
   // Расчет выхода нейросети
   double sum = Network.output.bias;
   for(int i = 0; i < HiddenNeurons; i++) {
      sum += Network.hidden[i].output * Network.output.weights[i];
   }
   Network.output.output = Sigmoid(sum);
   
   return Network.output.output;
}

Если бы мы могли заглянуть внутрь этой функции во время её работы, мы бы увидели нечто похожее на электрические импульсы, проходящие по нейронам мозга — информация проходит через сеть связей, преобразуясь и усиливаясь.

Функция активации: зажигаем нейроны

В обновленной версии индикатора мы заменили классическую сигмоиду на гиперболический тангенс (tanh). Эта функция имеет диапазон [-1, 1], что делает её особенно эффективной для моделирования хаотических систем, где важны как положительные, так и отрицательные значения.

double Tanh(double x) {
   return (MathExp(x) - MathExp(-x)) / (MathExp(x) + MathExp(-x));
}

Гиперболический тангенс обладает более крутым наклоном в центральной части, что позволяет сети быстрее обучаться и точнее улавливать резкие изменения в данных. Это критически важно для хаотических рынков, где переходы между состояниями могут происходить стремительно.

Нормализация данных: говорим на одном языке

Прежде чем подавать данные в нейронную сеть, необходимо их нормализовать — привести к единому масштабу. Это как перевод текста на понятный для собеседника язык. Если вы говорите на русском, а ваш собеседник понимает только английский, общения не получится.

double NormalizePrice(double price) {
   double min = ArrayMin(PriceHistory);
   double max = ArrayMax(PriceHistory);
   return (price - min) / (max - min);
}

Эта функция масштабирует все цены в диапазон от 0 до 1, что идеально подходит для входа нашей сигмоидной функции активации.

Расчёт осциллятора: момент истины

Наконец мы подошли к самому интересному — вычислению значения осциллятора. Как же мы его рассчитываем? По сути, мы сравниваем текущую цену с предсказанным аттрактором и выражаем отклонение в процентах.

// Рассчитываем значение осциллятора как отношение текущей цены к аттрактору
if(AttractorBuffer[i] > 0) {
   OscillatorBuffer[i] = (CurrentPriceBuffer[i] / AttractorBuffer[i] - 1.0) * 100.0;
} else {
   OscillatorBuffer[i] = 0; // Защита от деления на ноль
}

Эта простая формула говорит нам, насколько текущая цена отклонилась от своего "естественного" уровня. Если осциллятор показывает +30%, цена "перегрета" и может скоро вернуться к аттрактору. Если -30%, цена "переохлаждена" и может отскочить вверх.

Настраиваем индикатор под свои нужды

Помните старую поговорку "Один размер подходит всем"? В трейдинге это редко работает. Каждый рынок, каждый таймфрейм имеет свой характер, своё "настроение". И наш индикатор должен подстраиваться под эти особенности.

input int    InputNeurons = 10;     // Количество входных нейронов (исторические периоды)
input int    HiddenNeurons = 20;    // Количество нейронов в скрытом слое
input double LearningRate = 0.01;   // Скорость обучения
input int    TrainBars = 1000;      // Количество баров для обучения
input int    PredictionPeriod = 5;  // Период предсказания (в барах)
input bool   Smoothing = false;     // Применять сглаживание к осциллятору
input int    SmoothingPeriod = 3;   // Период сглаживания

Эти параметры — как регуляторы на дорогом усилителе звука. Хотите более чувствительный индикатор? Увеличьте количество нейронов или уменьшите период предсказания. Слишком много шума? Включите сглаживание.

Период предсказания: заглядывая в будущее

Особенно интересен параметр PredictionPeriod . Он определяет, насколько далеко в будущее мы пытаемся заглянуть. Если вы скальпер, работающий на минутных графиках, то значение 5 означает прогноз на 5 минут вперёд. Если вы позиционный трейдер на дневных графиках, то это 5 дней.

Я рекомендую экспериментировать с этим параметром. Начните с небольших значений и постепенно увеличивайте их, наблюдая за изменением поведения индикатора. Как и в настоящей науке, здесь нет готовых формул — только опыт и эксперименты.

Показатель Ляпунова: измеряем хаотичность рынка

Ключевым компонентом нашего обновлённого индикатора является показатель Ляпунова — мера чувствительности системы к начальным условиям. Этот показатель математически описывает знаменитый "эффект бабочки" — явление, когда небольшие изменения в начальных условиях приводят к значительным расхождениям в долгосрочной перспективе.

double CalculateLyapunovExponent(const double &close[], int bars) {
   double epsilon = 0.0001; // Малое возмущение
   double lyapunov = 0.0;
   int samples = MathMin(LyapunovPeriod, TrainBars/2);
   
   for(int i = 0; i < samples; i++) {
      int startIdx = MathRand() % (TrainBars - InputNeurons - PredictionPeriod);
      
      // Исходные входные данные
      double inputs1[];
      ArrayResize(inputs1, InputNeurons);
      for(int j = 0; j < InputNeurons; j++) {
         inputs1[j] = NormalizePrice(close[bars - TrainBars + startIdx + j]);
      }
      
      // Слегка возмущенные входные данные
      double inputs2[];
      ArrayResize(inputs2, InputNeurons);
      ArrayCopy(inputs2, inputs1);
      inputs2[MathRand() % InputNeurons] += epsilon;
      
      // Предсказания для обоих наборов данных
      double pred1 = ForwardPass(inputs1);
      double pred2 = ForwardPass(inputs2);
      
      // Расстояние между предсказаниями
      double distance = MathAbs(pred2 - pred1);
      
      // Показатель Ляпунова
      if(distance > 0) {
         lyapunov += MathLog(distance / epsilon);
      }
   }
   
   // Усредняем и нормализуем
   lyapunov = lyapunov / samples;
   
   // Ограничиваем значение для стабильности
   lyapunov = MathMax(-1.0, MathMin(1.0, lyapunov));
   
   return lyapunov;
}

Фрактальный шум: добавляем природную структуру

Одним из самых инновационных элементов нашего индикатора является включение фрактального шума, генерируемого алгоритмом смещения средней точки (Midpoint Displacement). Фрактальная геометрия, впервые применённая к финансовым рынкам Бенуа Мандельбротом, позволяет моделировать их естественную самоподобную структуру.

void GenerateFractalNoise(int size) {
   ArrayResize(FractalNoiseBuffer, size);
   
   // Начальные точки
   FractalNoiseBuffer[0] = 0;
   FractalNoiseBuffer[size-1] = 0;
   
   // Рекурсивное вычисление промежуточных точек
   MidpointDisplacement(FractalNoiseBuffer, 0, size-1, 1.0, FractalDimension);
   
   // Нормализация
   double min = ArrayMin(FractalNoiseBuffer, 0, size);
   double max = ArrayMax(FractalNoiseBuffer, 0, size);
   
   for(int i = 0; i < size; i++) {
      FractalNoiseBuffer[i] = 2.0 * (FractalNoiseBuffer[i] - min) / (max - min) - 1.0;
   }
}

Чем выше параметр фрактальной размерности (FractalDimension), тем более "зазубренным" и хаотичным становится шум, что позволяет точнее моделировать рынки с высокой волатильностью.

Применение индикатора на практике

Теперь, когда мы понимаем, как работает наш индикатор, давайте обсудим его практическое применение. Как и любой осциллятор, Neural Attractor Oscillator может использоваться для определения перекупленности и перепроданности рынка.

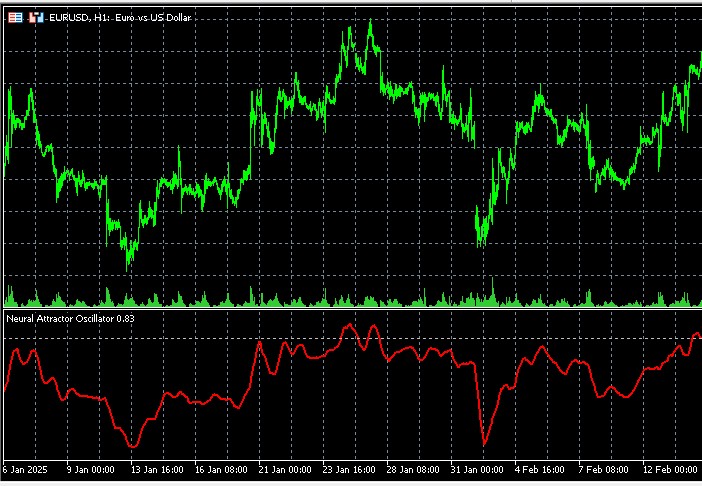
Представьте, что вы наблюдаете за маятником. Когда он отклоняется слишком далеко вправо, вы знаете, что вскоре он начнёт движение влево. Когда слишком далеко влево — вскоре пойдёт вправо. Так же работает и наш индикатор, только вместо механических сил, возвращающих маятник к центру, здесь действуют равновесные рыночные силы.

Сигналы на вход с учетом хаотичности

1. Сигнал на покупку: Когда осциллятор опускается ниже нижней границы аттрактора (которая динамически корректируется в зависимости от показателя Ляпунова) и начинает подниматься, это может быть хорошей точкой для входа в длинную позицию. При этом важно учитывать текущее значение показателя Ляпунова — чем оно ниже, тем надёжнее сигнал.
2. Сигнал на продажу: Когда осциллятор поднимается выше верхней границы аттрактора и начинает падать, это может указывать на хорошую точку для входа в короткую позицию. Опять же, низкий показатель Ляпунова повышает надёжность сигнала.
3. Дивергенции: Особенно ценный и высокоточный сигнал расхождения пиков индикатора и цены.

Помните, что в периоды высокой хаотичности (высокий показатель Ляпунова) даже сильные сигналы менее надёжны, и следует уменьшать размер позиции или вовсе воздерживаться от входа в рынок.

Расхождения в контексте теории хаоса

Хаос-аттрактор осциллятор предлагает новый взгляд на классические дивергенции. Когда цена формирует новый экстремум, а осциллятор нет, это может указывать не просто на ослабление тренда, а на изменение структуры аттрактора — точки равновесия, к которой стремится рынок.

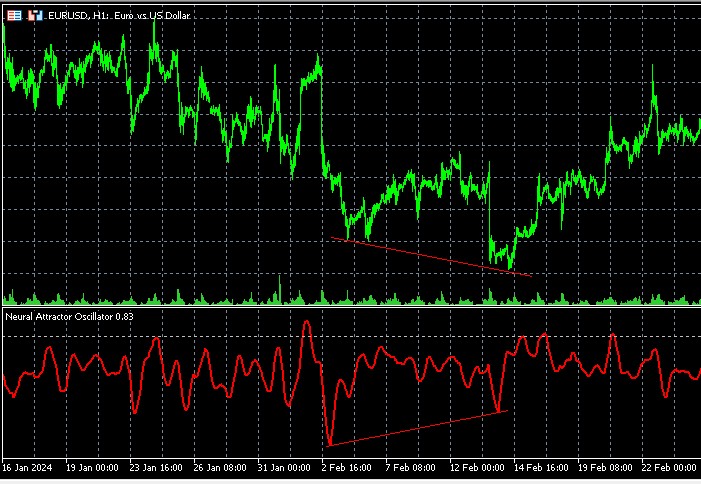
Особенно мощные сигналы возникают, когда дивергенция совпадает с изменением показателя Ляпунова — например, переход от положительного значения к отрицательному может указывать на формирование нового устойчивого тренда после периода хаотичности.

Оптимизация сети с моментом

В нашем обновлённом индикаторе мы применили технику оптимизации с моментом, которая значительно ускоряет процесс обучения и уменьшает вероятность застревания в локальных минимумах:

// Обновление весов выходного слоя с моментом
for(int j = 0; j < HiddenNeurons; j++) {
    double delta = LearningRate * Network.output.error * Network.hidden[j].output;
    Network.output.momentum[j] = momentum * Network.output.momentum[j] + (1.0 - momentum) * delta;
    Network.output.weights[j] += Network.output.momentum[j];
}

Метод момента работает как "инерция" в физическом мире — если сеть долго двигалась в определённом направлении при оптимизации, она будет продолжать движение в этом направлении даже при встрече с небольшими препятствиями (локальными минимумами). Это особенно полезно для хаотических систем, где ландшафт функции ошибки может быть очень сложным.

Будущие улучшения

Хотя наш индикатор уже является мощным инструментом, есть несколько направлений для дальнейшего развития концепции хаос-аттрактора:

1. Рекуррентные нейронные сети: Замена нашей прямой нейронной сети на рекуррентную (LSTM или GRU) может улучшить способность модели улавливать долгосрочные зависимости в хаотических системах.
2. Мультифрактальный анализ: Внедрение методов мультифрактального анализа для определения структуры волатильности на разных временных масштабах.
3. Анализ топологии аттракторов: Применение методов динамической топологии для идентификации и классификации странных аттракторов в ценовой динамике.
4. Квантовые алгоритмы: В будущем возможно применение квантовых вычислений для моделирования сложных хаотических систем, что может дать революционный прорыв в предсказании рыночных движений.

Ну и конечно, мы еще обязательно рассмотрим вопрос создания советника по данной системе. Вот так показывает себя черновой вариант - набросок эксперта:

В целом, система вполне работает — не особо круто, но и не ужасно.

Гибкие методы сглаживания

В обновлённой версии индикатора мы добавили выбор различных методов сглаживания, что позволяет трейдеру настраивать реакцию индикатора в зависимости от рыночных условий:

void ApplySmoothing(int rates_total, int prev_calculated, int period, ENUM_MA_METHOD method) {
   int start = prev_calculated == 0 ? InputNeurons + period : prev_calculated - 1;
   
   double temp[];
   ArrayResize(temp, rates_total);
   ArrayCopy(temp, OscillatorBuffer);
   
   for(int i = start; i < rates_total; i++) {
      switch(method) {
         case MODE_SMA: // Простое скользящее среднее
            {
               double sum = 0;
               for(int j = 0; j < period; j++) {
                  sum += temp[i - j];
               }
               OscillatorBuffer[i] = sum / period;
            }
            break;
            
         case MODE_EMA: // Экспоненциальное скользящее среднее
            {
               double alpha = 2.0 / (period + 1.0);
               OscillatorBuffer[i] = temp[i] * alpha + OscillatorBuffer[i-1] * (1.0 - alpha);
            }
            break;
            
         // ... другие методы ...
      }
   }
}

Для хаотических рынков с высоким показателем Ляпунова лучше использовать EMA, которое быстрее реагирует на изменения. Для более предсказуемых рынков с низким показателем Ляпунова, SMA может дать более надёжные сигналы с меньшим числом ложных срабатываний.

Заключение

Мы создали не просто очередной технический индикатор, а полноценную систему анализа рыночного хаоса. Chaos Attractor Oscillator соединяет в себе новейшие достижения теории хаоса, фрактальной геометрии и нейронных сетей, предоставляя трейдеру инструмент для навигации в сложных и непредсказуемых рыночных условиях.

Особая ценность этого индикатора заключается в его способности не только генерировать торговые сигналы, но и оценивать надёжность этих сигналов через показатель Ляпунова. Это даёт трейдеру возможность адаптировать свою стратегию к текущему состоянию рынка — быть агрессивным, когда система предсказуема, и осторожным, когда она хаотична.

В эпоху алгоритмической торговли и искусственного интеллекта преимущество получает тот, кто способен лучше моделировать сложную природу рынка. Chaos Attractor Oscillator — шаг в этом направлении, позволяющий увидеть порядок там, где другие видят лишь случайность.

Помните, что даже самый продвинутый индикатор — не магическая формула успеха. Торговля всегда требует дисциплины, управления рисками и понимания рыночного контекста. Но вооружившись инструментом, который позволяет заглянуть в саму природу рыночного хаоса, вы получаете значительное преимущество на пути к стабильной прибыли.

Удачи в торговле и пусть хаос-аттракторы будут с вами!