Нейросети в трейдинге: Контекстно-зависимое обучение, дополненное памятью (MacroHFT)

MetaTrader 5 — Торговые системы | 22 января 2025, 13:31

566

Dmitriy Gizlyk

Введение

Финансовые рынки привлекают огромное количество инвесторов, благодаря своей широкой доступности и потенциально высокой прибыльности. Среди всех доступных активов, криптовалюты выделяются своей исключительной волатильностью, что открывает уникальные возможности для получения значительной прибыли в короткие сроки. Дополнительным преимуществом является круглосуточный режим работы, который позволяет трейдерам быстро реагировать на изменения рыночной ситуации. Однако такая высокая волатильность несет в себе не только преимущества, но и существенные риски, что требует применения более сложных стратегий управления.

Для максимизации прибыли на криптовалютных рынках всё чаще используется высокочастотная торговля (HFT) — форма алгоритмической торговли, которая основывается на молниеносном выполнении сделок. HFT уже давно заняла лидирующие позиции на традиционных финансовых рынках, а в последнее время она активно применяется и в криптовалютной сфере. Высокочастотная торговля отличается не только скоростью выполнения операций, но и способностью обрабатывать огромные объёмы данных в реальном времени, что делает её незаменимой в условиях высокой динамики криптовалютных рынков.

Методы обучения с подкреплением (RL) становятся всё более популярными в сфере финансов, так как они позволяют решать сложные задачи последовательного принятия решений. RL-алгоритмы способны обрабатывать многомерные данные, учитывать различные параметры и адаптироваться к изменяющимся условиям. Тем не менее, несмотря на успехи в низкочастотной торговле, эффективные алгоритмы для высокочастотных криптовалютных рынков всё ещё находятся на стадии разработки. Особенностями криптовалютных рынков являются их высокая волатильность, нестабильность и необходимость учитывать долгосрочные горизонты торговли наряду с оперативным реагированием.

Существующие алгоритмы HFT для криптовалют сталкиваются с рядом проблем, которые ограничивают их эффективность. Во-первых, рынок часто рассматривается как единая стационарная система, а многие алгоритмы ограничиваются анализом тенденций, игнорируя волатильность. Такой подход затрудняет управление рисками и снижает точность прогнозирования. Во-вторых, многие стратегии склонны к переобучению из-за излишнего фокуса на узком наборе характеристик рынка. Это приводит к снижению их способности адаптироваться к новым рыночным условиям. Наконец, индивидуальные торговые политики агентов часто не обладают достаточной гибкостью для оперативного реагирования на резкие изменения, что особенно критично для рынков с высокой частотой данных.

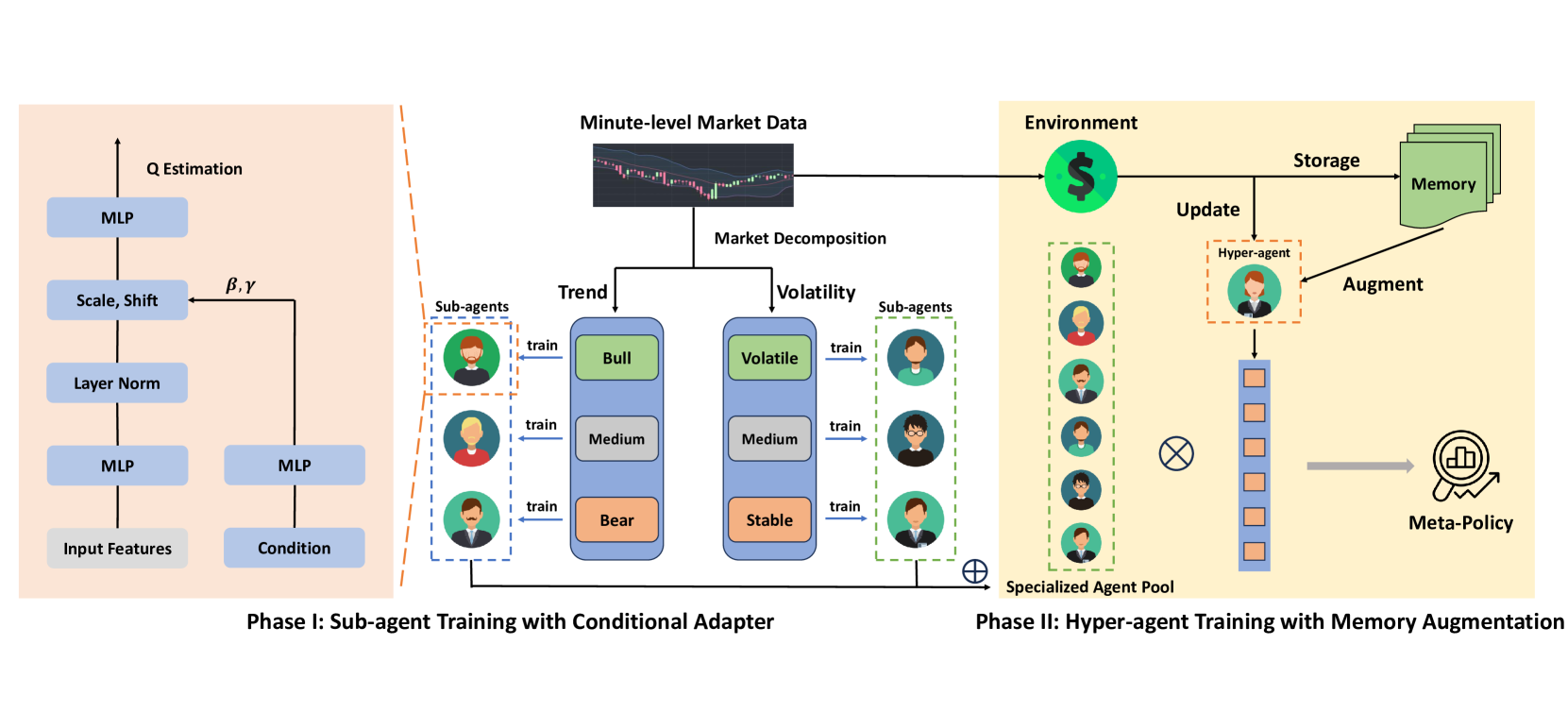
Один из вариантов решения указанных проблем был представлен в работе "MacroHFT: Memory Augmented Context-aware Reinforcement Learning On High Frequency Trading". Её авторы предложили фреймворк MacroHFT — инновационный подход, основанный на контекстно зависимом обучении с подкреплением. Этот фреймворк специально разработан для высокочастотной торговли криптовалютами на минутном таймфрейме. MacroHFT использует макроэкономическую информацию и другие контекстные данные для улучшения качества принимаемых решений. Процесс включает два ключевых этапа. На первом этапе рынок классифицируется на основе индикаторов тренда и волатильности. Для каждой категории рыночных условий обучаются специализированные субагенты, которые корректируют свои стратегии в зависимости от текущей ситуации. Такие субагенты обеспечивают гибкость и способность учитывать локальные особенности рынка.

На втором этапе создаётся гиперагент, который интегрирует стратегии субагентов и оптимизирует их использование в зависимости от динамики рынка. Гиперагент оснащён модулем памяти, который учитывает недавний опыт работы и позволяет развивать стабильные и адаптивные торговые стратегии. Это обеспечивает высокую устойчивость системы к резким изменениям рыночных условий и помогает минимизировать риски.

Алгоритм MacroHFT

Фреймворка MacroHFT является инновационной платформой для алгоритмической торговли, специально разработанной для криптовалютных рынков, с их высокой волатильностью и быстрыми изменениями. В основе работы фреймворка лежат методы обучения с подкреплением, которые позволяют создавать адаптивные алгоритмы, способные анализировать рыночные условия и прогнозировать их изменения. Главная идея заключается в интеграции специализированных субагентов, каждый из которых оптимизирован для определённого рыночного сценария, и гиперагента, который координирует их работу, обеспечивая согласованность и эффективность системы в целом.

В условиях высокой волатильности и постоянных изменений рыночной ситуации, применение одного агента обучения с подкреплением (RL) оказывается недостаточно эффективным. Это связано с тем, что рыночные условия могут меняться слишком быстро и непредсказуемо, а единый алгоритм не успевает адаптироваться под каждую новую ситуацию. Для решения этой проблемы авторы фреймворка MacroHFT предложили создать несколько специализированных субагентов, каждый из которых обучается на определённых рыночных условиях. Это позволяет построить более гибкую и адаптивную систему.

Основная идея заключается в сегментации и классификации рыночных данных с использованием двух ключевых параметров: тренда и волатильности. Для анализа рыночные данные разбиваются на блоки фиксированной длины. Эти блоки используются как для обучения, так и для тестирования. Затем, каждому блоку присваиваются метки, которые помогают определить, к какому типу рыночных условий он относится, что упрощает процесс обучения субагентов.

Процесс разметки данных делится на два этапа:

Определение меток тренда. Для выявления рыночного тренда используются данные каждого блока, которые пропускаются через фильтр низких частот. Это позволяет устранить шум и выделить основное направление движения цены. После этого, применяется линейная регрессия: наклон полученной линии служит индикатором тренда. На основе этого тренды классифицируются как положительные (бычий рынок), нейтральные (флэт) или отрицательные (медвежий рынок).
Определение меток волатильности. С целью оценки уровня волатильности, рассчитывается среднее значение изменений цен в рамках каждого блока. Полученные значения классифицируются по трём категориям: высокая волатильность, средняя и низкая. Классификация основывается на распределении данных и использовании квантилей для определения границ категорий.

Таким образом, каждый блок данных получает две метки: тренда и волатильности. Все данные делятся на шесть категорий, которые соответствуют комбинациям типов тренда (бычий, нейтральный, медвежий) и уровней волатильности (высокая, средняя, низкая). Это позволяет создать шесть обучающих подмножеств данных, каждое из которых предназначено для обучения субагентов под конкретные рыночные условия. После этого, аналогичная разметка применяется к тестовым данным, где используются пороговые значения, рассчитанные на основе обучающей выборки. Такой подход обеспечивает справедливую оценку эффективности каждого субагента.

Каждый субагент обучается на одном из шести подмножеств данных. Затем его производительность проверяется на тестовом наборе, соответствующем его категории. Это позволяет создать специализированных субагентов, каждый из которых оптимизирован для работы в определённых рыночных условиях. Например, один субагент будет наиболее эффективным на бычьем рынке с высокой волатильностью, а другой — на медвежьем рынке с низкой волатильностью. Такая модульная структура даёт возможность системе гибко адаптироваться к изменяющимся условиям и повышать свою эффективность.

Для обучения субагентов авторы фреймворка предлагают использовать метод Double Deep Q-Network (DDQN) с дуальной архитектурой, которая учитывает рыночные показатели, контекстные особенности и позицию трейдера. Эти данные обрабатываются отдельными слоями нейросети, после чего объединяются в общее представление. Полученное представление адаптируется с помощью Adaptive Layer Norm Block, который позволяет учитывать специфические условия рынка, обеспечивая гибкость и точность в принятии решений.

MacroHFT предусматривает создание шести субагентов, каждый из которых специализируется на конкретных рыночных условиях. Итоговые стратегии объединяются гиперагентом, который обеспечивает эффективность и адаптивность системы в условиях изменчивого криптовалютного рынка.

Гиперагент объединяет результаты работы субагентов для формирования гибкой и эффективной политики, способной адаптироваться к динамическим изменениям на рынке. Гиперагент объединяет их решения субагентов с помощью метаполитики, которая основана на весовой модели SoftMax. Такой подход минимизирует риск чрезмерной зависимости от одного субагента и учитывает мнения всех компонентов системы.

Одним из ключевых преимуществ гиперагента является использование технических индикаторов тренда и волатильности для быстрого принятия решений. Благодаря этому, он может оперативно реагировать на изменения рыночных условий. Однако, традиционные методы обучения на основе высокоуровневых MDP имеют свои сложности: высокая вариативность вознаграждений и редкие экстремальные рыночные изменения. Для решения этих проблем в гиперагент интегрирован модуль памяти.

Модуль памяти реализован в виде таблицы с ограниченным размером, где хранятся ключевые векторы состояний и действий. Новый опыт добавляется в память путём расчёта его значения на основе одношаговой Q-оценки. Если таблица заполняется, старые записи удаляются, чтобы сохранить наиболее актуальные данные. Во время поиска гиперагент находит наиболее релевантные записи с помощью вычисления L2-расстояния между текущим состоянием и сохранёнными ключами. Итоговое значение вычисляется как взвешенная сумма данных из памяти.

Модуль памяти также используется для улучшения оценки действий гиперагента. Это достигается путём модификации функции потерь, которая добавляет новый компонент для согласования оценок из памяти с текущими прогнозами гиперагента. Такой подход позволяет обучать более стабильные торговые стратегии, способные эффективно реагировать на внезапные изменения рыночных условий.

MacroHFT отличается продуманной архитектурой, которая делает его универсальным инструментом для торговли на различных рынках. Хотя он был разработан прежде всего для работы с криптовалютами, его подходы и алгоритмы могут быть адаптированы для использования на других финансовых рынках, включая фондовые или товарные рынки.

Авторская визуализация фреймворка MacroHFT представлена ниже.

Авторская визуализация фреймворка MacroHFT

Реализация средствами MQL5

После анализа теоретических аспектов фреймворка MacroHFT, мы переходим к практической части нашей статьи, в которой реализуем собственное видение предложенных подходов средствами MQL5.

В представленной реализации мы сохраняем основную концепцию иерархического построения модели, но вносим существенные изменения в архитектуру компонентов и процесс обучения. Во-первых, мы отказываемся от ручного разделения обучающей и тестовой выборок на блоки с метками тренда и уровня волатильности. Во-вторых, процесс обучения модели не разделяется на два отдельных этапа. Вместо этого мы реализуем одновременное обучение гиперагента и субагентов в рамках единого итерационного процесса. Мы предполагаем, что в процессе обучения гиперагент сможет самостоятельно классифицировать состояния окружающей среды и распределить роли между агентами.

Мы отказались от использования таблицы для организации памяти гиперагента, заменив её на объект трёхуровневой памяти, разработанный в рамках работы над фреймворком FinCon. Кроме того, мы приняли решение интегрировать ранее созданного агента-аналитика с более сложной и развитой архитектурой, чтобы эффективно реализовать функциональность субагентов. Таким образом, мы начинаем свою работу по реализации компонентов фреймворка MacroHFT с создания гиперагента.

Построение Гиперагента

В представленном авторами фреймворка MacroHFT описании функционала Гиперагента указано, что он анализирует текущее состояние окружающей среды, сопоставляет его с объектами в памяти и возвращает вероятностное распределение классификации анализируемого состояния. Это может быть классификация тренда или волатильности рыночного движения. Полученное вероятностное распределение используется для вычисления вклада каждого субагента в итоговое решение о совершении торговой операции, которое осуществляется путём взвешивания решений субагентов на основе их соответствия текущим рыночным условиям. Такой подход позволяет адаптировать общее решение в зависимости от доминирующих факторов.

Иными словами, нам предстоит создать компонент классификации анализируемого состояния окружающей среды, который будет учитывать контекст предшествующих состояний, хранящихся в памяти. Это достигается путём анализа последовательности изменений рыночных параметров и их корреляции с текущей ситуацией. Предшествующие состояния помогают выявить долгосрочные тренды и скрытые закономерности, что позволяет принимать более обоснованные решения при классификации текущего рыночного состояния.

Такого гиперагента мы создадим в рамках объекта CNeuronMacroHFTHyperAgent, структура которого представлена ниже.

class CNeuronMacroHFTHyperAgent  :  public CNeuronSoftMaxOCL
  {
protected:
   CNeuronMemoryDistil  cMemory;
   CNeuronRMAT          cStatePrepare;
   CNeuronTransposeOCL  cTranspose;
   CNeuronConvOCL       cScale;
   CNeuronBaseOCL       cMLP[2];
   //---
   virtual bool      feedForward(CNeuronBaseOCL *NeuronOCL) override;
   virtual bool      updateInputWeights(CNeuronBaseOCL *NeuronOCL) override;
   virtual bool      calcInputGradients(CNeuronBaseOCL *NeuronOCL) override;

public:
                     CNeuronMacroHFTHyperAgent(void) {};
                    ~CNeuronMacroHFTHyperAgent(void) {};
   //---
   virtual bool      Init(uint numOutputs, uint myIndex, COpenCLMy *open_cl,
                          uint window, uint window_key, uint units_count,
                          uint heads, uint layers, uint agents, uint stack_size,
                          ENUM_OPTIMIZATION optimization_type, uint batch);
   //---
   virtual int       Type(void) override   const   {  return defNeuronMacroHFTHyperAgent; }
   //---
   virtual bool      Save(int const file_handle) override;
   virtual bool      Load(int const file_handle) override;
   //---
   virtual bool      WeightsUpdate(CNeuronBaseOCL *source, float tau) override;
   virtual void      SetOpenCL(COpenCLMy *obj) override;
   //---
   virtual bool      Clear(void) override;
  };

В качестве родительского класса используется реализация слоя SoftMax. Эта функция была предложена авторами фреймворка для вычисления вероятностного распределения. Она играет ключевую роль в определении вклада каждого субагента в итоговое решение, обеспечивая точность и адаптивность модели.

В структуре гиперагента представлен стандартный набор виртуальных методов и несколько внутренних объектов, которые являются базой для построения алгоритма анализа текущего состояния окружающей среды. Подробнее с их функционалом мы ознакомимся в процессе реализации методов класса гиперагента.

Все внутренние объекты объявлены статично, что позволяет нам оставить пустыми конструктор и деструктор класса. А инициализация объявленных и унаследованных объектов осуществляется в методе Init. В параметрах данного метода передается ряд констант, которые позволяют однозначно определить архитектуру создаваемого объекта.

bool CNeuronMacroHFTHyperAgent::Init(uint numOutputs, uint myIndex, COpenCLMy *open_cl,
                                     uint window, uint window_key, uint units_count,
                                     uint heads, uint layers, uint agents, uint stack_size,
                                     ENUM_OPTIMIZATION optimization_type, uint batch)
  {
   if(!CNeuronSoftMaxOCL::Init(numOutputs, myIndex, open_cl, agents, optimization_type, batch))
      return false;
   SetHeads(1);
//---
   int index = 0;

В теле метода мы, как обычно, сначала вызываем одноименный метод родительского класса. В данном случае это слой функции SoftMax. Размер вектора результатов мы ожидаем получить равным количеству используемых субагентов. Необходимое значение получаем от вызывающей программы в параметрах метода.

Далее мы переходим к инициализации внутренних объектов. И первым инициализируем модуль памяти.

   int index = 0;
   if(!cMemory.Init(0, 0, OpenCL, window, window_key, units_count, heads, stack_size,
                                                                optimization, iBatch))
      return false;

Поиск зависимостей в данных анализируемого состояния окружающей среды мы планируем осуществить средствами трансформера с относительным кодирование.

   index++;
   if(!cStatePrepare.Init(0, index, OpenCL, window, window_key, units_count, heads, layers,
                                                                     optimization, iBatch))
      return false;

Следующим шагом является проекция анализируемого состояния окружающей среды в подпространство с размерностью, равной числу субагентов. Это требует создания эффективного механизма проекции, который сохранит все ключевые характеристики данных. На первый взгляд, можно использовать стандартный полносвязный или сверточный слой. Однако, учитывая специфику мультимодального временного ряда, важно учесть сохранение структуры унитарных последовательностей, которая содержат важную информацию. Эти данные могут потеряться при избыточной агрегации данных.

Выше мы использовали трансформер с относительным кодированием для анализа зависимостей между временными шагами. Теперь необходимо дополнить этот процесс, сохраняя детали отдельных унитарных последовательностей. Для этого сначала выполняется транспонирование данных, что обеспечивает удобство дальнейшей обработки унитарных последовательностей.

   index++;
   if(!cTranspose.Init(0, index, OpenCL, units_count, window, optimization, iBatch))
      return false;

Затем воспользуемся сверточным слоем, который позволит извлечь пространственные и временные особенности унитарных последовательностей, улучшая их интерпретацию. Нелинейность операции достигается использованием гиперболического тангенса в качестве функции активации.

   index++;
   if(!cScale.Init(4 * agents, index, OpenCL, 3, 1, 1, units_count - 2, window, optimization, iBatch))
      return false;
   cScale.SetActivationFunction(TANH);

После этого этапа наступает ключевой момент сжатия данных. Для уменьшения размерности используется двухслойная архитектура MLP. Первый слой отвечает за первичное снижение объёма данных, устраняя избыточные корреляции и шум. В этом нам помогает использование функции активации LReLU, которая позволяет избежать линейности преобразований. Второй слой завершает процесс сжатия, оптимизируя данные для дальнейшего анализа.

   index++;
   if(!cMLP[0].Init(agents, index, OpenCL, 4 * agents, optimization, iBatch))
      return false;
   cMLP[0].SetActivationFunction(LReLU);
   index++;
   if(!cMLP[1].Init(0, index, OpenCL, agents, optimization, iBatch))
      return false;
   cMLP[0].SetActivationFunction(None);
//---
   return true;
  }

Такой подход обеспечивает баланс между сохранением полезной информации и упрощением модели, что критически важно для эффективной работы гиперагента в условиях высокочастотной торговли.

Полученные данные мы планируем переносить в область вероятностей средствами родительского класса, которые были инициализированы выше. Поэтому на данном этапе мы можем вернуть логический результат вызывающей программе и завершить работу метода инициализации.

После завершения работы по инициализации объекта, мы переходим к построению алгоритма прямого прохода в рамках метода feedForward. Здесь все довольно просто и линейно.

bool CNeuronMacroHFTHyperAgent::feedForward(CNeuronBaseOCL *NeuronOCL)
  {
   if(!cMemory.FeedForward(NeuronOCL))
      return false;

В параметрах метода получаем указатель на объект исходных данных, содержащий мультимодальный тензор описания анализируемого состояния окружающей среды. Этот указатель сразу передаётся в одноимённый метод модуля памяти. Здесь статичное описание состояния окружающей среды обогащается информацией о недавней динамике, что позволяет создать более полное и актуальное представление для дальнейшего анализа. Интеграция этих данных обеспечивает более точное отслеживание изменений, происходящих в системе, и способствует улучшению эффективности алгоритмов обработки.

Обработанные на предыдущем этапе данные передаются в блок внимания, где определяются взаимозависимости между отдельными временными точками анализируемого временного ряда. Это позволяет выявить скрытые зависимости и повысить точность дальнейшего прогнозирования динамики ценового движения.

   if(!cStatePrepare.FeedForward(cMemory.AsObject()))
      return false;

После чего переходим к сжатию данных. Здесь сначала транспонируем результаты проведенного выше анализа.

   if(!cTranspose.FeedForward(cStatePrepare.AsObject()))
      return false;

Далее сначала сжимаем данные отдельных унитарных последовательностей с помощью сверточного слоя, что позволяет нам сохранить информацию об их структуре.

   if(!cScale.FeedForward(cTranspose.AsObject()))
      return false;

А затем проецируем анализируемое состояние окружающей среды в подпространство заданного размера с помощью MLP.

   if(!cMLP[0].FeedForward(cScale.AsObject()))
      return false;
   if(!cMLP[1].FeedForward(cMLP[0].AsObject()))
      return false;

Теперь нам необходимо перенести полученные значения в область вероятностей. Для этого мы воспользуемся средствами родительского класса SoftMax. Достаточно лишь вызвать одноименный метод родительского класса, передав в него результаты проведенной выше работы.

   return CNeuronSoftMaxOCL::feedForward(cMLP[1].AsObject());
  }

После чего возвращаем логический результат выполнения операций вызывающей программе и завершаем работу метода.

Как вы могли заметить, выше был представлен линейный алгоритм работы гиперагента. Алгоритмы методов обратного прохода имеют схожий линейный характер. Они относительно просты для самостоятельного изучения.

На этом предлагаю завершить рассмотрение принципов работы гиперагента. Полный код представленного класса, включая все его методы, доступен во вложении. Вы можете ознакомиться с ним для углубленного изучения и практического применения. А мы движемся дальше. И следующим шагом объединим агентов в едином фреймворке.

Построение фреймворка MacroHFT

На данном этапе мы имеем отдельные объекты субагентов и гиперагента. Настало время объединить их в единую целостную структуру, где будут построены алгоритмы обмена данными между компонентами модели. Эта задача будет реализована в рамках объекта CNeuronMacroHFT, который обеспечит оптимизацию процессов обработки данных. Структура нового объекта представлена ниже.

class CNeuronMacroHFT   :  public CNeuronBaseOCL
  {
protected:
   CNeuronTransposeOCL  cTranspose;
   CNeuronFinConAgent   caAgetnts[6];
   CNeuronMacroHFTHyperAgent  cHyperAgent;
   CNeuronBaseOCL       cConcatenated;
   //---
   virtual bool      feedForward(CNeuronBaseOCL *NeuronOCL) override;
   virtual bool      updateInputWeights(CNeuronBaseOCL *NeuronOCL) override;
   virtual bool      calcInputGradients(CNeuronBaseOCL *NeuronOCL) override;

public:
                     CNeuronMacroHFT(void) {};
                    ~CNeuronMacroHFT(void) {};
   //---
   virtual bool      Init(uint numOutputs, uint myIndex, COpenCLMy *open_cl,
                          uint window, uint window_key, uint units_count,
                          uint heads, uint layers, uint stack_size, uint nactions,
                          ENUM_OPTIMIZATION optimization_type, uint batch);
   //---
   virtual int       Type(void) override   const   {  return defNeuronMacroHFT; }
   //---
   virtual bool      Save(int const file_handle) override;
   virtual bool      Load(int const file_handle) override;
   //---
   virtual bool      WeightsUpdate(CNeuronBaseOCL *source, float tau) override;
   virtual void      SetOpenCL(COpenCLMy *obj) override;
   //---
   virtual bool      Clear(void) override;
  };

В структуре нового объекта представлен привычный набор переопределяемых виртуальных методов, что обеспечивает гибкость в реализации его функциональности. Среди внутренних объектов можно выделить гиперагента, играющего центральную роль в управлении, и массив из шести субагентов, каждый из которых отвечает за обработку определённых аспектов данных. Подробное описание функциональности внутренних объектов и логики их взаимодействия будет рассмотрено в процессе построения методов нового объекта.

Все внутренние объекты объявлены статично. Это позволяет нам оставить пустыми конструктор и деструктор класса. Инициализация объявленных и унаследованных объектов осуществляется в методе Init. В параметрах данного метода мы получаем ряд констант, которые дают однозначное представление об архитектуре создаваемого объекта.

bool CNeuronMacroHFT::Init(uint numOutputs, uint myIndex, COpenCLMy *open_cl,
                           uint window, uint window_key, uint units_count,
                           uint heads, uint layers, uint stack_size, uint nactions,
                           ENUM_OPTIMIZATION optimization_type, uint batch)
  {
   if(!CNeuronBaseOCL::Init(numOutputs, myIndex, open_cl, nactions, optimization_type, batch))
      return false;

В теле метода мы, как обычно, сначала вызываем одноимённый метод родительского класса, в котором уже реализован процесс инициализации унаследованных объектов и интерфейсов. В данном случае это полносвязный слой, от которого нам потребуются лишь базовые интерфейсы взаимодействия с внешними объектами модели. На выходе нашего нового объекта мы ожидаем получить итоговый тензор действия модели в соответствии с анализируемыми рыночными условиями. Поэтому в параметрах метода родительского класса указываем размерность пространства действий нашего Агента.

В представленной авторами организации работы субагентов предложено их разделение в зависимости от тренда и волатильности рынка. Мы же решили использовать разделение по углу обзора рынка. Наши субагенты получат разные проекции анализируемых рыночных данных. Для формирования таких проекций используется слой транспонирования данных.

   int index = 0;
   if(!cTranspose.Init(0, index, OpenCL, units_count, window, optimization, iBatch))
      return false;

Далее мы осуществляем инициализацию субагентов. Первая половина субагентов анализируют исходные данные в полученном от внешней программы представлении, а последняя — транспонированный их вид. Для осуществления процесса инициализации мы организуем 2 последовательных цикла с необходимым числом итераций.

   uint half = (caAgetnts.Size() + 1) / 2;
   for(uint i = 0; i < half; i++)
     {
      index++;
      if(!caAgetnts[i].Init(0, index, OpenCL, window, window_key, units_count, heads,
                            stack_size, nactions, optimization, iBatch))
         return false;
     }
   for(uint i = half; i < caAgetnts.Size(); i++)
     {
      index++;
      if(!caAgetnts[i].Init(0, index, OpenCL, units_count, window_key, window, heads,
                            stack_size, nactions, optimization, iBatch))
         return false;
     }

Затем мы инициализируем объект гиперагента. Он так же анализируем исходные данные в первичном их представлении.

   index++;
   if(!cHyperAgent.Init(0, index, OpenCL, window, window_key, units_count, heads, layers,
                        caAgetnts.Size(), stack_size, optimization, iBatch))
      return false;

Далее, согласно алгоритму фреймворка MacroHFT, нам предстоит осуществить взвешенное суммирование результатов работы субагентов. При этом веса генерируются гиперагентом. Данная операция легко выполняется умножением матрицы результатов работы субагентов на вектор весов, полученных от гиперагента. Только в нашем случае результаты работы субагентов хранятся в отдельных объектах. Создадим объект для конкатенации необходимых векторов в единую матрицу.

   index++;
   if(!cConcatenated.Init(0, index, OpenCL, caAgetnts.Size()*nactions, optimization, iBatch))
      return false;
//---
   return true;
  }

Непосредственное умножение матриц будет осуществляться в процессе прямого прохода. А сейчас мы возвращаем логический результат выполнения операций вызывающей программе и завершаем работу метода инициализации.

Следующим нашим шагом будет построение алгоритма прямого прохода в рамках метода feedForward. Как и ранее, в параметрах метода получаем указатель на объект исходных данных, которые мы сразу транспонируем.

bool CNeuronMacroHFT::feedForward(CNeuronBaseOCL *NeuronOCL)
  {
   if(!cTranspose.FeedForward(NeuronOCL))
      return false;

Далее одна половина субагентов работает с исходным представление анализируемого состояния окружающей среды, а вторая — с транспонированной проекцией.

   uint total = caAgetnts.Size();
   uint half = (total + 1) / 2;
   for(uint i = 0; i < half; i++)
      if(!caAgetnts[i].FeedForward(NeuronOCL))
         return false;

   for(uint i = half; i < total; i++)
      if(!caAgetnts[i].FeedForward(cTranspose.AsObject()))
         return false;

Тут же анализирует исходные данные и наш гиперагент.

   if(!cHyperAgent.FeedForward(NeuronOCL))
      return false;

Теперь нам необходимо собрать информацию от всех субагентов в единую матрицу.

   if(!Concat(caAgetnts[0].getOutput(), caAgetnts[1].getOutput(), caAgetnts[2].getOutput(),
              caAgetnts[3].getOutput(), cConcatenated.getPrevOutput(), Neurons(), Neurons(),
              Neurons(), Neurons(), 1) ||
      !Concat(cConcatenated.getPrevOutput(), caAgetnts[4].getOutput(), caAgetnts[5].getOutput(),
              cConcatenated.getOutput(), 4 * Neurons(), Neurons(), Neurons(), 1))
      return false;

На выходе мы получаем матрицу, в которой каждая отдельная строка представляет результаты работы одного субагента. Для корректного получения взвешенной суммы нам необходимо умножить вектор весов на полученную матрицу.

   if(!MatMul(cHyperAgent.getOutput(), cConcatenated.getOutput(), Output, 1, total, Neurons(), 1))
      return false;
//---
   return true;
  }

Результаты умножения записываем в буфер внешних интерфейсов, унаследованных от родительского класса и завершаем работу метода, предварительно вернув логический результат выполнения операций вызывающей программе.

Здесь стоит обратить внимание, что, несмотря на внесение некоторых конструктивных изменений, алгоритм прямого прохода полностью сохранил первоначальную идею авторов фреймворка MacroHFT. Однако этого не скажешь про построенный нами процесс обучения, о котором речь пойдет дальше.

Как указывалось ранее, авторы фреймворка разделили обучающую выборку на отдельные блоки в зависимости от тренда и волатильности рынка. Каждый субагент обучался на отдельной подвыборке. Мы же планируем обучать все агенты одновременно. Именно такой процесс будет построен в методах обратного прохода нашего класса.

Начнем мы реализацию процессов обратного прохода с построения алгоритма распределения градиентов ошибки между внутренними объектами нашего класса и исходными данными в соответствии с их влиянием на результат работы модели. Данная работа выполняется в рамках метода calcInputGradients.

bool CNeuronMacroHFT::calcInputGradients(CNeuronBaseOCL *NeuronOCL)
  {
   if(!NeuronOCL)
      return false;

В параметрах метода мы получаем указатель на тот же объект исходных данных, который получали и при прямом проходе. Только на этот раз нам предстоит передать в него соответствующий градиент ошибки. И в теле метода сразу проверяем актуальность полученного указателя, ведь в противном случае мы просто не сможем записать информацию в несуществующий объект. А в таком случае все дальнейшие операции теряют смысл.

Как вы знаете, информационный поток распределения градиента ошибки полностью соответствует операциям прямого прохода, только направлен в обратную сторону. И если прямой проход мы завершили операцией умножения матрицы результатов на вектор весов, то обратный проход начинается с распределения градиента ошибки через данную операцию.

   uint total = caAgetnts.Size();
   if(!MatMulGrad(cHyperAgent.getOutput(), cHyperAgent.getGradient(), cConcatenated.getOutput(),
                                 cConcatenated.getGradient(), Gradient, 1, total, Neurons(), 1))
      return false;

Здесь стоит обратить внимание, что в результате данной операции мы разделили градиент ошибки на 2 информационных потока. Один из них — информационный поток гиперагента. По нему мы можем сразу передать погрешность на уровень исходных данных.

   if(!NeuronOCL.calcHiddenGradients(cHyperAgent.AsObject()))
      return false;

Второй информационный поток относится к субагентам. При распределении градиента ошибки через операцию матричного умножения, мы получили значения погрешности на уровне конкатенированного объекта. Думаю, здесь очевидно, что наибольшие ошибки получил субагент, оказавший максимальное влияние на результат работы модели. Это позволяет нам осуществить распределение ролей между субагентами в процессе обучения на основании классификации анализируемых состояний окружающей среды, проведенной гиперагентом.

Теперь нам необходимо распределить полученные значения между соответствующими субагентами. Для этого выполним операции деконкатенации данных.

   if(!DeConcat(cConcatenated.getPrevOutput(), caAgetnts[4].getGradient(), caAgetnts[5].getGradient(),
                cConcatenated.getGradient(), 4 * Neurons(), Neurons(), Neurons(), 1) ||
      !DeConcat(caAgetnts[0].getGradient(), caAgetnts[1].getGradient(), caAgetnts[2].getGradient(),
                caAgetnts[3].getGradient(), cConcatenated.getPrevOutput(), Neurons(), Neurons(),
                Neurons(), Neurons(), 1))
      return false;

Далее мы можем передать градиент ошибки на уровень исходных данных по магистралям каждого отдельного субагента. Но здесь следует обратить внимание на 2 момента. Во-первых, в буфере градиентов объекта исходных данных уже содержится информация, полученная от гиперагента. И нам необходимо её сохранить. Для этого мы, как обычно, воспользуемся операциями подмены указателей на буфера данных, заменив буфер градиентов ошибки объекта исходных данных другим свободным.

   CBufferFloat *temp = NeuronOCL.getGradient();
   if(!temp ||
      !NeuronOCL.SetGradient(cTranspose.getPrevOutput(), false))
      return false;

Кроме того, не все наши субагенты напрямую работают с объектом исходные данных. Половина из них анализирует транспонированные данные. Следовательно, нам надо это учитывать в процессе распределения градиентов ошибки. Как и в случае прямого прохода, мы организуем 2 последовательных цикла. В первом мы работаем с субагентами прямого взаимодействия. Здесь мы опускаем градиент ошибки до уровня исходных данных и суммируем полученные данные с ранее накопленными.

   uint half = (total + 1) / 2;
   for(uint i = 0; i < half; i++)
     {
      if(!NeuronOCL.calcHiddenGradients(caAgetnts[i].AsObject()))
         return false;
      if(!SumAndNormilize(temp, NeuronOCL.getGradient(), temp, 1, false, 0, 0, 0, 1))
         return false;
     }

Второй цикл аналогичен первому, но добавляется шаг передачи градиента ошибки через слой транспонирования данных. Здесь обрабатывается вторая половина субагентов.

   for(uint i = half; i < total; i++)
     {
      if(!cTranspose.calcHiddenGradients(caAgetnts[i].AsObject()) ||
         !NeuronOCL.calcHiddenGradients(cTranspose.AsObject()))
         return false;
      if(!SumAndNormilize(temp, NeuronOCL.getGradient(), temp, 1, false, 0, 0, 0, 1))
         return false;
     }

После успешного завершения всех итераций указанных циклов, мы возвращаем указатели на буферы данных в исходное состояние. И завершаем работу метода, предварительно передав логический результат выполнения операций вызывающей программе.

На этом мы завершаем рассмотрение алгоритмов построения методов нашего нового объекта организации работы фреймворка MacroHFT. С полным кодом представленного класса и всех его методов вы можете ознакомиться во вложении.

Мы практически достигли предела формата статьи, но наша работа ещё не завершена. Предлагаю сделать небольшой перерыв, а начатую работу завершить в следующей статье. Там же мы проведем оценку реализованных подходов на реальных исторических данных.

Заключение

В данной статье мы познакомились с фреймворком MacroHFT, который представляет собой перспективное решение для высокочастотной торговли на криптовалютных рынках. Данный фреймворк учитывает макроэкономические контексты и особенности локальной рыночной динамики. Это делает его мощным инструментом для профессиональных трейдеров, стремящихся максимизировать свои доходы в условиях сложных и нестабильных рыночных условий.

В практической части мы реализовали свое видение основных компонентов рассмотренного фреймворка средствами MQL5. И в следующей статье мы доведём начатую работу до логического завершения с обязательной проверкой эффективности реализованных подходов на реальных исторических данных.

Ссылки

Программы, используемые в статье

#	Имя	Тип	Описание
1	Research.mq5	Советник	Советник сбора примеров
2	ResearchRealORL.mq5	Советник	Советник сбора примеров методом Real-ORL
3	Study.mq5	Советник	Советник обучения моделей
4	Test.mq5	Советник	Советник для тестирования модели
5	Trajectory.mqh	Библиотека класса	Структура описания состояния системы и архитектуры моделей
6	NeuroNet.mqh	Библиотека класса	Библиотека классов для создания нейронной сети
7	NeuroNet.cl	Библиотека	Библиотека кода OpenCL-программы

Прикрепленные файлы |

Загрузить ZIP

MQL5.zip (2376.99 KB)

Предупреждение: все права на данные материалы принадлежат MetaQuotes Ltd. Полная или частичная перепечатка запрещена.

Другие статьи автора

Перейти к обсуждению на форуме трейдеров

Разработка системы репликации (Часть 59): Новое будущее

Правильное понимание разных идей позволяет нам делать больше с наименьшими усилиями. В этой статье мы рассмотрим, почему необходимо настроить применение шаблона до того, как сервис начнет взаимодействовать с графиком. И что, если мы улучшим указатель мыши, чтобы иметь возможность делать больше вещей с его помощью?

От начального до среднего уровня: Переменные (III)

Сегодня мы рассмотрим, как использовать переменные и константы, предопределенные языком MQL5. Кроме того, мы проанализируем еще один особый тип переменных: функции. Умение правильно работать с этими переменными может определить разницу между работающим и неработающим приложением. Для того, чтобы понять представленное здесь, необходимо разобраться с материалом, который был рассмотрен в предыдущих статьях.

Алгоритм циклического партеногенеза — Cyclic Parthenogenesis Algorithm (CPA)

В данной статье рассмотрим новый популяционный алгоритм оптимизации CPA (Cyclic Parthenogenesis Algorithm), вдохновленный уникальной репродуктивной стратегией тлей. Алгоритм сочетает два механизма размножения — партеногенез и половое, а также использует колониальную структуру популяции с возможностью миграции между колониями. Ключевыми особенностями алгоритма являются адаптивное переключение между различными стратегиями размножения и система обмена информацией между колониями через механизм перелета.

Нейросимвольные системы в алготрейдинге: Объединение символьных правил и нейронных сетей

Статья рассказывает об опыте разработки гибридной торговой системы, объединяющей классический технический анализ с нейронными сетями. Автор подробно разбирает архитектуру системы — от базового анализа паттернов и структуры нейросети до механизмов принятия торговых решений, делясь реальным кодом и практическими наблюдениями.