Exemplo de CNA (Análise de Rede de Causalidade), SMOC (Controle Otimizado com Modelo Estocástico) e Teoria dos Jogos de Nash com Aprendizado Profundo

Introdução

Vamos passar pelo processo de adicionar Aprendizado Profundo a três Expert Advisors de negociação avançada. Esses três experts são EAs avançados publicados como artigos. 

Esses três artigos estão publicados em www.mql5.com

1. Aplicação da Teoria dos Jogos de Nash com Filtragem HMM em Negociação
2. Exemplo de Análise de Rede de Causalidade (CNA) e Modelo de Vetores Auto-Regressivos para Previsão de Eventos de Mercado
3. Exemplo de Otimização Estocástica e Controle Ótimo

Se você ainda não leu esses artigos, explicarei brevemente sobre o que são, mas recomendo fortemente a leitura completa dos artigos.

Teoria dos Jogos de Nash

O equilíbrio de Nash é considerado um dos componentes básicos da Teoria dos Jogos. 

Equilíbrio de Nash é um conceito da teoria dos jogos onde se assume que cada jogador conhece as estratégias de equilíbrio dos demais jogadores, e nenhum jogador tem algo a ganhar ao mudar apenas a sua própria estratégia.

Em um equilíbrio de Nash, a estratégia de cada jogador é ótima dado as estratégias de todos os outros jogadores. Um jogo pode ter múltiplos equilíbrios de Nash ou nenhum.

Análise de Rede de Causalidade

A Análise de Rede de Causalidade (CNA) é um método utilizado para entender e modelar relações causais complexas entre variáveis em um sistema. Quando aplicada aos mercados financeiros, pode ajudar a identificar como diferentes eventos e fatores de mercado influenciam uns aos outros, levando potencialmente a previsões mais precisas.

O robô utiliza Inferência de Causalidade Rápida.

Inferência de causalidade rápida é um conceito que combina inferência estatística veloz com análise causal. Ela visa tirar conclusões causais rapidamente a partir dos dados, equilibrando velocidade e compreensão causal. Essa abordagem é útil em cenários que exigem decisões rápidas baseadas em dados e, ao mesmo tempo, precisam de insights sobre relações de causa e efeito. As aplicações podem incluir análise de mercado em tempo real, decisões empresariais rápidas e estudos epidemiológicos ágeis. O método sacrifica certa profundidade de análise em prol da velocidade, tornando-o adequado para ambientes sensíveis ao tempo onde entender os vínculos causais é crucial.

Otimização Estocástica

A modelagem estocástica e a otimização de controle são técnicas matemáticas que ajudam a resolver problemas sob condições de incerteza. Elas encontram aplicação em finanças, engenharia, inteligência artificial e muitas outras áreas.

Modelagem estocástica é usada para descrever sistemas com elementos de aleatoriedade, como movimentos de preços no mercado de ações ou uma fila em um restaurante. Ela se baseia em variáveis aleatórias, distribuições de probabilidade e processos estocásticos. Métodos como Monte Carlo e cadeias de Markov podem modelar esses processos e prever seu comportamento.

A otimização de gestão ajuda a encontrar as melhores soluções para o gerenciamento de sistemas. Ela é usada para automatizar e melhorar o funcionamento de vários processos, desde a direção de veículos até a operação de plantas químicas. Os métodos básicos incluem o controlador quadrático linear, controle preditivo baseado em modelo e aprendizado por reforço.

Aprendizado Profundo

Aprendizado profundo aplicado à negociação utiliza redes neurais artificiais para analisar e prever tendências dos mercados financeiros. Aqui está um breve resumo:

1. Análise de dados: Modelos de Deep Learning processam grandes quantidades de dados financeiros, incluindo históricos de preços, volumes de negociação, indicadores econômicos e até sentimentos de notícias.
2. Reconhecimento de padrões: Esses modelos podem identificar padrões complexos e relações nos dados de mercado que podem não ser aparentes para operadores humanos ou métodos tradicionais de análise.
3. Previsão: Com base nos padrões identificados, os modelos de deep learning tentam prever movimentos futuros do mercado, tendências de preços ou estratégias de negociação ideais.
4. Negociação automatizada: Alguns sistemas utilizam aprendizado profundo para tomar decisões autônomas de negociação, executando operações com base nas previsões do modelo.
5. Gestão de risco: O aprendizado profundo pode ser usado para avaliar e gerenciar riscos de forma mais eficaz, analisando múltiplos fatores de risco simultaneamente.
6. Adaptabilidade: Esses modelos podem aprender continuamente e se adaptar às condições mutantes do mercado, potencialmente melhorando seu desempenho ao longo do tempo.
7. Negociação de alta frequência: O deep learning pode ser particularmente útil em cenários de negociação de alta frequência, onde decisões em frações de segundo são cruciais.

Embora o deep learning na negociação ofereça capacidades poderosas, é importante observar que os mercados são complexos e imprevisíveis. Esses modelos não são infalíveis e ainda exigem supervisão cuidadosa e gestão de riscos.

Por que deveríamos ter um EA com Aprendizado Profundo?

Faremos um modelo de Aprendizado Profundo com Python, criando um modelo ONNX, e adicionaremos esse modelo a cada um dos EAs, e compararemos os resultados com e sem Deep Learning.

Modelos ONNX serão usados porque podem ser facilmente criados em Python, e servem como ponte entre diferentes ecossistemas, promovendo flexibilidade e eficiência no desenvolvimento e implantação dos modelos. Python é uma maneira rápida de criar modelos ONNX ou fazer backtests de estratégias com agilidade. Para este artigo, usaremos Python 3.11.9.

Usaremos Aprendizado Profundo com esses EAs porque os resultados anteriores dos artigos poderiam ser melhores. Adicionaremos condições para que o EA execute ou não negociações caso os modelos de Deep Learning também indiquem isso.

O Script em Python

Usaremos este script .py, que cria um modelo de DL em ONNX e também possui métricas para verificar se o modelo foi corretamente desenvolvido. O DL apresenta problemas quando mal implementado, pois pode ocorrer subajuste ou sobreajuste, o que leva a previsões incorretas.

#python 3.11.9, tensorflow==2.12.0, keras==2.12.0,  tf2onnx==1.16.0
# python libraries
import MetaTrader5 as mt5
import tensorflow as tf
import numpy as np
import pandas as pd
import tf2onnx
#import tensorflow as tf
#import tf2onnx
import keras

print(f"TensorFlow version: {tf.__version__}")
print(f"Keras version: {keras.__version__}")
print(f"tf2onnx version: {tf2onnx.__version__}")


# input parameters

inp_history_size = 120

sample_size = inp_history_size*3*20
symbol = "EURUSD"
optional = "D1_2024"
inp_model_name = str(symbol)+"_"+str(optional)+".onnx" 

if not mt5.initialize():
    print("initialize() failed, error code =",mt5.last_error())
    quit()

# we will save generated onnx-file near the our script to use as resource
from sys import argv
data_path=argv[0]
last_index=data_path.rfind("\\")+1
data_path=data_path[0:last_index]
print("data path to save onnx model",data_path)

# and save to MQL5\Files folder to use as file
terminal_info=mt5.terminal_info()
file_path=terminal_info.data_path+"\\MQL5\\Files\\"
print("file path to save onnx model",file_path)

# set start and end dates for history data
from datetime import timedelta, datetime
#end_date = datetime.now()
end_date = datetime(2024, 1, 1, 0)
start_date = end_date - timedelta(days=inp_history_size*20)

# print start and end dates
print("data start date =",start_date)
print("data end date =",end_date)

# get rates
eurusd_rates = mt5.copy_rates_from(symbol, mt5.TIMEFRAME_D1, end_date, sample_size)

# create dataframe
df = pd.DataFrame(eurusd_rates)

# get close prices only
data = df.filter(['close']).values

# scale data
from sklearn.preprocessing import MinMaxScaler
scaler=MinMaxScaler(feature_range=(0,1))
scaled_data = scaler.fit_transform(data)

# training size is 80% of the data
training_size = int(len(scaled_data)*0.80) 
print("Training_size:",training_size)
train_data_initial = scaled_data[0:training_size,:]
test_data_initial = scaled_data[training_size:,:1]

# split a univariate sequence into samples
def split_sequence(sequence, n_steps):
    X, y = list(), list()
    for i in range(len(sequence)):
       # find the end of this pattern
       end_ix = i + n_steps
       # check if we are beyond the sequence
       if end_ix > len(sequence)-1:
          break
       # gather input and output parts of the pattern
       seq_x, seq_y = sequence[i:end_ix], sequence[end_ix]
       X.append(seq_x)
       y.append(seq_y)
    return np.array(X), np.array(y)

# split into samples
time_step = inp_history_size
x_train, y_train = split_sequence(train_data_initial, time_step)
x_test, y_test = split_sequence(test_data_initial, time_step)

# reshape input to be [samples, time steps, features] which is required for LSTM
x_train =x_train.reshape(x_train.shape[0],x_train.shape[1],1)
x_test = x_test.reshape(x_test.shape[0],x_test.shape[1],1)



# define model
from keras.models import Sequential
from keras.layers import Dense, Activation, Conv1D, MaxPooling1D, Dropout, Flatten, LSTM
from keras.metrics import RootMeanSquaredError as rmse
from tensorflow.keras import callbacks
model = Sequential()
model.add(Conv1D(filters=256, kernel_size=2, strides=1, padding='same', activation='relu', input_shape=(inp_history_size,1)))
model.add(MaxPooling1D(pool_size=2))
model.add(LSTM(100, return_sequences = True))
model.add(Dropout(0.3))
model.add(LSTM(100, return_sequences = False))
model.add(Dropout(0.3))
model.add(Dense(units=1, activation = 'sigmoid'))
model.compile(optimizer='adam', loss= 'mse' , metrics = [rmse()])

# Set up early stopping
early_stopping = callbacks.EarlyStopping(
    monitor='val_loss',
    patience=20,
    restore_best_weights=True,
)

# model training for 300 epochs
history = model.fit(x_train, y_train, epochs = 300 , validation_data = (x_test,y_test), batch_size=32, callbacks=[early_stopping], verbose=2)

# evaluate training data
train_loss, train_rmse = model.evaluate(x_train,y_train, batch_size = 32)
print(f"train_loss={train_loss:.3f}")
print(f"train_rmse={train_rmse:.3f}")

# evaluate testing data
test_loss, test_rmse = model.evaluate(x_test,y_test, batch_size = 32)
print(f"test_loss={test_loss:.3f}")
print(f"test_rmse={test_rmse:.3f}")

# Define a function that represents your model
@tf.function(input_signature=[tf.TensorSpec([None, inp_history_size, 1], tf.float32)])
def model_function(x):
    return model(x)

output_path = data_path+inp_model_name
# Convert the model to ONNX
onnx_model, _ = tf2onnx.convert.from_function(
    model_function, 
    input_signature=[tf.TensorSpec([None, inp_history_size, 1], tf.float32)],
    opset=13,
    output_path=output_path
)

print(f"Saved ONNX model to {output_path}")


# save model to ONNX
output_path = data_path+inp_model_name
onnx_model = tf2onnx.convert.from_keras(model, output_path=output_path)
print(f"saved model to {output_path}")

output_path = file_path+inp_model_name
onnx_model = tf2onnx.convert.from_keras(model, output_path=output_path)
print(f"saved model to {output_path}")

#prediction using testing data
test_predict = model.predict(x_test)
print(test_predict)
print("longitud total de la prediccion: ", len(test_predict))
print("longitud total del sample: ", sample_size)

plot_y_test = np.array(y_test).reshape(-1, 1)  # Selecciona solo el último elemento de cada muestra de prueba
plot_y_train = y_train.reshape(-1,1)
train_predict = model.predict(x_train)
#print(plot_y_test)

#calculate metrics
from sklearn import metrics
from sklearn.metrics import r2_score
#transform data to real values
value1=scaler.inverse_transform(plot_y_test)
#print(value1)
# Escala las predicciones inversas al transformarlas a la escala original
value2 = scaler.inverse_transform(test_predict.reshape(-1, 1))
#print(value2)
#calc score
score = np.sqrt(metrics.mean_squared_error(value1,value2))

print("RMSE         : {}".format(score))
print("MSE          :", metrics.mean_squared_error(value1,value2))
print("R2 score     :",metrics.r2_score(value1,value2))


#sumarize model
model.summary()

#Print error
value11=pd.DataFrame(value1)
value22=pd.DataFrame(value2)
#print(value11)
#print(value22)



value111=value11.iloc[:,:]
value222=value22.iloc[:,:]

print("longitud salida (tandas de 1 hora): ",len(value111) )
print("en horas son " + str((len(value111))*60*24)+ " minutos")
print("en horas son " + str(((len(value111)))*60*24/60)+ " horas")
print("en horas son " + str(((len(value111)))*60*24/60/24)+ " dias")


# Calculate error
error = value111 - value222

import matplotlib.pyplot as plt
# Plot error
plt.figure(figsize=(7, 6))
plt.scatter(range(len(error)), error, color='blue', label='Error')
plt.axhline(y=0, color='red', linestyle='--', linewidth=1)  # Línea horizontal en y=0
plt.title('Error de Predicción ' + str(symbol))
plt.xlabel('Índice de la muestra')
plt.ylabel('Error')
plt.legend()
plt.grid(True)
plt.savefig(str(symbol)+str(optional)+'.png') 

rmse_ = format(score)
mse_ = metrics.mean_squared_error(value1,value2)
r2_ = metrics.r2_score(value1,value2)

resultados= [rmse_,mse_,r2_]

# Abre un archivo en modo escritura
with open(str(symbol)+str(optional)+"results.txt", "w") as archivo:
    # Escribe cada resultado en una línea separada
    for resultado in resultados:
        archivo.write(str(resultado) + "\n")

# finish
mt5.shutdown()

#show iteration-rmse graph for training and validation
plt.figure(figsize = (7,10))
plt.plot(history.history['root_mean_squared_error'],label='Training RMSE',color='b')
plt.plot(history.history['val_root_mean_squared_error'],label='Validation-RMSE',color='g')
plt.xlabel("Iteration")
plt.ylabel("RMSE")
plt.title("RMSE" + str(symbol))
plt.legend()
plt.savefig(str(symbol)+str(optional)+'1.png') 

#show iteration-loss graph for training and validation
plt.figure(figsize = (7,10))
plt.plot(history.history['loss'],label='Training Loss',color='b')
plt.plot(history.history['val_loss'],label='Validation-loss',color='g')
plt.xlabel("Iteration")
plt.ylabel("Loss")
plt.title("LOSS" + str(symbol))
plt.legend()
plt.savefig(str(symbol)+str(optional)+'2.png') 

#show actual vs predicted (training) graph
plt.figure(figsize=(7,10))
plt.plot(scaler.inverse_transform(plot_y_train),color = 'b', label = 'Original')
plt.plot(scaler.inverse_transform(train_predict),color='red', label = 'Predicted')
plt.title("Prediction Graph Using Training Data" + str(symbol))
plt.xlabel("Hours")
plt.ylabel("Price")
plt.legend()
plt.savefig(str(symbol)+str(optional)+'3.png') 

#show actual vs predicted (testing) graph
plt.figure(figsize=(7,10))
plt.plot(scaler.inverse_transform(plot_y_test),color = 'b',  label = 'Original')
plt.plot(scaler.inverse_transform(test_predict),color='g', label = 'Predicted')
plt.title("Prediction Graph Using Testing Data" + str(symbol))
plt.xlabel("Hours")
plt.ylabel("Price")
plt.legend()
plt.savefig(str(symbol)+str(optional)+'4.png') 

A saída que este script .py gera se parece com isto:

177/177 - 51s - loss: 2.4565e-04 - root_mean_squared_error: 0.0157 - val_loss: 4.8860e-05 - val_root_mean_squared_error: 0.0070 - 51s/epoch - 291ms/step
177/177 [==============================] - 15s 82ms/step - loss: 1.0720e-04 - root_mean_squared_error: 0.0104
train_loss=0.000
train_rmse=0.010
42/42 [==============================] - 3s 74ms/step - loss: 4.4485e-05 - root_mean_squared_error: 0.0067
test_loss=0.000
test_rmse=0.007
Saved ONNX model to c:\XXXXXXXXXXXXXXX\EURUSD_D1_2024.onnx
saved model to c:\XXXXXXXXXXXXXXXX\EURUSD_D1_2024.onnx
saved model to C:\XXXXXXXXXX\MQL5\Files\EURUSD_D1_2024.onnx
42/42 [==============================] - 5s 80ms/step
[[0.40353602]
 [0.39568084]
 [0.39963558]
 ...
 [0.35914657]
 [0.3671721 ]
 [0.3618655 ]]
longitud total de la prediccion:  1320
longitud total del sample:  7200
177/177 [==============================] - 13s 72ms/step
RMSE         : 0.005155711558172936
MSE          : 2.6581361671078003e-05
R2 score     : 0.9915315181564703
Model: "sequential"
_________________________________________________________________
 Layer (type)                Output Shape              Param #
=================================================================
 conv1d (Conv1D)             (None, 120, 256)          768

 max_pooling1d (MaxPooling1D  (None, 60, 256)          0
 )

 lstm (LSTM)                 (None, 60, 100)           142800

 dropout (Dropout)           (None, 60, 100)           0

 lstm_1 (LSTM)               (None, 100)               80400

 dropout_1 (Dropout)         (None, 100)               0

 dense (Dense)               (None, 1)                 101

=================================================================
Total params: 224,069
Trainable params: 224,069
Non-trainable params: 0
________________________________________________________________

Este modelo pode estar com sobreajuste (overfitting), por causa destes resultados, isso pode estar no limite entre uma boa previsão e um modelo sobreajustado:

RMSE         : 0.005155711558172936
MSE          : 2.6581361671078003e-05
R2 score     : 0.9915315181564703

As principais métricas são estas três: R2, que fornece uma porcentagem dos resultados testados que foram boas previsões, e RMSE, MSE que são os erros. Se quiser saber mais sobre isso, você pode pesquisar no Google.

Como faremos isso para o mesmo símbolo (EURUSD), só precisamos fazer um único modelo de DL, e vamos testá-lo para 2024.

Selecionamos o período de tempo com time frame de 1 dia, para não sobrecarregar nossos computadores.

O script em Python também exibe alguns gráficos que são salvos (é outra maneira de verificar se os modelos estão ou não com sobreajuste ou subajuste).

Os gráficos devem se parecer com estes:

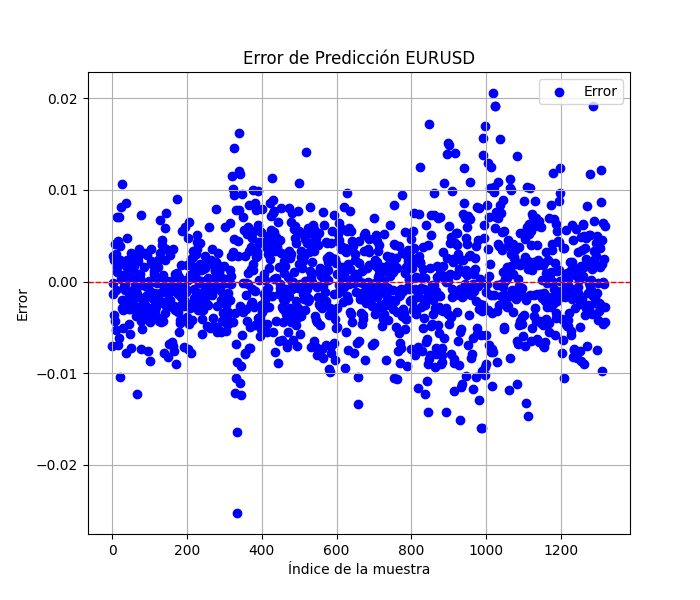
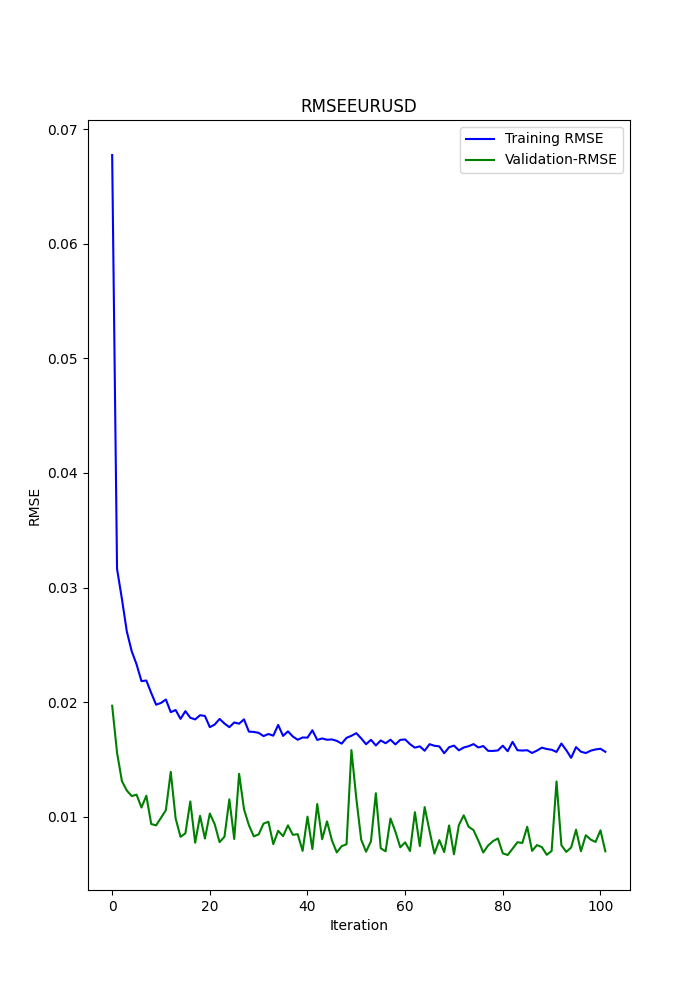
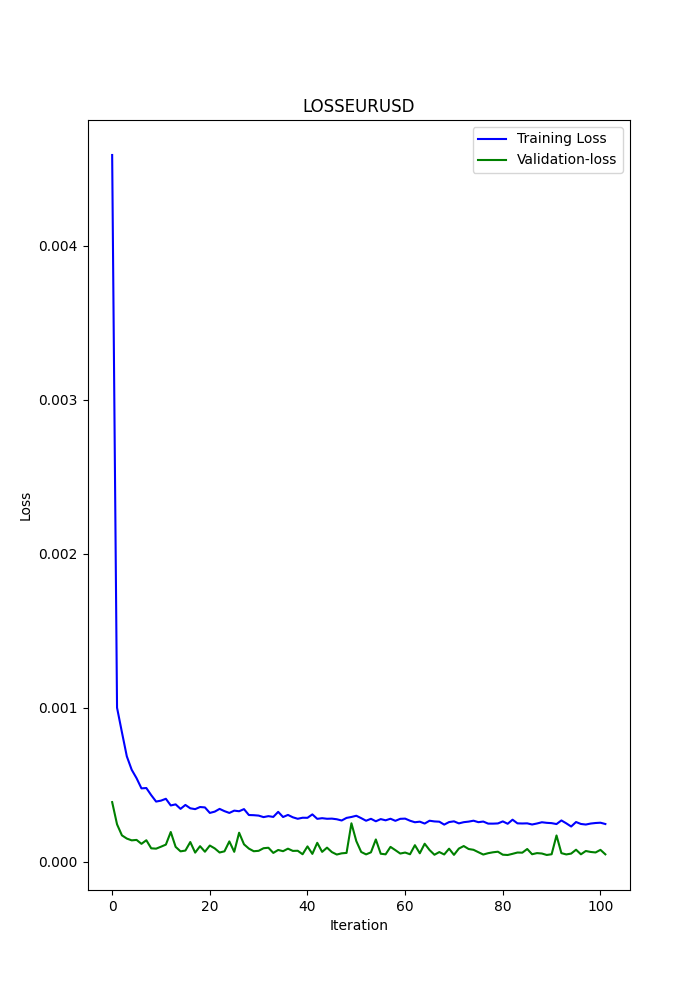
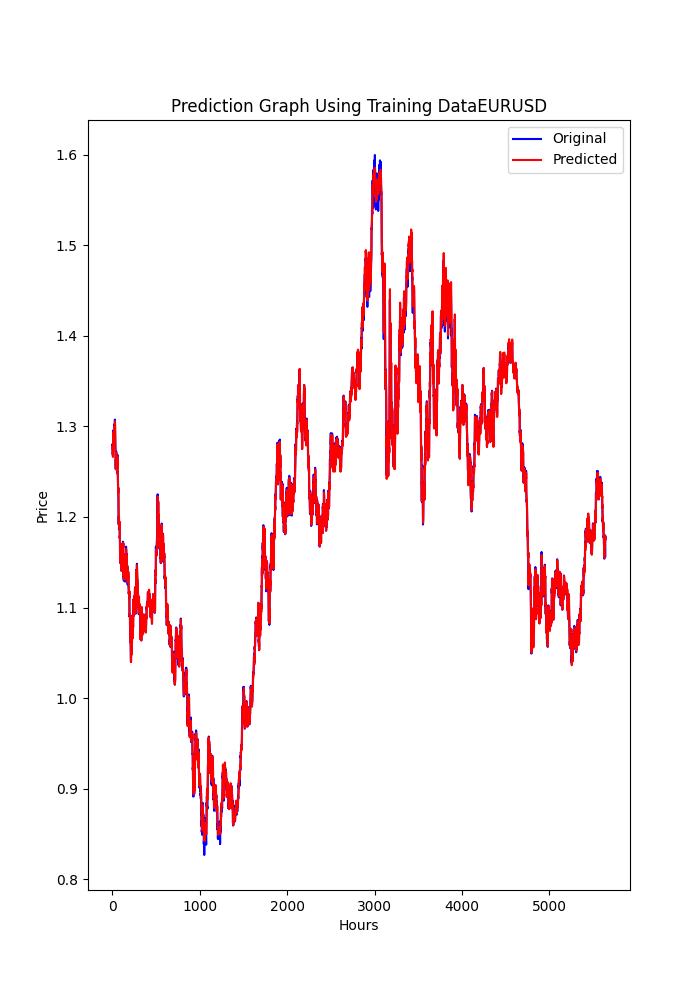
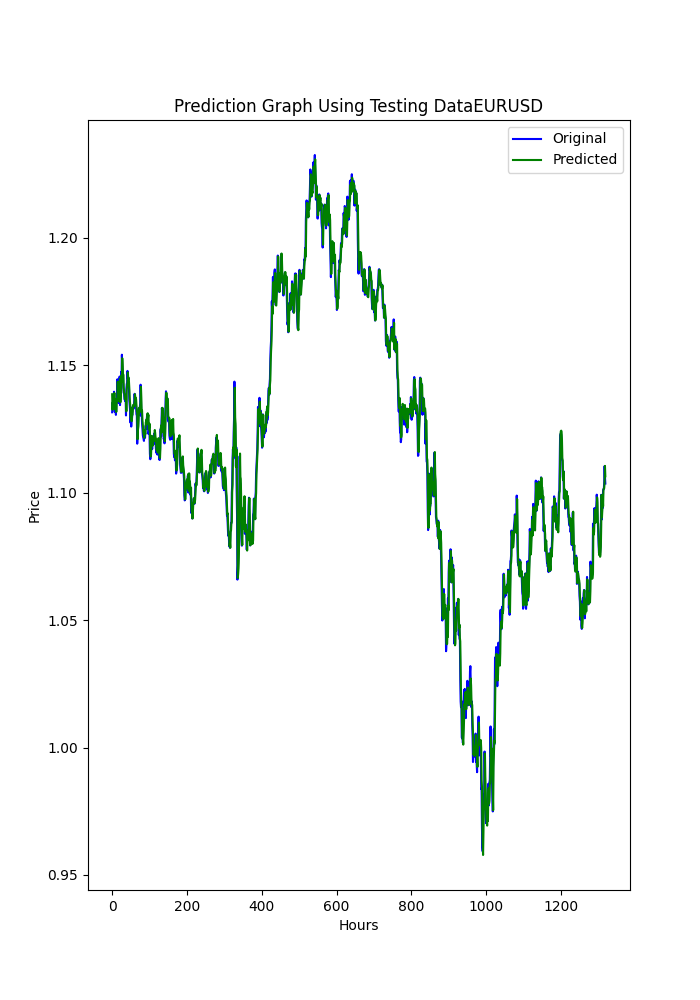
O script também salva um arquivo .txt onde as métricas anteriores são registradas na mesma ordem em que aparecem no terminal.

Para usar este script, você deve primeiro instalar o Python 3.11.9 e instalar estas bibliotecas com: pip install:

tensorflow==2.12.0, keras==2.12.0,  tf2onnx==1.16.0, MetaTrader5, pandas, numpy, scikit-learn, tf2onnx, keras

Recomendo fortemente o uso do Visual Studio Code, que você pode baixar pela Microsoft Store.

Talvez seja necessário instalar

Microsoft Visual C++ 2015 - 2022 Redistributable

Anexei o script .py, basta abri-lo no VSC e executá-lo.

If you want to change anything (another symbol, period from where to get the data or time period), change only this lines:

symbol = "EURUSD"
optional = "D1_2024"

O símbolo é óbvio, recomendo alterar "optional" para o time frame usado e a data final dos dados.

eurusd_rates = mt5.copy_rates_from(symbol, mt5.TIMEFRAME_D1, end_date, sample_size)

Nesta linha, é onde você altera o time frame, por exemplo, H1 (time frame de 1 hora).

Agora que temos o modelo ONNX de Deep Learning, podemos adicioná-lo aos EAs que já temos dos outros artigos.

Vou anexar o modelo DL ONNX (2024).

O que vamos adicionar aos EAs?

Modificações no CNA

Isto é básico, vou passar por este processo bem devagar.

Primeiro, no início, onde estão os parâmetros de entrada, devemos adicionar estas linhas:

#include <Trade\Trade.mqh>

#resource "/Files/EURUSD_D1.onnx" as uchar ExtModel[]

#define SAMPLE_SIZE 120

long     ExtHandle=INVALID_HANDLE;
int      ExtPredictedClass=-1;
datetime ExtNextBar=0;
datetime ExtNextDay=0;
float    ExtMin=0.0;
float    ExtMax=0.0;
CTrade   ExtTrade;
int dlsignal=-1;

//--- price movement prediction
#define PRICE_UP   0
#define PRICE_SAME 1
#define PRICE_DOWN 2

Lembre-se de modificar esta linha com o modelo ONNX que você criou (os scripts .py salvam o modelo em MQL5/Files/...).

#resource "/Files/EURUSD_D1_2024.onnx" as uchar ExtModel[]

No OnInit(), você deve adicionar isto:

//--- create a model from static buffer
   ExtHandle=OnnxCreateFromBuffer(ExtModel,ONNX_DEFAULT);
   if(ExtHandle==INVALID_HANDLE)
     {
      Print("OnnxCreateFromBuffer error ",GetLastError());
      return(INIT_FAILED);
     }

//--- since not all sizes defined in the input tensor we must set them explicitly
//--- first index - batch size, second index - series size, third index - number of series (only Close)
   const long input_shape[] = {1,SAMPLE_SIZE,1};
   if(!OnnxSetInputShape(ExtHandle,ONNX_DEFAULT,input_shape))
     {
      Print("OnnxSetInputShape error ",GetLastError());
      return(INIT_FAILED);
     }

//--- since not all sizes defined in the output tensor we must set them explicitly
//--- first index - batch size, must match the batch size of the input tensor
//--- second index - number of predicted prices (we only predict Close)
   const long output_shape[] = {1,1};
   if(!OnnxSetOutputShape(ExtHandle,0,output_shape))
     {
      Print("OnnxSetOutputShape error ",GetLastError());
      return(INIT_FAILED);
     }

Onde? Em qualquer lugar... não importa (apenas antes do retorno da função).

Na função OnDeinit, você também deve adicionar isto:

if(ExtHandle!=INVALID_HANDLE)
     {
      OnnxRelease(ExtHandle);
      ExtHandle=INVALID_HANDLE;
     }

Onde? Em qualquer lugar, isso libera o modelo ONNX.

Na função OnTick, você deve adicionar isto:

void OnTick()
  {
  //--- check new day
   if(TimeCurrent()>=ExtNextDay)
     {
      GetMinMax();
      //--- set next day time
      ExtNextDay=TimeCurrent();
      ExtNextDay-=ExtNextDay%PeriodSeconds(PERIOD_D1);
      ExtNextDay+=PeriodSeconds(PERIOD_D1);
     }

//--- check new bar
   if(TimeCurrent()<ExtNextBar)
      return;
//--- set next bar time
   ExtNextBar=TimeCurrent();
   ExtNextBar-=ExtNextBar%PeriodSeconds();
   ExtNextBar+=PeriodSeconds();
//--- check min and max
   float close=(float)iClose(_Symbol,_Period,0);
   if(ExtMin>close)
      ExtMin=close;
   if(ExtMax<close)
      ExtMax=close;
      
   PredictPrice();

Onde? No início, isso é importante porque o resultado da função PredictPrice() deve ser incorporado à lógica de execução de ordens.

Na função OnTick(), você também deve modificar a função que realiza as ordens, neste caso (CNA_DL), vamos mudar a linha original:

int signal = GenerateSignal(symbol, prediction);

para esta linha:

int signal = GenerateSignal(symbol, prediction, ExtPredictedClass);

ExtPredictedClass é o resultado da função PredictPrice() que adicionamos anteriormente.

Agora, também precisamos modificar a lógica da função GenerateSignal(), para que ela use a variável ExtPredictedClass:

Vamos ter que mudar o cabeçalho dessa função:

int GenerateSignal(string symbol, double prediction, int dlsgnl)

e adicionar a nova variável à lógica que decide as ordens, neste caso, aqui:from this:

disto:

   bool buy_condition =  prediction >  0.00001 && rsi < 30 && trend_strong  && volatility_ok && fastMA > slowMA;
   bool sell_condition = prediction < -0.00001 && rsi > 70 && trend_strong && volatility_ok && fastMA < slowMA;

para isto:

   bool buy_condition =  prediction >  0.00001 && rsi < 30 && trend_strong  && volatility_ok && fastMA > slowMA && dlsgnl==PRICE_UP;
   bool sell_condition = prediction < -0.00001 && rsi > 70 && trend_strong && volatility_ok && fastMA < slowMA && dlsgnl==PRICE_DOWN;

A última parte que precisamos modificar é esta:

Devemos adicionar estas funções ao script. Onde? Em qualquer lugar, no final, por exemplo.

//+------------------------------------------------------------------+
void PredictPrice(void)
  {
   static vectorf output_data(1);            // vector to get result
   static vectorf x_norm(SAMPLE_SIZE);       // vector for prices normalize

//--- check for normalization possibility
   if(ExtMin>=ExtMax)
     {
      Print("ExtMin>=ExtMax");
      ExtPredictedClass=-1;
      return;
     }
//--- request last bars
   if(!x_norm.CopyRates(_Symbol,_Period,COPY_RATES_CLOSE,1,SAMPLE_SIZE))
     {
      Print("CopyRates ",x_norm.Size());
      ExtPredictedClass=-1;
      return;
     }
   float last_close=x_norm[SAMPLE_SIZE-1];
//--- normalize prices
   x_norm-=ExtMin;
   x_norm/=(ExtMax-ExtMin);
//--- run the inference
   if(!OnnxRun(ExtHandle,ONNX_NO_CONVERSION,x_norm,output_data))
     {
      Print("OnnxRun");
      ExtPredictedClass=-1;
      return;
     }
//--- denormalize the price from the output value
   float predicted=output_data[0]*(ExtMax-ExtMin)+ExtMin;
//--- classify predicted price movement
   float delta=last_close-predicted;
   if(fabs(delta)<=0.00001)
      ExtPredictedClass=PRICE_SAME;
   else
     {
      if(delta<0)
         ExtPredictedClass=PRICE_UP;
      else
         ExtPredictedClass=PRICE_DOWN;
     }
  }
  
  
  
  void GetMinMax(void)
  {
   vectorf close;
   close.CopyRates(_Symbol,PERIOD_D1,COPY_RATES_CLOSE,0,SAMPLE_SIZE);
   ExtMin=close.Min();
   ExtMax=close.Max();
  }

Estas duas funções são chave para as previsões — uma faz as previsões, e a outra obtém o mínimo e o máximo do fechamento.

Modificações no SMOC

Tudo permanece o mesmo, e as mudanças são iguais às anteriores, exceto por estas:

Nos parâmetros de entrada, você não inicializa dlsignal nem adiciona CTrade:

#resource "/Files/EURUSD_D1.onnx" as uchar ExtModel[]

#define SAMPLE_SIZE 120

long     ExtHandle=INVALID_HANDLE;
int      ExtPredictedClass=-1;
datetime ExtNextBar=0;
datetime ExtNextDay=0;
float    ExtMin=0.0;
float    ExtMax=0.0;

//--- price movement prediction
#define PRICE_UP   0
#define PRICE_SAME 1
#define PRICE_DOWN 2

Na função OnTick(), teremos isto:

void OnTick()
  {
//--- check new day
   if(TimeCurrent()>=ExtNextDay)
     {
      GetMinMax();
      //--- set next day time
      ExtNextDay=TimeCurrent();
      ExtNextDay-=ExtNextDay%PeriodSeconds(PERIOD_D1);
      ExtNextDay+=PeriodSeconds(PERIOD_D1);
     }

//--- check new bar
   if(TimeCurrent()<ExtNextBar)
      return;
//--- set next bar time
   ExtNextBar=TimeCurrent();
   ExtNextBar-=ExtNextBar%PeriodSeconds();
   ExtNextBar+=PeriodSeconds();
//--- check min and max
   float close=(float)iClose(_Symbol,_Period,0);
   if(ExtMin>close)
      ExtMin=close;
   if(ExtMax<close)
      ExtMax=close;

   PredictPrice();

   static datetime lastBarTime = 0;
   datetime currentBarTime = iTime(Symbol(), PERIOD_CURRENT, 0);

// Only process on new bar
   if(currentBarTime == lastBarTime)
      return;

   lastBarTime = currentBarTime;

   double currentPrice = SymbolInfoDouble(Symbol(), SYMBOL_LAST);
   int decision = OptimalControl(currentPrice);

   string logMessage = StringFormat("New bar: Time=%s, Price=%f, Decision=%d",
                                    TimeToString(currentBarTime), currentPrice, decision);
   LogMessage(logMessage);

// Manage open order if exists
   if(orderTicket != 0)
     {
      ManageOpenOrder(decision, ExtPredictedClass);
     }

   if(orderTicket == 0 && decision != 0 && IsTrendFavorable(decision) && IsLongTermTrendFavorable(decision) && (ExtPredictedClass==PRICE_DOWN || ExtPredictedClass==PRICE_UP))
     {
      ExecuteTrade(decision, ExtPredictedClass);
     }
  }

Na função ManageOpenOrder(), faremos esta alteração:

void ManageOpenOrder(int decision, int dlsignal)
  {
   int barsOpen = iBars(Symbol(), PERIOD_CURRENT) - iBarShift(Symbol(), PERIOD_CURRENT, orderOpenTime);
   LogMessage(StringFormat("Bars open: %d for order ticket: %d", barsOpen, orderTicket));

   if(barsOpen >= maxBarsOpen ||
      (PositionGetInteger(POSITION_TYPE) == POSITION_TYPE_BUY && decision == -1 && dlsignal == PRICE_DOWN) ||
      (PositionGetInteger(POSITION_TYPE) == POSITION_TYPE_SELL && decision == 1 && dlsignal == PRICE_UP))
     {
      CloseOrder(orderTicket);
      orderTicket = 0;
      orderOpenTime = 0;
     }
   else
     {
      UpdateSLTP(orderTicket, decision);
     }
  }

Na função ExecuteTrade()

void ExecuteTrade(int decision, int dlsignal)
  {
   MqlTradeRequest request = {};
   MqlTradeResult result = {};
   double price;
   int decision1;
   
   

   if(decision == 1 && dlsignal == PRICE_UP)
     {
      price = SymbolInfoDouble(Symbol(), SYMBOL_ASK);
      request.type = ORDER_TYPE_BUY;
      decision1 = 1;
     }
   else
      if(decision == -1 && dlsignal == PRICE_DOWN)
        {
         price = SymbolInfoDouble(Symbol(), SYMBOL_BID);
         request.type = ORDER_TYPE_SELL;
        decision1 = -1;
        }
   double sl = CalculateDynamicSL(price, decision1);
   double tp = CalculateDynamicTP(price, decision1);



   double adjustedLotSize = AdjustLotSizeForDrawdown();
   request.volume = adjustedLotSize;

   request.action = TRADE_ACTION_DEAL;
   request.symbol = Symbol();
//request.volume = lotSize;
//request.type = (decision == 1 && dlsignal == PRICE_UP) ? ORDER_TYPE_BUY : ORDER_TYPE_SELL;
   request.price = price;
   request.sl = sl;
   request.tp = tp;
   request.deviation = 10;
   request.magic = 123456; // Magic number to identify orders from this EA
   request.comment = (decision == 1) ? "Buy Order" : "Sell Order";

   if(OrderSend(request, result))
     {
      Print((decision1 == 1 ? "Buy" : "Sell"), " Order Executed Successfully. Ticket: ", result.order);
      orderOpenTime = iTime(Symbol(), PERIOD_CURRENT, 0);
      orderTicket = result.order;
     }
   else
     {
      Print("Error executing Order: ", GetLastError());
     }
  }

E agora as modificações no script do Nash Equity

Modificações no Nash Equity

Todas as mudanças são iguais, exceto pela função OnTick(), que ficará assim:

void OnTick()
  {
//--- check new day
   if(TimeCurrent()>=ExtNextDay)
     {
      GetMinMax();
      //--- set next day time
      ExtNextDay=TimeCurrent();
      ExtNextDay-=ExtNextDay%PeriodSeconds(PERIOD_D1);
      ExtNextDay+=PeriodSeconds(PERIOD_D1);
     }

//--- check new bar
   if(TimeCurrent()<ExtNextBar)
      return;
//--- set next bar time
   ExtNextBar=TimeCurrent();
   ExtNextBar-=ExtNextBar%PeriodSeconds();
   ExtNextBar+=PeriodSeconds();
//--- check min and max
   float close=(float)iClose(_Symbol,_Period,0);
   if(ExtMin>close)
      ExtMin=close;
   if(ExtMax<close)
      ExtMax=close;

   PredictPrice();

   if(!IsNewBar())
      return; // Solo procesar en nueva barra

   MarketRegime hmmRegime = NOT_PRESENT;
   MarketRegime logLikelihoodRegime = NOT_PRESENT;
   DetectMarketRegime(hmmRegime, logLikelihoodRegime);

// Calcular señales para cada estrategia
   CalculateStrategySignals(_Symbol, TimeCurrent(), hmmRegime, logLikelihoodRegime);

// Verificar si la estrategia de Nash Equilibrium ha generado una señal
   if(strategies[3].enabled && strategies[3].signal != 0)
     {
      if(strategies[3].signal > 0 && ExtPredictedClass==PRICE_UP)
        {
         OpenBuyOrder(strategies[3].name);
        }
      else
         if(strategies[3].signal < 0 && ExtPredictedClass==PRICE_DOWN)
           {
            OpenSellOrder(strategies[3].name);
           }
     }

// Actualizar stops de seguimiento si es necesario
   if(UseTrailingStop)
     {
      UpdateTrailingStops();
     }
  }

Resultados
CNA_DL

Configurações

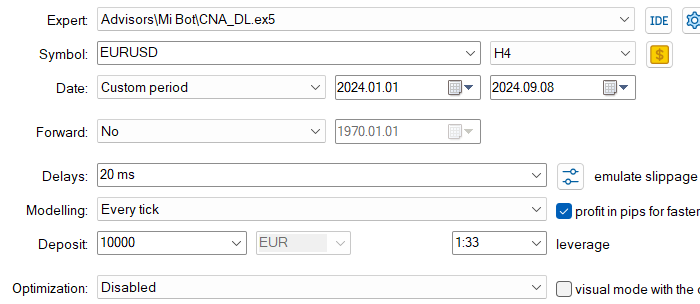
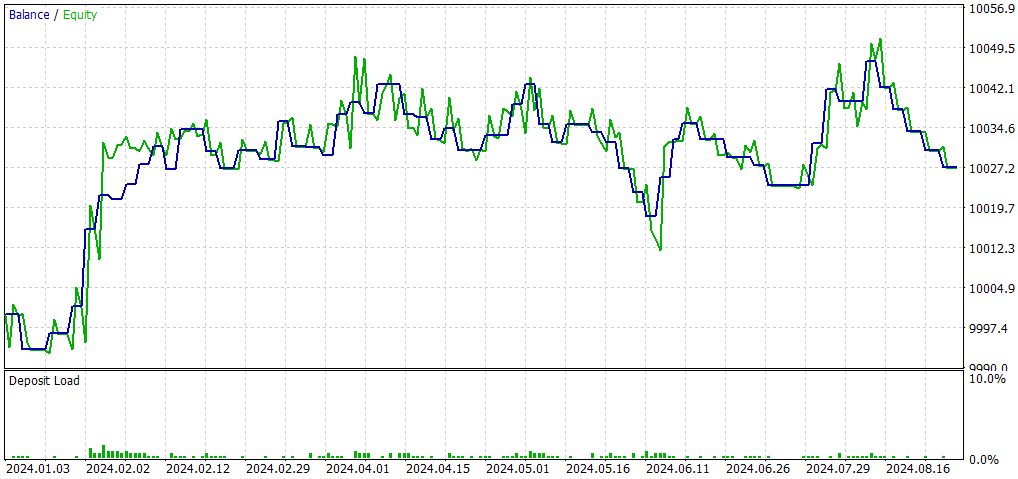
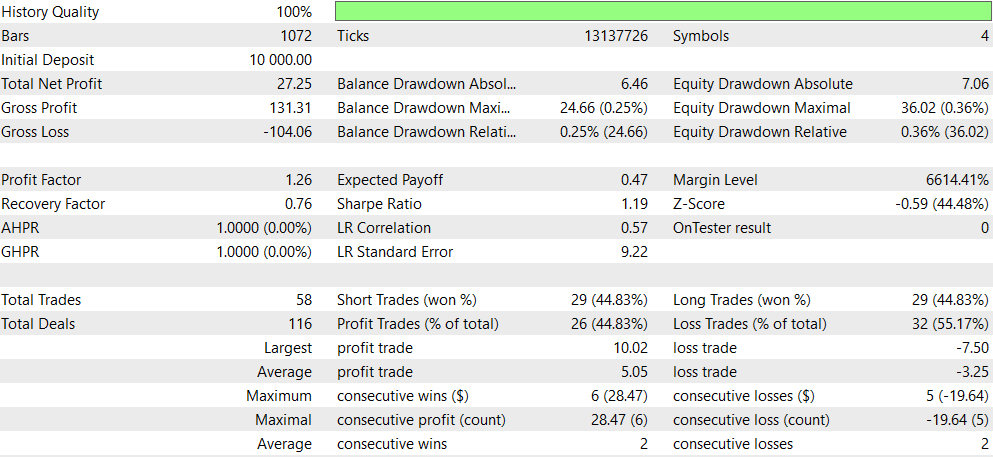
Comparado com o EA original (CNA_Final_v4):

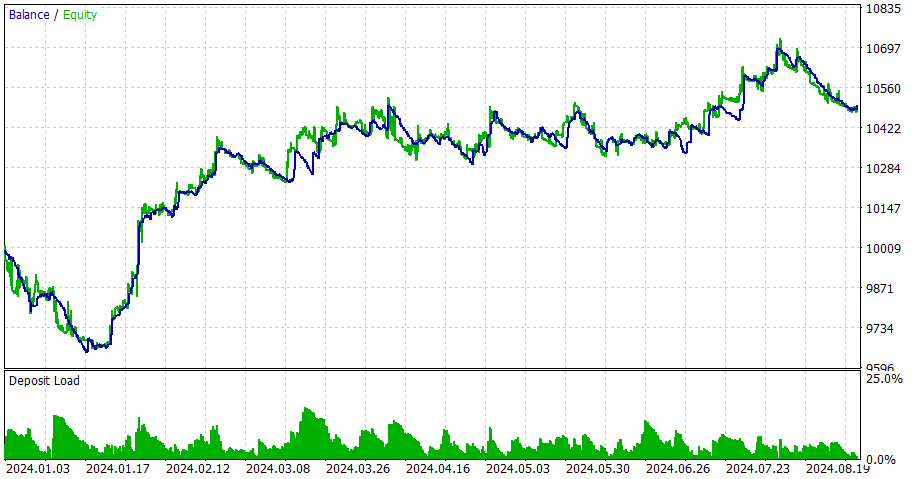
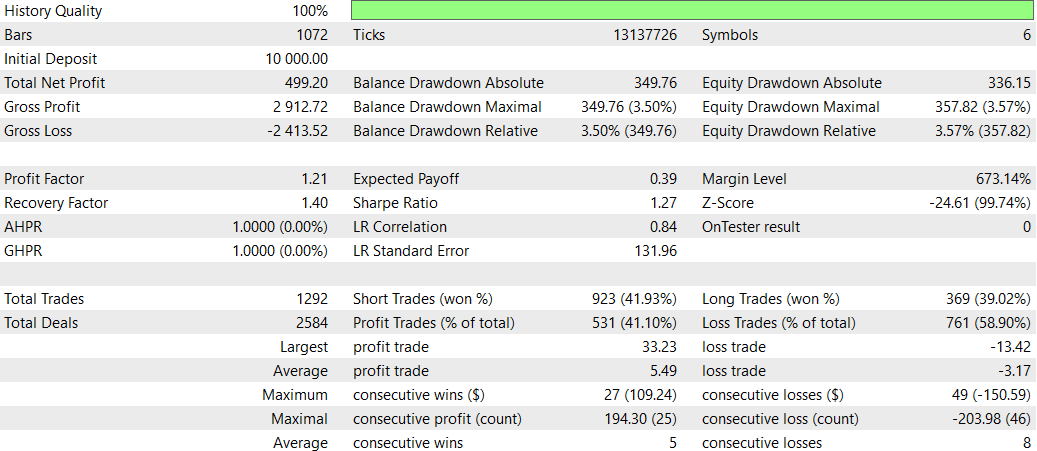
Comparação entre CNA com e sem Deep Learning

1. Lucratividade: O EA sem deep learning é significativamente mais lucrativo, mas também assume mais risco com rebaixamentos maiores.
2. Risco: O EA com deep learning tem rebaixamentos menores e parece mais conservador em sua abordagem.
3. Frequência de negociação: O EA sem deep learning negocia com muito mais frequência (1292 vs 58 negociações).
4. Taxa de acerto: O EA com deep learning tem uma taxa de acerto levemente melhor, mas ambas estão abaixo de 50%.
5. Tendência estratégica: O EA sem DL mostra forte preferência por operações vendidas (short), enquanto o EA com DL é mais equilibrado.
6. Consistência: O EA com DL parece mais consistente, com sequências menores de ganhos/perdas consecutivas.

Concluindo, o EA sem DL parece mais lucrativo, mas também mais arriscado, enquanto o EA com DL é mais conservador, com menores retornos e também menor risco. A escolha entre eles dependerá da tolerância ao risco e dos objetivos do investidor. O EA com DL pode ser preferido para operações mais estáveis e conservadoras, enquanto o EA sem DL pode ser escolhido para retornos potencialmente maiores com maior risco.

SMOC_DL

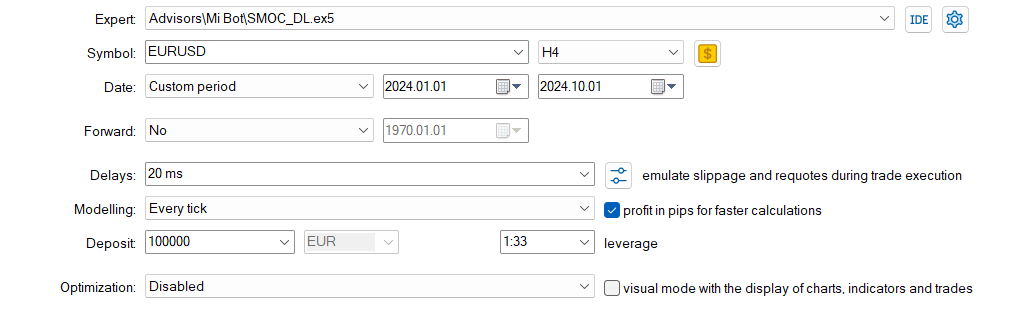
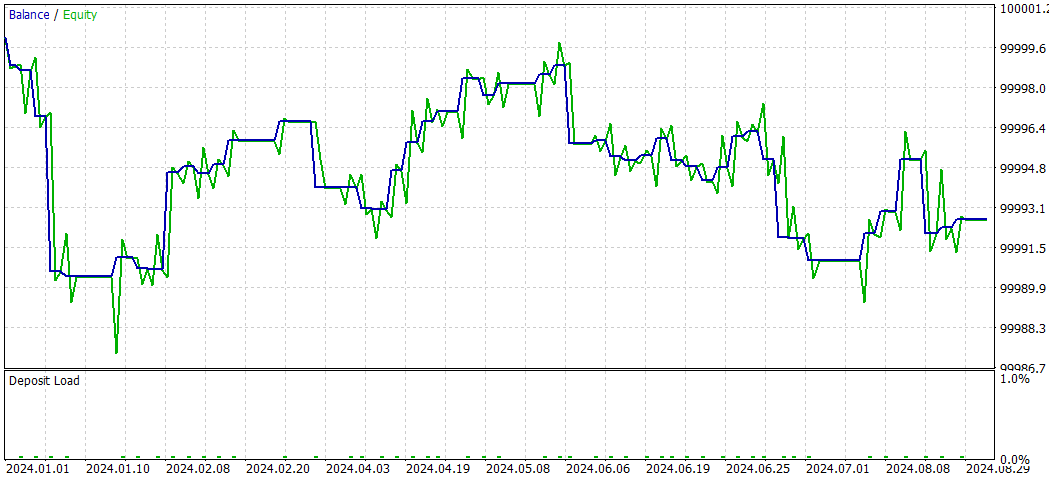
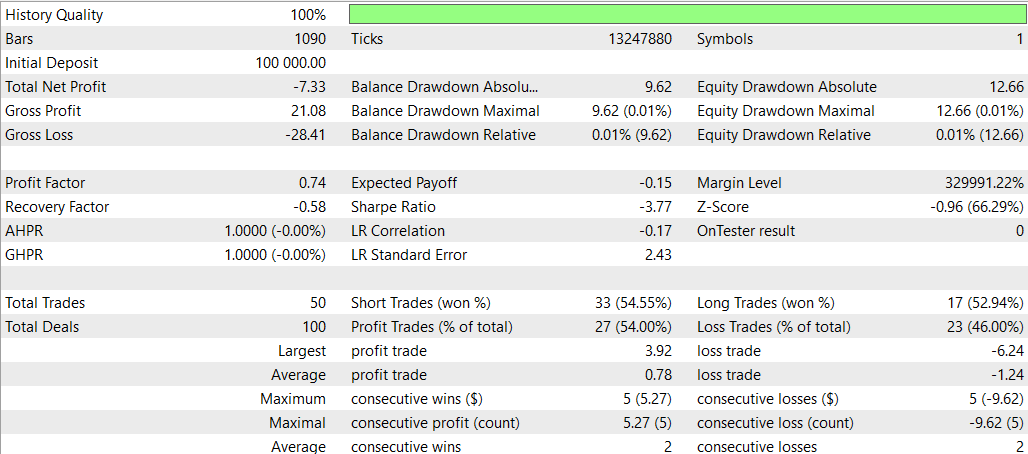
E agora o SMOC sem Deep Learning

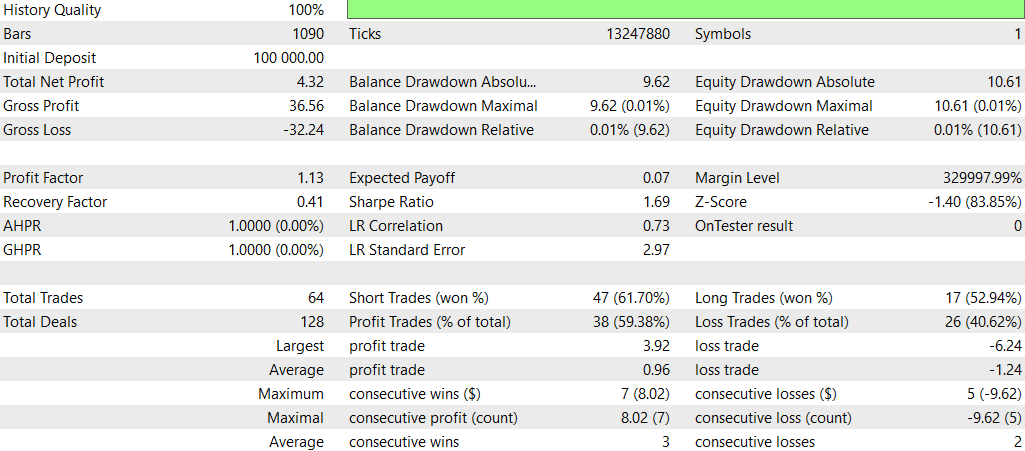
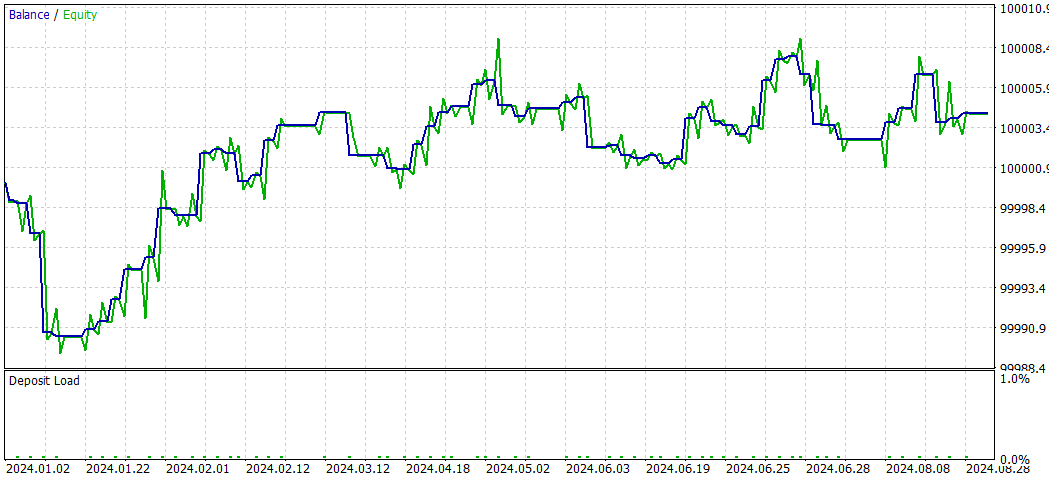
Comparação SMOC_DL vs SMOC:

1. Lucratividade: Estratégia 2 é lucrativa (4,32), enquanto a Estratégia 1 não é lucrativa (-7,33).
2. Retornos ajustados ao risco: Estratégia 2 tem índice de Sharpe positivo (1,69), indicando melhor desempenho ajustado ao risco em comparação à Estratégia 1, com índice negativo (-3,77).
3. Taxa de acerto: Estratégia 2 tem uma taxa de acerto maior (59,38%) contra 54% da Estratégia 1.
4. Número de negociações: Estratégia 2 executa mais negociações (64) que a Estratégia 1 (50), indicando potencialmente mais oportunidades identificadas.
5. Fator de lucro: Estratégia 2 tem fator de lucro acima de 1 (1,13), enquanto a Estratégia 1 está abaixo de 1 (0,74), sugerindo que a Estratégia 2 é mais eficaz em gerar lucros em relação às perdas.
6. Rebaixamento: Ambas as estratégias apresentam rebaixamentos baixos similares (0,01% da conta), indicando boa gestão de risco.
7. Distribuição das negociações: Ambas as estratégias têm preferência por operações vendidas, mas a Estratégia 2 tem distribuição mais equilibrada entre operações compradas e vendidas.

No geral, a Estratégia 2 parece superior em quase todos os aspectos, incluindo lucratividade, retorno ajustado ao risco, taxa de acerto e fator de lucro. Ela também realiza mais negociações, indicando melhor identificação de oportunidades. Ambas demonstram boa gestão de risco com baixos rebaixamentos. Com base nesses dados, a Estratégia 2 seria a escolha preferida entre as duas. Uma abordagem adequada para usar DL seria tentar outros prazos.

NASH_DL

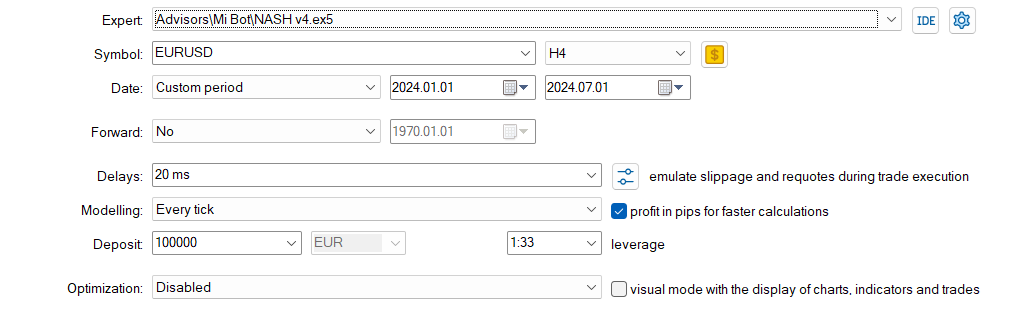
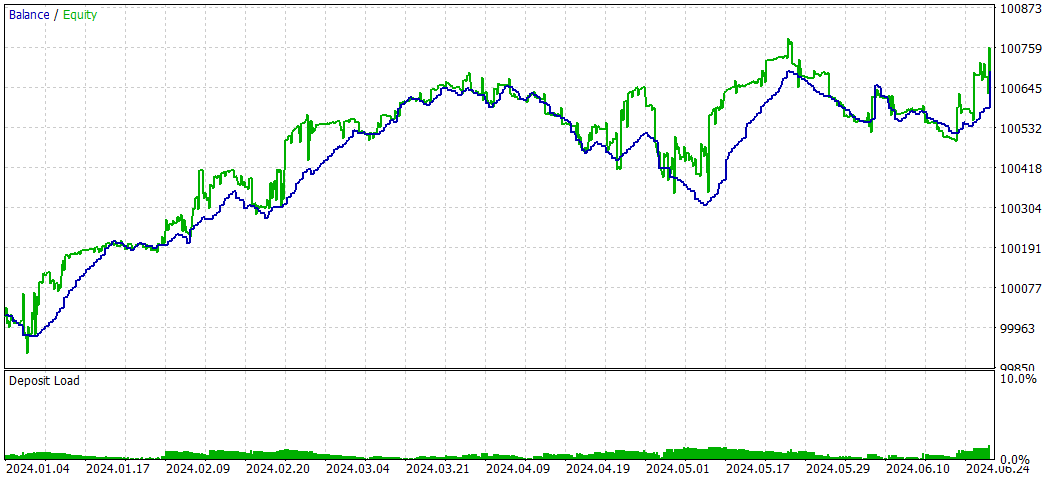
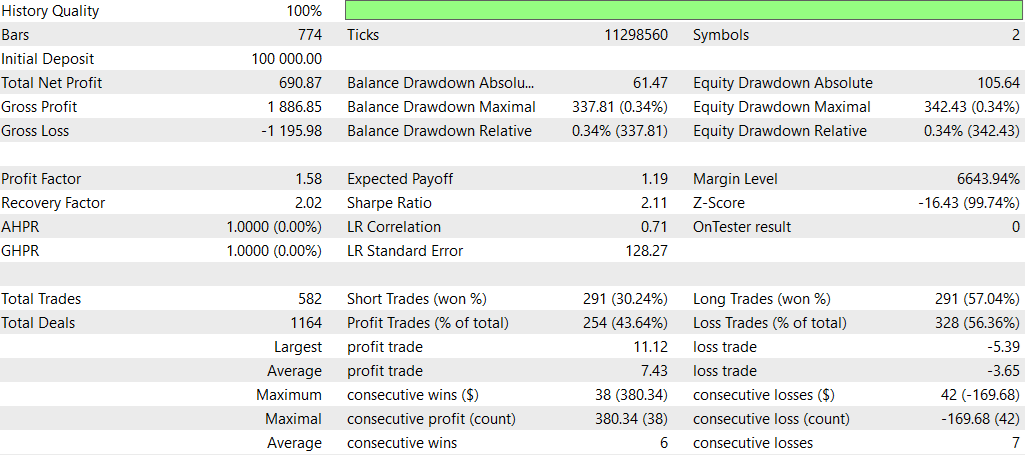
E agora sem Deep Learning:

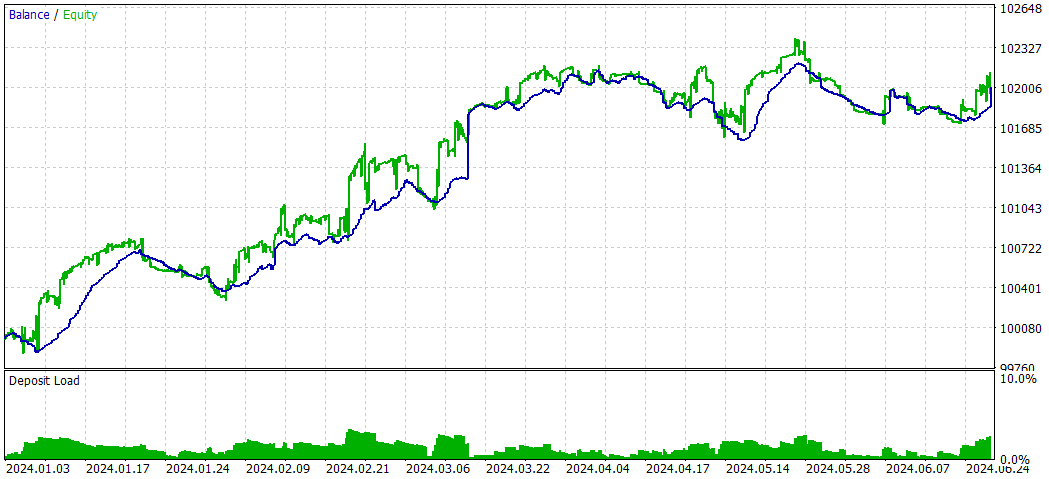
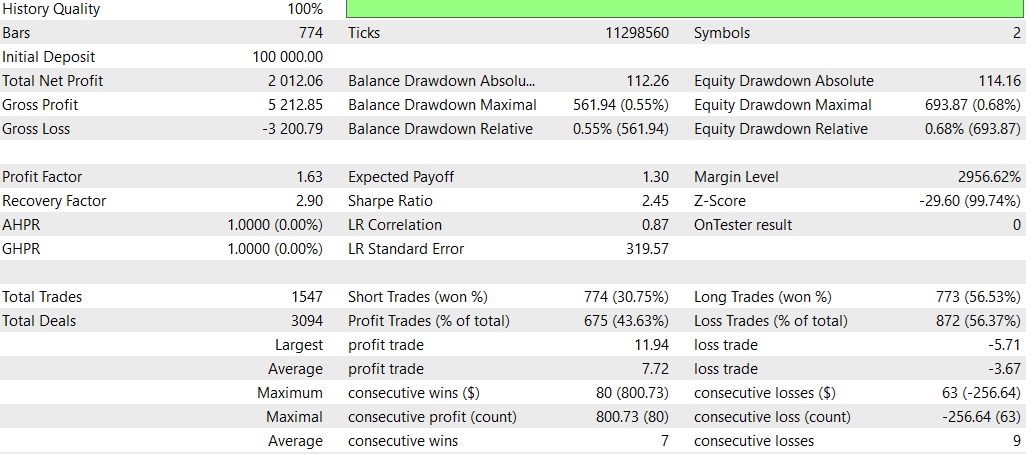
No geral, a estratégia sem DL teve desempenho melhor em termos de lucratividade total e retorno ajustado ao risco, apesar de apresentar maior rebaixamento máximo. Ela realizou mais operações e mostrou mais eficácia em posições compradas. A estratégia com DL foi mais conservadora, com rebaixamentos menores, mas também retornos mais baixos.

No entanto, é importante observar que essa comparação se baseia em apenas um período de backtest. Para conclusões mais robustas, seria necessário testar essas estratégias em múltiplos períodos e condições de mercado.

Conclusão

Este estudo explorou a integração de modelos de Deep Learning (DL) em três Expert Advisors (EAs) avançados de negociação: Análise de Rede de Causalidade (CNA), Otimização Estocástica e Controle Ótimo (SMOC) e Teoria dos Jogos de Nash. O processo envolveu a criação de modelos ONNX com Python e sua incorporação aos scripts MQL5 existentes.

Os resultados dessa integração foram variados entre as estratégias:

1. Para a estratégia CNA, a versão com DL mostrou operações mais conservadoras, com retornos menores, mas também menor risco em comparação à versão sem DL. Embora menos lucrativa, apresentou melhor consistência e abordagem mais equilibrada.
2. No caso do SMOC, a versão com DL superou significativamente sua contraparte sem DL. Mostrou maior lucratividade, maior taxa de acerto e retornos ajustados ao risco superiores, sugerindo que o modelo de DL aprimorou efetivamente a tomada de decisão da estratégia.
3. Para a abordagem baseada na Teoria dos Jogos de Nash, a versão sem DL teve desempenho geral melhor, com maior lucratividade total e retorno ajustado ao risco, mesmo com rebaixamento máximo mais alto. A versão com DL foi mais conservadora, com menos risco, porém com retornos menores.

Esses resultados destacam o potencial da integração de Deep Learning em estratégias de negociação, mas também reforçam a importância de uma implementação e testes cuidadosos. A eficácia da integração de DL varia conforme a estratégia utilizada e as condições de mercado.

É fundamental observar que estas conclusões se baseiam em períodos específicos de backtest e condições de mercado. Para conclusões mais sólidas, seria necessário realizar testes adicionais em diferentes períodos e cenários de mercado.

Concluindo, embora o Deep Learning possa aprimorar estratégias de negociação, sua integração deve ser feita com cautela e testes extensivos. Os resultados variados entre as estratégias sugerem que a eficácia do DL na negociação não é universal e depende fortemente da estratégia e do contexto de mercado. Pesquisas futuras podem explorar a otimização desses modelos de DL para diferentes time frames e condições de mercado, a fim de melhorar seu desempenho em diversos cenários de negociação.