交易中的多项式模型

引言

交易效率在很大程度上取决于市场数据的分析方法。正交多项式就是其中一种方法。这些多项式是数学函数，可用于解决与交易相关的若干问题。

最著名的正交多项式有勒让德多项式、切比雪夫多项式、拉盖尔多项式和埃尔米特多项式。这些多项式中的每一种都具有独特的性质，使其能够用于解决不同的问题。以下是它们的一些主要应用方式：

• 时间序列建模。正交多项式可用于描述时间序列。使用它们有助于识别趋势和其他模式。
• 回归分析。正交多项式可应用于回归分析。使用它们可以提高模型的质量，并使其更具可解释性。
• 预测。正交多项式可用于预测：如果当前趋势持续，价格将会如何变化。

下面我们来看看正交多项式在实践中是如何应用的。

正交多项式与指标

技术分析的全部要点归结为识别价格运动中的模式。但金融时间序列通常包含会掩盖这些模式的噪声。让我们看看正交多项式如何在市场环境中应用。

其基本思想是，这些多项式可用于将复杂信号分解为更简单的组成部分。这种分解使我们能够滤除噪声并识别趋势。

举例来说，我将使用勒让德多项式来制作一个基于它的平滑指标。这些多项式的一般方程及其定义域由以下表达式给出：

我将使用最高为9次的多项式。这对于平滑处理来说是完全足够的，而使用更高次的多项式反而可能引入噪声，并掩盖价格运动的主要趋势。本文所使用的多项式方程已在表格中给出。

n	勒让德多项式
0	1
1	x
2	(3*x^2-1)/2
3	(5*x^3-3*x)/2
4	(35*x^4-30*x^2+3)/8
5	(63*x^5-70*x^3+15*x)/8
6	(231*x^6-315*x^4+105*x^2-5)/16
7	(429*x^7-693*x^5+315*x^3-35*x)/16
8	(6435*x^8-12012*x^6+6930*x^4-1260*x^2+35)/128
9	(12155*x^9-25740*x^7+18018*x^5-4620*x^3+315*x)/128

首先，我需要将价格指数转换到这些多项式的定义域内。为此，我对每个索引 i 应用移位函数：

之后，我为每个 x[i] 值计算我感兴趣的所有多项式的值。例如，我将计算一个周期为3的2次多项式的值：

现在我需要引入一个针对离散性的修正。1次及更高次多项式的值之和应该等于零。为了满足这个条件，我需要计算修正值：

我利用这个修正值来调整多项式的值：

现在，最有趣的部分开始了。任何时间序列都可以被分解为一系列带有特定权重的多项式之和：

这些权重本身可以按如下方式计算：

这看起来可能有些奇怪，甚至有点吓人。事实上，一切都很简单。我们以一个周期为 N 的0次多项式为例。它在所有点的值都等于1。而它的权重将是：

这就是简单移动平均线（SMA） 的方程。更高次多项式的权重则等同于一些具有特殊选定比率的振荡器。换句话说，正交多项式就是简单移动平均线加上一些巧妙计算出的附加项。勒让德多项式对噪声具有很强的鲁棒性，在排序应用中表现出色。例如，一次勒让德多项式看起来是这样的。

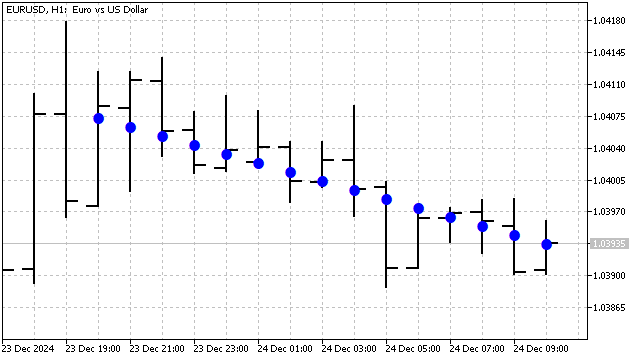
除了勒让德多项式，切比雪夫多项式也可用于趋势检测和平滑。这类多项式有两种类型。它们在边界处的表现彼此不同。这些多项式的主要优点在于它们对价格突变的敏感性。这些多项式的方程非常简单：

n	第一类切比雪夫多项式	第二类切比雪夫多项式
0	1	1
1	x	2*x
2	2*x^2-1	4*x^2-1
3	4*x^3-3*x	8*x^3-4*x
4	8*x^4-8*x^2+1	16*x^4-12*x^2+1
5	16*x^5-20*x^3+5*x	32*x^5-32*x^3+6*x
6	32*x^6-48*x^4+18*x^2-1	64*x^6-80*x^4+24*x^2-1
7	64*x^7-112*x^5+56*x^3-7*x	128*x^7-192*x^5+80*x^3-8*x
8	128*x^8-256*x^6+160*x^4-32*x^2+1	256*x^8-448*x^6+240*x^4-40*x^2+1
9	256*x^9-576*x^7+432*x^5-120*x^3+9*x	512*x^9-1024*x^7+672*x^5-160*x^3+10*x

这就是使用3次切比雪夫多项式进行平滑处理的效果。

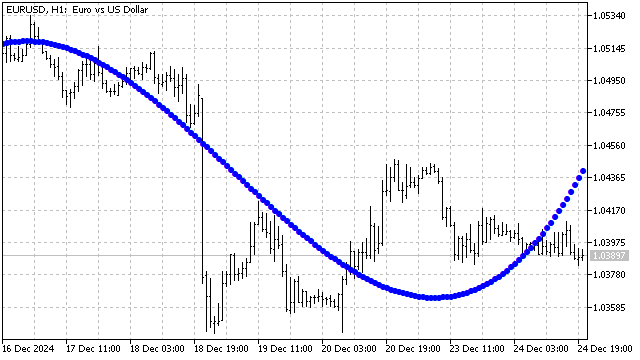
到目前为止，我们讨论的定义域为 +/-1 的多项式，但也存在其他定义域的多项式。例如，拉盖尔多项式的定义域是所有非负实数。它的方程如下所示：

n	拉盖尔多项式
0	1
1	-x+1
2	(x^2-4*x+2)/2
3	(-x^3+9*x^2-18*x+6)/6
4	(x^4-16*x^3+72*x^2-96*x+24)/24
5	(-x^5+25*x^4-200*x^3+600*x^2-600*x+120)/120
6	(x^6-36*x^5+450*x^4-2400*x^3+5400*x^2-4320*x+720)/720
7	(-x^7+49*x^6-882*x^5+7350*x^4-29400*x^3+52920*x^2-35280*x+5040)/5040
8	(x^8-64*x^7+1568*x^6-18816*x^5+117600*x^4-376320*x^3+564480*x^2-322560*x+40320)/40320
9	(-x^9+81*x^8-2592*x^7+42336*x^6-381024*x^5+1905120*x^4-5080320*x^3+6531840*x^2-3265920*x+362880)/362880

其自变量的平移函数如下所示：

这一变化导致拉盖尔多项式的行为不仅取决于其次数，还取决于其周期。这种多项式对近期的价格变化很敏感。例如，下图展示了5次拉盖尔多项式在图表上的形态：

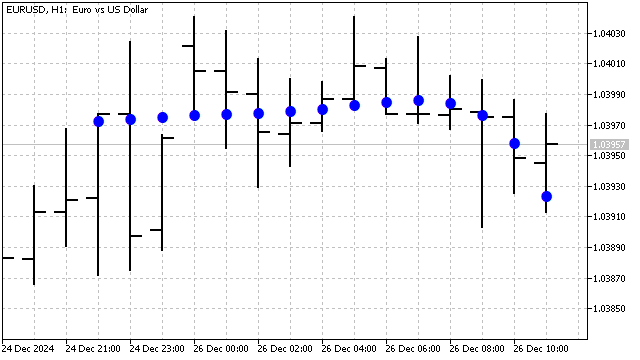
正交性的另一个有趣例子是埃尔米特多项式。这些多项式在数学和物理学的许多领域都有应用。这些多项式对所有实数值的自变量都有定义，其方程如下所示：

n	埃尔米特多项式
0	1
1	x
2	x^2-1
3	x^3-3*x
4	x^4-6*x^2+3
5	x^5-10*x^3+15*x
6	x^6-15*x^4+45*x^2-15
7	x^7-21*x^5+105*x^3-105*x
8	x^8-28*x^6+210*x^4-420*x^2+105
9	x^9-36*x^7+378*x^5-1260*x^3+945*x

平移函数将价格值进行中心化处理：

结果，我们得到了一个平滑滤波器，其效率取决于多项式的次数及其周期。

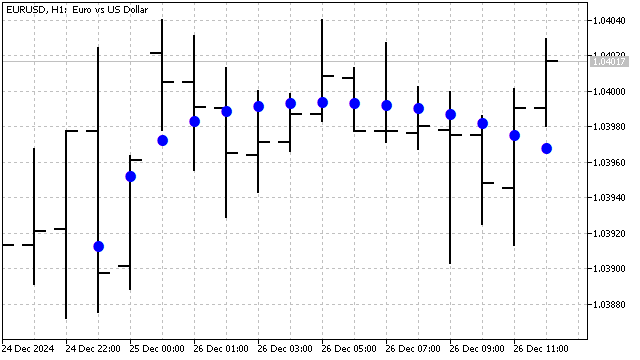
我们已经研究了基本的经典正交多项式。但完全有可能创建出自定义版本的多项式。例如，一个结合了切比雪夫多项式和埃尔米特多项式优点的多项式，其方程由下式给出：

n	雪夫多项式-埃尔米特多项式
0	1
1	2*x
2	4*x^2-2
3	8*x^3-12*x
4	16*x^4-48*x^2+12
5	32*x^5-160*x^3+120*x
6	64*x^6-480*x^4+720*x^2-120
7	128*x^7-1344*x^5+3360*x^3-1680*x
8	256*x^8-3584*x^6+13440*x^4-13440*x^2+1680
9	512*x^9-9216*x^7+48384*x^5-80640*x^3+30240*x

该多项式对非线性趋势——如二次、三次曲线等——非常敏感。下图展示了9次切比雪夫-埃尔米特多项式的图形形态：

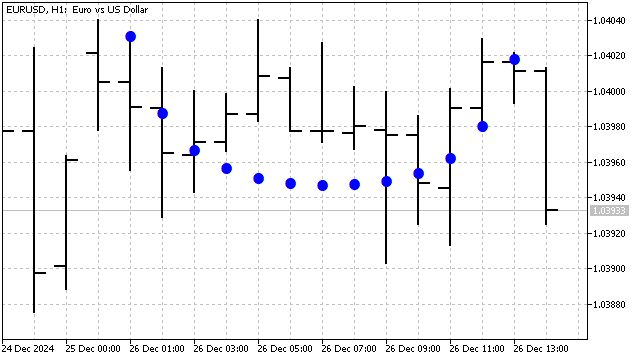
使用正交多项式能带来诸多优势。

• 稳定性与去相关性。多项式的正交性确保了它们对模型参数变化的稳定性。每个多项式都相互独立，这使得时间序列的每个组成部分都可以被单独建模和研究。
• 可解释性。每个正交多项式都对应着其自身的价格行为模型。多项式的权重系数使我们能够识别出最重要的模型，并专注于这些模型。
• 适应性与高效性。正交多项式会根据时间序列的具体数值进行调整。新价格的出现会导致权重系数的变化，从而使多项式模型能够适应市场的当前状态。而非线性多项式的使用，使得这种调整过程非常高效。

正交多项式唯一一个可被视为缺点的特征是，它们会处理其定义域内的所有价格。换句话说，基于此类多项式构建的指标会“重绘”。在我看来，这并非一个缺点——当新数据到来时，指标只是在寻找最佳拟合。

使用正交多项式也存在一些限制。指标的周期应大于多项式的次数。出于实际应用的目的，我们可以将多项式的次数限制在3次。这个指标结合了SMA（简单移动平均线）、线性趋势以及两条抛物线——二次和三次曲线。这足以平滑处理相当复杂的市场情况。但是，通过增加指标的周期，我们也可以相应地提高多项式的次数。

现在，让我们来看一些正交多项式在交易中的应用实例。

交易策略

基于正交多项式，交易者可以创建各种交易策略。例如，使用基于正交多项式的多项式回归，交易者不仅可以分析过去的价格走势，还能创建一个能够适应市场当前变化的模型。

作为一个例子，我们来看几个基于均值偏离的交易策略。

我们采用最简单的策略——当价格与SMA（简单移动平均线）交叉时开仓。我们将移动平均线替换为正交多项式，而开仓和平仓的规则保持不变：

• 价格自下而上穿越多项式——开买单，同时平卖单。
• 价格自上而下穿越多项式——开卖单，同时平买单。

尽管策略简单，但相当有效。

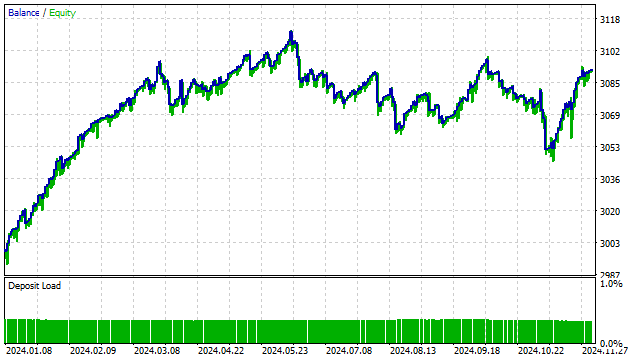
让我们稍微将这个策略复杂化，用某个多项式的值来替代价格。换句话说，我们将得到一个类似于两条SMA交叉的策略。结果在一定程度上是可预测的：在所有可能的选项中，策略优化器最终选择了正交多项式。

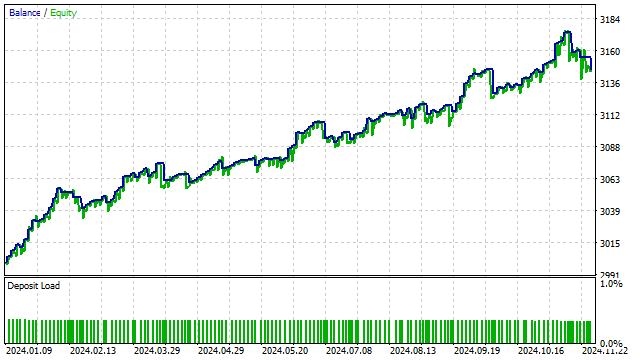
多项式模型也可用于更复杂的策略中。如果策略中使用了任何指标，你都可以尝试用正交多项式来替换它们。这样的替换可能会改善策略的表现。

我将使用商品通道指数(CCI)指标作为例子。它的经典方程如下所示：

我将对这个指标做一些小小的改动。正如我之前所说：SMA（简单移动平均线）是一个0次多项式。我将用任意次数的正交多项式来替代SMA。相应地，我将计算相对于这个多项式的平均绝对偏差。最终得到的指标如下：

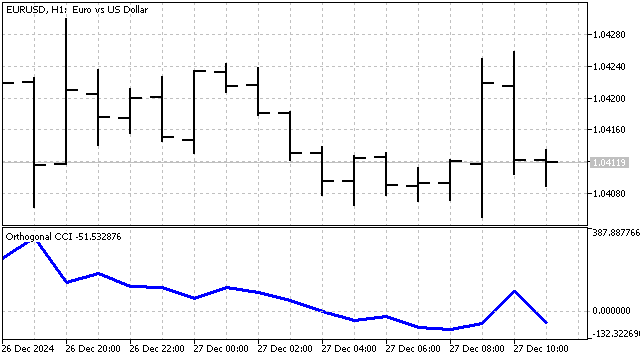
交易策略将与经典策略类似：

• 如果指标低于指定水平并持续下降，则开买单；
• 如果指标高于指定水平并持续上升，则开卖单；
• 在相反信号出现时平仓。

使用3次多项式对该策略进行测试的结果如下：

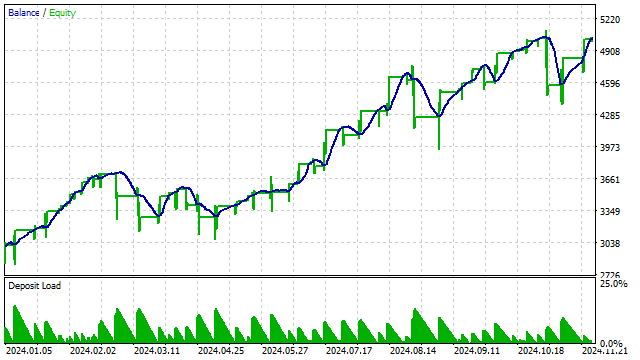
其他指标也可以基于正交多项式来构建。例如，我想构建一个与RSI等效的指标。其原理很简单：首先，我构建一个多项式，然后计算有多少价格位于该多项式之上。基于这个数量，我就可以判断价格是处于超买还是超卖状态。

我用这个指标创建一个简单的策略：

• 如果指标达到超买或超卖水平，则开仓；
• 如果指标回到中心区域，则平仓。

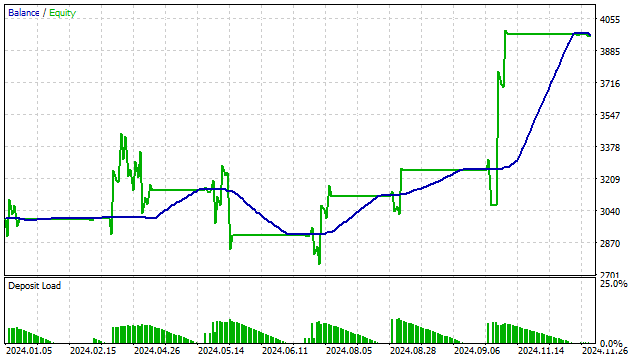
此外，正交多项式还可以集成到各种机器学习算法中。多项式函数的灵活性使机器学习算法能够发现数据中的复杂关系。 

例如，多项式可用于从源数据中生成新的特征。正交多项式能够对时间序列的不同组成部分提供独立的估计。由于这一特性，它们可以减少过拟合。这可以提高训练数据的质量，并提升模型的性能。

你可以任取一个神经网络，并将正交多项式的权重比值输入给它。但在这种情况下，有必要构建一个完整的多项式系统：从1次多项式开始，到N-1次多项式结束，其中N是所处理的价格数量。

结论

正交多项式是分析金融时间序列的强大工具。它们提供了诸多优势，并使我们能够评估市场的变化。在交易策略中使用正交多项式可以提高其效率，并改善交易结果。

撰写本文时使用了以下程序。

名称	类型	说明
正交多项式	指标	在图表上模拟正交多项式 Type - 多项式类型 iPeriod - 多项式周期（不小于2） N - 多项式次数，可接受值为 0 - 9 Shift - 指标偏移
正交多项式EA	EA	实现一种基于价格与多项式交叉的交易策略
正交多项式EA2	EA	实现一种基于两个多项式交叉的交易策略
正交 CCI	指标	CCI指标，其中可以使用正交多项式来替代简单移动平均线
正交 CCI EA	EA	实现一种基于CCI正交变体的策略
正交 RSI	指标	使用正交多项式来确定超买/超卖状况
正交 RSI EA	EA	实现一种基于RSI正交版本的策略