Polynomiale Modelle im Handel

Einführung

Die Effizienz des Handels hängt weitgehend von den Methoden zur Analyse der Marktdaten ab. Eine dieser Methoden sind orthogonale Polynome. Diese Polynome sind mathematische Funktionen, die zur Lösung einer Reihe von Problemen im Zusammenhang mit dem Handel verwendet werden können.

Die bekanntesten orthogonalen Polynome sind die Legendre-, Tschebyscheff-, Laguerre- und Hermite-Polynome. Jedes dieser Polynome hat einzigartige Eigenschaften, die es ermöglichen, sie zur Lösung verschiedener Probleme zu verwenden. Im Folgenden werden einige der wichtigsten Verwendungszwecke genannt:

• Simulation von Zeitreihen. Orthogonale Polynome können zur Beschreibung von Zeitreihen verwendet werden. Ihre Verwendung kann helfen, Trends und andere Muster zu erkennen.
• Regression. Orthogonale Polynome können in der Regressionsanalyse verwendet werden. Ihre Verwendung ermöglicht es uns, die Qualität des Modells zu verbessern und es besser interpretierbar zu machen.
• Vorhersage. Mit Hilfe von orthogonalen Polynomen lassen sich Vorhersagen darüber treffen, wie hoch der Preis sein wird, wenn die derzeitigen Trends anhalten.

Sehen wir uns an, wie orthogonale Polynome in der Praxis angewendet werden können.

Orthogonale Polynome und Indikatoren

Bei der technischen Analyse geht es vor allem darum, Muster in den Kursbewegungen zu erkennen. Finanzielle Zeitreihen enthalten jedoch in der Regel Rauschen, das diese Muster verschleiert. Schauen wir uns an, wie orthogonale Polynome in einem Marktumfeld angewendet werden können.

Der Grundgedanke ist, dass diese Polynome verwendet werden können, um komplexe Signale in einfachere Komponenten zu zerlegen. Diese Zerlegung ermöglicht es uns, Rauschen auszusortieren und Trends zu erkennen.

Als Beispiel werde ich Legendre Polynome verwenden, um einen darauf basierenden Glättungsindikator zu erstellen. Die allgemeine Gleichung dieser Polynome und ihr Definitionsbereich sind durch die folgenden Ausdrücke gegeben:

Ich werde Polynome bis zum 9. Grad verwenden. Dies ist für die Glättung völlig ausreichend, und die Verwendung von Polynomen höheren Grades kann Rauschen hinzufügen und die Haupttrends in der Preisbewegung verbergen. Die hier verwendeten Polynomgleichungen sind in der Tabelle aufgeführt.

n	Legendre-Polynome
0	1
1	x
2	(3*x^2-1)/2
3	(5*x^3-3*x)/2
4	(35*x^4-30*x^2+3)/8
5	(63*x^5-70*x^3+15*x)/8
6	(231*x^6-315*x^4+105*x^2-5)/16
7	(429*x^7-693*x^5+315*x^3-35*x)/16
8	(6435*x^8-12012*x^6+6930*x^4-1260*x^2+35)/128
9	(12155*x^9-25740*x^7+18018*x^5-4620*x^3+315*x)/128

Zunächst muss ich die Preisindizes in den Bereich dieser Polynome umwandeln. Zu diesem Zweck wende ich die Verschiebungsfunktion für jeden i-Index an:

Danach berechne ich die Werte aller Polynome, die mich interessieren, für jeden Wert von x[i]. Ich werde zum Beispiel den Wert eines Polynoms 2. Grades mit der Periode 3 berechnen:

Jetzt muss ich eine Korrektur wegen der diskreten Daten vornehmen. Die Summe der Werte eines Polynoms vom Grad 1 und höher sollte gleich Null sein. Um diese Bedingung zu erfüllen, muss ich die Korrektur berechnen:

Mit dieser Korrektur passe ich die Werte des Polynoms an:

Jetzt beginnt der interessanteste Teil. Jede Zeitreihe kann in eine Summe von Polynomen mit einem bestimmten Gewicht zerlegt werden:

Die Gewichte selbst können wie folgt berechnet werden:

Es sieht seltsam und ein wenig unheimlich aus. Im Grunde ist alles ganz einfach. Nehmen wir ein Polynom vom Grad 0 mit der Periode N. Seine Werte in allen Punkten sind gleich 1. Und sein Gewicht wird sein:

Dies ist die Gleichung des SMA. Die Gewichte von Polynomen höherer Ordnung entsprechen einigen Oszillatoren mit speziell ausgewählten Verhältnissen. Mit anderen Worten: Orthogonale Polynome sind SMA mit einigen geschickt berechneten Ergänzungen. Legendre-Polynome sind sehr robust gegenüber Rauschen und eignen sich hervorragend für Sortieranwendungen. Das Legendre-Polynom ersten Grades sieht zum Beispiel wie folgt aus.

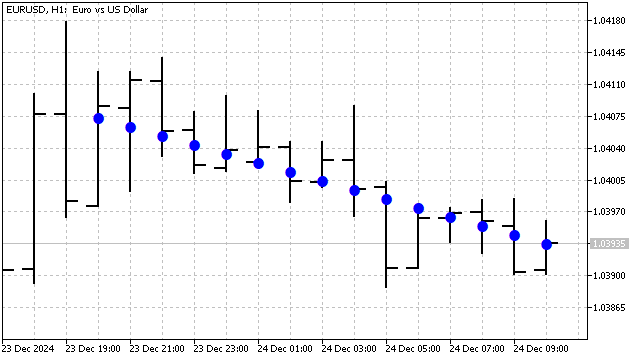
Tschebyschow-Polynome können auch zur Trenderkennung und Glättung verwendet werden. Es gibt zwei Arten von solchen Polynomen. Sie unterscheiden sich voneinander durch ihr Verhalten an den Rändern. Der Hauptvorteil dieser Polynome ist ihre Empfindlichkeit gegenüber plötzlichen Preisänderungen. Die Gleichung für diese Polynome ist sehr einfach:

n	Polynome der ersten Art	Polynome der zweiten Art
0	1	1
1	x	2*x
2	2*x^2-1	4*x^2-1
3	4*x^3-3*x	8*x^3-4*x
4	8*x^4-8*x^2+1	16*x^4-12*x^2+1
5	16*x^5-20*x^3+5*x	32*x^5-32*x^3+6*x
6	32*x^6-48*x^4+18*x^2-1	64*x^6-80*x^4+24*x^2-1
7	64*x^7-112*x^5+56*x^3-7*x	128*x^7-192*x^5+80*x^3-8*x
8	128*x^8-256*x^6+160*x^4-32*x^2+1	256*x^8-448*x^6+240*x^4-40*x^2+1
9	256*x^9-576*x^7+432*x^5-120*x^3+9*x	512*x^9-1024*x^7+672*x^5-160*x^3+10*x

So sieht die Glättung mit dem Tschebyscheff-Polynom 3. Grades aus.

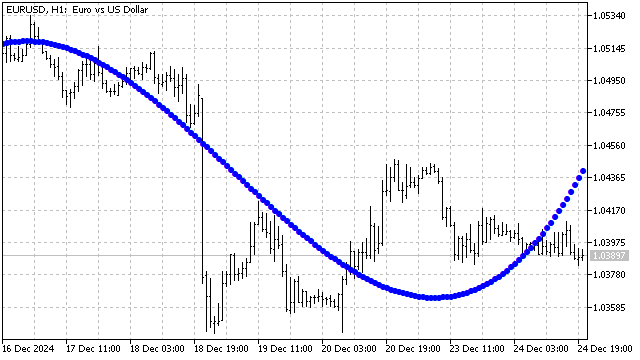
Bisher haben wir Polynome mit dem Definitionsbereich von +/-1 betrachtet, aber es gibt auch Polynome mit anderen Bereichen. Beispielsweise ist das Laguerre-Polynom für alle nichtnegativen Werte des Arguments definiert. Die Gleichung sieht wie folgt aus:

n	Laguerre-Polynome
0	1
1	-x+1
2	(x^2-4*x+2)/2
3	(-x^3+9*x^2-18*x+6)/6
4	(x^4-16*x^3+72*x^2-96*x+24)/24
5	(-x^5+25*x^4-200*x^3+600*x^2-600*x+120)/120
6	(x^6-36*x^5+450*x^4-2400*x^3+5400*x^2-4320*x+720)/720
7	(-x^7+49*x^6-882*x^5+7350*x^4-29400*x^3+52920*x^2-35280*x+5040)/5040
8	(x^8-64*x^7+1568*x^6-18816*x^5+117600*x^4-376320*x^3+564480*x^2-322560*x+40320)/40320
9	(-x^9+81*x^8-2592*x^7+42336*x^6-381024*x^5+1905120*x^4-5080320*x^3+6531840*x^2-3265920*x+362880)/362880

Und die Verschiebung für ihr Argument sieht wie folgt aus:

Diese Änderung führt zu der Tatsache, dass das Verhalten des Laguerre-Polynoms nicht nur vom Grad, sondern auch von seiner Periodenlänge abhängt. Dieses Polynom reagiert empfindlich auf aktuelle Preisänderungen. So sieht zum Beispiel das Laguerre-Polynom fünften Grades auf einem Chart aus:

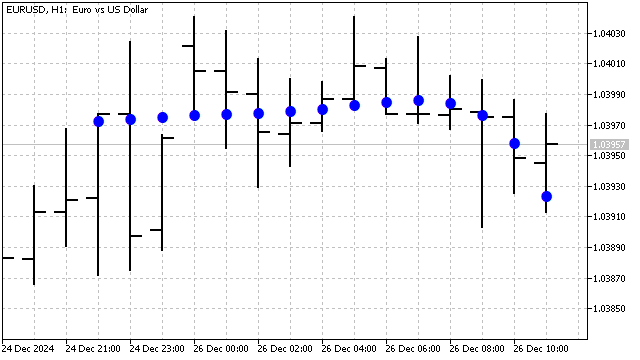
Ein weiteres interessantes Beispiel für Orthogonalität ist das Hermitesches Polynom. Dieses Polynom wird in vielen Bereichen der Mathematik und Physik verwendet. Dieses Polynom ist für beliebige Werte des Arguments definiert, und ihre Gleichungen sehen wie folgt aus:

n	Hermitesches Polynome
0	1
1	x
2	x^2-1
3	x^3-3*x
4	x^4-6*x^2+3
5	x^5-10*x^3+15*x
6	x^6-15*x^4+45*x^2-15
7	x^7-21*x^5+105*x^3-105*x
8	x^8-28*x^6+210*x^4-420*x^2+105
9	x^9-36*x^7+378*x^5-1260*x^3+945*x

Die Verschiebefunktion zentriert die Preiswerte:

Als Ergebnis haben wir einen Glättungsfilter erhalten, dessen Effizienz vom Grad des Polynoms und seiner Periode abhängt.

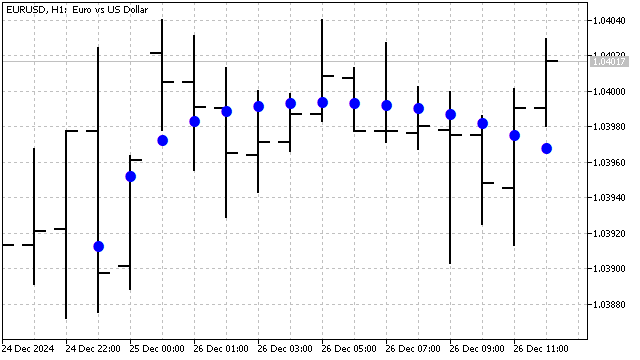
Wir haben die grundlegenden klassischen orthogonalen Polynome betrachtet. Aber es ist durchaus möglich, eine eigene Version solcher Polynome zu erstellen. Ein Polynom, das die Vorteile des Tschebyscheff- und des Hermite-Polynoms vereint, ist beispielsweise durch die folgende Gleichung gegeben:

n	Tschebyscheff-Hermit-Polynome
0	1
1	2*x
2	4*x^2-2
3	8*x^3-12*x
4	16*x^4-48*x^2+12
5	32*x^5-160*x^3+120*x
6	64*x^6-480*x^4+720*x^2-120
7	128*x^7-1344*x^5+3360*x^3-1680*x
8	256*x^8-3584*x^6+13440*x^4-13440*x^2+1680
9	512*x^9-9216*x^7+48384*x^5-80640*x^3+30240*x

Dieses Polynom ist empfindlich gegenüber nichtlinearen Trends – quadratisch, kubisch usw. So sieht das Tschebyscheff-Hermite-Polynom 9. Grades in einer Grafik aus:

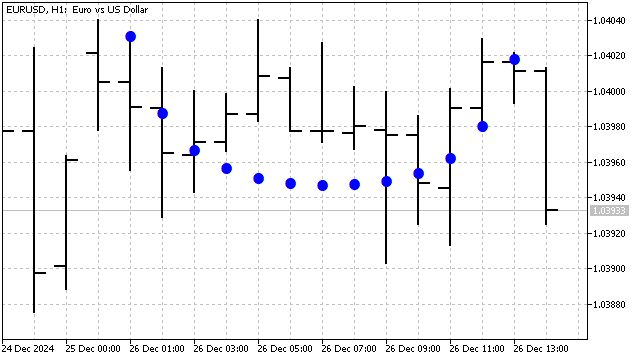
Die Verwendung von orthogonalen Polynomen bietet eine Reihe von Vorteilen.

• Stabilität und De-Korrelation. Die Orthogonalität der Polynome gewährleistet ihre Stabilität gegenüber Änderungen der Modellparameter. Jedes Polynom ist unabhängig von den anderen, wodurch jede Komponente der Zeitreihe separat modelliert und untersucht werden kann.
• Interpretierbarkeit. Jedes orthogonale Polynom entspricht einem eigenen Modell des Preisverhaltens. Die Gewichtungsverhältnisse der Polynome ermöglichen es uns, die wichtigsten Modelle zu identifizieren und uns auf sie zu konzentrieren.
• Anpassungsfähigkeit und Effizienz. Orthogonale Polynome werden an bestimmte Werte der Zeitreihe angepasst. Das Auftreten neuer Preise führt zu einer Änderung der Gewichtungsrelationen, wodurch sich das Polynommodell an die aktuelle Marktlage anpasst. Und die Verwendung nichtlinearer Polynome macht diese Anpassung effizient.

Das einzige Merkmal orthogonaler Polynome, das als Nachteil angesehen werden kann, ist, dass diese Polynome alle Preise innerhalb des Polynoms behandeln. Mit anderen Worten: Ein auf solchen Polynomen aufgebauter Indikator „zeichnet". Meiner Meinung nach ist diese Eigenschaft kein Nachteil – der Indikator findet einfach den besten Näherungswert, wenn neue Daten eintreffen.

Die Verwendung von orthogonalen Polynomen bringt einige Einschränkungen mit sich. Die Indikatorperiode sollte größer sein als der Grad des Polynoms. Für praktische Zwecke können wir uns auf den 3. Grad des Polynoms beschränken. Dieser Indikator kombiniert SMA, linearen Trend und zwei Parabeln – quadratisch und kubisch. Dies reicht aus, um recht komplexe Situationen zu glätten. Indem wir die Indikatorperiode erhöhen, können wir aber auch den Grad des Polynoms erhöhen.

Betrachten wir nun einige Beispiele für die Anwendung von orthogonalen Polynomen im Handel.

Handelsstrategien

Auf der Grundlage orthogonaler Polynome können Händler verschiedene Handelsstrategien entwickeln. Mit Hilfe der polynomialen Regression, die auf orthogonalen Polynomen basiert, kann ein Händler beispielsweise nicht nur vergangene Kursbewegungen analysieren, sondern auch ein Modell erstellen, das sich an aktuelle Marktveränderungen anpassen kann.

Betrachten wir als Beispiel mehrere Handelsstrategien, die auf Abweichungen vom Mittelwert basieren.

Nehmen wir die einfachste Strategie: Positionen werden eröffnet, wenn der Kurs den SMA kreuzt. Wir werden den gleitenden Durchschnitt durch ein orthogonales Polynom ersetzen, wobei die Regeln für die Eröffnung und Schließung von Positionen unverändert bleiben:

• Der Preis kreuzt das Polynom von unten nach oben – Öffnen Sie eine Kaufposition, schließen Sie eine Verkaufsposition.
• Der Preis kreuzt das Polynom von oben nach unten – Öffnen Sie eine Verkaufsposition, schließen Sie eine Kaufposition.

Trotz ihrer Einfachheit ist diese Strategie recht effizient.

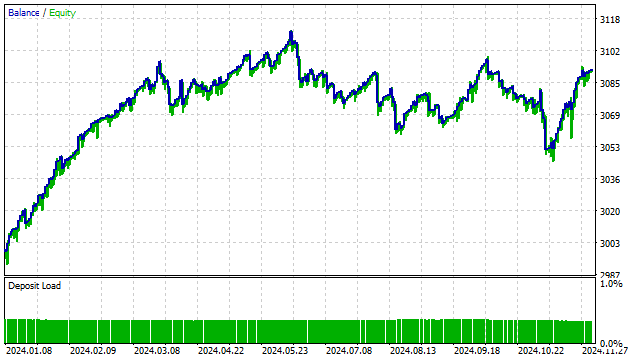
Wir wollen diese Strategie etwas komplizierter gestalten und den Preis durch den Wert eines Polynoms ersetzen. Mit anderen Worten, wir erhalten ein Analogon der Strategie mit dem Schnittpunkt von zwei SMAs. Das Ergebnis ist einigermaßen vorhersehbar: Von allen möglichen Optionen bevorzugte der Strategieoptimierer orthogonale Polynome.

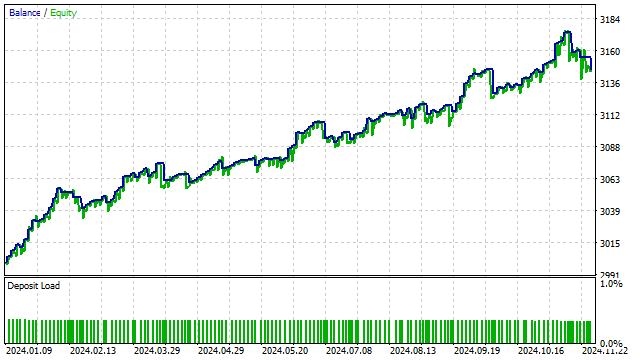
Polynomiale Modelle können auch für komplexere Strategien verwendet werden. Wenn die Strategie irgendwelche Indikatoren verwendet, können Sie versuchen, diese durch orthogonale Polynome zu ersetzen. Ein solcher Ersatz könnte die Strategie verbessern.

Ich werde den Indikator Commodity Channel Index (CCI) als Beispiel verwenden. Die klassische Gleichung sieht wie folgt aus:

Ich werde einige kleinere Änderungen an diesem Indikator vornehmen. Wie ich bereits sagte: SMA ist ein Polynom vom Grad 0. Anstelle von SMA werde ich ein orthogonales Polynom beliebigen Grades verwenden. Dementsprechend werde ich die mittlere absolute Abweichung relativ zu diesem Polynom berechnen. Der daraus resultierende Indikator sieht wie folgt aus:

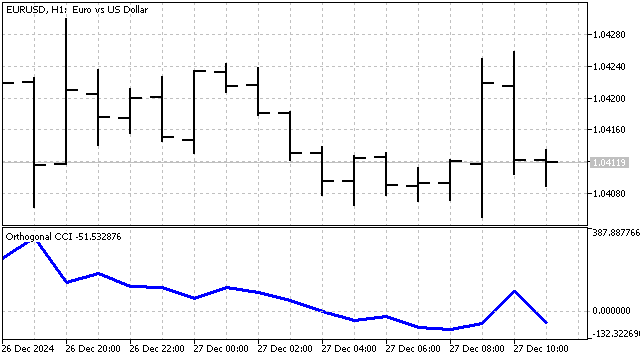
Die Handelsstrategie wird der klassischen ähneln:

• eine Kaufposition eröffnen, wenn der Indikator unter dem angegebenen Niveau liegt und weiter sinkt;
• eine Verkaufsposition eröffnen, wenn der Indikator über dem angegebenen Niveau liegt und weiter steigt;
• Positionen bei einem entgegengesetzte Signal schließen.

Das Ergebnis der Prüfung einer solchen Strategie mit einem Polynom 3. Grades:

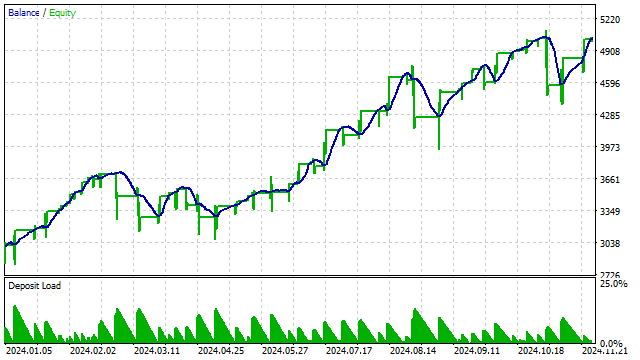
Auch andere Indikatoren können auf der Grundlage orthogonaler Polynome konstruiert werden. Ich möchte zum Beispiel ein Äquivalent zum RSI konstruieren. Das Prinzip ist einfach: Zuerst bilde ich ein Polynom, und dann zähle ich, wie viele Preise oberhalb dieses Polynoms liegen. Aus dieser Zahl schließe ich, dass der Kurs überkauft/überverkauft ist.

Ich verwende den Indikator, um eine einfache Strategie zu entwickeln:

• eine Position eröffnen, wenn der Indikator das überkaufte oder überverkaufte Niveau erreicht hat;
• Positionen schließen, wenn der Indikator in der Mitte steht.

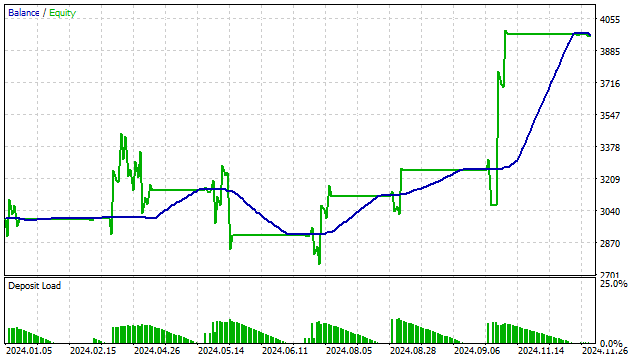
Außerdem können orthogonale Polynome in verschiedene Algorithmen des maschinellen Lernens integriert werden. Die Flexibilität von Polynomfunktionen ermöglicht es Algorithmen für maschinelles Lernen, komplexe Beziehungen in Daten zu erkennen. 

Zum Beispiel können Polynome verwendet werden, um neue Merkmale aus den Quelldaten zu erzeugen. Orthogonale Polynome liefern unabhängige Schätzungen der verschiedenen Komponenten einer Zeitreihe. Aufgrund dieser Eigenschaft können sie die Überanpassung reduzieren. Dies kann die Qualität der Trainingsdaten verbessern und die Leistung der Modelle steigern.

Man nehme ein beliebiges neuronales Netz und füttere es mit den Werten der Gewichtungsverhältnisse der orthogonalen Polynome. In diesem Fall ist es jedoch erforderlich, ein vollständiges System von Polynomen zu konstruieren, das mit einem Polynom 1. Grades beginnt und mit N-1 endet, wobei N die Anzahl der verarbeiteten Preise ist.

Schlussfolgerung

Orthogonale Polynome sind ein leistungsfähiges Instrument zur Analyse von Finanzzeitreihen. Sie bieten eine Reihe von Vorteilen und ermöglichen es uns, Veränderungen auf dem Markt zu bewerten. Die Verwendung orthogonaler Polynome in Handelsstrategien kann deren Effizienz und die Handelsergebnisse verbessern.

Die folgenden Programme wurden bei der Erstellung dieses Artikels verwendet.

Name	Typ	Beschreibung
Orthogonale Polynome	Indikator	simuliert orthogonale Polynome auf einem Graphen Type – Polynomtyp iPeriod – Periodenlänge des Polynoms (nicht kleiner als 2) N – Grad des Polynoms, zulässige Werte 0 – 9 Shift – Indikatorverschiebung
EA Orthogonal polynomials	EA	implementiert eine Handelsstrategie, die auf dem Schnittpunkt von Preis und Polynom basiert
EA Orthogonal polynomials 2	EA	setzt eine Strategie für den Schnittpunkt zweier Polynome um
Orthogonal CCI	Indikator	CCI, bei dem orthogonale Polynome anstelle von SMA verwendet werden können
EA Orthogonal CCI	EA	setzt eine Strategie um, die auf der orthogonalen Variante der CCI basiert
Orthogonal RSI	Indikator	bestimmt überkaufte/überverkaufte Bedingungen mithilfe orthogonaler Polynome
EA Orthogonal RSI	EA	setzt eine Strategie um, die auf der orthogonalen Version des RSI basiert