MQL5 Wizard Techniques you should know (Part 51): Reinforcement Learning with SAC

Introduction

Soft Actor Critic (SAC) is yet another reinforcement learning algorithm that we are considering, having looked at a few already that included proximal policy optimization, deep-Q-networks, SARSA, and others. This algorithm though, like some that we have already looked at, uses neural networks, but with some important caveat. The total number of networks used are three, and these are: 2 critic networks and an actor network. The two critic networks make reward forecasts (Q-Values) when inputted with an action and an environment state, and the minimum of the outputs of these 2 networks is used in modulating the loss function used for training the actor network.

The inputs to the actor network are environment state coordinates, with the output being 2-fold. A mean vector, and a log-standard-deviation vector. By using the Gaussian process, these two vectors are used to derive a probability distribution for the possible actions open to the actor. And so, while the 2 critic networks can be trained traditionally, the actor network clearly is a different kettle of fish. There is quite a bit to get into here, so let’s first reiterate the basics before going any further. The two critic networks for input take the current state of the environment and an action. Their output is an estimate of the expected return (Q-value) for taking that action in that state. The use of two critics helps in reducing overestimation bias, a common problem with Q-learning.

The actor network has the current environment state as its input. Its output is effectively a probability distribution over possible actions, with this distribution being stochastic so as to encourage exploration. I use the phrase ‘effectively’ because the actual outputs of the actor network are two vectors that need to be fed to a Gaussian probability distribution to get the weights of each action. In MQL5, we accomplish this as follows:

//+------------------------------------------------------------------+
// Function to compute the Gaussian probability distribution and log
// probabilities
//+------------------------------------------------------------------+
vectorf CSignalSAC::LogProbabilities(vectorf &Mean, vectorf &Log_STD)
{  vectorf _log_probs;
   // Compute standard deviations from log_std
   vectorf _std = exp(Log_STD);
   // Sample actions and compute log probabilities
   float _z = float(rand() % USHORT_MAX / USHORT_MAX); // Generate N(0, 1) sample
   // Sample action using reparameterization trick: action = mean + std * N(0, 1)
   vectorf _actions = Mean + (_std * _z);
   // Compute log probability of the sampled action
   vectorf _variance = _std * _std;
   vectorf _diff = _actions - Mean;
   _log_probs = -0.5f * (log(2.0f * M_PI * _variance) + (_diff * _diff) / _variance);
   return(_log_probs);
}

How SAC Works

With that said, SAC works like most reinforcement learning algorithms. First there is action selection where the actor samples an action from the probability distribution of the actor network outputs. This is followed by ‘environment interaction’ where the agent takes the sampled action in the environment and performs an observation of its next state and reward. This is then followed by the critic update, where the two critic networks are updated by a loss function that uses a comparison between predicted Q-values and target Q-values. However, as already noted above the actor network update is a novelty in that it is updates using a policy gradient that aims to maximize expected return, by taking into consideration the entropy of the policy distribution. This is meant to encourage exploration and prevent premature convergence to suboptimal solutions.

Entropy of policy distribution in SAC measures the randomness or uncertainty. In SAC, higher entropy corresponds to more exploration actions while lower entropy is meant to emphasize deterministic choices. The outputs for the actor network in SAC are inherently a stochastic policy which is parametrized by a probability distribution, which in our case (for this article) is the Gaussian distribution. The entropy of this distribution paints a picture of the actions an agent might take when presented with a specific state (the inputs).

The significance of this is to encourage agent exploration, as is typical with most reinforcement learning algorithms, so as to reduce the risk of premature convergence to suboptimal policies. This therefore creates an exploration-exploitation balance. SAC incorporates an entropy term into its policy optimization objective so as to maximize both expected rewards and entropy. The objective equation is as follows:

Where:

• α: Entropy temperature, balancing reward maximization and exploration.
• logπ(a∣s): Log-probability of the action, (the output of our function whose code is shared above) which depends on both μ and log(σ).
• Q(s,a): Is the minimum Q-value of the two outputs of the critic networks.

Higher entropy tends to lead to more robust decision-making in environments with incomplete information, since it prevents over-fitting to particular scenarios. So, maximizing entropy is a good thing in SAC. Besides improved exploration since the agent is encouraged to try a wider range of actions or the avoiding of suboptimal policies that prevent getting stuck in local optima, it inherently serves as a form of regularization by preventing overly deterministic policies that are prone to fail in unforeseen scenarios. Also, gradual entropy adjustments often lead to smoother policy updates, ensuring stable training and convergence.

The temperature controlling parameter is very sensitive to the entropy and learning process of the actor network that it is worth mentioning why. For our purposes we are fixing this at 0.5 as can be seen in the Logarithm probabilities function, whose MQL5 code is shared above. However, the temperature parameter alpha dictates how much weight is given to energy in the objective. As higher alpha encourages exploration while a lower value promotes deterministic policies or exploitation. So, assigning this as 0.5, for our purposes, does strike a form of balance.

It is often the case, though, that SAC uses an automatic entropy tuning mechanism that dynamically adjusts alpha to maintain a target entropy level, adapting a balance between exploration and exploitation. The practical implications of this are: robust learning across tasks; creation of generalization policies that are adept with incomplete information (stochastic policies); and the provision of a foundation for continual learning. The potential trade-offs of this are majorly two. Too much exploration and computational cost.

Excessive entropy can lead to inefficient learning through the over emphasis of exploratory actions at the cost of exploiting known high-reward strategies. This will always come on the back of calculating and optimizing entropy terms, which add computational overhead compared to algorithms that just focus on reward maximization. The actor network outputs two vectors MU and Log-STD as mentioned above, so how do these affect this entropy?

MU represents the central tendency of the policy’s action distribution. It does not directly affect entropy, however it in a sense defines the mean behaviour of the policy. The Log-STD, on the other hand, controls the spread or uncertainty of the action distribution and directly influences entropy. A higher Log-STD means a broader, more uncertain action distribution, while a lower Log-STD points to the opposite. What then does the magnitude of a given action in the Log-STD have to do with likelihood of selection?

The specifics are determined by the Gaussian process, as already mentioned, however a low Log-STD often implies the actor network is confident about the optimal action, MU. This often implies less variability in sampled actions. Actions sampled will be more tightly concentrated around the corresponding MU value of this action that has a low Log-STD reading, which would encourage more exploitation of policies around this action. So, while low Log-STD readings do not directly make an action more likely, it in essence narrows the scope of potential actions, thus increasing the chance of actions close to MU being chosen.

There are also some practical adjustments that are often applied to entropy. Firstly, since Log-STD directly determines entropy, for stable training SAC typically bounds log(σ) within a range to avoid extremely high or low entropy. This is done with the ‘z’ parameter shown in our Log Probabilities function above. Secondly the tuning of alpha, (which we set to 0.5f, in our Log Probabilities function) is crucial in striking the explore-exploit balance as mentioned. To this end, quite often automatic alpha adjustment is used as a means of dynamically striking an exploitation-exploration balance.

This is achieved by using an entropy target H. The equation below defines this:

Where:

• alpha (α t ): Is the current temperature that controls the weight of the entropy term in the objective, with higher values encouraging exploration while smaller values lean to exploitation.

• alpha (αt+1 ): Is the updated temperature parameter after feedback from the current entropy relative to the target has been included.

• lambda (λ): Is a learning rate for the alpha adjustment process that controls how quickly alpha adapts to deviations from the entropy target H.

• E (E a~π ): Is the expectation from actions sampled from the current policy plan.

• Log(a|s): Is the Log probability for the action-a at state-s under the current policy. It quantifies uncertainty of the policy’s action selection.

• H target : Serves as the target entropy value of the policy. It is often assigned based on the action space’s dimensionality (number & scope of available actions) in cases where the actions are discrete such as the (buy, sell, hold implementations we have considered this far); it can also be scaled if the actions are continuous (for example if we were to have 2 dimensioned market orders both scaled from 0.01 to 0.10 for position sizing of two securities to be bought concurrently with values being a percentage of free margin).

So, the use of automatic alpha adjustment, even though not explored in our implementation for this article ensures the agent adapts dynamically to changes in the environment, omits the need for manual alpha tuning, and promotes efficient learning through the maintenance of a preset exploration-exploitation tradeoff.

SAC vs DQN comparison

We have so far considered another reinforcement learning algorithm that uses a single neural network, namely the Deep-Q-Networks, so what advantages if any are in the offing for using SAC with its multiple networks? To make the case for SAC, let’s consider a use case scenario of a Robot manipulation task. So, here is the task: a robotic-arm is required to hold and move objects to specified target locations. The joints of its arms would be assigned continuous action spaces that quantify necessary torque and angle adjustments, etc.

The challenges with using a DQN in this case is that firstly, DQN is best suited for discrete action spaces. Trying to extend it to accommodate a continuous space would lead to an exponential growth in the number of available discrete actions for higher dimensional action spaces, making training too expensive and inefficient. DQNs also rely on epsilon-greedy strategies at balancing exploration and exploitation, and these may struggle to work efficiently in the discretized higher dimension spaces. Finally, DQN is prone to overestimation bias which could lead to some instability when training, especially in complex environments with high variability in reward.

SAC would be better suited in this case, primarily for its continuous action space support. This is manifest in the way SAC optimizes stochastic policy over continuous action spaces, which eliminates the need for action discretization (or classification). This leads to smooth and precise control of the robot’s arm. The three networks in SAC work in synergy, where the actor network generates a stochastic policy to set the distribution (probabilistic weighting) of the continuous actions. This promotes efficiency while also avoiding premature exploration.

On their part, the critic networks, engage a twin Q-value estimation method that helps avoid the over estimation bias by forwarding the minimum-value in back propagating to the actor network. This stabilizes training and ensures more accurate results. In summary, the entropy-augmented objective that encourages more exploration (especially when paired with automatic temperature tuning as argued above with alpha) plus the robustness and stability afforded by SAC’s ability to deal with high dimensional action spaces do clearly put it a step above DQN. To this end, publicized performance examples of Open AI’s Gym Reacher and Fetch tasks clearly indicate that DQN struggles to produce smooth arm motions because of its discretized action outputs and poor exploration, with policies converging a lot t suboptimal strategies. On the other hand, SAC does generate smooth precise actions, with a stochastic policy which leads to faster task completion, fewer collisions, and better adaptation to the changing of object positions or target locations, again thanks to the stochastic policy approach.

Python and TensorFlow

For this article, unlike the past machine learning pieces, we are taking a plunge into Python’s TensorFlow. MQL5, the parent language by MetaQuotes obviously remains relevant as the wizard assembled Expert advisors rely on it a lot. For new readers, there are guides here and here on how to use the code attached at the end of this article to assemble an Expert Advisor. Python though is certainly encroaching on MQL5’s relevance and dominance as the go-to programming language when developing financial models. A quick reconnaissance could indicate that MetaQuotes needs to simply put out more libraries out on python in order to keep apace with innovation and to continue to reassert their dominance. 

However, I am old enough to remember the introduction of MetaTrader 5 in 09(?). And the painstakingly slow adoption they received from their customers despite all the advantages it offered. I can therefore empathize why they would be hesitant with rolling out and maintaining active libraries on python. With that said, the innovations being fronted here are mostly from the ‘customers’ (i.e. the python community) and not MetaQuotes as was the case with MetaTrader 5 where positions as opposed to orders were being rolled out. So, perhaps they need to heed this with some urgency? Time will tell but in the meantime the efficiency benefits of using not just TensorFlow, but even PyTorch when not only developing but most importantly training networks is actually gargantuan!

In my opinion, MetaQuotes can explore corporate sponsorships, becoming a contributor, or even creating fork projects for the key python libraries of Pandas, NumPy, and Sci-Kit; and among other things allow the reading of its highly compressed file formats of *.*hcc, and *.*tkc. But these are general thoughts, returning to TensorFlow though firstly, it offers advanced deep learning capabilities that are primarily two-fold. On the software front and on the GPU/ hardware end.  

MQL5 does support OpenCL, so it can be argued the two languages could go toe to toe, however the same can certainly not be said about Python’s advanced libraries and tools for building, training and optimizing deep learning models. These libraries include support for complex architectures like SAC via TensorFlow Agents.

It also features rich ecosystem with prebuilt tools such as stable -baseline for furthering reinforcement learning (besides tensor-agents); allows flexibility & experimentation since one can rapidly prototype and test a wide variety of model implementations; Is highly reproducible and easily debugged (especially when one engages tools like Tensor-Board for visualizing and training matrices/kernels; It offers interoperability with exportable formats like ONNX; and has a very vast and growing community support plus regular updates.

SAC can be implemented in python in arguably a wide variety of ways. For purposes of illustrating the core principles, we will just dwell on two approaches. The first of these manually defines the three principal networks of SAC and by using for loop iterations(s) trains and tests the SAC model. The second uses the already mentioned tensor-agents that come with the python library and are specifically meant to aid in reinforcement learning.

The steps in the manual iterative approach are: designing the SAC components in TensorFlow/ Keras where for the actor network this involves defining a neural network that outputs a stochastic policy for Gaussian Sampling; for the critic networks this means constructing 2 Q-value networks for twin Q-learning to manage the over estimation bias; and the defining of n entropy regularization regime for efficient exploration. For our purposes as mentioned above our entropy is utilizing a fixed value of alpha at 0.5. The opening source that covers these is as follows:

import numpy as np
import pandas as pd

from sklearn.model_selection import train_test_split

import tensorflow as tf

print("Num GPUs Available: ", len(tf.config.list_physical_devices('GPU')))

from tensorflow.keras import optimizers
from tensorflow.keras.layers import Input
from tensorflow.keras import layers
from tensorflow import keras
import tf2onnx
import onnx

import os

# Define the actor network
def ActorNetwork(state_dim, action_dim, hidden_units=256):
    """
    Creates a simple SAC actor network.
    
    :param state_dim: The dimension of the state space.
    :param action_dim: The dimension of the action space.
    :param hidden_units: The number of hidden units in each layer.
    :return: A Keras model representing the actor network.
    """
    # Input layer
    state_input = layers.Input(shape=(state_dim, ))
    
    # Hidden layers (Dense layers with ReLU activation)
    x = layers.Dense(hidden_units, activation='relu')(state_input)
    x = layers.Dense(hidden_units, activation='relu')(x)
    
    # Output layer: output means (mu) and log standard deviation (log_std) for Gaussian distribution
    
    output_size = action_dim + action_dim
    stacked_mean_logs = layers.Dense(output_size)(x)
    
    # Create the model

    actor_model = tf.keras.Model(inputs=state_input, outputs=stacked_mean_logs)
    
    return actor_model

# Define the critic network
def CriticNetwork(state_dim, action_dim, hidden_units=256):
    """
    Creates a simple SAC critic network (Q-value approximation).
    
    :param state_dim: The dimension of the state space.
    :param action_dim: The dimension of the action space.
    :param hidden_units: The number of hidden units in each layer.
    :return: A Keras model representing the critic network.
    """
    
    input_size = state_dim + action_dim
    state_action_inputs = layers.Input(shape=(None, input_size, 1))  # Concatenate state and action
    
    # Hidden layers (Dense layers with ReLU activation)
    x = layers.Dense(hidden_units, activation='relu')(state_action_inputs)
    x = layers.Dense(hidden_units, activation='relu')(x)
    
    # Output layer: Q-value for the given state-action pair
    q_value_output = layers.Dense(1)(x)  # Single output for Q-value
    
    # Create the model 
    critic_model = tf.keras.Model(inputs=state_action_inputs, outputs=q_value_output)
    
    return critic_model

After this, we would need to train the SAC model in TensorFlow/ Keras. This would typically involve using an old MetaTrader 5 library to import MetaTrader 5 data from the MetaTrader terminal, and then parcelling this data into testing and training data. We’re using a two-thirds training ratio, which leaves one-third for testing. We simulate the trade setup of MetaTrader 5 in a tedious and highly inefficient for loop that is as expected sized to a number of epochs and the training data size. Furthermore, we aim to optimize the actor and critic networks with the SAC objective function, including the entropy term. The code involved in this is shared below:

# Filter the DataFrame to keep only the '<state>' column
df = pd.read_csv(name_csv)

states = df.filter(['<STATE>']).astype(int).values
# Extract the '<state>' column as an integer array
rewards = df.filter(['<REWARD>']).values

states_size = int(len(states)*(2.0/3.0))
actor_x_train = states[0:states_size,:]
actor_x_test = states[states_size:,:1]
rewards_size = int(len(rewards)*(2.0/3.0))
critic_y_train = rewards[0:rewards_size,:]
critic_y_test = rewards[rewards_size:,:1]

# Initialize networks and optimizers
input_dim = 1  # 2 states, of 3 gradations are flattened into a single index
output_dim = 3  # possible actions buy, sell, hold
actor = ActorNetwork(input_dim, output_dim)
critic1 = CriticNetwork(input_dim, output_dim)  # Input paired with action
critic2 = CriticNetwork(input_dim, output_dim)  # Input paired with action

critic_optimizer_1 = tf.keras.optimizers.Adam(learning_rate=0.001)
critic_optimizer_2 = tf.keras.optimizers.Adam(learning_rate=0.001)
actor_optimizer = tf.keras.optimizers.Adam(learning_rate=0.001)

# Training loop
for e in range(epoch_size):
    train_critic_loss1 = 0
    train_critic_loss2 = 0
    train_actor_loss = 0
    
    for i in range(actor_x_train.shape[0]):
        input_state = tf.expand_dims(actor_x_train[i], axis=0)  # Select a single sample and maintain batch dim
        target_q = tf.expand_dims(critic_y_train[i], axis=0)

        # Actor forward pass and sampling
        with tf.GradientTape(persistent=True) as tape:

            actor_output = actor(input_state)
            # Split the vector into mean and log_std
            mu = actor_output[:, :output_dim]     # First 3 values
            log_std = actor_output[:, output_dim:]  # Last 3 values
            std = tf.exp(log_std)
            sampled_action = tf.random.normal(shape=mu.shape, mean=mu, stddev=std)  # Sample action from Gaussian

            # Concatenate the state and action tensors
            in_state = tf.convert_to_tensor(tf.cast(input_state, dtype=tf.float32), dtype=tf.float32)  # Ensure it's a tensor
            in_action = tf.convert_to_tensor(tf.cast(sampled_action, dtype=tf.float32), dtype=tf.float32)
            
            # Concatenate along the last axis
            critic_raw_input = tf.concat([in_state, in_action], axis=-1)  # Ensure correct axis
            critic_input = tf.reshape(critic_raw_input, [-1, 1, 4, 1])  # -1 infers the batch size dynamically

            q_value1 = critic1(critic_input)
            q_value2 = critic2(critic_input)

            # Critic loss (mean squared error)
            critic_loss1 = tf.reduce_mean((tf.cast(q_value1, tf.float32) - tf.cast(target_q, tf.float32)) ** 2)
            critic_loss2 = tf.reduce_mean((tf.cast(q_value2, tf.float32) - tf.cast(target_q, tf.float32)) ** 2)

            # Actor loss (maximize expected Q-value based on minimum critic output)
            min_q_value = tf.minimum(q_value1, q_value2)  # Take the minimum Q-value
            actor_loss = tf.reduce_mean(min_q_value)  # Maximize expected Q-value (negative for minimization)

        # Backpropagation
        critic_gradients1 = tape.gradient(critic_loss1, critic1.trainable_variables)
        critic_gradients2 = tape.gradient(critic_loss2, critic2.trainable_variables)
        actor_gradients = [-grad for grad in tape.gradient(actor_loss, actor.trainable_variables)]

        del tape  # Free up resources from persistent GradientTape
        
        critic_optimizer_1.apply_gradients(zip(critic_gradients1, critic1.trainable_variables))
        critic_optimizer_2.apply_gradients(zip(critic_gradients2, critic2.trainable_variables))
        actor_optimizer.apply_gradients(zip(actor_gradients, actor.trainable_variables))
        
        # Accumulate losses for epoch summary
        train_critic_loss1 += critic_loss1.numpy()
        train_critic_loss2 += critic_loss2.numpy()
        train_actor_loss += actor_loss.numpy()

    print(f"  Epoch {e + 1}/{epoch_size}:")
    print(f"  Train Critic Loss 1: {train_critic_loss1 / actor_x_train.shape[0]:.4f}")
    print(f"  Train Critic Loss 2: {train_critic_loss2 / actor_x_train.shape[0]:.4f}")
    print(f"  Train Actor Loss: {train_actor_loss / actor_x_train.shape[0]:.4f}")
    print("-" * 40)

critic2.summary()
critic1.summary()
actor.summary()

Post-training, we would be open to exporting our model, that comprises three networks, into ONNX. ONNX which s an abbreviation of Open Neural Network Exchange provides an open standard for machine learning interoperability where models trained in python using various libraries like PyTorch or SciKit-Learn can be exported to this format for use across a wider variety of platforms and programming languages of which is MQL5. This compatibility removes the need to replicate complex machine learning logic, which saves on time and reduces on errors.

Importation of ONNX as a resource allows for the compilation of a single ex5 file that includes the ONNX machine learning model and MQL5 trade execution logic, so traders do not have to grapple with multiple files. With that said, the export process from python to ONNX has. Number of options, one of which is tf2onnx, but it is not the only one as there are: onnxmltools, skl2onnx, transformers.onnx (for hugging face), and mxnet.contrib.onnx.  What is crucial at the export stage though is to ensure that the input and output layers’ shapes of each network are properly logged and recorded because in MQL5 this information is crucial in accurately initializing the respective ONNX handles for each network. We do this as follows:

# Check input and output layer shapes for importing ONNX
import onnxruntime as ort

session_critic2 = ort.InferenceSession(path_critic2_onnx)
session_critic1 = ort.InferenceSession(path_critic1_onnx)
session_actor = ort.InferenceSession(path_actor_onnx)

for i in session_critic2.get_inputs():
    print(f"in critic2 Name: {i.name}, Shape: {i.shape}, Type: {i.type}")

for i in session_critic1.get_inputs():
    print(f"in critic1 Name: {i.name}, Shape: {i.shape}, Type: {i.type}")

for i in session_actor.get_inputs():
    print(f"in actor Name: {i.name}, Shape: {i.shape}, Type: {i.type}")
    

for o in session_critic2.get_outputs():
    print(f"out critic2 Name: {o.name}, Shape: {o.shape}, Type: {o.type}")

for o in session_critic1.get_outputs():
    print(f"out critic1 Name: {o.name}, Shape: {o.shape}, Type: {o.type}")

for o in session_actor.get_outputs():
    print(f"out actor Name: {o.name}, Shape: {o.shape}, Type: {o.type}")

The performance of the python code with this implementation that uses for loops as indicated above is far from efficient, in fact, it is very similar to MQL5 because the use of tensors/ graphs is not properly capitalized on. It, however, is necessary in that the TensorFlow fit function that often is used to harness the training efficiencies of TensorFlow would not have been applicable in this case given the fact that in backpropagation, the outputs of the 2 critic networks (the Q values) are used to train the actor network. The actor network does not have target vectors or target dataset like the critic networks or most typical neural network.

The second approach for implementing this uses tensor-agents, which are inbuilt libraries for handling reinforcement within TensorFlow and python. We look at this in proper depth in upcoming articles, but suffice to say the initialization does not just cover the constituent networks but also considers the environment and the agents. Crucial aspects to Reinforcement Learning that could be overlooked if one is overly focused on network training efficiency.

Combining with MQL5

We do import our exported ONNX models into MQL5 s resources, which presents us with the following header to our custom signal class file.

//+------------------------------------------------------------------+
//|                                                    SignalSAC.mqh |
//|                   Copyright 2009-2017, MetaQuotes Software Corp. |
//|                                              http://www.mql5.com |
//+------------------------------------------------------------------+
#include <Expert\ExpertSignal.mqh>
#include <My\Cql.mqh>
#resource "Python/EURUSD_H1_D1_critic2.onnx" as uchar __CRITIC_2[]
#resource "Python/EURUSD_H1_D1_critic1.onnx" as uchar __CRITIC_1[]
#resource "Python/EURUSD_H1_D1_actor.onnx" as uchar __ACTOR[]
#define  __ACTIONS 3
#define  __ENVIONMENTS 3

The data we exported to python was for the symbol EURUSD on the hourly time frame from 2023.12.12 to 2024.12.12. The training was for two thirds of the time, which comes to eight months, meaning we trained from 2023.12.12 to 2024.08.12. We can therefore run tests going forward from 2024.08.12. This comes to a period barely over 4 months, which is really not that long but because we are using the 1-hour timeframe, it could be significant.

Since the back propagation is already done in python, we're including no special input parameters for optimization on these forwards walk run. Our class interface therefore is as follows:

//+------------------------------------------------------------------+
//| SACs CSignalSAC.                                                 |
//| Purpose: Soft Actor Critic for Reinforcement-Learning.           |
//|            Derives from class CExpertSignal.                     |
//+------------------------------------------------------------------+
//+------------------------------------------------------------------+
//|                                                                  |
//+------------------------------------------------------------------+
class CSignalSAC   : public CExpertSignal
{
protected:

   long                          m_critic_2_handle;
   long                          m_critic_1_handle;
   long                          m_actor_handle;

public:
   void                          CSignalSAC(void);
   void                          ~CSignalSAC(void);

   //--- methods of setting adjustable parameters

   //--- method of verification of arch
   virtual bool      ValidationSettings(void);
   //--- method of creating the indicator and timeseries
   virtual bool      InitIndicators(CIndicators *indicators);
   //--- methods of checking if the market models are formed
   virtual int       LongCondition(void);
   virtual int       ShortCondition(void);

protected:
   vectorf           GetOutput();
   vectorf           LogProbabilities(vectorf &Mean, vectorf &Log_STD);
};

We do initialize and validate the input and output layer sizes of each ONNX models follows:

//+------------------------------------------------------------------+
//| Validation arch protected data.                                  |
//+------------------------------------------------------------------+
bool CSignalSAC::ValidationSettings(void)
{  if(!CExpertSignal::ValidationSettings())
      return(false);
//--- initial data checks
   if(m_period > PERIOD_H1)
   {  Print(" time frame too large ");
      return(false);
   }
   ResetLastError();
   if(m_critic_2_handle == INVALID_HANDLE)
   {  Print("Crit 2 OnnxCreateFromBuffer error ", GetLastError());
      return(false);
   }
   if(m_critic_1_handle == INVALID_HANDLE)
   {  Print("Crit 1 OnnxCreateFromBuffer error ", GetLastError());
      return(false);
   }
   if(m_actor_handle == INVALID_HANDLE)
   {  Print("Actor OnnxCreateFromBuffer error ", GetLastError());
      return(false);
   }
   // Set input shapes
   const long _critic_in_shape[] = {1, 4, 1};
   const long _actor_in_shape[] = {1};
   // Set output shapes
   const long _critic_out_shape[] = {1, 4, 1, 1};
   const long _actor_out_shape[] = {1, 6};
   if(!OnnxSetInputShape(m_critic_2_handle, ONNX_DEFAULT, _critic_in_shape))
   {  Print("Crit 2  OnnxSetInputShape error ", GetLastError());
      return(false);
   }
   if(!OnnxSetOutputShape(m_critic_2_handle, 0, _critic_out_shape))
   {  Print("Crit 2  OnnxSetOutputShape error ", GetLastError());
      return(false);
   }
   if(!OnnxSetInputShape(m_critic_1_handle, ONNX_DEFAULT, _critic_in_shape))
   {  Print("Crit 1 OnnxSetInputShape error ", GetLastError());
      return(false);
   }
   if(!OnnxSetOutputShape(m_critic_1_handle, 0, _critic_out_shape))
   {  Print("Crit 1 OnnxSetOutputShape error ", GetLastError());
      return(false);
   }
   if(!OnnxSetInputShape(m_actor_handle, ONNX_DEFAULT, _actor_in_shape))
   {  Print("Actor OnnxSetInputShape error ", GetLastError());
      return(false);
   }
   if(!OnnxSetOutputShape(m_actor_handle, 0, _actor_out_shape))
   {  Print("Actor OnnxSetOutputShape error ", GetLastError());
      return(false);
   }
//read best weights
//--- ok
   return(true);
}

On the layer shapes it is noteworthy we had to make changes that eased our export to ONNX even though they went against the base logic of SAC. First, the actor network is meant to export 2 vectors mean vectors and a log-standard deviation vector. Having to define these in ONNX layer shape would have been error-prone, so we combined them into a single vector within python, as indicted in the for-loop code above. Also, the inputs to the critic networks re 2-fold, the environment state and the action probability distribution as provided by the actor network. This too can typically b defined s 2 tensors, however for simplicity we again combined these too into a single 4-sized vector. Our get output function is as follows:

//+------------------------------------------------------------------+
//| This function calculates the next actions to be selected from    |
//| the Reinforcement Learning Cycle.                                |
//+------------------------------------------------------------------+
vectorf CSignalSAC::GetOutput()
{  vectorf _out;
   int _load = 1;
   static vectorf _x_states(1);
   _out.Init(__ACTIONS);
   _out.Fill(0.0);
   vector _in, _in_row, _in_row_old, _in_col, _in_col_old;
   if
   (
      _in_row.Init(_load) &&
      _in_row.CopyRates(m_symbol.Name(), PERIOD_H1, 8, 0, _load) &&
      _in_row.Size() == _load
      &&
      _in_row_old.Init(_load) &&
      _in_row_old.CopyRates(m_symbol.Name(), PERIOD_H1, 8, 1, _load) &&
      _in_row_old.Size() == _load
      &&
      _in_col.Init(_load) &&
      _in_col.CopyRates(m_symbol.Name(), PERIOD_D1, 8, 0, _load) &&
      _in_col.Size() == _load
      &&
      _in_col_old.Init(_load) &&
      _in_col_old.CopyRates(m_symbol.Name(), PERIOD_D1, 8, 1, _load) &&
      _in_col_old.Size() == _load
   )
   {  _in_row -= _in_row_old;
      _in_col -= _in_col_old;
      Cql *QL;
      Sql _RL;
      _RL.actions  = __ACTIONS;//buy, sell, do nothing
      _RL.environments = __ENVIONMENTS;//bullish, bearish, flat
      QL = new Cql(_RL);
      vector _e(_load);
      QL.Environment(_in_row, _in_col, _e);
      delete QL;
      _x_states[0] = float(_e[0]);
      static matrixf _y_mu_logstd(6, 1);
//--- run the inference
      ResetLastError();
      if(!OnnxRun(m_actor_handle, ONNX_NO_CONVERSION, _x_states, _y_mu_logstd))
      {  Print("Actor OnnxConversion error ", GetLastError());
         return(_out);
      }
      else
      {  vectorf _mu(__ACTIONS), _logstd(__ACTIONS);
         _mu.Fill(0.0); _logstd.Fill(0.0);
         for(int i=0;i<__ACTIONS;i++)
         {  _mu[i] = _y_mu_logstd[i][0];
            _logstd[i] = _y_mu_logstd[i+__ACTIONS][0];
         }
         _out = LogProbabilities(_mu, _logstd);
      }
   }
   return(_out);
}

We are sticking with the same model we have been using this far, of 9-environment states and 3 possible actions. In order to process the probability distribution of the actions, we need the log probabilities function whose code was shared at the beginning of this piece.  Compiling with the wizard and performing a test run for the remaining 4 months of the data window does present us with the following report:

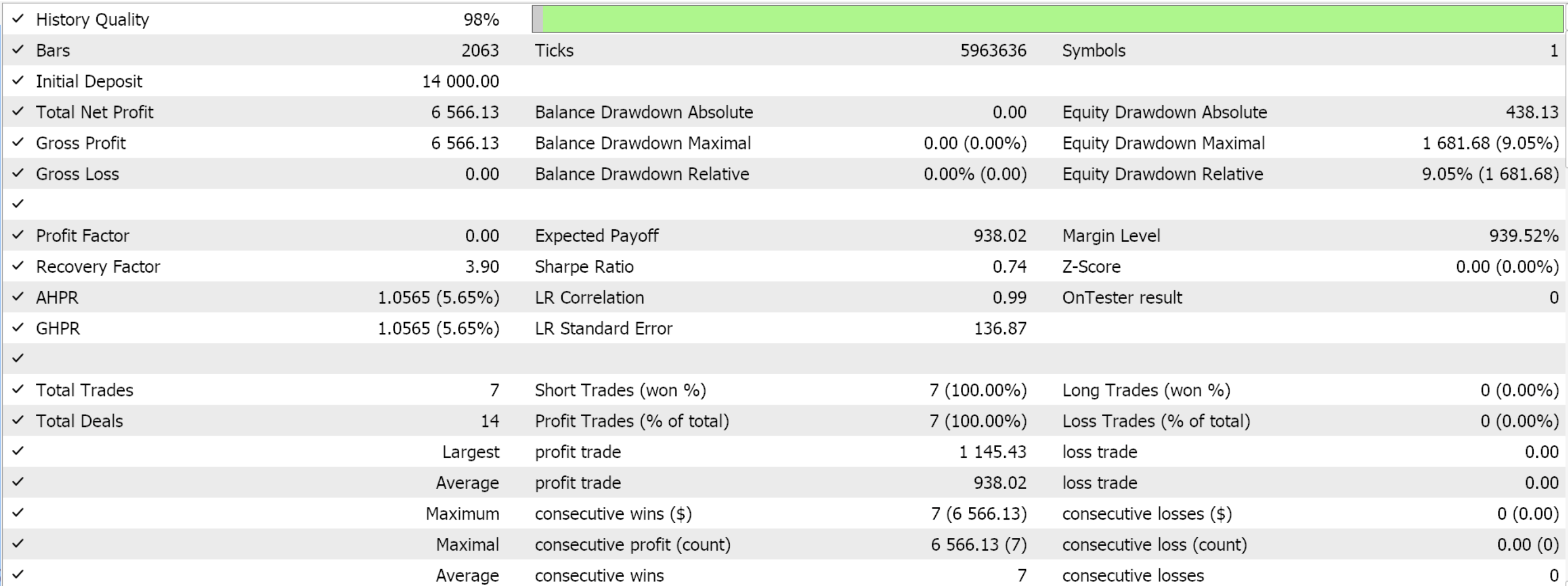
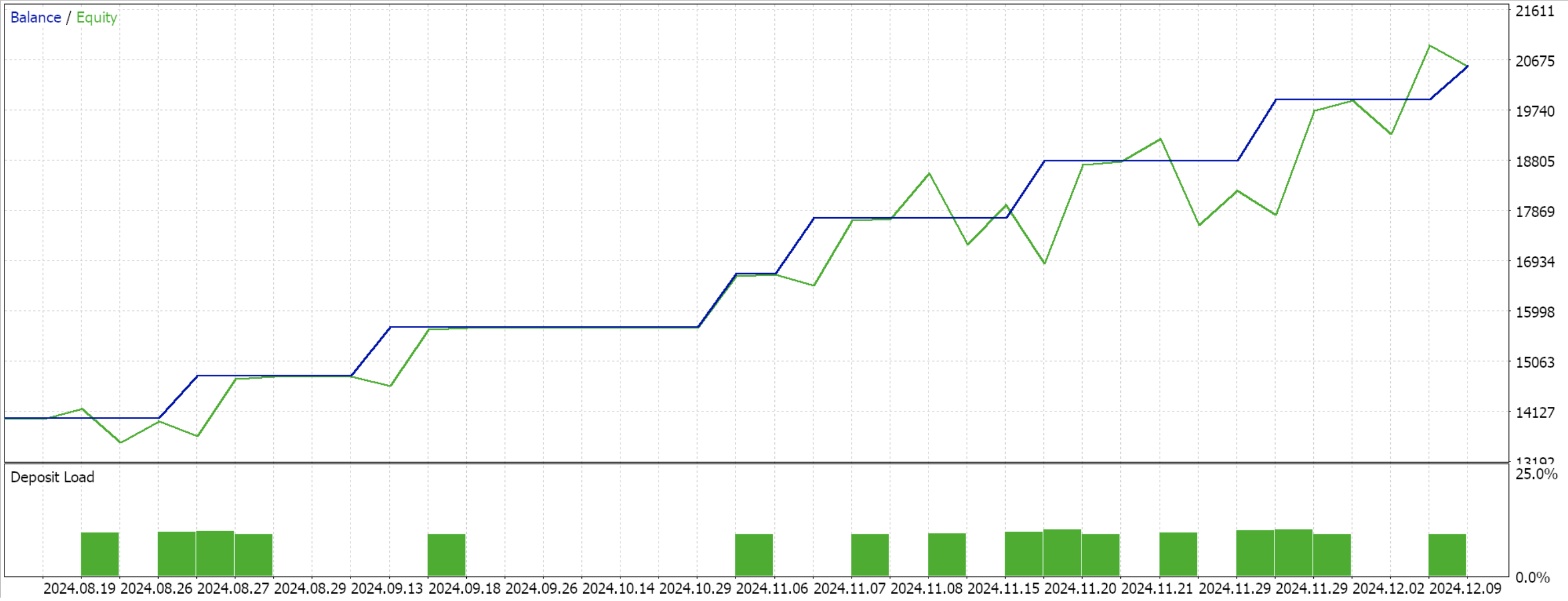
Conclusion

We have looked with a very basic implementation scenario of reinforcement learnings SAC in python that did not utilize the tensor-agent library and thus use the efficiencies it entails. This approach lays out the SAC basics and highlights why the back propagation is a bit protracted, since it involves pairing multiple networks and one of these does not have a typical training dataset. SAC in principle is meant to safely promote more exploration through entropy as modulated by the alpha parameter (which we applied in the Gaussian Distribution). The reader is therefore invited to explore this more by considering a non-fixed alpha, such as the automated adjustment that has a target entropy value. We should also be delving into examples of these in future articles.

File Name	Description
WZ_51.mq5	Wizard Assembled Expert Advisor whose header serves to show files used
SignalWZ_51.mqh	Custom Signal Class File
EURUSD_H1_D1_critic2.onnx	Critic 2 ONNX network
EURUSD_H1_D1_critic1.onnx	Critic 1 ONNX network
EURUSD_H1_D1_actor.onnx	Actor Network