Técnicas do MQL5 Wizard que você deve conhecer (Parte 54): Aprendizado por Reforço com SAC híbrido e Tensores

Introdução

Soft Actor Critic (SAC) é um dos algoritmos utilizados em Aprendizado por Reforço ao treinar uma rede neural. Recapitulando, o aprendizado por reforço é um método emergente de treinamento em aprendizado de máquina, ao lado do aprendizado supervisionado e do não supervisionado.

Replay Buffer

O replay buffer é um componente muito importante do algoritmo off-policy SAC em Aprendizado por Reforço, pois mantém experiências passadas de estado, ação, recompensa, próximo estado e o indicador de término (para registrar se um episódio foi concluído ou continua) em mini-lotes de amostras para treinamento. Seu principal objetivo é descorrelacionar diversas experiências, permitindo que o agente aprenda a partir de um conjunto mais diverso de vivências, o que tende a melhorar a estabilidade do aprendizado e a eficiência de amostragem.

Na implementação do SAC, podemos usar a linguagem MQL5, mas as redes criadas não seriam tão eficientes para treinar quanto aquelas criadas em Python com bibliotecas open-source como TensorFlow ou PyTorch. Portanto, como vimos no último artigo sobre aprendizado por reforço, onde Python foi usado para modelar uma rede SAC rudimentar, continuamos com Python, mas desta vez buscando explorar e aproveitar seus grafos de tensores. Em princípio, há duas maneiras de implementar um replay buffer em Python. A abordagem manual ou a abordagem baseada em tensores. 

Na abordagem manual, estruturas de dados básicas do Python, como listas ou arrays NumPy, são utilizadas. Já no método baseado em tensores, frameworks de deep learning como TensorFlow ou PyTorch são empregados, sendo essa abordagem mais eficiente para aceleração por GPU devido à integração transparente com pipelines de treinamento de redes neurais. Na abordagem manual, o replay buffer é construído com arrays ‘NumPy’, o que é simples e eficaz para problemas de pequena escala. Isso poderia ser tratado da seguinte forma:

import numpy as np

class ReplayBuffer:
    def __init__(self, max_size, state_dim, action_dim):
        self.max_size = max_size
        self.states = np.zeros((max_size, state_dim), dtype=np.float32)
        self.actions = np.zeros((max_size, action_dim), dtype=np.float32)
        self.rewards = np.zeros(max_size, dtype=np.float32)
        self.next_states = np.zeros((max_size, state_dim), dtype=np.float32)
        self.dones = np.zeros(max_size, dtype=np.float32)
        self.ptr = 0
        self.size = 0

    def add(self, state, action, reward, next_state, done):
             
        ...

    def sample(self, batch_size):
        idx = np.random.randint(0, self.size, size=batch_size)
        return (
            self.states[idx],
            ...

             self.dones[idx],
        )

Embora essa abordagem seja relativamente direta de implementar e também muito semelhante ao que utilizamos no artigo anterior sobre SAC, ela pode não escalar bem para problemas maiores ou aceleração por GPU.

Com o método baseado em tensores, o replay buffer é codificado com PyTorch ou TensorFlow. Este último, na minha experiência (até agora), parece um pouco problemático. Consegui configurar uma GPU para funcionar com TensorFlow, mas a natureza específica de toda a cadeia de drivers e versões de bibliotecas de software associadas que precisam estar presentes para uma versão específica não apenas do TensorFlow, mas também do Python ao usar uma GPU específica, é certamente avassaladora.

Tentei usar PyTorch depois, e talvez graças à experiência anterior com TensorFlow, o processo foi muito mais tranquilo. A integração do PyTorch no treinamento de redes neurais com aceleração por GPU é tão fluida que um conjunto de dados de quase um milhão de linhas, quando alimentado em uma rede relativamente complexa com 10 milhões de parâmetros, pode ter uma única época executada em cerca de 4 minutos em uma NVIDIA T4 bastante básica. Podemos realizar uma implementação rudimentar em Python da seguinte forma:

import torch

class ReplayBuffer:
    def __init__(self, max_size, state_dim, action_dim):
        self.max_size = max_size
        self.states = torch.zeros((max_size, state_dim), dtype=torch.float32)
        ...

        self.ptr = 0
        self.size = 0

    def add(self, state, action, reward, next_state, done):
        self.states[self.ptr] = torch.tensor(state, dtype=torch.float32)
        self.actions[self.ptr] = torch.tensor(action, dtype=torch.float32)
        self.rewards[self.ptr] = torch.tensor(reward, dtype=torch.float32)
        self.next_states[self.ptr] = torch.tensor(next_state, dtype=torch.float32)
        self.dones[self.ptr] = torch.tensor(done, dtype=torch.float32)
        self.ptr = (self.ptr + 1) % self.max_size
        self.size = min(self.size + 1, self.max_size)

    def sample(self, batch_size):
        idx = torch.randint(0, self.size, (batch_size,))
        return (
            self.states[idx],
            self.actions[idx],
            self.rewards[idx],
            self.next_states[idx],
            self.dones[idx],
        )

Esse método é muito eficiente, pois se integra diretamente aos pipelines de autograd e otimização do PyTorch. Resumindo a comparação entre manual e tensor: a abordagem manual tem como vantagens a simplicidade de implementação e nenhuma dependência de frameworks de deep learning. As desvantagens, por outro lado, são escalabilidade limitada e ausência de aceleração por GPU. Na abordagem baseada em tensores, as vantagens incluem integração transparente com redes neurais, aceleração por GPU e suporte a problemas de grande escala, enquanto as desvantagens seriam a necessidade de familiaridade razoável com implementações complexas de TensorFlow/PyTorch.

Como regra, portanto, deve-se escolher a abordagem considerando a escala do problema e a disponibilidade de hardware; métodos baseados em tensores são preferidos para problemas de grande escala ou treinamento em GPU. Além disso, se seu ambiente possui estados de tamanho variável, como imagens, então o método baseado em tensores é mais adequado. Adicionalmente, o SAC pode ser aprimorado com Prioritized Experience Replay (PER), onde a amostragem do replay buffer é baseada na importância relativa de cada estado no buffer, medida pelo erro de diferença temporal ou outras métricas-chave. A implementação de PER é mais fácil com replay buffers baseados em tensores, pois permite atualizações e amostragens de prioridade eficientes.

Como em qualquer listagem de código, antes da implantação é sempre uma boa ideia realizar testes e depuração; com um replay buffer, isso pode ser feito adicionando dados fictícios e verificando se a amostragem funciona corretamente. Além disso, deve-se garantir que o replay buffer lide com casos extremos, como estar vazio ou cheio. Asserções em Python ou testes unitários podem ser usados para validar a funcionalidade. Quando o replay buffer estiver pronto, o próximo passo é a integração ao loop de treinamento SAC, armazenando experiências após cada etapa de treinamento e, em seguida, amostrando mini-lotes para atualizações.

Frequentemente busca-se um equilíbrio ao definir o tamanho do replay buffer, pois ele deve ser grande o suficiente para armazenar um conjunto diverso de experiências, mas não tão grande a ponto de desacelerar o processo de amostragem. O replay buffer pode ser otimizado para velocidade e memória usando estruturas de dados eficientes como tensores do PyTorch; evitando cópias desnecessárias de dados; e pré-alocando memória para o buffer. O profiling do replay buffer pode ajudar a identificar e resolver gargalos de desempenho.

Resumindo, um buffer SAC bem implementado é essencial para o sucesso do SAC e de muitos algoritmos off-policy. Ele garante treinamento estável e eficiente ao fornecer experiências diversas e descorrelacionadas.

Rede de Críticos

Nos algoritmos SAC, a rede crítica estima o valor Q (ou valor estado-ação, ou a próxima ação a ser tomada pelo ator) quando recebe o estado atual do ambiente e a escolha de ação do ator. O SAC utiliza duas dessas redes críticas para reduzir o viés de superestimação e também melhorar a estabilidade do aprendizado. Como uma rede neural que recebe como entrada dois conjuntos de dados limitados — a distribuição de probabilidades de ações da rede ator e as ‘coordenadas’ dos estados do ambiente — a escolha entre usar NumPy ou tensores dependerá do tamanho do problema (definido pelo tamanho da rede e volume de dados de treinamento) e também da disponibilidade de hardware.

Em uma implementação manual sem tensores das redes críticas, o NumPy é útil para operações de matriz e atualizações de gradiente. Em casos onde as redes possuem menos de 5 camadas com tamanhos não superiores a 15 cada, ou para fins educacionais e ilustrativos, essa pode ser uma solução viável. Com essa abordagem, as passagens de propagação direta e retropropagação são implementadas manualmente, o que pode ser propenso a erros e não tão eficiente ao escalar para grandes conjuntos de dados. Isso é o que uma implementação manual em Python poderia parecer:

import numpy as np

class CriticNetwork:
    def __init__(self, state_dim, action_dim, hidden_dim=256):
        self.state_dim = state_dim
        self.action_dim = action_dim
        self.hidden_dim = hidden_dim

        # Initialize weights and biases
        self.W1 = np.random.randn(state_dim + action_dim, hidden_dim)
        self.b1 = np.zeros(hidden_dim)
        self.W2 = np.random.randn(hidden_dim, hidden_dim)
        self.b2 = np.zeros(hidden_dim)
        self.W3 = np.random.randn(hidden_dim, 1)
        self.b3 = np.zeros(1)

    def forward(self, state, action):
        x = np.concatenate([state, action], axis=-1)
        x = np.maximum(0, x @ self.W1 + self.b1)  # ReLU activation
        x = np.maximum(0, x @ self.W2 + self.b2)  # ReLU activation
        q_value = x @ self.W3 + self.b3
        return q_value

    def update(self, states, actions, targets, learning_rate=1e-3):
        # Manual gradient descent (simplified)
        q_values = self.forward(states, actions)
        error = q_values - targets
        # Backpropagation and weight updates (not shown for brevity)

Como já observado, essa abordagem não é escalável para grandes redes ou conjuntos de dados e não possui aceleração por GPU. Se, por outro lado, optarmos por usar tensores com PyTorch, poderemos aproveitar diferenciação automática e aceleração por GPU. Essas propriedades são muito favoráveis para problemas de grande escala e implementações em nível de produção. Um exemplo de código muito básico disso poderia ser:

import torch
import torch.nn as nn
import torch.nn.functional as F

class CriticNetwork(nn.Module):
    def __init__(self, state_dim, action_dim, hidden_dim=256):
        super(CriticNetwork, self).__init__()
        self.fc1 = nn.Linear(state_dim + action_dim, hidden_dim)
        self.fc2 = nn.Linear(hidden_dim, hidden_dim)
        self.fc3 = nn.Linear(hidden_dim, 1)

    def forward(self, state, action):
        x = torch.cat([state, action], dim=-1)
        x = F.relu(self.fc1(x))
        x = F.relu(self.fc2(x))
        q_value = self.fc3(x)
        return q_value

O PyTorch, em particular, possui algumas bibliotecas cruciais, como ‘torch.optim’ para lidar com otimização da rede e ‘torch.nn’ para definir a arquitetura da rede. Tudo isso é realizado de forma altamente escalável e eficiente.

Assim, embora a abordagem manual seja possível, como mostrado anteriormente, oferecendo simplicidade e ausência de dependência de frameworks de deep learning, sua incapacidade de escalar ou aproveitar adequadamente GPUs é uma limitação à adoção.

O uso de tensores nas redes críticas apresenta vantagens e desvantagens semelhantes às discutidas para o replay buffer, o que implica, de forma geral, que a abordagem manual é mais adequada quando os problemas são muito pequenos e o objetivo é ensinar as nuances das redes neurais. Na prática, porém, tensores são mais viáveis pelos motivos já apresentados.

As redes SAC utilizam duas redes críticas (frequentemente chamadas Q1 e Q2) para mitigar viés de superestimação. O valor Q-alvo é determinado como o mínimo entre os dois valores Q produzidos pelas redes. Para ilustrar, as redes críticas, assim como parte da saída da rede ator, produzem um vetor com recompensas estimadas para cada ação disponível.

Naturalmente, dentro de cada vetor, o índice/ação com maior valor indicaria a maior recompensa prevista. O propósito principal das redes críticas é determinar de forma conservadora o gradiente para retropropagação da rede ator.

Durante a atualização da rede ator, o gradiente da função objetivo é calculado e retropropagado pela rede ator a partir do mínimo entre os dois valores Q. A escolha do mínimo garante que o ator seja otimizado para escolher ações robustas a erros de superestimação nas redes críticas.

Essas redes críticas, que fornecem o gradiente para a função objetivo que atualiza a rede ator, também precisam ser treinadas. Mas, como estimam recompensas futuras a partir de ações, como seu alvo de treinamento é estabelecido? A resposta é que, nas atualizações dos críticos, o SAC não usa diretamente o mínimo dos dois valores Q. Em vez disso, realiza-se uma atualização para cada crítico (Q1 e Q2) usando o alvo derivado da equação de Bellman suave.

class DoubleCriticNetwork(nn.Module):
    def __init__(self, state_dim, action_dim, hidden_dim=256):
        super(DoubleCriticNetwork, self).__init__()
        self.Q1 = CriticNetwork(state_dim, action_dim, hidden_dim)
        self.Q2 = CriticNetwork(state_dim, action_dim, hidden_dim)

    def forward(self, state, action):
        q1 = self.Q1(state, action)
        q2 = self.Q2(state, action)
        return q1, q2

Além disso, as redes-alvo no SAC são outro conjunto separado de redes (uma para cada crítico Q1 e Q2) usadas para calcular os valores Q-alvo que são fundamentais na retropropagação dessas redes críticas. Elas próprias são atualizadas lentamente via média de Polyak, para garantir estabilidade durante o treinamento. O uso de redes-alvo surge da necessidade de fornecer um alvo estável para a equação de Bellman; sem isso, argumenta-se que as estimativas de valor Q das redes críticas divergiriam ou oscilariam devido ao ciclo de feedback entre valores Q e alvos.

for target_param, param in zip(target_critic.parameters(), critic.parameters()):
    target_param.data.copy_(tau * param.data + (1 - tau) * target_param.data)
```
where `tau` is the polyak averaging coefficient (e.g., 0.005).

A função de perda dos críticos seria então o erro quadrático médio (MSE) entre o valor Q previsto e o valor Q-alvo, conforme estabelecido pela equação de Bellman com ajuda das redes-alvo mencionadas.

target_q_value = reward + (1 - done) * gamma * min(Q1_target(next_state, next_action), Q2_target(next_state, next_action))
```
where `gamma` is the discount factor.

Para treinar os críticos, um mini-lote é amostrado do replay buffer e o valor Q-alvo é calculado. Com isso, as redes críticas são atualizadas por descida de gradiente. Um otimizador como Adam pode ser usado para tornar o treinamento mais eficiente.

optimizer = torch.optim.Adam(critic.parameters(), lr=learning_rate)

Depuração e testes podem ser realizados fornecendo entradas fictícias e verificando a forma e os valores de saída. Deve-se garantir que a rede consiga superajustar um pequeno conjunto de dados. Como já mencionado, asserções em Python podem ser usadas para validar dados de entrada. As redes críticas são integradas ao loop de treinamento SAC computando valores Q, atualizando a perda do crítico e sincronizando as redes-alvo. É importante garantir que a rede crítica seja atualizada em conjunto com as redes ator e valor, razão pela qual tensores — e particularmente GPUs — são tão relevantes aqui.

Algumas dicas extras de otimização também podem ser aplicadas às redes críticas. Primeiro, normalização de lote ou de camada. Segundo, experimentar diferentes funções de ativação como ReLU ou Leaky pode produzir resultados distintos dependendo dos dados e da arquitetura utilizada. Além disso, hiperparâmetros como taxa de aprendizado e profundidade da rede podem ser ajustados. Monitorar a perda do crítico durante o treinamento é importante para detectar problemas como overfitting e instabilidade.

Para concluir, a rede crítica é um componente crucial do SAC, essencial para estimar valores Q e orientar as atualizações de política do ator. Uma rede crítica bem implementada garante aprendizado estável e eficiente.

Redes de Valor

Essa rede, também chamada de função valor-estado, é uma parte opcional do SAC que podemos optar por usar. Seu propósito é estimar a recompensa cumulativa esperada de um estado sob a política atual usando a função valor suave. Embora o uso de uma rede de valor seja “opcional”, ela traz diversas vantagens quando implementada corretamente. Primeiro, por incorporar explicitamente entropia, a função valor suave incentiva a política a explorar de forma mais eficiente. Além disso, tende a fornecer um alvo de treinamento mais suave, ajudando a estabilizar o processo de aprendizado.

Essa estabilidade é muito benéfica quando se trabalha com dados de entrada de alta dimensão (vetores maiores que 10), espaços de ação contínuos (por exemplo, (0.14, 0.67, 1.51) em vez de (comprar, vender, manter)) ou ambientes com múltiplos ótimos locais (situação em que diferentes configurações de pesos parecem boas em conjuntos distintos, mas não generalizam).

Resumindo, redes de valor no SAC estimam o retorno esperado de um estado independentemente da ação, ajudando a reduzir a variância das estimativas de valor Q ao fornecer um alvo suave. Os argumentos sobre uso de tensores versus abordagem manual são semelhantes aos discutidos para a rede crítica. Muitas implementações modernas de SAC não utilizam rede de valor, concentrando-se nas duas redes-alvo dos críticos.

Além de usar uma única rede de valor para moderar os alvos de treinamento dos críticos, também poderíamos usar duas redes de valor. Nesse cenário, tanto uma rede de valor quanto uma rede de valor alvo são usadas para estimar a função de valor, que prevê o retorno esperado (recompensa cumulativa) de qualquer estado dado. A rede de valor alvo, em particular, é usada para estabilizar o treinamento, não apenas neste caso, mas também com redes Deep-QN. Por ser uma cópia da rede de valores, ela é atualizada com menos frequência e fornece um alvo estável para o treinamento.

Rede de atores

Esta é a rede principal, também chamada de rede de política. Ela recebe como entrada os estados do ambiente e produz dois vetores, média e desvio padrão, que servem como parâmetros de uma distribuição de probabilidade sobre ações, permitindo amostragem estocástica. As duas redes críticas, suas redes-alvo correspondentes e a rede de valor (se usada) auxiliam na retropropagação e treinamento desta rede.

Sendo uma rede central no SAC, o uso de tensores traz benefícios significativos. Além disso, como todas as redes mencionadas contribuem para o treinamento da rede ator, o uso de GPUs para paralelizar e permitir treinamento simultâneo dessas múltiplas redes é algo que deve ser explorado, pois oferece grandes ganhos de eficiência.

import torch
import torch.nn as nn
import torch.nn.functional as F
import torch.distributions as dist

class ActorNetwork(nn.Module):
    def __init__(self, state_dim, action_dim, hidden_dim=256):
        super(ActorNetwork, self).__init__()
        self.fc1 = nn.Linear(state_dim, hidden_dim)
        self.fc2 = nn.Linear(hidden_dim, hidden_dim)
        self.fc_mean = nn.Linear(hidden_dim, action_dim)
        self.fc_log_std = nn.Linear(hidden_dim, action_dim)

    def forward(self, state):
        x = F.relu(self.fc1(state))
        x = F.relu(self.fc2(x))
        mean = self.fc_mean(x)
        log_std = self.fc_log_std(x)
        return mean, log_std

    def sample_action(self, state):
        mean, log_std = self.forward(state)
        std = torch.exp(log_std)
        normal = dist.Normal(mean, std)
        action = normal.rsample()  # Reparameterization trick
        return torch.tanh(action), normal.log_prob(action).sum(dim=-1, keepdim=True)

A rede ator, como já observamos no último artigo sobre SAC, produz dois ‘vetores’ principais de dados: a média e o desvio padrão de uma distribuição Gaussiana. Esses dois são combinados para determinar a próxima ação de forma estocástica, o que é importante para exploração e otimização em espaços de ação contínuos. A média representa o centro da distribuição de ações, enquanto o desvio padrão controla a dispersão ou aleatoriedade da distribuição. Esses dois elementos definem uma distribuição Gaussiana a partir da qual as ações podem ser selecionadas. O código Python abaixo ajuda a realizar isso.

import torch

def select_action(mean, log_std):
    """
    Given the SAC actor's output (mean and log_std), this function selects an action index.
    
    Args:
        mean (torch.Tensor): Mean of the action distribution, shape (n_actions,)
        log_std (torch.Tensor): Log standard deviation, shape (n_actions,)

    Returns:
        int: The index of the selected action.
    """
    std = log_std.exp()  # Convert log standard deviation back to standard deviation
    ....  
    return selected_index

# Example inputs
mean = torch.tensor([0.2, -0.5, 1.0, 0.3])  # Example mean values for 4 actions
log_std = torch.tensor([-1.0, -0.7, -0.2, -0.5])  # Example log std values

# Select action
action_index = select_action(mean, log_std)
print("Selected Action Index:", action_index)

Na prática, porém, precisaríamos executar essa função no MQL5, pois após treinar o modelo em Python ele seria exportado como um arquivo ONNX, e como ONNX suas saídas em qualquer passagem direta seriam semelhantes às usadas no treinamento em Python. Assim, como essas duas saídas seriam recebidas no MQL5, essa função de seleção de ação também precisaria estar em MQL5.

Essas duas saídas definem uma distribuição Gaussiana ou Normal a partir da qual as ações são escolhidas. A escolha das ações é feita de forma estocástica para incentivar a exploração, de modo que o agente não escolha sempre a mesma ação para um determinado estado. Durante a retropropagação, para eficiência, utiliza-se reparametrização para que os gradientes possam fluir através do processo de amostragem.

Além disso, a partir da função Python acima, como a maioria das ações em aplicações do mundo real possui limites ou restrições, o SAC aplica a função Tanh para comprimir as ações amostradas ao intervalo de -1 a +1. Isso garante que a ação permaneça dentro de um intervalo gerenciável, preservando a natureza estocástica do processo.

Agente

O agente no SAC, representado aqui como a classe agent em Python, combina a otimização da política (rede ator) com a aproximação da função valor (o pareamento das duas redes críticas, da rede de valor e da rede alvo de valor). O agente deve ser altamente eficiente em amostragem e capaz de lidar com espaços de ação contínuos. Isso ocorre porque ele reúne não apenas essas redes, mas também o replay buffer com o objetivo de aprender uma ‘política ótima’ ou pesos e vieses adequados para a rede ator.

Dada a natureza de visão geral de alto nível do agente, talvez seja desnecessário dizer que tensores são essenciais se o treinamento da rede deve ser realizado com alguma eficiência. Abaixo está uma descrição em Python de como isso poderia ser feito:

import torch
import torch.nn.functional as F
import torch.optim as optim

class SACAgent:
    def __init__(self, state_dim, action_dim, hidden_dim=256, replay_buffer_size=1e6, batch_size=256, gamma=0.99, tau=0.005, alpha=0.2):
        self.state_dim = state_dim
        ...

        self.alpha = alpha

        # Initialize networks and replay buffer
        self.actor = ActorNetwork(state_dim, action_dim, hidden_dim)
        ....

        self.value_optimizer = optim.Adam(self.value_network.parameters(), lr=3e-4)

    def select_action(self, state):
        state = torch.FloatTensor(state).unsqueeze(0)
        action, _ = self.actor.sample_action(state)
        return action.detach().numpy()[0]

    def update(self):
        # Sample a batch from the replay buffer
        states, actions, rewards, next_states, dones = self.replay_buffer.sample(self.batch_size)

        # Convert to tensors
        states = torch.FloatTensor(states)
        ...

        dones = torch.FloatTensor(dones).unsqueeze(1)

        # Update value network
        target_value = self.target_value_network(next_states)
        ...

        # Update critic networks
        q1_value = self.critic1(states, actions)
             
        ...

        self.critic2_optimizer.step()

        # Update actor network
        new_actions, log_probs = self.actor.sample_action(states)
             
        ...

        self.actor_optimizer.step()

        # Update target networks
        for target_param, param in zip(self.target_value_network.parameters(), self.value_network.parameters()):
            target_param.data.copy_(self.tau * param.data + (1 - self.tau) * target_param.data)

Como estamos usando tensores com PyTorch, é importante enfatizar que a atribuição manual de um dispositivo GPU, se disponível, contribui significativamente para garantir que os tensores sejam executados da forma mais eficiente possível.

Ambiente

O ambiente é onde os conjuntos de dados de treinamento e alvo/ação são definidos. Ele essencialmente define o problema que o agente está tentando resolver, fornecendo estado, recompensa e sinal de término ao agente com base em suas ações. O ambiente pode ser implementado manualmente (ou seja, a partir de primeiros princípios) ou por herança usando bibliotecas como o Gym da OpenAI para ambientes padronizados. Um ambiente baseado em tensores poderia ser implementado da seguinte forma:

import torch

class TensorEnvironment:
    def __init__(self):
        self.state_space = 4  # Example: state dimension
        self.action_space = 2  # Example: action dimension
        self.state = torch.zeros(self.state_space)  # Initial state

    def reset(self):
        self.state = torch.randn(self.state_space)  # Reset to a random state
        return self.state

    def step(self, action):
        # Define transition dynamics and reward function
        next_state = self.state + action  # Simple transition
        ...

        self.state = next_state
        return next_state, reward, done, {}

    def render(self):
        print(f"State: {self.state}")

Em seguida, utiliza-se um loop para coletar experiências e atualizar o agente periodicamente:

for episode in range(num_episodes):
    state = env.reset()
    episode_reward = 0
    for step in range(max_steps):
        action = agent.select_action(state)
        next_state, reward, done, _ = env.step(action)
        agent.replay_buffer.add(state, action, reward, next_state, done)
        state = next_state
        episode_reward += reward
        if len(agent.replay_buffer) > batch_size:
            agent.update()
        if done:
            break
    print(f"Episode {episode}, Reward: {episode_reward}")

Montagem e testes no Wizard

Testamos nosso SAC híbrido baseado em tensores que, além de possuir uma rede ator e duas redes críticas, utiliza uma rede de valor e uma rede alvo de valor no lugar das duas redes alvo que treinam os críticos. Utilizamos o par EURUSD no timeframe de 4 horas para o ano de 2023.

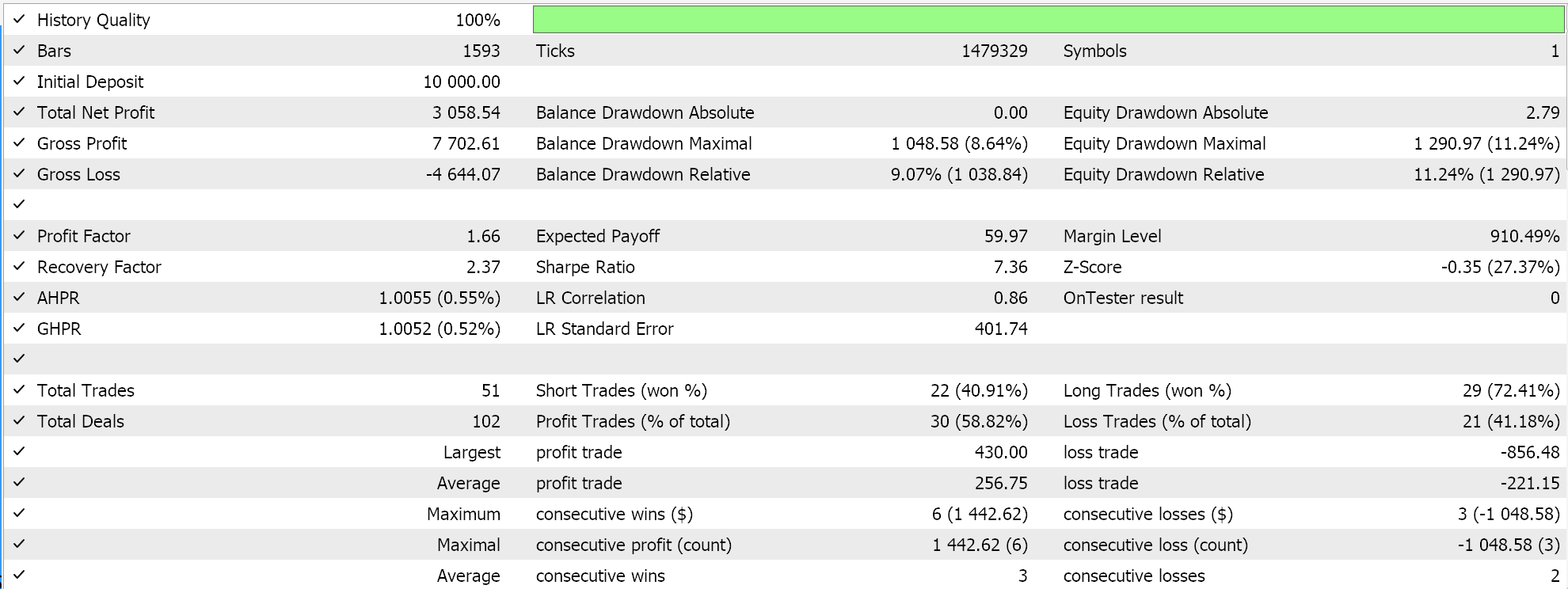
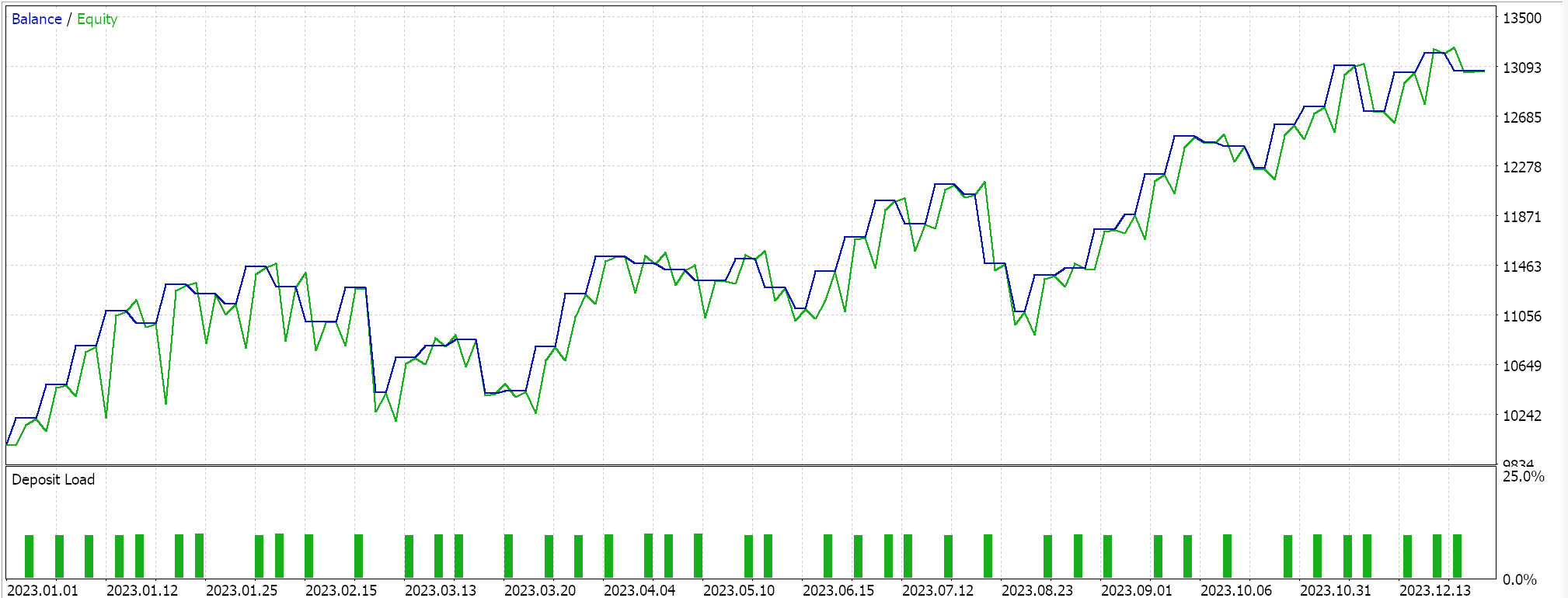
Tanto o TensorFlow quanto o PyTorch permitem não apenas o treinamento de modelos, mas também sua validação cruzada. O TensorFlow permite passar valores de dados de validação x e y para sua função fit, enquanto o PyTorch essencialmente permite o mesmo ao passar esses dados para um data_loader. Uma execução de teste em um Expert Advisor compilado no MQL5 que não realiza validação cruzada (ou inferência) nos fornece os seguintes resultados para EURUSD ao longo de 2023:

Utilizamos, como no último artigo sobre SAC, o ONNX para exportar o modelo do Python e importá-lo para o MQL5. Estamos lidando com cinco redes neurais e, ainda assim, apenas uma realiza as previsões necessárias, enquanto as outras quatro auxiliam apenas na retropropagação. A rede necessária e exportada é a rede ator. Essa rede, contudo, produz não um, mas dois vetores, como já mencionado: A média e o desvio padrão. Portanto, antes de podermos usar o modelo ONNX no MQL5, precisamos definir com precisão os formatos de saída desse modelo. O formato de entrada é direto. Definimos os formatos no MQL5 da seguinte maneira:

//+------------------------------------------------------------------+
//| Validation arch protected data.                                  |
//+------------------------------------------------------------------+
bool CSignalSAC::ValidationSettings(void)
{  if(!CExpertSignal::ValidationSettings())
      return(false);
//--- initial data checks
   if(m_period != PERIOD_H4)
   {  Print(" time frame should be H4 ");
      return(false);
   }
   if(m_actor_handle == INVALID_HANDLE)
   {  Print("Actor OnnxCreateFromBuffer error ", GetLastError());
      return(false);
   }
   // Set input shapes
   const long _actor_in_shape[] = {1, __STATES};
   // Set output shapes
   const long _actor_out_shape[] = {1, __ACTIONS};
   if(!OnnxSetInputShape(m_actor_handle, ONNX_DEFAULT, _actor_in_shape))
   {  Print("Actor OnnxSetInputShape error ", GetLastError());
      return(false);
   }
   if(!OnnxSetOutputShape(m_actor_handle, 0, _actor_out_shape))
   {  Print("Actor OnnxSetOutputShape error ", GetLastError());
      return(false);
   }
   if(!OnnxSetOutputShape(m_actor_handle, 1, _actor_out_shape))
   {  Print("Actor OnnxSetOutputShape error ", GetLastError());
      return(false);
   }
//read best weights
//--- ok
   return(true);
}

Isso é tratado na função de validação da nossa classe de sinal personalizada, pois o modelo ONNX não será executado se esses formatos não estiverem definidos corretamente. Novos leitores podem encontrar guias sobre como montar um Expert Advisor a partir de um arquivo de sinal personalizado *.*mqh aqui e aqui.

Conclusão

Implementamos um algoritmo de aprendizado por reforço Soft Actor Critic em Python com o auxílio de tensores. Os tensores são cruciais em aprendizado de máquina porque proporcionam grandes ganhos de eficiência no treinamento de modelos, um aspecto muito importante especialmente para traders. O tamanho dos conjuntos de dados de treinamento e a necessidade de redes mais elaboradas tendem a levar a processos de treinamento mais lentos. Essa limitação é superada não apenas pelo uso de tensores, mas também pelo aproveitamento do poder das GPUs.

Nome	Descrição
hybrid_sac.mq5	Expert Advisor montado no Wizard com cabeçalho mostrando os arquivos utilizados
SignlWZ_54.mqh	Arquivo de Classe de Sinal Personalizada
model.onnx	Arquivo de Rede ONNX