您应当知道的 MQL5 向导技术（第 51 部分）：配以 SAC 的强化学习

概述

柔性参与者评论者（SAC）是我们正研究的另一种强化学习算法，我们曾考察过一些算法，包括近端政略优化、深度 Q-网络、SARSA，等等。不过，该算法就像我们曾考察过的一些算法，使用神经网络，但伴随一些重要警告。用到的网络总数为三个，分别是：两个评论者网络，和一个参与者网络。当输入动作和环境状态时，两个评论者网络会做出奖励预测（Q-值），且这两个网络的输出中的最小值被用作调制训练参与者网络的损失函数。

参与者网络的输入是环境状态坐标，输出为两叠。平均向量、和对数标准差向量。通过使用高斯过程，这两个向量用于推导参与者可能采取动作的概率分布。故此，虽然两个评论者网络能够按照传统进行训练，但参与者网络显然是另一码事。此处有很多东西要讨论，故我们先重申一下基础知识，然后再深入。两个评论者网络从输入取得环境的当前状态和一个动作。它们的输出是考虑该状态下所采取动作的预期回报（Q-值）的估测。使用两个评论者有助于降低高估偏差，这是 Q-学习的常见问题。

参与者网络将当前环境状态作为其输入。它的输出是有效的可能动作的概率分布，这种分布是随机的，故可鼓励探索。我使用“有效”这个词，是因为参与者网络的实际输出是两个向量，需要投喂至高斯概率分布，才能获得每个动作的权重。我们按如下方式完成 MQL5 版本：

//+------------------------------------------------------------------+
// Function to compute the Gaussian probability distribution and log
// probabilities
//+------------------------------------------------------------------+
vectorf CSignalSAC::LogProbabilities(vectorf &Mean, vectorf &Log_STD)
{  vectorf _log_probs;
   // Compute standard deviations from log_std
   vectorf _std = exp(Log_STD);
   // Sample actions and compute log probabilities
   float _z = float(rand() % USHORT_MAX / USHORT_MAX); // Generate N(0, 1) sample
   // Sample action using reparameterization trick: action = mean + std * N(0, 1)
   vectorf _actions = Mean + (_std * _z);
   // Compute log probability of the sampled action
   vectorf _variance = _std * _std;
   vectorf _diff = _actions - Mean;
   _log_probs = -0.5f * (log(2.0f * M_PI * _variance) + (_diff * _diff) / _variance);
   return(_log_probs);
}

SAC 如何工作

话虽如此，SAC 的工作与大多数强化学习算法一样。首先是动作选择，其中参与者从参与者网络输出的概率分布中抽取一个动作。随后是“环境交互”，其中智代执行在环境中抽取的动作，并观察其下一个状态和奖励。然后跟随评论者更新，其中两个评论者网络按损失函数进行更新，其在预测 Q-值、和目标 Q-值之间比较。然而，如上注解，参与者网络更新是一个新颖之处，因为它采用政略梯度进行更新，旨在参考政策分布的熵来最大化预期回报。意即，为了鼓励探索，并防止过早收敛到次优解。

在 SAC 中政策分布的熵衡量随机性或不确定性。在 SAC 中，较高的熵对应于更多的探索动作，而较低的熵意味着强调判定性选择。在 SAC 中参与者网络的输出本质上是一种随机政策，其由概率分布参数化，在我们的例子中（对于本文）是高斯分布。该分布的熵涂绘出智代在特定状态（输入）下可能采取动作的景象。

其含义在于鼓励智代探索，如同大多数典型的强化学习算法，如此这般来降低过早收敛到次优政策的风险。因此，在探索与利用之间创造了平衡。SAC 将一个熵项纳入其政策优化意向，如此最大化预期回报和熵。意向方程如下：

其中：

• α：熵温度，平衡奖励最大化和探索。
• logπ(a∣s)：动作的对数概率，（我们的函数输出，其代码已在上面分享），它取决于 μ 和 log(σ)。
• Q(s,a)：是评论者网络的两个输出的最小 Q-值。

在信息不完整的环境中，较高的熵往往会导致更稳健的决策制定，因为它可防止过度拟合特定场景。故此，最大化熵在 SAC 中是一件好事。除了改进探索之外，因为鼓励智代尝试更广泛的动作、或避免次优政策，以便防止陷入局部最优状态，它本质上是一种正则化形式，防止过度判定性政策在不可预见的场景下易于失败。此外，逐渐熵调整通常会导致政策更新更加顺畅，确保稳定的训练和收敛。

温度控制参数对于参与者网络的熵、和学习过程非常敏感，这是值得提及的原因。出于我们的目的，我们将其固定为 0.5，正如对数概率函数所示，其 MQL5 代码已在上面分享。然而，温度参数 alpha 规定了意向中能量的权重。正如较高的 alpha 鼓励探索，而较低的值则促进判定性正策或利用。故此，就我们的目的，将其赋值 0.5，这就达到某种平衡。

然而，SAC 经常使用自动熵调谐机制，即动态调整 alpha，以便维持目标熵水平，从而在探索和开发之间达至平衡。这样做的实际意义是：跨任务的稳健学习；创建普适政策来熟练处理不完整信息（随机策略）；以及为持续学习奠定基础。其潜在权衡主要是两点。过多的探索和计算成本。

泛滥的熵会导致利用已知的高回报策略为代价，过度强调探索性动作，从而导致学习效率低下。这将始终在计算和优化熵项的背后遇到，与仅专注奖励最大化的算法相比，熵项会增加计算开销。如上所述，参与者网络输出两个向量 MU 和 Log-STD，那么它们如何影响这个熵呢？

MU 代表政策动作分布的向心趋势。它不会直接影响熵，然而在某种意义上它定义了政策的平均行为。另一方面，Log-STD 控制动作分布的扩散或不确定性，并直接影响熵。较高的 Log-STD 意味着更广泛、更不确定的动作分布，而较低的 Log-STD 则指向对立。那么，Log-STD 中给定动作的量级、与选择的可能性有什么关系呢？

如前所述，细节由高斯过程判定，不过低 Log-STD 往往意味着参与者网络对最优动作 MU 很信任。这通常意味着所抽取动作的可变性较低。所抽取动作将更紧密地集中在该动作的相应 MU 值周围，该值具有较低的 Log-STD 读数，这将鼓励利用更多围绕该动作的政策。故此，虽然低 Log-STD 读数不会直接令动作有更多可能性，但它本质上收窄了潜在动作的纵深，从而增加了选择接近 MU 的动作的机会。

还有一些经常应用于熵的实际调整。首先，由于 Log-STD 直接判定熵，为了稳定训练 SAC，通常将 log(σ) 限制在一定范围内，以边避免熵值极高或极低。这是由上面的对数概率函数中所示的 “z” 参数完成的。其次，alpha 的调整（我们在对数概率函数中将其设置为 0.5f），对于实现如前所述的探索-利用平衡至关重要。为此，自动 alpha 调整经常被当作动态实现开发-探索平衡的一种手段。

这是通过使用熵目标 H 来达成的。下面的方程定义了这一点：

其中：

• alpha (α t )：是当前温度，控制意向中熵项的权重，较高的值鼓励探索，而较小的值倾向于利用。

• alpha (αt+1 )：是更新的温度参数，来自当前熵相对于所包含目标的反馈之后。

• lambda (λ)：是 alpha 调整过程的学习率，控制 alpha 适应距熵目标 H 的偏离速度。

• E (E a~π )：是从当前政策计划中抽取的动作预期。

• Log(a|s)：是动作-a 在当前政策下状态-s 的对数概率。它量化了选择政策动作的不确定性。

• H target：用作政策的目标熵值。动作是离散的处境下，它通常基于动作空间的维度（可用动作的数量和纵深）进行赋值，诸如（买入、卖出、持有，我们到目前为止已经考虑过的实现）；如果动作是连续的，也可对其进行缩放（例如，如果我们有 2 个维度的市价单，均从 0.01 缩放到 0.10，用作同时购买两种证券的开仓规模，其值是可用保证金的百分比）。

故此，运用自动 alpha 调整，即使我们在本文中的实现中没有进行探讨，也可以确保智代动态适配环境的变化，省略了手工调整 alpha 的需要，并通过维护预设的探索-利用权衡来促进高效学习。

SAC 与 DQN 比较

到目前为止，我们已研究了另一种实用单一神经网络的强化学习算法，即 深度-Q-网络，如此这般把 SAC 与其多个网络一起使用能提供什么优势呢？为了给 SAC 建档，我们研究一个机器人任务操控的用例场景。那么，任务是这样的：需要机械臂来固定物体，并将其移动到指定的目标位置。其手臂的关节会在连续动作空间进行分配，即量化必要的扭矩和角度调整、等等。

在这种情况下使用 DQN 的挑战在于，首先，DQN 最适合离散动作空间。尝试扩展它来适应连续空间，将导致更高维度动作空间的可用离散动作数量呈指数级增长，从而令训练过于昂贵、且效率低下。DQN 还依赖于 ε-贪婪策略来平衡探索和利用，而这些或许难以在离散化的高维空间中有效工作。最后，DQN 易于出现高估偏差，这可能导致训练时出现一些不稳定性，尤其是在奖励变化较大的复杂环境当中。

在这种情况下，SAC 更适合，主要是因为其连续动作空间支持。这体现在 SAC 优化连续动作空间的随机政策的方式上，其剔除了动作离散化（或分类）的需求。这就导致了机器人手臂的控制更平稳和精确。SAC 中的三个网络协同工作，其中参与者网络生成一个随机政策来设置连续动作的分布（概率加权）。这就提高了效率，同时也避免了过早的探索。

就评论者网络而言，它们采用了一种孪生 Q-值估算方法，其将最小值反向传播到参与者网络，帮助避免过度估算偏差。这可稳定训练，并确保更准确的结果。总之，鼓励更多探索的熵增强意向（特别是当与上面与 alpha 论证的自动温度调整配对时），加上 SAC 处理高维动作空间的能力所提供的健壮性和稳定性，令其比 DQN 高出一筹。为此，Open AI 的 Gym Reacher 和 Fetch 任务的公开性能示例清楚地表明，DQN 由于其离散化的动作输出、和糟糕的探索，政策多次收敛到次优策略，难以产生流畅的手臂运动。另一方面，SAC 依据随机策略生成了平滑的精确动作，这导致任务完成更快，冲突更少，并更好地适配物体位置、或目标位置的变化，这要再次归功于随机政策方式。

Python 和 TensorFlow

至于本文，不同于过去的机器学习文章，我们将深入研究 Python 的 TensorFlow。MQL5 是 MetaQuotes 的亲本语言，显然保有相关性，因而由向导汇编的智能系统大量依赖它。对于新读者，这里和这里的指南都是关于如何使用本文末尾所附代码来汇编智能系统。不过，作为开发金融模型时首选的编程语言，Python 无疑正在侵占 MQL5 的相关性和主导地位。快速侦察能表明，简单地在 MetaQuotes 上发布更多 python 函数库，以边跟上创新的步伐，并继续重申其主导地位。 

然而，我岁数已足够老了，还记得 09 年引入 MetaTrader 5？尽管它提供了所有优势，但从客户那里，采用它们的进度非常缓慢。因此，我能理解为什么他们会犹豫是否要积极推出和维护 python 函数库。话虽如此，此处展示的创新主要来自“客户”（即 python 社区），而非 MetaQuotes，正如 MetaTrader 5，其中推出的仓位，与订单对立。那么，也许他们需要紧急关注这一点？时间会证明一切，但与此同时，不仅使用 TensorFlow，甚至使用 PyTorch 也能带来效率优势，不仅开发网络、最重要的是训练网络，实际提升都是巨大的！

以我观点，MetaQuotes 可以探寻企业赞助，成为贡献者，甚至为 Pandas、NumPy 和 Sci-Kit 的关键 python 函数库创建分支项目；除此之外，还允许读取其高度压缩的文件格式 *.*HCC 和 *.*TKC。但这都是普遍性的想法，回到 TensorFlow，首先，它主要提供了两个方面的高级深度学习能力。在软件前端，以及 GPU 硬件端。  

MQL5 支持 OpenCL，故可说这两种语言能针锋相对，不过有关 Python 用来构建、训练、和优化深度学习模型的高级库和工具，肯定不能这样说。这些函数库包括支持复杂架构，例如通过 TensorFlow 智代 的 SAC。

它还具有丰富的生态系统和预构建工具，诸如进一步强化学习的稳定基线（张量智代之外）；允许灵活性和实验性，因为能够快速实现原型设计、及测试各种模型；具有高度可重复性、并易于调试（尤其是当使用 Tensor-Board 等工具来可视化、并训练矩阵/内核时）；它还提供与 ONNX 等可导出格式的互操作性；并拥有非常广泛、且不断增长的社区支持，以及定期更新。

SAC 能够在 python 中以多种方式实现。为了概括核心原则目的，我们将仅讨论两种方式。其中第一个手工定义 SAC 的三个主网络，并通过使用 for 循环来迭代训练和测试 SAC 模型。第二个使用曾提到的 python 函数库附带的张量智代，专门帮助强化学习。

手工迭代方式中的步骤是：在 TensorFlow/Keras 中设计 SAC 组件，其中对于参与者网络，这涉及定义一个神经网络，其为高斯采样输出随机政策；对于评论者网络，这意味着为孪生 Q-学习构造 2 个 Q-值网络，来管理高估偏差；以及定义 n 熵正则化制度，以边实现高效探索。如上所述，出于我们的目的，我们的熵采用 0.5 的固定 alpha 值。涵盖这些内容的开源如下：

import numpy as np
import pandas as pd

from sklearn.model_selection import train_test_split

import tensorflow as tf

print("Num GPUs Available: ", len(tf.config.list_physical_devices('GPU')))

from tensorflow.keras import optimizers
from tensorflow.keras.layers import Input
from tensorflow.keras import layers
from tensorflow import keras
import tf2onnx
import onnx

import os

# Define the actor network
def ActorNetwork(state_dim, action_dim, hidden_units=256):
    """
    Creates a simple SAC actor network.
    
    :param state_dim: The dimension of the state space.
    :param action_dim: The dimension of the action space.
    :param hidden_units: The number of hidden units in each layer.
    :return: A Keras model representing the actor network.
    """
    # Input layer
    state_input = layers.Input(shape=(state_dim, ))
    
    # Hidden layers (Dense layers with ReLU activation)
    x = layers.Dense(hidden_units, activation='relu')(state_input)
    x = layers.Dense(hidden_units, activation='relu')(x)
    
    # Output layer: output means (mu) and log standard deviation (log_std) for Gaussian distribution
    
    output_size = action_dim + action_dim
    stacked_mean_logs = layers.Dense(output_size)(x)
    
    # Create the model

    actor_model = tf.keras.Model(inputs=state_input, outputs=stacked_mean_logs)
    
    return actor_model

# Define the critic network
def CriticNetwork(state_dim, action_dim, hidden_units=256):
    """
    Creates a simple SAC critic network (Q-value approximation).
    
    :param state_dim: The dimension of the state space.
    :param action_dim: The dimension of the action space.
    :param hidden_units: The number of hidden units in each layer.
    :return: A Keras model representing the critic network.
    """
    
    input_size = state_dim + action_dim
    state_action_inputs = layers.Input(shape=(None, input_size, 1))  # Concatenate state and action
    
    # Hidden layers (Dense layers with ReLU activation)
    x = layers.Dense(hidden_units, activation='relu')(state_action_inputs)
    x = layers.Dense(hidden_units, activation='relu')(x)
    
    # Output layer: Q-value for the given state-action pair
    q_value_output = layers.Dense(1)(x)  # Single output for Q-value
    
    # Create the model 
    critic_model = tf.keras.Model(inputs=state_action_inputs, outputs=q_value_output)
    
    return critic_model

此后，我们需要在 TensorFlow/Keras 中训练 SAC 模型。典型情况下涉及使用旧的 MetaTrader 5 库从 MetaTrader 终端导入 MetaTrader 5 数据，然后将这些数据打包到测试和训练数据之中。我们使用三分之二的比例进行训练，剩下三分之一用于测试。我们在一个繁琐、且效率极低的 for 循环中模拟了 MetaTrader 5 的交易设置，该循环的大小符合预期，以边适配多个局次、和训练数据大小。甚至，我们旨在调用 SAC 意向函数，包括熵项，来优化参与者和评论者网络。下面分享其中涉及的代码：

# Filter the DataFrame to keep only the '<state>' column
df = pd.read_csv(name_csv)

states = df.filter(['<STATE>']).astype(int).values
# Extract the '<state>' column as an integer array
rewards = df.filter(['<REWARD>']).values

states_size = int(len(states)*(2.0/3.0))
actor_x_train = states[0:states_size,:]
actor_x_test = states[states_size:,:1]
rewards_size = int(len(rewards)*(2.0/3.0))
critic_y_train = rewards[0:rewards_size,:]
critic_y_test = rewards[rewards_size:,:1]

# Initialize networks and optimizers
input_dim = 1  # 2 states, of 3 gradations are flattened into a single index
output_dim = 3  # possible actions buy, sell, hold
actor = ActorNetwork(input_dim, output_dim)
critic1 = CriticNetwork(input_dim, output_dim)  # Input paired with action
critic2 = CriticNetwork(input_dim, output_dim)  # Input paired with action

critic_optimizer_1 = tf.keras.optimizers.Adam(learning_rate=0.001)
critic_optimizer_2 = tf.keras.optimizers.Adam(learning_rate=0.001)
actor_optimizer = tf.keras.optimizers.Adam(learning_rate=0.001)

# Training loop
for e in range(epoch_size):
    train_critic_loss1 = 0
    train_critic_loss2 = 0
    train_actor_loss = 0
    
    for i in range(actor_x_train.shape[0]):
        input_state = tf.expand_dims(actor_x_train[i], axis=0)  # Select a single sample and maintain batch dim
        target_q = tf.expand_dims(critic_y_train[i], axis=0)

        # Actor forward pass and sampling
        with tf.GradientTape(persistent=True) as tape:

            actor_output = actor(input_state)
            # Split the vector into mean and log_std
            mu = actor_output[:, :output_dim]     # First 3 values
            log_std = actor_output[:, output_dim:]  # Last 3 values
            std = tf.exp(log_std)
            sampled_action = tf.random.normal(shape=mu.shape, mean=mu, stddev=std)  # Sample action from Gaussian

            # Concatenate the state and action tensors
            in_state = tf.convert_to_tensor(tf.cast(input_state, dtype=tf.float32), dtype=tf.float32)  # Ensure it's a tensor
            in_action = tf.convert_to_tensor(tf.cast(sampled_action, dtype=tf.float32), dtype=tf.float32)
            
            # Concatenate along the last axis
            critic_raw_input = tf.concat([in_state, in_action], axis=-1)  # Ensure correct axis
            critic_input = tf.reshape(critic_raw_input, [-1, 1, 4, 1])  # -1 infers the batch size dynamically

            q_value1 = critic1(critic_input)
            q_value2 = critic2(critic_input)

            # Critic loss (mean squared error)
            critic_loss1 = tf.reduce_mean((tf.cast(q_value1, tf.float32) - tf.cast(target_q, tf.float32)) ** 2)
            critic_loss2 = tf.reduce_mean((tf.cast(q_value2, tf.float32) - tf.cast(target_q, tf.float32)) ** 2)

            # Actor loss (maximize expected Q-value based on minimum critic output)
            min_q_value = tf.minimum(q_value1, q_value2)  # Take the minimum Q-value
            actor_loss = tf.reduce_mean(min_q_value)  # Maximize expected Q-value (negative for minimization)

        # Backpropagation
        critic_gradients1 = tape.gradient(critic_loss1, critic1.trainable_variables)
        critic_gradients2 = tape.gradient(critic_loss2, critic2.trainable_variables)
        actor_gradients = [-grad for grad in tape.gradient(actor_loss, actor.trainable_variables)]

        del tape  # Free up resources from persistent GradientTape
        
        critic_optimizer_1.apply_gradients(zip(critic_gradients1, critic1.trainable_variables))
        critic_optimizer_2.apply_gradients(zip(critic_gradients2, critic2.trainable_variables))
        actor_optimizer.apply_gradients(zip(actor_gradients, actor.trainable_variables))
        
        # Accumulate losses for epoch summary
        train_critic_loss1 += critic_loss1.numpy()
        train_critic_loss2 += critic_loss2.numpy()
        train_actor_loss += actor_loss.numpy()

    print(f"  Epoch {e + 1}/{epoch_size}:")
    print(f"  Train Critic Loss 1: {train_critic_loss1 / actor_x_train.shape[0]:.4f}")
    print(f"  Train Critic Loss 2: {train_critic_loss2 / actor_x_train.shape[0]:.4f}")
    print(f"  Train Actor Loss: {train_actor_loss / actor_x_train.shape[0]:.4f}")
    print("-" * 40)

critic2.summary()
critic1.summary()
actor.summary()

训练后，我们还要把模型（由三个网络组成）导出到 ONNX 之中。ONNX 是 Open Neural Network Exchange 的缩写，为机器学习互操作性提供了一种开放标准，由 python 训练的模型都可利用 PyTorch 或 SciKit-Learn 等各种函数库导出这种格式，从而在更广泛的平台和编程语言中所用，其中包括 MQL5。这种兼容性消除了复制复杂机器学习逻辑的需要，从而节省了时间，并降低了出错。

允许编译单个 ex5 文件导入 ONNX 作为资源，其中包括 ONNX 机器学习模型、和 MQL5 交易执行逻辑，故交易者无需处理多个文件。如此说，从 python 到 ONNX 的导出过程已经完成。选项数量，其中之一是 tf2onnx，但它不是唯一的选项：onnxmltools、skl2onnx、transformers.onnx（用于 HuggingFace）、和 mxnet.contrib.onnx。不过，在导出阶段至关重要的是确保正确记载和录制每个网络的输入层和输出层的形状，因为在 MQL5 中，该信息对于准确初始化每个网络的相应 ONNX 句柄至关重要。我们如下行事：

# Check input and output layer shapes for importing ONNX
import onnxruntime as ort

session_critic2 = ort.InferenceSession(path_critic2_onnx)
session_critic1 = ort.InferenceSession(path_critic1_onnx)
session_actor = ort.InferenceSession(path_actor_onnx)

for i in session_critic2.get_inputs():
    print(f"in critic2 Name: {i.name}, Shape: {i.shape}, Type: {i.type}")

for i in session_critic1.get_inputs():
    print(f"in critic1 Name: {i.name}, Shape: {i.shape}, Type: {i.type}")

for i in session_actor.get_inputs():
    print(f"in actor Name: {i.name}, Shape: {i.shape}, Type: {i.type}")
    

for o in session_critic2.get_outputs():
    print(f"out critic2 Name: {o.name}, Shape: {o.shape}, Type: {o.type}")

for o in session_critic1.get_outputs():
    print(f"out critic1 Name: {o.name}, Shape: {o.shape}, Type: {o.type}")

for o in session_actor.get_outputs():
    print(f"out actor Name: {o.name}, Shape: {o.shape}, Type: {o.type}")

如上所述，以 python 代码的 for 循环实现的性能远非高效，事实上，它与 MQL5 非常相似，原因在于张量/图形的使用并未得到恰当的利用。然而，这是必要的，即利用 TensorFlow 训练效率的 TensorFlow 拟合函数在这种情况下并不适用，在于反向传播中，2 个评论者网络的输出（Q-值）也被用于训练参与者网络。参与者网络没有像评论者网络，或更典型的神经网络那样的目标向量，或目标数据集。

实现这一点的第二种方式使用张量智代，其为 TensorFlow 和 python 中处理强化的内置函数库。我们将在接下来的文章中对此进行适当深度的研究，但足以说明初始化不仅涵盖了成分网络，还考虑了环境和智代。如果过分专注网络训练效率，则强化学习的关键方面可能会被忽视。

与 MQL5 结合

我们将导出的 ONNX 模型作为 MQL5 的资源导入，在我们的自定义信号类文件里如下标头所示。

//+------------------------------------------------------------------+
//|                                                    SignalSAC.mqh |
//|                   Copyright 2009-2017, MetaQuotes Software Corp. |
//|                                              http://www.mql5.com |
//+------------------------------------------------------------------+
#include <Expert\ExpertSignal.mqh>
#include <My\Cql.mqh>
#resource "Python/EURUSD_H1_D1_critic2.onnx" as uchar __CRITIC_2[]
#resource "Python/EURUSD_H1_D1_critic1.onnx" as uchar __CRITIC_1[]
#resource "Python/EURUSD_H1_D1_actor.onnx" as uchar __ACTOR[]
#define  __ACTIONS 3
#define  __ENVIONMENTS 3

我们导出到 python 的是品种 EURUSD 于 2023.12.12 至 2024.12.12 间 H1 时间帧的数据。训练时间为三分之二，即八个月，这意味着我们据 2023.12.12 到 2024.08.12 进行训练。因此，我们能从 2024.08.12 开始进行前向测试。这段区间勉强超过 4 个月，确实不太长，但因为我们采用的是 H1 时间帧，所以它可能很重要。

由于反向传播已经在 python 中完成，故我们没有包含优化这些向前漫游的特殊输入参数。我们的类接口如下：

//+------------------------------------------------------------------+
//| SACs CSignalSAC.                                                 |
//| Purpose: Soft Actor Critic for Reinforcement-Learning.           |
//|            Derives from class CExpertSignal.                     |
//+------------------------------------------------------------------+
//+------------------------------------------------------------------+
//|                                                                  |
//+------------------------------------------------------------------+
class CSignalSAC   : public CExpertSignal
{
protected:

   long                          m_critic_2_handle;
   long                          m_critic_1_handle;
   long                          m_actor_handle;

public:
   void                          CSignalSAC(void);
   void                          ~CSignalSAC(void);

   //--- methods of setting adjustable parameters

   //--- method of verification of arch
   virtual bool      ValidationSettings(void);
   //--- method of creating the indicator and timeseries
   virtual bool      InitIndicators(CIndicators *indicators);
   //--- methods of checking if the market models are formed
   virtual int       LongCondition(void);
   virtual int       ShortCondition(void);

protected:
   vectorf           GetOutput();
   vectorf           LogProbabilities(vectorf &Mean, vectorf &Log_STD);
};

我们如下进行初始化，并验证每个 ONNX 模型的输入层和输出层大小：

//+------------------------------------------------------------------+
//| Validation arch protected data.                                  |
//+------------------------------------------------------------------+
bool CSignalSAC::ValidationSettings(void)
{  if(!CExpertSignal::ValidationSettings())
      return(false);
//--- initial data checks
   if(m_period > PERIOD_H1)
   {  Print(" time frame too large ");
      return(false);
   }
   ResetLastError();
   if(m_critic_2_handle == INVALID_HANDLE)
   {  Print("Crit 2 OnnxCreateFromBuffer error ", GetLastError());
      return(false);
   }
   if(m_critic_1_handle == INVALID_HANDLE)
   {  Print("Crit 1 OnnxCreateFromBuffer error ", GetLastError());
      return(false);
   }
   if(m_actor_handle == INVALID_HANDLE)
   {  Print("Actor OnnxCreateFromBuffer error ", GetLastError());
      return(false);
   }
   // Set input shapes
   const long _critic_in_shape[] = {1, 4, 1};
   const long _actor_in_shape[] = {1};
   // Set output shapes
   const long _critic_out_shape[] = {1, 4, 1, 1};
   const long _actor_out_shape[] = {1, 6};
   if(!OnnxSetInputShape(m_critic_2_handle, ONNX_DEFAULT, _critic_in_shape))
   {  Print("Crit 2  OnnxSetInputShape error ", GetLastError());
      return(false);
   }
   if(!OnnxSetOutputShape(m_critic_2_handle, 0, _critic_out_shape))
   {  Print("Crit 2  OnnxSetOutputShape error ", GetLastError());
      return(false);
   }
   if(!OnnxSetInputShape(m_critic_1_handle, ONNX_DEFAULT, _critic_in_shape))
   {  Print("Crit 1 OnnxSetInputShape error ", GetLastError());
      return(false);
   }
   if(!OnnxSetOutputShape(m_critic_1_handle, 0, _critic_out_shape))
   {  Print("Crit 1 OnnxSetOutputShape error ", GetLastError());
      return(false);
   }
   if(!OnnxSetInputShape(m_actor_handle, ONNX_DEFAULT, _actor_in_shape))
   {  Print("Actor OnnxSetInputShape error ", GetLastError());
      return(false);
   }
   if(!OnnxSetOutputShape(m_actor_handle, 0, _actor_out_shape))
   {  Print("Actor OnnxSetOutputShape error ", GetLastError());
      return(false);
   }
//read best weights
//--- ok
   return(true);
}

在层形状上，值得注意的是，我们必须进行更改，以简化我们导出 ONNX，即使它们违背了 SAC 的基本逻辑。首先，参与者网络旨在导出 2 个向量的平均向量，及一个对数标准差向量。若在 ONNX 层形状中定义这些很容易出错，故我们在 python 中将它们组合成一个向量，如上面的 for 循环代码中所述。此外，评论者网络的输入是 2-叠，即参与者网络提供的环境状态、及动作概率分布。这通常也可以定义为 2 个张量，但为了简单起见，我们再次将它们组合成一个大小为 4 的向量。我们的 GetOutput 函数如下：

//+------------------------------------------------------------------+
//| This function calculates the next actions to be selected from    |
//| the Reinforcement Learning Cycle.                                |
//+------------------------------------------------------------------+
vectorf CSignalSAC::GetOutput()
{  vectorf _out;
   int _load = 1;
   static vectorf _x_states(1);
   _out.Init(__ACTIONS);
   _out.Fill(0.0);
   vector _in, _in_row, _in_row_old, _in_col, _in_col_old;
   if
   (
      _in_row.Init(_load) &&
      _in_row.CopyRates(m_symbol.Name(), PERIOD_H1, 8, 0, _load) &&
      _in_row.Size() == _load
      &&
      _in_row_old.Init(_load) &&
      _in_row_old.CopyRates(m_symbol.Name(), PERIOD_H1, 8, 1, _load) &&
      _in_row_old.Size() == _load
      &&
      _in_col.Init(_load) &&
      _in_col.CopyRates(m_symbol.Name(), PERIOD_D1, 8, 0, _load) &&
      _in_col.Size() == _load
      &&
      _in_col_old.Init(_load) &&
      _in_col_old.CopyRates(m_symbol.Name(), PERIOD_D1, 8, 1, _load) &&
      _in_col_old.Size() == _load
   )
   {  _in_row -= _in_row_old;
      _in_col -= _in_col_old;
      Cql *QL;
      Sql _RL;
      _RL.actions  = __ACTIONS;//buy, sell, do nothing
      _RL.environments = __ENVIONMENTS;//bullish, bearish, flat
      QL = new Cql(_RL);
      vector _e(_load);
      QL.Environment(_in_row, _in_col, _e);
      delete QL;
      _x_states[0] = float(_e[0]);
      static matrixf _y_mu_logstd(6, 1);
//--- run the inference
      ResetLastError();
      if(!OnnxRun(m_actor_handle, ONNX_NO_CONVERSION, _x_states, _y_mu_logstd))
      {  Print("Actor OnnxConversion error ", GetLastError());
         return(_out);
      }
      else
      {  vectorf _mu(__ACTIONS), _logstd(__ACTIONS);
         _mu.Fill(0.0); _logstd.Fill(0.0);
         for(int i=0;i<__ACTIONS;i++)
         {  _mu[i] = _y_mu_logstd[i][0];
            _logstd[i] = _y_mu_logstd[i+__ACTIONS][0];
         }
         _out = LogProbabilities(_mu, _logstd);
      }
   }
   return(_out);
}

迄今为止，我们一如既往坚持使用相同模型，即 9 种环境状态、和 3 种可能的动作。为了处理动作的概率分布，我们需要对数概率函数，其代码已在本文开头分享。使用向导进行编译，并对数据窗口的剩余 4 个月执行测试运行，会向我们呈现以下报告：

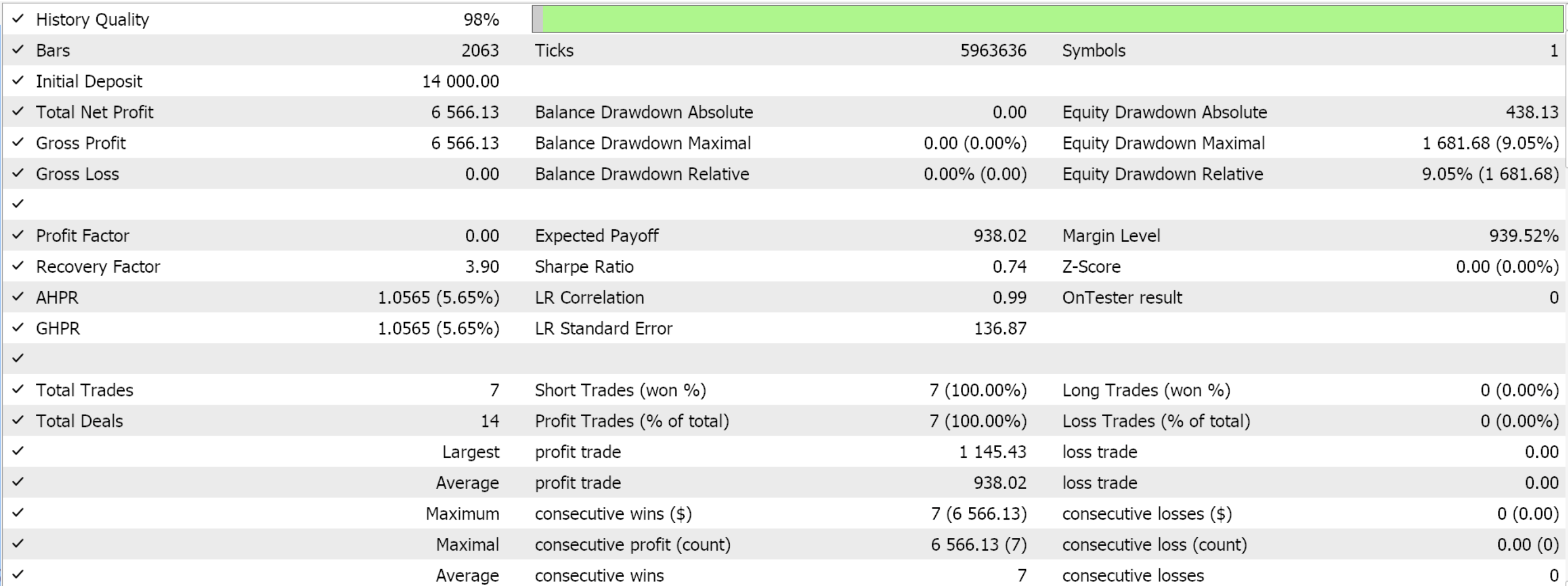
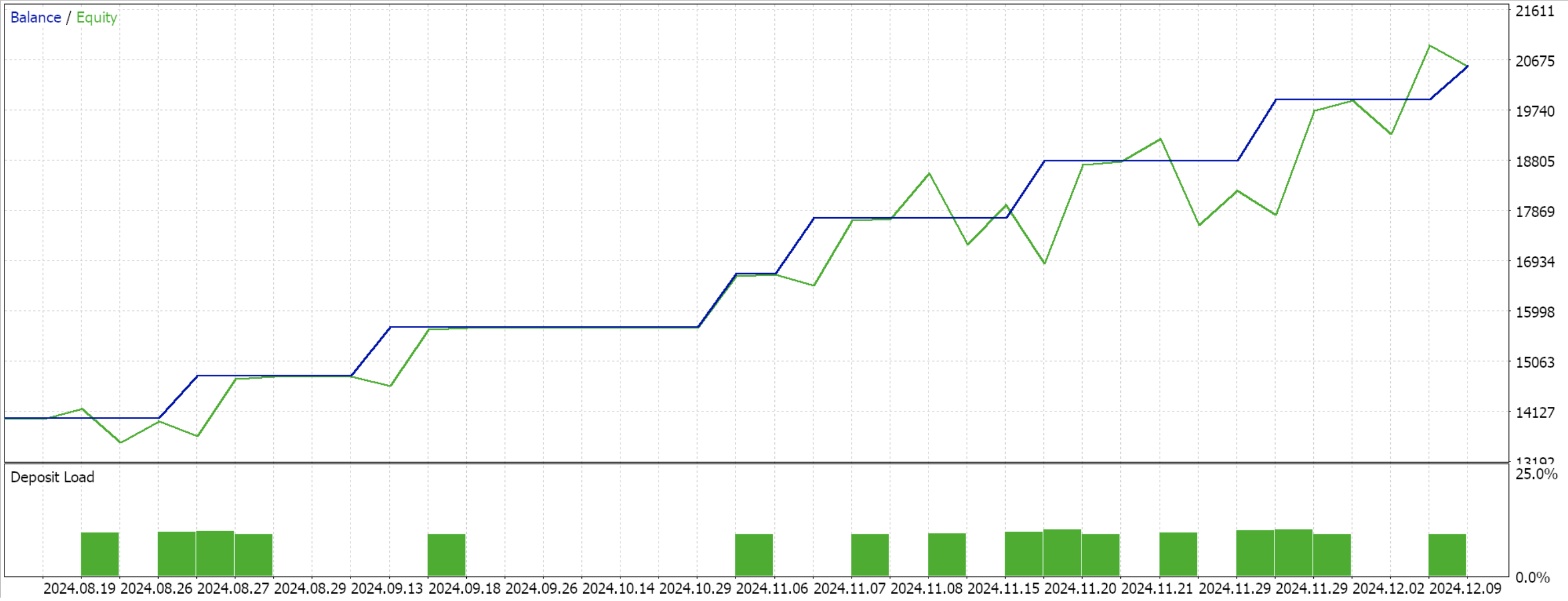
结束语

我们考察了一个非常基本的 python 强化学习 SAC 实现场景，其未用张量智代函数库，从而利用它所带来的效率。该方式阐述了 SAC 的基础，并强调了为什么反向传播有点旷日持久，因为它涉及多个网络配对，而其中并不存在典型的训练数据集。SAC 原则上旨在通过由 alpha 参数（我们在高斯分布中应用的）调制的熵，来安全地促进更多的探索。因此，邀请读者来研究一个非固定 alpha，以便更多地探索这一点，譬如具有目标熵值的自动调整。我们还会在以后的文章中深入这些示例。

文件名	描述
WZ_51.mq5	向导汇编的智能系统，所示文件作为头文件
SignalWZ_51.mqh	自定义信号类文件
EURUSD_H1_D1_critic2.onnx	评论者 2 ONNX 网络
EURUSD_H1_D1_critic1.onnx	评论者 1 ONNX 网络
EURUSD_H1_D1_actor.onnx	参与者网络