Características del Wizard MQL5 que debe conocer (Parte 51): Aprendizaje por refuerzo con SAC

Introducción

Soft Actor Critic (SAC) es otro algoritmo de aprendizaje por refuerzo que estamos considerando, después de haber analizado algunos otros, entre los que se incluyen Proximal Policy Optimization (PPO), Deep-Q-Networks (DQN), SARSA y otros. Sin embargo, este algoritmo, al igual que algunos que ya hemos visto, utiliza redes neuronales, pero con una salvedad importante. El número total de redes utilizadas es tres, y estas son: dos redes críticas y una red de actores. Las dos redes críticas realizan predicciones de recompensa (valores Q) cuando se les introduce una acción y un estado del entorno, y el mínimo de las salidas de estas dos redes se utiliza para modular la función de pérdida empleada para entrenar la red de actores.

Las entradas a la red de actores son coordenadas del estado del entorno, y la salida es doble. Un vector medio y un vector de desviación estándar logarítmica. Mediante el uso del proceso gaussiano, estos dos vectores se utilizan para derivar una distribución de probabilidad para las posibles acciones que puede realizar el actor. Así pues, mientras que las dos redes críticas pueden entrenarse de forma tradicional, la red de actores es claramente harina de otro costal. Hay bastante que abordar aquí, así que primero reiteremos los conceptos básicos antes de continuar. Las dos redes críticas para la entrada toman el estado actual del entorno y una acción. Su resultado es una estimación del rendimiento esperado (valor Q) de realizar esa acción en ese estado. El uso de dos críticos ayuda a reducir el sesgo de sobreestimación, un problema habitual en el aprendizaje Q.

La red de actores tiene como entrada el estado actual del entorno. Su resultado es, efectivamente, una distribución de probabilidad sobre las posibles acciones, siendo esta distribución estocástica para fomentar la exploración. Utilizo la expresión «efectivamente» porque los resultados reales de la red de actores son dos vectores que deben introducirse en una distribución de probabilidad gaussiana para obtener los pesos de cada acción. En MQL5, lo hacemos de la siguiente manera:

//+------------------------------------------------------------------+
// Function to compute the Gaussian probability distribution and log
// probabilities
//+------------------------------------------------------------------+
vectorf CSignalSAC::LogProbabilities(vectorf &Mean, vectorf &Log_STD)
{  vectorf _log_probs;
   // Compute standard deviations from log_std
   vectorf _std = exp(Log_STD);
   // Sample actions and compute log probabilities
   float _z = float(rand() % USHORT_MAX / USHORT_MAX); // Generate N(0, 1) sample
   // Sample action using reparameterization trick: action = mean + std * N(0, 1)
   vectorf _actions = Mean + (_std * _z);
   // Compute log probability of the sampled action
   vectorf _variance = _std * _std;
   vectorf _diff = _actions - Mean;
   _log_probs = -0.5f * (log(2.0f * M_PI * _variance) + (_diff * _diff) / _variance);
   return(_log_probs);
}

Cómo funciona SAC

Dicho esto, SAC funciona como la mayoría de los algoritmos de aprendizaje por refuerzo. En primer lugar, está la selección de acciones, en la que el actor toma una muestra de una acción de la distribución de probabilidad de las salidas de la red de actores. A continuación, se produce la «interacción con el entorno», en la que el agente lleva a cabo la acción muestreada en el entorno y realiza una observación de su siguiente estado y recompensa. A continuación, se realiza la actualización de los críticos, en la que las dos redes de críticos se actualizan mediante una función de pérdida que utiliza una comparación entre los valores Q previstos y los valores Q objetivo. Sin embargo, como ya se ha señalado anteriormente, la actualización de la red de actores es una novedad, ya que se trata de actualizaciones que utilizan un gradiente de política que tiene como objetivo maximizar el rendimiento esperado, teniendo en cuenta la entropía de la distribución de la política. El objetivo es fomentar la exploración y evitar la convergencia prematura hacia soluciones subóptimas.

La entropía de la distribución de políticas en SAC mide la aleatoriedad o la incertidumbre. En SAC, una mayor entropía se corresponde con más acciones de exploración, mientras que una menor entropía se utiliza para enfatizar las elecciones deterministas. Los resultados de la red de actores en SAC son, por naturaleza, una política estocástica parametrizada por una distribución de probabilidad, que en nuestro caso (para este artículo) es la distribución gaussiana. La entropía de esta distribución describe las acciones que un agente podría llevar a cabo cuando se enfrenta a una situación específica (las entradas).

La importancia de esto radica en fomentar la exploración del agente, como es habitual en la mayoría de los algoritmos de aprendizaje por refuerzo, con el fin de reducir el riesgo de convergencia prematura hacia políticas subóptimas. Esto crea, por lo tanto, un equilibrio entre exploración y explotación. SAC incorpora un término de entropía en su objetivo de optimización de políticas con el fin de maximizar tanto las recompensas esperadas como la entropía. La ecuación objetiva es la siguiente:

Donde:

• α: Temperatura de entropía, equilibrando la maximización de la recompensa y la exploración.
• logπ(a∣s): Probabilidad logarítmica de la acción (el resultado de nuestra función cuyo código se ha compartido anteriormente), que depende tanto de μ como de log(σ).
• Q(s,a): Es el valor Q mínimo de las dos salidas de las redes críticas.

Una mayor entropía tiende a conducir a una toma de decisiones más sólida en entornos con información incompleta, ya que evita el sobreajuste a escenarios concretos. Por lo tanto, maximizar la entropía es algo positivo en SAC. Además de mejorar la exploración, ya que se anima al agente a probar una gama más amplia de acciones o a evitar políticas subóptimas que impiden quedarse estancado en óptimos locales, sirve inherentemente como una forma de regularización al evitar políticas excesivamente deterministas que son propensas a fallar en escenarios imprevistos. Además, los ajustes graduales de la entropía suelen dar lugar a actualizaciones de políticas más fluidas, lo que garantiza una formación y una convergencia estables.

El parámetro de control de la temperatura es muy sensible a la entropía y al proceso de aprendizaje de la red de actores, por lo que vale la pena mencionar por qué. Para nuestros fines, lo fijamos en 0.5, como se puede ver en la función Probabilidades logarítmicas, cuyo código MQL5 se ha compartido anteriormente. Sin embargo, el parámetro de temperatura alfa determina cuánto peso se le da a la energía en el objetivo. Un alfa más alto fomenta la exploración, mientras que un valor más bajo promueve políticas deterministas o la explotación. Por lo tanto, asignarle un valor de 0.5, para nuestros propósitos, supone alcanzar una especie de equilibrio.

Sin embargo, a menudo ocurre que SAC utiliza un mecanismo automático de ajuste de entropía que adapta dinámicamente el alfa para mantener un nivel de entropía objetivo, equilibrando la exploración y la explotación. Las implicaciones prácticas de esto son: un aprendizaje sólido en todas las tareas; la creación de políticas de generalización que se adapten a la información incompleta (políticas estocásticas); y el establecimiento de una base para el aprendizaje continuo. Las posibles desventajas de esto son principalmente dos. Demasiada exploración y coste computacional.

Una entropía excesiva puede conducir a un aprendizaje ineficaz al dar demasiada importancia a las acciones exploratorias en detrimento del aprovechamiento de estrategias conocidas y altamente rentables. Esto siempre vendrá acompañado del cálculo y la optimización de los términos de entropía, lo que añade una sobrecarga computacional en comparación con los algoritmos que solo se centran en la maximización de la recompensa. La red de actores genera dos vectores MU y Log-STD, como se ha mencionado anteriormente, ¿cómo afectan estos a la entropía?

MU representa la tendencia central de la distribución de la acción de la política. No afecta directamente a la entropía, pero en cierto sentido define el comportamiento medio de la política. Por otro lado, el Log-STD controla la dispersión o incertidumbre de la distribución de la acción e influye directamente en la entropía. Un Log-STD más alto significa una distribución de acciones más amplia e incierta, mientras que un Log-STD más bajo apunta a lo contrario. ¿Qué relación tiene entonces la magnitud de una acción determinada en el Log-STD con la probabilidad de selección?

Los detalles específicos los determina el proceso gaussiano, como ya se ha mencionado, sin embargo, un Log-STD bajo suele implicar que la red de actores está segura de la acción óptima, MU. Esto a menudo implica una menor variabilidad en las acciones muestreadas. Las acciones muestreadas se concentrarán más estrechamente en torno al valor MU correspondiente a esta acción, que tiene una lectura Log-STD baja, lo que fomentaría un mayor aprovechamiento de las políticas relacionadas con esta acción. Por lo tanto, aunque los valores bajos de Log-STD no aumentan directamente la probabilidad de que se realice una acción, en esencia reducen el alcance de las acciones potenciales, lo que aumenta la probabilidad de que se elijan acciones cercanas a MU.

También hay algunos ajustes prácticos que se aplican a menudo a la entropía. En primer lugar, dado que Log-STD determina directamente la entropía, para un entrenamiento estable, SAC suele limitar log(σ) dentro de un rango para evitar una entropía extremadamente alta o baja. Esto se hace con el parámetro «z» que se muestra en nuestra función de probabilidades de registro anterior. En segundo lugar, el ajuste de alfa (que establecemos en 0.5f en nuestra función de probabilidades logarítmicas) es crucial para lograr el equilibrio entre exploración y explotación mencionado anteriormente. Con este fin, a menudo se utiliza el ajuste automático alfa como medio para lograr de forma dinámica un equilibrio entre la explotación y la exploración.

Esto se consigue utilizando un objetivo de entropía H. La siguiente ecuación lo define:

Donde:

• alpha (α t ): Es la temperatura actual que controla el peso del término de entropía en el objetivo, donde los valores más altos fomentan la exploración, mientras que los valores más bajos se inclinan hacia la explotación.

• alpha (αt+1 ): Es el parámetro de temperatura actualizado después de incluir la retroalimentación de la entropía actual en relación con el objetivo.

• lambda (λ): Es una tasa de aprendizaje para el proceso de ajuste alfa que controla la rapidez con la que alfa se adapta a las desviaciones del objetivo de entropía H.

• E (E a~π ): Es la expectativa derivada de las medidas incluidas en el plan de políticas actual.

• Log(a|s): Es la probabilidad logarítmica de la acción a en el estado s bajo la política actual. Cuantifica la incertidumbre de la selección de acciones de la política.

• H: Sirve como valor de entropía objetivo de la política. A menudo se asigna en función de la dimensionalidad del espacio de acción (número y alcance de las acciones disponibles) en los casos en que las acciones son discretas, como las implementaciones de compra, venta y mantenimiento que hemos considerado hasta ahora; también se puede escalar si las acciones son continuas (por ejemplo, si tuviéramos órdenes de mercado bidimensionales escaladas de 0.01 a 0.10 para el tamaño de la posición de dos valores que se comprarán simultáneamente con valores que son un porcentaje del margen libre).

Por lo tanto, el uso del ajuste automático de alfa, aunque no se ha explorado en nuestra implementación para este artículo, garantiza que el agente se adapte dinámicamente a los cambios en el entorno, elimina la necesidad de ajustar manualmente el alfa y promueve un aprendizaje eficiente mediante el mantenimiento de un equilibrio preestablecido entre exploración y explotación.

Comparación entre SAC y DQN

Hasta ahora hemos considerado otro algoritmo de aprendizaje por refuerzo que utiliza una única red neuronal, concretamente las Deep-Q-Networks (DQN). Entonces, ¿qué ventajas, si las hay, ofrece el uso de SAC con sus múltiples redes? Para defender el SAC, consideremos un caso práctico de una tarea de manipulación con robots. Así pues, esta es la tarea: se necesita un brazo robótico para sujetar y mover objetos a ubicaciones específicas. A las articulaciones de sus brazos se les asignarían espacios de acción continuos que cuantifican los ajustes necesarios de par y ángulo, etc.

Los retos que plantea el uso de una DQN en este caso son, en primer lugar, que la DQN es más adecuada para espacios de acción discretos. Intentar ampliarlo para acomodar un espacio continuo conduciría a un crecimiento exponencial del número de acciones discretas disponibles para espacios de acción de mayor dimensión, lo que haría que el entrenamiento resultara demasiado costoso e ineficaz. Las DQN también se basan en estrategias epsilon-greedy para equilibrar la exploración y la explotación, y estas pueden tener dificultades para funcionar de manera eficiente en los espacios discretizados de mayor dimensión. Por último, DQN es propenso a un sesgo de sobreestimación que podría provocar cierta inestabilidad durante el entrenamiento, especialmente en entornos complejos con una alta variabilidad en las recompensas.

En este caso, el SAC sería más adecuado, principalmente por su apoyo continuo al espacio de acción. Esto se manifiesta en la forma en que SAC optimiza la política estocástica sobre espacios de acción continuos, lo que elimina la necesidad de discretizar (o clasificar) las acciones. Esto permite un control suave y preciso del brazo del robot. Las tres redes de SAC funcionan en sinergia, donde la red de actores genera una política estocástica para establecer la distribución (ponderación probabilística) de las acciones continuas. Esto promueve la eficiencia y evita la exploración prematura.

Por su parte, las redes críticas utilizan un método de estimación del valor Q doble que ayuda a evitar el sesgo de sobreestimación al reenviar el valor mínimo en la propagación hacia atrás a la red de actores. Esto estabiliza el entrenamiento y garantiza resultados más precisos. En resumen, el objetivo aumentado por la entropía que fomenta una mayor exploración (especialmente cuando se combina con el ajuste automático de la temperatura, como se ha argumentado anteriormente con alfa), junto con la robustez y la estabilidad que proporciona la capacidad de SAC para manejar espacios de acción de alta dimensión, lo sitúan claramente un paso por delante de DQN. A tal fin, los ejemplos de rendimiento publicados de las tareas Reacher y Fetch de Open AI Gym indican claramente que DQN tiene dificultades para producir movimientos fluidos del brazo debido a sus salidas de acción discretizadas y a su escasa exploración, con políticas que convergen en gran medida en estrategias subóptimas. Por otro lado, SAC genera acciones precisas y fluidas, con una política estocástica que permite completar las tareas más rápidamente, reducir las colisiones y adaptarse mejor a los cambios en la posición de los objetos o la ubicación de los objetivos, gracias, una vez más, al enfoque de política estocástica.

Python y TensorFlow

Para este artículo, a diferencia de los anteriores artículos sobre aprendizaje automático, nos sumergimos en TensorFlow de Python. MQL5, el lenguaje principal de MetaQuotes, sigue siendo relevante, ya que los asesores expertos creados por el asistente dependen en gran medida de él. Para los nuevos lectores, hay guías aquí y aquí sobre cómo utilizar el código adjunto al final de este artículo para montar un Asesor Experto. Sin embargo, Python está sin duda mermando la relevancia y el dominio de MQL5 como lenguaje de programación preferido para el desarrollo de modelos financieros. Un rápido reconocimiento podría indicar que MetaQuotes simplemente necesita publicar más librerías en Python para mantenerse al día con la innovación y seguir reafirmando su dominio. 

Sin embargo, tengo la edad suficiente para recordar la introducción de MetaTrader 5 en 2009 (?). Y la lenta y laboriosa aceptación que recibieron por parte de sus clientes a pesar de todas las ventajas que ofrecía. Por lo tanto, puedo entender por qué dudan en implementar y mantener librerías activas en Python. Dicho esto, las innovaciones que se presentan aquí provienen en su mayoría de los «clientes» (es decir, la comunidad Python) y no de MetaQuotes, como fue el caso de MetaTrader 5, donde se implementaron posiciones en lugar de órdenes. Entonces, ¿quizás deberían prestar atención a esto con cierta urgencia? El tiempo lo dirá, pero mientras tanto, las ventajas en términos de eficiencia que ofrece el uso no solo de TensorFlow, sino también de PyTorch, no solo en el desarrollo, sino sobre todo en el entrenamiento de redes, son realmente enormes.

En mi opinión, MetaQuotes puede explorar patrocinios corporativos, convertirse en colaborador o incluso crear proyectos derivados para las librerías clave de Python de Pandas, NumPy y Sci-Kit; y, entre otras cosas, permitir la lectura de sus formatos de archivo altamente comprimidos *.hcc y *.tkc. Pero estas son reflexiones generales. Volviendo a TensorFlow, en primer lugar, ofrece capacidades avanzadas de aprendizaje profundo que son principalmente de dos tipos. En cuanto al software y al GPU/hardware.  

MQL5 es compatible con OpenCL, por lo que se podría argumentar que ambos lenguajes están al mismo nivel, pero no se puede decir lo mismo de las librerías y herramientas avanzadas de Python para crear, entrenar y optimizar modelos de aprendizaje profundo. Estas librerías incluyen soporte para arquitecturas complejas como SAC a través de los agentes de TensorFlow.

También cuenta con un rico ecosistema con herramientas preconstruidas, como una base estable para promover el aprendizaje por refuerzo (además de los agentes tensoriales); permite flexibilidad y experimentación, ya que se pueden crear rápidamente prototipos y probar una amplia variedad de implementaciones de modelos; Es altamente reproducible y fácil de depurar (especialmente cuando se utilizan herramientas como Tensor-Board para visualizar y entrenar matrices/kernels); ofrece interoperabilidad con formatos exportables como ONNX; y cuenta con un apoyo comunitario muy amplio y creciente, además de actualizaciones periódicas.

SAC se puede implementar en Python de muchas formas diferentes. A fin de ilustrar los principios fundamentales, nos centraremos únicamente en dos enfoques. El primero de ellos define manualmente las tres redes principales del SAC y, mediante iteraciones de bucles for, entrena y prueba el modelo SAC. El segundo utiliza los ya mencionados agentes tensoriales que vienen con la librería Python y que están específicamente diseñados para ayudar en el aprendizaje por refuerzo.

Los pasos del enfoque iterativo manual son: diseñar los componentes SAC en TensorFlow/Keras, donde para la red de actores esto implica definir una red neuronal que genere una política estocástica para el muestreo gaussiano; para las redes críticas, esto significa construir dos redes de valor Q para el aprendizaje Q gemelo con el fin de gestionar el sesgo de sobreestimación; y definir el régimen de regularización de entropía n para una exploración eficiente. Para nuestros fines, tal y como se ha mencionado anteriormente, nuestra entropía utiliza un valor fijo de alfa de 0.5. La fuente inicial que cubre estos aspectos es la siguiente:

import numpy as np
import pandas as pd

from sklearn.model_selection import train_test_split

import tensorflow as tf

print("Num GPUs Available: ", len(tf.config.list_physical_devices('GPU')))

from tensorflow.keras import optimizers
from tensorflow.keras.layers import Input
from tensorflow.keras import layers
from tensorflow import keras
import tf2onnx
import onnx

import os

# Define the actor network
def ActorNetwork(state_dim, action_dim, hidden_units=256):
    """
    Creates a simple SAC actor network.
    
    :param state_dim: The dimension of the state space.
    :param action_dim: The dimension of the action space.
    :param hidden_units: The number of hidden units in each layer.
    :return: A Keras model representing the actor network.
    """
    # Input layer
    state_input = layers.Input(shape=(state_dim, ))
    
    # Hidden layers (Dense layers with ReLU activation)
    x = layers.Dense(hidden_units, activation='relu')(state_input)
    x = layers.Dense(hidden_units, activation='relu')(x)
    
    # Output layer: output means (mu) and log standard deviation (log_std) for Gaussian distribution
    
    output_size = action_dim + action_dim
    stacked_mean_logs = layers.Dense(output_size)(x)
    
    # Create the model

    actor_model = tf.keras.Model(inputs=state_input, outputs=stacked_mean_logs)
    
    return actor_model

# Define the critic network
def CriticNetwork(state_dim, action_dim, hidden_units=256):
    """
    Creates a simple SAC critic network (Q-value approximation).
    
    :param state_dim: The dimension of the state space.
    :param action_dim: The dimension of the action space.
    :param hidden_units: The number of hidden units in each layer.
    :return: A Keras model representing the critic network.
    """
    
    input_size = state_dim + action_dim
    state_action_inputs = layers.Input(shape=(None, input_size, 1))  # Concatenate state and action
    
    # Hidden layers (Dense layers with ReLU activation)
    x = layers.Dense(hidden_units, activation='relu')(state_action_inputs)
    x = layers.Dense(hidden_units, activation='relu')(x)
    
    # Output layer: Q-value for the given state-action pair
    q_value_output = layers.Dense(1)(x)  # Single output for Q-value
    
    # Create the model 
    critic_model = tf.keras.Model(inputs=state_action_inputs, outputs=q_value_output)
    
    return critic_model

Después de esto, tendríamos que entrenar el modelo SAC en TensorFlow/Keras. Esto normalmente implicaría utilizar una antigua librería de MetaTrader 5 para importar datos de MetaTrader 5 desde el terminal MetaTrader y, a continuación, dividir estos datos en datos de prueba y datos de entrenamiento. Estamos utilizando una proporción de entrenamiento de dos tercios, lo que deja un tercio para las pruebas. Simulamos la configuración comercial de MetaTrader 5 en un bucle for tedioso y altamente ineficiente que, como era de esperar, tiene un tamaño determinado por el número de épocas y el tamaño de los datos de entrenamiento. Además, nuestro objetivo es optimizar las redes de actores y críticos con la función objetivo SAC, incluyendo el término de entropía. El código relacionado con esto se comparte a continuación:

# Filter the DataFrame to keep only the '<state>' column
df = pd.read_csv(name_csv)

states = df.filter(['<STATE>']).astype(int).values
# Extract the '<state>' column as an integer array
rewards = df.filter(['<REWARD>']).values

states_size = int(len(states)*(2.0/3.0))
actor_x_train = states[0:states_size,:]
actor_x_test = states[states_size:,:1]
rewards_size = int(len(rewards)*(2.0/3.0))
critic_y_train = rewards[0:rewards_size,:]
critic_y_test = rewards[rewards_size:,:1]

# Initialize networks and optimizers
input_dim = 1  # 2 states, of 3 gradations are flattened into a single index
output_dim = 3  # possible actions buy, sell, hold
actor = ActorNetwork(input_dim, output_dim)
critic1 = CriticNetwork(input_dim, output_dim)  # Input paired with action
critic2 = CriticNetwork(input_dim, output_dim)  # Input paired with action

critic_optimizer_1 = tf.keras.optimizers.Adam(learning_rate=0.001)
critic_optimizer_2 = tf.keras.optimizers.Adam(learning_rate=0.001)
actor_optimizer = tf.keras.optimizers.Adam(learning_rate=0.001)

# Training loop
for e in range(epoch_size):
    train_critic_loss1 = 0
    train_critic_loss2 = 0
    train_actor_loss = 0
    
    for i in range(actor_x_train.shape[0]):
        input_state = tf.expand_dims(actor_x_train[i], axis=0)  # Select a single sample and maintain batch dim
        target_q = tf.expand_dims(critic_y_train[i], axis=0)

        # Actor forward pass and sampling
        with tf.GradientTape(persistent=True) as tape:

            actor_output = actor(input_state)
            # Split the vector into mean and log_std
            mu = actor_output[:, :output_dim]     # First 3 values
            log_std = actor_output[:, output_dim:]  # Last 3 values
            std = tf.exp(log_std)
            sampled_action = tf.random.normal(shape=mu.shape, mean=mu, stddev=std)  # Sample action from Gaussian

            # Concatenate the state and action tensors
            in_state = tf.convert_to_tensor(tf.cast(input_state, dtype=tf.float32), dtype=tf.float32)  # Ensure it's a tensor
            in_action = tf.convert_to_tensor(tf.cast(sampled_action, dtype=tf.float32), dtype=tf.float32)
            
            # Concatenate along the last axis
            critic_raw_input = tf.concat([in_state, in_action], axis=-1)  # Ensure correct axis
            critic_input = tf.reshape(critic_raw_input, [-1, 1, 4, 1])  # -1 infers the batch size dynamically

            q_value1 = critic1(critic_input)
            q_value2 = critic2(critic_input)

            # Critic loss (mean squared error)
            critic_loss1 = tf.reduce_mean((tf.cast(q_value1, tf.float32) - tf.cast(target_q, tf.float32)) ** 2)
            critic_loss2 = tf.reduce_mean((tf.cast(q_value2, tf.float32) - tf.cast(target_q, tf.float32)) ** 2)

            # Actor loss (maximize expected Q-value based on minimum critic output)
            min_q_value = tf.minimum(q_value1, q_value2)  # Take the minimum Q-value
            actor_loss = tf.reduce_mean(min_q_value)  # Maximize expected Q-value (negative for minimization)

        # Backpropagation
        critic_gradients1 = tape.gradient(critic_loss1, critic1.trainable_variables)
        critic_gradients2 = tape.gradient(critic_loss2, critic2.trainable_variables)
        actor_gradients = [-grad for grad in tape.gradient(actor_loss, actor.trainable_variables)]

        del tape  # Free up resources from persistent GradientTape
        
        critic_optimizer_1.apply_gradients(zip(critic_gradients1, critic1.trainable_variables))
        critic_optimizer_2.apply_gradients(zip(critic_gradients2, critic2.trainable_variables))
        actor_optimizer.apply_gradients(zip(actor_gradients, actor.trainable_variables))
        
        # Accumulate losses for epoch summary
        train_critic_loss1 += critic_loss1.numpy()
        train_critic_loss2 += critic_loss2.numpy()
        train_actor_loss += actor_loss.numpy()

    print(f"  Epoch {e + 1}/{epoch_size}:")
    print(f"  Train Critic Loss 1: {train_critic_loss1 / actor_x_train.shape[0]:.4f}")
    print(f"  Train Critic Loss 2: {train_critic_loss2 / actor_x_train.shape[0]:.4f}")
    print(f"  Train Actor Loss: {train_actor_loss / actor_x_train.shape[0]:.4f}")
    print("-" * 40)

critic2.summary()
critic1.summary()
actor.summary()

Tras la formación, estaríamos dispuestos a exportar nuestro modelo, que comprende tres redes, a ONNX. ONNX, abreviatura de Open Neural Network Exchange, proporciona un estándar abierto para la interoperabilidad del aprendizaje automático, en el que los modelos entrenados en Python utilizando diversas librerías como PyTorch o SciKit-Learn pueden exportarse a este formato para su uso en una mayor variedad de plataformas y lenguajes de programación, entre los que se encuentra MQL5. Esta compatibilidad elimina la necesidad de replicar la compleja lógica del aprendizaje automático, lo que ahorra tiempo y reduce los errores.

La importación de ONNX como recurso permite la compilación de un único archivo ex5 que incluye el modelo de aprendizaje automático ONNX y la lógica de ejecución de operaciones MQL5, por lo que los operadores no tienen que lidiar con múltiples archivos. Dicho esto, el proceso de exportación de Python a ONNX tiene. Número de opciones, una de las cuales es tf2onnx, pero no es la única, ya que también existen: onnxmltools, skl2onnx, transformers.onnx (para hugging face) y mxnet.contrib.onnx. Sin embargo, lo que es crucial en la etapa de exportación es asegurarse de que las formas de las capas de entrada y salida de cada red se registren y almacenen correctamente, ya que en MQL5 esta información es crucial para inicializar con precisión los respectivos manejadores ONNX para cada red. Lo hacemos de la siguiente manera:

# Check input and output layer shapes for importing ONNX
import onnxruntime as ort

session_critic2 = ort.InferenceSession(path_critic2_onnx)
session_critic1 = ort.InferenceSession(path_critic1_onnx)
session_actor = ort.InferenceSession(path_actor_onnx)

for i in session_critic2.get_inputs():
    print(f"in critic2 Name: {i.name}, Shape: {i.shape}, Type: {i.type}")

for i in session_critic1.get_inputs():
    print(f"in critic1 Name: {i.name}, Shape: {i.shape}, Type: {i.type}")

for i in session_actor.get_inputs():
    print(f"in actor Name: {i.name}, Shape: {i.shape}, Type: {i.type}")
    

for o in session_critic2.get_outputs():
    print(f"out critic2 Name: {o.name}, Shape: {o.shape}, Type: {o.type}")

for o in session_critic1.get_outputs():
    print(f"out critic1 Name: {o.name}, Shape: {o.shape}, Type: {o.type}")

for o in session_actor.get_outputs():
    print(f"out actor Name: {o.name}, Shape: {o.shape}, Type: {o.type}")

El rendimiento del código Python con esta implementación que utiliza bucles «for» como se ha indicado anteriormente dista mucho de ser eficiente; de hecho, es muy similar al de MQL5, ya que no se aprovecha adecuadamente el uso de tensores/gráficos. Sin embargo, es necesario porque la función fit de TensorFlow, que a menudo se utiliza para aprovechar la eficiencia de entrenamiento de TensorFlow, no habría sido aplicable en este caso, dado que en la retropropagación se utilizan los resultados de las dos redes críticas (los valores Q) para entrenar la red de actores. La red de actores no tiene vectores objetivo ni conjuntos de datos objetivo como las redes críticas o la mayoría de las redes neuronales típicas.

El segundo enfoque para implementar esto utiliza agentes tensoriales, que son librerías integradas para gestionar el refuerzo dentro de TensorFlow y Python. Analizaremos este tema en profundidad en próximos artículos, pero basta con decir que la inicialización no solo abarca las redes constituyentes, sino que también tiene en cuenta el entorno y los agentes. Aspectos cruciales del aprendizaje por refuerzo que podrían pasarse por alto si se presta demasiada atención a la eficiencia del entrenamiento de la red.

En combinación con MQL5

Importamos nuestros modelos ONNX exportados a los recursos de MQL5, lo que nos presenta el siguiente encabezado en nuestro archivo de clase de señal personalizado.

//+------------------------------------------------------------------+
//|                                                    SignalSAC.mqh |
//|                   Copyright 2009-2017, MetaQuotes Software Corp. |
//|                                              http://www.mql5.com |
//+------------------------------------------------------------------+
#include <Expert\ExpertSignal.mqh>
#include <My\Cql.mqh>
#resource "Python/EURUSD_H1_D1_critic2.onnx" as uchar __CRITIC_2[]
#resource "Python/EURUSD_H1_D1_critic1.onnx" as uchar __CRITIC_1[]
#resource "Python/EURUSD_H1_D1_actor.onnx" as uchar __ACTOR[]
#define  __ACTIONS 3
#define  __ENVIONMENTS 3

Los datos que exportamos a Python correspondían al símbolo EURUSD en el marco temporal horario desde el 12/12/2023 hasta el 12/12/2024. La formación duró dos tercios del tiempo, lo que equivale a ocho meses, es decir, nos formamos desde el 12 de diciembre de 2023 hasta el 12 de agosto de 2024. Por lo tanto, podemos realizar pruebas a partir del 12 de agosto de 2024. Esto supone un periodo de apenas más de cuatro meses, lo que realmente no es mucho tiempo, pero dado que estamos utilizando un marco temporal de una hora, podría ser significativo.

Dado que la propagación hacia atrás ya se ha realizado en Python, no incluimos ningún parámetro de entrada especial para la optimización en estas ejecuciones hacia adelante. Por lo tanto, nuestra interfaz de clase es la siguiente:

//+------------------------------------------------------------------+
//| SACs CSignalSAC.                                                 |
//| Purpose: Soft Actor Critic for Reinforcement-Learning.           |
//|            Derives from class CExpertSignal.                     |
//+------------------------------------------------------------------+
//+------------------------------------------------------------------+
//|                                                                  |
//+------------------------------------------------------------------+
class CSignalSAC   : public CExpertSignal
{
protected:

   long                          m_critic_2_handle;
   long                          m_critic_1_handle;
   long                          m_actor_handle;

public:
   void                          CSignalSAC(void);
   void                          ~CSignalSAC(void);

   //--- methods of setting adjustable parameters

   //--- method of verification of arch
   virtual bool      ValidationSettings(void);
   //--- method of creating the indicator and timeseries
   virtual bool      InitIndicators(CIndicators *indicators);
   //--- methods of checking if the market models are formed
   virtual int       LongCondition(void);
   virtual int       ShortCondition(void);

protected:
   vectorf           GetOutput();
   vectorf           LogProbabilities(vectorf &Mean, vectorf &Log_STD);
};

Inicializamos y validamos los tamaños de las capas de entrada y salida de cada modelo ONNX de la siguiente manera:

//+------------------------------------------------------------------+
//| Validation arch protected data.                                  |
//+------------------------------------------------------------------+
bool CSignalSAC::ValidationSettings(void)
{  if(!CExpertSignal::ValidationSettings())
      return(false);
//--- initial data checks
   if(m_period > PERIOD_H1)
   {  Print(" time frame too large ");
      return(false);
   }
   ResetLastError();
   if(m_critic_2_handle == INVALID_HANDLE)
   {  Print("Crit 2 OnnxCreateFromBuffer error ", GetLastError());
      return(false);
   }
   if(m_critic_1_handle == INVALID_HANDLE)
   {  Print("Crit 1 OnnxCreateFromBuffer error ", GetLastError());
      return(false);
   }
   if(m_actor_handle == INVALID_HANDLE)
   {  Print("Actor OnnxCreateFromBuffer error ", GetLastError());
      return(false);
   }
   // Set input shapes
   const long _critic_in_shape[] = {1, 4, 1};
   const long _actor_in_shape[] = {1};
   // Set output shapes
   const long _critic_out_shape[] = {1, 4, 1, 1};
   const long _actor_out_shape[] = {1, 6};
   if(!OnnxSetInputShape(m_critic_2_handle, ONNX_DEFAULT, _critic_in_shape))
   {  Print("Crit 2  OnnxSetInputShape error ", GetLastError());
      return(false);
   }
   if(!OnnxSetOutputShape(m_critic_2_handle, 0, _critic_out_shape))
   {  Print("Crit 2  OnnxSetOutputShape error ", GetLastError());
      return(false);
   }
   if(!OnnxSetInputShape(m_critic_1_handle, ONNX_DEFAULT, _critic_in_shape))
   {  Print("Crit 1 OnnxSetInputShape error ", GetLastError());
      return(false);
   }
   if(!OnnxSetOutputShape(m_critic_1_handle, 0, _critic_out_shape))
   {  Print("Crit 1 OnnxSetOutputShape error ", GetLastError());
      return(false);
   }
   if(!OnnxSetInputShape(m_actor_handle, ONNX_DEFAULT, _actor_in_shape))
   {  Print("Actor OnnxSetInputShape error ", GetLastError());
      return(false);
   }
   if(!OnnxSetOutputShape(m_actor_handle, 0, _actor_out_shape))
   {  Print("Actor OnnxSetOutputShape error ", GetLastError());
      return(false);
   }
//read best weights
//--- ok
   return(true);
}

En cuanto a las formas de las capas, cabe destacar que tuvimos que realizar cambios que facilitaron nuestra exportación a ONNX, aunque iban en contra de la lógica básica de SAC. En primer lugar, la red de actores está destinada a exportar dos vectores: vectores medios y un vector de desviación estándar logarítmica. Tener que definir estos en la forma de capa ONNX habría sido propenso a errores, por lo que los combinamos en un único vector dentro de Python, como se indica en el código del bucle «for» anterior. Además, las entradas a las redes críticas son dobles: el estado del entorno y la distribución de probabilidad de acción proporcionada por la red de actores. Esto también se puede definir típicamente como 2 tensores, sin embargo, para simplificar, los hemos combinado de nuevo en un único vector de tamaño 4. Nuestra función de obtención de resultados es la siguiente:

//+------------------------------------------------------------------+
//| This function calculates the next actions to be selected from    |
//| the Reinforcement Learning Cycle.                                |
//+------------------------------------------------------------------+
vectorf CSignalSAC::GetOutput()
{  vectorf _out;
   int _load = 1;
   static vectorf _x_states(1);
   _out.Init(__ACTIONS);
   _out.Fill(0.0);
   vector _in, _in_row, _in_row_old, _in_col, _in_col_old;
   if
   (
      _in_row.Init(_load) &&
      _in_row.CopyRates(m_symbol.Name(), PERIOD_H1, 8, 0, _load) &&
      _in_row.Size() == _load
      &&
      _in_row_old.Init(_load) &&
      _in_row_old.CopyRates(m_symbol.Name(), PERIOD_H1, 8, 1, _load) &&
      _in_row_old.Size() == _load
      &&
      _in_col.Init(_load) &&
      _in_col.CopyRates(m_symbol.Name(), PERIOD_D1, 8, 0, _load) &&
      _in_col.Size() == _load
      &&
      _in_col_old.Init(_load) &&
      _in_col_old.CopyRates(m_symbol.Name(), PERIOD_D1, 8, 1, _load) &&
      _in_col_old.Size() == _load
   )
   {  _in_row -= _in_row_old;
      _in_col -= _in_col_old;
      Cql *QL;
      Sql _RL;
      _RL.actions  = __ACTIONS;//buy, sell, do nothing
      _RL.environments = __ENVIONMENTS;//bullish, bearish, flat
      QL = new Cql(_RL);
      vector _e(_load);
      QL.Environment(_in_row, _in_col, _e);
      delete QL;
      _x_states[0] = float(_e[0]);
      static matrixf _y_mu_logstd(6, 1);
//--- run the inference
      ResetLastError();
      if(!OnnxRun(m_actor_handle, ONNX_NO_CONVERSION, _x_states, _y_mu_logstd))
      {  Print("Actor OnnxConversion error ", GetLastError());
         return(_out);
      }
      else
      {  vectorf _mu(__ACTIONS), _logstd(__ACTIONS);
         _mu.Fill(0.0); _logstd.Fill(0.0);
         for(int i=0;i<__ACTIONS;i++)
         {  _mu[i] = _y_mu_logstd[i][0];
            _logstd[i] = _y_mu_logstd[i+__ACTIONS][0];
         }
         _out = LogProbabilities(_mu, _logstd);
      }
   }
   return(_out);
}

Seguiremos utilizando el mismo modelo que hemos utilizado hasta ahora, con 9 estados ambientales y 3 acciones posibles. Para procesar la distribución de probabilidad de las acciones, necesitamos la función de probabilidades logarítmicas cuyo código se compartió al principio de este artículo. Al compilar con el asistente y realizar una prueba para los 4 meses restantes de la ventana de datos, obtenemos el siguiente informe:

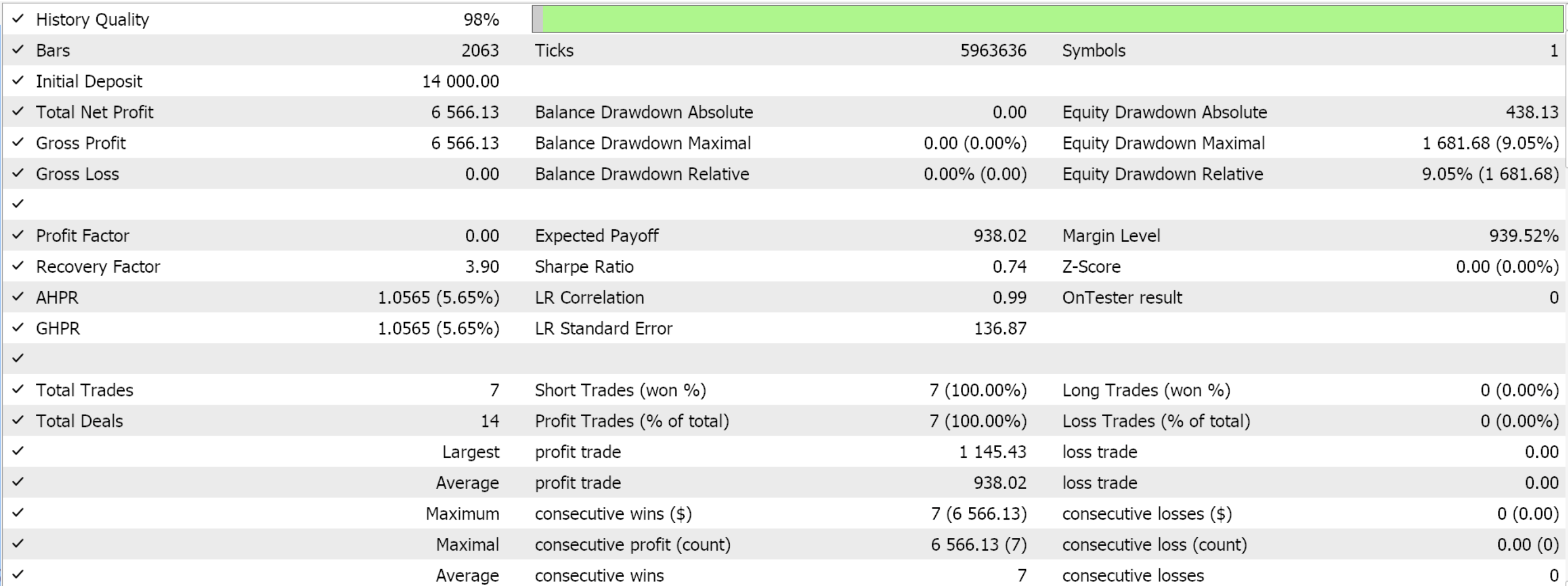
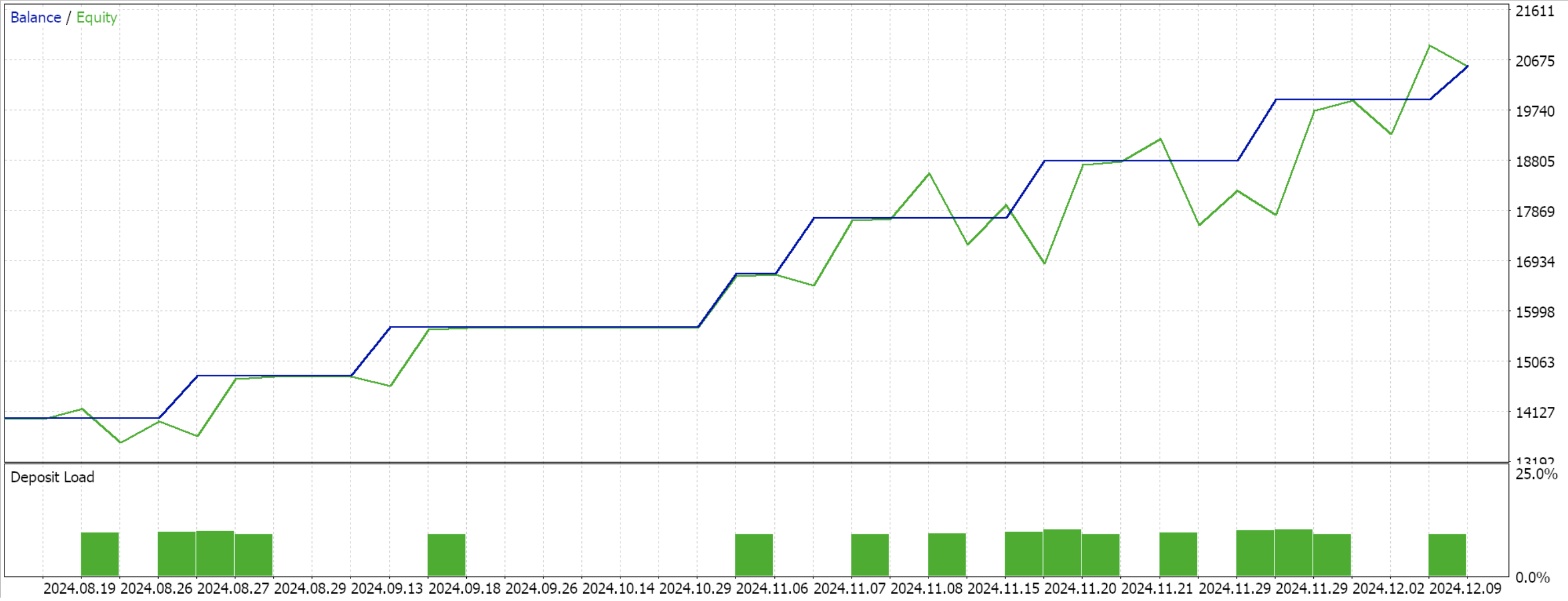
Conclusión

Hemos analizado un escenario de implementación muy básico del aprendizaje por refuerzo SAC en Python que no utilizaba la librería tensor-agent y, por lo tanto, no aprovechaba las eficiencias que esta conlleva. Este enfoque expone los fundamentos del SAC y destaca por qué la retropropagación es un poco prolongada, ya que implica emparejar múltiples redes y una de ellas no tiene un conjunto de datos de entrenamiento típico. En principio, el SAC tiene como objetivo promover de forma segura una mayor exploración a través de la entropía modulada por el parámetro alfa (que aplicamos en la distribución gaussiana). Por lo tanto, se invita al lector a explorar esto más a fondo considerando un alfa no fijo, como el ajuste automático que tiene un valor de entropía objetivo. También deberíamos profundizar en ejemplos de esto en futuros artículos.

Nombre del archivo	Descripción
WZ_51.mq5	Asistente para crear asesores expertos cuyo encabezado sirve para mostrar los archivos utilizados.
SignalWZ_51.mqh	Archivo de clase de señal personalizado.
EURUSD_H1_D1_critic2.onnx	Red ONNX de Crítico 2.
EURUSD_H1_D1_critic1.onnx	Red ONNX de Crítico 1.
EURUSD_H1_D1_actor.onnx	Red de actores.