Criando barras 3D com base em tempo, preço e volume
60
0
Introdução
Já se passaram seis meses desde que comecei este projeto. Seis meses desde a ideia, que parecia boba, então não dei muita atenção, apenas comentei com alguns traders conhecidos sobre a ideia de criar esse tipo de cotação.
Tudo começou com uma pergunta simples: por que os traders insistem em analisar um mercado tridimensional olhando para gráficos bidimensionais? Price action, análise técnica, teoria das ondas: todos esses conceitos se baseiam na projeção do mercado em um plano. Mas e se tentássemos ver a estrutura real do preço, volume e tempo?
No meu trabalho com sistemas algorítmicos, frequentemente percebia que os indicadores tradicionais perdem conexões cruciais entre preço e volume.
A ideia das barras 3D não surgiu de imediato. Primeiro foi uma experiência com visualização 3D da profundidade do mercado. Depois vieram os primeiros esboços de clusters volume-preço. E quando adicionei o componente temporal e construí a primeira barra 3D, ficou claro que se tratava de uma nova forma de enxergar o mercado.
Hoje quero compartilhar com vocês os resultados desse trabalho. Vou mostrar como Python e MetaTrader 5 permitem construir barras volumétricas em tempo real. Vou explicar a matemática por trás dos cálculos e como usar essa informação na prática de trading.
O que diferencia uma barra 3D
Enquanto olharmos para o mercado pela lente dos gráficos bidimensionais, perderemos o mais importante: sua estrutura real. A análise técnica tradicional trabalha com projeções de preço-tempo, volume-tempo, mas nunca mostra o quadro completo da interação entre esses componentes.
A análise 3D é fundamentalmente diferente porque permite ver o mercado como um todo integrado. Quando construímos uma barra volumétrica, criamos literalmente um "molde" do estado do mercado, onde cada dimensão carrega uma informação essencial:
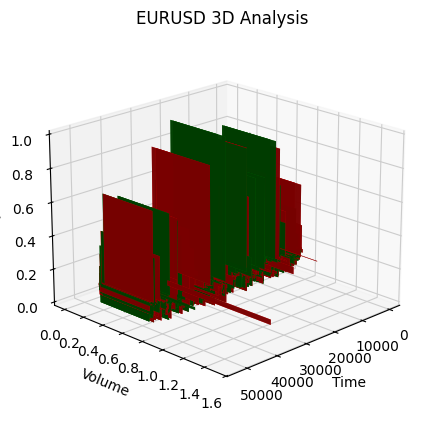
- a altura da barra mostra a amplitude do movimento do preço
- a largura reflete a escala temporal
- a profundidade visualiza a distribuição do volume
Por que isso é importante? Imagine dois movimentos de preço idênticos no gráfico. Em uma representação bidimensional, eles parecem iguais. Mas ao adicionarmos o componente de volume, o cenário muda completamente, pois um movimento pode ser sustentado por um volume massivo, formando uma barra profunda e estável, enquanto o outro é apenas um pico superficial com suporte mínimo de negociações reais.
A abordagem integrada por meio das barras 3D resolve um problema clássico da análise técnica: o atraso nos sinais. A estrutura volumétrica da barra começa a se formar desde os primeiros ticks, permitindo identificar o surgimento de um movimento forte muito antes que ele apareça no gráfico convencional. Na prática, temos uma ferramenta de análise preditiva baseada não em padrões históricos, mas na dinâmica real das negociações em andamento.
A análise multidimensional de dados não é apenas uma visualização bonita, mas sim uma nova forma de entender a microestrutura do mercado. Cada barra 3D contém informações sobre:
- a distribuição do volume dentro da faixa de preço
- a velocidade de acumulação de posições
- os desequilíbrios entre compradores e vendedores
- a volatilidade em nível micro
- o momentum do movimento
Todos esses componentes atuam como um mecanismo único, permitindo enxergar a verdadeira natureza do movimento do preço. Onde a análise técnica clássica vê apenas uma vela ou uma barra, a análise 3D revela uma estrutura complexa de interação entre oferta e demanda.
Fórmulas de cálculo das principais métricas. Princípios básicos da construção das barras 7D. A lógica da unificação das diversas dimensões em um único sistema
O modelo matemático das barras 3D surgiu da análise da microestrutura real do mercado. Cada barra no sistema pode ser representada como uma figura volumétrica, onde:
class Bar3D: def __init__(self): self.price_range = None # Диапазон цены self.time_period = None # Временной интервал self.volume_profile = {} # Профиль объема по ценам self.direction = None # Направление движения self.momentum = None # Импульс self.volatility = None # Волатильность self.spread = None # Средний спред
O ponto-chave é o cálculo do perfil volumétrico dentro da barra. Ao contrário das barras clássicas, aqui analisamos a distribuição do volume entre os níveis de preço.
def calculate_volume_profile(self, ticks_data): volume_by_price = defaultdict(float) for tick in ticks_data: price_level = round(tick.price, 5) volume_by_price[price_level] += tick.volume # Нормализуем профиль total_volume = sum(volume_by_price.values()) for price in volume_by_price: volume_by_price[price] /= total_volume return volume_by_price
O momentum do movimento é calculado como uma combinação da velocidade de variação do preço e do volume:
def calculate_momentum(self): price_velocity = (self.close - self.open) / self.time_period volume_intensity = self.total_volume / self.time_period self.momentum = price_velocity * volume_intensity * self.direction
A análise da volatilidade dentro da barra recebe atenção especial. Utilizamos uma fórmula modificada do ATR, que leva em conta a microestrutura do movimento:
def calculate_volatility(self, tick_data): tick_changes = np.diff([tick.price for tick in tick_data]) weighted_std = np.std(tick_changes * [tick.volume for tick in tick_data[1:]]) time_factor = np.sqrt(self.time_period) self.volatility = weighted_std * time_factor
A diferença fundamental em relação às barras clássicas é que todas as métricas são calculadas em tempo real, permitindo visualizar a formação da estrutura da barra:
def update_bar(self, new_tick): self.update_price_range(new_tick.price) self.update_volume_profile(new_tick) self.recalculate_momentum() self.update_volatility(new_tick) # Пересчитываем объемный центр тяжести self.volume_poc = self.calculate_poc()
A unificação de todas as dimensões ocorre através de um sistema de coeficientes de peso, ajustáveis para cada ativo específico:
def calculate_bar_strength(self): return (self.momentum_weight * self.normalized_momentum + self.volatility_weight * self.normalized_volatility + self.volume_weight * self.normalized_volume_concentration + self.spread_weight * self.normalized_spread_factor)
Na prática de trading, esse modelo matemático permite observar aspectos do mercado como:
- desequilíbrios na acumulação de volume
- anomalias na velocidade de formação do preço
- zonas de consolidação e rompimento
- a verdadeira força da tendência através das características volumétricas
Cada barra 3D deixa de ser apenas um ponto no gráfico para se tornar um indicador completo do estado do mercado em um momento específico.
Análise detalhada do algoritmo de criação das barras 3D. Particularidades do trabalho com MetaTrader 5. Especificidades no tratamento dos dados
Após depurar o algoritmo principal, finalmente cheguei à parte mais interessante: a implementação das barras multidimensionais em tempo real. Admito, no início isso pareceu uma tarefa complicada. O MetaTrader 5 não é exatamente amigável com scripts externos, e a documentação, em alguns pontos, deixa muito a desejar. Mas vou explicar como consegui superar isso.
Comecei com uma estrutura básica para armazenar os dados. Após várias iterações, nasceu a seguinte classe:
class Bar7D: def __init__(self): self.time = None self.open = None self.high = None self.low = None self.close = None self.tick_volume = 0 self.volume_profile = {} self.direction = 0 self.trend_count = 0 self.volatility = 0 self.momentum = 0
O mais difícil foi descobrir como calcular corretamente o tamanho do bloco. Depois de muitos experimentos, cheguei à seguinte fórmula:
def calculate_brick_size(symbol_info, multiplier=45): spread = symbol_info.spread point = symbol_info.point min_price_brick = spread * multiplier * point # Адаптивная корректировка под волатильность atr = calculate_atr(symbol_info.name) if atr > min_price_brick * 2: min_price_brick = atr / 2 return min_price_brick
Também tive bastante dor de cabeça com os volumes. Inicialmente, pensei em usar um tamanho fixo para o volume_brick, mas rapidamente percebi que isso não funcionava. A solução veio na forma de um algoritmo adaptativo:
def adaptive_volume_threshold(tick_volume, history_volumes): median_volume = np.median(history_volumes) std_volume = np.std(history_volumes) if tick_volume > median_volume + 2 * std_volume: return median_volume + std_volume return max(tick_volume, median_volume / 2)
Já no cálculo das métricas estatísticas, acho que exagerei um pouco:
def calculate_stats(df): df['ma_5'] = df['close'].rolling(5).mean() df['ma_20'] = df['close'].rolling(20).mean() df['volume_ma_5'] = df['tick_volume'].rolling(5).mean() df['price_volatility'] = df['price_change'].rolling(10).std() df['volume_volatility'] = df['tick_volume'].rolling(10).std() df['trend_strength'] = df['trend_count'] * df['direction'] # Наверное, это уже лишнее df['zscore_price'] = stats.zscore(df['close'], nan_policy='omit') df['zscore_volume'] = stats.zscore(df['tick_volume'], nan_policy='omit') return df
Engraçado, mas o mais difícil acabou não sendo escrever o código, e sim depurá-lo em condições reais.
Aqui está o resultado final da função, que também inclui a normalização no intervalo de 3 a 9. Por que 3 a 9? Tanto Gann quanto Tesla afirmavam que havia certa magia nesses números. E eu pessoalmente vi um trader em uma plataforma conhecida que supostamente criou um script de reversão bem-sucedido baseado nesses números. Não vou me aprofundar em teorias conspiratórias ou misticismo, só vou testar:
def create_true_3d_renko(symbol, timeframe, min_spread_multiplier=45, volume_brick=500, lookback=20000): """ Creates 3D Renko bars with extended analytics """ rates = mt5.copy_rates_from_pos(symbol, timeframe, 0, lookback) if rates is None: print(f"Error getting data for {symbol}") return None, None df = pd.DataFrame(rates) df['time'] = pd.to_datetime(df['time'], unit='s') if df.isnull().any().any(): print("Missing values detected, cleaning...") df = df.dropna() if len(df) == 0: print("No data for analysis after cleaning") return None, None symbol_info = mt5.symbol_info(symbol) if symbol_info is None: print(f"Failed to get symbol info for {symbol}") return None, None try: min_price_brick = symbol_info.spread * min_spread_multiplier * symbol_info.point if min_price_brick <= 0: print("Invalid block size") return None, None except AttributeError as e: print(f"Error getting symbol parameters: {e}") return None, None # Convert time to numeric and scale everything scaler = MinMaxScaler(feature_range=(3, 9)) # Convert datetime to numeric (seconds from start) df['time_numeric'] = (df['time'] - df['time'].min()).dt.total_seconds() # Scale all numeric data together columns_to_scale = ['time_numeric', 'open', 'high', 'low', 'close', 'tick_volume'] df[columns_to_scale] = scaler.fit_transform(df[columns_to_scale]) renko_blocks = [] current_price = float(df.iloc[0]['close']) current_tick_volume = 0 current_time = df.iloc[0]['time'] current_time_numeric = float(df.iloc[0]['time_numeric']) current_spread = float(symbol_info.spread) current_type = 0 prev_direction = 0 trend_count = 0 try: for idx, row in df.iterrows(): if pd.isna(row['tick_volume']) or pd.isna(row['close']): continue current_tick_volume += float(row['tick_volume']) volume_bricks = int(current_tick_volume / volume_brick) price_diff = float(row['close']) - current_price if pd.isna(price_diff) or pd.isna(min_price_brick): continue price_bricks = int(price_diff / min_price_brick) if volume_bricks > 0 or abs(price_bricks) > 0: direction = np.sign(price_bricks) if price_bricks != 0 else 1 if direction == prev_direction: trend_count += 1 else: trend_count = 1 renko_block = { 'time': current_time, 'time_numeric': float(row['time_numeric']), 'open': float(row['open']), 'close': float(row['close']), 'high': float(row['high']), 'low': float(row['low']), 'tick_volume': float(row['tick_volume']), 'direction': float(direction), 'spread': float(current_spread), 'type': float(current_type), 'trend_count': trend_count, 'price_change': price_diff, 'volume_intensity': float(row['tick_volume']) / volume_brick, 'price_velocity': price_diff / (volume_bricks if volume_bricks > 0 else 1) } if volume_bricks > 0: current_tick_volume = current_tick_volume % volume_brick if price_bricks != 0: current_price += min_price_brick * price_bricks prev_direction = direction renko_blocks.append(renko_block) except Exception as e: print(f"Error processing data: {e}") if len(renko_blocks) == 0: return None, None if len(renko_blocks) == 0: print("Failed to create any blocks") return None, None result_df = pd.DataFrame(renko_blocks) # Scale derived metrics to same range derived_metrics = ['price_change', 'volume_intensity', 'price_velocity', 'spread'] result_df[derived_metrics] = scaler.fit_transform(result_df[derived_metrics]) # Add analytical metrics using scaled data result_df['ma_5'] = result_df['close'].rolling(5).mean() result_df['ma_20'] = result_df['close'].rolling(20).mean() result_df['volume_ma_5'] = result_df['tick_volume'].rolling(5).mean() result_df['price_volatility'] = result_df['price_change'].rolling(10).std() result_df['volume_volatility'] = result_df['tick_volume'].rolling(10).std() result_df['trend_strength'] = result_df['trend_count'] * result_df['direction'] # Scale moving averages and volatility ma_columns = ['ma_5', 'ma_20', 'volume_ma_5', 'price_volatility', 'volume_volatility', 'trend_strength'] result_df[ma_columns] = scaler.fit_transform(result_df[ma_columns]) # Add statistical metrics and scale them result_df['zscore_price'] = stats.zscore(result_df['close'], nan_policy='omit') result_df['zscore_volume'] = stats.zscore(result_df['tick_volume'], nan_policy='omit') zscore_columns = ['zscore_price', 'zscore_volume'] result_df[zscore_columns] = scaler.fit_transform(result_df[zscore_columns]) return result_df, min_price_brickE aqui está como ficou a série de barras obtidas em escala unificada. Não parece muito estacionária, não é mesmo?!
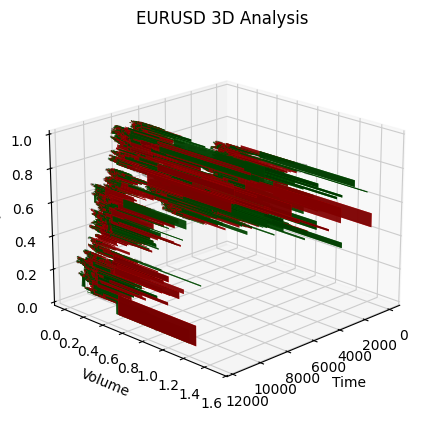
Obviamente, essa série não me satisfez, pois minha meta era criar uma série mais ou menos estacionária, e especificamente uma série tempo-volume-preço estacionária. E o que fiz a seguir foi:
Introduzimos a dimensão de volatilidade e começamos a experimentar
Durante a implementação da função create_stationary_4d_features, segui um caminho completamente diferente. Ao contrário das barras 3D originais, onde simplesmente escalávamos os dados para o intervalo de 3 a 9, aqui me concentrei em criar séries verdadeiramente estacionárias.
A ideia central da função é criar uma representação quadridimensional do mercado por meio de características estacionárias. Em vez de uma simples normalização, cada dimensão é transformada de forma específica para atingir a estacionaridade:
- 1. Dimensão temporal: aqui utilizei uma transformação trigonométrica, convertendo as horas em senóides e cossenóides. As fórmulas sin(2π * hora/24) e cos(2π * hora/24) criam características cíclicas, eliminando totalmente o problema da sazonalidade diária.
- 2. Dimensão de preço: em vez de valores absolutos, são usadas as variações relativas dos preços. No código, isso é feito através do cálculo do preço típico (high + low + close)/3 e posterior cálculo dos retornos e suas acelerações. Esse método torna a série estacionária, independentemente do nível de preços.
- 3. Dimensão de volume: aqui há um ponto interessante, pois não usamos simplesmente as variações de volume, mas seus incrementos relativos. Isso é importante porque os volumes costumam ter distribuição bastante irregular. No código, isso é feito com o uso sequencial de pct_change() e diff().
- 4. Dimensão de volatilidade: aqui implementei uma transformação em duas etapas, isto é, primeiro, o cálculo da volatilidade móvel por meio do desvio padrão dos retornos; depois, o cálculo das variações relativas dessa volatilidade. Na prática, obtemos a "volatilidade da volatilidade".
Cada bloco de dados é formado em uma janela deslizante de 20 períodos. Esse número não é aleatório, foi escolhido como um compromisso entre manter a estrutura local dos dados e garantir a significância estatística dos cálculos.
Todas as características calculadas são, no final, escaladas para o intervalo de 3 a 9, mas isso já é uma transformação secundária, aplicada a séries que já foram tornadas estacionárias. Isso permite manter compatibilidade com a implementação original das barras 3D, mesmo utilizando uma abordagem completamente diferente na etapa de pré-processamento dos dados.
Um ponto especialmente importante é preservar todas as métricas-chave da função original: médias móveis, volatilidade, escores-z. Isso permite que a nova implementação seja usada como substituta direta da função original, entregando dados mais qualificados e estacionários.
Como resultado, obtemos um conjunto de características que não apenas são estacionárias do ponto de vista estatístico, mas também preservam todas as informações relevantes sobre a estrutura do mercado. Essa abordagem torna os dados muito mais adequados para aplicação de métodos de aprendizado de máquina e análise estatística, sem perder a conexão com o contexto original do trading.
Aqui está a função:
def create_true_3d_renko(symbol, timeframe, min_spread_multiplier=45, volume_brick=500, lookback=20000): """ Creates 4D stationary features with same interface as 3D Renko """ rates = mt5.copy_rates_from_pos(symbol, timeframe, 0, lookback) if rates is None: print(f"Error getting data for {symbol}") return None, None df = pd.DataFrame(rates) df['time'] = pd.to_datetime(df['time'], unit='s') if df.isnull().any().any(): print("Missing values detected, cleaning...") df = df.dropna() if len(df) == 0: print("No data for analysis after cleaning") return None, None symbol_info = mt5.symbol_info(symbol) if symbol_info is None: print(f"Failed to get symbol info for {symbol}") return None, None try: min_price_brick = symbol_info.spread * min_spread_multiplier * symbol_info.point if min_price_brick <= 0: print("Invalid block size") return None, None except AttributeError as e: print(f"Error getting symbol parameters: {e}") return None, None scaler = MinMaxScaler(feature_range=(3, 9)) df_blocks = [] try: # Time dimension df['time_sin'] = np.sin(2 * np.pi * df['time'].dt.hour / 24) df['time_cos'] = np.cos(2 * np.pi * df['time'].dt.hour / 24) df['time_numeric'] = (df['time'] - df['time'].min()).dt.total_seconds() # Price dimension df['typical_price'] = (df['high'] + df['low'] + df['close']) / 3 df['price_return'] = df['typical_price'].pct_change() df['price_acceleration'] = df['price_return'].diff() # Volume dimension df['volume_change'] = df['tick_volume'].pct_change() df['volume_acceleration'] = df['volume_change'].diff() # Volatility dimension df['volatility'] = df['price_return'].rolling(20).std() df['volatility_change'] = df['volatility'].pct_change() for idx in range(20, len(df)): window = df.iloc[idx-20:idx+1] block = { 'time': df.iloc[idx]['time'], 'time_numeric': scaler.fit_transform([[float(df.iloc[idx]['time_numeric'])]]).item(), 'open': float(window['price_return'].iloc[-1]), 'high': float(window['price_acceleration'].iloc[-1]), 'low': float(window['volume_change'].iloc[-1]), 'close': float(window['volatility_change'].iloc[-1]), 'tick_volume': float(window['volume_acceleration'].iloc[-1]), 'direction': np.sign(window['price_return'].iloc[-1]), 'spread': float(df.iloc[idx]['time_sin']), 'type': float(df.iloc[idx]['time_cos']), 'trend_count': len(window), 'price_change': float(window['price_return'].mean()), 'volume_intensity': float(window['volume_change'].mean()), 'price_velocity': float(window['price_acceleration'].mean()) } df_blocks.append(block) except Exception as e: print(f"Error processing data: {e}") if len(df_blocks) == 0: return None, None if len(df_blocks) == 0: print("Failed to create any blocks") return None, None result_df = pd.DataFrame(df_blocks) # Scale all features features_to_scale = [col for col in result_df.columns if col != 'time' and col != 'direction'] result_df[features_to_scale] = scaler.fit_transform(result_df[features_to_scale]) # Add same analytical metrics as in original function result_df['ma_5'] = result_df['close'].rolling(5).mean() result_df['ma_20'] = result_df['close'].rolling(20).mean() result_df['volume_ma_5'] = result_df['tick_volume'].rolling(5).mean() result_df['price_volatility'] = result_df['price_change'].rolling(10).std() result_df['volume_volatility'] = result_df['tick_volume'].rolling(10).std() result_df['trend_strength'] = result_df['trend_count'] * result_df['direction'] # Scale moving averages and volatility ma_columns = ['ma_5', 'ma_20', 'volume_ma_5', 'price_volatility', 'volume_volatility', 'trend_strength'] result_df[ma_columns] = scaler.fit_transform(result_df[ma_columns]) # Add statistical metrics and scale them result_df['zscore_price'] = stats.zscore(result_df['close'], nan_policy='omit') result_df['zscore_volume'] = stats.zscore(result_df['tick_volume'], nan_policy='omit') zscore_columns = ['zscore_price', 'zscore_volume'] result_df[zscore_columns] = scaler.fit_transform(result_df[zscore_columns]) return result_df, min_price_brick
E é assim que isso se apresenta em 2D:
Em seguida, vamos tentar criar um modelo 3D interativo para os preços 3D usando o plotly. Ao lado, devemos observar o gráfico bidimensional comum. Aqui está o código:
import plotly.graph_objects as go from plotly.subplots import make_subplots def create_interactive_3d(df, symbol, save_dir): """ Creates interactive 3D visualization with smoothed data and original price chart """ try: save_dir = Path(save_dir) # Smooth all series with MA(100) df_smooth = df.copy() smooth_columns = ['close', 'tick_volume', 'price_volatility', 'volume_volatility'] for col in smooth_columns: df_smooth[f'{col}_smooth'] = df_smooth[col].rolling(window=100, min_periods=1).mean() # Create subplots: 3D view and original chart side by side fig = make_subplots( rows=1, cols=2, specs=[[{'type': 'scene'}, {'type': 'xy'}]], subplot_titles=(f'{symbol} 3D View (MA100)', f'{symbol} Original Price'), horizontal_spacing=0.05 ) # Add 3D scatter plot fig.add_trace( go.Scatter3d( x=np.arange(len(df_smooth)), y=df_smooth['tick_volume_smooth'], z=df_smooth['close_smooth'], mode='markers', marker=dict( size=5, color=df_smooth['price_volatility_smooth'], colorscale='Viridis', opacity=0.8, showscale=True, colorbar=dict(x=0.45) ), hovertemplate= "Time: %{x}<br>" + "Volume: %{y:.2f}<br>" + "Price: %{z:.5f}<br>" + "Volatility: %{marker.color:.5f}", name='3D View' ), row=1, col=1 ) # Add original price chart fig.add_trace( go.Candlestick( x=np.arange(len(df)), open=df['open'], high=df['high'], low=df['low'], close=df['close'], name='OHLC' ), row=1, col=2 ) # Add smoothed price line fig.add_trace( go.Scatter( x=np.arange(len(df_smooth)), y=df_smooth['close_smooth'], line=dict(color='blue', width=1), name='MA100' ), row=1, col=2 ) # Update 3D layout fig.update_scenes( xaxis_title='Time', yaxis_title='Volume', zaxis_title='Price', camera=dict( up=dict(x=0, y=0, z=1), center=dict(x=0, y=0, z=0), eye=dict(x=1.5, y=1.5, z=1.5) ) ) # Update 2D layout fig.update_xaxes(title_text="Time", row=1, col=2) fig.update_yaxes(title_text="Price", row=1, col=2) # Update overall layout fig.update_layout( width=1500, # Double width to accommodate both plots height=750, showlegend=True, title_text=f"{symbol} Combined Analysis" ) # Save interactive HTML fig.write_html(save_dir / f'{symbol}_combined_view.html') # Create additional plots with smoothed data (unchanged) fig2 = make_subplots(rows=2, cols=2, subplot_titles=('Smoothed Price', 'Smoothed Volume', 'Smoothed Price Volatility', 'Smoothed Volume Volatility')) fig2.add_trace( go.Scatter(x=np.arange(len(df_smooth)), y=df_smooth['close_smooth'], name='Price MA100'), row=1, col=1 ) fig2.add_trace( go.Scatter(x=np.arange(len(df_smooth)), y=df_smooth['tick_volume_smooth'], name='Volume MA100'), row=1, col=2 ) fig2.add_trace( go.Scatter(x=np.arange(len(df_smooth)), y=df_smooth['price_volatility_smooth'], name='Price Vol MA100'), row=2, col=1 ) fig2.add_trace( go.Scatter(x=np.arange(len(df_smooth)), y=df_smooth['volume_volatility_smooth'], name='Volume Vol MA100'), row=2, col=2 ) fig2.update_layout( height=750, width=750, showlegend=True, title_text=f"{symbol} Smoothed Data Analysis" ) fig2.write_html(save_dir / f'{symbol}_smoothed_analysis.html') print(f"Interactive visualizations saved in {save_dir}") except Exception as e: print(f"Error creating interactive visualization: {e}") raise
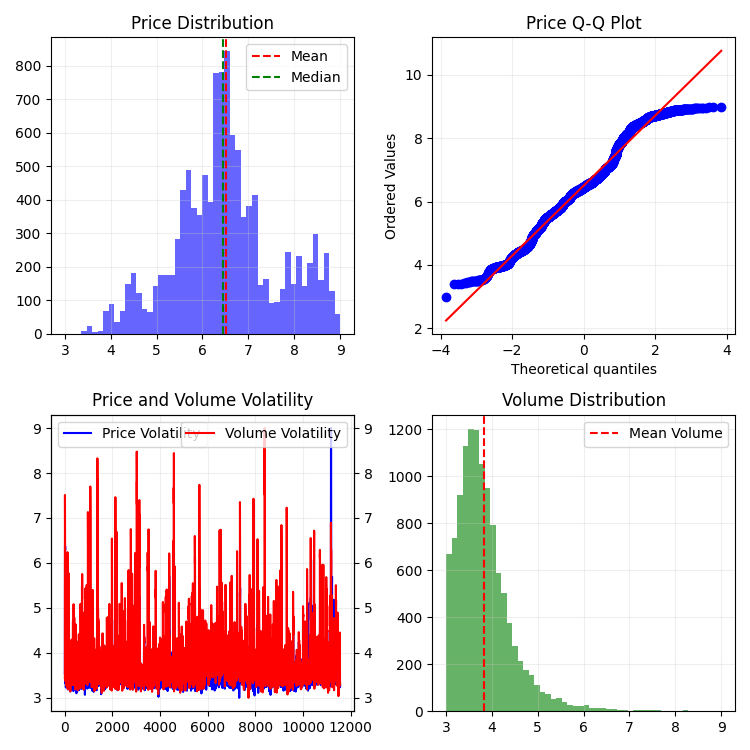
Assim se apresenta nossa nova série de preços:
No geral, o visual é muito interessante. Podemos ver certas sequências de agrupamento de preços ao longo do tempo e picos de agrupamento de preços em volume. Ou seja, cria-se a sensação — e isso é diretamente confirmado pela experiência de traders experientes — de que, quando o mercado está instável, quando volumes gigantes estão sendo negociados, quando a volatilidade dispara, estamos lidando com um valor atípico perigoso, algo que foge à estatística: os famosos riscos de cauda. Por isso, aqui conseguimos identificar imediatamente esse tipo de saída do preço “para fora da normalidade”, nesse tipo de coordenada. E só por isso, já agradeço à ideia dos gráficos multidimensionais de preço!
Repare nisso:
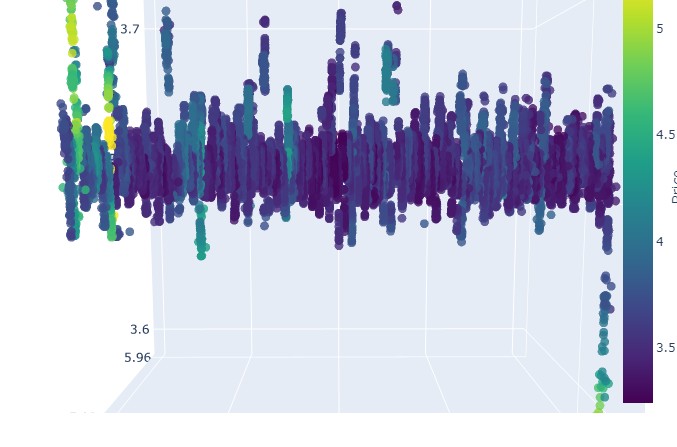
Vamos agora examinar o paciente (o gráfico 3D)
Agora proponho fazermos uma visualização. Mas não do nosso futuro brilhante sob uma palmeira ao lado do terminal, e sim dos gráficos de preços 3D. Vamos dividir as situações em três clusters: tendência de alta, tendência de baixa, reversão de alta para baixa e reversão de baixa para alta. Para isso, será necessário alterar um pouco o código: não precisaremos mais dos números das barras, pois vamos carregar dados por datas específicas. Na prática, basta passarmos a usar mt5.copy_rates_range.
def create_true_3d_renko(symbol, timeframe, start_date, end_date, min_spread_multiplier=45, volume_brick=500): """ Creates 4D stationary features with same interface as 3D Renko """ rates = mt5.copy_rates_range(symbol, timeframe, start_date, end_date) if rates is None: print(f"Error getting data for {symbol}") return None, None df = pd.DataFrame(rates) df['time'] = pd.to_datetime(df['time'], unit='s') if df.isnull().any().any(): print("Missing values detected, cleaning...") df = df.dropna() if len(df) == 0: print("No data for analysis after cleaning") return None, None symbol_info = mt5.symbol_info(symbol) if symbol_info is None: print(f"Failed to get symbol info for {symbol}") return None, None try: min_price_brick = symbol_info.spread * min_spread_multiplier * symbol_info.point if min_price_brick <= 0: print("Invalid block size") return None, None except AttributeError as e: print(f"Error getting symbol parameters: {e}") return None, None scaler = MinMaxScaler(feature_range=(3, 9)) df_blocks = [] try: # Time dimension df['time_sin'] = np.sin(2 * np.pi * df['time'].dt.hour / 24) df['time_cos'] = np.cos(2 * np.pi * df['time'].dt.hour / 24) df['time_numeric'] = (df['time'] - df['time'].min()).dt.total_seconds() # Price dimension df['typical_price'] = (df['high'] + df['low'] + df['close']) / 3 df['price_return'] = df['typical_price'].pct_change() df['price_acceleration'] = df['price_return'].diff() # Volume dimension df['volume_change'] = df['tick_volume'].pct_change() df['volume_acceleration'] = df['volume_change'].diff() # Volatility dimension df['volatility'] = df['price_return'].rolling(20).std() df['volatility_change'] = df['volatility'].pct_change() for idx in range(20, len(df)): window = df.iloc[idx-20:idx+1] block = { 'time': df.iloc[idx]['time'], 'time_numeric': scaler.fit_transform([[float(df.iloc[idx]['time_numeric'])]]).item(), 'open': float(window['price_return'].iloc[-1]), 'high': float(window['price_acceleration'].iloc[-1]), 'low': float(window['volume_change'].iloc[-1]), 'close': float(window['volatility_change'].iloc[-1]), 'tick_volume': float(window['volume_acceleration'].iloc[-1]), 'direction': np.sign(window['price_return'].iloc[-1]), 'spread': float(df.iloc[idx]['time_sin']), 'type': float(df.iloc[idx]['time_cos']), 'trend_count': len(window), 'price_change': float(window['price_return'].mean()), 'volume_intensity': float(window['volume_change'].mean()), 'price_velocity': float(window['price_acceleration'].mean()) } df_blocks.append(block) except Exception as e: print(f"Error processing data: {e}") if len(df_blocks) == 0: return None, None if len(df_blocks) == 0: print("Failed to create any blocks") return None, None result_df = pd.DataFrame(df_blocks) # Scale all features features_to_scale = [col for col in result_df.columns if col != 'time' and col != 'direction'] result_df[features_to_scale] = scaler.fit_transform(result_df[features_to_scale]) # Add same analytical metrics as in original function result_df['ma_5'] = result_df['close'].rolling(5).mean() result_df['ma_20'] = result_df['close'].rolling(20).mean() result_df['volume_ma_5'] = result_df['tick_volume'].rolling(5).mean() result_df['price_volatility'] = result_df['price_change'].rolling(10).std() result_df['volume_volatility'] = result_df['tick_volume'].rolling(10).std() result_df['trend_strength'] = result_df['trend_count'] * result_df['direction'] # Scale moving averages and volatility ma_columns = ['ma_5', 'ma_20', 'volume_ma_5', 'price_volatility', 'volume_volatility', 'trend_strength'] result_df[ma_columns] = scaler.fit_transform(result_df[ma_columns]) # Add statistical metrics and scale them result_df['zscore_price'] = stats.zscore(result_df['close'], nan_policy='omit') result_df['zscore_volume'] = stats.zscore(result_df['tick_volume'], nan_policy='omit') zscore_columns = ['zscore_price', 'zscore_volume'] result_df[zscore_columns] = scaler.fit_transform(result_df[zscore_columns]) return result_df, min_price_brick
Aqui está nosso código modificado:
def main(): try: # Initialize MT5 if not mt5.initialize(): print("MetaTrader5 initialization error") return # Analysis parameters symbols = ["EURUSD", "GBPUSD"] timeframes = { "M15": mt5.TIMEFRAME_M15 } # 7D analysis parameters params = { "min_spread_multiplier": 45, "volume_brick": 500 } # Date range for data fetching start_date = datetime(2017, 1, 1) end_date = datetime(2018, 2, 1) # Analysis for each symbol and timeframe for symbol in symbols: print(f"\nAnalyzing symbol {symbol}") # Create symbol directory symbol_dir = Path('charts') / symbol symbol_dir.mkdir(parents=True, exist_ok=True) # Get symbol info symbol_info = mt5.symbol_info(symbol) if symbol_info is None: print(f"Failed to get symbol info for {symbol}") continue print(f"Spread: {symbol_info.spread} points") print(f"Tick: {symbol_info.point}") # Analysis for each timeframe for tf_name, tf in timeframes.items(): print(f"\nAnalyzing timeframe {tf_name}") # Create timeframe directory tf_dir = symbol_dir / tf_name tf_dir.mkdir(exist_ok=True) # Get and analyze data print("Getting data...") df, brick_size = create_true_3d_renko( symbol=symbol, timeframe=tf, start_date=start_date, end_date=end_date, min_spread_multiplier=params["min_spread_multiplier"], volume_brick=params["volume_brick"] ) if df is not None and brick_size is not None: print(f"Created {len(df)} 7D bars") print(f"Block size: {brick_size}") # Basic statistics print("\nBasic statistics:") print(f"Average volume: {df['tick_volume'].mean():.2f}") print(f"Average trend length: {df['trend_count'].mean():.2f}") print(f"Max uptrend length: {df[df['direction'] > 0]['trend_count'].max()}") print(f"Max downtrend length: {df[df['direction'] < 0]['trend_count'].max()}") # Create visualizations print("\nCreating visualizations...") create_visualizations(df, symbol, tf_dir) # Save data csv_file = tf_dir / f"{symbol}_{tf_name}_7d_data.csv" df.to_csv(csv_file) print(f"Data saved to {csv_file}") # Results analysis trend_ratio = len(df[df['direction'] > 0]) / len(df[df['direction'] < 0]) print(f"\nUp/Down bars ratio: {trend_ratio:.2f}") volume_corr = df['tick_volume'].corr(df['price_change'].abs()) print(f"Volume-Price change correlation: {volume_corr:.2f}") # Print warnings if anomalies detected if df['price_volatility'].max() > df['price_volatility'].mean() * 3: print("\nWARNING: High volatility periods detected!") if df['volume_volatility'].max() > df['volume_volatility'].mean() * 3: print("WARNING: Abnormal volume spikes detected!") else: print(f"Failed to create 3D bars for {symbol} on {tf_name}") print("\nAnalysis completed successfully!") except Exception as e: print(f"An error occurred: {e}") import traceback print(traceback.format_exc()) finally: mt5.shutdown()
Vamos pegar o primeiro trecho de dados, euro-dólar, de 1º de janeiro de 2017 a 1º de fevereiro de 2018. Um fortíssimo bull market, de fato. Pronto para ver como isso aparece nas barras 3D?
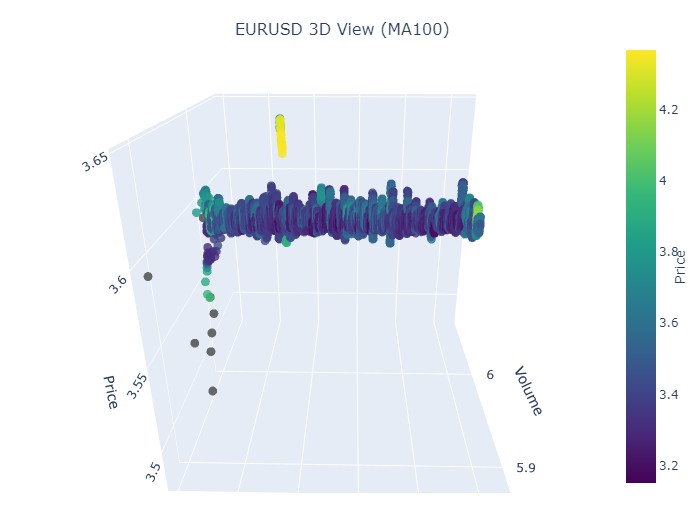
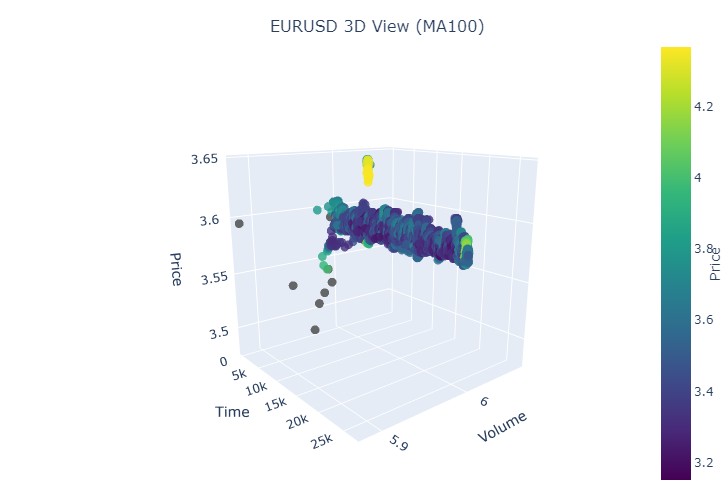
Aqui está mais uma visualização:
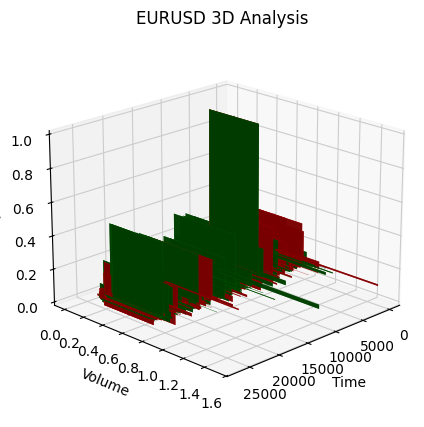
Vamos observar o início da tendência de alta:
E o seu fim:
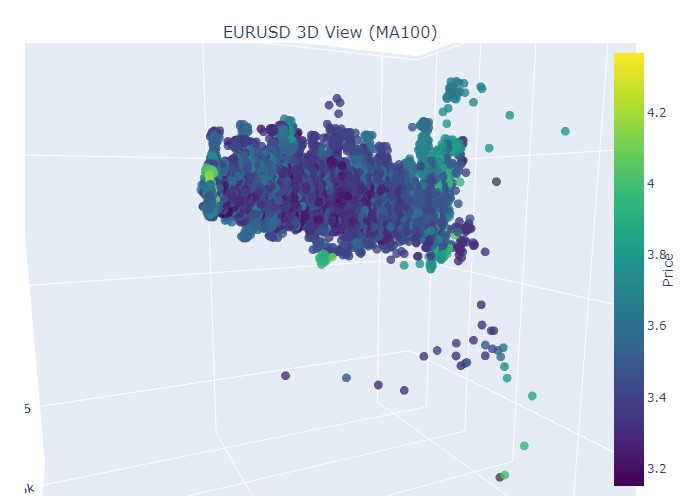
Agora vejamos a tendência de baixa. De 1º de fevereiro de 2018 a 20 de março de 2020:
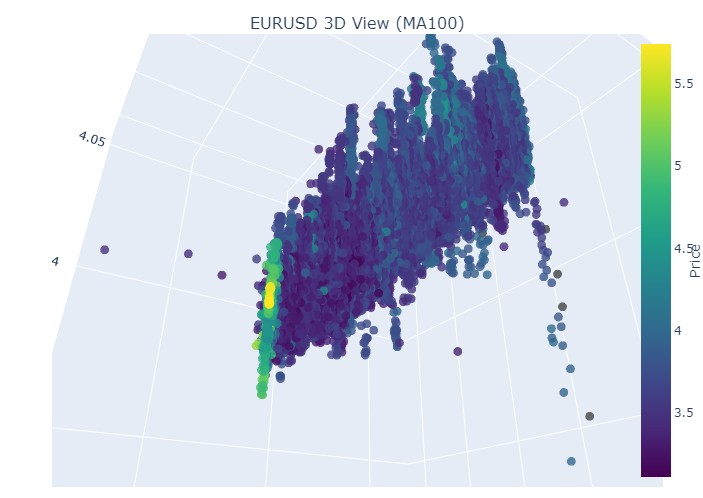
Aqui está o início do bear market:
E aqui, o seu encerramento:
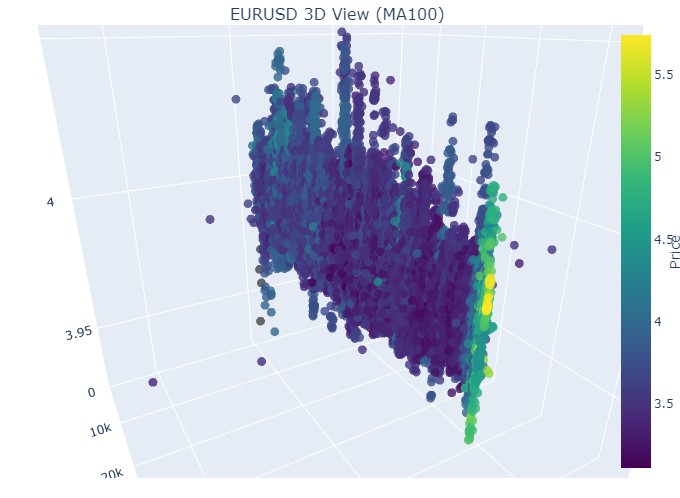
Então, o que vemos: ambas as tendências (tanto a de alta quanto a de baixa), no formato 3D, começaram como uma região de pontos com densidade 3D concentrada. E o fim de ambas as tendências foi marcado por uma coloração amarela intensa e destacada.
Para descrever esse fenômeno e o comportamento dos preços do par de moedas, como o euro-dólar, em cenários de tendências de alta e de baixa, podemos usar a seguinte fórmula universal:
P(t) = P_0 + \int_{t_0}^{t} A \cdot e^{k(t-u)} \cdot V(u) \, du + N(t)
onde:
- P(t) — preço da moeda no momento t
- P_0 — preço inicial no momento t₀
- A — amplitude da tendência, representando a magnitude da variação do preço
- k — coeficiente que define a velocidade da variação (com k > 0 temos tendência de alta, com k < 0 temos tendência de baixa)
- V(u) — volume de negociações no momento u, que afeta a atividade do mercado e pode ampliar a relevância da mudança de preço
- N(t) — ruído aleatório, que representa oscilações imprevisíveis do mercado
Explicação textual
Essa fórmula descreve como o preço da moeda varia com o tempo, em função de diversos fatores. O preço inicial serve como ponto de partida, após o qual o integral leva em conta a influência da amplitude e velocidade da tendência, expondo o preço a um crescimento ou queda exponencial conforme o valor de k. O volume de negociações, representado pela função V(u), adiciona uma dimensão extra, mostrando que a atividade no mercado também afeta diretamente a variação do preço.
Assim, esse modelo permite visualizar os movimentos de preços em diferentes contextos de tendência, representando-os em um espaço 3D onde tempo, preço e volume compõem uma representação rica da atividade de mercado. A intensidade das cores nesse modelo pode indicar a força da tendência, sendo que cores mais vibrantes correspondem a maiores valores na derivada do preço e no volume negociado, sinalizando movimentos intensos de volume fluindo pelo mercado.
Como se representa a reversão
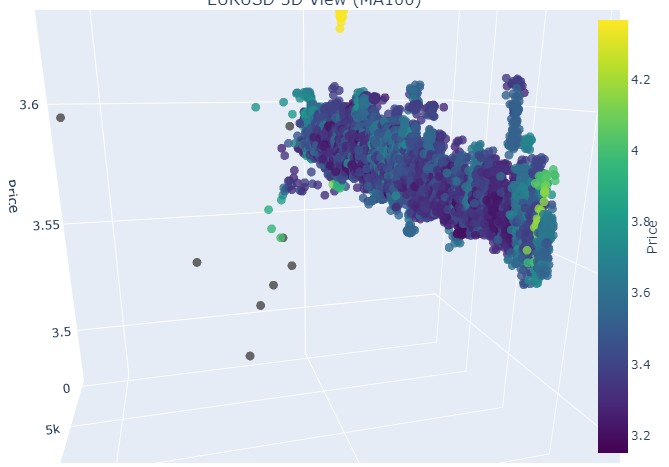
Aqui está o período de 14 a 28 de novembro, com uma reversão nas cotações ocorrendo aproximadamente no meio desse intervalo. Como isso aparece nas coordenadas 3D? Assim:
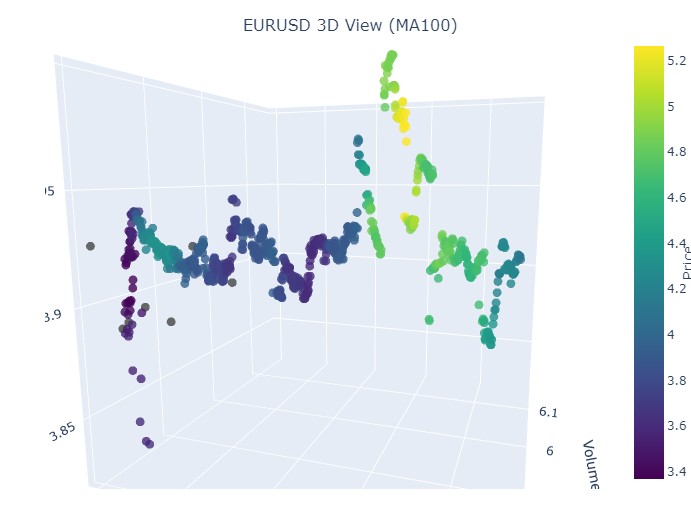
Vemos novamente o já familiar tom amarelo no momento da reversão e a elevação da coordenada normalizada de preços. Agora vejamos outro trecho de preço com reversão de tendência, de 13 de setembro de 2024 a 10 de outubro do mesmo ano:
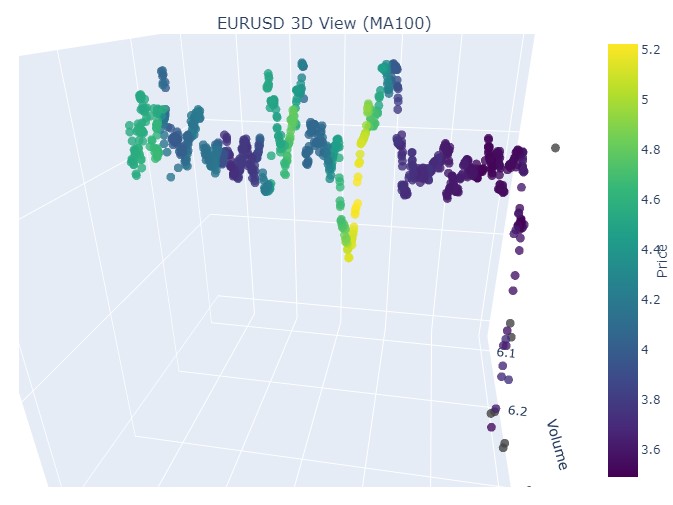
Mais uma vez, a mesma imagem, mas agora o amarelo e seu acúmulo estão posicionados na parte inferior. Interessante? Interessante. Seguimos?
Seguimos! De 19 de agosto de 2024 a 30 de agosto de 2024, exatamente no meio desse período ocorre uma reversão de tendência. Vamos dar uma olhada nas nossas coordenadas?
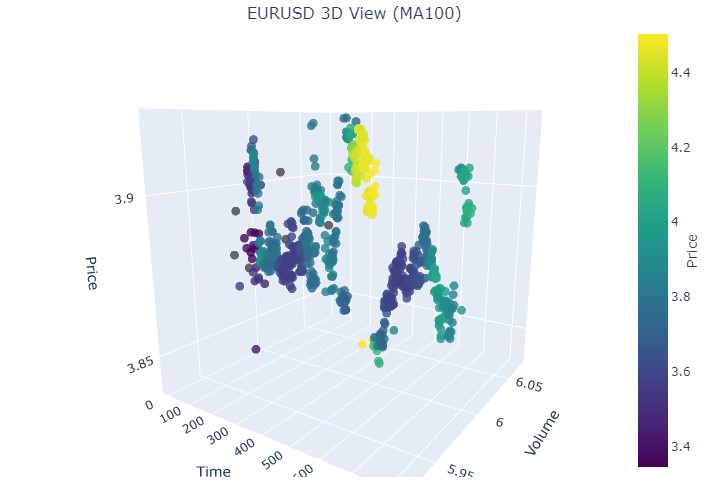
Mais uma vez, exatamente o mesmo padrão. Vamos analisar o período de 17 de julho de 2024 a 8 de agosto de 2024. Será que o modelo indicará sinais de uma reversão iminente?
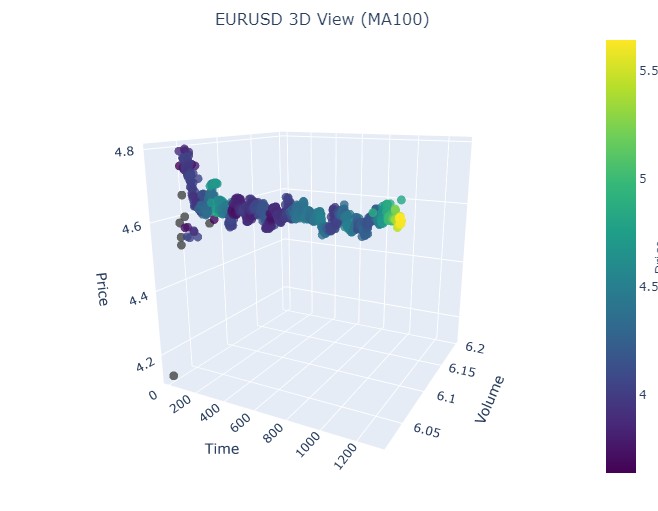
Mostrou ou não? O que você acha?
E o último período: de 21 de abril a 10 de agosto de 2023. Foi aí que a tendência de alta chegou ao fim.
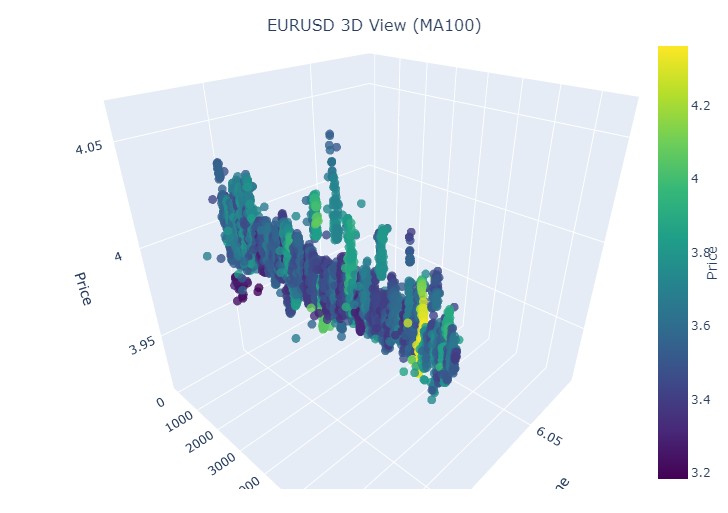
Mais uma vez, o conhecido tom amarelo está presente.
Sobre os clusters amarelos
Durante o desenvolvimento das barras 3D, me deparei com uma característica extremamente interessante: os clusters amarelos de volume e volatilidade. Não vou negar, fiquei totalmente fascinado pelo comportamento deles no gráfico! Após analisar uma tonelada de dados históricos (mais precisamente, mais de 400 mil barras entre 2022 e 2024), percebi algo surpreendente.
A princípio, nem acreditei no que estava vendo: de cerca de 100 mil barras amarelas, quase todas (97%) estavam próximas de reversões de preço. E isso funcionava dentro de uma margem de cerca de três barras. Curiosamente, ao analisar todas as reversões — foram cerca de 169 mil — apenas 40% delas apresentaram barras amarelas. Ou seja, a presença de uma barra amarela quase garante uma reversão, embora nem toda reversão venha acompanhada dela.
Ao explorar mais a fundo os padrões de tendência, notei um comportamento claro. No início e durante a tendência, há poucas barras amarelas, apenas barras 3D normais agrupadas de forma densa. Porém, logo antes da reversão, os clusters amarelos brilham no gráfico.
Isso fica especialmente evidente em tendências longas. Basta observar a valorização do euro-dólar entre o início de 2017 e fevereiro de 2018, e depois a queda até março de 2020. Em ambos os casos, os clusters amarelos surgiram antes da reversão, e sua posição no espaço 3D praticamente indicava a direção futura do preço!
Testei isso também em períodos curtos, selecionando alguns trechos de 2 a 3 semanas ao longo de 2024. E sabe o que aconteceu? Funcionou como um relógio! Sempre antes de uma reversão, lá estavam as barras amarelas, como se estivessem alertando: “Ei, amigo, o mercado está prestes a virar!”
Isso não é apenas mais um indicador. Acredito que encontramos algo realmente importante na própria estrutura do mercado: como os volumes se distribuem e como a volatilidade muda antes da inversão de uma tendência. Agora, quando vejo clusters amarelos no gráfico 3D, sei que é hora de me preparar para uma reversão!
Considerações finais
Encerrando nosso estudo sobre as barras tridimensionais, não posso deixar de destacar o quanto esse mergulho profundo mudou minha compreensão da microestrutura de mercado. O que começou como um experimento de visualização se transformou em uma nova maneira de ver e entender o mercado.
Trabalhando neste projeto, percebi constantemente o quanto estamos limitados pela representação tradicional bidimensional dos preços. A transição para a análise tridimensional abriu horizontes completamente novos para compreender as relações entre preço, volume e tempo. O que mais me impressionou foi a clareza com que os padrões que precedem eventos importantes no mercado se revelam no espaço tridimensional.
A descoberta mais significativa foi a capacidade de detectar precocemente potenciais reversões de tendência. O acúmulo característico de volumes e a mudança na coloração na representação tridimensional mostraram-se indicadores surpreendentemente confiáveis de alterações futuras na tendência. E isso não é apenas uma observação teórica: validamos essa constatação em inúmeros exemplos históricos.
O modelo matemático que desenvolvemos permite não apenas visualizar, mas também quantificar a dinâmica do mercado. A integração de tecnologias modernas de visualização e ferramentas de programação tornou possível aplicar esse método na negociação real. Eu uso essas ferramentas todos os dias, e elas transformaram profundamente a minha abordagem à análise de mercado.
No entanto, acredito que estamos apenas no começo. Este projeto abriu a porta para o universo da análise multidimensional da microestrutura do mercado, e tenho plena confiança de que futuras pesquisas nesse campo trarão ainda muitas descobertas valiosas. Talvez o próximo passo seja integrar aprendizado de máquina para o reconhecimento automático de padrões tridimensionais, ou desenvolver novas estratégias de trading baseadas nessa análise multidimensional.
No fim das contas, o maior valor deste estudo não está nos gráficos sofisticados nem nas fórmulas complexas, mas no novo entendimento de mercado que ele proporciona. Como pesquisador, estou profundamente convencido de que o futuro da análise técnica está justamente na abordagem multidimensional da leitura de dados de mercado.
Traduzido do russo pela MetaQuotes Ltd.
Artigo original: https://www.mql5.com/ru/articles/16555
Do básico ao intermediário: Indicador (V)
Redes neurais em trading: Modelo adaptativo multiagente (MASA)
Simulação de mercado (Parte 21): Iniciando o SQL (IV)
Ciclos e trading
- Aplicativos de negociação gratuitos
- 8 000+ sinais para cópia
- Notícias econômicas para análise dos mercados financeiros
Você concorda com a política do site e com os termos de uso