MetaTrader 5 / Trading systems
Русский 中文 Español Deutsch 日本語 Português
preview
Neural Networks in Trading: Hierarchical Vector Transformer (HiVT)

Neural Networks in Trading: Hierarchical Vector Transformer (HiVT)

MetaTrader 5 — Trading systems |
3 244 0
Dmitriy Gizlyk
Dmitriy Gizlyk

Introduction

The challenges in autonomous driving significantly overlap with those faced by traders. Navigating dynamic environments with safe maneuvers is a critical task for autonomous vehicles. To achieve this, these vehicles must comprehend their surroundings and predict future events on the road. However, accurately forecasting the maneuvers of nearby road users, such as cars, bicycles, and pedestrians, is a complex problem, particularly when their goals or intentions remain unknown. In multi-agent traffic scenarios, an agent's behavior is shaped by intricate interactions with other agents, further complicated by map-dependent traffic rules. Understanding the diverse behaviors of multiple agents in a scene is, therefore, extremely challenging.

Recent research uses a vectorized approach for more compact scene representation by extracting sets of vectors or points from trajectories and map elements. However, existing vectorized methods struggle with real-time motion prediction in fast-changing traffic conditions. Because such methods are usually sensitive to coordinate system shifts. To mitigate this issue, scenes are normalized to center on the target agent and align with its direction of movement. This approach becomes problematic when predicting the motion of a large number of agents, as the high computational costs of repeated scene normalization and feature recomputation for each target agent become a bottleneck. Additionally, existing methods model the relationships between all elements across spatial and temporal dimensions to capture detailed interactions between vectorized elements. This inevitably leads to excessive computational overhead as the number of elements increases. Since accurate real-time prediction is critical for autonomous driving safety, many researchers are looking to take this process to the next level by developing a new framework that enables faster and more precise multi-agent motion forecasting.

One such approach was presented in the paper "HiVT: Hierarchical Vector Transformer for Multi-Agent Motion Prediction". This method leverages symmetries and a hierarchical structure for multi-agent motion prediction. The authors of HiVT decompose the motion prediction task into multiple stages and hierarchically model interactions between elements using a Transformer-based architecture.

In the first stage, the model avoids costly modeling of interactions between all elements by extracting contextual features locally. The entire scene is divided into a set of local regions, each centered on a modeled agent. Contextual features are extracted from local vectorized elements in each agent-centric region, containing rich information relevant to the central agent.

In the second stage, to compensate for the limitations of local fields of view and capture long-range dependencies, a global information transfer mechanism between agent-centric regions is introduced. The authors employ a Transformer equipped with geometric connections between local coordinate systems to achieve this.

The combined local and global representations enable the decoder to predict the future trajectories of all agents in a single forward pass of the model. To further exploit the symmetry of the task, the authors introduce a scene representation that is invariant to global coordinate system shifts, using relative positions to describe all vectorized elements. Based on this scene representation, they implement rotation-invariant cross-attention modules for spatial learning, which allow the model to learn local and global representations independently of scene orientation.


1. HiVT Algorithm

The HiVT method begins by representing the road scene as a collection of vectorized elements. Based on this scene representation, the model hierarchically aggregates spatiotemporal information. The road scene consists of agents and map information. For structured scene representation, vectorized elements are first extracted, including trajectory segments of road agents and lane segments from map data.

A vectorized element is associated with semantic and geometric attributes. Unlike previous vectorized methods, where the geometrical attributes of agents or lanes include absolute point positions, the authors avoid absolute positions and instead describe geometric attributes using relative positions. This makes the scene entirely a set of vectors. Specifically, the trajectory of agent i is represented as "pt,i - pt-1,i", where pt,i is the location of the agent i at time step t.

For a lane segment xi, the geometrical attribute is defined as p1,xi - p0,xi, where p0,xi and p1,xi are start and end coordinates of xi. Converting the set of points into a set of vectors naturally ensures translation invariance. However, relative positional information between elements is lost. To preserve spatial relationships, relative position vectors are introduced for agent-agent and agent-lane pairs. For example, the position vector of agent j relative to agent i at time step t is ptj - pti, fully describing their spatial relationship while maintaining translation invariance. This scene representation ensures that any applied learning functions adhere to translation invariance without losing information.

To accurately predict future agent trajectories in a high-dynamic environment, the model must effectively learn spatiotemporal dependencies among numerous vectorized elements. The Transformer has demonstrated potential in capturing long-term dependencies between elements across various tasks. However, applying Transformers directly to spatiotemporal elements results in a computational complexity of O((NT + L)^2), where N, T and L are the numbers of agents, historical time steps, and lane segments, respectively. To efficiently extract information from a large number of elements, HiVT factorizes spatial and temporal dimensions by modeling spatial relationships locally at each time step. Specifically, the space is divided into N local regions, each centered on an agent. Within each local region, the central agent's local environment is represented by neighboring agents' trajectories and local lane segments. Local information is aggregated into a feature vector for each region, modeling agent-agent interactions at each time step, temporal dependencies for each agent, and agent-lane interactions at the current time step. After aggregation, the feature vector contains rich information related to the central agent. This reduces computational complexity from O((NT + L)^2) to O(NT^2 + TN^2 + NL) due to the factorization of spatial and temporal dimensions and then further reduces to O(NT^2 + TNk + Nl) by limiting the radius of local regions where k < N and l < L.

While the local encoder extracts rich representations, its information volume is constrained by local regions. To prevent degradation in prediction quality, the authors introduce a global interaction module that compensates for limited local receptive fields and captures scene-level dynamics with message passing between local regions. This global interaction module significantly enhances the model's expressiveness with a computational cost of O(N^2), which is relatively lightweight compared to the local encoder.

The multi-agent motion prediction problem exhibits translational and rotational symmetries. Existing methods renormalize all vectorized elements relative to each agent and make multiple predictions per agent to achieve invariance. This paradigm scales linearly with the number of agents. In contrast, HiVT can predict all agents' motions in a single forward pass while maintaining invariance by using an invariant scene representation and rotation-robust spatial learning modules.

The Agent-Agent Interaction Module captures relationships between the central and neighboring agents in each local region at each time step. To exploit problem symmetries, the authors propose a rotation-invariant cross-attention block, which aggregates spatial information. Specifically, they use the final trajectory segment of the central agent pT,i — pT-1,i as a reference vector for the local region and rotate all local vectors according to the reference orientation ʘi. The rotated vectors and their associated semantic attributes are processed using a multi-layer perceptron (MLP) to obtain embeddings for the central agent zti and any neighboring agent ztij at any time step t.

Since all geometric attributes are normalized relative to the central agent before being fed into the MLP, these embeddings are rotation-invariant. In addition to trajectory segments, the input function фnbr(•) also includes relative position vectors of neighboring agents concerning the central agent, making neighbor embeddings spatially aware. The central agent's embedding is then transformed into a Query vector, while neighbor embeddings are used to compute Key and Value entities. The resulting entities are utilized in the attention block.

Unlike classical Transformer, the HiVT authors propose a feature fusion function that integrates environmental features with the central agent's features zti. This enables the attention block to better control feature updates. Similar to the original Transformer architecture, the proposed attention block can be extended to multiple attention heads. The output of the multi-head attention block is passed through an MLP block to obtain the spatial embedding sti of agent i at time step t.

In addition, the authors of the method use data normalization by layer before each block and residual connections after each block. In practice, this module can be implemented using efficient parallel learning operations across all local regions and time steps.

Further capture of temporal information of each local region is implemented using a temporal Transformer encoder, which follows the Agent-Agent interaction module. For any central agent i, the initial sequence of this module consists of embeddings sti, received from the Agent-Agent interaction module at different time steps. The authors of the method add an additional trainable token sT+1 to the end of the original sequence. Then they add the learnable positional encoding to all tokens and place the tokens in a matrix Si, which is fed into the temporal attention block.

The temporal learning module also consists of alternating blocks of multi-headed attention and MLP blocks.

The local structure of the map can indicate the future intentions of the central agent. Therefore, local map information is added to the central agent's embedding. To do this, the method first rotates local road segments and the vectors of the relative positions of the road agent at the current time step T. The rotated vectors are then encoded using an MLP. Using the spatiotemporal features of the central agent as Query and road segment features encoded using an MLP as Key-Value vectors, cross-attention Agent-Road is implemented similarly to the approaches described above.

The authors of the method additionally apply an MLP block to obtain the final local embedding hi of the central agent i. After sequentially modeling Agent-Agent interactions, temporal dependencies, and Agent-Road interactions, the embeddings encapsulate enriched information related to the central agents of the local regions.

In the next stage of the HiVT algorithm, the local embeddings are processed within the global interaction module to capture long-range dependencies in the scene. Since local features are extracted in agent-centered coordinate systems, the global interaction module must account for geometric relationships between different frames when exchanging information across local regions. To achieve this, the authors extend the Transformer encoder to incorporate differences between local coordinate systems. When transmitting information from agent j to agent i, the authors use an MLP to obtain a pairwise embedding, which is then included in the vector transformation.

To model pairwise global interactions, the same spatial attention mechanism used in the local encoder is applied, followed by an MLP block that outputs a global representation for each agent.

The predicted motion of traffic agents is inherently multimodal. Therefore, the authors propose parameterizing the distribution of future trajectories as a mixture model, where each component follows a Laplace distribution. Predictions are generated for all agents in a single forward pass. For each agent i of each component f, MLP takes local and global representations as inputs. It then outputs the agent's location and its associated uncertainty at each future time step in the local coordinate system. The output tensor of the regression head has dimensions [F, N, H, 4], where F is the number of mixture components, N is the number of agents in the scene, and H is the prediction horizon in future time steps. An MLP is also used here. It is followed by a Softmax function, which determines the mixture model coefficients for each agent.

Authors' visualization of the HiVT method is presented below.



2. Implementation in MQL5

We have reviewed the comprehensive algorithm proposed by the HiVT authors. We now shift to the practical aspect of implementing our interpretation of these methods using MQL5.

It is important to note that the approaches proposed by the HiVT authors differ significantly from the mechanisms we have previously employed. As a result, we are about to undertake a substantial amount of work.

2.1 Vectorization of the Initial State


We begin by organizing the process of state vectorization. Of course, we have previously explored various state vectorization algorithms, including piecewise-linear time series representation, data segmentation, and different embedding techniques. However, in this case, the authors propose a radically different approach. We will implement it on the OpenCL side in the HiVTPrepare kernel.

__kernel void HiVTPrepare(__global const float *data,
                          __global float2 *output
                         )
  {
   const size_t t = get_global_id(0);
   const size_t v = get_global_id(1);
   const size_t total_v = get_global_size(1);

In the kernel parameters, we use only two pointers to global data buffers: one for the input values and another for the operation results.

It is important to note that, unlike the input data, we use the vector type float2 for the results buffer. Previously, we employed this type for complex values. However, in this case, we do not utilize complex number mathematics. Instead, the choice of this data type is driven by the need to handle scene rotation in a two-dimensional space. Using a two-element vector allows us to conveniently store coordinates and displacement within the plane.

As you may have noticed, the kernel parameters do not explicitly include constants that define the dimensions of the input and output tensors. We plan to derive this information from the two-dimensional task space. The first dimension will indicate the depth of the analyzed history, while the second will specify the number of univariate time series in the multimodal sequence being processed.

This approach is based on the assumption that our multimodal sequence consists of a collection of one-dimensional univariate time series.

Within the kernel body, we identify the current thread across all dimensions of the task space. We then determine the offset constants within the global data buffers accordingly.

   const int shift_data = t * total_v;
   const int shift_out = shift_data * total_v;

To clarify the offset in the result buffer, it is worth telling a little about the algorithm that we plan to implement in this kernel.

As mentioned in the theoretical part, the authors of the HiVT method proposed replacing absolute values with relative ones with rotation of the scene around the central agent.

Following this logic, we first determine the bias of each agent at a given time step.

   float value = data[shift_data + v + total_v] - data[shift_data + v];

Next, we calculate the angle of inclination of the obtained displacement. Naturally, determining the inclination angle in a plane requires two displacement coordinates. However, the input data contains only a single value. Since we are working with a time series, we can derive the second displacement coordinate by assuming a unit step along the time axis. That is, we take "1" as the displacement along the time axis for a single step.

   const float theta = atan(value);

Now we can determine the sine and cosine of the angle to construct the rotation matrix.

   const float cos_theta = cos(theta);
   const float sin_theta = sin(theta);

After that, we can rotate the movement vector of the central agent.

   const float2 main = Rotate(value, cos_theta, sin_theta);

Since we need to perform rotation for all agents, I moved this operation into a separate function.

Please note that as a result of rotation, we get a displacement along 2 coordinate axes. To store the data, we use a vector variable float2.

Next, we run a loop over all agents present at a given time step.

   for(int a = 0; a < total_v; a++)
     {
      float2 o = main;
      if(a != v)
         o -= Rotate(data[shift_data + a + total_v] - data[shift_data + a], cos_theta, sin_theta);
      output[shift_out + a] = o;
     }
  }

In the body of the loop for the central agent, we save its movement, and for the other agents we calculate their movement relative to the central one. To do this, we first determine the shift of each agent. We rotate it in accordance with the rotation matrix of the central agent. And we subtract the resulting displacement from the central agent's motion vector.

Thus, for each agent at each time step we obtain a scene description tensor of 2 columns (coordinates on the plane) with the number of rows equal to the number of analyzed univariate series.

It is worth mentioning here that the authors of the method limited the number of agents to the radius of the local segment. We didn't do this, since the divergence of indicator values often gives quite good trading signals.

2.2 Attention Within a Single Time Step


The next question that we faced in the process of implementing the proposed approaches was the organization of attention mechanisms between agents within a separate time step.

We have previously implemented attention mechanisms within individual variables. But this is a "vertical" analysis. And in this case we need a "horizontal" analysis. We could, of course, solve this problem by creating a new "horizontal attention" class, but this is a rather labor-intensive approach.

There is a faster solution. We could transpose the original data and use existing "vertical attention" solutions. Yet, there is a nuance. In this case, the existing algorithm for transposing two-dimensional matrices is not suitable. Therefore, we will create an algorithm for transposing a three-dimensional tensor. In this transposition process, we swap the 1st and 2nd dimensions, while the 3rd remains unchanged.

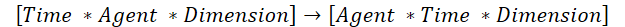
This is exactly what we need to use the existing "vertical attention" algorithms.

To organize this process, we will create a TransposeRCD kernel.

__kernel void TransposeRCD(__global const float *matrix_in, ///<[in] Input matrix
                           __global float *matrix_out ///<[out] Output matrix
                          )
  {
   const int r = get_global_id(0);
   const int c = get_global_id(1);
   const int d = get_global_id(2);
   const int rows = get_global_size(0);
   const int cols = get_global_size(1);
   const int dimension = get_global_size(2);
//---
   matrix_out[(c * rows + r)*dimension + d] = matrix_in[(r * cols + c) * dimension + d];
  }

I must say that the kernel algorithm almost completely repeats the similar kernel for transposing a two-dimensional matrix. Only one more dimension of the task space is added. Accordingly, the offset in the data buffers is adjusted taking into account the added dimension.

The same can be said about the CNeuronTransposeRCDOCL class structure. Here we use the 2D matrix transpose class CNeuronTransposeOCL as a parent. 

class CNeuronTransposeRCDOCL  :  public CNeuronTransposeOCL
  {
protected:
   virtual bool      feedForward(CNeuronBaseOCL *NeuronOCL) override;
   virtual bool      calcInputGradients(CNeuronBaseOCL *NeuronOCL) override;

public:
                     CNeuronTransposeRCDOCL(void){};
                    ~CNeuronTransposeRCDOCL(void){};
   //---
   virtual bool      Init(uint numOutputs, uint myIndex, COpenCLMy *open_cl, 
                          uint count, uint window, uint dimension, 
                          ENUM_OPTIMIZATION optimization_type, uint batch);
   //---
   virtual int       Type(void) const { return defNeuronTransposeRCDOCL; }
  };

Note that we do not declare any additional variables or objects in the class body. To implement the process, the inherited ones are quite sufficient for us. This allows us to override only the kernel call methods, while all other functionality is covered by the methods of the parent class. Therefore, we will not consider in detail the algorithms of the class methods. I suggest you examine them on your own. The complete code of this class and all its methods is included in the attached files.

2.3 Agent-Agent Attention Block


Next we move on to the implementation of the Agent-Agent attention block. Within the framework of this block, it is assumed that attention is constructed between local embeddings of agents within one time step. The three-dimensional tensor transposition class created above has greatly simplified our work. However, the use of the method of feature unification control mechanism proposed by the authors requires adjustment of the algorithm.

To organize the processes of the specified attention block, we will create a new class CNeuronHiVTAAEncoder. In this case, we will use the independent variable attention layer CNeuronMVMHAttentionMLKV as the parent class.

class CNeuronHiVTAAEncoder : public CNeuronMVMHAttentionMLKV
  {
protected:
   virtual bool      feedForward(CNeuronBaseOCL *NeuronOCL) override;
   //---
   virtual bool      calcInputGradients(CNeuronBaseOCL *prevLayer) override;
   virtual bool      updateInputWeights(CNeuronBaseOCL *NeuronOCL) override;

public:
                     CNeuronHiVTAAEncoder(void){};
                    ~CNeuronHiVTAAEncoder(void){};
   //---
   virtual bool      Init(uint numOutputs, uint myIndex, COpenCLMy *open_cl, 
                          uint window, uint window_key, uint heads, uint heads_kv, 
                          uint units_count, uint layers, uint layers_to_one_kv, uint variables, 
                          ENUM_OPTIMIZATION optimization_type, uint batch);
   //---
   virtual int       Type(void)   const   {  return defNeuronMVMHAttentionMLKV;   }
  };

As you can see, we do not declare additional variables or objects in the structure of this class. The parent class structure is more than enough. The CNeuronMVMHAttentionMLKV class uses dynamic collections of data buffers, which, in turn, are operated on by the class methods. And we can add as many data buffers as we need to the existing collections.

Initialization of a new instance of our class object is implemented in the Init method.

bool CNeuronHiVTAAEncoder::Init(uint numOutputs, uint myIndex, COpenCLMy *open_cl, 
                                uint window, uint window_key, uint heads, uint heads_kv, 
                                uint units_count, uint layers, uint layers_to_one_kv, uint variables, 
                                ENUM_OPTIMIZATION optimization_type, uint batch)
  {
   if(!CNeuronBaseOCL::Init(numOutputs, myIndex, open_cl, window * units_count * variables, 
                                                                   optimization_type, batch))
      return false;

In the method parameters, we receive the main constants that allow us to accurately determine the architecture of the object specified by the user. In the body of the method, we call the same method of the neural layer base class.

Note that we are calling a method of the base class, not the direct parent. his is because we still have to redefine some data buffers later.

After successful execution of the parent class method, we save the constants of the object architecture definition received from the external program into internal variables.

   iWindow = fmax(window, 1);
   iWindowKey = fmax(window_key, 1);
   iUnits = fmax(units_count, 1);
   iHeads = fmax(heads, 1);
   iLayers = fmax(layers, 1);
   iHeadsKV = fmax(heads_kv, 1);
   iLayersToOneKV = fmax(layers_to_one_kv, 1);
   iVariables = variables;

Next, we immediately calculate the constants that determine the sizes of internal objects.

   uint num_q = iWindowKey * iHeads * iUnits * iVariables;      //Size of Q tensor
   uint num_kv = iWindowKey * iHeadsKV * iUnits * iVariables;   //Size of KV tensor
   uint q_weights = (iWindow * iHeads + 1) * iWindowKey;        //Size of weights' matrix of Q tenzor
   uint kv_weights = (iWindow * iHeadsKV + 1) * iWindowKey;     //Size of weights' matrix of KV tenzor
   uint scores = iUnits * iUnits * iHeads * iVariables;         //Size of Score tensor
   uint mh_out = iWindowKey * iHeads * iUnits * iVariables;     //Size of multi-heads self-attention
   uint out = iWindow * iUnits * iVariables;                    //Size of attention out tensore
   uint w0 = (iWindowKey * iHeads + 1) * iWindow;               //Size W0 weights matrix
   uint gate = (2 * iWindow + 1) * iWindow;                     //Size of weights' matrix gate layer
   uint self = (iWindow + 1) * iWindow;                         //Size of weights' matrix self layer

The algorithm is basically inherited from the parent class, only some minor edits have been made.

After completing the preparatory work, we create a loop with a number of iterations equal to the specified number of nested layers. In the body of this loop, at each iteration, we create objects necessary to perform the functionality of each individual nested layer.

   for(uint i = 0; i < iLayers; i++)
     {
      CBufferFloat *temp = NULL;
      for(int d = 0; d < 2; d++)
        {
         //--- Initilize Q tensor
         temp = new CBufferFloat();
         if(CheckPointer(temp) == POINTER_INVALID)
            return false;
         if(!temp.BufferInit(num_q, 0))
            return false;
         if(!temp.BufferCreate(OpenCL))
            return false;
         if(!QKV_Tensors.Add(temp))
            return false;

Here we first create buffers for intermediate data and results of individual blocks, as well as for recording the corresponding error gradients.

Note that the data buffer and the corresponding error gradients have the same size. Therefore, in order to reduce manual labor, we will create a nested loop of 2 iterations. During the first iteration of the loop, we create data buffers, and during the second one, we create buffers of the corresponding error gradients.

First we create a buffer to write Query entities to. This is followed by Key and Value buffers.

         //--- Initilize KV tensor
         if(i % iLayersToOneKV == 0)
           {
            temp = new CBufferFloat();
            if(CheckPointer(temp) == POINTER_INVALID)
               return false;
            if(!temp.BufferInit(num_kv, 0))
               return false;
            if(!temp.BufferCreate(OpenCL))
               return false;
            if(!K_Tensors.Add(temp))
               return false;
            temp = new CBufferFloat();
            if(CheckPointer(temp) == POINTER_INVALID)
               return false;
            if(!temp.BufferInit(num_kv, 0))
               return false;
            if(!temp.BufferCreate(OpenCL))
               return false;
            if(!V_Tensors.Add(temp))
               return false;
            temp = new CBufferFloat();
            if(CheckPointer(temp) == POINTER_INVALID)
               return false;
            if(!temp.BufferInit(2 * num_kv, 0))
               return false;
            if(!temp.BufferCreate(OpenCL))
               return false;
            if(!KV_Tensors.Add(temp))
               return false;
           }

The algorithms for creating and initializing data buffers are completely identical. The only difference is that our algorithm provides the ability to use one Key-Value tensor for multiple nested layers. Therefore, before creating buffers, we check the necessity of this action on the current layer.

Next we initialize a buffer of dependency coefficients between objects.

         //--- Initialize scores
         temp = new CBufferFloat();
         if(CheckPointer(temp) == POINTER_INVALID)
            return false;
         if(!temp.BufferInit(scores, 0))
            return false;
         if(!temp.BufferCreate(OpenCL))
            return false;
         if(!S_Tensors.Add(temp))
            return false;

And the multi-headed attention output buffer.

         //--- Initialize multi-heads attention out
         temp = new CBufferFloat();
         if(CheckPointer(temp) == POINTER_INVALID)
            return false;
         if(!temp.BufferInit(mh_out, 0))
            return false;
         if(!temp.BufferCreate(OpenCL))
            return false;
         if(!AO_Tensors.Add(temp))
            return false;

On accordance with the Multi-Head Self-Attention algorithm, the results of multi-headed attention are compressed to the original data level using a projection layer. We create a buffer to save the resulting projection.

         //--- Initialize attention out
         temp = new CBufferFloat();
         if(CheckPointer(temp) == POINTER_INVALID)
            return false;
         if(!temp.BufferInit(out, 0))
            return false;
         if(!temp.BufferCreate(OpenCL))
            return false;
         if(!FF_Tensors.Add(temp))
            return false;

The algorithm described up to this point almost completely repeats the method of the parent class. But further on come the changes introduced to implement the mechanism for managing the unification of features. Here, according to the proposed algorithm, we first have to concatenate the source data with the results of the attention block.

         //--- Initialize Concatenate
         temp = new CBufferFloat();
         if(CheckPointer(temp) == POINTER_INVALID)
            return false;
         if(!temp.BufferInit(2 * out, 0))
            return false;
         if(!temp.BufferCreate(OpenCL))
            return false;
         if(!FF_Tensors.Add(temp))
            return false;

The results are then used to calculate control coefficients.

         //--- Initialize Gate
         temp = new CBufferFloat();
         if(CheckPointer(temp) == POINTER_INVALID)
            return false;
         if(!temp.BufferInit(out, 0))
            return false;
         if(!temp.BufferCreate(OpenCL))
            return false;
         if(!FF_Tensors.Add(temp))
            return false;

After that we make a projection of the original data.

         //--- Initialize Self
         temp = new CBufferFloat();
         if(CheckPointer(temp) == POINTER_INVALID)
            return false;
         if(!temp.BufferInit(out, 0))
            return false;
         if(!temp.BufferCreate(OpenCL))
            return false;
         if(!FF_Tensors.Add(temp))
            return false;

At the end of the nested loop, we create an output buffer of the current nested layer.

         //--- Initialize Out
         if(i == iLayers - 1)
           {
            if(!FF_Tensors.Add(d == 0 ? Output : Gradient))
               return false;
            continue;
           }
         temp = new CBufferFloat();
         if(CheckPointer(temp) == POINTER_INVALID)
            return false;
         if(!temp.BufferInit(out, 0))
            return false;
         if(!temp.BufferCreate(OpenCL))
            return false;
         if(!FF_Tensors.Add(temp))
            return false;
        }

It should be noted here that we create output and gradient buffers only for intermediate internal layers. For the last nested layer, we simply copy the pointers to the corresponding buffers of our class.

After creating the intermediate result buffers and corresponding error gradients, we initialize the training parameter matrices. We will have several of them. First, it is the Query entity generation matrix.

      //--- Initilize Q weights
      temp = new CBufferFloat();
      if(CheckPointer(temp) == POINTER_INVALID)
         return false;
      if(!temp.Reserve(q_weights))
         return false;
      float k = (float)(1 / sqrt(iWindow + 1));
      for(uint w = 0; w < q_weights; w++)
        {
         if(!temp.Add(GenerateWeight() * 2 * k - k))
            return false;
        }
      if(!temp.BufferCreate(OpenCL))
         return false;
      if(!QKV_Weights.Add(temp))
         return false;

Here we first create a buffer and then fill it with random parameters. These parameters will be optimized during the model training process.

Similarly, we create Key and Value entity generation parameters. However, we do not generate matrices for each nested layer.

      //--- Initialize K weights
      if(i % iLayersToOneKV == 0)
        {
         temp = new CBufferFloat();
         if(CheckPointer(temp) == POINTER_INVALID)
            return false;
         if(!temp.Reserve(kv_weights))
            return false;
         for(uint w = 0; w < kv_weights; w++)
           {
            if(!temp.Add(GenerateWeight() * 2 * k - k))
               return false;
           }
         if(!temp.BufferCreate(OpenCL))
            return false;
         if(!K_Weights.Add(temp))
            return false;
         //---
         temp = new CBufferFloat();
         if(CheckPointer(temp) == POINTER_INVALID)
            return false;
         if(!temp.Reserve(kv_weights))
            return false;
         for(uint w = 0; w < kv_weights; w++)
           {
            if(!temp.Add(GenerateWeight() * 2 * k - k))
               return false;
           }
         if(!temp.BufferCreate(OpenCL))
            return false;
         if(!V_Weights.Add(temp))
            return false;
        }

In addition, we will need a projection matrix of the multi-headed attention results.

      //--- Initialize Weights0
      temp = new CBufferFloat();
      if(CheckPointer(temp) == POINTER_INVALID)
         return false;
      if(!temp.Reserve(w0))
         return false;
      for(uint w = 0; w < w0; w++)
        {
         if(!temp.Add(GenerateWeight() * 2 * k - k))
            return false;
        }
      if(!temp.BufferCreate(OpenCL))
         return false;
      if(!FF_Weights.Add(temp))
         return false;

Here we also add parameters for the feature combination control block.

      //--- Initialize Gate Weights
      temp = new CBufferFloat();
      if(CheckPointer(temp) == POINTER_INVALID)
         return false;
      if(!temp.Reserve(gate))
         return false;
      k = (float)(1 / sqrt(2 * iWindow + 1));
      for(uint w = 0; w < gate; w++)
        {
         if(!temp.Add(GenerateWeight() * 2 * k - k))
            return false;
        }
      if(!temp.BufferCreate(OpenCL))
         return false;
      if(!FF_Weights.Add(temp))
         return false;

And projections of the source data.

      //--- Self
      temp = new CBufferFloat();
      if(CheckPointer(temp) == POINTER_INVALID)
         return false;
      if(!temp.Reserve(self))
         return false;
      k = (float)(1 / sqrt(iWindow + 1));
      for(uint w = 0; w < self; w++)
        {
         if(!temp.Add(GenerateWeight() * 2 * k - k))
            return false;
        }
      if(!temp.BufferCreate(OpenCL))
         return false;
      if(!FF_Weights.Add(temp))
         return false;

Next, we need to add data buffers to write momentum at the weight matrix level that will be used in the parameter optimization process.

      //---
      for(int d = 0; d < (optimization == SGD ? 1 : 2); d++)
        {
         temp = new CBufferFloat();
         if(CheckPointer(temp) == POINTER_INVALID)
            return false;
         if(!temp.BufferInit((d == 0 || optimization == ADAM ? q_weights : iWindowKey * iHeads), 0))
            return false;
         if(!temp.BufferCreate(OpenCL))
            return false;
         if(!QKV_Weights.Add(temp))
            return false;
         if(i % iLayersToOneKV == 0)
           {
            temp = new CBufferFloat();
            if(CheckPointer(temp) == POINTER_INVALID)
               return false;
            if(!temp.BufferInit((d == 0 || optimization == ADAM ? kv_weights : iWindowKey * iHeadsKV), 0))
               return false;
            if(!temp.BufferCreate(OpenCL))
               return false;
            if(!K_Weights.Add(temp))
               return false;
            //---
            temp = new CBufferFloat();
            if(CheckPointer(temp) == POINTER_INVALID)
               return false;
            if(!temp.BufferInit((d == 0 || optimization == ADAM ? kv_weights : iWindowKey * iHeadsKV), 0))
               return false;
            if(!temp.BufferCreate(OpenCL))
               return false;
            if(!V_Weights.Add(temp))
               return false;
           }
         temp = new CBufferFloat();
         if(CheckPointer(temp) == POINTER_INVALID)
            return false;
         if(!temp.BufferInit((d == 0 || optimization == ADAM ? w0 : iWindow), 0))
            return false;
         if(!temp.BufferCreate(OpenCL))
            return false;
         if(!FF_Weights.Add(temp))
            return false;
         //--- Initilize Gate Momentum
         temp = new CBufferFloat();
         if(CheckPointer(temp) == POINTER_INVALID)
            return false;
         if(!temp.BufferInit((d == 0 || optimization == ADAM ? gate : 2 * iWindow), 0))
            return false;
         if(!temp.BufferCreate(OpenCL))
            return false;
         if(!FF_Weights.Add(temp))
            return false;
         //--- Initilize Self Momentum
         temp = new CBufferFloat();
         if(CheckPointer(temp) == POINTER_INVALID)
            return false;
         if(!temp.BufferInit((d == 0 || optimization == ADAM ? self : iWindow), 0))
            return false;
         if(!temp.BufferCreate(OpenCL))
            return false;
         if(!FF_Weights.Add(temp))
            return false;
        }
     }

After successful initialization of nested layer objects, we create an additional buffer that will be used to temporarily record intermediate results.

   if(!Temp.BufferInit(MathMax(2 * num_kv, out), 0))
      return false;
   if(!Temp.BufferCreate(OpenCL))
      return false;
//---
   return true;
  }

Complete the method execution. After that we return the boolean result of the method operations to the calling program.

The next step, after initializing the object, is to construct a feed-forward pass algorithm, which is implemented in the feedForward method.

bool CNeuronHiVTAAEncoder::feedForward(CNeuronBaseOCL *NeuronOCL)
  {
   if(CheckPointer(NeuronOCL) == POINTER_INVALID)
      return false;

In the parameters of this method, we receive a pointer to the object with the initial data and immediately check the relevance of the received pointer. Upon successful completion of this control, we run a loop in which we implement the sequential execution of operations of each nested layer.

   CBufferFloat *kv = NULL;
   for(uint i = 0; (i < iLayers && !IsStopped()); i++)
     {
      //--- Calculate Queries, Keys, Values
      CBufferFloat *inputs = (i == 0 ? NeuronOCL.getOutput() : FF_Tensors.At(10 * i - 6));
      CBufferFloat *q = QKV_Tensors.At(i * 2);
      if(IsStopped() || 
         !ConvolutionForward(QKV_Weights.At(i * (optimization == SGD ? 2 : 3)), inputs, q, 
                                                       iWindow, iWindowKey * iHeads, None))
         return false;

First we generate Query entities. Then, if necessary, we form a Key-Value tensor.

      if((i % iLayersToOneKV) == 0)
        {
         uint i_kv = i / iLayersToOneKV;
         kv = KV_Tensors.At(i_kv * 2);
         CBufferFloat *k = K_Tensors.At(i_kv * 2);
         CBufferFloat *v = V_Tensors.At(i_kv * 2);
         if(IsStopped() || 
           !ConvolutionForward(K_Weights.At(i_kv * (optimization == SGD ? 2 : 3)), inputs, k, 
                                                        iWindow, iWindowKey * iHeadsKV, None))
            return false;
         if(IsStopped() || 
            !ConvolutionForward(V_Weights.At(i_kv * (optimization == SGD ? 2 : 3)), inputs, v, 
                                                         iWindow, iWindowKey * iHeadsKV, None))
            return false;
         if(IsStopped() || 
            !Concat(k, v, kv, iWindowKey * iHeadsKV * iVariables, iWindowKey * iHeadsKV * iVariables, iUnits))
            return false;
        }

After forming the tensors of the required entities, we can compute the results of multi-headed attention.

      //--- Score calculation and Multi-heads attention calculation
      CBufferFloat *temp = S_Tensors.At(i * 2);
      CBufferFloat *out = AO_Tensors.At(i * 2);
      if(IsStopped() || !AttentionOut(q, kv, temp, out))
         return false;

Then we compress them to the dimension of the initial data.

      //--- Attention out calculation
      temp = FF_Tensors.At(i * 10);
      if(IsStopped() || 
         !ConvolutionForward(FF_Weights.At(i * (optimization == SGD ? 6 : 9)), out, temp, 
                                                       iWindowKey * iHeads, iWindow, None))
         return false;

To compute the control coefficients, we first concatenate the results of the attention block and the initial data.

      //--- Concat
      out = FF_Tensors.At(i * 10 + 1);
      if(IsStopped() || !Concat(temp, inputs, out, iWindow, iWindow, iUnits))
         return false;

Then we compute the control coefficients.

      //--- Gate
      if(IsStopped() || 
         !ConvolutionForward(FF_Weights.At(i * (optimization == SGD ? 6 : 9) + 1), out, 
                                 FF_Tensors.At(i * 10 + 2), 2 * iWindow, iWindow, SIGMOID))
         return false;

Then we just need to make a projection of the original inputs.

      //--- Self
      if(IsStopped() || 
         !ConvolutionForward(FF_Weights.At(i * (optimization == SGD ? 6 : 9) + 2), inputs, 
                                         FF_Tensors.At(i * 10 + 3), iWindow, iWindow, None))
         return false;

After that we combine the obtained projection with the results of the attention block, taking into account the control coefficients.

      //--- Out
      if(IsStopped() || 
        !GateElementMult(FF_Tensors.At(i * 10 + 3), temp, FF_Tensors.At(i * 10 + 2), 
                                                          FF_Tensors.At(i * 10 + 4)))
         return false; 
     }
//---
   return true;
  }

After that we move on to working with the next nested layer on a new iteration of the cycle.

After successfully completing the operations of all nested layers within the block, we finalize the method's execution and return a logical result to the caller, indicating the completion status of the operations.

This completes our work on implementing the feed-forward algorithm. I suggest you familiarize yourself with the algorithms of the backpropagation methods independently. You can find the full code of all classes and their methods, as well as all programs used in preparing the article, in the attachment.


Conclusion

In this article, we explored a rather interesting and promising method of Hierarchical Vector Transformer (HiVT), which was proposed to predict the movement of multiple agents. This method offers an effective approach to solving the forecasting problem by decomposing the problem into stages of local context extraction and global interaction modeling.

The authors of the method took a comprehensive approach to solving the problem and proposed a number of approaches to improve the effectiveness of the proposed model. Unfortunately, the amount of work to implement the proposed approaches exceeds the format of the article. So, this part only covered the preparatory work. The work started will be completed in the next article. The results of testing the proposed approaches on real historical data will also be presented in the second part.


References

  • HiVT: Hierarchical Vector Transformer for Multi-Agent Motion Prediction
  • Other articles from this series

    • Programs used in the article

    # Issued to Type Description
    1 Research.mq5 EA Example collection EA
    2 ResearchRealORL.mq5
    		 EA
    		 EA for collecting examples using the Real-ORL method
    3 Study.mq5 EA Model training EA
    4 StudyEncoder.mq5 EA
    		 Encoder training EA
    5 Test.mq5 EA Model testing EA
    6 Trajectory.mqh Class library System state description structure
    7 NeuroNet.mqh Class library A library of classes for creating a neural network
    8 NeuroNet.cl Code Base OpenCL program code library

    Translated from Russian by MetaQuotes Ltd.
    Original article: https://www.mql5.com/ru/articles/15688

    Attached files |
    Download ZIP
    MQL5.zip (1699.15 KB)
    Warning: All rights to these materials are reserved by MetaQuotes Ltd. Copying or reprinting of these materials in whole or in part is prohibited.

    Other articles by this author

    Go to discussion
    Build Self Optimizing Expert Advisors in MQL5 (Part 6): Self Adapting Trading Rules (II) Build Self Optimizing Expert Advisors in MQL5 (Part 6): Self Adapting Trading Rules (II)
    This article explores optimizing RSI levels and periods for better trading signals. We introduce methods to estimate optimal RSI values and automate period selection using grid search and statistical models. Finally, we implement the solution in MQL5 while leveraging Python for analysis. Our approach aims to be pragmatic and straightforward to help you solve potentially complicated problems, with simplicity.
    From Basic to Intermediate: WHILE and DO WHILE Statements From Basic to Intermediate: WHILE and DO WHILE Statements
    In this article, we will take a practical and very visual look at the first loop statement. Although many beginners feel intimidated when faced with the task of creating loops, knowing how to do it correctly and safely can only come with experience and practice. But who knows, maybe I can reduce your troubles and suffering by showing you the main issues and precautions to take when using loops in your code.
    Introduction to MQL5 (Part 14): A Beginner's Guide to Building Custom Indicators (III) Introduction to MQL5 (Part 14): A Beginner's Guide to Building Custom Indicators (III)
    Learn to build a Harmonic Pattern indicator in MQL5 using chart objects. Discover how to detect swing points, apply Fibonacci retracements, and automate pattern recognition.
    Automating Trading Strategies in MQL5 (Part 12): Implementing the Mitigation Order Blocks (MOB) Strategy Automating Trading Strategies in MQL5 (Part 12): Implementing the Mitigation Order Blocks (MOB) Strategy
    In this article, we build an MQL5 trading system that automates order block detection for Smart Money trading. We outline the strategy’s rules, implement the logic in MQL5, and integrate risk management for effective trade execution. Finally, we backtest the system to assess its performance and refine it for optimal results.