
Redes neurais em trading: Injeção de informação global em canais independentes (InjectTST)
Introdução
Recentemente, os modelos de previsão de séries temporais multimodais baseados na arquitetura Transformer têm sido amplamente aceitos, tornando-se uma das arquiteturas mais populares para modelar séries temporais. Cada vez mais, esses modelos adotam abordagens de canais independentes, nas quais a sequência de cada canal é modelada separadamente dos outros.
A independência de canal tem duas vantagens:
- Supressão de ruído: modelos independentes de canal podem se concentrar na previsão de canais individuais, sem se distrair com o ruído dos outros canais.
- Redução do desvio de distribuição: a independência de canal pode ajudar a mitigar o problema de desvio de distribuição da série temporal.
Ao mesmo tempo, a mistura de canais tem se mostrado menos eficaz no enfrentamento desses problemas, o que leva a uma redução no desempenho do modelo. No entanto, a mistura de canais possui algumas vantagens únicas:
- Alta capacidade informativa: os modelos de mistura de canais são excelentes para captar as dependências entre os canais e podem fornecer mais informações para prever valores subsequentes.
- Especificidade de canal: a otimização simultânea de vários canais em modelos de mistura permite que o modelo capture completamente as características distintivas de cada canal.
Além disso, como a abordagem de independência de canais analisa canais separados usando um modelo geral, o modelo não pode diferenciar entre os canais e, em sua maioria, aprende padrões gerais de múltiplos canais. Isso leva à perda da especificidade de canal, podendo impactar negativamente a previsão de séries temporais multimodais.
Portanto, o desenvolvimento de um modelo eficaz que combine as vantagens da independência de canais e da mistura de canais, permitindo aproveitar os benefícios de ambas as abordagens (redução de ruído, mitigação de desvio de distribuição, alta capacidade informativa e especificidade de canal), é fundamental para melhorar ainda mais a eficiência na previsão de séries temporais multimodais.
No entanto, o desenvolvimento de tal modelo representa um desafio complexo. Primeiramente, os modelos independentes de canais, por natureza, contradizem as dependências entre eles. Embora o ajuste fino de um modelo geral para cada canal possa resolver a questão da especificidade de canal, isso resulta em um aumento significativo no tempo de treinamento. Em segundo lugar, os métodos existentes de supressão de ruído e mitigação de desvio de distribuição ainda não conseguem tornar os frameworks de mistura de canais tão confiáveis quanto os modelos independentes de canal.
Uma solução para esses problemas foi proposta no artigo "InjectTST: A Transformer Method of Injecting Global Information into Independent Channels for Long Time Series Forecasting", que apresenta um método de injeção de informação global em séries temporais multimodais em canais independentes (InjectTST). Os autores evitam o modelamento explícito das dependências entre os canais para a previsão de séries temporais multimodais. Em vez disso, mantêm a estrutura de independência de canal como base, enquanto a informação global (mistura de canais) é inserida seletivamente em cada um. Isso possibilita uma mistura implícita de canais.
Cada canal individual pode selecionar informações globais úteis e evitar aquelas com ruído, o que permite manter alta capacidade informativa e supressão de ruído. Como a independência de canal é mantida como base, o desvio de distribuição também pode ser reduzido.
Além disso, os autores introduzem um identificador de canal no InjectTST para resolver a questão da especificidade de canal.
1. Algoritmo InjectTST
Com o objetivo de construir previsões Y para um horizonte de planejamento T, analisamos os valores históricos de uma série temporal multimodal X, que contém L etapas temporais. Cada etapa temporal é representada por um vetor de dimensão M.
Para resolver esse problema, utilizando as vantagens tanto da independência de canais quanto da mistura de canais, é utilizado o complexo e multinível algoritmo InjectTST.
Na primeira etapa do algoritmo, aplica-se o mecanismo de segmentação dos dados brutos em uma estrutura independente de canal. Em seguida, é realizada uma projeção linear com codificação posicional treinável.
A plataforma independente de canais processa os canais utilizando um modelo geral. Como resultado, o modelo não consegue diferenciar entre os canais, aprendendo apenas padrões gerais, sem especificidade de canal. Para resolver esse problema, os autores do InjectTST introduzem um identificador de canal, que é um tensor treinável.
Após a projeção linear dos patches para tokens, tensores com codificação posicional e com o identificador de canal são adicionados aos tokens.
Os dados processados dessa maneira são enviados para o codificador Transformer para uma representação de alto nível.
Vale destacar que, neste caso, o codificador Transformer opera em uma estrutura de independência de canais, ou seja, os tokens de cada canal são analisados separadamente. Não há mistura de informações entre os canais.
O identificador de canal representa as características distintivas de cada um, permitindo que o modelo diferencie os canais e obtenha uma representação única para cada um deles.
Paralelamente à estrutura independente de canais, na rota de mistura de canais, a sequência original X primeiro passa por um módulo global de mistura para obter informações globais. Como o objetivo principal do InjectTST é inserir informações globais em cada canal, a obtenção dessas informações é uma questão fundamental. Os autores do método apresentaram dois tipos de módulos globais de mistura, denominados CaT (canal como token) e PaT (patch como token).
O módulo CaT projeta cada canal diretamente em um token. Em resumo, aplica-se uma projeção linear a todos os valores do canal.
O módulo global de mistura PaT recebe patches como entrada. Primeiro, os patches relacionados às etapas temporais correspondentes da sequência multimodal analisada são agrupados. Em seguida, uma projeção linear é aplicada aos patches agrupados, combinando basicamente informações no nível dos patches. Depois, adiciona-se a codificação posicional e os dados são enviados ao codificador Transformer para a fusão das informações entre os patches e as informações globais.
Os experimentos conduzidos pelos autores mostram que o módulo PaT é mais estável, enquanto o módulo CaT se destaca em alguns conjuntos de dados específicos.
Um dos desafios do método InjectTST é inserir informações globais em cada canal com impacto mínimo na confiabilidade do modelo. No Transformer convencional, a atenção cruzada permite que a sequência-alvo se concentre de maneira seletiva e livre na informação contextual de outra fonte, conforme sua relevância. Com base nesse entendimento, a estrutura de atenção cruzada pode ser adequada para a injeção de informações globais em séries temporais multimodais. Dessa forma, a informação global misturada entre os canais pode ser tratada como contexto. Os autores do método utilizam a estrutura de atenção cruzada para inserir informações globais em cada canal.
Aqui vale destacar que os autores do método introduzem uma conexão residual opcional para o módulo de atenção contextual. Geralmente, a conexão residual pode tornar o modelo ligeiramente instável. Contudo, ela pode melhorar significativamente o desempenho em alguns conjuntos de dados específicos.
De modo geral, a informação global é inserida no módulo de atenção contextual sob a forma de Key e Value, enquanto a informação de canal é fornecida como Query.
Após o processamento com atenção cruzada, os dados são enriquecidos com informações globais. Para a geração de valores previstos, é adicionada uma camada linear final.
Os autores do InjectTST propõem um processo de treinamento em três etapas. Na etapa de pré-treinamento, as séries temporais originais são mascaradas aleatoriamente, e o objetivo é prever as partes mascaradas. Na etapa de ajuste fino, a camada linear de pré-treinamento do InjectTST é substituída por uma camada de previsão, e o ajuste fino dessa camada é realizado enquanto o restante da rede é congelado. Na última etapa, todo o modelo InjectTST é ajustado finamente.
A seguir, é apresentada a visualização autoral do método.

2. Implementação em MQL5
Após explorar os aspectos teóricos do método InjectTST, passamos à implementação prática da nossa visão dos conceitos apresentados, utilizando MQL5.
É importante ressaltar que a implementação proposta neste artigo não é a única correta. Além disso, a implementação descrita reflete minha interpretação pessoal dos materiais apresentados no artigo original e pode não coincidir com a visão dos próprios autores. O mesmo se aplica aos resultados obtidos.
Ao iniciarmos a implementação dos conceitos propostos, é relevante notar que já analisamos anteriormente várias arquiteturas baseadas em Transformer utilizando a abordagem de independência de canais. Nessas arquiteturas, apenas as previsões eram realizadas de forma independente para cada canal, enquanto o bloco Transformer era empregado para estudar as dependências entre canais. Isso pode ser comparado aos módulos globais de mistura CaT.
Entretanto, os autores do método utilizam a arquitetura Transformer na estrutura de independência de canais, evitando a transferência de informações entre os canais nessa etapa. Teoricamente, podemos implementar este algoritmo organizando um ciclo para processar sequências unidimensionais separadas. Contudo, essa abordagem é extensiva e leva a um aumento no número de operações sequenciais, que cresce à medida que aumenta o número de variáveis analisadas nos dados multimodais originais.
Em nosso trabalho, buscamos realizar o máximo possível de operações em fluxos paralelos. Portanto, nesta implementação, criaremos uma nova camada capaz de realizar análises independentes de canais individuais.
Bloco de análise independente de canais individuais
A funcionalidade de análise independente de canais individuais será implementada na classe CNeuronMVMHAttentionMLKV, que herda a funcionalidade básica de outro bloco multicamadas de atenção multi-cabeças, CNeuronMLMHAttentionOCL. A estrutura da nova classe é apresentada a seguir:
class CNeuronMVMHAttentionMLKV : public CNeuronMLMHAttentionOCL { protected: uint iLayersToOneKV; ///< Number of inner layers to 1 KV uint iHeadsKV; ///< Number of heads KV uint iVariables; ///< Number of variables CCollection KV_Tensors; ///< The collection of tensors of Keys and Values CCollection K_Tensors; ///< The collection of tensors of Keys CCollection K_Weights; ///< The collection of Matrix of K weights to previous layer CCollection V_Tensors; ///< The collection of tensors of Values CCollection V_Weights; ///< The collection of Matrix of V weights to previous layer CBufferFloat Temp; //--- virtual bool feedForward(CNeuronBaseOCL *NeuronOCL) override; virtual bool AttentionOut(CBufferFloat *q, CBufferFloat *kv, CBufferFloat *scores, CBufferFloat *out); virtual bool AttentionInsideGradients(CBufferFloat *q, CBufferFloat *q_g, CBufferFloat *kv, CBufferFloat *kv_g, CBufferFloat *scores, CBufferFloat *gradient); //--- virtual bool calcInputGradients(CNeuronBaseOCL *prevLayer) override; virtual bool updateInputWeights(CNeuronBaseOCL *NeuronOCL) override; public: CNeuronMVMHAttentionMLKV(void) {}; ~CNeuronMVMHAttentionMLKV(void) {}; //--- virtual bool Init(uint numOutputs, uint myIndex, COpenCLMy *open_cl, uint window, uint window_key, uint heads, uint heads_kv, uint units_count, uint layers, uint layers_to_one_kv, uint variables, ENUM_OPTIMIZATION optimization_type, uint batch); //--- virtual int Type(void) const { return defNeuronMVMHAttentionMLKV; } //--- virtual bool Save(int const file_handle); virtual bool Load(int const file_handle); virtual bool WeightsUpdate(CNeuronBaseOCL *source, float tau); virtual void SetOpenCL(COpenCLMy *obj); };
Nesta classe, adicionamos três variáveis:
- iLayersToOneKV — número de camadas para um único tensor Key-Value;
- iHeadsKV — número de cabeças de atenção no tensor Key-Value;
- iVariables — número de sequências unitárias na série temporal multimodal.
Além disso, adicionamos cinco coleções de buffers de dados, cujas finalidades serão exploradas durante a implementação. Todos os objetos internos são declarados como estáticos, o que permite manter o construtor e o destrutor da classe "vazios". A inicialização de todas as variáveis e objetos internos é realizada no método Init.
bool CNeuronMVMHAttentionMLKV::Init(uint numOutputs, uint myIndex, COpenCLMy *open_cl, uint window, uint window_key, uint heads, uint heads_kv, uint units_count, uint layers, uint layers_to_one_kv, uint variables, ENUM_OPTIMIZATION optimization_type, uint batch) { if(!CNeuronBaseOCL::Init(numOutputs, myIndex, open_cl, window * units_count * variables, optimization_type, batch)) return false;
Os parâmetros deste método devem incluir as principais constantes que permitem identificar de forma única a arquitetura da classe a ser inicializada. Entre elas:
- window — tamanho do vetor de representação de um elemento da sequência de uma série temporal unitária;
- window_key — tamanho do vetor de representação interna da entidade
- heads — número de cabeças de atenção da entidade Query;
- heads_kv — número de cabeças de atenção no tensor Key-Value concatenado;
- units_count — tamanho da sequência analisada;
- layers — número de camadas aninhadas no bloco;
- layers_to_one_kv — número de camadas aninhadas que operam em um único tensor Key-Value;
- variables — número de sequências unitárias na série temporal multimodal.
No corpo do método, chamamos imediatamente o método de mesmo nome da classe base pai, onde ocorre a inicialização das variáveis e objetos herdados. Além disso, esse método já contém os controles mínimos necessários para os dados recebidos pelo programa chamador.
Após a execução bem-sucedida do método da classe pai, armazenamos os parâmetros recebidos nas variáveis internas.
iWindow = fmax(window, 1); iWindowKey = fmax(window_key, 1); iUnits = fmax(units_count, 1); iHeads = fmax(heads, 1); iLayers = fmax(layers, 1); iHeadsKV = fmax(heads_kv, 1); iLayersToOneKV = fmax(layers_to_one_kv, 1); iVariables = variables;
Em seguida, definimos as principais constantes que determinam a arquitetura dos objetos aninhados.
uint num_q = iWindowKey * iHeads * iUnits * iVariables; //Size of Q tensor uint num_kv = iWindowKey * iHeadsKV * iUnits * iVariables; //Size of KV tensor uint q_weights = (iWindow * iHeads + 1) * iWindowKey; //Size of weights' matrix of Q tenzor uint kv_weights = (iWindow * iHeadsKV + 1) * iWindowKey; //Size of weights' matrix of K/V tenzor uint scores = iUnits * iUnits * iHeads * iVariables; //Size of Score tensor uint mh_out = iWindowKey * iHeads * iUnits * iVariables; //Size of multi-heads self-attention uint out = iWindow * iUnits * iVariables; //Size of out tensore uint w0 = (iWindowKey * iHeads + 1) * iWindow; //Size W0 weights' matrix uint ff_1 = 4 * (iWindow + 1) * iWindow; //Size of weights' matrix 1-st feed forward layer uint ff_2 = (4 * iWindow + 1) * iWindow; //Size of weights' matrix 2-nd feed forward layer
E aqui é relevante mencionar algumas abordagens que propomos para a implementação desta classe. Primeiramente, decidimos construir uma nova classe sem alterar o programa OpenCL. Em outras palavras, apesar dos novos requisitos, toda a classe é construída com base nos kernels existentes.
Para isso, inicialmente, separamos a geração das entidades Key e Value. Vale lembrar que, anteriormente, essas entidades eram geradas em um único processo direto de passagem pelo bloco convolucional e armazenadas sequencialmente no buffer para cada elemento da sequência. No entanto, ao construir a atenção global, essa abordagem não é mais aceitável. Porém, ao organizar o trabalho em canais separados, obtemos uma sequência alternada de Key/Value para cada canal, o que não é ideal para análises posteriores e não se alinha com os algoritmos anteriormente desenvolvidos. Assim, geramos as entidades separadamente e, em seguida, as concatenamos em um único tensor.
É importante destacar que dividimos a geração das entidades em dois estágios, cujo número independe do número de variáveis analisadas ou de cabeças de atenção.
Outro ponto é que os autores do método InjectTST preveem o uso de um único codificador Transformer para todos os canais. Portanto, também utilizamos as mesmas matrizes de pesos para todos eles. Dessa forma, o tamanho das matrizes de pesos permanece inalterado, independentemente da quantidade de canais.
Com isso, concluímos nosso trabalho preparatório e organizamos um laço com um número de iterações igual ao número de camadas aninhadas.
for(uint i = 0; i < iLayers; i++) { CBufferFloat *temp = NULL;
No corpo do laço, organizamos um laço interno para criar buffers dos resultados de operações intermediárias e dos gradientes de erro correspondentes.
for(int d = 0; d < 2; d++) { //--- Initilize Q tensor temp = new CBufferFloat(); if(CheckPointer(temp) == POINTER_INVALID) return false; if(!temp.BufferInit(num_q, 0)) return false; if(!temp.BufferCreate(OpenCL)) return false; if(!QKV_Tensors.Add(temp)) return false;
Primeiro, criamos o buffer do tensor Query. O algoritmo para criá-lo é idêntico para todos os casos. Inicialmente, criamos uma nova instância de um objeto de buffer. Inicializamos esse buffer com valores zero e um tamanho especificado. Depois, criamos uma cópia do buffer no contexto OpenCL e adicionamos um ponteiro para ele na coleção correspondente. Durante cada etapa, controlamos o processo de execução das operações.
Como planejamos usar um único tensor Key-Value para análise em várias camadas aninhadas, os buffers correspondentes são criados com uma periodicidade definida.
//--- Initilize KV tensor if(i % iLayersToOneKV == 0) { temp = new CBufferFloat(); if(CheckPointer(temp) == POINTER_INVALID) return false; if(!temp.BufferInit(num_kv, 0)) return false; if(!temp.BufferCreate(OpenCL)) return false; if(!K_Tensors.Add(temp)) return false; temp = new CBufferFloat(); if(CheckPointer(temp) == POINTER_INVALID) return false; if(!temp.BufferInit(num_kv, 0)) return false; if(!temp.BufferCreate(OpenCL)) return false; if(!V_Tensors.Add(temp)) return false; temp = new CBufferFloat(); if(CheckPointer(temp) == POINTER_INVALID) return false; if(!temp.BufferInit(2 * num_kv, 0)) return false; if(!temp.BufferCreate(OpenCL)) return false; if(!KV_Tensors.Add(temp)) return false; }
Vale notar que, nesta etapa, criamos três buffers: Key, Value e o tensor concatenado Key-Value.
O próximo passo é criar o buffer dos coeficientes de atenção.
//--- Initialize scores temp = new CBufferFloat(); if(CheckPointer(temp) == POINTER_INVALID) return false; if(!temp.BufferInit(scores, 0)) return false; if(!temp.BufferCreate(OpenCL)) return false; if(!S_Tensors.Add(temp)) return false;
Em seguida, criamos o buffer dos resultados da atenção multi-cabeças.
//--- Initialize multi-heads attention out temp = new CBufferFloat(); if(CheckPointer(temp) == POINTER_INVALID) return false; if(!temp.BufferInit(mh_out, 0)) return false; if(!temp.BufferCreate(OpenCL)) return false; if(!AO_Tensors.Add(temp)) return false;
Posteriormente, criamos os buffers para compressão da atenção multi-cabeças e para o bloco FeedForward.
//--- Initialize attention out temp = new CBufferFloat(); if(CheckPointer(temp) == POINTER_INVALID) return false; if(!temp.BufferInit(out, 0)) return false; if(!temp.BufferCreate(OpenCL)) return false; if(!FF_Tensors.Add(temp)) return false; //--- Initialize Feed Forward 1 temp = new CBufferFloat(); if(CheckPointer(temp) == POINTER_INVALID) return false; if(!temp.BufferInit(4 * out, 0)) return false; if(!temp.BufferCreate(OpenCL)) return false; if(!FF_Tensors.Add(temp)) return false; //--- Initialize Feed Forward 2 if(i == iLayers - 1) { if(!FF_Tensors.Add(d == 0 ? Output : Gradient)) return false; continue; } temp = new CBufferFloat(); if(CheckPointer(temp) == POINTER_INVALID) return false; if(!temp.BufferInit(out, 0)) return false; if(!temp.BufferCreate(OpenCL)) return false; if(!FF_Tensors.Add(temp)) return false; }
Após a inicialização dos buffers dos resultados intermediários e seus gradientes, passamos à inicialização das matrizes de pesos. O algoritmo para sua inicialização é semelhante ao processo de criação dos buffers de dados, com a diferença de que as matrizes são preenchidas com valores aleatórios.
A primeira matriz gerada é a de pesos da entidade Query.
//--- Initilize Q weights temp = new CBufferFloat(); if(CheckPointer(temp) == POINTER_INVALID) return false; if(!temp.Reserve(q_weights)) return false; float k = (float)(1 / sqrt(iWindow + 1)); for(uint w = 0; w < q_weights; w++) { if(!temp.Add(GenerateWeight() * 2 * k - k)) return false; } if(!temp.BufferCreate(OpenCL)) return false; if(!QKV_Weights.Add(temp)) return false;
A periodicidade de criação das matrizes de pesos das entidades Key e Value segue a mesma frequência dos buffers correspondentes.
//--- Initilize K weights if(i % iLayersToOneKV == 0) { temp = new CBufferFloat(); if(CheckPointer(temp) == POINTER_INVALID) return false; if(!temp.Reserve(kv_weights)) return false; float k = (float)(1 / sqrt(iWindow + 1)); for(uint w = 0; w < kv_weights; w++) { if(!temp.Add(GenerateWeight() * 2 * k - k)) return false; } if(!temp.BufferCreate(OpenCL)) return false; if(!K_Weights.Add(temp)) return false; //--- temp = new CBufferFloat(); if(CheckPointer(temp) == POINTER_INVALID) return false; if(!temp.Reserve(kv_weights)) return false; for(uint w = 0; w < kv_weights; w++) { if(!temp.Add(GenerateWeight() * 2 * k - k)) return false; } if(!temp.BufferCreate(OpenCL)) return false; if(!V_Weights.Add(temp)) return false; }
Adicionamos, em seguida, a matriz de compressão das cabeças de atenção.
//--- Initilize Weights0 temp = new CBufferFloat(); if(CheckPointer(temp) == POINTER_INVALID) return false; if(!temp.Reserve(w0)) return false; for(uint w = 0; w < w0; w++) { if(!temp.Add(GenerateWeight() * 2 * k - k)) return false; } if(!temp.BufferCreate(OpenCL)) return false; if(!FF_Weights.Add(temp)) return false;
E do bloco FeedForward.
//--- Initilize FF Weights temp = new CBufferFloat(); if(CheckPointer(temp) == POINTER_INVALID) return false; if(!temp.Reserve(ff_1)) return false; for(uint w = 0; w < ff_1; w++) { if(!temp.Add(GenerateWeight() * 2 * k - k)) return false; } if(!temp.BufferCreate(OpenCL)) return false; if(!FF_Weights.Add(temp)) return false; //--- temp = new CBufferFloat(); if(CheckPointer(temp) == POINTER_INVALID) return false; if(!temp.Reserve(ff_2)) return false; k = (float)(1 / sqrt(4 * iWindow + 1)); for(uint w = 0; w < ff_2; w++) { if(!temp.Add(GenerateWeight() * 2 * k - k)) return false; } if(!temp.BufferCreate(OpenCL)) return false; if(!FF_Weights.Add(temp)) return false;
Após isso, criamos outro laço interno, onde adicionamos buffers para os momentos no nível dos coeficientes de peso. A quantidade de buffers criados depende do método de atualização dos parâmetros.
for(int d = 0; d < (optimization == SGD ? 1 : 2); d++) { temp = new CBufferFloat(); if(CheckPointer(temp) == POINTER_INVALID) return false; if(!temp.BufferInit((d == 0 || optimization == ADAM ? q_weights : iWindowKey * iHeads), 0)) return false; if(!temp.BufferCreate(OpenCL)) return false; if(!QKV_Weights.Add(temp)) return false; if(i % iLayersToOneKV == 0) { temp = new CBufferFloat(); if(CheckPointer(temp) == POINTER_INVALID) return false; if(!temp.BufferInit((d == 0 || optimization == ADAM ? kv_weights : iWindowKey * iHeadsKV), 0)) return false; if(!temp.BufferCreate(OpenCL)) return false; if(!K_Weights.Add(temp)) return false; //--- temp = new CBufferFloat(); if(CheckPointer(temp) == POINTER_INVALID) return false; if(!temp.BufferInit((d == 0 || optimization == ADAM ? kv_weights : iWindowKey * iHeadsKV), 0)) return false; if(!temp.BufferCreate(OpenCL)) return false; if(!V_Weights.Add(temp)) return false; } temp = new CBufferFloat(); if(CheckPointer(temp) == POINTER_INVALID) return false; if(!temp.BufferInit((d == 0 || optimization == ADAM ? w0 : iWindow), 0)) return false; if(!temp.BufferCreate(OpenCL)) return false; if(!FF_Weights.Add(temp)) return false; //--- Initilize FF Weights temp = new CBufferFloat(); if(CheckPointer(temp) == POINTER_INVALID) return false; if(!temp.BufferInit((d == 0 || optimization == ADAM ? ff_1 : 4 * iWindow), 0)) return false; if(!temp.BufferCreate(OpenCL)) return false; if(!FF_Weights.Add(temp)) return false; temp = new CBufferFloat(); if(CheckPointer(temp) == POINTER_INVALID) return false; if(!temp.BufferInit((d == 0 || optimization == ADAM ? ff_2 : iWindow), 0)) return false; if(!temp.BufferCreate(OpenCL)) return false; if(!FF_Weights.Add(temp)) return false; } }
Ao final do método de inicialização, adicionamos um buffer para armazenar dados temporários e retornamos um resultado lógico à função chamadora, indicando o sucesso das operações realizadas.
if(!Temp.BufferInit(MathMax(2 * num_kv, out), 0)) return false; if(!Temp.BufferCreate(OpenCL)) return false; //--- return true; }
Depois de inicializar o objeto, avançamos para a organização dos algoritmos de propagação para frente. Aqui, é necessário mencionar o uso dos kernels criados anteriormente, especialmente o kernel de propagação para frente do bloco de atenção cruzada MH2AttentionOut, cujo algoritmo de enfileiramento para execução está implementado no método AttentionOut. Reforçamos que o algoritmo de enfileiramento do kernel não foi alterado. No entanto, nossa tarefa é utilizá-lo para realizar a análise de canais independentes.
Primeiro, vejamos como nosso kernel trabalha com cabeças de atenção individuais. Ele as processa de forma independente em fluxos separados. Aparentemente, isso é exatamente o que precisamos. Então, podemos tratar os canais independentes como se fossem cabeças de atenção.
bool CNeuronMVMHAttentionMLKV::AttentionOut(CBufferFloat *q, CBufferFloat *kv, CBufferFloat *scores, CBufferFloat *out) { if(!OpenCL) return false; //--- uint global_work_offset[3] = {0}; uint global_work_size[3] = {iUnits/*Q units*/, iUnits/*K units*/, iHeads * iVariables}; uint local_work_size[3] = {1, iUnits, 1};
O restante do algoritmo do método permanece o mesmo. Passamos os parâmetros necessários ao kernel.
ResetLastError(); if(!OpenCL.SetArgumentBuffer(def_k_MH2AttentionOut, def_k_mh2ao_q, q.GetIndex())) { printf("Error of set parameter kernel %s: %d; line %d", __FUNCTION__, GetLastError(), __LINE__); return false; } if(!OpenCL.SetArgumentBuffer(def_k_MH2AttentionOut, def_k_mh2ao_kv, kv.GetIndex())) { printf("Error of set parameter kernel %s: %d; line %d", __FUNCTION__, GetLastError(), __LINE__); return false; } if(!OpenCL.SetArgumentBuffer(def_k_MH2AttentionOut, def_k_mh2ao_score, scores.GetIndex())) { printf("Error of set parameter kernel %s: %d; line %d", __FUNCTION__, GetLastError(), __LINE__); return false; } if(!OpenCL.SetArgumentBuffer(def_k_MH2AttentionOut, def_k_mh2ao_out, out.GetIndex())) { printf("Error of set parameter kernel %s: %d; line %d", __FUNCTION__, GetLastError(), __LINE__); return false; } if(!OpenCL.SetArgument(def_k_MH2AttentionOut, def_k_mh2ao_dimension, (int)iWindowKey)) { printf("Error of set parameter kernel %s: %d; line %d", __FUNCTION__, GetLastError(), __LINE__); return false; }
Certificamo-nos de ajustar a quantidade de cabeças do tensor Key-Value.
if(!OpenCL.SetArgument(def_k_MH2AttentionOut, def_k_mh2ao_heads_kv, (int)(iHeadsKV * iVariables))) { printf("Error of set parameter kernel %s: %d; line %d", __FUNCTION__, GetLastError(), __LINE__); return false; }
Depois, colocamos o kernel na fila de execução.
if(!OpenCL.SetArgument(def_k_MH2AttentionOut, def_k_mh2ao_mask, 0)) { printf("Error of set parameter kernel %s: %d; line %d", __FUNCTION__, GetLastError(), __LINE__); return false; } if(!OpenCL.Execute(def_k_MH2AttentionOut, 3, global_work_offset, global_work_size, local_work_size)) { printf("Error of execution kernel %s: %d", __FUNCTION__, GetLastError()); return false; } //--- return true; }
Finalizamos o método, mas isso é apenas uma parte do algoritmo de propagação para frente. O algoritmo completo será implementado no método feedForward.
bool CNeuronMVMHAttentionMLKV::feedForward(CNeuronBaseOCL *NeuronOCL) { if(CheckPointer(NeuronOCL) == POINTER_INVALID) return false;
Os parâmetros do método incluem um ponteiro para o objeto da camada neural anterior, que contém os dados de entrada para o nosso algoritmo. Esperamos receber como dados de entrada um tensor tridimensional contendo informações sobre o comprimento da sequência, o número de sequências unitárias e o tamanho da janela de análise de um elemento.
No corpo do método, verificamos a validade do ponteiro recebido e organizamos um laço para iterar sobre as camadas aninhadas do módulo.
CBufferFloat *kv = NULL; for(uint i = 0; (i < iLayers && !IsStopped()); i++) { //--- Calculate Queries, Keys, Values CBufferFloat *inputs = (i == 0 ? NeuronOCL.getOutput() : FF_Tensors.At(6 * i - 4));
Primeiro, declaramos um ponteiro local para o buffer dos dados de entrada, no qual armazenamos o ponteiro necessário. Depois, extraímos da coleção o buffer correspondente ao nível de análise do módulo para a entidade Query e gravamos nele os dados gerados a partir dos dados de entrada.
CBufferFloat *q = QKV_Tensors.At(i * 2); if(IsStopped() || !ConvolutionForward(QKV_Weights.At(i * (optimization == SGD ? 2 : 3)), inputs, q, iWindow, iWindowKey * iHeads, None)) return false;
O próximo passo é verificar se é necessário gerar um novo tensor Key-Value. Se for o caso, começamos definindo o deslocamento nas coleções correspondentes.
if((i % iLayersToOneKV) == 0) { uint i_kv = i / iLayersToOneKV;
Em seguida, extraímos os ponteiros para os buffers necessários.
kv = KV_Tensors.At(i_kv * 2); CBufferFloat *k = K_Tensors.At(i_kv * 2); CBufferFloat *v = V_Tensors.At(i_kv * 2);
Depois disso, geramos sequencialmente as entidades Key e Value.
if(IsStopped() || !ConvolutionForward(K_Weights.At(i_kv * (optimization == SGD ? 2 : 3)), inputs, k, iWindow, iWindowKey * iHeadsKV, None)) return false; if(IsStopped() || !ConvolutionForward(V_Weights.At(i_kv * (optimization == SGD ? 2 : 3)), inputs, v, iWindow, iWindowKey * iHeadsKV, None)) return false;
E concatenamos os tensores gerados ao longo da primeira dimensão (elementos da sequência).
if(IsStopped() || !Concat(k, v, kv, iWindowKey * iHeadsKV * iVariables, iWindowKey * iHeadsKV * iVariables, iUnits)) return false; }
Vale destacar que, com essa organização dos dados, obtemos um buffer que pode ser representado como um tensor de cinco dimensões: Units * [Key, Value] * Variable * HeadsKV * Window_Key. O tensor da entidade Query tem uma dimensão comparável, mas em vez de [Key, Value], temos [Query]. Ao agruparmos as dimensões Variable e Heads em uma única dimensão chamada "Variable * Heads", as dimensões dos tensores se tornam compatíveis com a atenção multi-cabeças convencional (Multi-Heads Self-Attention).
É importante lembrar que, no contexto do OpenCL, trabalhamos com buffers de dados unidimensionais. A divisão dos dados em um tensor multidimensional é apenas declarativa, para facilitar a compreensão da sequência dos dados. Em geral, a sequência dos dados no buffer segue do último para o primeiro dimensionamento.
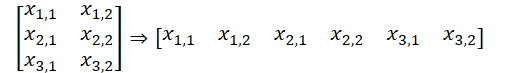
Isso nos permite usar os kernels criados anteriormente no programa OpenCL para analisar canais independentes. Extraímos os ponteiros para os buffers necessários das coleções e executamos o algoritmo Multi-Heads Self-Attention. O método necessário foi ajustado previamente.
//--- Score calculation and Multi-heads attention calculation CBufferFloat *temp = S_Tensors.At(i * 2); CBufferFloat *out = AO_Tensors.At(i * 2); if(IsStopped() || !AttentionOut(q, kv, temp, out)) return false;
Depois, reformatamos mentalmente os resultados da atenção multi-cabeças em um tensor [Units * Variable] * Heads * Window_Key e projetamos os dados para coincidir com as dimensões dos dados originais.
//--- Attention out calculation temp = FF_Tensors.At(i * 6); if(IsStopped() || !ConvolutionForward(FF_Weights.At(i * (optimization == SGD ? 6 : 9)), out, temp, iWindowKey * iHeads, iWindow, None)) return false; //--- Sum and normilize attention if(IsStopped() || !SumAndNormilize(temp, inputs, temp, iWindow, true)) return false;
Em seguida, somamos os resultados obtidos aos dados originais e normalizamos os valores calculados.
Depois, realizamos as operações do bloco FeedForward no mesmo estilo e avançamos para a próxima iteração do laço.
//--- Feed Forward inputs = temp; temp = FF_Tensors.At(i * 6 + 1); if(IsStopped() || !ConvolutionForward(FF_Weights.At(i * (optimization == SGD ? 6 : 9) + 1), inputs, temp, iWindow, 4 * iWindow, LReLU)) return false; out = FF_Tensors.At(i * 6 + 2); if(IsStopped() || !ConvolutionForward(FF_Weights.At(i * (optimization == SGD ? 6 : 9) + 2), temp, out, 4 * iWindow, iWindow, activation)) return false; //--- Sum and normilize out if(IsStopped() || !SumAndNormilize(out, inputs, out, iWindow, true)) return false; } //--- return true; }
Após a conclusão bem-sucedida das operações de todas as camadas aninhadas do bloco, encerramos o método e retornamos um resultado lógico de sucesso para a função chamadora.
Após a implementação dos métodos de propagação para frente, geralmente passamos à construção dos algoritmos de propagação reversa. Hoje, quero sugerir que você examine por conta própria a implementação proposta, disponível no anexo. Durante a implementação dos métodos de propagação reversa, foram utilizados os mesmos conceitos descritos anteriormente na implementação dos métodos de propagação para frente. É importante ressaltar que as operações de propagação reversa são realizadas estritamente de acordo com o algoritmo de propagação para frente, mas em ordem inversa.
Além disso, no anexo, você encontrará a implementação da classe CNeuronMVCrossAttentionMLKV, cujos algoritmos, em sua maioria, repetem os algoritmos semelhantes da classe CNeuronMVMHAttentionMLKV, mas são complementados com funcionalidades de atenção cruzada.
Gostaria de lembrar que as classes implementadas, CNeuronMVMHAttentionMLKV e CNeuronMVCrossAttentionMLKV, são apenas blocos componentes de um algoritmo mais complexo, o InjectTST, cujos aspectos teóricos foram apresentados anteriormente. O próximo passo do nosso trabalho será a criação de uma nova classe, onde implementaremos o algoritmo completo do InjectTST.
2.2 Implementação do InjectTST
O algoritmo completo do InjectTST será construído dentro da classe CNeuronInjectTST, que herda a funcionalidade básica da classe mãe do neurônio de camada totalmente conectada, CNeuronBaseOCL. A estrutura da nova classe é apresentada a seguir:
class CNeuronInjectTST : public CNeuronBaseOCL { protected: CNeuronPatching cPatching; CNeuronLearnabledPE cCIPosition; CNeuronLearnabledPE cCMPosition; CNeuronMVMHAttentionMLKV cChanelIndependentAttention; CNeuronMLMHAttentionMLKV cChanelMixAttention; CNeuronMVCrossAttentionMLKV cGlobalInjectionAttention; CBufferFloat cTemp; //--- virtual bool feedForward(CNeuronBaseOCL *NeuronOCL) override; //--- virtual bool calcInputGradients(CNeuronBaseOCL *NeuronOCL) override; virtual bool updateInputWeights(CNeuronBaseOCL *NeuronOCL) override; //--- public: CNeuronInjectTST(void) {}; ~CNeuronInjectTST(void) {}; //--- virtual bool Init(uint numOutputs, uint myIndex, COpenCLMy *open_cl, uint window, uint window_key, uint heads, uint heads_kv, uint units_count, uint layers, uint layers_to_one_kv, uint variables, ENUM_OPTIMIZATION optimization_type, uint batch); //--- virtual int Type(void) const { return defNeuronInjectTST; } //--- virtual bool Save(int const file_handle); virtual bool Load(int const file_handle); //--- virtual bool WeightsUpdate(CNeuronBaseOCL *source, float tau); virtual void SetOpenCL(COpenCLMy *obj); //--- virtual CBufferFloat *getWeights(void) override; };
Nessa classe, observamos uma quantidade considerável de objetos internos, mas nenhuma variável. Isso ocorre porque a classe implementa uma espécie de "montagem modular" do algoritmo, cujo principal funcional se baseia nos objetos internos. Todas as constantes que definem a arquitetura do bloco são usadas apenas no método de inicialização da classe e armazenadas dentro dos objetos aninhados, cuja funcionalidade será detalhada durante a implementação dos algoritmos.
Todos os objetos internos da classe são declarados como estáticos, o que permite que os construtores e destrutores da classe permaneçam vazios. A inicialização de todos os objetos aninhados e herdados é realizada no método Init.
bool CNeuronInjectTST::Init(uint numOutputs, uint myIndex, COpenCLMy *open_cl, uint window, uint window_key, uint heads, uint heads_kv, uint units_count, uint layers, uint layers_to_one_kv, uint variables, ENUM_OPTIMIZATION optimization_type, uint batch) { if(!CNeuronBaseOCL::Init(numOutputs, myIndex, open_cl, window * units_count * variables, optimization_type, batch)) return false; SetActivationFunction(None);
Como de costume, os parâmetros deste método incluem as principais constantes que definem a arquitetura do objeto a ser criado. No corpo do método, chamamos imediatamente o método de mesmo nome da classe mãe, no qual já estão implementados os controles básicos dos parâmetros recebidos e a inicialização dos objetos herdados.
Em seguida, realizamos a inicialização dos objetos internos seguindo a sequência de propagação para frente do algoritmo InjectTST. Na visualização do método apresentada anteriormente pelos autores, fica evidente que os dados recebidos são usados em dois fluxos de informação: os blocos de canais independentes e o de mistura global. Em ambos os blocos, os dados recebidos são segmentados inicialmente. Na minha implementação, decidi evitar a duplicação do processo de segmentação, realizando-o apenas uma vez antes da bifurcação dos fluxos de informação.
if(!cPatching.Init(0, 0, OpenCL, window, window, window, units_count, variables, optimization, iBatch)) return false; cPatching.SetActivationFunction(None);
Nesta implementação, optei por utilizar parâmetros iguais: tamanho do segmento, passo da janela do segmento e tamanho do embedding do segmento. Assim, o tamanho do buffer dos dados originais antes e depois da segmentação permanece o mesmo. No entanto, a sequência dos dados no buffer foi alterada. O tensor de dados, anteriormente com duas dimensões L * V , foi reformatado para três dimensões L/p x V x p, onde L representa o comprimento da sequência multimodal dos dados originais, V é o número de variáveis analisadas e p é o tamanho do segmento.
Aos tokens dos segmentos no bloco de canais independentes, os autores do método adicionam dois tensores treináveis: codificação posicional e identificação de canal. A soma dessas duas informações resulta em um valor, e por isso, em minha implementação, decidi usar uma única camada de codificação posicional treinável, que aprende a posição de cada elemento individual no tensor dos dados originais.
if(!cCIPosition.Init(0, 1, OpenCL, window * units_count * variables, optimization, iBatch)) return false; cCIPosition.SetActivationFunction(None);
No bloco de mistura global, o algoritmo também utiliza codificação posicional. Inicializamos uma camada semelhante para o segundo fluxo de informações.
if(!cCMPosition.Init(0, 2, OpenCL, window * units_count * variables, optimization, iBatch)) return false; cCMPosition.SetActivationFunction(None);
A estrutura de canais independentes foi construída com o uso do bloco de atenção de canais independentes CNeuronMVMHAttentionMLKV.
if(!cChanelIndependentAttention.Init(0, 3, OpenCL, window, window_key, heads, heads_kv, units_count, layers, layers_to_one_kv, variables, optimization, iBatch)) return false; cChanelIndependentAttention.SetActivationFunction(None);
Já para o bloco de mistura global, utilizamos o bloco de atenção previamente criado, CNeuronMLMHAttentionMLKV.
if(!cChanelMixAttention.Init(0, 4, OpenCL, window * variables, window_key, heads, heads_kv, units_count, layers, layers_to_one_kv, optimization, iBatch)) return false; cChanelMixAttention.SetActivationFunction(None);
É importante observar que, neste caso, o tamanho da janela do vetor analisado de um elemento corresponde ao produto do tamanho do segmento pelo número de variáveis analisadas, o que segue a abordagem da mistura de canais.
A injeção de informações globais nos canais independentes é realizada dentro do bloco de atenção cruzada.
if(!cGlobalInjectionAttention.Init(0, 5, OpenCL, window, window_key, heads, window * variables, heads_kv, units_count, units_count, layers, layers_to_one_kv, variables, 1, optimization, iBatch)) return false; cGlobalInjectionAttention.SetActivationFunction(None);
Note que, neste caso, o número de séries unitárias no contexto é especificado como 1, uma vez que estamos lidando com canais mistos.
Ao final do método de inicialização, realizamos a substituição dos buffers de dados, permitindo eliminar a cópia excessiva entre os buffers da classe e os objetos internos.
if(!SetOutput(cGlobalInjectionAttention.getOutput(), true) || !SetGradient(cGlobalInjectionAttention.getGradient(), true) ) return false;
Inicializamos um buffer auxiliar para armazenar dados intermediários e retornamos um resultado lógico indicando o sucesso das operações à função chamadora.
if(!cTemp.BufferInit(cPatching.Neurons(), 0) || !cTemp.BufferCreate(OpenCL) ) return false; //--- return true; }
Após inicializar o objeto da classe, avançamos para a construção do algoritmo de propagação para frente do nosso modelo. Os principais marcos do algoritmo já foram discutidos durante a implementação do método de inicialização, e agora só precisamos descrevê-los no método feedForward.
bool CNeuronInjectTST::feedForward(CNeuronBaseOCL *NeuronOCL) { if(!cPatching.FeedForward(NeuronOCL)) return false;
Os parâmetros do método incluem um ponteiro para o objeto da camada anterior, que transmite os dados originais. O ponteiro recebido é imediatamente encaminhado ao método de mesmo nome da camada aninhada de segmentação de dados.
Observe que, nesta etapa, não verificamos a validade do ponteiro recebido, pois os controles necessários já estão implementados no método da camada de segmentação, tornando uma verificação adicional desnecessária.
O próximo passo é adicionar a codificação posicional aos dados segmentados.
if(!cCIPosition.FeedForward(cPatching.AsObject()) || !cCMPosition.FeedForward(cPatching.AsObject()) ) return false;
Depois disso, os dados passam primeiro pelo bloco de canais independentes.
if(!cChanelIndependentAttention.FeedForward(cCIPosition.AsObject())) return false;
E em seguida pelo bloco de mistura global.
if(!cChanelMixAttention.FeedForward(cCMPosition.AsObject())) return false;
Vale destacar que, apesar da sequência de execução, esses são dois fluxos de informação independentes. Somente no bloco de atenção contextual ocorre a injeção de dados globais nos canais independentes.
if(!cGlobalInjectionAttention.FeedForward(cCIPosition.AsObject(), cCMPosition.getOutput())) return false; //--- return true; }
A camada de decisão foi posicionada fora da classe CNeuronInjectTST.
Como você pode ver, o método de propagação para frente é bastante conciso e legível, o que era esperado para uma implementação de "montagem modular" do algoritmo. Os métodos de propagação reversa foram construídos de forma semelhante, e sugiro que você os explore por conta própria. Lembro que o código completo de todas as classes e métodos descritos está anexado. Nele, você também encontrará o código completo de todos os programas usados na elaboração deste artigo.
2.3 Arquitetura dos modelos treináveis
Acima, implementamos os principais algoritmos do método InjectTST utilizando MQL5 e agora podemos incorporar os conceitos propostos em nossos próprios modelos. O método em questão foi proposto para previsão de séries temporais, e, assim como em outros métodos de previsão de séries temporais analisados anteriormente, tentaremos aplicar os conceitos propostos ao modelo de Codificador do estado do ambiente. Como você sabe, a descrição da arquitetura desse modelo está apresentada no método CreateEncoderDescriptions.
bool CreateEncoderDescriptions(CArrayObj *&encoder) { //--- CLayerDescription *descr; //--- if(!encoder) { encoder = new CArrayObj(); if(!encoder) return false; }
Nos parâmetros desse método, recebemos um ponteiro para o objeto de matriz dinâmica para gravar a arquitetura do modelo. No corpo do método, verificamos imediatamente a validade do ponteiro recebido e, se necessário, criamos um novo objeto de matriz dinâmica. Em seguida, começamos a descrever a arquitetura do modelo a ser criado.
Primeiro, inserimos uma camada totalmente conectada básica, que serve para gravar os dados de entrada.
//--- Input layer if(!(descr = new CLayerDescription())) return false; descr.type = defNeuronBaseOCL; int prev_count = descr.count = (HistoryBars * BarDescr); descr.activation = None; descr.optimization = ADAM; if(!encoder.Add(descr)) { delete descr; return false; }
Como de costume, planejamos alimentar o modelo com dados brutos não processados. A primeira etapa de processamento ocorre na camada de normalização em lote, onde as informações de diferentes distribuições são ajustadas para uma forma comparável.
//--- layer 1 if(!(descr = new CLayerDescription())) return false; descr.type = defNeuronBatchNormOCL; descr.count = prev_count; descr.batch = 1e4; descr.activation = None; descr.optimization = ADAM; if(!encoder.Add(descr)) { delete descr; return false; }
Em seguida, posicionamos a nossa nova camada de canais independentes com injeção global.
//--- layer 2 if(!(descr = new CLayerDescription())) return false; descr.type = defNeuronInjectTST; descr.window = PatchSize; //Patch window descr.window_out = 8; //Window Key
Para especificar o tamanho do segmento, adicionamos a constante PatchSize. O tamanho da sequência é calculado com base na profundidade do histórico analisado e no tamanho do segmento.
prev_count = descr.count = (HistoryBars + descr.window - 1) / descr.window; //Units
O número de cabeças de atenção para as entidades Query, Key e Value, bem como o número de sequências unitárias, será registrado em uma matriz.
{
int temp[] =
{
4, //Heads
2, //Heads KV
BarDescr //Variables
};
ArrayCopy(descr.heads, temp);
}
Todos os blocos internos conterão quatro camadas empilhadas.
descr.layers = 4; //Layers
E um único tensor Key-Value será utilizado por dois blocos aninhados.
descr.step = 2; //Layers to 1 KV descr.batch = 1e4; descr.activation = None; descr.optimization = ADAM; if(!encoder.Add(descr)) { delete descr; return false; }
Em seguida, adicionamos a camada de previsão de valores futuros. Lembramos que, na saída do bloco InjectTST, obtemos um tensor de dimensão L/p * V * p. Para realizar a previsão de dados nos canais independentes, precisamos primeiro transpor os dados.
//--- layer 3 if(!(descr = new CLayerDescription())) return false; descr.type = defNeuronTransposeOCL; descr.count = prev_count; descr.window = PatchSize * BarDescr; descr.activation = None; descr.optimization = ADAM; if(!encoder.Add(descr)) { delete descr; return false; }
Após isso, utilizamos um MLP de duas camadas para realizar a previsão nos canais independentes.
//--- layer 4 if(!(descr = new CLayerDescription())) return false; descr.type = defNeuronConvOCL; descr.count = PatchSize * BarDescr; descr.window = prev_count; descr.window_out = NForecast; descr.activation = LReLU; descr.optimization = ADAM; if(!encoder.Add(descr)) { delete descr; return false; } //--- layer 5 if(!(descr = new CLayerDescription())) return false; descr.type = defNeuronConvOCL; descr.count = BarDescr; descr.window = PatchSize * NForecast; descr.window_out = NForecast; descr.activation = TANH; descr.optimization = ADAM; if(!encoder.Add(descr)) { delete descr; return false; }
Nesse processo, reduzimos a dimensionalidade dos dados para Variables * Forecast. Assim, podemos retornar os valores previstos ao formato dos dados originais.
//--- layer 6 if(!(descr = new CLayerDescription())) return false; descr.type = defNeuronTransposeOCL; descr.count = BarDescr; descr.window = NForecast; descr.activation = None; descr.optimization = ADAM; if(!encoder.Add(descr)) { delete descr; return false; }
Adicionamos também indicadores estatísticos extraídos dos dados originais durante o processo de normalização.
//--- layer 7 if(!(descr = new CLayerDescription())) return false; descr.type = defNeuronRevInDenormOCL; descr.count = BarDescr * NForecast; descr.activation = None; descr.optimization = ADAM; descr.layers = 1; if(!encoder.Add(descr)) { delete descr; return false; }
Além disso, aplicamos os conceitos do método FreDF para alinhar os valores previstos das séries unitárias no domínio da frequência.
//--- layer 8 if(!(descr = new CLayerDescription())) return false; descr.type = defNeuronFreDFOCL; descr.window = BarDescr; descr.count = NForecast; descr.step = int(true); descr.probability = 0.7f; descr.activation = None; descr.optimization = ADAM; if(!encoder.Add(descr)) { delete descr; return false; } //--- return true; }
As arquiteturas dos modelos Ator e Crítico foram transferidas sem alterações de trabalhos anteriores. Por isso, não vamos nos aprofundar na descrição delas agora.
Além disso, não alteramos a camada de entrada nem a camada de resultados na nova arquitetura do Codificador do estado do ambiente. Isso nos permite reutilizar, sem modificações, todos os programas criados anteriormente para interagir com o ambiente e treinar modelos. Consequentemente, também podemos usar o conjunto de dados de treinamento previamente coletado para o treinamento inicial dos modelos.
Lembro que o código completo de todas as classes e métodos apresentados, bem como o código completo de todos os programas utilizados na preparação deste artigo, está disponível no anexo.
3. Testes
Implementamos acima os conceitos do método InjectTST utilizando MQL5 e também demonstramos um exemplo de uso da nova classe na modelagem do Codificador do Estado do Ambiente. Agora, podemos proceder à avaliação da eficácia do modelo com base em dados históricos reais.
Como anteriormente, começamos treinando o modelo do Codificador do estado do ambiente para prever o movimento futuro de preços em um horizonte de planejamento definido. Durante o experimento, utilizamos como conjunto de dados de treinamento os dados históricos de 2023 para o par EURUSD no timeframe H1.
O Codificador do Estado do Ambiente analisa apenas os dados históricos de preços do ativo, sem influência direta das ações do Agente. Assim, o treinamento do modelo é realizado até atingir os resultados desejados ou até que o erro de previsão atinja um "platô".
Abaixo, apresentamos uma visualização comparativa da trajetória prevista em relação à trajetória real do movimento de preços.
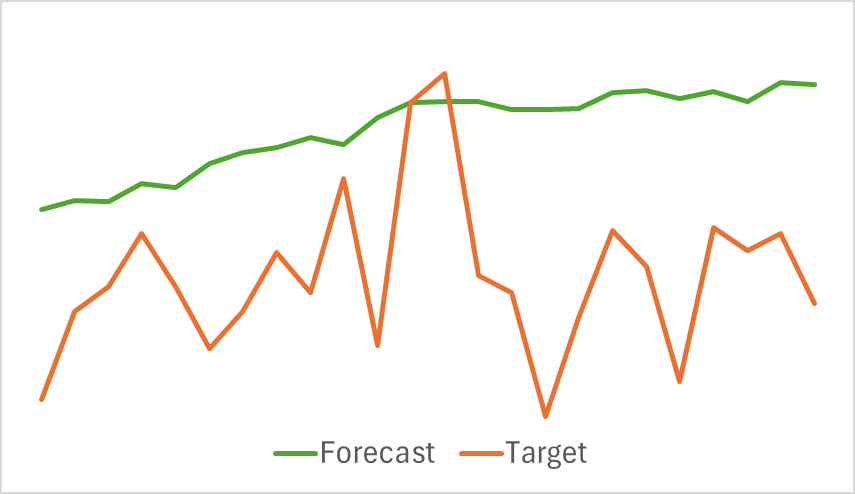
Como pode ser observado no gráfico apresentado, a trajetória prevista está deslocada para cima e apresenta oscilações menos pronunciadas. No entanto, é possível identificar coincidências nas direções das tendências gerais. Talvez esse não seja o melhor modelo para prever movimentos de preços futuros em comparação com os modelos analisados anteriormente. Avançaremos, então, para a segunda etapa do treinamento dos modelos e verificaremos se este Codificador pode ajudar o Ator a construir uma estratégia lucrativa.
O treinamento dos modelos Ator e Crítico é realizado de maneira iterativa. Inicialmente, algumas épocas de treinamento são executadas no conjunto de dados existente. Em seguida, durante a interação com o ambiente, utilizando a política atual do Ator, o conjunto de dados de treinamento é atualizado. Isso nos permite enriquecer o conjunto de dados de treinamento com recompensas reais das ações derivadas da política atual do Ator. Consequentemente, nas etapas seguintes do treinamento, conseguimos aprimorar a função de recompensa do Crítico e avaliar as ações do Ator com mais precisão, indicando um vetor de ajuste para melhorar a eficiência da política atual. Essas iterações se repetem até que o resultado desejado seja atingido.
Para avaliar a eficácia da política treinada do Ator, realizamos uma execução de teste do EA para interação com o ambiente no testador de estratégias do MetaTrader 5. O teste foi realizado com dados históricos de janeiro de 2024, mantendo os outros parâmetros inalterados. Os resultados do teste estão apresentados abaixo.
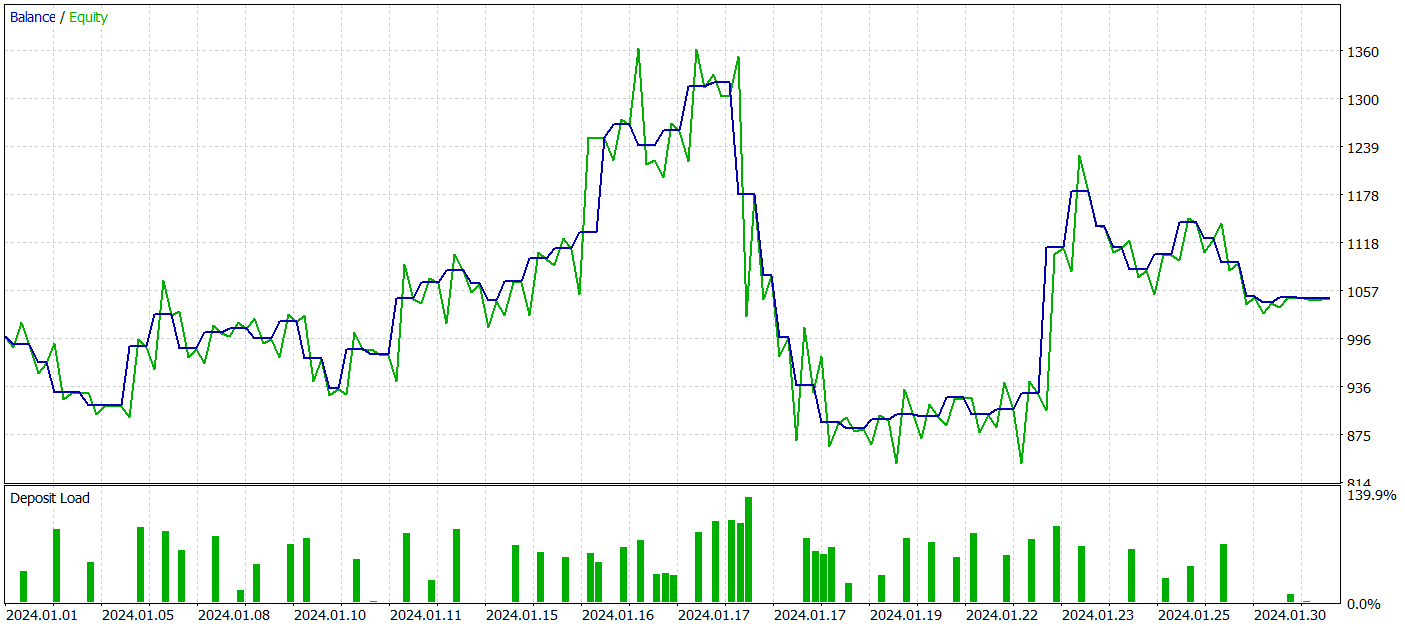
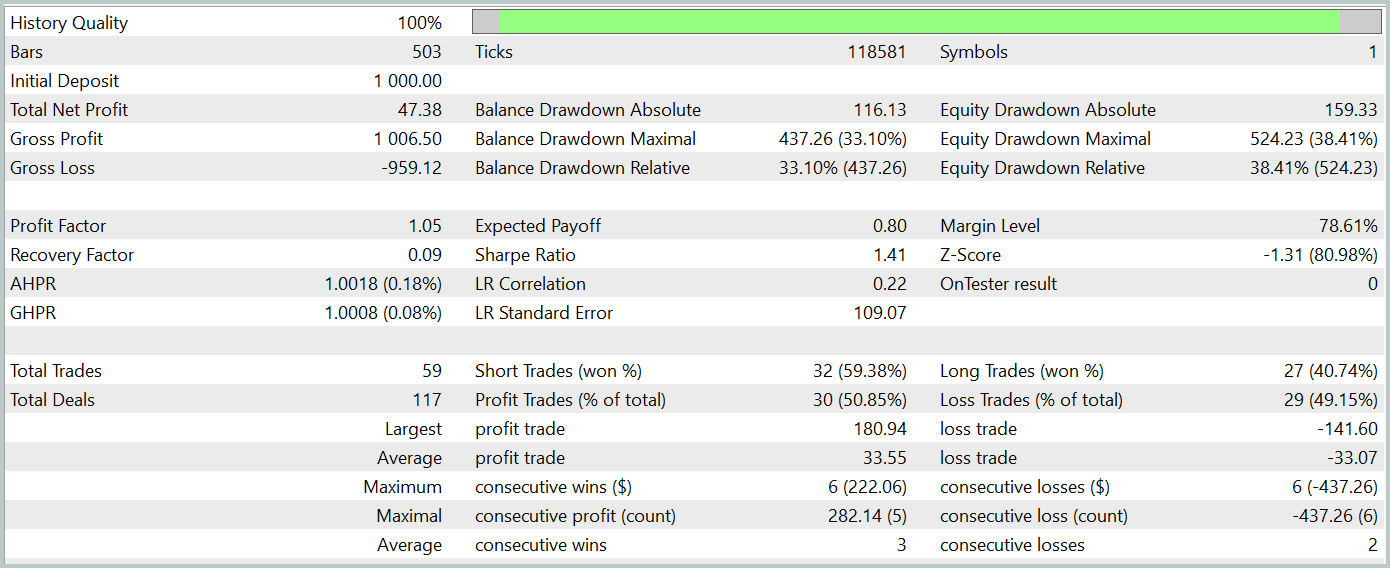
Durante o período de teste, o modelo obteve um pequeno lucro. Foram realizadas 59 operações, das quais 30 foram encerradas com lucro. O lucro máximo e o lucro médio por operação lucrativa superaram os valores correspondentes das operações perdedoras. Assim, o fator de lucro foi de 1,05. No entanto, o gráfico do saldo não apresenta uma tendência claramente definida. Durante o teste, o saldo diminuiu mais de 33%.
Considerações finais
Neste artigo, exploramos o novo método de previsão de séries temporais InjectTST, desenvolvido para melhorar a qualidade das previsões de séries temporais longas através da injeção de informações globais em canais de dados independentes.
Na parte prática, implementamos os conceitos propostos utilizando MQL5 e os incorporamos ao modelo de Codificador do estado do ambiente. Embora tenhamos realizado um trabalho extenso, os resultados ficaram aquém das expectativas.
Para identificar as razões dos resultados tão baixos, é necessário realizar uma análise detalhada. No entanto, é bastante provável que uma das razões seja a tentativa de treinar o modelo de previsão dos estados futuros do ambiente de maneira direta, ou seja, "de forma bruta". Vale lembrar que os autores do método recomendaram um treinamento em três etapas para o modelo.
Referências
- InjectTST: A Transformer Method of Injecting Global Information into Independent Channels for Long Time Series Forecasting
- Outros artigos da série
Programas utilizados no artigo
| # | Nome | Tipo | Descrição |
|---|---|---|---|
| 1 | Research.mq5 | Expert Advisor | EA para coleta de exemplos |
| 2 | ResearchRealORL.mq5 | Expert Advisor | EA para coleta de exemplos pelo método Real-ORL |
| 3 | Study.mq5 | Expert Advisor | EA para treinamento de Modelos |
| 4 | StudyEncoder.mq5 | Expert Advisor | EA para treinamento do Codificador |
| 5 | Test.mq5 | Expert Advisor | EA para testar o modelo |
| 6 | Trajectory.mqh | Biblioteca de classe | Estrutura de descrição do estado do sistema |
| 7 | NeuroNet.mqh | Biblioteca de classe | Biblioteca de classes para criação de redes neurais |
| 8 | NeuroNet.cl | Biblioteca | Biblioteca de código do programa OpenCL |
Traduzido do russo pela MetaQuotes Ltd.
Artigo original: https://www.mql5.com/ru/articles/15498
Aviso: Todos os direitos sobre esses materiais pertencem à MetaQuotes Ltd. É proibida a reimpressão total ou parcial.
Esse artigo foi escrito por um usuário do site e reflete seu ponto de vista pessoal. A MetaQuotes Ltd. não se responsabiliza pela precisão das informações apresentadas nem pelas possíveis consequências decorrentes do uso das soluções, estratégias ou recomendações descritas.
 Analisando exemplos de estratégias de trading no terminal do cliente
Analisando exemplos de estratégias de trading no terminal do cliente
 Colmeia artificial de abelhas (ABHA): Testes e resultados
Colmeia artificial de abelhas (ABHA): Testes e resultados
 Redes neurais em trading: Modelos de espaço de estados
Redes neurais em trading: Modelos de espaço de estados
 Do básico ao intermediário: Template e Typename (IV)
Do básico ao intermediário: Template e Typename (IV)
- Aplicativos de negociação gratuitos
- 8 000+ sinais para cópia
- Notícias econômicas para análise dos mercados financeiros
Você concorda com a política do site e com os termos de uso