Redes neurais em trading: Modelo universal de geração de trajetórias (UniTraj)

Introdução

A análise do comportamento de múltiplos agentes é importante em várias áreas, como finanças, direção autônoma e sistemas de videomonitoramento. Para compreender as ações desses agentes, é necessário resolver uma série de tarefas essenciais, como o rastreamento de objetos, a identificação, a modelagem de trajetórias e o reconhecimento de ações. A modelagem de trajetórias é fundamental para a análise dos movimentos dos agentes. Apesar das dificuldades relacionadas à dinâmica do ambiente e às sutis interações entre agentes, houve avanços significativos recentemente na solução desse problema. Os principais progressos se concentram em três áreas-chave: previsão de trajetórias, recuperação de dados ausentes e modelagem espaço-temporal.

No entanto, a maioria das abordagens é especializada para tarefas específicas, o que dificulta sua generalização para outras aplicações. A solução de algumas dessas tarefas exige o uso de dependências espaço-temporais tanto diretas quanto reversas, que geralmente não são consideradas em modelos focados em previsão. Embora outros algoritmos tenham resolvido o problema do cálculo condicional de trajetórias multiagentes, frequentemente ignoram as trajetórias futuras dos agentes, limitando sua utilidade prática na compreensão completa dos movimentos. A previsão de trajetórias futuras é essencial para o planejamento de ações subsequentes, não apenas para reconstruir trajetórias históricas.

No artigo "Deciphering Movement: Unified Trajectory Generation Model for Multi-Agent", é apresentado o modelo universal Unified TrajectoryGeneration (UniTraj), que integra diversas tarefas de manipulação de trajetórias em uma estrutura comum. Em particular, os autores do método unificam diferentes tipos de dados brutos em uma única forma padronizada: uma trajetória arbitrária e incompleta, acompanhada por uma máscara que indica a visibilidade de cada agente em cada instante de tempo. O modelo processa uniformemente os dados brutos de cada tarefa como trajetórias mascaradas, buscando gerar trajetórias completas a partir das incompletas.

Para modelar dependências espaço-temporais em diferentes representações de trajetórias, os autores do método propuseram o módulo Ghost Spatial Masking (GSM), integrado ao codificador baseado em Transformer. Aproveitando as capacidades dos mais recentes modelos populares de espaço de estados (SSM), especialmente o modelo Mamba, os autores adaptam e aprimoram essa abordagem em um codificador temporal bidirecional Mamba para a geração de longo prazo de trajetórias multiagentes. Além disso, eles introduziram um módulo simples, porém eficaz, chamado Bidirectional Temporal Scaled (BTS), que varre amplamente as trajetórias enquanto preserva a integridade das relações temporais na sequência. Os resultados experimentais apresentados no artigo confirmam o excelente desempenho estável do método proposto.

1. Algoritmo UniTraj

Para processar diferentes condições iniciais dentro de uma única estrutura, os autores propõem um modelo generativo unificado de trajetória, que trata qualquer entrada arbitrária como uma sequência de trajetória mascarada. As áreas visíveis da trajetória são usadas como restrições ou dados brutos, enquanto as áreas ausentes são o alvo da solução da tarefa generativa. Assim, o seguinte problema é definido:

É necessário determinar a trajetória completa X[N, T, D], onde N — o número de agentes, T representa o comprimento da trajetória e D — a dimensionalidade dos estados dos agentes. Denotamos o estado do agente i no momento t como xi,t[D]. Além disso, utiliza-se uma matriz binária de mascaramento M[N, T]. A variável mi,t assume o valor 1, se a localização do agente i for conhecida no tempo t e 0 caso contrário. Dessa forma, a trajetória é dividida pela máscara em dois segmentos: a área visível, definida como Xv=X⊙M, e a área ausente, definida como Xm=X⊙(1−M). A tarefa consiste em criar a trajetória completa Y'={X'v,X'm}, onde X'v — a trajetória reconstruída e X'm — a trajetória gerada novamente. Para manter a consistência, os autores referem-se à trajetória original como a verdade fundamental Y=X={Xv, Xm}.

De forma mais rigorosa, o objetivo é treinar um modelo generativo f(⋅) com parâmetros θ, de modo que ele gere a trajetória completa Y'.

A abordagem geral para estimar os parâmetros do modelo θ envolve a decomposição do produto das distribuições conjuntas da trajetória e a maximização da verossimilhança logarítmica.

Consideremos o uso do agente i no instante de tempo t com a posição xi,t. Primeiro, calculamos a velocidade relativa 𝒗i,t, subtraindo as coordenadas dos passos temporais adjacentes. Para locais ausentes, preenchemos os valores com 0 por meio da multiplicação elemento a elemento pela máscara. Além disso, definimos o vetor de categoria única 𝒄i,t para representar as categorias dos agentes. Essa categorização é essencial em jogos esportivos, nos quais os jogadores podem adotar estratégias ofensivas ou defensivas específicas. As características do agente são projetadas em um vetor de características de alta dimensionalidade, denominado 𝒇i,xt. Os vetores de características originais são calculados da seguinte forma:

onde φx(⋅) — uma função de projeção com pesos 𝐖x, ⊙ representa a multiplicação elemento a elemento e ⊕ indica concatenação.

Os autores do método implementaram φx(⋅) utilizando MLP. Essa abordagem permite incorporar informações sobre posição, velocidade, visibilidade e categorias para a extração de características espaciais e sua posterior análise.

Ao contrário de outras tarefas de modelagem sequencial, é essencial considerar interações sociais densas. As pesquisas existentes sobre interações humanas utilizam, predominantemente, mecanismos de atenção, como atenção cruzada e atenção baseada em grafos, para capturar essa dinâmica. No entanto, dado que o UniTraj resolve uma única tarefa com dados brutos arbitrários e incompletos, é fundamental que o modelo proposto aprenda padrões espaço-temporais ausentes. Assim, os autores apresentam um novo e eficiente módulo Ghost Spatial Masking (GSM) para abstrair e generalizar estruturas espaciais de dados ausentes. Esse módulo pode ser perfeitamente integrado ao Transformer sem adicionar complexidade à sua estrutura.

Transformer foi originalmente proposto para modelar dependências temporais em dados sequenciais, e os autores UniTraj aplicam um design multicabeça de Self-Attention na dimensão espacial. Em cada instante de tempo, o embedding de cada um dos N agentes é considerado e passado como entrada para o Codificador Transformer. Essa abordagem tem como objetivo extrair características espaciais invariantes à ordem dos agentes, considerando qualquer possível rearranjo que possa ocorrer na prática. Portanto, nesse caso, é preferível substituir a codificação posicional senoidal por uma totalmente treinável.

Como resultado, o codificador Transformer gera características espaciais Fs,xt para todos os agentes em cada instante de tempo t. Em seguida, essas características são concatenadas ao longo da dimensão temporal para obter as características espaciais de toda a trajetória.

Considerando a capacidade do modelo Mamba de capturar dependências temporais de longo prazo, os autores UniTraj o adaptaram para integração à infraestrutura proposta. No entanto, adaptar o modelo Mamba para a geração de trajetórias unificadas é um desafio complexo, principalmente devido à ausência de uma arquitetura especificamente ajustada para modelagem de trajetórias. A modelagem eficiente de trajetórias exige a captura cuidadosa de características espaço-temporais, o que se torna ainda mais difícil diante da incompletude das trajetórias.

Para aumentar a eficácia da extração de características temporais, preservando as relações ausentes, é introduzida a Mamba temporal bidirecional. Essa adaptação inclui vários blocos residuais Mamba combinados com o módulo inovador Bidirectional Temporal Scaled (BTS).

Inicialmente, a máscara M é processada ao longo de toda a trajetória. Expandimos essa máscara ao longo da dimensão temporal para gerar M', o que facilita o aprendizado das relações temporais ausentes, utilizando tanto a máscara original quanto sua versão invertida no módulo BTS. Esse processo gera a matriz de escalonamento S e sua versão inversa S'. Em particular, para o agente i no instante de tempo t, si,t é calculado da seguinte forma:

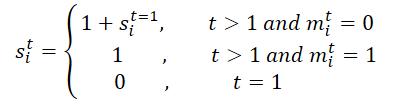
Em seguida, projetamos a matriz de escalonamento S e sua versão invertida S' na matriz de características da seguinte maneira:

onde φs(⋅) — funções de projeção com pesos 𝐖s.

Os autores do método implementaram φs(⋅) utilizando MLP com a função de ativação ReLU. A matriz de escalonamento proposta é projetada para calcular a distância entre a última observação e o instante atual, ajudando a quantificar o impacto das lacunas temporais, especialmente ao lidar com padrões ausentes complexos. A ideia central é que o impacto de uma variável ausente por um determinado período diminui com o tempo. O uso da função exponencial negativa e da ReLU garante que essa influência se atenua monotonamente dentro de um intervalo razoável entre 0 e 1.

O processo de codificação descrito acima é projetado para definir os parâmetros da distribuição gaussiana para a aproximação do posterior. Mais especificamente, a média μq e o desvio padrão σq da distribuição gaussiana posterior são calculados da seguinte maneira:

Realizamos então a amostragem das variáveis latentes 𝒁 a partir da distribuição gaussiana a priori 𝒩(0, I).

Para melhorar a capacidade do modelo de gerar trajetórias plausíveis, combinamos a função Fz,x com a variável latente 𝒁 antes de alimentá-la no decodificador. Em seguida, o processo de geração de trajetórias é calculado da seguinte forma:

onde φdec — função de decodificação, implementada usando MLP.

Diante de uma trajetória arbitrária e incompleta, o modelo UniTraj gera uma trajetória completa. Durante o treinamento, são calculados o erro de reconstrução para as áreas visíveis e o erro de recuperação dos dados mascarados.

A visualização do método proposto no UniTraj é apresentada abaixo.

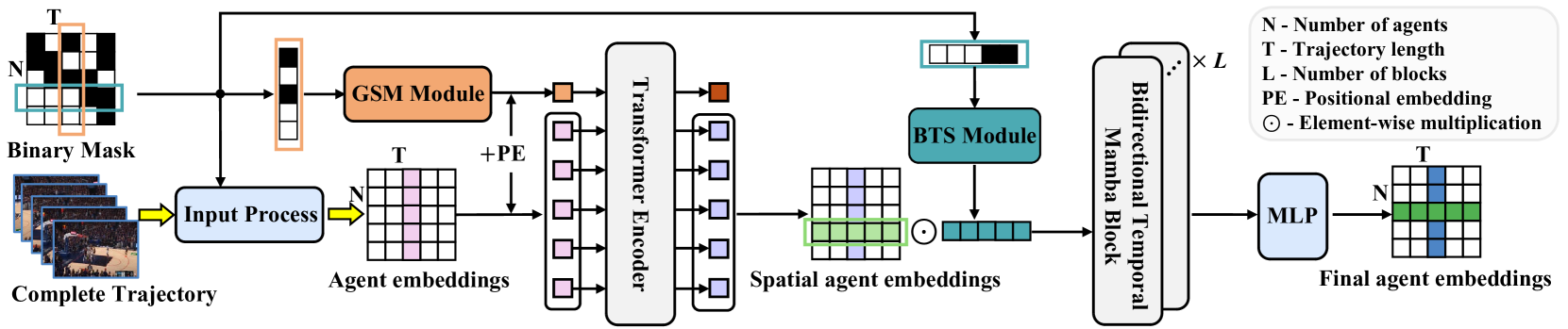
2. Implementação em MQL5

Após analisar a descrição teórica do método UniTraj, como de costume, partimos para a parte prática do artigo, na qual implementamos nossa visão sobre as abordagens propostas utilizando MQL5. Desde o início, é importante destacar que o algoritmo proposto difere estruturalmente dos métodos analisados anteriormente.

O primeiro aspecto a considerar é o processo de mascaramento. Ao fornecer os dados brutos para o modelo, os autores propõem preparar adicionalmente uma máscara que define quais dados o modelo pode ver e quais devem ser gerados. Isso adiciona uma carga extra de trabalho e, ao mesmo tempo, aumenta o tempo de tomada de decisão, o que é indesejável. Portanto, seria ideal gerar a máscara dentro do próprio modelo.

O segundo ponto é a transmissão da trajetória completa para o modelo. Se essa informação pode ser obtida durante o teste, na fase de utilização real isso não é possível. Claro, embora o modelo permita o mascaramento de dados ausentes seguido de reconstrução, de qualquer forma, precisamos fornecer um tensor de maior volume. O que leva ao aumento do consumo de memória e dos custos adicionais na transmissão desse volume. Isso resulta em maior consumo de memória e custos adicionais na transmissão de dados extras, impactando novamente no tempo de tomada de decisão.

Uma possível alternativa seria limitar a transmissão apenas aos dados históricos durante o treinamento e a operação. No entanto, essa abordagem sacrificaria uma parte significativa da funcionalidade do método proposto.

Por isso, decidimos dividir o volume de dados transmitidos em duas partes: dados históricos e a trajetória futura. A trajetória futura é fornecida apenas durante o treinamento do modelo para a extração de dependências espaço-temporais. Já na fase de utilização do modelo, o tensor dos valores futuros não é transmitido, e o modelo opera exclusivamente no modo de previsão de dados.

Além disso, nesta implementação, tivemos que fazer algumas adaptações na parte do programa OpenCL.

2.1 Adaptações no programa OpenCL

Na primeira etapa do nosso trabalho, preparamos novos kernels no programa OpenCL. Primeiramente, criamos o kernel UniTrajPrepare, responsável pela preparação de dados. Dentro desse kernel, concatenamos os dados históricos com as informações conhecidas sobre o movimento futuro, considerando o mascaramento.

Nos parâmetros do kernel, recebemos ponteiros para cinco buffers de dados: 4 contêm dados brutos e 1 armazena os resultados. Além disso, definimos os tamanhos da profundidade da história analisada e do horizonte de planejamento.

__kernel void UniTrajPrepare(__global const float *history,
                             __global const float *h_mask,
                             __global const float *future,
                             __global const float *f_mask,
                             __global float *output,
                             const int h_total,
                             const int f_total
                            )
  {
   const size_t i = get_global_id(0);
   const size_t v = get_global_id(1);
   const size_t variables = get_global_size(1);

A execução do kernel ocorrerá em um espaço bidimensional de tarefas. A primeira dimensão corresponderá ao maior dos dois intervalos temporais (profundidade do histórico e horizonte de planejamento). A segunda dimensão indicará o número de parâmetros analisados.

No corpo do kernel, primeiramente identificamos o fluxo dentro do espaço de tarefas definido e determinamos o deslocamento nos buffers de dados.

   const int shift_in = i * variables + v;
   const int shift_out = 3 * shift_in;
   const int shift_f_out = 3 * (h_total * variables + v);

Em seguida, trabalhamos com os dados históricos. Primeiro, calculamos a taxa de variação do parâmetro considerando a máscara. Depois, armazenamos no buffer de resultados o valor do parâmetro ajustado pela máscara, a velocidade calculada anteriormente e a máscara em si.

//--- history
   if(i < h_total)
     {
      float mask = h_mask[shift_in];
      float h = history[shift_in];
      float v = (i < (h_total - 1) && mask != 0 ? (history[shift_in + variables] - h) * mask : 0);
      if(isnan(v) || isinf(v))
         v = h = mask = 0;
      output[shift_out] = h * mask;
      output[shift_out + 1] = v;
      output[shift_out + 2] = mask;
     }

Parâmetros semelhantes também são calculados para os valores futuros.

//--- future
   if(i < f_total)
     {
      float mask = f_mask[shift_in];
      float f = future[shift_in];
      float v = (i < (f_total - 1) && mask != 0 ? (future[shift_in + variables] - f) * mask : 0);
      if(isnan(v) || isinf(v))
         v = f = mask = 0;
      output[shift_f_out + shift_out] = f * mask;
      output[shift_f_out + shift_out + 1] = v;
      output[shift_f_out + shift_out + 2] = mask;
     }
  }

Depois, armazenamos o kernel de propagação reversa das operações mencionadas acima, UniTrajPrepareGrad.

__kernel void UniTrajPrepareGrad(__global float *history_gr,
                                 __global float *future_gr,
                                 __global const float *output,
                                 __global const float *output_gr,
                                 const int h_total,
                                 const int f_total
                                )
  {
   const size_t i = get_global_id(0);
   const size_t v = get_global_id(1);
   const size_t variables = get_global_size(1);

É importante observar que não especificamos ponteiros para os buffers de dados brutos e máscaras nos parâmetros do método de propagação reversa. Em vez disso, utilizamos o buffer de resultados do kernel de propagação para frente UniTrajPrepare, no qual esses dados já foram armazenados. Além disso, não transmitimos o gradiente do erro para o nível das máscaras, pois isso não faz sentido.

O espaço de tarefas do kernel de propagação reversa é idêntico ao descrito acima para o kernel de propagação para frente.

No corpo do kernel, identificamos o fluxo atual no espaço de tarefas e determinamos o deslocamento nos buffers de dados.

   const int shift_in = i * variables + v;
   const int shift_out = 3 * shift_in;
   const int shift_f_out = 3 * (h_total * variables + v);

Assim como no kernel de propagação para frente, dividimos o trabalho em duas etapas. Primeiro, distribuímos o gradiente do erro para o nível dos dados históricos.

//--- history
   if(i < h_total)
     {
      float mask = output[shift_out + 2];
      float grad = 0;
      if(mask > 0)
        {
         grad = output_gr[shift_out] * mask;
         grad -= (i < (h_total - 1) && mask != 0 ? (output_gr[shift_out + 1]) * mask : 0);
         grad += (i > 0 ? output[shift_out + 1 - 3 * variables] * output[shift_out + 2 - 3 * variables] : 0);
         if(isnan(grad) || isinf(grad))
            grad = 0;
         //---
        }
      history_gr[shift_in] = grad;
     }

Depois, transmitimos o gradiente do erro para os valores previstos conhecidos.

//--- future
   if(i < f_total)
     {
      float mask = output[shift_f_out + shift_out + 2];
      float grad = 0;
      if(mask > 0)
        {
         grad = output_gr[shift_f_out + shift_out] * mask;
         grad -= (i < (h_total - 1) && mask != 0 ? (output_gr[shift_f_out + shift_out + 1]) * mask : 0);
         grad += (i > 0 ? output[shift_f_out + shift_out + 1 - 3 * variables] * 
                          output[shift_f_out + shift_out + 2 - 3 * variables] : 0);
         if(isnan(grad) || isinf(grad))
            grad = 0;
         //---
        }
      future_gr[shift_in] = grad;
     }
  }

Outro algoritmo que precisamos implementar no lado do OpenCL é a criação da matriz de escalonamento. No kernel UniTrajBTS, calculamos as matrizes de escalonamento direta e reversa.

Aqui, também utilizamos os resultados do kernel de preparação de dados como dados brutos. Com base nesses dados, calculamos o deslocamento a partir do último valor não mascarado nas direções direta e reversa e armazenamos essas informações nos buffers correspondentes. 

__kernel void UniTrajBTS(__global const float * concat_inp,
                         __global float * d_forw,
                         __global float * d_bakw,
                         const int total
                        )
  {
   const size_t i = get_global_id(0);
   const size_t v = get_global_id(1);
   const size_t variables = get_global_size(1);

O espaço de tarefas será bidimensional. No entanto, a primeira dimensão terá apenas dois fluxos, correspondentes ao cálculo das matrizes de escalonamento direta e reversa. Na segunda dimensão, indicaremos o número de variáveis analisadas, como antes.

Após identificar o fluxo no espaço de tarefas, dividimos o algoritmo do kernel conforme o valor da primeira dimensão.

   if(i == 0)
     {
      const int step = variables * 3;
      const int start = v * 3 + 2;
      float last = 0;
      d_forw[v] = 0;
      for(int p = 1; p < total; p++)
        {
         float m = concat_inp[start + p * step];
         d_forw[p * variables + v] = last = 1 + (1 - m) * last;
        }
     }

No cálculo da matriz de escalonamento direta, determinamos o deslocamento até a máscara do primeiro elemento da variável analisada e o passo até o próximo elemento. Em seguida, criamos um laço para percorrer sequencialmente as máscaras do elemento analisado e calcular os coeficientes de escalonamento de acordo com a fórmula especificada.

O algoritmo para a matriz de escalonamento reversa é idêntico. A única diferença é que determinamos o deslocamento até o último elemento e, então, seguimos no sentido inverso.

   else
     {
      const int step = -(variables * 3);
      const int start = (total - 1) * variables + v * 3 + 2;
      float last = 0;
      d_bakw[(total - 1) + v] = 0;
      for(int p = 1; p < total; p++)
        {
         float m = concat_inp[start + p * step];
         d_bakw[(total - 1 - p) * variables + v] = last = 1 + (1 - m) * last;
        }
     }
  }

É importante notar que o algoritmo apresentado opera apenas com máscaras, nas quais a distribuição do gradiente do erro não faz sentido. Por esse motivo, não criamos um kernel de propagação reversa para este algoritmo. Com isso, concluímos o trabalho no lado do programa OpenCL. O código completo está disponível no anexo.

2.2 Implementação do algoritmo UniTraj

Após a realização dos trabalhos preparatórios no programa OpenCL, partimos para a implementação das abordagens propostas no programa principal. A seguir, apresentamos a estrutura da classe CNeuronUniTraj, na qual integramos o algoritmo UniTraj.

class CNeuronUniTraj    :  public CNeuronBaseOCL
  {
protected:
   uint              iVariables;
   float             fDropout;
   //---
   CBufferFloat      cHistoryMask;
   CBufferFloat      cFutureMask;
   CNeuronBaseOCL    cData;
   CNeuronLearnabledPE cPE;
   CNeuronMVMHAttentionMLKV   cEncoder;
   CNeuronBaseOCL    cDForw;
   CNeuronBaseOCL    cDBakw;
   CNeuronConvOCL    cProjDForw;
   CNeuronConvOCL    cProjDBakw;
   CNeuronBaseOCL    cDataDForw;
   CNeuronBaseOCL    cDataDBakw;
   CNeuronBaseOCL    cConcatDataDForwBakw;
   CNeuronMambaBlockOCL cSSM[4];
   CNeuronConvOCL    cStat;
   CNeuronTransposeOCL cTranspStat;
   CVAE              cVAE;
   CNeuronTransposeOCL cTranspVAE;
   CNeuronConvOCL    cDecoder[2];
   CNeuronTransposeOCL cTranspResult;
   //---
   virtual bool      Prepare(const CBufferFloat* history, const CBufferFloat* future);
   virtual bool      PrepareGrad(CBufferFloat* history_gr, CBufferFloat* future_gr);
   virtual bool      BTS(void);
   //---
   virtual bool      feedForward(CNeuronBaseOCL *NeuronOCL) override { return feedForward(NeuronOCL, NULL); }
   virtual bool      feedForward(CNeuronBaseOCL *NeuronOCL, CBufferFloat *SecondInput) override;
   //---
   virtual bool      calcInputGradients(CNeuronBaseOCL *NeuronOCL) override 
                                       { return calcInputGradients(NeuronOCL, NULL, NULL, None); }
   virtual bool      updateInputWeights(CNeuronBaseOCL *NeuronOCL) override 
                                       { return updateInputWeights(NeuronOCL, NULL); }
   virtual bool      calcInputGradients(CNeuronBaseOCL *NeuronOCL, CBufferFloat *SecondInput, 
                                                                   CBufferFloat *SecondGradient, 
                                                            ENUM_ACTIVATION SecondActivation = None) override;
   virtual bool      updateInputWeights(CNeuronBaseOCL *NeuronOCL, CBufferFloat *second) override;
   //---

public:
                     CNeuronUniTraj(void) {};
                    ~CNeuronUniTraj(void) {};
   //---
   virtual bool      Init(uint numOutputs, uint myIndex, COpenCLMy *open_cl, 
                          uint window, uint window_key, uint heads, uint units_count, 
                          uint forecast, float dropout, ENUM_OPTIMIZATION optimization_type, uint batch);
   //---
   virtual int       Type(void)   const   {  return defNeuronUniTrajOCL; }
   //---
   virtual bool      Save(int const file_handle);
   virtual bool      Load(int const file_handle);
   //---
   virtual bool      WeightsUpdate(CNeuronBaseOCL *source, float tau);
   virtual void      SetOpenCL(COpenCLMy *obj);
  };

Como pode ser observado, a estrutura da classe declara um grande número de objetos internos, cujas funcionalidades serão conhecidas à medida que os métodos forem implementados. Todos os objetos são declarados como estáticos. Isso nos permite deixar o construtor e o destrutor da classe vazios, delegando ao sistema a responsabilidade de gerenciar a memória.

A inicialização de todos os objetos internos é realizada no método Init, cujos parâmetros contêm as principais constantes que permitem identificar de forma única a arquitetura do objeto.

bool CNeuronUniTraj::Init(uint numOutputs, uint myIndex, COpenCLMy *open_cl, 
                          uint window, uint window_key, uint heads, uint units_count, 
                          uint forecast, float dropout, ENUM_OPTIMIZATION optimization_type, uint batch)
  {
   if(!CNeuronBaseOCL::Init(numOutputs, myIndex, open_cl, window * (units_count + forecast), 
                                                                   optimization_type, batch))
      return false;

No corpo do método, seguindo a prática estabelecida, primeiro chamamos o método com o mesmo nome da classe pai, onde já foram implementados os controles mínimos necessários para a inicialização dos objetos herdados.

Após a execução bem-sucedida das operações da classe pai, armazenamos as constantes recebidas do programa externo, incluindo o número de variáveis analisadas nos dados brutos e a proporção de elementos mascarados durante o treinamento.

   iVariables = window;
   fDropout = MathMax(MathMin(dropout, 1), 0);

Em seguida, passamos para a inicialização dos objetos declarados. Primeiro, criamos os buffers de mascaramento para os dados históricos e previstos.

   if(!cHistoryMask.BufferInit(iVariables * units_count, 1) ||
      !cHistoryMask.BufferCreate(OpenCL))
      return false;
   if(!cFutureMask.BufferInit(iVariables * forecast, 1) ||
      !cFutureMask.BufferCreate(OpenCL))
      return false;

Depois, inicializamos a camada interna dos dados brutos concatenados.

   if(!cData.Init(0, 0, OpenCL, 3 * iVariables * (units_count + forecast), optimization, iBatch))
      return false;

Criamos também uma camada de codificação posicional treinável de tamanho correspondente.

   if(!cPE.Init(0, 1, OpenCL, cData.Neurons(), optimization, iBatch))
      return false;

O próximo passo é o Codificador Transformer, responsável pela extração das dependências espaço-temporais.

   if(!cEncoder.Init(0, 2, OpenCL, 3, window_key, heads, (heads + 1) / 2, iVariables, 1, 1, 
                                                  (units_count + forecast), optimization, iBatch))
      return false;

Vale destacar que os autores do método realizaram uma série de experimentos e concluíram que o desempenho ideal é alcançado com 1 bloco do Codificador Transformer e 4 blocos Mamba. Por isso, neste caso, utilizamos apenas 1 camada de codificação.

É importante destacar que o tamanho da janela dos dados brutos é igual a "3", correspondendo a três parâmetros de um único indicador a cada instante (valor, velocidade e máscara). O número de elementos na sequência é definido de acordo com a quantidade de variáveis analisadas, enquanto o número de canais independentes corresponde à profundidade total dos dados históricos analisados e da previsão. Dessa forma, avaliamos as dependências entre os indicadores analisados dentro de um único instante temporal.

Em seguida, passamos ao bloco BTS e criamos os objetos para as matrizes de escalonamento direta e reversa.

   if(!cDForw.Init(0, 3, OpenCL, iVariables * (units_count + forecast), optimization, iBatch))
      return false;;
   if(!cDBakw.Init(0, 4, OpenCL, iVariables * (units_count + forecast), optimization, iBatch))
      return false;

Nesse mesmo momento, adicionamos camadas convolucionais para projetar os dados das matrizes.

   if(!cProjDForw.Init(0, 5, OpenCL, 1, 1, 3, iVariables, (units_count + forecast), optimization, iBatch))
      return false;
   cProjDForw.SetActivationFunction(SIGMOID);
   if(!cProjDBakw.Init(0, 6, OpenCL, 1, 1, 3, iVariables, (units_count + forecast), optimization, iBatch))
      return false;
   cProjDBakw.SetActivationFunction(SIGMOID);

As projeções resultantes serão multiplicadas elemento a elemento pelos resultados do Codificador Transformer, e os resultados dessas operações serão armazenados nos objetos subsequentes.

   if(!cDataDForw.Init(0, 7, OpenCL, cData.Neurons(), optimization, iBatch))
      return false;
   if(!cDataDBakw.Init(0, 8, OpenCL, cData.Neurons(), optimization, iBatch))
      return false;

Depois disso, planejamos concatenar os dados obtidos em um único tensor.

   if(!cConcatDataDForwBakw.Init(0, 9, OpenCL, 2 * cData.Neurons(), optimization, iBatch))
      return false;

Esse tensor será então enviado para o bloco SSM. Como mencionado anteriormente, esse bloco inicializa quatro camadas sequenciais Mamba.

   for(uint i = 0; i < cSSM.Size(); i++)
     {
      if(!cSSM[i].Init(0, 10 + i, OpenCL, 6 * iVariables, 12 * iVariables, 
                                 (units_count + forecast), optimization, iBatch))
         return false;
     }

Os autores do método sugerem o uso de conexões residuais para as camadas Mamba. Aqui, vamos um pouco além e utilizamos a classe CNeuronMambaBlockOCL, que foi criada durante o desenvolvimento do método TrajLLM.

Os resultados obtidos são projetados nos indicadores estatísticos da distribuição alvo.

   uint id = 10 + cSSM.Size();
   if(!cStat.Init(0, id, OpenCL, 6, 6, 12, iVariables * (units_count + forecast), optimization, iBatch))
      return false;

No entanto, antes de realizar a amostragem e a reparametrização dos valores, precisamos modificar ligeiramente a ordem dos dados. Para isso, utilizamos uma camada de transposição.

   id++;
   if(!cTranspStat.Init(0, id, OpenCL, iVariables * (units_count + forecast), 12, optimization, iBatch))
      return false;
   id++;
   if(!cVAE.Init(0, id, OpenCL, cTranspStat.Neurons() / 2, optimization, iBatch))
      return false;

Os valores amostrados são convertidos para a dimensionalidade dos canais de informação independentes.

   id++;
   if(!cTranspVAE.Init(0, id, OpenCL, cVAE.Neurons() / iVariables, iVariables, optimization, iBatch))
      return false;

Os dados então passam pelo decodificador, cuja saída é a sequência alvo gerada.

   id++;
   uint w = cTranspVAE.Neurons() / iVariables;
   if(!cDecoder[0].Init(0, id, OpenCL, w, w, 2 * (units_count + forecast), iVariables, optimization, iBatch))
      return false;
   cDecoder[0].SetActivationFunction(LReLU);
   id++;
   if(!cDecoder[1].Init(0, id, OpenCL, 2 * (units_count + forecast), 2 * (units_count + forecast), 
                                                 (units_count + forecast), iVariables, optimization, iBatch))
      return false;
   cDecoder[1].SetActivationFunction(TANH);

Agora, resta apenas ajustar o resultado obtido para a dimensionalidade dos dados brutos.

   id++;
   if(!cTranspResult.Init(0, id, OpenCL, iVariables, (units_count + forecast), optimization, iBatch))
      return false;

Para evitar operações desnecessárias de cópia de dados, substituímos os ponteiros nos buffers de dados.

   if(!SetOutput(cTranspResult.getOutput(), true) ||
      !SetGradient(cTranspResult.getGradient(), true))
      return false;
   SetActivationFunction((ENUM_ACTIVATION)cDecoder[1].Activation());
//---
   return true;
  }

É fundamental monitorar o processo de execução em cada etapa. Ao final do método, retornamos um valor lógico indicando o sucesso da operação para o programa que fez a chamada.

Após concluir a inicialização da instância da classe, passamos à implementação dos métodos de propagação para frente. Primeiramente, fazemos uma breve preparação, no qual arrumamos a fila de execução dos kernels criados anteriormente.  Aqui, utilizamos algoritmos já estabelecidos, que podem ser consultados no anexo. Neste artigo, propomos analisar o método de alto nível feedForward, no qual descrevemos o algoritmo de forma abrangente.

bool CNeuronUniTraj::feedForward(CNeuronBaseOCL *NeuronOCL, CBufferFloat *SecondInput)
  {
   if(!NeuronOCL)
      return false;

Nos parâmetros do método, recebemos ponteiros para dois objetos contendo os valores históricos e previstos. No corpo do método, verificamos imediatamente a validade do ponteiro para os dados históricos. Como mencionado anteriormente, os dados históricos sempre estão presentes. No entanto, os valores previstos podem ou não estar disponíveis.

Em seguida, iniciamos a geração do tensor de mascaramento aleatório para os dados históricos.

//--- Create History Mask
   int total = cHistoryMask.Total();
   if(!cHistoryMask.BufferInit(total, 1))
      return false;
   if(bTrain)
     {
      for(int i = 0; i < int(total * fDropout); i++)
         cHistoryMask.Update(RND(total), 0);
     }
   if(!cHistoryMask.BufferWrite())
      return false;

É importante destacar que o mascaramento ocorre apenas durante o treinamento. Na prática, utilizamos todas as informações disponíveis.

Depois, fazemos um processo semelhante para os valores previstos. No entanto, há um detalhe importante: se houver valores previstos, geramos um tensor de mascaramento aleatório. Caso contrário, ou seja, na ausência de informações sobre o movimento futuro, preenchemos todo o tensor de mascaramento com valores zero.

//--- Create Future Mask
   total = cFutureMask.Total();
   if(!cFutureMask.BufferInit(total, (!SecondInput ? 0 : 1)))
      return false;
   if(bTrain && !!SecondInput)
     {
      for(int i = 0; i < int(total * fDropout); i++)
         cFutureMask.Update(RND(total), 0);
     }
   if(!cFutureMask.BufferWrite())
      return false;

Após a geração dos tensores de mascaramento, podemos prosseguir com a etapa de preparação e concatenação dos dados.

//--- Prepare Data
   if(!Prepare(NeuronOCL.getOutput(), SecondInput))
      return false;

Em seguida, adicionamos a codificação posicional e enviamos os dados ao codificador Transformer/

//--- Encoder
   if(!cPE.FeedForward(cData.AsObject()))
      return false;
   if(!cEncoder.FeedForward(cPE.AsObject()))
      return false;

De acordo com o algoritmo UniTraj, utilizamos o bloco BTS. Criamos as matrizes de escalonamento direta e reversa.

//--- BTS
   if(!BTS())
      return false;

Realizamos suas projeções.

   if(!cProjDForw.FeedForward(cDForw.AsObject()))
      return false;
   if(!cProjDBakw.FeedForward(cDBakw.AsObject()))
      return false;

Multiplicamos pelos resultados do Codificador.

   if(!ElementMult(cEncoder.getOutput(), cProjDForw.getOutput(), cDataDForw.getOutput()))
      return false;
   if(!ElementMult(cEncoder.getOutput(), cProjDBakw.getOutput(), cDataDBakw.getOutput()))
      return false;

E combinamos os valores obtidos em um único tensor.

   if(!Concat(cDataDForw.getOutput(), cDataDBakw.getOutput(), cConcatDataDForwBakw.getOutput(),
              3, 3, cData.Neurons() / 3))
      return false;

Analisamos os dados dentro do modelo de espaço de estados.

//--- SSM
   if(!cSSM[0].FeedForward(cConcatDataDForwBakw.AsObject()))
      return false;
   for(uint i = 1; i < cSSM.Size(); i++)
      if(!cSSM[i].FeedForward(cSSM[i - 1].AsObject()))
         return false;

Depois disso, obtemos a projeção dos indicadores estatísticos da distribuição alvo.

//--- VAE
   if(!cStat.FeedForward(cSSM[cSSM.Size() - 1].AsObject()))
      return false;

E amostramos valores a partir da distribuição especificada.

   if(!cTranspStat.FeedForward(cStat.AsObject()))
      return false;
   if(!cVAE.FeedForward(cTranspStat.AsObject()))
      return false;

O decodificador gera a sequência alvo.

//--- Decoder
   if(!cTranspVAE.FeedForward(cVAE.AsObject()))
      return false;
   if(!cDecoder[0].FeedForward(cTranspVAE.AsObject()))
      return false;
   if(!cDecoder[1].FeedForward(cDecoder[0].AsObject()))
      return false;
   if(!cTranspResult.FeedForward(cDecoder[1].AsObject()))
      return false;
//---
   return true;
  }

Que então ajustamos para a dimensionalidade dos dados brutos. 

Como mencionado anteriormente, no método de inicialização do objeto, substituímos os ponteiros nos buffers de dados. Dessa forma, nesta etapa, não é necessário copiar os valores obtidos dos objetos internos para os buffers herdados da classe. Para finalizar o método de propagação para frente, basta retornar o resultado lógico da execução para o programa que fez a chamada.

Concluímos o trabalho de construção do algoritmo de propagação para frente. O próximo passo é gerar os processos de propagação reversa, que seguem exatamente a mesma lógica da propagação para frente, mas com o fluxo de informações na direção oposta. Eles correspondem integralmente ao processo de propagação para frente, porém o fluxo de informações ocorre em sentido inverso. No entanto, ainda há um volume significativo de trabalho a ser realizado e o formato do artigo possui limitações de tamanho. Por isso, deixo os métodos de propagação reversa para estudo independente. Lembro que o código completo desta classe e de todos os seus métodos está disponível no anexo.

2.3 Arquitetura dos modelos

Após a implementação dos algoritmos do método UniTraj, passamos agora à sua aplicação dentro de nossos modelos. Assim como outros métodos de análise de trajetórias baseadas em dados históricos, o algoritmo proposto será utilizado dentro do modelo do Codificador do Estado do Ambiente. Vale lembrar que a arquitetura desse modelo é definida no método CreateEncoderDescriptions.

bool CreateEncoderDescriptions(CArrayObj *&encoder)
  {
//---
   CLayerDescription *descr;
//---
   if(!encoder)
     {
      encoder = new CArrayObj();
      if(!encoder)
         return false;
     }

O método recebe da aplicação externa um ponteiro para um objeto de array dinâmico, no qual a arquitetura do modelo será registrada. No corpo do método, verificamos imediatamente a validade do ponteiro recebido e, se necessário, criamos um novo objeto. Em seguida, passamos à descrição da solução arquitetônica.

Primeiro, utilizamos uma camada totalmente conectada, onde registramos os dados brutos.

//--- Encoder
   encoder.Clear();
//--- Input layer
   if(!(descr = new CLayerDescription()))
      return false;
   descr.type = defNeuronBaseOCL;
   int prev_count = descr.count = (HistoryBars * BarDescr);
   descr.activation = None;
   descr.optimization = ADAM;
   if(!encoder.Add(descr))
     {
      delete descr;
      return false;
     }

Aqui, armazenamos informações sobre o movimento histórico dos preços e os valores dos indicadores analisados em uma profundidade histórica especificada. Os dados são recebidos do terminal "como estão", sem qualquer processamento prévio. Obviamente, esses dados terão escalas diferentes e não serão diretamente comparáveis. Portanto, aplicamos uma camada de normalização em lote para torná-los compatíveis.

//--- layer 1
   if(!(descr = new CLayerDescription()))
      return false;
   descr.type = defNeuronBatchNormOCL;
   descr.count = prev_count;
   descr.batch = 1e4;
   descr.activation = None;
   descr.optimization = ADAM;
   if(!encoder.Add(descr))
     {
      delete descr;
      return false;
     }

Os dados normalizados são então enviados diretamente para o bloco UniTraj. Definimos a taxa de mascaramento em 50% dos dados recebidos. 

//--- layer 2
   if(!(descr = new CLayerDescription()))
      return false;
   descr.type = defNeuronUniTrajOCL;
   descr.window = BarDescr;                          //window
   descr.window_out = EmbeddingSize;                 //Inside Dimension
   descr.count = HistoryBars;                        //Units
   descr.layers = NForecast;                         //Forecast
   descr.step=4;                                     //Heads
   descr.probability=0.5f;                           //DropOut
   descr.batch = 1e4;
   descr.activation = None;
   descr.optimization = ADAM;
   if(!encoder.Add(descr))
     {
      delete descr;
      return false;
     }

Na saída do bloco, obtemos uma trajetória-alvo expandida, contendo tanto os dados históricos reconstruídos quanto os valores previstos para o horizonte de planejamento especificado. Adicionamos indicadores estatísticos dos dados brutos, extraídos durante a normalização, aos dados obtidos.

//--- layer 3
   if(!(descr = new CLayerDescription()))
      return false;
   descr.type = defNeuronRevInDenormOCL;
   descr.count = BarDescr * (NForecast+HistoryBars);
   descr.activation = None;
   descr.optimization = ADAM;
   descr.layers = 1;
   if(!encoder.Add(descr))
     {
      delete descr;
      return false;
     }

Em seguida, ajustamos os valores previstos na área de frequência.

//--- layer 4
   if(!(descr = new CLayerDescription()))
      return false;
   descr.type = defNeuronFreDFOCL;
   descr.window = BarDescr;
   descr.count =  NForecast+HistoryBars;
   descr.step = int(true);
   descr.probability = 0.7f;
   descr.activation = None;
   descr.optimization = ADAM;
   if(!encoder.Add(descr))
     {
      delete descr;
      return false;
     }
//---
   return true;
  }

Graças à arquitetura integrada do novo bloco CNeuronUniTraj, conseguimos descrever o modelo de forma concisa e eficiente, sem comprometer suas capacidades.

É importante mencionar que o aumento do tamanho do tensor de saída do modelo Codificador do Estado do Ambiente exigiu ajustes pontuais nos modelos Ator e Crítico. No entanto, essas alterações são mínimas e podem ser conferidas no anexo. Já as modificações no programa de treinamento do Codificador foram mais significativas.

2.4 Programa de treinamento do modelo

As alterações feitas na arquitetura do modelo Codificador do Estado do Ambiente, juntamente com as abordagens de treinamento propostas pelos autores do UniTraj, levaram à necessidade de ajustar o EA de treinamento da seguinte forma: ...\Experts\UniTraj\StudyEncoder.mq5.

A primeira alteração foi feita no bloco de controle do modelo, mais especificamente na verificação do tamanho da camada de saída. Trata-se de uma correção pontual no método de inicialização do EA.

   Encoder.getResults(Result);
   if(Result.Total() != (NForecast+HistoryBars) * BarDescr)
     {
      PrintFormat("The scope of the Encoder does not match the forecast state count (%d <> %d)",
                                             (NForecast+HistoryBars) * BarDescr, Result.Total());
      return INIT_FAILED;
     }

No entanto, como se pode imaginar, a principal reformulação ocorreu no método de treinamento Train.

void Train(void)
  {
//---
   vector<float> probability = GetProbTrajectories(Buffer, 0.9);

Como antes, no corpo do método, primeiro geramos um vetor de probabilidades para a escolha das trajetórias durante o treinamento, com base nos retornos obtidos. O objetivo dessa operação é dar maior peso às trajetórias mais lucrativas, permitindo assim o aprendizado de uma estratégia mais rentável.

Depois disso, declaramos as variáveis necessárias.

   vector<float> result, target, state;
   bool Stop = false;
   const int Batch = 1000;
   int b = 0;
//---
   uint ticks = GetTickCount();

E elaboramos o sistema de ciclos de treinamento dos modelos.

   for(int iter = 0; (iter < Iterations && !IsStopped() && !Stop); iter += b)
     {
      int tr = SampleTrajectory(probability);
      int start = (int)((MathRand() * MathRand() / MathPow(32767, 2)) * (Buffer[tr].Total - 5 - NForecast));
      if(start <= 0)
         continue;

Vale lembrar que o bloco Mamba possui um caráter recorrente, o que influencia diretamente seu processo de treinamento. Primeiro, amostramos uma trajetória do buffer de replicação e selecionamos o estado inicial do treinamento. Em seguida, fazemos um laço aninhado para percorrer sequencialmente os estados da trajetória selecionada.

      for(b = 0; (b < Batch && (iter + b) < Iterations); b++)
        {
         int i = start + b;
         if(i >= MathMin(Buffer[tr].Total, Buffer_Size) - NForecast)
            break;

Primeiro, carregamos do buffer de replay os dados históricos dos parâmetros analisados.

         state.Assign(Buffer[tr].States[i].state);
         if(MathAbs(state).Sum() == 0)
            break;
         bState.AssignArray(state);

Imediatamente após, carregamos os valores reais subsequentes.

         //--- Collect target data
         if(!Result.AssignArray(Buffer[tr].States[i + NForecast].state))
            continue;
         if(!Result.Resize(BarDescr * NForecast))
            continue;

Depois, dividimos aleatoriamente o processo de treinamento em dois fluxos com uma probabilidade de 50%.

         //--- State Encoder
         if((MathRand() / 32767.0) < 0.5)
           {
            if(!Encoder.feedForward((CBufferFloat*)GetPointer(bState), 1, false, (CBufferFloat*)NULL))
              {
               PrintFormat("%s -> %d", __FUNCTION__, __LINE__);
               Stop = true;
               break;
              }
           }

No primeiro caso, como anteriormente, fornecemos apenas os dados históricos ao modelo e realizamos a propagação para frente. No segundo caso, fornecemos ao modelo também os valores reais subsequentes do movimento futuro dos preços. Dessa forma, o modelo recebe como entrada informações completas sobre os estados históricos e futuros do sistema.

         else
           {
            if(Result.GetIndex()>=0)
              Result.BufferWrite();
            if(!Encoder.feedForward((CBufferFloat*)GetPointer(bState), 1, false, Result))
              {
               PrintFormat("%s -> %d", __FUNCTION__, __LINE__);
               Stop = true;
               break;
              }
           }

É importante ressaltar que nosso algoritmo inclui o mascaramento aleatório de 50% dos dados recebidos durante o treinamento. Dessa forma, o modelo aprende a reconstruir os dados mascarados.

Na saída do modelo, obtemos a trajetória completa representada por um único tensor. Por isso, combinamos os dois buffers de dados brutos em um único tensor e o utilizamos na propagação reversa do modelo. Durante essa etapa, ajustamos os parâmetros treináveis do modelo para minimizar o erro geral de reconstrução e previsão dos dados.

         //--- Collect target data
         if(!bState.AddArray(Result))
            continue;
         if(!Encoder.backProp((CBufferFloat*)GetPointer(bState), (CBufferFloat*)NULL))
           {
            PrintFormat("%s -> %d", __FUNCTION__, __LINE__);
            Stop = true;
            break;
           }

Agora, resta apenas informar o usuário sobre o progresso do treinamento e avançar para a próxima iteração do sistema de ciclos.

         //---
         if(GetTickCount() - ticks > 500)
           {
            double percent = double(iter + b) * 100.0 / (Iterations);
            string str = StringFormat("%-14s %6.2f%% -> Error %15.8f\n", "Encoder", 
                                          percent, Encoder.getRecentAverageError());
            Comment(str);
            ticks = GetTickCount();
           }
        }
     }

Após a conclusão bem-sucedida de todas as iterações do treinamento, limpamos o campo de comentários no gráfico do ativo, registramos os resultados do treinamento no log do terminal e iniciamos o processo de finalização do modelo.

   Comment("");
//---
   PrintFormat("%s -> %d -> %-15s %10.7f", __FUNCTION__, __LINE__, "Encoder", Encoder.getRecentAverageError());
   ExpertRemove();
//---
  }

No modo de utilização do modelo, não fornecemos valores previstos como entrada. Por esse motivo, o programa de treinamento da política do Ator permaneceu inalterado. O código completo de todas as classes e programas utilizados para preparar este artigo está disponível no anexo.

3. Testes

Acima, analisamos a descrição teórica do novo método para lidar com sequências temporais multimodais UniTraj. Também implementamos nossa visão sobre as abordagens propostas utilizando MQL5. Agora, passamos para a etapa final do nosso trabalho, na qual avaliamos a eficácia dos métodos propostos para a solução de nossas tarefas.

Apesar das mudanças na arquitetura do modelo e no programa de treinamento do Codificador do Estado do Ambiente, a estrutura do conjunto de dados de treinamento permaneceu inalterada. Isso nos permite iniciar o treinamento do modelo utilizando os mesmos conjuntos de dados anteriormente coletados.

Vale lembrar que, para treinar os modelos, utilizamos dados históricos reais do par EURUSD no timeframe H1, abrangendo todo o ano de 2023. Os parâmetros de todos os indicadores analisados foram mantidos nos valores padrão.

Na primeira etapa, treinamos o Codificador do Estado do Ambiente. Como mencionado anteriormente, não é necessário atualizar o conjunto de dados de treinamento durante o treinamento do Codificador, e o modelo é treinado até alcançar os resultados desejados. É importante ressaltar que o modelo resultante não é leve e que seu treinamento demanda tempo. No entanto, o processo ocorre de forma relativamente estável, e ao final do treinamento, obtivemos uma projeção visualmente satisfatória do movimento futuro dos preços.

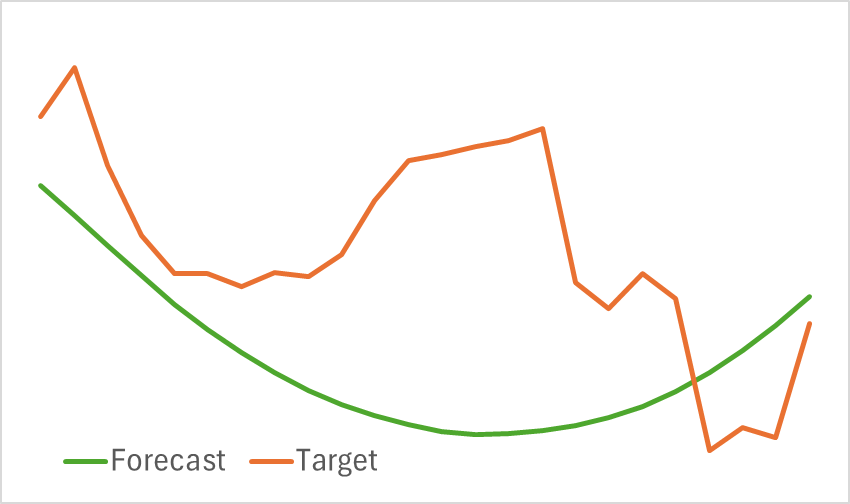
Vale notar que a linha de previsão de movimento ficou bastante suavizada. O mesmo pode ser dito sobre a trajetória reconstruída, que evidencia a eliminação significativa do ruído nos dados brutos. O impacto dessa suavização na aprendizagem de uma política lucrativa para o Ator será analisado na próxima etapa do treinamento dos modelos.

A segunda etapa do teste envolve o treinamento iterativo dos modelos Ator e Crítico. Nesta fase, buscamos construir uma política lucrativa para o Ator, baseada na análise do movimento previsto dos preços, fornecido pelo Codificador do Estado do Ambiente. O Codificador retorna tanto o movimento previsto quanto a trajetória histórica reconstruída.

Para testar o desempenho dos modelos treinados, utilizamos dados históricos de janeiro de 2024, mantendo todos os demais parâmetros inalterados.

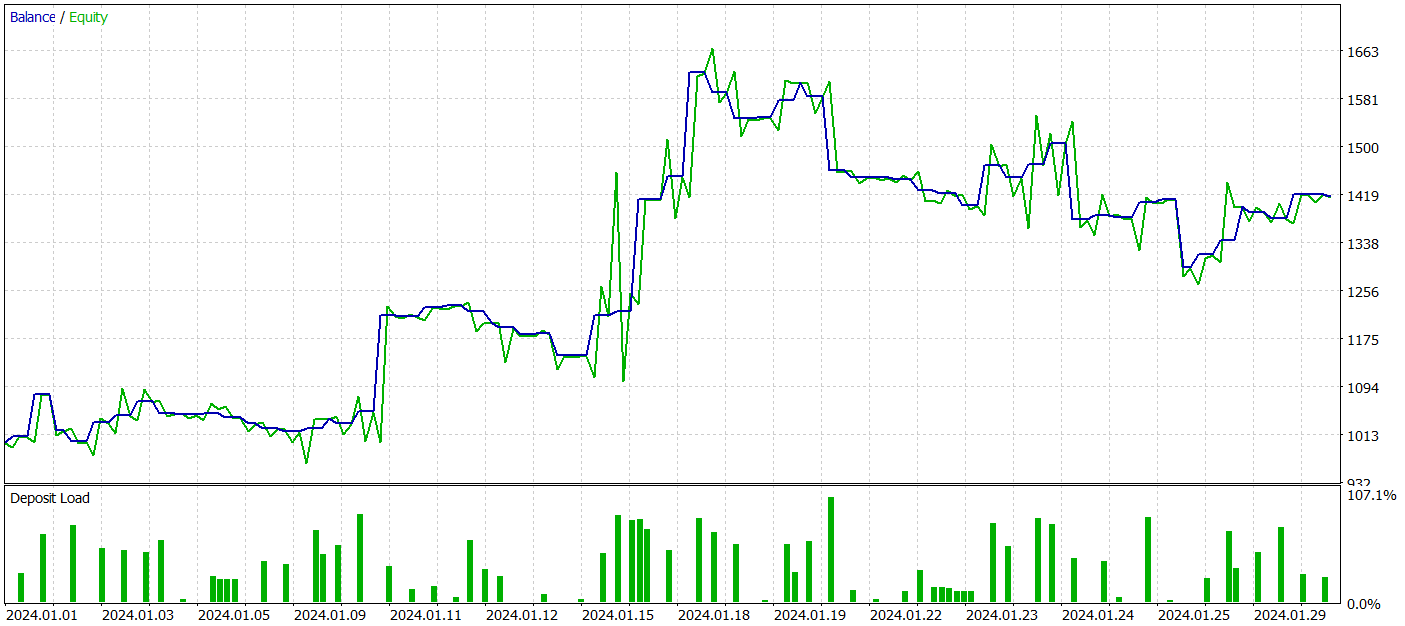
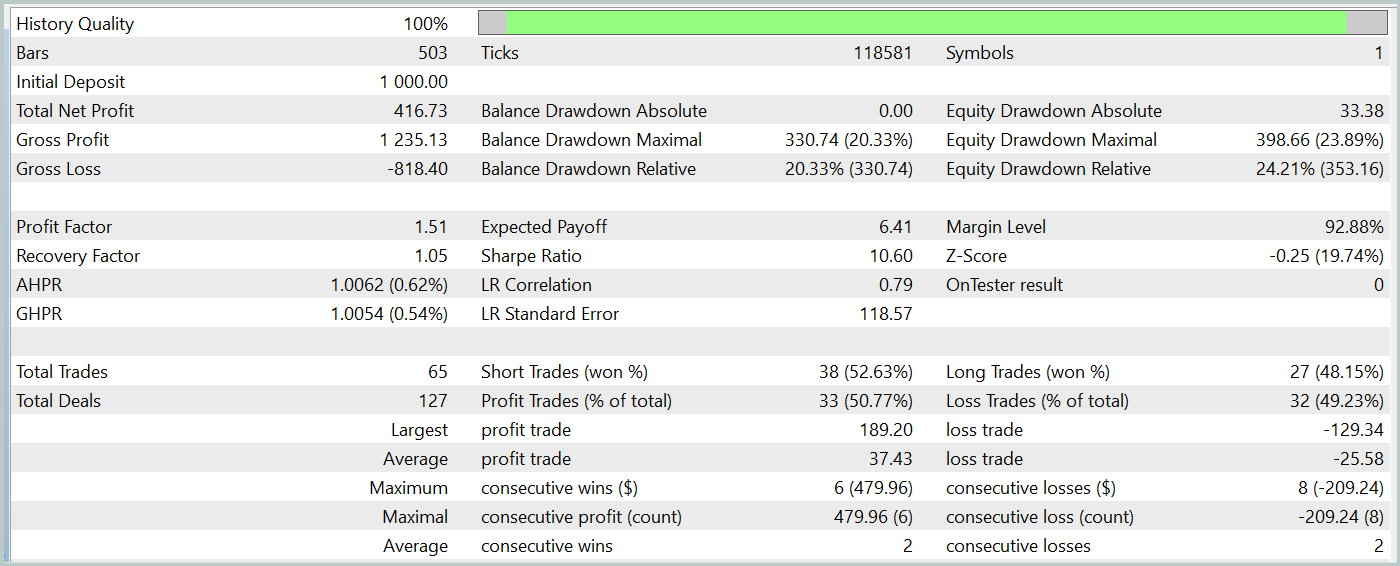
Durante o período de teste, o modelo treinado do Ator gerou um lucro superior a 40%, com um rebaixamento máximo no patrimônio (equity) de pouco mais de 24%. Foram realizadas 65 operações, das quais 33 (aproximadamente metade) foram encerradas com lucro. Além disso, devido ao aumento significativo do lucro máximo e médio por operação em relação às perdas, o fator de lucro foi registrado em 1,51. Obviamente, um período de teste de apenas um mês e 65 operações não é suficiente para garantir rendimentos consistentes no longo prazo. No entanto, de modo geral, o resultado obtido superou o desempenho do método Traj-LLM.

Considerações finais

O método UniTraj, analisado neste artigo, demonstra um grande potencial como ferramenta universal para o processamento de trajetórias de agentes em diferentes cenários. Essa abordagem resolve um dos principais desafios da modelagem: a adaptação do modelo a múltiplas tarefas, o que resulta em um desempenho superior aos métodos tradicionais. A padronização no tratamento de dados mascarados torna UniTraj uma solução flexível e eficiente.

Na parte prática deste artigo, implementamos as abordagens propostas utilizando MQL5. Integramos essas abordagens ao modelo do Codificador do Estado do Ambiente. Treinamos o modelo e o testamos com dados históricos reais. Os resultados obtidos demonstram a eficácia dos métodos propostos, permitindo sua aplicação no desenvolvimento de estratégias de negociação reais.

Referências

Deciphering Movement: Unified Trajectory Generation Model for Multi-Agent

Outros artigos da série

Programas utilizados no artigo

#	Nome	Tipo	Descrição
1	Research.mq5	Expert Advisor	EA para coleta de exemplos
2	ResearchRealORL.mq5	Expert Advisor	EA para coleta de exemplos pelo método Real-ORL
3	Study.mq5	Expert Advisor	EA para treinamento de modelos
4	StudyEncoder.mq5	Expert Advisor	EA para treinamento do Codificador
5	Test.mq5	Expert Advisor	EA para teste do modelo
6	Trajectory.mqh	Biblioteca de classe	Estrutura de descrição do estado do sistema
7	NeuroNet.mqh	Biblioteca de classe	Biblioteca de classes para criação de redes neurais
8	NeuroNet.cl	Biblioteca	Biblioteca de código do programa OpenCL