Redes neurais em trading: Otimização de LSTM para fins de previsão de séries temporais multivariadas (DA-CG-LSTM)

Introdução

Os mercados financeiros não são apenas números nas telas. Trata-se de um ambiente dinâmico, no qual cada tick, cada candle, cada variação no volume de negociações reflete emoções humanas, expectativas, medos e esperanças. Compreender esse ritmo, aprender a prever para onde o preço irá, essa é a tarefa que desafia os traders.

O foco está nas séries temporais multivariadas. Esta é a forma clássica de representar os dados de mercado: preço do ativo ao longo do tempo, volume de negociação, indicadores, notícias. Todos esses são dados que podem ser analisados, modelados e usados para previsão.

Até recentemente, o mercado se baseava em métodos clássicos consagrados, como ARIMA, SARIMA e outros. Esses modelos são convenientes, compreensíveis e não exigem recursos computacionais exorbitantes. Lidavam bem com padrões sazonais e dependências lineares, especialmente em condições de mercado estáveis. Mas o mercado financeiro não é estacionário. Aqui tudo se mistura: as notícias influenciam as expectativas, o humor dos investidores muda em segundos, operações algorítmicas geram efeitos de ressonância, e tudo isso dá origem a dependências complexas, não lineares e frequentemente caóticas. Os modelos tradicionais podem indicar a direção, mas não revelam os detalhes.

Com a chegada dos métodos de aprendizado profundo, o cenário mudou drasticamente. As redes neurais recorrentes (RNN) possibilitaram levar em conta o histórico das variações, mas também não eram uma solução definitiva. Sua limitação fundamental é a chamada "memória curta". Em outras palavras, esses modelos só conseguem processar um contexto temporal limitado. À medida que cresce o comprimento da sequência original, eles rapidamente esquecem informações importantes do início da série temporal.

Para resolver esse problema, foram desenvolvidas arquiteturas aprimoradas, como a LSTM (Long Short-Term Memory) e a GRU (Gated Recurrent Unit). Esses modelos deram às redes neurais algo como memória, a capacidade de reter informações relevantes ao longo de intervalos temporais maiores.

No entanto, mesmo essas arquiteturas têm suas limitações. Apesar da capacidade de captar dependências em períodos mais longos, elas continuam sensíveis à qualidade dos dados de entrada. Especialmente problemáticas são as situações em que picos de mercado de curto prazo têm papel decisivo. Tais mutações frequentemente não são captadas pela memória longa do modelo, principalmente quando não vêm acompanhadas de alterações significativas no contexto de longo prazo.

Com o objetivo de superar essas limitações, foi proposto o mecanismo de atenção (attention). Ele permitiu que os modelos se concentrassem de forma eficaz nas partes mais relevantes da série temporal, independentemente de quão distantes estivessem do momento atual. Diferente do LSTM, os mecanismos de atenção não exigem o processamento sequencial de todos os passos temporais e podem focar diretamente nas informações realmente importantes. Isso melhorou de forma significativa a capacidade das redes neurais de captar dependências de longo prazo, especialmente em séries temporais multivariadas e complexas.

Mas aqui também há uma armadilha: tais modelos captam bem as dependências de longo prazo, mas tendem a ignorar sinais de curto prazo que podem ser criticamente importantes. O mercado financeiro não tolera demora, pois um único título de notícia pode fazer o preço disparar ou despencar. Se o modelo não reage a essas mutações, ele perde a oportunidade de ajustar a posição a tempo.

Os autores do trabalho "A Dual-Staged Attention Based Conversion-Gated Long Short Term Memory for Multivariable Time Series Prediction" tentaram unir o melhor dos dois mundos e propuseram um novo framework: o Dual-Staged Attention Conversion-Gated LSTM (DA-CG-LSTM). O modelo utiliza um mecanismo de atenção duplo. Na primeira etapa, ele avalia a relevância dos atributos e dos intervalos de tempo; em seguida, após o processamento por um bloco especial CG-LSTM, reanalisa as dependências temporais, reforçando os sinais importantes e atenuando os irrelevantes.

Um benefício adicional do modelo é a forma refinada com que ele lida com as funções de ativação, o que ajuda a manter a informação de longo prazo e a responder aos picos de curto prazo.

Algoritmo DA-CG-LSTM

O framework DA-CG-LSTM é um modelo capaz de extrair a essência de séries temporais multivariadas. Sua arquitetura combina dois níveis de atenção e um bloco recorrente modificado, no formato Conversion-Gated LSTM. Isso torna o modelo especialmente eficaz em tarefas de previsão de processos dinâmicos e multivariados.

Tudo começa com o fornecimento da sequência temporal multivariada de dados brutos como entrada do modelo. Essa sequência é representada por uma matriz X = [x1, x2, ..., xT] ∈ RT*n, onde cada linha xt é um vetor com n características no instante t. Mas o modelo não processa essas informações às cegas. Primeiro, ele aprende a identificar quais atributos e quais instantes temporais, nesse histórico, são realmente importantes. Assim começa a primeira etapa, a atenção de entrada.

Primeiro, os atributos são analisados dentro de cada instante de tempo. O modelo calcula o grau de importância de cada característica xkt no passo temporal t pela fórmula:

Aqui, We e be representam pesos e viés treináveis de uma camada linear aplicada a cada vetor de características dos dados brutos xt. Essa camada permite transformar os dados originais em uma representação oculta mais informativa, adequada para a avaliação de relevância. Além disso, o vetor ve, também treinável, atua como uma máscara de atenção interpretável, pois ele é usado para calcular a pontuação escalar de importância. Essa estrutura oferece ao modelo a capacidade de classificar os atributos de forma flexível, com base em sua contribuição, o que é especialmente importante ao lidar com séries temporais multivariadas e ruidosas.

Os coeficientes de importância obtidos são normalizados com a função SoftMax, transformando o conjunto de escores em uma distribuição probabilística sobre os atributos:

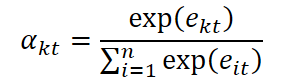
Com isso, é ajustado o vetor de dados originais x̃t, no qual cada atributo é escalado de acordo com sua relevância.

Mas não paramos por aí. A etapa seguinte envolve a análise da importância de cada passo temporal, determinando quais pontos no tempo devem ser enfatizados durante o processamento. Para isso, é usada uma estrutura análoga:

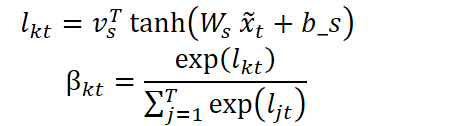
A sequência resultante consiste em representações ponderadas no tempo:

Assim, antes mesmo do processamento recorrente, o modelo já se concentra nas informações que considera realmente relevantes.

Em seguida, a sequência é encaminhada para o bloco recorrente modificado CG-LSTM. É nesse ponto que ocorre o segundo nível da "mágica". No mecanismo LSTM padrão, os autores do framework trabalharam nas funções de ativação das portas de entrada e de esquecimento. Essa modificação tem como objetivo aumentar a sensibilidade do modelo a picos relacionados a mutações de curto prazo, ao mesmo tempo em que reforça a capacidade de retenção de informações de longo prazo.

No bloco LSTM clássico, a porta de entrada utiliza uma função sigmoide para decidir quais informações devem ser retidas. No entanto, a sigmoide tende à saturação: quando os valores de entrada são muito baixos ou muito altos, sua derivada se aproxima de zero, o que reduz a eficiência do treinamento. Os autores do DA-CG-LSTM propuseram usar uma combinação da sigmoide com a tangente hiperbólica, expressa pela seguinte fórmula:

Essa estrutura ajuda a evitar a saturação nas fases iniciais do treinamento e a manter a sensibilidade a oscilações fracas, mas significativas. No contexto das séries temporais financeiras, isso é especialmente relevante, já que, por exemplo, uma variação brusca no volume de negociações ou um pico de volatilidade pode sinalizar uma mudança no regime de mercado, e a detecção oportuna desses padrões oferece ao modelo uma vantagem na previsão.

As portas de esquecimento do CG-LSTM também foram modificadas. Diferentemente do bloco LSTM padrão, aqui foi utilizada uma função que combina a sigmoide com a tangente hiperbólica inversa:

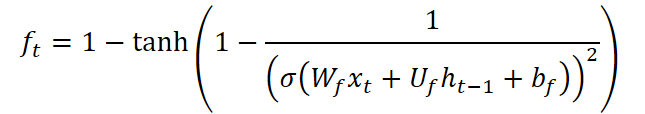
Essa fórmula possui uma propriedade única: a derivada da função assume valores no intervalo de 0 até aproximadamente 2,89, gerando um efeito de dispersão dos dados. Em outras palavras, o modelo se torna capaz de esquecer de forma mais agressiva informações irrelevantes ou obsoletas, concentrando-se, assim, em mudanças recentes. Isso é particularmente valioso em ambientes de mercado, nos quais eventos passados rapidamente perdem relevância, e o sucesso depende da reação a sinais atuais.

Na saída do bloco CG-LSTM, obtém-se a sequência (h1, h2, ..., hT), em que cada ht carrega informações de curto e longo prazo. No entanto, não basta apenas armazenar, pois é essencial recuperar corretamente essas informações. Essa é a função do segundo nível de atenção: a atenção temporal.

Nesse estágio, o modelo "revê" sua própria memória. Ele calcula a relevância de cada estado oculto hj em relação ao momento atual. Os valores obtidos são normalizados por meio da função SoftMax. Com base neles, é criado um vetor de contexto, a quintessência de toda a história temporal, que será processado por um segundo bloco CG-LSTM.

De posse do estado oculto atual ht e do contexto enriquecido ct, o modelo gera a previsão final:

Aqui, f representa, em geral, uma camada totalmente conectada ou outra estrutura de saída do modelo.

A arquitetura DA-CG-LSTM não é apenas inteligente, é criteriosa. O modelo não memoriza tudo indiscriminadamente, mas faz escolhas conscientes. Ele não reage a qualquer ruído, mas aprende a distinguir picos de padrões reais. Em tarefas de previsão financeira, isso é especialmente relevante. O sistema é capaz de captar sinais semelhantes a eventos anteriores, reconhecer sua intensidade e ajustar a previsão com base nisso.

Assim, o DA-CG-LSTM se apresenta como um organismo vivo e dinâmico, que aprende, adapta-se e tira conclusões a partir de uma análise estruturada da informação. Sua força não está apenas nas equações formais, mas na clareza conceitual:

Atenção + Memória + Interpretação = Previsão com Sentido

A visualização original do framework DA-CG-LSTM é apresentada a seguir.

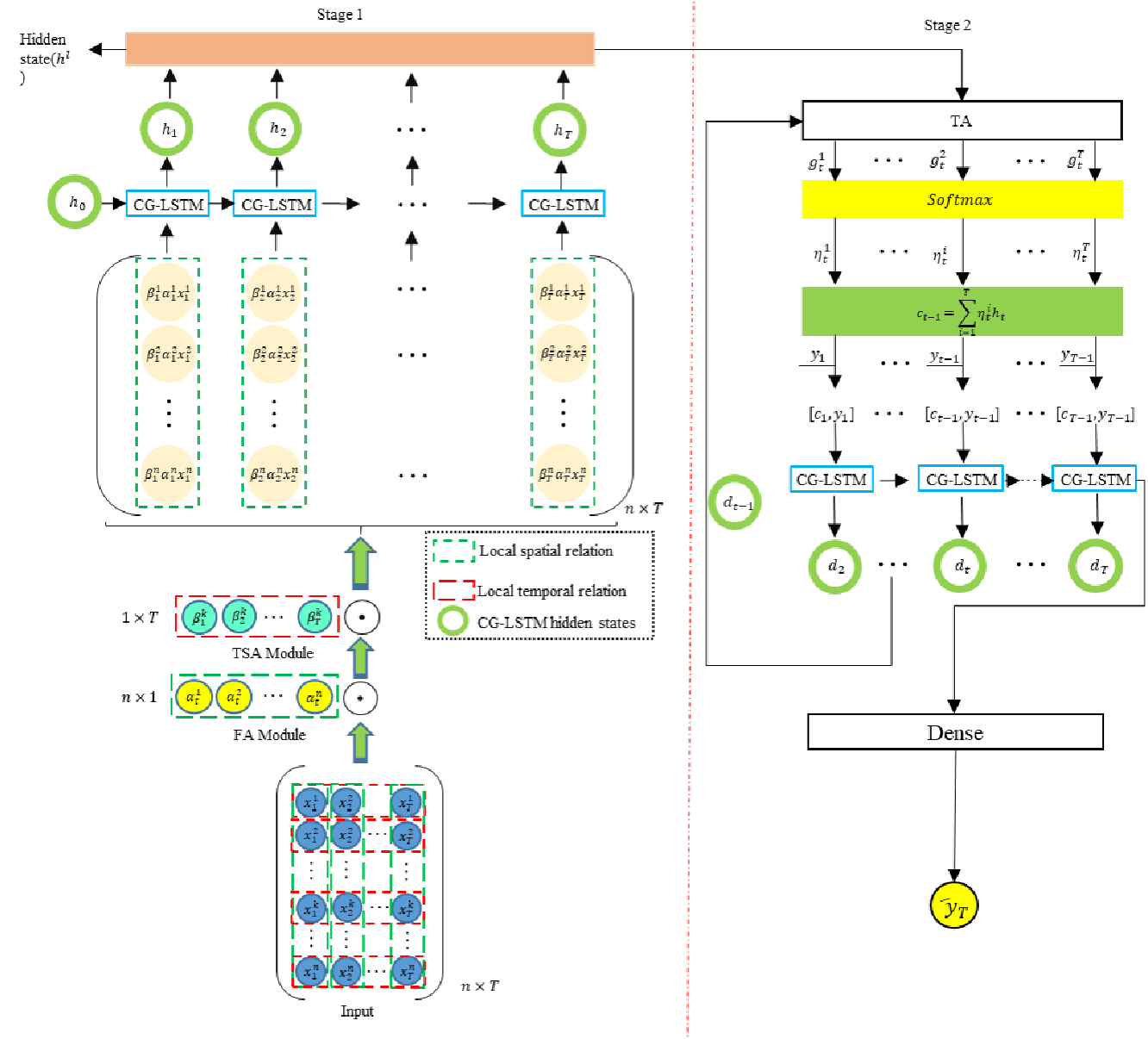
Implementação em MQL5

Após analisar os aspectos teóricos do framework DA-CG-LSTM, passamos à parte prática do nosso trabalho, na qual exploraremos uma possível implementação da proposta utilizando MQL5.

Começaremos desenvolvendo o bloco CG-LSTM modificado, cuja visualização original é apresentada abaixo.

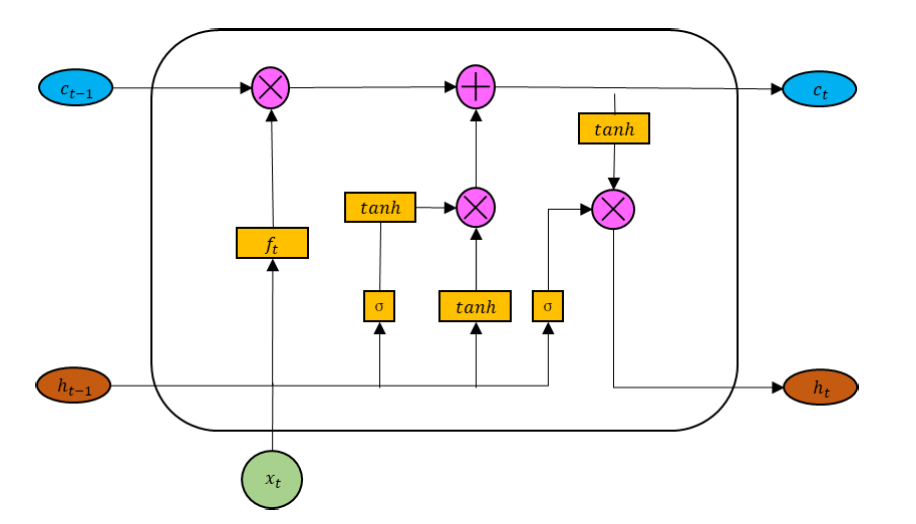
Aqui, vale destacar que, de maneira análoga ao bloco LSTM clássico, o tensor dos dados de entrada é concatenado ao estado oculto do bloco, formado no passo temporal anterior. O tensor resultante é utilizado para gerar 4 entidades: três portas e a representação do novo contexto. Para formar cada uma dessas entidades, é utilizada uma camada linear. No entanto, os resultados das camadas lineares são passados por funções de ativação distintas, conferindo a elas a devida não linearidade.

O uso de quatro funções de ativação diferentes para a formação das entidades mencionadas nos leva à necessidade de criar quatro camadas totalmente conectadas, chamadas de forma sequencial. Convenhamos, essa não é a melhor abordagem. Em nossos trabalhos, buscamos constantemente maneiras de maximizar a paralelização das operações, o que permite acelerar o processo de treinamento dos modelos e a tomada de decisões durante a utilização prática.

Para isso, ao desenvolver o bloco LSTM clássico, organizamos todo o processo de propagação para frente dentro de um único kernel. Nesse processo, o cálculo dos valores de cada entidade era realizado em fluxos paralelos dentro do grupo de trabalho, com os valores sendo compartilhados por meio do armazenamento dos dados na memória local. Essa implementação demonstrou ser eficaz. No entanto, ao incorporar sequências mais complexas de funções de ativação, como as propostas pelos autores do framework DA-CG-LSTM, nos deparamos com a necessidade de criar buffers adicionais para armazenar valores intermediários, além da maior complexidade do algoritmo como um todo.

Portanto, nesta implementação, optamos por uma abordagem alternativa. Para isso, dividiremos o processo de propagação para frente em duas etapas. Na primeira etapa, realizamos o cálculo de todas as quatro entidades sem aplicar funções de ativação. Podemos utilizar aqui uma camada totalmente conectada simples ou uma camada convolucional, cujo tensor de saída seja múltiplo da quantidade de entidades a serem formadas. No caso de dados de entrada multivariados, o uso da camada convolucional é mais vantajoso, pois permite a execução de operações independentes para sequências unitárias distintas.

Na segunda etapa, organizamos propriamente o funcionamento do bloco CG-LSTM, aplicando as funções de ativação apropriadas aos dados obtidos e estruturando os processos internos do bloco.

Acredito que está claro: começaremos com a implementação da segunda etapa no contexto do OpenCL.

Modificação do programa OpenCL

Primeiramente, organizamos o processo de propagação para frente da nossa versão do bloco CG-LSTM dentro do kernel CSLSTM_FeedForward. Nos parâmetros desse kernel, recebemos apenas os ponteiros para três buffers de dados.

Um desses buffers contém os dados de entrada (concatenated), onde estão reunidos os valores das quatro componentes antes da aplicação das funções de ativação. Com o objetivo de minimizar a latência no acesso à memória global e acelerar a leitura dos valores, os dados nesse buffer são representados no formato float4 — um tipo vetorial que permite ler quatro elementos consecutivos em uma única operação. Essa organização garante um uso mais eficiente da largura de banda da memória e acelera os cálculos, especialmente quando se trabalha com grandes volumes de dados de entrada.

Os outros dois buffers são destinados ao armazenamento do contexto e dos resultados.

__kernel void CSLSTM_FeedForward(__global const float4* __attribute__((aligned(16))) concatenated,
                                 __global float *memory,
                                 __global float *output)
  {
   uint id = (uint)get_global_id(0);
   uint total = (uint)get_global_size(0);       // hidden size
   uint idv = (uint)get_global_id(1);
   uint total_v = (uint)get_global_size(1);     // variables

A execução desse kernel é planejada em um espaço bidimensional de tarefas, sem a criação de grupos de trabalho. A primeira dimensão indica o tamanho do estado oculto da célula, enquanto a segunda representa a quantidade de sequências unitárias nos dados de entrada. No corpo do kernel, identificamos imediatamente o fluxo de execução em todas as dimensões do espaço de tarefas.

Com base nos dados obtidos, determinamos o deslocamento nos buffers e lemos diretamente para uma variável local o bloco correspondente dos dados de entrada.

uint shift = id + total * idv;
float4 concat = concatenated[shift];

Em seguida, aplicamos as funções de ativação necessárias a todas as entidades.

float fg = 1 - Activation(1 - 1 / pow(Activation(concat.s0, ActFunc_SIGMOID), 2), ActFunc_TANH);
float ig = Activation(Activation(concat.s1, ActFunc_SIGMOID), ActFunc_TANH);
float nc = Activation(concat.s2, ActFunc_TANH);
float og = Activation(concat.s3, ActFunc_SIGMOID);

Depois disso, atualizamos os valores do contexto e do estado oculto.

float mem = IsNaNOrInf(memory[shift] * fg + ig * nc, 0);
float out = IsNaNOrInf(og * Activation(mem, ActFunc_TANH), 0);

Os valores obtidos são gravados nos elementos apropriados dos buffers globais de dados, e o kernel é finalizado.

 memory[shift] = mem;
 output[shift] = out;
} 

O código do kernel ficou compacto e de fácil leitura, em grande parte graças ao uso de um método auxiliar para seleção da função de ativação. Essa solução não apenas simplifica a lógica do corpo principal do kernel, como também torna o código mais modular e expansível. Além disso, a introdução de um mecanismo de verificação da correção dos valores obtidos aumenta a confiabilidade de toda a cadeia computacional.

Concluído o trabalho com o kernel de propagação para frente, passamos à construção dos processos de propagação reversa. É fácil perceber que, durante a propagação para frente, não foram utilizados parâmetros treináveis. Todos eles foram alocados na camada neural usada na primeira etapa. Portanto, para implementar as operações da propagação reversa, basta distribuir corretamente o gradiente do erro entre os participantes do processo. Essas operações são executadas no kernel CSLSTM_CalcHiddenGradient.

Os parâmetros do kernel de distribuição do gradiente de erro são complementados com os buffers apropriados, mantendo-se o mesmo espaço de tarefas.

__kernel void CSLSTM_CalcHiddenGradient(__global const float4* __attribute__((aligned(16))) concatenated,
                                        __global float4* __attribute__((aligned(16))) grad_concat,
                                        __global const float* memory,
                                        __global const float* grad_output
                                       )
  {
   uint id = get_global_id(0);
   uint total = get_global_size(0);
   uint idv = get_global_id(1);
   uint shift = id + total * idv;

No corpo do kernel, identificamos o fluxo atual em todas as dimensões do espaço de tarefas e determinamos imediatamente o deslocamento nos buffers até os elementos correspondentes.

É importante observar que o cálculo das derivadas das funções de ativação complexas propostas pelos autores do framework DA-CG-LSTM requer uma série de valores intermediários, os quais optamos por não armazenar durante a execução das operações de propagação para frente. É evidente que armazenar esses valores exigiria recursos significativos de memória. Além disso, o acesso aos buffers globais de dados é uma operação relativamente custosa. No entanto, graças ao fato de que o principal volume das operações matriciais foi delegado à camada neural interna da primeira etapa, conseguimos calcular com facilidade e rapidez os valores necessários com base nas entidades antes da aplicação das funções de ativação.

Para isso, lemos os dados originais (pré-ativação) para uma variável local e reexecutamos as funções, desta vez armazenando os resultados intermediários em variáveis locais. 

   float4 concat = concatenated[shift];                    // Pre-activation values for all 4 gates
// --- Forward reconstruction of gates ---
   float fg_s = Activation(concat.s0, ActFunc_SIGMOID);
   float fg = 1.0f - Activation(1.0f - 1.0f / pow(fg_s, 2), ActFunc_TANH);  // Forget gate (ft)
   float ig_s = Activation(concat.s1, ActFunc_SIGMOID);
   float ig = Activation(ig_s, ActFunc_TANH);              // Input gate (it)
   float nc = Activation(concat.s2, ActFunc_TANH);         // New content (ct~)
   float og = Activation(concat.s3, ActFunc_SIGMOID);      // Output gate (ot)
   float mem = memory[shift];                              // New memory state (ct)
   float mem_t = Activation(mem, ActFunc_TANH);            // tanh(ct)

Em seguida, por retropropagação, calculamos o valor da memória no passo temporal anterior.

// --- Reconstruct previous memory state (t-1) ---
   float prev_mem = IsNaNOrInf((mem - ig * nc) / fg, 0);

Concluída essa etapa de preparação, passamos diretamente às operações de distribuição do gradiente do erro. Aqui, começamos lendo o valor do gradiente na saída do módulo a partir do buffer global para uma variável local.

// --- Gradients computation ---
   float out_g = grad_output[shift];

Distribuímos então esse valor entre as portas de saída e a memória de contexto, utilizando as derivadas das respectivas funções de ativação.

float og_g = Deactivation(out_g * mem_t, og, ActFunc_SIGMOID);
float mem_g = Deactivation(out_g * og, mem_t, ActFunc_TANH);

Na sequência, distribuímos o gradiente do erro da memória de contexto entre a projeção do novo contexto e as portas de entrada.

float nc_g = Deactivation(mem_g * ig, nc, ActFunc_TANH);
float ig_g = Deactivation(Deactivation(mem_g * nc, ig, ActFunc_TANH), ig_s, ActFunc_SIGMOID);

Atente-se às etapas de aplicação das derivadas das funções de ativação durante o ajuste sequencial do gradiente do erro nas portas de entrada.

Por fim, resta-nos propagar o gradiente do erro até os valores das portas de esquecimento, antes da aplicação da função de ativação. Como mencionado anteriormente, aqui os autores do framework DA-CG-LSTM propuseram o uso de uma função de ativação bastante complexa. Consequentemente, a distribuição do gradiente do erro será feita em várias etapas.

Primeiramente, determinamos o erro das portas de esquecimento com base no gradiente da memória de contexto e seu valor anterior.

// ∂L/∂fg = ∂L/∂ct * mem_(t-1)
   float fg_g = mem_g * prev_mem;

O valor obtido é então ajustado pela derivada da função de ativação da tangente hiperbólica e da expressão interna complexa.

// Derivative of the complex forget gate:
// f(z) = 1 - tanh(1 - 1 / σ(z)^2)
   float fg_s_g = 2 / pow(fg_s, 3) * Deactivation(-fg_g, fg, ActFunc_TANH);
   fg_g = Deactivation(fg_s_g, fg_s, ActFunc_SIGMOID);

Em seguida, aplicamos a derivada da sigmoide.

Os valores finais são armazenados nos respectivos elementos do buffer global de dados.

// --- Write back gradients ---
   grad_concat[shift] = (float4)(fg_g, ig_g, nc_g, og_g);
  }

Com isso, encerramos o trabalho do lado do programa OpenCL. O código completo pode ser consultado no anexo.

Criação do objeto CG-LSTM

Agora passamos para a etapa de trabalho no lado do programa principal. Aqui, criaremos um novo objeto chamado CNeuronCGLSTMOCL, no qual será estruturado o funcionamento do nosso bloco CG-LSTM. A estrutura do novo objeto é apresentada a seguir.

class CNeuronCGLSTMOCL : public CNeuronBaseOCL
  {
protected:
   CNeuronBaseOCL    cConcatenateInputs;
   CNeuronConvOCL    cProjection;
   //---
   virtual bool      CSLSTM_feedForward(void);
   virtual bool      CSLSTM_CalcHiddenGradient(void);
   //---
   virtual bool      feedForward(CNeuronBaseOCL *NeuronOCL) override;
   virtual bool      updateInputWeights(CNeuronBaseOCL *NeuronOCL) override;
   virtual bool      calcInputGradients(CNeuronBaseOCL *NeuronOCL) override;

public:
                     CNeuronCGLSTMOCL(void) {};
                    ~CNeuronCGLSTMOCL(void) {};
   //---
   virtual bool      Init(uint numOutputs, uint myIndex, COpenCLMy *open_cl, uint numNeurons,
                          ENUM_OPTIMIZATION optimization_type, uint batch) override;
   virtual bool      Init(uint numOutputs, uint myIndex, COpenCLMy *open_cl,
                          uint count, uint window, uint variables, 
                          ENUM_OPTIMIZATION optimization_type, uint batch);
   //---
   virtual bool      Save(int const file_handle) override;
   virtual bool      Load(int const file_handle) override;
   //---
   virtual int       Type(void) override  const    {  return defNeuronCGLSTMOCL; }
   virtual bool      Clear(void) override;
   virtual CBufferFloat *getLSTMWeights(void) { return cProjection.GetWeightsConv(); }
   virtual void      SetOpenCL(COpenCLMy *obj) override;
   virtual bool      WeightsUpdate(CNeuronBaseOCL *source, float tau) override;
  };

Na estrutura apresentada da nova classe, observamos o conjunto habitual de métodos sobrescrevíveis e 2 objetos internos, cuja funcionalidade será detalhada mais adiante, no decorrer da implementação dos métodos da classe. Todos os objetos internos são declarados de forma estática, o que nos permite deixar vazios o construtor e o destrutor da classe. A inicialização direta dos objetos declarados e herdados ocorre no método Init.

Nos parâmetros do método de inicialização, recebemos um conjunto de constantes que permitem interpretar de forma inequívoca a arquitetura do objeto que está sendo criado.

bool CNeuronCGLSTMOCL::Init(uint numOutputs, uint myIndex, COpenCLMy *open_cl,
                            uint count, uint window, uint variables,
                            ENUM_OPTIMIZATION optimization_type, uint batch)
  {
   if(!CNeuronBaseOCL::Init(numOutputs, myIndex, open_cl, count * variables, optimization_type, batch))
      return false;
   SetActivationFunction(None);

Parte dos valores recebidos é imediatamente repassada ao método homônimo da classe base, onde já estão organizados os processos de verificação dos parâmetros e a inicialização dos objetos herdados.

Note que, aqui também, indicamos explicitamente a ausência de função de ativação para o objeto que está sendo criado.

Após a execução bem-sucedida das operações do método da classe base, passamos à preparação do funcionamento dos objetos declarados. Neste caso, são apenas dois. Um deles é uma camada totalmente conectada, responsável por registrar o tensor concatenado dos dados de entrada com o estado oculto das últimas operações da propagação para frente.

if(!cConcatenateInputs.Init(0, 0, OpenCL, (count + window) * variables, optimization, iBatch))
   return false;
cConcatenateInputs.SetActivationFunction(None);

E, aqui também, indicamos explicitamente a ausência de função de ativação.

O segundo é uma camada convolucional que projeta o tensor concatenado nas quatro entidades.

if(!cProjection.Init(0, 1, OpenCL, count + window, count + window, count * 4, 1, variables, optimization, iBatch))
   return false;
cProjection.SetActivationFunction(None);

Como já discutido anteriormente, essa camada não utiliza função de ativação, o que também é indicado de forma explícita.

A inicialização da camada convolucional merece atenção especial. Durante sua criação, definimos explicitamente o comprimento da sequência como igual a um. À primeira vista, isso pode parecer uma limitação; no entanto, por trás dessa decisão há uma clara intenção arquitetural: ao mesmo tempo, indicamos a quantidade de sequências unitárias (independentes) que serão processadas em paralelo.

Essa abordagem permite atribuir a cada sequência unitária seu próprio conjunto de parâmetros treináveis, uma matriz de pesos separada. Isso garante independência total em sua análise e aprendizado. Cada sequência pode ser treinada em seu próprio contexto, reagindo a padrões e estruturas específicas, sem compartilhar parâmetros com as demais. Como resultado, obtemos uma representação dos dados de entrada mais expressiva, adaptável e estruturalmente flexível, especialmente em tarefas nas quais diferentes subsequências temporais carregam funções semânticas distintas ou refletem o comportamento de fatores de mercado específicos.

Esse tipo de isolamento dos parâmetros também desempenha um papel importante no processo de aprendizado. Em primeiro lugar, ele reduz a interferência mútua entre os canais, o que diminui o risco de sobreajuste a padrões dominantes. Em segundo lugar, cada sequência unitária pode se concentrar nas propriedades específicas dos seus próprios dados. Esse tipo de aprendizado diferenciado torna o modelo não apenas mais preciso em tarefas específicas, mas também muito mais robusto frente a mudanças nas condições de mercado.

Além disso, o aprendizado independente dos filtros unitários favorece a capacidade de generalização, pois o modelo passa a memorizar menos e a identificar com mais frequência padrões recorrentes. Isso é especialmente relevante em séries temporais financeiras, onde os dados históricos podem conter eventos únicos e pouco representativos. Ao decompor o processo de aprendizado em múltiplos ramos isolados, o modelo se torna capaz de reconhecer sinais típicos do mercado mesmo em situações novas, nunca antes encontradas.

E, naturalmente, uma característica essencial dos modelos recorrentes é o uso dos próprios dados do ciclo anterior de propagação para frente. Por isso, limpamos todos os buffers de dados e apenas então encerramos o método de inicialização.

   if(!Clear())
      return false;
//---
   return true;
  }

O próximo passo do nosso trabalho é a construção dos processos de propagação para frente, os quais organizamos dentro do método feedForward. Posso dizer que aqui tudo é bastante simples. Nos parâmetros do método, recebemos um ponteiro para o objeto de dados de entrada, cuja validade verificamos imediatamente.

bool CNeuronCGLSTMOCL::feedForward(CNeuronBaseOCL *NeuronOCL)
  {
   if(!NeuronOCL)
      return false;

Em seguida, extraímos das configurações da camada de projeção as dimensões do tensor de dados de entrada e do estado oculto.

int hidden = (int)cProjection.GetFilters() / 4;
int inputs = (int)cProjection.GetWindow() - hidden;
int variables = (int)cProjection.GetVariables();

Depois disso, concatenamos os dados de entrada com os resultados do ciclo anterior de propagação para frente, no contexto das sequências unitárias.

if(!Concat(NeuronOCL.getOutput(), getOutput(), cConcatenateInputs.getOutput(), inputs, hidden, variables))
   return false;

Os valores obtidos são então projetados nas quatro entidades.

if(!cProjection.FeedForward(cConcatenateInputs.AsObject()))
   return false;

E agora, basta apenas chamar o método encapsulador responsável por enfileirar o kernel de propagação para frente CSLSTM_feedForward na fila de execução.

 return CSLSTM_feedForward();
}

Os métodos de enfileiramento de kernels foram criados segundo a estrutura que você já conhece. Por esse motivo, não abordaremos em detalhes o algoritmo correspondente nesta etapa do artigo.

Após concluir a construção do método de propagação para frente, passamos à implementação dos processos de propagação reversa. Como você sabe, esse processo se divide em duas etapas: distribuição do gradiente do erro e otimização dos parâmetros treináveis.

Neste caso, os parâmetros treináveis estão presentes apenas na camada de projeção dos dados concatenados. Logo, o processo de otimização dos parâmetros do modelo se reduz à chamada do método homônimo da projeção.

bool CNeuronCGLSTMOCL::updateInputWeights(CNeuronBaseOCL *NeuronOCL)
  {
   return cProjection.UpdateInputWeights(cConcatenateInputs.AsObject());
  }

O algoritmo do método de distribuição do gradiente de erro entre os participantes do processo, calcInputGradients, apresenta um pouco mais de complexidade. Nos parâmetros do método, recebemos um ponteiro para o objeto de dados de entrada. Esse é o mesmo objeto que foi analisado durante a propagação para frente. A diferença agora é que precisamos transmitir a ele o gradiente do erro, de acordo com a influência dos dados de entrada sobre o resultado final da execução do modelo.

bool CNeuronCGLSTMOCL::calcInputGradients(CNeuronBaseOCL *NeuronOCL)
  {
   if(!NeuronOCL)
      return false;

No corpo do método, verificamos imediatamente a validade do ponteiro recebido. A necessidade dessa verificação de controle já foi discutida diversas vezes em artigos anteriores.

Em seguida, de maneira semelhante ao método de propagação para frente, determinamos as dimensões dos dados de entrada e do estado oculto.

int hidden = (int)cProjection.GetFilters() / 4;
int inputs = (int)cProjection.GetWindow() - hidden;
int variables = (int)cProjection.GetVariables();

Primeiro, distribuímos o gradiente do erro entre as entidades, chamando o método encapsulador que adiciona o respectivo kernel à fila de execução.

if(!CSLSTM_CalcHiddenGradient())
   return false;

Depois, propagamos o gradiente do erro até o nível do tensor concatenado dos dados de entrada.

if(!cConcatenateInputs.calcHiddenGradients(cProjection.AsObject()))
   return false;

E, por meio da operação de desconcatenação reversa, extraímos o gradiente do erro relativo aos dados de entrada.

if(!DeConcat(NeuronOCL.getGradient(), getPrevOutput(), cConcatenateInputs.getGradient(),
                                                             inputs, hidden, variables))
   return false;

Aqui, vale observar que, durante a inicialização dos objetos internos, desativamos propositalmente as funções de ativação. No entanto, isso não exclui a possibilidade de que os dados de entrada utilizem uma função de ativação. Por isso, verificamos se há uma função de ativação definida para os dados de entrada e, se necessário, ajustamos os gradientes do erro obtidos utilizando as derivadas correspondentes.

   if(NeuronOCL.Activation() != None)
      if(!DeActivation(NeuronOCL.getOutput(), NeuronOCL.getGradient(), NeuronOCL.getGradient(),
                                                                       NeuronOCL.Activation()))
         return false;
//---
   return true;
  }

Em seguida, encerramos o método, retornando previamente o resultado lógico da execução das operações para o programa chamador.

Com isso, finalizamos a análise dos algoritmos de construção do método da nossa nova classe CNeuronCGLSTMOCL. O código completo dessa classe e de todos os seus métodos pode ser consultado no anexo.

Pouco a pouco, quase sem percebermos, chegamos ao limite de volume desta parte do artigo. No entanto, a conclusão lógica desta pesquisa exige continuidade. Faremos uma breve pausa. A próxima parte está por vir, e ela será igualmente rica em conteúdo. 

Considerações finais

Neste artigo, exploramos os aspectos teóricos do framework DA-CG-LSTM. Diferentemente dos modelos tradicionais, sua arquitetura incorpora diversos mecanismos inovadores, como o CG-LSTM e o mecanismo de atenção duplo, que proporcionam uma extração mais profunda e precisa das dependências nos dados. Esses componentes permitem lidar de forma eficaz com dependências temporais complexas, considerando tanto padrões de longo prazo quanto de curto prazo.

Na parte prática do artigo, apresentamos nossa visão sobre a implementação do bloco CG-LSTM utilizando MQL5. No entanto, nosso trabalho ainda não está concluído, e daremos continuidade a ele no próximo artigo, até completarmos o desenvolvimento de forma lógica e funcional.

Referências

• A Dual-Staged Attention Based Conversion-Gated Long Short Term Memory for Multivariable Time Series Prediction
• Demais artigos da série

Programas utilizados no artigo

#	Nome	Tipo	Descrição
1	Research.mq5	EA	EA para coleta de exemplos
2	ResearchRealORL.mq5	EA	EA para coleta de exemplos via método Real-ORL
3	Study.mq5	EA	EA para treinamento offline de modelos
4	StudyOnline.mq5	EA	EA para treinamento online de modelos
4	Test.mq5	EA	EA para teste do modelo
5	Trajectory.mqh	Biblioteca de classe	Estrutura de descrição do estado do sistema e arquitetura dos modelos
6	NeuroNet.mqh	Biblioteca de classe	Biblioteca de classes para criação de rede neural
7	NeuroNet.cl	Biblioteca	Biblioteca de código do programa OpenCL