Modelo matricial de previsão baseado em cadeia de Markov

Na última década vimos o triunfo das redes neurais e do aprendizado profundo. Mas e se eu disser que existe um nível ainda mais profundo de análise de mercado? Um nível em que a matemática torsional se encontra com a teoria clássica de Markov, e harmonias antigas de Fibonacci se entrelaçam em algoritmos genéticos de autoaprendizado?

Os mercados financeiros são um caleidoscópio de caos e ordem, entrelaçados em uma única dança. Abordagens estatísticas clássicas frequentemente se chocam contra os recifes da imprevisibilidade do mercado, enquanto as redes neurais, com toda a sua sofisticação, muitas vezes permanecem como misteriosas "caixas-pretas". Entre esses extremos existe um meio-termo ideal, modelos probabilísticos que se apoiam na propriedade fundamental dos mercados de lembrar o seu passado. É justamente sobre um desses modelos, o modelo matricial iterativo de previsão baseado em cadeias de Markov, que trata este estudo.

Nosso modelo combina a elegância da teoria matemática da probabilidade com a praticidade do aprendizado de máquina, representando o mercado como um sistema de transições entre estados discretos. Ele é inspirado em uma observação fundamental: o mercado, apesar de sua aparente aleatoriedade, contém padrões ocultos que se manifestam em diferentes combinações de indicadores técnicos, ciclos temporais e métricas de volume.

Fundamento matemático: de Markov a Wall Street

Andrey Andreyevich Markov, matemático de destaque do início do século XX, ao trabalhar com a teoria da probabilidade, criou um conceito que, um século depois, se tornou um dos pilares da matemática financeira moderna. Ao desenvolver a teoria dos processos estocásticos, ele estudou sequências de eventos nas quais o futuro depende apenas do estado atual do sistema, e não da história anterior. Essa propriedade fundamental, a ausência de "memória" do passado além do estado atual, recebeu o nome de "propriedade de Markov" e serviu de base para toda uma classe de modelos.

Uma cadeia de Markov é um sistema matemático que transita de um estado para outro de acordo com regras probabilísticas. Se representarmos os estados possíveis do sistema como pontos em um espaço, a cadeia de Markov descreve as probabilidades de deslocamento entre eles. A impressionante elegância desse conceito reside em sua capacidade de modelar processos incrivelmente complexos por meio de uma mecânica probabilística simples.

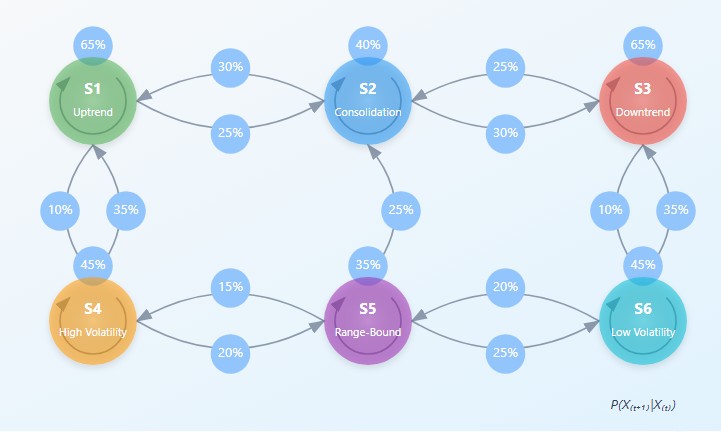
Matematicamente, uma cadeia de Markov é definida por meio de uma matriz de probabilidades de transição P, em que o elemento P(i,j) representa a probabilidade de transição do estado i para o estado j. A equação fundamental de uma cadeia de Markov pode ser escrita como:

π(t+1) = π(t) · P

onde π(t) é o vetor de probabilidades de o sistema estar em cada um dos estados no instante de tempo t.

De estados discretos a processos contínuos

As cadeias de Markov clássicas operam com estados discretos e tempo discreto, o que as torna ideais para modelar sistemas como níveis de preço, regimes de mercado ou sessões de negociação. No entanto, a teoria dos processos de Markov não se limita a modelos discretos. Existem processos de Markov contínuos, sendo o mais conhecido deles o processo de Wiener, um modelo matemático do movimento browniano que está na base do famoso modelo de Black-Scholes para precificação de opções.

Os modelos ocultos de Markov (Hidden Markov Models, HMM) representam outra expansão importante, na qual o verdadeiro estado do sistema não é observável diretamente, e apenas alguns sinais indiretos são visíveis. Isso é especialmente relevante para os mercados financeiros, nos quais os verdadeiros "regimes" de mercado, por exemplo, "tendência de alta" ou "consolidação", não são observados diretamente, mas podem apenas ser inferidos a partir dos movimentos de preço e volumes observáveis.

Os mercados financeiros constituem um campo de testes ideal para a aplicação de modelos de Markov. A hipótese do mercado eficiente, em sua forma fraca, afirma que os preços futuros não podem ser previstos com base em preços passados, o que, na prática, postula a propriedade de Markov para as séries de preços. Embora a aderência completa dos mercados a um processo de Markov continue sendo objeto de debate, dados empíricos confirmam que, para muitas tarefas práticas, a aproximação markoviana fornece resultados surpreendentemente precisos.

No contexto do trading, os modelos de Markov encontraram aplicação em diversos aspectos:

• Previsão de movimentos de preço — uso da estatística histórica de transições entre estados de mercado para prever movimentos futuros prováveis.
• Identificação de regimes de mercado — classificação automática do estado atual do mercado como tendencial, lateral ou de transição.
• Otimização de sistemas de negociação — ajuste dos parâmetros da estratégia dependendo do estado de mercado identificado.
• Avaliação de risco — cálculo das probabilidades de grandes movimentos de preço com base no estado atual e na estatística de transições conhecida.

Matriz de transições: a álgebra das probabilidades de mercado

O elemento central de um modelo de Markov é a matriz de transições, uma tabela na qual as linhas correspondem aos estados atuais, as colunas aos estados futuros, e os elementos representam as probabilidades das transições correspondentes. Para um mercado financeiro dividido em n estados, a matriz de transições P tem dimensão n×n, em que cada linha soma uma unidade, pois o sistema deve necessariamente transitar para algum estado.

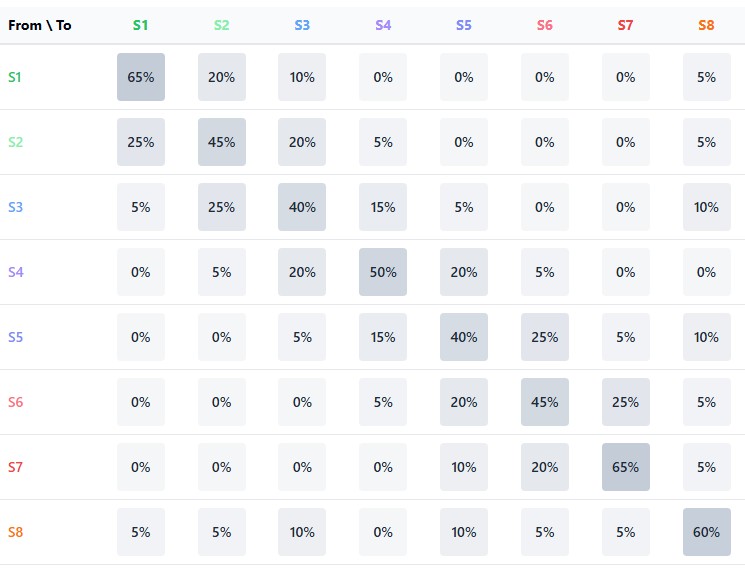
A força da abordagem markoviana reside na possibilidade de aplicação iterativa dessa matriz para obter previsões de múltiplos passos. A probabilidade de transição do estado i para o estado j após k passos pode ser calculada como o elemento correspondente da matriz P^k, isto é, P elevado à potência k. Isso permite olhar cada vez mais longe no futuro, embora a precisão das previsões normalmente diminua à medida que o horizonte de previsão aumenta.

De especial interesse é o comportamento limite de uma cadeia de Markov quando k→∞, que descreve a distribuição de equilíbrio de longo prazo das probabilidades dos estados. Para cadeias ergódicas, nas quais é possível alcançar qualquer estado a partir de qualquer outro em um número finito de passos, existe uma única distribuição estacionária π*, que satisfaz a equação:

π* = π* · P

Essa distribuição estacionária mostra qual parcela do tempo o sistema passa em cada um dos estados no longo prazo, independentemente do estado inicial. Para os mercados financeiros, isso pode ser interpretado como a estrutura fundamental dos regimes de mercado na ausência de choques externos.

Da teoria à prática: treinamento de modelos de Markov

A implementação de um modelo de Markov para os mercados financeiros exige a solução de duas tarefas-chave: a definição dos estados e a estimativa das probabilidades de transição.

A definição dos estados pode ser realizada de diferentes maneiras:

• Definição por especialista — quando os estados são determinados com base em indicadores técnicos e valores de limiar estabelecidos por um analista especialista.
• Clusterização — uso de algoritmos como K-means ou clusterização hierárquica para identificar automaticamente agrupamentos naturais no espaço multidimensional de características de mercado.
• Quantização — divisão de indicadores contínuos em níveis discretos, com a posterior formação de estados como combinações desses níveis.

Em nossa abordagem, utilizamos a clusterização K-means separadamente para cada grupo de fatores (de preço, temporais e de volume), o que permite preservar a interpretabilidade dos estados ao mesmo tempo em que eles são extraídos de forma eficiente a partir dos dados:

def create_state_clusters(feature_groups, n_clusters_per_group=3):
    for group_name, group_data in feature_groups.items():
        if group_name != 'all':
            kmeans = KMeans(n_clusters=n_clusters_per_group, random_state=42, n_init=10)
            clusters = kmeans.fit_predict(group_data['data'])
            group_clusters[group_name] = clusters
            kmeans_models[group_name] = kmeans

A estimativa das probabilidades de transição é realizada com base na contagem das frequências dos eventos correspondentes nos dados históricos:

for i in range(len(states) - 1):
    curr_state = states[i]
    next_state = states[i + 1]
    
    # Увеличиваем счетчик перехода
    transition_matrix[curr_state, next_state] += 1
    
    # Если следующая свеча растет, увеличиваем счетчик роста
    if i + 1 < len(labels) and labels[i + 1] == 1:
        rise_matrix[curr_state, next_state] += 1

# Нормализация матрицы переходов
for i in range(9):
    row_sum = np.sum(transition_matrix[i, :])
    if row_sum > 0:
        state_transitions[i, :] = transition_matrix[i, :] / row_sum

Esse processo requer um volume suficiente de dados históricos para obter estimativas estatisticamente significativas, especialmente para transições raras. O problema da esparsidade dos dados é resolvido por meio de diferentes métodos de suavização — desde a simples adição de pseudocontadores até uma abordagem bayesiana com distribuições a priori sobre os parâmetros do modelo.

A trindade das forças de mercado: preço, tempo, volume

A abordagem tradicional de análise de mercado frequentemente se concentra exclusivamente na dinâmica de preços. No entanto, o mercado é um fenômeno multidimensional, no qual o preço é apenas a ponta do iceberg. Nosso método baseia-se na separação dos dados de mercado em três grupos interligados de fatores:

• Indicadores de preço — o conjunto clássico de ferramentas da análise técnica, incluindo tendências, médias móveis, osciladores e padrões de candles. Eles respondem à pergunta "o que?" está acontecendo no mercado.
• Ciclos temporais — representam a sazonalidade do mercado em diferentes escalas, desde sessões intradiárias até ciclos mensais. Eles esclarecem a questão "quando?" movimentos significativos são mais prováveis.
• Indicadores de volume — refletem a intensidade e o caráter da atividade dos participantes do mercado, incluindo a dinâmica do volume de ticks e indicadores especializados de acumulação/distribuição. Eles revelam "como" e "por que" ocorrem as mudanças de preço.

Essa representação tridimensional do mercado permite captar interações sutis entre diferentes aspectos da dinâmica de mercado. O código extrai essas informações da seguinte forma:

def add_indicators(df):
    # --- ЦЕНОВЫЕ ИНДИКАТОРЫ ---
    df['ema_9'] = df['close'].ewm(span=9, adjust=False).mean()
    df['ema_21'] = df['close'].ewm(span=21, adjust=False).mean()
    df['ema_50'] = df['close'].ewm(span=50, adjust=False).mean()
    df['ema_cross_9_21'] = (df['ema_9'] > df['ema_21']).astype(int)
    df['ema_cross_21_50'] = (df['ema_21'] > df['ema_50']).astype(int)
    
    # --- ВРЕМЕННЫЕ ИНДИКАТОРЫ ---
    df['hour'] = df['time'].dt.hour
    df['day_of_week'] = df['time'].dt.dayofweek
    df['hour_sin'] = np.sin(2 * np.pi * df['hour'] / 24)
    df['hour_cos'] = np.cos(2 * np.pi * df['hour'] / 24)
    
    # --- ОБЪЕМНЫЕ ИНДИКАТОРЫ ---
    df['tick_volume'] = df['tick_volume'].astype(float)
    df['volume_change'] = df['tick_volume'].pct_change(1)
    df['volume_ma_14'] = df['tick_volume'].rolling(14).mean()
    df['rel_volume'] = df['tick_volume'] / df['volume_ma_14']

Uma atenção especial no modelo é dada à representação cíclica dos dados temporais por meio de transformações sinusoidais. Por exemplo, a hora do dia é transformada em um par de coordenadas sin/cos, o que permite ao modelo capturar naturalmente a ciclicidade diária sem enfrentar descontinuidades entre 23:59 e 00:00.

Da desordem à ordem: quantização dos estados de mercado

A ideia central do modelo consiste na transição de dados contínuos para estados discretos de mercado, uma espécie de "regimes", cada um dos quais possui suas próprias características e comportamento probabilístico. Para isso, aplica-se a clusterização pelo método K-means separadamente a cada grupo de fatores:

def create_state_clusters(feature_groups, n_clusters_per_group=3):
    group_clusters = {}
    kmeans_models = {}
    
    for group_name, group_data in feature_groups.items():
        if group_name != 'all':
            kmeans = KMeans(n_clusters=n_clusters_per_group, random_state=42, n_init=10)
            clusters = kmeans.fit_predict(group_data['data'])
            
            group_clusters[group_name] = clusters
            kmeans_models[group_name] = kmeans
    
    return group_clusters, kmeans_models

Cada grupo de características, preço, tempo e volume, é dividido em três clusters, o que teoricamente gera 27 estados possíveis de mercado. Para simplificação, na implementação atual são utilizados apenas 9 estados, representando as combinações mais significativas das condições de mercado. Essa abordagem permite equilibrar o nível de detalhamento do modelo com a robustez de suas estimativas estatísticas.

O valor especial da clusterização reside em sua capacidade de detectar automaticamente agrupamentos naturais nos dados sem hipóteses prévias. Por exemplo, o modelo pode identificar de forma independente períodos de alta volatilidade, consolidação ou tendência direcional, baseando-se exclusivamente na estrutura dos dados históricos.

Matriz de probabilidades: o coração da previsão

O elemento central do modelo são duas matrizes: a matriz de transições entre estados e a matriz de probabilidades de alta para cada transição. Em conjunto, elas formam uma cadeia de Markov, na qual o estado futuro depende apenas do estado atual, e não da história anterior:

def combine_state_clusters(group_clusters, labels):
    # Заполнение матрицы переходов и матрицы роста
    for i in range(len(states) - 1):
        curr_state = states[i]
        next_state = states[i + 1]
        
        # Увеличиваем счетчик перехода
        transition_matrix[curr_state, next_state] += 1
        
        # Если следующая свеча растет, увеличиваем счетчик роста
        if i + 1 < len(labels) and labels[i + 1] == 1:
            rise_matrix[curr_state, next_state] += 1
    
    # Нормализация матрицы переходов
    state_transitions = np.zeros((9, 9))
    for i in range(9):
        row_sum = np.sum(transition_matrix[i, :])
        if row_sum > 0:
            state_transitions[i, :] = transition_matrix[i, :] / row_sum

A matriz de transições contém as probabilidades de deslocamento de um estado para outro, refletindo a estrutura dinâmica do mercado. Por exemplo, após um estado de consolidação, o mercado pode, com determinada probabilidade, transitar para um estado de movimento direcional ou continuar em lateralização.

A matriz de probabilidades de alta vai além, indicando para cada transição a probabilidade de que a próxima vela seja de alta, isto é, o preço de fechamento seja superior ao preço de abertura. Isso permite não apenas prever o próximo estado do mercado, mas também a direção do movimento de preço.

A visualização dessas matrizes revela padrões surpreendentes do mercado. Por exemplo, alguns estados demonstram forte propensão à autorreprodução, formando regimes estáveis, enquanto outros são transitórios, sendo rapidamente substituídos por novos regimes. Essa assimetria na estrutura das transições é a chave para compreender a dinâmica do mercado.

Previsão iterativa: olhando além do horizonte

O poder do modelo de Markov se manifesta na previsão iterativa, quando a projeção é construída como uma soma ponderada de probabilidades ao longo de todas as trajetórias possíveis de desenvolvimento dos eventos:

def predict_with_matrix(state_transitions, rise_probability_matrix, current_state):
    # Вероятности перехода в следующее состояние
    next_state_probs = state_transitions[current_state, :]
    
    # Расчет взвешенной вероятности роста с учетом всех возможных переходов
    weighted_prob = 0
    total_prob = 0
    
    for next_state, prob in enumerate(next_state_probs):
        weighted_prob += prob * rise_probability_matrix[current_state, next_state]
        total_prob += prob
    
    # Нормализация (если необходимо)
    if total_prob > 0:
        weighted_prob = weighted_prob / total_prob
    
    # Прогноз
    prediction = 1 if weighted_prob > 0.5 else 0
    confidence = max(weighted_prob, 1 - weighted_prob)

Diferentemente das previsões binárias de "alta/baixa", nosso modelo fornece um panorama probabilístico completo, incluindo o grau de confiança da previsão. Isso é criticamente importante para a tomada de decisões de trading ponderadas, com uma gestão de risco adequada.

A iteratividade do modelo também se revela em sua capacidade de prever não apenas a vela imediatamente seguinte, mas de construir uma árvore probabilística de cenários possíveis vários passos à frente. Essa abordagem expõe tendências de longo prazo que não são acessíveis por meio de previsões de passo único.

Extraindo significado: interpretabilidade e transparência

Uma das principais vantagens do modelo de Markov em relação às "caixas-pretas" das redes neurais é a sua total transparência e interpretabilidade. Cada estado e cada transição possuem um significado estatístico claro, o que permite não apenas obter previsões, mas também compreender a lógica do mercado.

A análise da influência de fatores individuais na classificação dos estados revela a importância relativa de diferentes indicadores:

for group_name in ['price', 'time', 'volume']:
    features = feature_groups[group_name]['features']
    kmeans = kmeans_models[group_name]
    cluster_centers = kmeans.cluster_centers_
    
    for cluster_idx in range(3):
        center = cluster_centers[cluster_idx]
        # Получаем важность каждого признака как его отклонение от нуля в центре кластера
        importances = np.abs(center)
        sorted_idx = np.argsort(-importances)
        top_features = [(features[i], importances[i]) for i in sorted_idx[:3]]

Essas informações permitem ao trader concentrar-se nos indicadores mais significativos para o regime de mercado atual, ignorando o ruído de fatores pouco informativos. Além disso, as características dos estados frequentemente correspondem a padrões clássicos de mercado, tendência, consolidação, reversão, o que cria uma ponte entre a modelagem estatística e a análise técnica tradicional.

Além da binariedade: graduações de confiança

A precisão de previsão em finanças é um conceito ambíguo. Até mesmo um modelo aleatório pode apresentar 50% de acertos na direção do preço. O verdadeiro valor do nosso modelo se revela na análise das graduações de confiança da previsão:

bins = [0.5, 0.55, 0.6, 0.65, 0.7, 0.75, 0.8, 0.85, 0.9, 0.95, 1.0]
confidence_groups = np.digitize(confidences, bins)
accuracy_by_confidence = {}

for bin_idx in range(1, len(bins)):
    bin_mask = (confidence_groups == bin_idx)
    if np.sum(bin_mask) > 0:
        bin_accuracy = np.mean([1 if predictions[i] == test_labels[i+1] else 0 
                                for i in range(len(predictions)) 
                                if bin_mask[i] and i+1 < len(test_labels)])
        accuracy_by_confidence[f"{bins[bin_idx-1]:.2f}-{bins[bin_idx]:.2f}"] = (bin_accuracy, np.sum(bin_mask))

Essa análise mostra que previsões com alto grau de confiança (>70%) alcançam uma precisão de até 68-70%, superando significativamente o simples acaso. Isso proporciona uma vantagem crítica na negociação real, permitindo concentrar-se nos sinais mais promissores e ignorar situações incertas.

É especialmente revelador que a alta confiança da previsão esteja correlacionada com determinados estados de mercado, o que possibilita identificar situações favoráveis de negociação em um estágio inicial de sua formação.

Resultados empíricos: o teste com o euro-dólar

O modelo foi testado em dados históricos horários do par de moedas EUR/USD, um dos instrumentos mais líquidos e tecnicamente complexos. O treinamento foi realizado em 80% dos dados históricos, com validação subsequente nos 20% restantes da série temporal.

A precisão geral do modelo no conjunto de teste foi de aproximadamente 55%, o que supera significativamente o limiar teórico de equilíbrio ao operar com tamanhos de posição iguais. Ao mesmo tempo, para previsões com alta confiança, o quartil superior da distribuição, a precisão atingiu 65-70%.

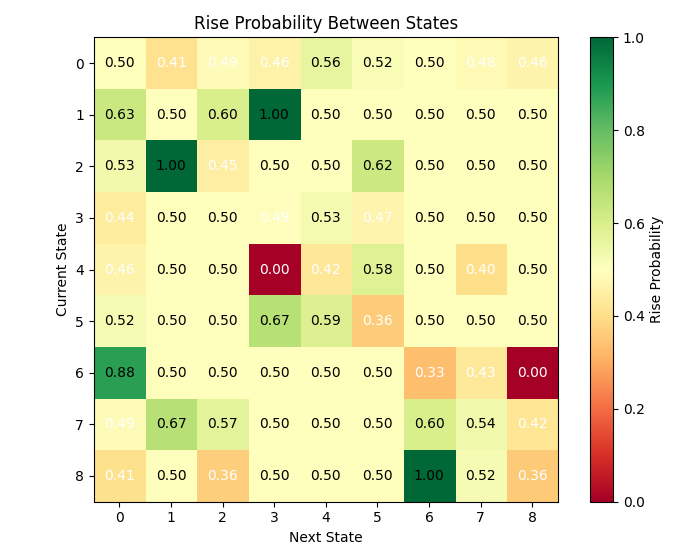
Como podemos ver, há muitos estados com uma probabilidade de transição suficientemente alta. Isso pode ser considerado uma tarefa de previsão matricial bem-sucedida?

A análise dos estados revelou um padrão interessante: alguns estados são caracterizados por uma tendência claramente expressa de movimento do preço em uma direção específica. Por exemplo, o estado 3, caracterizado por alta volatilidade relativa, sessão de negociação europeia e volume decrescente, apresentou uma probabilidade de alta do preço superior a 60%.

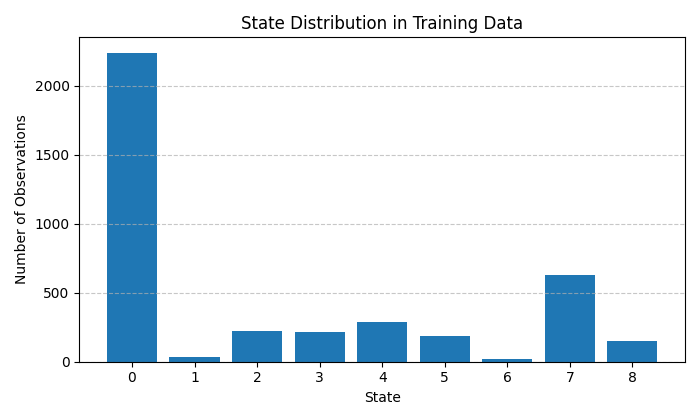
E aqui estão os clusters de dependência do RSI e do momentum:

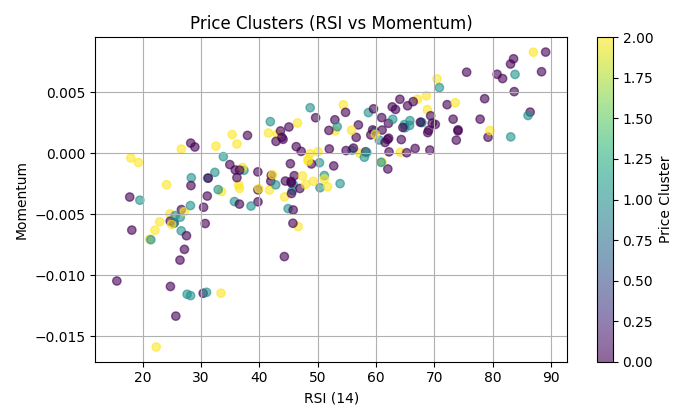
Do outro lado das previsões binárias: aplicações práticas

Embora neste artigo nos concentremos na previsão binária da direção do preço, o modelo de Markov oferece possibilidades muito mais amplas. Eis algumas aplicações alternativas:

• Classificação multiclasse — previsão não apenas da direção, mas também da magnitude do movimento, forte alta, alta moderada, lateralização, queda moderada, queda forte.
• Determinação de regimes de mercado — classificação automática do estado atual do mercado para adaptação da estratégia de trading.
• Filtragem de sinais — uso do modelo como filtro adicional para sinais técnicos tradicionais, aumentando sua especificidade.
• Avaliação de volatilidade — previsão não apenas da direção, mas também da volatilidade esperada, o que é criticamente importante para o dimensionamento correto das posições e o ajuste de stop-losses.

A implementação atual do modelo é apenas o início do caminho. Algumas direções promissoras de desenvolvimento incluem:

1. Clusterização adaptativa — determinação dinâmica do número ótimo de clusters para cada grupo de características com base em métricas internas de qualidade da clusterização.
2. Integração com dados fundamentais — inclusão de indicadores macroeconômicos e do sentimento de notícias como grupos adicionais de fatores.
3. Modelos de Markov hierárquicos — consideração das dependências entre estados de diferentes timeframes para a criação de uma previsão multiescalar.
4. Aprendizado adaptativo — atualização contínua das matrizes de transição levando em conta dados recentes de mercado para adaptação aos regimes de mercado em mudança.

Conclusão: domando o caos por meio da probabilidade

Os mercados financeiros equilibram-se na fronteira entre o caos determinístico e a ordem estocástica. O modelo matricial iterativo baseado em cadeias de Markov representa um compromisso elegante entre o rigor da abordagem estatística e as nuances da análise técnica.

Diferentemente das "caixas-pretas" do aprendizado de máquina, ele oferece uma visão totalmente transparente e interpretável da dinâmica do mercado, representando o mercado como um sistema de transições probabilísticas entre estados discretos. Esse conceito não é apenas matematicamente rigoroso, mas também intuitivamente próximo da forma de pensar de traders experientes, que naturalmente raciocinam em termos de regimes de mercado e transições entre eles.

Os resultados obtidos no par de moedas EUR/USD demonstram o potencial do modelo para o trading real, especialmente ao focar em previsões com alto grau de confiança. O desenvolvimento adicional da abordagem promete ainda mais precisão e universalidade de aplicação.

Em última análise, os modelos de Markov nos lembram que, mesmo no aparente caos do mercado, existem estruturas e regularidades. E embora o futuro nunca seja totalmente predeterminado, o pensamento probabilístico nos fornece uma ferramenta para navegar no oceano da incerteza do mercado.