Neuronale Netze im Handel: Vereinheitlichtes Trajektoriengenerierungsmodell (UniTraj)
Einführung
Die Analyse des Verhaltens von Multi-Agenten spielt eine entscheidende Rolle in verschiedenen Bereichen, darunter Finanzen, autonomes Fahren und Überwachungssysteme. Um die Handlungen von Agenten zu verstehen, müssen mehrere wichtige Aufgaben gelöst werden: Objektverfolgung, Identifizierung, Modellierung von Trajektorien und Handlungserkennung. Die Modellierung von Trajektorien ist besonders wichtig für die Analyse von Agentenbewegungen. Trotz der Komplexität, die mit der Umweltdynamik und den subtilen Interaktionen zwischen den Akteuren verbunden ist, wurden in letzter Zeit bedeutende Fortschritte bei der Lösung dieses Problems erzielt. Die wichtigsten Errungenschaften konzentrieren sich auf drei Schlüsselbereiche: Trajektorievorhersage, Wiederherstellung fehlender Daten und räumlich-zeitliche Modellierung.
Die meisten Ansätze bleiben jedoch auf bestimmte Aufgaben spezialisiert. Das macht es schwierig, sie auf andere Probleme zu verallgemeinern. Einige Aufgaben erfordern sowohl vorwärts- als auch rückwärtsgerichtete räumlich-zeitliche Abhängigkeiten, die in prognoseorientierten Modellen oft übersehen werden. Einige Algorithmen haben sich zwar erfolgreich mit der bedingten Berechnung von Multiagententrajektorien befasst, doch berücksichtigen sie häufig nicht die zukünftigen Trajektorien. Diese Einschränkung schränkt ihre praktische Anwendbarkeit für ein umfassendes Verständnis von Bewegungen ein, bei denen die Vorhersage künftiger Bewegungsabläufe für die Planung nachfolgender Handlungen wesentlich ist, anstatt lediglich vergangene Bewegungsabläufe zu rekonstruieren.
Der Artikel „Movement: Unified Trajectory Generation Model for Multi-Agent“ stellt das Modell Unified TrajectoryGeneration (UniTraj) Modell vor, ein universelles Rahmenwerk, das verschiedene trajektorienbezogene Aufgaben in ein einheitliches Schema integriert. Konkret fassen die Autoren verschiedene Arten von Eingabedaten in einem einzigen einheitlichen Format zusammen: eine beliebige unvollständige Trajektorie mit einer Maske, die die Sichtbarkeit jedes Agenten in jedem Zeitschritt angibt. Das Modell verarbeitet alle Aufgabeneingaben einheitlich als maskierte Trajektorien und versucht, aus unvollständigen Trajektorien vollständige zu generieren.
Um räumlich-zeitliche Abhängigkeiten in verschiedenen Trajektoriendarstellungen zu modellieren, führen die Autoren das Modul Ghost Spatial Masking (GSM) ein, das in einen Transformer-basierten Encoder eingebettet ist. Die Autoren nutzen die Fähigkeiten aktueller populärer State-Space-Modelle (SSM), insbesondere des Mamba-Modells, und adaptieren und erweitern es zu einem bidirektionalen temporalen Encoder Mamba für die langfristige Generierung von Multi-Agenten-Trajektorien. Darüber hinaus schlagen sie ein einfaches, aber effektives Bidirectional Temporal Scaled (BTS) Modul vor, das Trajektorien umfassend scannt und dabei zeitliche Beziehungen innerhalb der Sequenz beibehält. Die in der Arbeit vorgestellten experimentellen Ergebnisse bestätigen die robuste und außergewöhnliche Leistung der vorgeschlagenen Methode.
1. Der Algorithmus UniTraj
Um verschiedene Anfangsbedingungen in einem einzigen Rahmen zu behandeln, schlagen die Autoren ein einheitliches generatives Trajektorienmodell vor, das jede beliebige Eingabe als maskierte Trajektoriensequenz behandelt. Die sichtbaren Bereiche der Trajektorie dienen als Randbedingungen oder Eingabedaten, während fehlende Bereiche zu Zielen für die generative Aufgabe werden. Dieser Ansatz führt zu der folgenden Problemstellung:
Es ist notwendig, die vollständige Trajektorie X[N, T, D] zu bestimmen, wobei N die Anzahl der Agenten, T die Länge der Trajektorie und D die Dimension der Zustände der Agenten ist. Der Zustand des Agenten i im Zeitschritt t wird als xi,t[D] bezeichnet. Außerdem verwendet der Algorithmus eine binäre Maskierungsmatrix M[N, T]. Die Variable mi,t ist gleich 1, wenn der Standort des Agenten i zum Zeitpunkt t bekannt ist, und 0 andernfalls. So wird die Trajektorie durch die Maske in zwei Segmente unterteilt: den sichtbaren Bereich, definiert als Xv=X⊙M, und den fehlenden Bereich, definiert als Xm=X⊙(1−M). Ziel ist es, eine vollständige Trajektorie Y'={X'v,X'm} zu erstellen, wobei X'v eine rekonstruierte Trajektorie und X'm die neu generierte Trajektorie ist. Aus Gründen der Konsistenz bezeichnen die Autoren die ursprüngliche Trajektorie als die Grundwahrheit (ground truth) Y=X={Xv, Xm}.
Formaler ausgedrückt, besteht das Ziel darin, ein generatives Modell f(⋅) mit den Parametern θ zu trainieren, um die vollständige Trajektorie Y' auszugeben.
Der allgemeine Ansatz zur Schätzung der Modellparameter θ beinhaltet die Faktorisierung der gemeinsamen Trajektorienverteilung und die Maximierung der Log-Likelihood.
Nehmen wir an, Agent i befindet sich im Zeitschritt t und hat die Position xi,t. Zunächst wird die relative Geschwindigkeit 𝒗i,t, durch Subtraktion der Koordinaten benachbarter Zeitschritte berechnet. Für fehlende Stellen werden die Werte durch elementweise Multiplikation mit der Maske mit Null aufgefüllt. Zusätzlich wird ein Ein-Kategorie-Vektor 𝒄i,t definiert, der die Agentenkategorien repräsentiert. Diese Kategorisierung ist in Sportszenarien, in denen Spieler bestimmte offensive oder defensive Strategien anwenden können, von entscheidender Bedeutung. Agentenmerkmale werden in einen hochdimensionalen Merkmalsvektor 𝒇i,xt projiziert. Die Vektoren der Ausgangsmerkmale werden wie folgt berechnet:
![]()
wobei φx(⋅) eine Projektionsfunktion mit den Gewichten 𝐖x ist, ⊙ die elementweise Multiplikation darstellt und ⊕ die Verkettung bezeichnet.
Die Autoren der Methode implementierten φx(⋅) mit Hilfe von MLP. Bei diesem Ansatz werden Informationen über Position, Geschwindigkeit, Sichtbarkeit und Kategorie berücksichtigt, um räumliche Merkmale für die anschließende Analyse zu extrahieren.
Im Gegensatz zu anderen sequenziellen Modellierungsaufgaben ist es entscheidend, dichte soziale Interaktionen zu berücksichtigen. Bestehende Studien über menschliche Interaktionen verwenden vorwiegend Aufmerksamkeitsmechanismen wie Kreuzaufmerksamkeit und graphbasierte Aufmerksamkeit, um diese Dynamik zu erfassen. Da UniTraj jedoch eine einheitliche Aufgabe mit willkürlich unvollständigen Eingabedaten behandelt, muss das vorgeschlagene Modell räumlich-zeitliche fehlende Muster untersuchen. Die Autoren führen das Modul Ghost Spatial Masking (GSM) ein, um räumliche Strukturen fehlender Daten zu abstrahieren und zu verallgemeinern. Dieses Modul fügt sich nahtlos in die Transformer-Architektur ein, ohne die Modellkomplexität zu erhöhen.
Ursprünglich für die Modellierung zeitlicher Abhängigkeiten in sequentiellen Daten entwickelt, wendet der Transformer-Encoder in UniTraj ein mehrköpfiges Self-Attention-Design in der räumlichen Dimension an. In jedem Zeitschritt wird die Einbettung jedes der N Agenten als Eingabe für den Transformer-Encoder verarbeitet. Dieser Ansatz extrahiert ordnungsinvariante räumliche Merkmale von Agenten und berücksichtigt dabei alle möglichen Permutationen der Agentenanordnung in praktischen Szenarien. Daher ist es besser, die sinusförmige Positionskodierung durch eine vollständig trainierbare Kodierung zu ersetzen.
Als Ergebnis gibt der Transformer-Encoder räumliche Merkmale Fs,xt für alle Agenten zu jedem Zeitschritt t aus. Diese Merkmale werden dann entlang der zeitlichen Dimension verkettet, um räumliche Darstellungen für die gesamte Trajektorie zu erhalten.
Da Mamba in der Lage ist, langfristige zeitliche Abhängigkeiten zu erfassen, haben die Autoren von UniTraj es für die Integration in den vorgeschlagenen Rahmen angepasst. Die Anpassung von Mamba für eine einheitliche Trajektoriengenerierung ist jedoch aufgrund des Fehlens einer trajektorenspezifischen Architektur eine Herausforderung. Eine wirksame Trajektorienmodellierung erfordert die Erfassung von raum-zeitlichen Merkmalen bei gleichzeitiger Behandlung fehlender Daten, was den Prozess erschwert.
Um die Extraktion zeitlicher Merkmale zu verbessern und gleichzeitig fehlende Beziehungen zu erhalten, wird eine bidirektionale temporale Mamba eingeführt. Diese Anpassung umfasst mehrere Mamba-Restblöcke sowie ein Bidirectional Temporal Scaled (BTS) Modul.
Zunächst wird die Maske M für die gesamte Trajektorie bearbeitet. Sie wird entlang der zeitlichen Dimension entfaltet, um M' zu erzeugen, was das Erlernen fehlender zeitlicher Beziehungen erleichtert, indem sowohl ursprüngliche als auch umgekehrte Masken im BTS-Modul verwendet werden. Dieser Prozess erzeugt eine Skalierungsmatrix S und ihre Inverse S'. Für den Agenten i im Zeitschritt t wird si,t wie folgt berechnet:
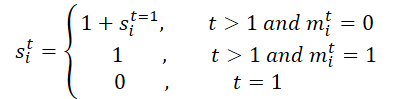
Anschließend werden die Skalierungsmatrix S und ihre Inverse S' auf die Merkmalsmatrix projiziert:
![]()
wobei φs(⋅) die Projektionsfunktionen mit den Gewichten 𝐖s darstellt.
Die Autoren implementieren φs(⋅) mit MLP und der Aktivierungsfunktion ReLU. Die vorgeschlagene Skalierungsmatrix berechnet den Abstand zwischen der letzten Beobachtung und dem aktuellen Zeitschritt und quantifiziert so die Auswirkungen von zeitlichen Lücken, insbesondere bei komplexen fehlenden Mustern. Die wichtigste Erkenntnis ist, dass der Einfluss einer Variable im Laufe der Zeit abnimmt, wenn sie über einen bestimmten Zeitraum hinweg fehlt. Durch die Verwendung einer negativen Exponentialfunktion und ReLU wird sichergestellt, dass der Einfluss innerhalb eines angemessenen Bereichs zwischen 0 und 1 monoton abnimmt.
Der Kodierungsprozess zielt darauf ab, die Parameter einer Gauß-Verteilung für das approximative Posterior zu bestimmen. Konkret werden der Mittelwert μq und die Standardabweichung σq der posterioren Gaußschen Verteilung wie folgt berechnet:
![]()
Die latenten Variablen 𝒁 werden aus einer a priori Gauß-Verteilung 𝒩(0, I) abgeleitet.
Um die Fähigkeit des Modells, plausible Trajektorien zu erzeugen, zu verbessern, kombinieren wir diese Funktion Fz,x mit der latenten Variable 𝒁, bevor wir sie in den Decoder einspeisen. Der Prozess der Trajektoriengenerierung wird dann wie folgt berechnet:
![]()
wobei φdec die Decoderfunktion ist, die mit Hilfe eines MLP implementiert wird.
Bei Vorliegen einer beliebigen unvollständigen Trajektorie erzeugt das Modell UniTraj eine vollständige Trajektorie. Während des Trainingsprozesses werden der Rekonstruktionsfehler für sichtbare Bereiche und der Wiederherstellungsfehler für maskierte Daten berechnet.
Im Folgenden wird die Visualisierung der Methode UniTraj durch den Autor vorgestellt.
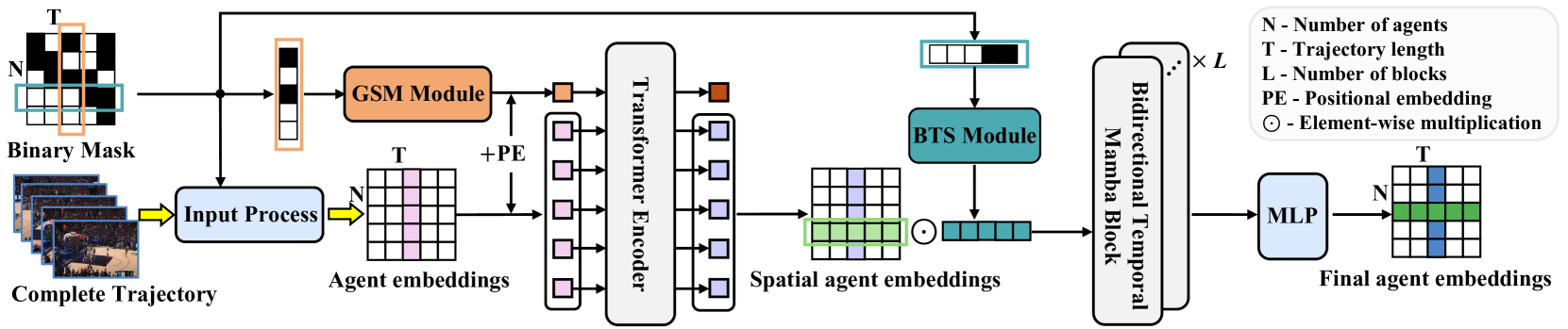
2. Implementation in MQL5
Nach der Betrachtung der theoretischen Aspekte der Methode UniTraj gehen wir zum praktischen Teil unseres Artikels über, in dem wir unsere Vision der vorgeschlagenen Ansätze mit MQL5 umsetzen. Es ist wichtig, darauf hinzuweisen, dass sich der vorgeschlagene Algorithmus strukturell von den bisher untersuchten Methoden unterscheidet.
Der erste bemerkenswerte Unterschied ist das Maskierungsverfahren. Bei der Übergabe von Eingabedaten an das Modell schlagen die Autoren vor, eine zusätzliche Maske zu erstellen, die festlegt, welche Daten das Modell sehen kann und welche es erzeugen muss. Dadurch wird der Arbeitsablauf um einen zusätzlichen Schritt erweitert und die Entscheidungszeit verlängert, was unerwünscht ist. Deshalb wollen wir die Maskenerstellung in das Modell selbst integrieren.
Der zweite Aspekt ist die Übermittlung der vollständigen Trajektorie an das Modell. Eine vollständige Trajektorie kann zwar während der Tests ermittelt werden, ist aber im realen Einsatz nicht möglich. Das Modell ermöglicht es, fehlende Daten zu maskieren und anschließend zu rekonstruieren, aber wir müssen dem Modell immer noch einen größeren Tensor zur Verfügung stellen. Dies führt zu einem erhöhten Speicherverbrauch und zusätzlichem Overhead bei der Datenübertragung, was sich letztlich auf die Verarbeitungsgeschwindigkeit auswirkt. Eine mögliche Lösung besteht darin, die Übertragung zu begrenzen
sowohl bei der Training als auch beim Einsatz nur auf historische Daten zurückgreifen. Dies würde jedoch einen erheblichen Teil der Funktionsweise der Methode beeinträchtigen.
Um ein Gleichgewicht zwischen Effizienz und Genauigkeit herzustellen, habe ich beschlossen, die Datenübertragung in zwei Teile zu unterteilen: historische Daten und die zukünftige Trajektorie. Letztere wird nur während der Trainingsphase zur Verfügung gestellt, um räumlich-zeitliche Abhängigkeiten zu extrahieren. Während der Echtzeitausführung wird der zukünftige Trajektorientensor weggelassen, und das Modell arbeitet in einem prädiktiven Modus.
Außerdem erforderte diese Implementierung bestimmte Änderungen auf der OpenCL-Seite.
2.1 Erweiterungen des OpenCL-Programms
Als ersten Schritt in unserer Implementierung bereiten wir neue Kernel-Funktionen innerhalb des OpenCL-Programms vor. Die wichtigste Ergänzung ist der Kernel UniTrajPrepare, der für die Vorverarbeitung der Daten zuständig ist. Dieser Kernel verknüpft historische Daten mit der bekannten zukünftigen Trajektorie und wendet dabei die entsprechende Maskierung an.
Die Kernelparameter enthalten Zeiger auf 5 Datenpuffer: 4 für Eingabedaten und eine für Ausgabeergebnisse. Außerdem sind Parameter erforderlich, die die Tiefe der historischen Datenanalyse und den Planungshorizont festlegen.
__kernel void UniTrajPrepare(__global const float *history, __global const float *h_mask, __global const float *future, __global const float *f_mask, __global float *output, const int h_total, const int f_total ) { const size_t i = get_global_id(0); const size_t v = get_global_id(1); const size_t variables = get_global_size(1);
Wir planen die Ausführung des Kernels in einem zweidimensionalen Aufgabenraum. Die erste Dimension ist die Größe des größeren der beiden Zeiträume (Geschichtstiefe und Planungshorizont). Die zweite Dimension gibt die Anzahl der analysierten Parameter an.
Im Kernelkörper identifizieren wir zunächst einen Thread in einem bestimmten Aufgabenbereich. Wir bestimmen auch den Offset in den Datenpuffern.
const int shift_in = i * variables + v; const int shift_out = 3 * shift_in; const int shift_f_out = 3 * (h_total * variables + v);
Als Nächstes arbeiten wir mit historischen Daten. Hier bestimmen wir zunächst die Änderungsrate des Parameters unter Berücksichtigung der Maske. Und dann speichern wir den Parameterwert im Ergebnispuffer unter Berücksichtigung des Maximalwerts, der zuvor berechneten Geschwindigkeit und der Maske selbst.
//--- history if(i < h_total) { float mask = h_mask[shift_in]; float h = history[shift_in]; float v = (i < (h_total - 1) && mask != 0 ? (history[shift_in + variables] - h) * mask : 0); if(isnan(v) || isinf(v)) v = h = mask = 0; output[shift_out] = h * mask; output[shift_out + 1] = v; output[shift_out + 2] = mask; }
Wir berechnen ähnliche Parameter für zukünftige Werte.
//--- future if(i < f_total) { float mask = f_mask[shift_in]; float f = future[shift_in]; float v = (i < (f_total - 1) && mask != 0 ? (future[shift_in + variables] - f) * mask : 0); if(isnan(v) || isinf(v)) v = f = mask = 0; output[shift_f_out + shift_out] = f * mask; output[shift_f_out + shift_out + 1] = v; output[shift_f_out + shift_out + 2] = mask; } }
Als Nächstes speichern wir den Kernel des umgekehrten Durchlaufs der oben genannten Operationen: UniTrajPrepareGrad.
__kernel void UniTrajPrepareGrad(__global float *history_gr, __global float *future_gr, __global const float *output, __global const float *output_gr, const int h_total, const int f_total ) { const size_t i = get_global_id(0); const size_t v = get_global_id(1); const size_t variables = get_global_size(1);
Beachten Sie, dass wir in den Parametern der Methode für den Rückwärtsdurchgang keine Zeiger auf die Quelldaten und Maskenpuffer angeben. Stattdessen verwenden wir den Ergebnispuffer von UniTrajPrepare, dem Kernel des Vorwärtsdurchgangs, in dem die angegebenen Daten gespeichert werden. Außerdem wird der Fehlergradient nicht an die Maskenebene weitergegeben, da dies nicht sinnvoll ist.
Der Aufgabenbereich des Kerns des Rückwärtsdurchgangs ist identisch mit dem oben für den Kernel des Vorwärtsdurchgangs beschriebenen.
Im Kernelkörper identifizieren wir den aktuellen Thread im Aufgabenraum und bestimmen den Offset in den Datenpuffern.
const int shift_in = i * variables + v; const int shift_out = 3 * shift_in; const int shift_f_out = 3 * (h_total * variables + v);
Ähnlich wie beim Kernel des Vorwärtsdurchgangs organisieren wir die Arbeit in 2 Stufen. Zunächst verteilen wir den Fehlergradienten auf die Ebene der historischen Daten.
//--- history if(i < h_total) { float mask = output[shift_out + 2]; float grad = 0; if(mask > 0) { grad = output_gr[shift_out] * mask; grad -= (i < (h_total - 1) && mask != 0 ? (output_gr[shift_out + 1]) * mask : 0); grad += (i > 0 ? output[shift_out + 1 - 3 * variables] * output[shift_out + 2 - 3 * variables] : 0); if(isnan(grad) || isinf(grad)) grad = 0; //--- } history_gr[shift_in] = grad; }
Und dann übertragen wir den Fehlergradienten auf die bekannten vorhergesagten Werte.
//--- future if(i < f_total) { float mask = output[shift_f_out + shift_out + 2]; float grad = 0; if(mask > 0) { grad = output_gr[shift_f_out + shift_out] * mask; grad -= (i < (h_total - 1) && mask != 0 ? (output_gr[shift_f_out + shift_out + 1]) * mask : 0); grad += (i > 0 ? output[shift_f_out + shift_out + 1 - 3 * variables] * output[shift_f_out + shift_out + 2 - 3 * variables] : 0); if(isnan(grad) || isinf(grad)) grad = 0; //--- } future_gr[shift_in] = grad; } }
Ein weiterer Algorithmus, den wir auf der OpenCL-Seite implementieren müssen, ist die Erstellung einer Skalierungsmatrix. Im Kernel von UniTrajBTS berechnen wir die direkten und inversen Skalierungsmatrizen.
Auch hier verwenden wir die Ergebnisse des Datenaufbereitungs-Kernel als Input. Anhand seiner Daten berechnen wir den Versatz zum letzten unmaskierten Wert in Vorwärts- und Rückwärtsrichtung, den wir in den entsprechenden Datenpuffern speichern.
__kernel void UniTrajBTS(__global const float * concat_inp, __global float * d_forw, __global float * d_bakw, const int total ) { const size_t i = get_global_id(0); const size_t v = get_global_id(1); const size_t variables = get_global_size(1);
Wir verwenden einen zweidimensionalen Aufgabenraum. In der ersten Dimension werden wir jedoch nur 2 Threads haben, die der Berechnung der direkten und inversen Skalierungsmatrix entsprechen. In der zweiten Dimension geben wir wie zuvor die Anzahl der zu analysierenden Variablen an.
Nachdem wir den Thread im Aufgabenraum identifiziert haben, teilen wir den Kernel-Algorithmus je nach Wert der ersten Dimension auf.
if(i == 0) { const int step = variables * 3; const int start = v * 3 + 2; float last = 0; d_forw[v] = 0; for(int p = 1; p < total; p++) { float m = concat_inp[start + p * step]; d_forw[p * variables + v] = last = 1 + (1 - m) * last; } }
Bei der Berechnung der direkten Skalierungsmatrix bestimmen wir den Offset zur Maske des ersten Elements der analysierten Variablen und den Schritt zum nächsten Element. Anschließend werden die Masken des analysierten Elements nacheinander durchlaufen und die Skalierungskoeffizienten nach der vorgegebenen Formel berechnet.
Für die inverse Skalierungsmatrix bleibt der Algorithmus identisch. Nur dass wir den Versatz zum letzten Element ermitteln und in umgekehrter Reihenfolge iterieren.
else { const int step = -(variables * 3); const int start = (total - 1) * variables + v * 3 + 2; float last = 0; d_bakw[(total - 1) + v] = 0; for(int p = 1; p < total; p++) { float m = concat_inp[start + p * step]; d_bakw[(total - 1 - p) * variables + v] = last = 1 + (1 - m) * last; } } }
Beachten Sie, dass der vorgestellte Algorithmus nur mit Masken funktioniert, für die die Verteilung des Fehlergradienten nicht sinnvoll ist. Aus diesem Grund erstellen wir für diesen Algorithmus keinen Kernel für einen Rückwärtsdurchgang. Damit sind unsere Operationen auf der Programmseite von OpenCL abgeschlossen. Den vollständigen Code finden Sie im Anhang.
2.2 Implementierung des UniTraj-Algorithmus
Nach den vorbereitenden Arbeiten auf der OpenCL-Programmseite gehen wir dazu über, die vorgeschlagenen Ansätze auf der Seite des Hauptprogramms zu implementieren. Der Algorithmus UniTraj wird in der Klasse CNeuronUniTraj implementiert. Seine Struktur wird im Folgenden dargestellt.
class CNeuronUniTraj : public CNeuronBaseOCL { protected: uint iVariables; float fDropout; //--- CBufferFloat cHistoryMask; CBufferFloat cFutureMask; CNeuronBaseOCL cData; CNeuronLearnabledPE cPE; CNeuronMVMHAttentionMLKV cEncoder; CNeuronBaseOCL cDForw; CNeuronBaseOCL cDBakw; CNeuronConvOCL cProjDForw; CNeuronConvOCL cProjDBakw; CNeuronBaseOCL cDataDForw; CNeuronBaseOCL cDataDBakw; CNeuronBaseOCL cConcatDataDForwBakw; CNeuronMambaBlockOCL cSSM[4]; CNeuronConvOCL cStat; CNeuronTransposeOCL cTranspStat; CVAE cVAE; CNeuronTransposeOCL cTranspVAE; CNeuronConvOCL cDecoder[2]; CNeuronTransposeOCL cTranspResult; //--- virtual bool Prepare(const CBufferFloat* history, const CBufferFloat* future); virtual bool PrepareGrad(CBufferFloat* history_gr, CBufferFloat* future_gr); virtual bool BTS(void); //--- virtual bool feedForward(CNeuronBaseOCL *NeuronOCL) override { return feedForward(NeuronOCL, NULL); } virtual bool feedForward(CNeuronBaseOCL *NeuronOCL, CBufferFloat *SecondInput) override; //--- virtual bool calcInputGradients(CNeuronBaseOCL *NeuronOCL) override { return calcInputGradients(NeuronOCL, NULL, NULL, None); } virtual bool updateInputWeights(CNeuronBaseOCL *NeuronOCL) override { return updateInputWeights(NeuronOCL, NULL); } virtual bool calcInputGradients(CNeuronBaseOCL *NeuronOCL, CBufferFloat *SecondInput, CBufferFloat *SecondGradient, ENUM_ACTIVATION SecondActivation = None) override; virtual bool updateInputWeights(CNeuronBaseOCL *NeuronOCL, CBufferFloat *second) override; //--- public: CNeuronUniTraj(void) {}; ~CNeuronUniTraj(void) {}; //--- virtual bool Init(uint numOutputs, uint myIndex, COpenCLMy *open_cl, uint window, uint window_key, uint heads, uint units_count, uint forecast, float dropout, ENUM_OPTIMIZATION optimization_type, uint batch); //--- virtual int Type(void) const { return defNeuronUniTrajOCL; } //--- virtual bool Save(int const file_handle); virtual bool Load(int const file_handle); //--- virtual bool WeightsUpdate(CNeuronBaseOCL *source, float tau); virtual void SetOpenCL(COpenCLMy *obj); };
Wie Sie sehen können, deklariert die Klassenstruktur eine große Anzahl interner Objekte, deren Funktionsweise wir Schritt für Schritt erkunden werden, wenn wir mit der Methodenimplementierung fortfahren. Alle Objekte werden statisch deklariert. So können wir den Konstruktor und den Destruktor der Klasse leer lassen, während die Speicheroperationen an das System delegiert werden.
Alle internen Objekte werden in der Methode Init initialisiert. In seinen Parametern finden wir die wichtigsten Konstanten, die es uns ermöglichen, die Architektur des Objekts eindeutig zu identifizieren.
bool CNeuronUniTraj::Init(uint numOutputs, uint myIndex, COpenCLMy *open_cl, uint window, uint window_key, uint heads, uint units_count, uint forecast, float dropout, ENUM_OPTIMIZATION optimization_type, uint batch) { if(!CNeuronBaseOCL::Init(numOutputs, myIndex, open_cl, window * (units_count + forecast), optimization_type, batch)) return false;
Innerhalb des Hauptteils der Methode rufen wir, der gängigen Konvention folgend, zunächst die gleichnamige Methode der Elternklasse auf, die bereits die wesentlichen Initialisierungskontrollen für geerbte Objekte implementiert.
Nach der erfolgreichen Ausführung der Operationen der übergeordneten Klasse speichern wir die vom externen Programm erhaltenen Konstanten. Dazu gehören die Anzahl der analysierten Variablen in den Eingabedaten und der Anteil der während des Trainingsprozesses maskierten Elemente.
iVariables = window; fDropout = MathMax(MathMin(dropout, 1), 0);
Als Nächstes gehen wir zur Initialisierung der deklarierten Objekte über. Hier legen wir zunächst Puffer an, um historische und prognostizierte Daten zu maskieren.
if(!cHistoryMask.BufferInit(iVariables * units_count, 1) || !cHistoryMask.BufferCreate(OpenCL)) return false; if(!cFutureMask.BufferInit(iVariables * forecast, 1) || !cFutureMask.BufferCreate(OpenCL)) return false;
Dann initialisieren wir die innere Schicht der verketteten Quelldaten.
if(!cData.Init(0, 0, OpenCL, 3 * iVariables * (units_count + forecast), optimization, iBatch)) return false;
Und erstellen Sie eine ähnlich große, erlernbare Schicht für die Kodierung von Positionen.
if(!cPE.Init(0, 1, OpenCL, cData.Neurons(), optimization, iBatch)) return false;
Darauf folgt der Transformer-Encoder, der zur Extraktion räumlich-zeitlicher Abhängigkeiten verwendet wird.
if(!cEncoder.Init(0, 2, OpenCL, 3, window_key, heads, (heads + 1) / 2, iVariables, 1, 1, (units_count + forecast), optimization, iBatch)) return false;
Es ist erwähnenswert, dass die Autoren eine Reihe von Experimenten durchgeführt haben und zu dem Schluss gekommen sind, dass die optimale Leistung der Methode erreicht wird, wenn ein einziger Block des Transformer-Encoders und vier Mamba Blöcke verwendet werden. Daher verwenden wir in diesem Fall nur eine Encoder-Ebene.
Außerdem ist zu beachten, dass die Größe des Eingabefensters auf „3“ eingestellt ist, was drei Parametern eines einzelnen Indikators bei jedem Zeitschritt entspricht (Wert, Geschwindigkeit und Maske). Die Sequenzlänge wird durch die Anzahl der analysierten Variablen bestimmt, während die Anzahl der unabhängigen Kanäle auf die Gesamttiefe der analysierten Historie und des Prognosehorizonts festgelegt wird. Auf diese Weise können wir die Abhängigkeiten zwischen den analysierten Indikatoren innerhalb eines einzigen Zeitschritts bewerten.
Als Nächstes gehen wir zum BTS-Modul über, wo wir die vorwärts- und rückwärtsgerichteten Skalierungsmatrizen erstellen.
if(!cDForw.Init(0, 3, OpenCL, iVariables * (units_count + forecast), optimization, iBatch)) return false;; if(!cDBakw.Init(0, 4, OpenCL, iVariables * (units_count + forecast), optimization, iBatch)) return false;
Dann fügen wir Faltungsschichten für die Projektion dieser Matrizen hinzu.
if(!cProjDForw.Init(0, 5, OpenCL, 1, 1, 3, iVariables, (units_count + forecast), optimization, iBatch)) return false; cProjDForw.SetActivationFunction(SIGMOID); if(!cProjDBakw.Init(0, 6, OpenCL, 1, 1, 3, iVariables, (units_count + forecast), optimization, iBatch)) return false; cProjDBakw.SetActivationFunction(SIGMOID);
Die sich ergebenden Projektionen werden Element für Element mit den Ergebnissen der Arbeit des Encoders multipliziert und die Ergebnisse der Operationen werden in die folgenden Objekte geschrieben.
if(!cDataDForw.Init(0, 7, OpenCL, cData.Neurons(), optimization, iBatch)) return false; if(!cDataDBakw.Init(0, 8, OpenCL, cData.Neurons(), optimization, iBatch)) return false;
Wir planen dann, die resultierenden Daten zu einem einzigen Tensor zu verketten.
if(!cConcatDataDForwBakw.Init(0, 9, OpenCL, 2 * cData.Neurons(), optimization, iBatch)) return false;
Wir übergeben diesen Tensor an den SSM-Block. Wie bereits erwähnt, werden in diesem Block 4 aufeinanderfolgende Mamba-Schichten initialisiert.
for(uint i = 0; i < cSSM.Size(); i++) { if(!cSSM[i].Init(0, 10 + i, OpenCL, 6 * iVariables, 12 * iVariables, (units_count + forecast), optimization, iBatch)) return false; }
Hier schlagen die Autoren der Methode vor, Restverbindungen zur Mamba-Schicht zu verwenden. Wir gehen noch ein wenig weiter und verwenden die Klasse CNeuronMambaBlockOCL, die wir bei der Arbeit mit der Methode TrajLLM erstellt haben.
Wir projizieren die erhaltenen Ergebnisse auf statistische Variablen der Zielverteilung.
uint id = 10 + cSSM.Size(); if(!cStat.Init(0, id, OpenCL, 6, 6, 12, iVariables * (units_count + forecast), optimization, iBatch)) return false;
Doch bevor wir die Werte abfragen und neu parametrisieren, müssen wir die Daten neu anordnen. Hierfür verwenden wir die Transponierungsebene.
id++; if(!cTranspStat.Init(0, id, OpenCL, iVariables * (units_count + forecast), 12, optimization, iBatch)) return false; id++; if(!cVAE.Init(0, id, OpenCL, cTranspStat.Neurons() / 2, optimization, iBatch)) return false;
Wir übersetzen die abgefragten Werte in die Dimension der unabhängigen Informationskanäle.
id++; if(!cTranspVAE.Init(0, id, OpenCL, cVAE.Neurons() / iVariables, iVariables, optimization, iBatch)) return false;
Dann leiten wir die Daten durch den Decoder und erhalten am Ausgang die generierte Zielsequenz.
id++; uint w = cTranspVAE.Neurons() / iVariables; if(!cDecoder[0].Init(0, id, OpenCL, w, w, 2 * (units_count + forecast), iVariables, optimization, iBatch)) return false; cDecoder[0].SetActivationFunction(LReLU); id++; if(!cDecoder[1].Init(0, id, OpenCL, 2 * (units_count + forecast), 2 * (units_count + forecast), (units_count + forecast), iVariables, optimization, iBatch)) return false; cDecoder[1].SetActivationFunction(TANH);
Jetzt müssen wir nur noch das erhaltene Ergebnis in die Dimension der ursprünglichen Daten umrechnen.
id++; if(!cTranspResult.Init(0, id, OpenCL, iVariables, (units_count + forecast), optimization, iBatch)) return false;
Um unnötige Datenkopiervorgänge zu vermeiden, tauschen wir die Zeiger auf die Datenpuffer.
if(!SetOutput(cTranspResult.getOutput(), true) || !SetGradient(cTranspResult.getGradient(), true)) return false; SetActivationFunction((ENUM_ACTIVATION)cDecoder[1].Activation()); //--- return true; }
In jeder Phase sorgen wir für eine ordnungsgemäße Überwachung des Ausführungsprozesses, und nach Abschluss der Methode geben wir einen booleschen Wert an das aufrufende Programm zurück, der den Erfolg der Methode anzeigt.
Sobald die Initialisierung der Klasseninstanz abgeschlossen ist, gehen wir zur Implementierung der Methoden für die Weitergabe über. Zunächst führen wir einen kurzen Vorbereitungsschritt durch, um die Ausführung der zuvor erstellten Kernel in eine Warteschlange zu stellen. Dabei stützen wir uns auf bewährte Algorithmen, die Sie in den beigefügten Materialien unabhängig voneinander überprüfen können. In diesem Artikel möchte ich mich jedoch auf die hochrangige Methode FeedForward konzentrieren, bei der wir den gesamten Algorithmus in groben Zügen skizzieren.
bool CNeuronUniTraj::feedForward(CNeuronBaseOCL *NeuronOCL, CBufferFloat *SecondInput) { if(!NeuronOCL) return false;
In den Methodenparametern erhalten wir Zeiger auf 2 Objekte, die historische und prognostizierte Werte enthalten. Im Hauptteil der Methode wird sofort die Relevanz des Zeigers auf historische Daten geprüft. Wie Sie sich erinnern, gibt es nach unserer Logik immer historische Daten. Es kann aber sein, dass es keine vorhergesagten Werte gibt.
Als Nächstes organisieren wir den Prozess der Erzeugung eines zufälligen Maskierungstensors aus historischen Daten.
//--- Create History Mask int total = cHistoryMask.Total(); if(!cHistoryMask.BufferInit(total, 1)) return false; if(bTrain) { for(int i = 0; i < int(total * fDropout); i++) cHistoryMask.Update(RND(total), 0); } if(!cHistoryMask.BufferWrite()) return false;
Beachten Sie, dass die Maskierung nur während des Trainingsprozesses angewendet wird. In einer Einsatzsituation nutzen wir alle verfügbaren Informationen.
Anschließend führen wir ein ähnliches Verfahren für die vorhergesagten Werte ein. Es gibt jedoch eine wichtige Nuance. Wenn Prognosewerte verfügbar sind, wird ein zufälliger Maskierungstensor erstellt. In Ermangelung von Informationen über zukünftige Bewegungen füllen wir den gesamten Maskierungstensor mit Nullwerten.
//--- Create Future Mask total = cFutureMask.Total(); if(!cFutureMask.BufferInit(total, (!SecondInput ? 0 : 1))) return false; if(bTrain && !!SecondInput) { for(int i = 0; i < int(total * fDropout); i++) cFutureMask.Update(RND(total), 0); } if(!cFutureMask.BufferWrite()) return false;
Sobald die Maskierungstensoren erstellt sind, können wir die Datenvorbereitung und die Verkettung durchführen.
//--- Prepare Data if(!Prepare(NeuronOCL.getOutput(), SecondInput)) return false;
Dann fügen wir eine Positionskodierung hinzu und übergeben sie an den Transformer Encoder.
//--- Encoder if(!cPE.FeedForward(cData.AsObject())) return false; if(!cEncoder.FeedForward(cPE.AsObject())) return false;
Als Nächstes verwenden wir gemäß dem Algorithmus UniTraj den BTS-Block. Erstellen wir vorwärts und invers skalierende Matrizen.
//--- BTS if(!BTS()) return false;
Lassen Sie uns ihre Prognosen erstellen.
if(!cProjDForw.FeedForward(cDForw.AsObject())) return false; if(!cProjDBakw.FeedForward(cDBakw.AsObject())) return false;
Wir multiplizieren sie mit den Ergebnissen der Arbeit des Encoders.
if(!ElementMult(cEncoder.getOutput(), cProjDForw.getOutput(), cDataDForw.getOutput())) return false; if(!ElementMult(cEncoder.getOutput(), cProjDBakw.getOutput(), cDataDBakw.getOutput())) return false;
Dann kombinieren wir die erhaltenen Werte zu einem einzigen Tensor.
if(!Concat(cDataDForw.getOutput(), cDataDBakw.getOutput(), cConcatDataDForwBakw.getOutput(), 3, 3, cData.Neurons() / 3)) return false;
Analysieren wir die Daten in einem Zustandsraummodell.
//--- SSM if(!cSSM[0].FeedForward(cConcatDataDForwBakw.AsObject())) return false; for(uint i = 1; i < cSSM.Size(); i++) if(!cSSM[i].FeedForward(cSSM[i - 1].AsObject())) return false;
Daraufhin erhalten wir eine Projektion der statistischen Indikatoren der Zielverteilung.
//--- VAE if(!cStat.FeedForward(cSSM[cSSM.Size() - 1].AsObject())) return false;
Dann ziehen wir Werte aus einer bestimmten Verteilung.
if(!cTranspStat.FeedForward(cStat.AsObject())) return false; if(!cVAE.FeedForward(cTranspStat.AsObject())) return false;
Der Decoder erzeugt die Zielsequenz.
//--- Decoder if(!cTranspVAE.FeedForward(cVAE.AsObject())) return false; if(!cDecoder[0].FeedForward(cTranspVAE.AsObject())) return false; if(!cDecoder[1].FeedForward(cDecoder[0].AsObject())) return false; if(!cTranspResult.FeedForward(cDecoder[1].AsObject())) return false; //--- return true; }
Anschließend transponieren wir sie in die Dimension der Eingangsdaten.
Wie Sie sich erinnern, haben wir in der Methode der Objektinitialisierung die Zeiger auf die Datenpuffer ausgetauscht, sodass in diesem Stadium keine Notwendigkeit mehr besteht, empfangene Werte von internen Objekten in die geerbten Puffer unserer Klasse zu kopieren. Um die Feedforward-Methode abzuschließen, müssen wir nur das boolesche Ausführungsergebnis an das aufrufende Programm zurückgeben.
Nachdem der Vorwärtsdurchgangs-Algorithmus erstellt wurde, besteht der nächste Schritt in der Regel darin, die Prozesse der Rückwärtsdurchgänge zu organisieren. Diese Prozesse spiegeln den Vorwärtsdurchgang wider, aber der Datenfluss ist umgekehrt. In Anbetracht des Umfangs unserer Arbeit und des begrenzten Formats des Artikels werden wir hier jedoch nicht im Detail auf den Rückwärtsdurchgang eingehen. Stattdessen überlasse ich sie dem Selbststudium. Zur Erinnerung: Den vollständigen Code für diese Klasse und alle ihre Methoden finden Sie im Anhang.
2.3 Modellarchitektur
Nachdem wir unsere Interpretation des Algorithmus von UniTraj umgesetzt haben, fahren wir nun mit seiner Integration in unsere Modelle fort. Wie andere Methoden der Trajektorienanalyse, die auf historische Daten angewandt werden, werden wir den vorgeschlagenen Algorithmus in ein Umgebungszustands-Kodierungsmodell einbinden. Die Architektur dieses Modells wird in der Methode CreateEncoderDescriptions definiert.
bool CreateEncoderDescriptions(CArrayObj *&encoder) { //--- CLayerDescription *descr; //--- if(!encoder) { encoder = new CArrayObj(); if(!encoder) return false; }
Diese Methode erhält vom externen Programm einen Zeiger auf ein dynamisches Array-Objekt als Parameter, in dem wir die Modellarchitektur angeben. Im Hauptteil der Methode prüfen wir sofort die Relevanz des empfangenen Zeigers und erstellen gegebenenfalls ein neues Objekt. Danach gehen wir zur Beschreibung der architektonischen Lösung über.
Die erste Komponente, die wir implementieren, ist eine vollständig verbundene Schicht, die die Eingabedaten speichert.
//--- Encoder encoder.Clear(); //--- Input layer if(!(descr = new CLayerDescription())) return false; descr.type = defNeuronBaseOCL; int prev_count = descr.count = (HistoryBars * BarDescr); descr.activation = None; descr.optimization = ADAM; if(!encoder.Add(descr)) { delete descr; return false; }
In dieser Phase werden Informationen über historische Kursbewegungen und die Werte der analysierten Indikatoren über eine vordefinierte historische Tiefe aufgezeichnet. Diese Roheingaben werden vom Terminal „wie sie sind“ ohne jegliche Vorverarbeitung abgerufen. Natürlich können solche Daten sehr uneinheitlich sein. Um dies zu beheben, wenden wir eine Batch-Normalisierungsebene an, um die Werte auf eine vergleichbare Skala zu bringen.
//--- layer 1 if(!(descr = new CLayerDescription())) return false; descr.type = defNeuronBatchNormOCL; descr.count = prev_count; descr.batch = 1e4; descr.activation = None; descr.optimization = ADAM; if(!encoder.Add(descr)) { delete descr; return false; }
Wir übertragen die normalisierten Daten sofort in unseren neuen Block UniTraj. Hier setzen wir den Maskierungskoeffizienten auf 50 % der empfangenen Daten.
//--- layer 2 if(!(descr = new CLayerDescription())) return false; descr.type = defNeuronUniTrajOCL; descr.window = BarDescr; //window descr.window_out = EmbeddingSize; //Inside Dimension descr.count = HistoryBars; //Units descr.layers = NForecast; //Forecast descr.step=4; //Heads descr.probability=0.5f; //DropOut descr.batch = 1e4; descr.activation = None; descr.optimization = ADAM; if(!encoder.Add(descr)) { delete descr; return false; }
Am Ausgang des Blocks erhalten wir eine beliebige Zieltrajektorie, die sowohl wiederhergestellte historische Daten als auch Prognosewerte für einen bestimmten Planungshorizont enthält. Zu den erhaltenen Daten fügen wir statistische Variablen der Eingabedaten hinzu, die bei der Normalisierung der Daten entfernt wurden.
//--- layer 3 if(!(descr = new CLayerDescription())) return false; descr.type = defNeuronRevInDenormOCL; descr.count = BarDescr * (NForecast+HistoryBars); descr.activation = None; descr.optimization = ADAM; descr.layers = 1; if(!encoder.Add(descr)) { delete descr; return false; }
Dann gleichen wir die vorhergesagten Werte im Frequenzbereich ab.
//--- layer 4 if(!(descr = new CLayerDescription())) return false; descr.type = defNeuronFreDFOCL; descr.window = BarDescr; descr.count = NForecast+HistoryBars; descr.step = int(true); descr.probability = 0.7f; descr.activation = None; descr.optimization = ADAM; if(!encoder.Add(descr)) { delete descr; return false; } //--- return true; }
Dank der umfassenden Architektur unseres neuen Blocks CNeuronUniTraj bleibt die Beschreibung des erstellten Modells übersichtlich und strukturiert, ohne seine Fähigkeiten zu beeinträchtigen.
Es ist anzumerken, dass die erhöhte Tensorgröße des Umgebungszustands-Encoder-Modells geringfügige Anpassungen sowohl des Akteurs- als auch des Kritiker-Modells erforderte. Diese Änderungen sind jedoch minimal und können in den beigefügten Unterlagen unabhängig voneinander überprüft werden. Die Änderungen am Trainingsprogramm für das Encoder-Modell sind jedoch umfangreicher.
2.4 Modellschulungsprogramm
Die Änderungen an der Architektur des Umweltzustands-Encoder-Modells sowie die von den Autoren von UniTraj vorgeschlagenen Trainingsansätze erfordern eine Aktualisierung des EA für das Modell-Training „...\Experts\UniTraj\StudyEncoder.mq5“.
Die erste Anpassung bestand darin, den Block zur Modellvalidierung zu ändern, um die Größe der Ausgabeschicht zu überprüfen. Dies war eine gezielte Aktualisierung im Rahmen der EA-Initialisierungsmethode.
Encoder.getResults(Result); if(Result.Total() != (NForecast+HistoryBars) * BarDescr) { PrintFormat("The scope of the Encoder does not match the forecast state count (%d <> %d)", (NForecast+HistoryBars) * BarDescr, Result.Total()); return INIT_FAILED; }
Aber wie Sie sich denken können, ist die Hauptarbeit in der Trainingsmethode des Modells - Train - erforderlich.
void Train(void) { //--- vector<float> probability = GetProbTrajectories(Buffer, 0.9);
Die Methode erzeugt zunächst einen Wahrscheinlichkeitsvektor für die Auswahl von Trajektorien während des Trainings auf der Grundlage der erzielten Erträge. Das Wesentliche dieses Vorgangs besteht darin, profitablen Trajektorien häufiger den Vorrang zu geben, damit das Modell eine profitablere Strategie erlernen kann.
Als Nächstes deklarieren wir die notwendigen Variablen.
vector<float> result, target, state; bool Stop = false; const int Batch = 1000; int b = 0; //--- uint ticks = GetTickCount();
Und wir schaffen ein System von Modellschulungszyklen.
for(int iter = 0; (iter < Iterations && !IsStopped() && !Stop); iter += b) { int tr = SampleTrajectory(probability); int start = (int)((MathRand() * MathRand() / MathPow(32767, 2)) * (Buffer[tr].Total - 5 - NForecast)); if(start <= 0) continue;
Es ist wichtig zu beachten, dass der Mamba-Block einen wiederkehrenden Charakter hat, der seinen Trainingsprozess beeinflusst. Zu Beginn wird eine einzelne Trajektorie aus dem Erfahrungswiedergabepuffer entnommen und ein Startzustand für das Training ausgewählt. Anschließend erstellen wir eine verschachtelte Schleife, in der wir die Zustände entlang der gewählten Trajektorie sequentiell durchlaufen.
for(b = 0; (b < Batch && (iter + b) < Iterations); b++) { int i = start + b; if(i >= MathMin(Buffer[tr].Total, Buffer_Size) - NForecast) break;
Wir laden zunächst die historischen Daten der analysierten Parameter aus dem Erfahrungswiedergabepuffer.
state.Assign(Buffer[tr].States[i].state); if(MathAbs(state).Sum() == 0) break; bState.AssignArray(state);
Dann laden wir die nachfolgenden, wahren Werte.
//--- Collect target data if(!Result.AssignArray(Buffer[tr].States[i + NForecast].state)) continue; if(!Result.Resize(BarDescr * NForecast)) continue;
Danach teilen wir den Lernprozess zufällig in 2 Threads mit einer Wahrscheinlichkeit von 50% auf.
//--- State Encoder if((MathRand() / 32767.0) < 0.5) { if(!Encoder.feedForward((CBufferFloat*)GetPointer(bState), 1, false, (CBufferFloat*)NULL)) { PrintFormat("%s -> %d", __FUNCTION__, __LINE__); Stop = true; break; } }
Im ersten Fall werden wie bisher nur historische Daten in das Modell eingespeist und ein Feedforward-Durchgang durchgeführt. Im zweiten Fall liefern wir dem Modell auch die tatsächlichen zukünftigen Werte der Preisbewegungen. Dies bedeutet, dass das Modell vollständige reale Informationen sowohl über historische als auch über zukünftige Systemzustände erhält.
else { if(Result.GetIndex()>=0) Result.BufferWrite(); if(!Encoder.feedForward((CBufferFloat*)GetPointer(bState), 1, false, Result)) { PrintFormat("%s -> %d", __FUNCTION__, __LINE__); Stop = true; break; } }
Zur Erinnerung: Unser Algorithmus maskiert die Eingabedaten während des Trainings zu 50 % zufällig. Dieser Modus zwingt das Modell zu lernen, wie die maskierten Werte wiederhergestellt werden können.
Am Ausgang des Modells erhalten wir die vollständige Trajektorie als einen einzigen Tensor, also verschmelzen wir die beiden Quelldatenpuffer zu einem einzigen Tensor und verwenden ihn für den Backpropagation-Durchgang des Modells. Dabei passen wir die trainierten Parameter des Modells an, um die Datenwiederherstellung und den Vorhersagefehler insgesamt zu minimieren.
//--- Collect target data if(!bState.AddArray(Result)) continue; if(!Encoder.backProp((CBufferFloat*)GetPointer(bState), (CBufferFloat*)NULL)) { PrintFormat("%s -> %d", __FUNCTION__, __LINE__); Stop = true; break; }
Jetzt müssen wir den Nutzer nur noch über den Fortschritt des Trainingsprozesses informieren und mit der nächsten Iteration des Schleifensystems fortfahren.
//--- if(GetTickCount() - ticks > 500) { double percent = double(iter + b) * 100.0 / (Iterations); string str = StringFormat("%-14s %6.2f%% -> Error %15.8f\n", "Encoder", percent, Encoder.getRecentAverageError()); Comment(str); ticks = GetTickCount(); } } }
Nachdem alle Iterationen der Modelltrainingsschleifen erfolgreich abgeschlossen wurden, löschen wir das Kommentarfeld auf dem Chart des Symbols. Wir geben die Trainingsergebnisse in das Terminalprotokoll ein und initialisieren die Modellvervollständigung.
Comment(""); //--- PrintFormat("%s -> %d -> %-15s %10.7f", __FUNCTION__, __LINE__, "Encoder", Encoder.getRecentAverageError()); ExpertRemove(); //--- }
Bei der Einführung des Modells ist es nicht vorgesehen, vorhergesagte Werte als Eingabe zu verwenden. Daher bleibt das Schulungsprogramm für die Politik des Akteurs unverändert. Den vollständigen Code aller hier verwendeten Programme finden Sie im Anhang.
3. Tests
In den vorangegangenen Abschnitten haben wir die theoretischen Grundlagen der Methode UniTraj für die Arbeit mit multimodalen Zeitreihen untersucht. Wir haben unsere Interpretation mit MQL5 umgesetzt. Nun gehen wir zur letzten Phase über, in der wir die Wirksamkeit dieser Ansätze für unsere spezifischen Aufgaben bewerten.
Trotz der Änderungen an der Architektur und dem Trainingsprogramm des Umweltzustands-Encoder-Modells bleibt die Struktur des Trainingsdatensatzes unverändert. So können wir mit dem Training unter Verwendung zuvor gesammelter Datensätze beginnen.
Auch hier verwenden wir zum Trainieren der Modelle reale historische Daten des EURUSD-Instruments mit dem Zeitrahmen H1 für das gesamte Jahr 2023. Alle Indikatorparameter wurden auf ihre Standardwerte gesetzt.
In diesem Stadium trainieren wir das Encoder-Modell. Wie bereits erwähnt, ist es nicht erforderlich, den Trainingsdatensatz während des Encoder-Trainings zu aktualisieren. Das Modell wird so lange trainiert, bis die gewünschte Leistung erreicht ist. Das Modell kann nicht als leichtgewichtig bezeichnet werden. Seine Training braucht daher Zeit. Der Prozess läuft jedoch reibungslos ab. Als Ergebnis erhalten wir eine visuell vernünftige Projektion der zukünftigen Preisentwicklung.
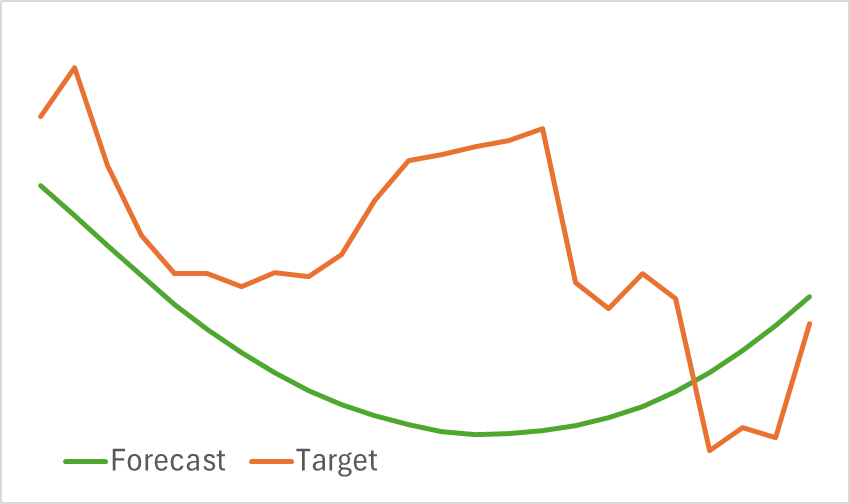
Allerdings ist die vorhergesagte Trajektorie deutlich geglättet. Dasselbe gilt für die rekonstruierte Trajektorie. Dies deutet auf eine erhebliche Verringerung des Rauschens in den Originaldaten hin. In der nächsten Phase des Modelltrainings wird festgestellt, ob diese Glättung für die Entwicklung einer rentablen Politik der Akteure von Vorteil ist.
In der zweiten Phase werden die Modelle Akteur und Kritiker iterativ trainiert. In diesem Stadium müssen wir auf der Grundlage der vorhergesagten Preisentwicklung, die durch den Umweltzustands-Codierer generiert wird, eine profitable Akteurspolitik finden. Der Encoder gibt sowohl prognostizierte als auch rekonstruierte historische Preisbewegungen aus.
Um die trainierten Modelle zu testen, haben wir historische Daten vom Januar 2024 verwendet und alle anderen Parameter unverändert gelassen.
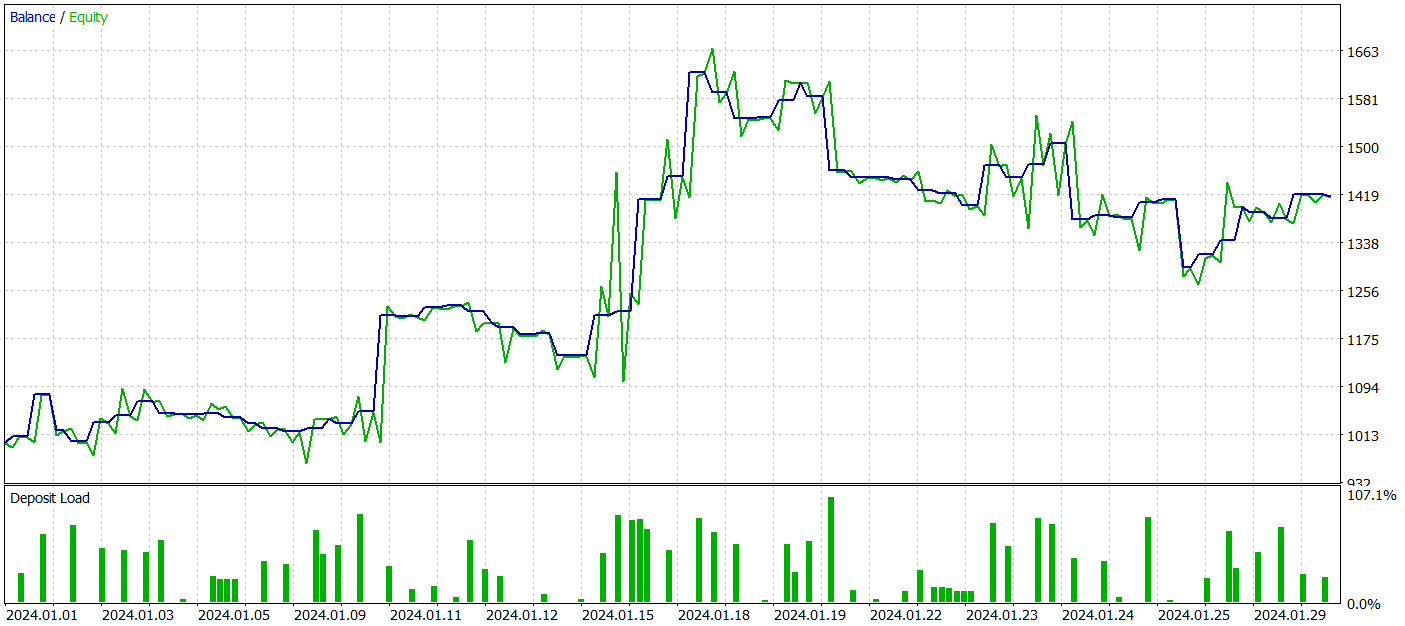
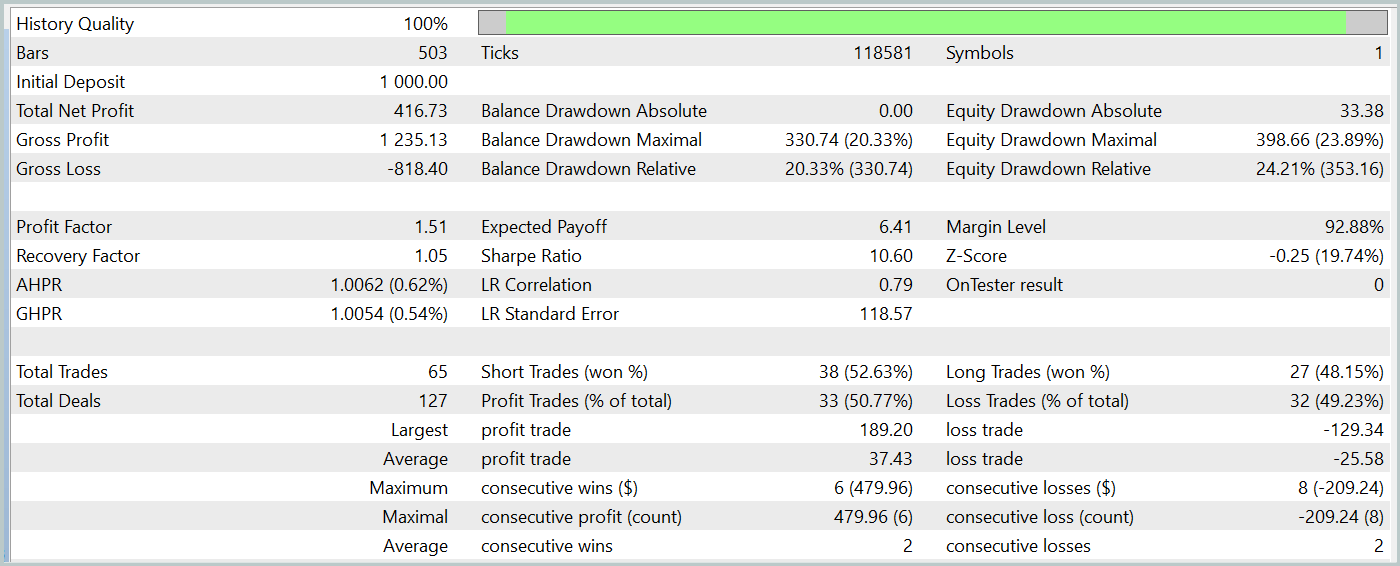
Während des Testzeitraums erzielte unser trainiertes Akteursmodell über 40 % Gewinn bei einem maximalen Drawdown von knapp über 24 %. Der EA führte insgesamt 65 Handelsgeschäfte aus, von denen 33 mit einem Gewinn abgeschlossen wurden. Da die maximalen und durchschnittlichen Gewinnwerte die entsprechenden Verlustvariablen übersteigen, wurde der Gewinnfaktor mit 1,51 ermittelt. Natürlich reichen ein einmonatiger Testzeitraum und 65 Handelsgeschäfte nicht aus, um langfristige Stabilität zu garantieren. Die Ergebnisse übertreffen jedoch die mit der Traj-LLM-Methode erzielten.
Schlussfolgerung
Die in dieser Studie vorgestellte Methode UniTraj zeigt ihr Potenzial als vielseitiges Werkzeug zur Verarbeitung von Agententrajektorien in verschiedenen Szenarien. Mit diesem Ansatz wird ein zentrales Problem angegangen: die Anpassung von Modellen an mehrere Aufgaben, wodurch die Leistung im Vergleich zu herkömmlichen Methoden verbessert wird. Die einheitliche Handhabung von maskierten Eingabedaten macht UniTraj zu einer flexiblen und effizienten Lösung.
Im praktischen Teil haben wir die vorgeschlagenen Ansätze in MQL5 implementiert und in das Environmental State Encoder-Modell integriert. Wir haben die Modelle anhand echter historischer Daten trainiert und getestet. Die erzielten Ergebnisse zeigen die Effektivität der vorgeschlagenen Ansätze, sodass sie für die Entwicklung realer Handelsstrategien verwendet werden können.
Referenzen
Programme, die im diesem Artikel verwendet werden
| # | Name | Typ | Beschreibung |
|---|---|---|---|
| 1 | Research.mq5 | EA | EA-Beispielsammlung |
| 2 | ResearchRealORL.mq5 | EA | EA zum Sammeln von Beispielen mit der Real-ORL-Methode |
| 3 | Study.mq5 | EA | Trainings-EA des Modells |
| 4 | StudyEncoder.mq5 | EA | Trainings-EA des Encoders |
| 5 | Test.mq5 | EA | Modeltest-EA |
| 6 | Trajectory.mqh | Klassenbibliothek | Struktur der Systemzustandsbeschreibung |
| 7 | NeuroNet.mqh | Klassenbibliothek | Eine Bibliothek von Klassen zur Erstellung eines neuronalen Netzes |
| 8 | NeuroNet.cl | Code Base | OpenCL-Programmcode-Bibliothek |
Übersetzt aus dem Russischen von MetaQuotes Ltd.
Originalartikel: https://www.mql5.com/ru/articles/15648
Warnung: Alle Rechte sind von MetaQuotes Ltd. vorbehalten. Kopieren oder Vervielfältigen untersagt.
Dieser Artikel wurde von einem Nutzer der Website verfasst und gibt dessen persönliche Meinung wieder. MetaQuotes Ltd übernimmt keine Verantwortung für die Richtigkeit der dargestellten Informationen oder für Folgen, die sich aus der Anwendung der beschriebenen Lösungen, Strategien oder Empfehlungen ergeben.
 Entwicklung eines Replay-Systems (Teil 61): Den Dienst abspielen (II)
Entwicklung eines Replay-Systems (Teil 61): Den Dienst abspielen (II)
 Ensemble-Methoden zur Verbesserung von Klassifizierungsaufgaben in MQL5
Ensemble-Methoden zur Verbesserung von Klassifizierungsaufgaben in MQL5
 Von der Grundstufe bis zur Mittelstufe: IF ELSE
Von der Grundstufe bis zur Mittelstufe: IF ELSE
 Entwicklung des Swing Entries Monitoring (EA)
Entwicklung des Swing Entries Monitoring (EA)
- Freie Handelsapplikationen
- Über 8.000 Signale zum Kopieren
- Wirtschaftsnachrichten für die Lage an den Finanzmärkte
Sie stimmen der Website-Richtlinie und den Nutzungsbedingungen zu.