Do básico ao intermediário: Recursividade

Introdução

O conteúdo exposto aqui, visa e tem como objetivo, pura e simplesmente a didática. De modo algum deve ser encarado como uma aplicação final, onde o objetivo não seja o estudo dos conceitos aqui mostrados.

No artigo anterior Do básico ao intermediário: União (II), foi explicado como poderíamos utilizar uniões para conseguir resolver um problema do qual muitos dizem não ser possível de ser feito, ou mesmo resolvido, utilizando para isto MQL5 puro e simples.

Apesar de muitos de vocês, meus caros leitores, imaginarem que aquele tipo de coisa somente é possível de ser feita, sendo um programador extremamente experiente. Ao meu ver, e na minha maneira de entender as coisas. Aquele tipo de material visto é algo básico. Sendo perfeitamente possível de ser criado, por qualquer estudante de programação com nível básico de conhecimento.

Porém estamos em um momento em que as coisas começam a explodir, nos dando diversas possibilidades de uso e de coisas que podemos fazer. Mesmo que grande parte, ainda não se sinta seguro o suficiente para se aventurar em uma programação, que pode parecer um pouco ousada. Com base no que já foi mostrado, de fato é possível programar diversas coisas. Desde que não façamos uso de eventos. Já que ainda não foi explicado como trabalhar e utilizar os eventos de maneira adequada.

Lembrando mais uma vez, que o MetaTrader 5, é sim um programa baseado em eventos. E as aplicações que nele são executadas, também são baseadas em eventos. Salvo dois tipos que não utiliza normalmente eventos de maneira geral. Um são os scripts, que tem sido disponibilizado nos anexos. O outro são os serviços. No caso deste último iremos tratar dele em um momento mais oportuno. Já que mexer e programar serviços envolve conhecer em detalhes como o MetaTrader 5 funciona. Mas serviços de fato são um tipo de aplicação, que ao meu ver é o mais avançado que podemos criar voltados ao uso do MetaTrader 5.

Porém assim como estes dois, temos ainda os indicadores e Expert Advisor. Ambos são voltados a programação baseada em eventos. E no atual momento, não é adequado ainda falar dos mesmos. No entanto, temos outros temas para serem explicados. E eles ainda fazem parte do que considero a base para a formação de um bom profissional voltado ao mercado de programação.

Digo isto, pois muitos acreditam, já estar prontos para entrar neste mercado. Porém quanto são colocados a prova, falham de maneira miserável. E muitas vezes acham que o mundo foi injusto com eles. Porém a verdade é que eles não estavam devidamente preparados para enfrentar os desafios que um bom programador consegue lidar. E isto de maneira simples, rápida e eficiente.

Um laço especial

Ok, durante alguns artigos, expliquei comandos voltados a trabalhar com laços. Basicamente no MQL5, assim como em diversas outras linguagens, temos três deles. Os primeiros e ao meu ver mais simples são os comandos while e o casal do while. Além destes dois, temos também o comando for. Porém, toda via e, entretanto, existe uma quarta forma de se criar laços. Sendo esta disponível em quase todas linguagens de programação. Pelo menos a única linguagem que me lembro não ter como utilizar esta quarta forma, foi o BASIC. Isto por que BASIC não é uma linguagem estruturada. Voltada a trabalhar com funções e procedimentos. Mas isto não nos importa e não nos interessa aqui. Já que estamos mexendo com MQL5. E sendo esta linguagem, uma linguagem estruturada. Podemos utilizar funções e procedimentos dentro dela. E isto nos permite utilizar o que é a quarta forma de se criar um laço.

Normalmente laços são criados de duas maneiras. Usando os comandos voltados para isto, e usando uma função ou procedimento. Sim, meu caro leitor, parece bem maluco usar uma função ou procedimento para se criar um laço. Mas isto por incrível que possa parecer, é muito mais comum do que você imagina.

Quando usamos um comando voltado para criar interações a fim de obter um laço. Dizemos que estamos utilizando um modo interativo, de efetuar as interações. E quando usamos funções ou procedimentos para o mesmo objetivo, dizemos que estamos utilizando um modo recursivo. Saber e entender como se criar esta recursividade é algo que todo iniciante deveria de fato procurar aprender. Isto pelo simples motivo, de que um laço recursivo é consideravelmente mais simples de entender do que um laço interativo.

Mas então, por que somente agora estou falando sobre isto? O motivo, é que para entender com criar e como utilizar este aparato, que é o uso da recursividade em seus códigos. Demanda um bom domínio sobre certas coisas. Como utilização do comando if, assim como um bom entendimento sobre variáveis e constantes. Tempo de vida, transferência de valores. Mas principalmente um bom domínio sobre os tipos de dados e suas limitações. Já que dependendo do que será feito, precisamos escolher da melhor maneira possível qual o tipo mais adequado em determinados casos. Isto para evitar ambiguidades que possam a vir a prejudicar uma interação recursiva.

Perceba o seguinte meu caro leitor. Diferente de um laço interativo, onde tudo é feito ali perto, do código que estamos utilizando. Um laço recursivo, pode ter o seu ponto chave em um procedimento ou função muito distante de onde realmente estamos olhando no código. E se algum tipo e erro ou falha vier a acontecer, muitas das vezes você terá que navegar por todo o código até chegar ao ponto onde tudo irá de fato começar a retornar. E nem sempre isto é uma tarefa do qual iniciantes costumam dar conta de resolver. Isto por conta da própria natureza da recursividade. Pois ela não parece de fato, ser o que realmente é. Ou seja, um laço. Só que um laço do tipo especial.

Para começar a entender isto melhor. Precisamos partir para um exemplo. Mas antes de fazer isto, um último recado: Todo laço interativo, pode ser refeito como sendo um laço recursivo. E todo laço recursivo, pode ser feito como sendo um laço interativo. Porém o nível de dificuldade envolvida para tornar um em outro. Depende da própria natureza do laço. Mas no geral, laços interativos são mais rápidos durante a fase de execução do código. Porém os laços recursivos são mais simples de programar. Então uma coisa compensa a outra. O tempo que se gasta para transformar um laço recursivo em um interativo, pode não valer o ganho em termos de performance da aplicação. Então no geral, vale a regra do bom senso e do menor custo possível. Dito isto, podemos começar.

E vamos começar com um exemplo bem simples para ser fácil de entender como a coisa acontece na prática. Este é visto logo abaixo.

01. //+------------------------------------------------------------------+
02. #property copyright "Daniel Jose"
03. //+------------------------------------------------------------------+
04. void OnStart(void)
05. {
06.     Recursive(5);
07. }
08. //+------------------------------------------------------------------+
09. void Recursive(uchar arg)
10. {
11.     Print(__FUNCTION__, " ", __LINE__, "  :: ", arg);
12.     arg--;
13.     if (arg > 0)
14.         Recursive(arg);
15.     Print(__FUNCTION__, " ", __LINE__, "  :: ", arg);
16. }
17. //+------------------------------------------------------------------+

Código 01

Quando executado este código 01, irá gerar o que você pode observar na imagem logo abaixo.

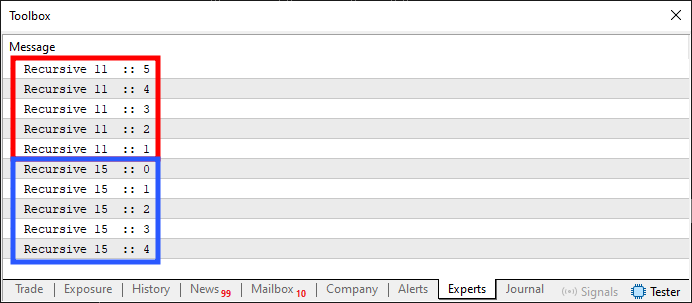
Imagem 01

Mas que coisa maluca foi esta? Bem, meu caro leitor, é isto que uma rotina recursiva de fato faz. Parece ser algo bem maluco. Porém isto muitas das vezes é exatamente o que queremos e procuramos fazer. Veja que este mesmo resultado visto na imagem 01, poderia ser conseguido utilizando laços. Mas foi conseguido usando justamente algo que em programação é chamado de recursividade. Ou seja, quando uma função ou procedimento chama a sim ou outra, com intuito de criar um laço entre elas. Muitos colocam a recursividade como algo inerente a somente uma função ou procedimento. Porém, ela não necessariamente está ligada a isto. O único critério que precisa ser atendido é que exista um laço, sem que façamos uso de um comando voltado a criar um laço. Um outro exemplo de recursividade bastante interessante é visto logo abaixo.

01. //+------------------------------------------------------------------+
02. #property copyright "Daniel Jose"
03. //+------------------------------------------------------------------+
04. void OnStart(void)
05. {
06.     Print("Result: ", Fibonacci(7));
07. }
08. //+------------------------------------------------------------------+
09. uint Fibonacci(uint arg)
10. {
11.     if (arg <= 1)
12.         return arg;
13. 
14.     Print(__FUNCTION__, " ", __LINE__, "  :: ", arg);
15. 
16.     return Fibonacci(arg - 1) + Fibonacci(arg - 2);
17. }
18. //+------------------------------------------------------------------+

Código 02

Talvez este seja o exemplo mais típico, quando se estuda recursividade. Isto por que este código 02, exemplifica muito bem o que seria a recursividade. Ao executar este código, teremos o resultado visto logo abaixo.

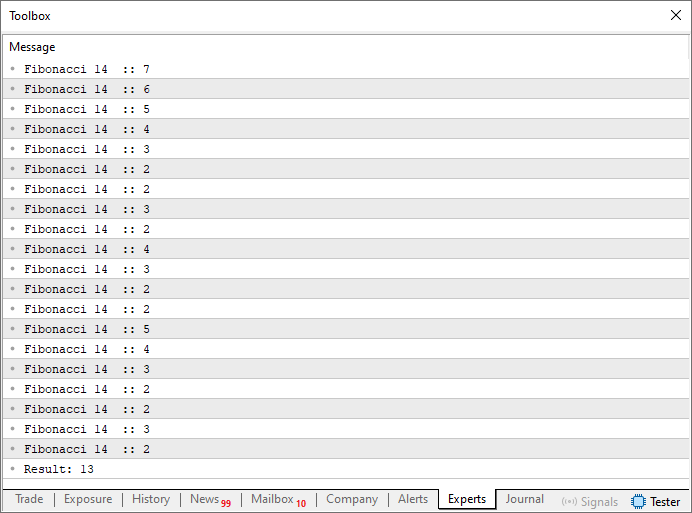
Imagem 02

Ou seja, o sétimo valor na sequência de Fibonacci é o treze. E de fato, se você olhar, ou já conhecer a sequência, sabe que este é mesmo o sétimo valor na sequência. Mas por que este código funcionou, a ponto de calcular o sétimo valor? Sinceramente não estou conseguindo entender como isto foi possível. Bem meu caro leitor, o motivo é que na linha 16, temos o que seria a fatoração mínima que precisa ser feita a fim de conseguir calcular o valor de Fibonacci. Se você procurar a expressão matemática, que de fato permite calcular o valor de Fibonacci, irá ver algo do tipo mostrado logo abaixo.

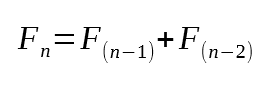
Imagem 03

Agora olhe novamente a linha 16. Consegue notar alguma semelhança entre a expressão matemática da imagem 03 com esta linha 16? Isto é que usamos para criar uma rotina recursiva. Ou seja, reduzimos o trabalho até encontrar um ponto onde a resposta venha a convergir para um valor mínimo. E que valor mínimo é este? Bem, meu caro leitor, no caso da sequência Fibonacci, este valor pode ser zero ou um. E é isto que estamos testando na linha 11.

Repare o seguinte fato: Da mesma maneira que o código 01, fizemos uma contagem, primeiro regressiva e logo depois aparentemente uma contagem progressiva. A mesma coisa acontece aqui no código 02. Só que em duas etapas. A primeira etapa é quando iremos calcular o valor de arg menos um. Então fazemos uma serie de chamadas até que a linha 12 seja executada. A cada chamada feita, a linha 14 será executada, e nos mostrará qual o valor em arg. Por conta disto temos no primeiro momento uma sequência regressiva em uma unidade. Logo tudo isto irá retornar e teremos a chamada seguindo uma redução em duas unidades. Sei que aparece muito complicado entender isto. Então vamos mudar alguns pontos no código 02, a fim de tornar mais simples de visualizar, como de fato este código 02, consegue fazer com que o cálculo aconteça e o resultado correto possa ser obtido. Para isto vamos usar o código visto logo abaixo.

01. //+------------------------------------------------------------------+
02. #property copyright "Daniel Jose"
03. //+------------------------------------------------------------------+
04. void OnStart(void)
05. {
06.     Print("Result: ", Fibonacci(5, 0, 0));
07. }
08. //+------------------------------------------------------------------+
09. uint Fibonacci(uint arg, uint call, int who)
10. {
11.     uint value = 0;
12. 
13.     Print(__FUNCTION__, " ", __LINE__, " Entry point [ ", call," ]  ARG: ", arg, " WHO: ", who);
14. 
15.     if (arg <= 1)
16.     {
17.         Print(__FUNCTION__, " ", __LINE__, " Number Callback [ ", call," ]  ARG: ", arg, " WHO: ", who);
18. 
19.         return arg;
20.     }
21. 
22.     value += Fibonacci(arg - 1, call + 1, 1);
23. 
24.     Print(__FUNCTION__, " ", __LINE__, " Value = ", value, "  >> New call with arg: ", arg);
25. 
26.     value += Fibonacci(arg - 2, call + 1, 2);
27. 
28.     Print(__FUNCTION__, " ", __LINE__, " General Return = ", value);
29. 
30.     return value;
31. }
32. //+------------------------------------------------------------------+

Código 03

Neste momento peço desculpas a todos. Mas infelizmente não tem outra maneira de explicar, e mostrar de uma forma mais fácil, o que de fato está ocorrendo aqui. Sendo assim a imagem da execução deste código 03 é mostrada logo abaixo.

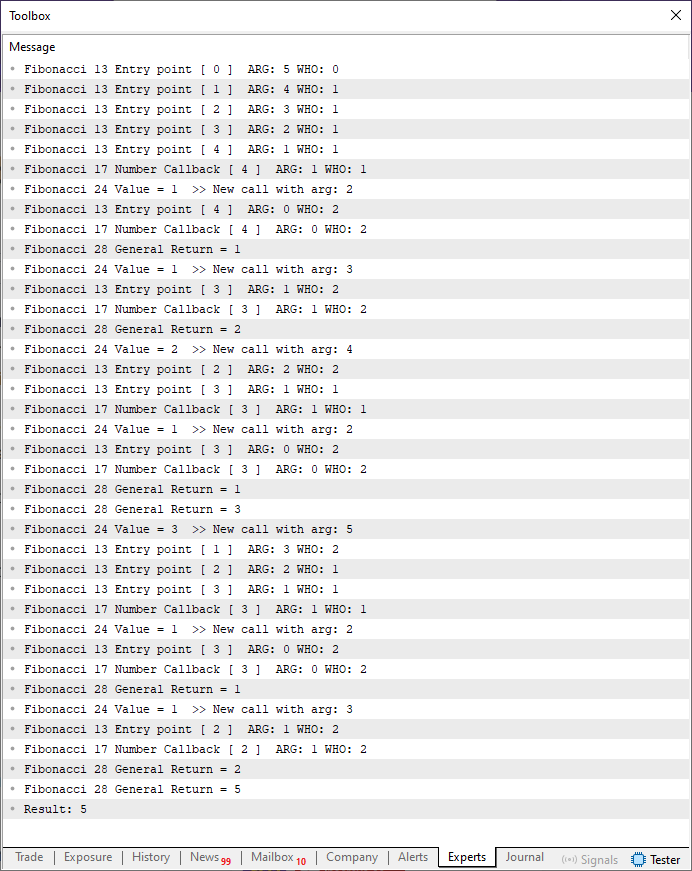
Imagem 04

Sei que esta imagem 04 é um tanto quanto comprida. Porém, é necessário notar que mudei a execução de sete para cinco elementos. O que pode não parecer muito, mas diminui bastante a quantidade de coisas para serem observadas aqui. Mas ainda assim, você precisa entender o seguinte meu caro leitor. Cada vez que a linha 13 é executada, significa que estamos entrando na função. E que podemos ter um retorno imediato, ou uma nova chamada. Porém uma coisa que neste primeiro momento pode parecer estranha, é justamente o valor da linha 11. Muitos podem imaginar que isto irá atrapalhar o resultado final. No entanto, se você pensa assim, é por que não tem a devida noção do que a recursividade de fato faz com a função ou procedimento onde ela é aplicada.

Devido justamente a isto, é que estou mostrando nesta imagem 04, de maneira o mais detalhada possível, o que está ocorrendo. Isto a ponto de fazer com que o código 02 consiga calcular o valor correto.

Ok, como é necessário prestar atenção ao que será explicado. Peço para você, meu caro e estimado leitor, de remova qualquer tipo de distração, ou algo que possa lhe distrair, durante esta explicação. Isto por que, funções ou procedimentos recursivos são bem fáceis de se tornarem confusos no primeiro contato que estamos tendo com este tipo de programação.

Então com base na imagem 04, vamos entender o que está de fato ocorrendo aqui. Primeiro, quando a linha seis é executada, estaremos chamando a função Fibonacci como se esta fosse de fato um laço. Não um laço interativo, mas um laço recursivo. Este é o primeiro ponto que você precisa de fato compreender.

O próximo ponto, é entender que precisamos de uma condição limitadora. Assim como aconteceu no código 01. Todo e qualquer laço, que pretenda utilizar recursividade, precisa de uma condição limite. No caso a condição limite é a que está sendo definida na linha 15. Eu sei, que foi dito que a recursividade, precisa ficar reduzida a uma expressão simples. Porém quem de fato evita de que um laço recursivo, venha de fato a se tornar um laço infinito, é a condição de limite. Uma coisa nada tem a ver com a outra. Cuidado, para não utilizar os conceitos de maneira errada. Então novamente: 

Quem gera a recursividade é a implementação de uma expressão matemática mínima. Mas quem limita a recursividade é a condição que evita o surgimento do laço infinito.

Assim sendo, quem limita a recursividade, no código 04 é a linha 15. Quem cria a recursividade, são as linhas 22 e 26. Já no código 02, a limitação seria a linha 11 e quem estaria criando a recursividade seria a linha 16.

Ok, então vamos entender como isto de fato funciona. Como nosso argumento inicial é igual a cinco. Teremos a execução da linha 13 logo depois, a linha 22. Ao fazermos isto, esta linha 22 irá chamar novamente a linha nove, criando assim um loop. Porém preste atenção ao fato de que durante a chamada na linha 22, estaremos reduzindo o argumento em uma unidade. Então nossa pilha começará a ser construída. Chamada após chamada até que em algum momento, a linha 15 se tornará verdadeira.

Neste momento temos algo interessante acontecendo. Pois, estaremos executando a quarta chamada, empilhando valores cada vez menores no argumento. Então quando a linha 15 for verdadeira, a linha 17 será executada, nos mostrando qual o valor atual no argumento. Assim como qual está sendo o número de chamadas naquele exato momento. Como o valor é igual a um, retornamos este valor para o chamador. Porém o chamador NÃO É A LINHA SEIS. Mas sim a linha 22. Lembre-se de que empilhamos uma serie de chamadas. Agora começamos a desempilhar as mesmas. Com isto o primeiro valor retornado é um, sendo ele somado a variável value. E esta variável não irá perder seu valor entre as chamadas. Mas irá montar um novo valor a cada nova chamada. Para entender isto melhor, seria necessário explicar como uma pilha funciona. Mas este tipo de coisa, ao meu entender é algo um pouco mais avançado. Porém isto não irá lhe impedir de entender como a recursividade funciona. É só prestar atenção.

Ok, então já calculamos qual seria o primeiro valor. No entanto, pela expressão mostrada na imagem 03, temos que calcular novamente a função da linha nove. Por conta disto, temos uma nova chamada, que neste caso se encontra na linha 26. Agora preste muita, mas muita atenção mesmo, senão será impossível entender a recursividade de funções compostas, como esta que calcula o Fibonacci.

A chamada da linha 22, foi reduzindo o valor de arg de um em um. Porém, quando arg foi igual a um, na chamada seguinte. O valor de arg, presente na linha 22, ou seja, na chamada anterior, continua sendo igual a dois. Assim quando a linha 24 for executada, devido ao fato de que arg era igual a um, na chamada da linha 22. Não estaremos de fato lidando com arg na linha 24 igual a um, mas sim igual a dois.

Este tipo de coisa, na primeira vez que se ouve falar, é muito confusa. Sei disto. E justamente por conta disto, estou usando a recursividade mais simples que existe. Assim como também, mostrei o que acontece no código 01. Onde executamos uma contagem regressiva em um primeiro momento e depois, uma contagem progressiva. Porém a contagem progressiva somente surgir devido ao fato de que havíamos empilhado valores. Assim quando começamos a desempilhar estes mesmos valores, tivemos a ilusão de que uma contagem progressiva acabou ocorrendo. Sendo que na verdade ela não foi de fato implementada. Tudo foi devido a uma condição própria do uso de chamadas recursivas.

Muito bem, então vamos com calma. Na chamada da linha 26, neste exato momento, arg é igual a dois. Porém, como estamos reduzindo arg em duas unidades, antes de chamarmos novamente a função. Quando a linha 13 for executada, teremos um valor igual a zero. Neste caso a linha 15 será verdadeira e a função irá retornar. Com isto a linha 28 irá imprimir um valor igual a um. Ou seja, calculamos o Fibonacci do primeiro elemento da sequência.

Agora lembre-se, empilhamos cinco chamadas, e somente retornamos da primeira. Assim agora na linha 22, teremos value igual a um. Mas espere, ela já não era igual a um? Não meu caro leitor. A variável value era igual a um na chamada que acabamos de finalizar. Como a função retornou, agora voltamos a linha 22. E antes disto value era igual a zero. Agora ela é igual a um. Com isto, executamos a linha 24. E como desempilhamos uma chamada, agora arg é igual a dois. Isto na linha 24. Não perca o fio da meada. Bem, como arg é igual a dois, e precisamos executar a linha 26, onde iremos subtrair duas unidades deste argumento. Agora a função irá receber arg igual a zero. Mas WHO igual a dois. Isto por que estamos fazendo a chamada pela linha 26.

Como arg é igual a zero. Então a linha 15 é verdadeira e retornamos zero na linha 19. Agora, como voltamos a linha 26, somamos o valor um calculado anteriormente com este novo valor zero. Com isto temos o valor igual a um. Ou seja, acabamos de calcular o segundo elemento da sequência Fibonacci.

E voltamos para a linha 22, já que desempilhamos apenas dois valores, precisamos desempilhar cinco. Com o valor um sendo atribuído a variável value. Mas arg agora é igual a três. Esta agora é a parte realmente interessante. Isto por que como arg é igual a três, ao subtrairmos dois na linha 26, teremos a função recebendo o valor um. E como isto tornar verdadeira a linha 15, iremos retornar um na linha 19. Assim a variável value agora é igual a dois.

E conseguimos desta forma calcular o que seria o terceiro elemento da sequência. Falta desempilhar outros dois elementos. Novamente voltamos a linha 22, só que agora esta variável value é igual a dois. E arg é igual a quatro. Bem o que vai acontecer quando a linha 26 for executada. Adivinha? A função Fibonacci, será chamada novamente, mas agora com arg igual a dois. Lembre-se de que subtraímos dois na linha 26 antes de chamar a função.

Ok, como arg neste momento é igual a dois, a linha 15 irá falhar, fazendo com que a linha 22 seja executada mais uma vez. Só que neste ponto a variável value é igual a zero, e não igual a dois. Este outro valor foi armazenado na pilha. Muito bem, como arg é igual a dois, e precisamos subtrair um antes de efetuar a chamada, termos arg igual a um na linha 15, e retornamos um. Agora value na linha 22 é um, e a linha 26 será executada. Neste ponto arg que é dois, será subtraída de dois, e a função será chamada. Como já se sabe, isto irá retornar zero. E a linha 30 irá fazer com que o valor um seja retornado. Mas retornado para onde? Bem, meu caro leitor, será retornado para a linha 26, que fez a chamada. Lembre-se de que neste momento value é igual a dois. Como o retorno foi um, agora value é igual a três. E com isto acabamos de calcular o que seria o quarto elemento da sequência. Falta um. (RISOS)

Аcredito que seu cérebro tá começando a se embananar, com estes retornos e chamadas. Mas neste último elemento, vamos fazer diferente. Já que tudo será uma imensa repetição dos passos. Isto por que, agora na linha 26, o valor de arg é igual a cinco e value é igual a três. Como arg, precisará ser subtraído de dois e teremos uma serie nova de chamadas. Tudo que você precisa entender acredito que foi explicado.

Mas como você pode ter notado. Existe uma questão que foi dita no começo deste artigo. Que é justamente o fato de que a recursividade é simples de ser programada. Porém é mais lenta de ser executada. No entanto, podemos gerar um código equivalente que usa a interação ao invés de usar a recursividade. Com isto ganhamos em velocidade ao custo de tornar o código um pouco mais complexo.

Para provar isto, vamos ver como seria feito este tipo de código, cujo propósito é calcular a sequência Fibonacci. Existem diversa forma de se fazer isto. Mas logo abaixo, você pode ver uma destas maneiras.

01. //+------------------------------------------------------------------+
02. #property copyright "Daniel Jose"
03. //+------------------------------------------------------------------+
04. void OnStart(void)
05. {
06.     const uchar who = 6;
07. 
08.     Print("Result: ", Fibonacci_Recursive(who));
09.     Print("Result: ", Fibonacci_Interactive(who));
10. }
11. //+------------------------------------------------------------------+
12. uint Fibonacci_Recursive(uint arg)
13. {
14.     if (arg <= 1)
15.         return arg;
16. 
17.     return Fibonacci_Recursive(arg - 1) +  Fibonacci_Recursive(arg - 2);
18. }
19. //+------------------------------------------------------------------+
20. uint Fibonacci_Interactive(uint arg)
21. {
22.     uint v, i, c;
23. 
24.     for (c = 0, i = 0, v = 1; c < arg; i += v, c += 2)
25.         v += i;
26. 
27.     return (c == arg ? i : v);
28. }
29. //+------------------------------------------------------------------+

Código 04

Note que aqui estamos trabalhando com as duas maneiras de trabalhar com laços. A primeira é usando a recursividade, já a segunda é usando a interatividade. Pergunto: Qual você acha ser mais simples de entender? Dada esta resposta. Qual você acha que é a mais rápida em termos de tempo de execução? Isto levando em conta o que você já sabe sobre ambos métodos de se fazer o mesmo tipo de cálculo.

Como sei que muitos podem achar um tanto quanto estranho esta função interativa, que está sendo implementada na linha 20. Vou dar uma rápida explicada na mesma.

Na linha 22 declaramos as variáveis que iremos precisar. Já na linha 24 entramos no laço principal de cálculo. Esta daqui é a parte divertida. Observe que iniciamos os valores antes de efetuar qualquer cálculo. Agora veja o seguinte fato: Quando o elemento a ser buscado é ímpar, ou seja, se estamos procurando o primeiro, terceiro, quinto, sétimo elemento, e assim por diante, teremos o valor da variável v apontando para o valor correto. Porém, quando os elementos a serem buscados são pares, temos o valor de i apontando para o resultado correto. Mas por que?

O motivo é que, a variável c estará sendo incrementada de duas em duas unidades. Isto para que não ultrapassemos o resultado correto. Mas como a cada interação, teremos que somar o valor anterior com um novo valor, e não estamos fazendo a troca entre os valores de i e v. Temos este pequeno detalhe nesta função interativa. Existem forma de implementar a mesma, sem que tal questão venha a surgir. Porém acho desnecessário fazer isto. Já que a interação do laço, já me diz qual será o próximo valor e o valor atual. Sendo assim, tudo que preciso fazer é usar um operador ternário, para retornar o resultado correto. Sem que este pequeno ajuste fosse feito, poderíamos estar olhando para o próximo elemento da sequência ou para o antigo elemento da sequência. Tudo iria depender se o argumento, ou elemento buscado seria par ou ímpar. E se estaríamos usando o valor de i ou de v.

Como prova de que este código 04, de fato funciona. Logo na sequência, podemos ver a resposta da execução do mesmo. Para obter outros valores e assim testar ambas formas de calcular a serie Fibonacci. Basta mudar o valor da constante da linha seis. Mas lembre-se de outro detalhe: A serie Fibonacci, cresce de maneira muito rápida. E como existe limitações devido aos tipos utilizados. Tome cuidado para não exagerar, e querer ver um elemento muito distante. Pois irá acabar criando problemas no resultado final.

Imagem 05

Existem forma e maneiras de se corrigir isto. Nos permitindo mostrar qualquer valor numérico possível de ser colocado na memória de um computador. Mas como isto é um assunto, que ao meu ver é um pouco mais avançado. Vou deixar para mostrar isto em outro momento mais oportuno. Mas só para aguçar a sua curiosidade sobre o tema. Como você imagina que programadores, conseguem calcular o valor de PI, ou de outras constantes irracionais com milhares de casas decimais? Sendo que usando os tipos normalmente vistos em programas de computadores. Não temos como alcançar tal tipo de objetivo.

Como eu disse, este tipo de coisa é um pouco mais avançada. Necessitando que você entenda certos conceitos que ainda não foram explicados. Não que com o conhecimento já mostrado até aqui, isto não seja possível. Pois se isto fosse tido, seria uma grande mentira. Já que sim, é possível fazer isto, com os conceitos já mostrados até aqui, entre eles, este de usar recursividade. Porém o trabalho de implementar o código seria bem maior. Já que seria necessário adaptar certas coisas a um formato não muito natural de ser entendido logo de início.

Considerações finais

Este artigo, teve como objetivo apresentar um conceito de programação muito interessante e bem divertido. Porém que deve ser tratado com extremo respeito. Já que um mal uso, ou mal entendimento do que foi mostrado aqui, torna programas relativamente simples em algo desnecessariamente complicado. Porém o bom uso, e a perfeita adequação do que foi mostrado aqui, em situações igualmente adequadas. Torna a recursividade um grande aliado para resolver questões que de outra forma seria muito mais trabalhoso e demorado.

Como regra geral, use a recursividade sempre que for possível, ou tiver uma expressão matemática, na qual você não consegue enxergar uma forma interativa de a escrever. Mas lembre-se de que a grande quantidade de chamadas entre cada fatoração que precisa ser efetuada, pode tornar seu código mais lento que o normal. Quando isto ocorrer, procure tornar a recursividade em um laço interativo. Que apesar de ser mais complicado no princípio de ser criado. É consideravelmente mais rápido durante a execução do código. Ainda mais quando temos series de dados muito grandes para serem calculadas ou ajustadas de uma dada maneira.