Consultor Especialista Auto-Otimizável com MQL5 e Python (Parte V): Modelos de Markov Profundos

MetaTrader 5 — Exemplos | 18 agosto 2025, 07:06

Em nossa discussão anterior sobre Cadeias de Markov, vinculada aqui, mostramos como usar uma matriz de transição para entender o comportamento probabilístico do mercado. Nossa matriz de transição resumiu muitas informações para nós. Ela não apenas nos guiou sobre quando comprar e vender, como também nos informou se nosso mercado apresentava fortes tendências ou se era predominantemente de reversão à média. Na discussão de hoje, vamos mudar nossa definição de estado do sistema, das médias móveis usadas na nossa primeira discussão, para o Indicador de Força Relativa (RSI).

Quando a maioria das pessoas aprende a operar usando o RSI, é instruída a comprar sempre que o RSI atinge 30 e vender quando atinge 70. Alguns membros da comunidade podem questionar se essa é realmente a melhor decisão em todos os mercados. Todos sabemos que não se pode operar todos os mercados da mesma maneira. Este artigo mostrará como você pode construir suas próprias Cadeias de Markov para aprender, de forma algorítmica, regras de negociação ideais. E mais: as regras aprendidas ajustam-se dinamicamente aos dados que você coleta do mercado no qual pretende operar.

Visão Geral da Estratégia de Trading

O RSI é amplamente utilizado por analistas técnicos para identificar níveis extremos de preço. Normalmente, os preços de mercado tendem a reverter para suas médias. Portanto, sempre que analistas de preço encontram um ativo pairando em níveis extremos de RSI, eles normalmente apostam contra a tendência dominante. Essa estratégia foi levemente adaptada em muitas versões diferentes, todas derivadas de uma mesma fonte. A limitação dessa estratégia é que o que pode ser considerado um nível forte de RSI em um mercado não é necessariamente um nível forte para todos os mercados.

Para ilustrar esse ponto, a Fig. 1 abaixo mostra como o desvio padrão do valor do RSI evolui em 2 mercados diferentes. A linha azul representa o desvio padrão médio do RSI no mercado XPDUSD, enquanto a linha laranja representa o mercado NZDJPY. É amplamente conhecido, por todos os traders experientes, que o mercado de metais preciosos é significativamente volátil. Portanto, podemos ver uma disparidade clara nas mudanças dos níveis do RSI entre os dois mercados. O que pode ser considerado uma leitura alta de RSI em um par de moedas, como o par NZDUSD, pode ser considerado ruído de mercado comum ao negociar um instrumento mais volátil, como o XPDUSD.

Logo se torna evidente que cada mercado pode ter seu próprio nível de interesse no indicador RSI. Em outras palavras, ao utilizarmos o indicador RSI, o nível ótimo para entrar em uma operação depende do símbolo que está sendo negociado. Portanto, como podemos aprender, de forma algorítmica, em qual nível de RSI devemos comprar ou vender? Podemos empregar nossa matriz de transição para responder a essa pergunta para qualquer símbolo que tivermos em mente.

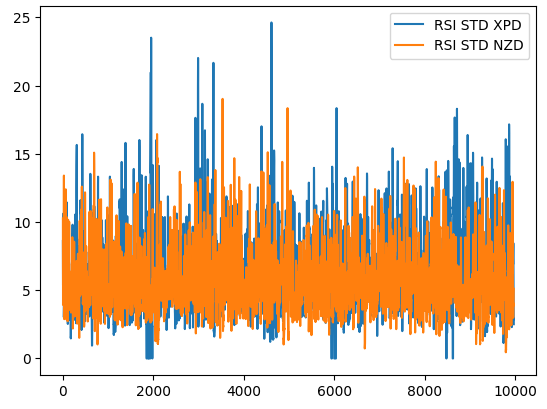
Fig 1: A volatilidade móvel do indicador RSI no mercado XPDUSD (linha azul) e no mercado NZDUSD (linha laranja).

Visão Geral da Metodologia

Para aprender nossa estratégia a partir dos dados que possuímos, primeiramente coletamos 300.000 linhas de dados M1 usando a biblioteca MetaTrader 5 para Python. Rotulamos os dados e, em seguida, dividimos em conjuntos de treino e teste. No conjunto de treino, agrupamos as leituras do RSI em 10 intervalos, de 0-10, 11-20, linearmente até 91-100. Registramos como o preço se comportou no futuro, ao passar por cada grupo no RSI. Os dados de treino mostraram que os preços tinham maior tendência de valorização sempre que passavam pela zona de 41-50 no RSI, e maior tendência de desvalorização na zona de 61-70.

Usamos essa matriz de transição estimada para construir um modelo ganancioso (“greedy”) que sempre selecionava o resultado mais provável a partir das distribuições anteriores. Nosso modelo simples obteve 52% de acurácia no conjunto de teste. Outra vantagem dessa abordagem é a sua interpretabilidade: conseguimos entender facilmente como o modelo toma decisões. Além disso, é cada vez mais comum que modelos de IA usados em setores importantes sejam explicáveis, e você pode ter certeza de que essa família de modelos probabilísticos não trará problemas de conformidade.

Avançando, nosso interesse não estava apenas na acurácia geral do modelo. Na verdade, estávamos interessados nas acurácias individuais das 10 zonas que identificamos no conjunto de treino. Nenhuma das 2 zonas que apresentaram maiores distribuições no treino se mostrou confiável na validação. No conjunto de validação, obtivemos a maior precisão ao comprar na faixa 11-20 e vender na faixa 71-80. Obtivemos níveis de acurácia de 51,4% e 75,8%, respectivamente. Selecionamos essas zonas como as ideais para abrir posições de compra e venda no par NZDJPY.

Por fim, criamos um Expert Advisor MQL5 que implementou os resultados da nossa análise em Python. Também implementamos 2 formas de encerrar posições no nosso aplicativo. Demos ao usuário a opção de fechar posições quando o RSI entrasse em uma zona que prejudicasse a posição aberta ou, alternativamente, encerrar quando o preço cruzasse a média móvel.

Coleta e Limpeza dos Dados

Vamos começar importando as bibliotecas necessárias.

#Let's get started
import MetaTrader5       as mt5
import pandas            as pd
import numpy             as np
import seaborn           as sns
import matplotlib.pyplot as plt
import pandas_ta         as ta

Verifique se o Terminal pode ser acessado.

mt5.initialize()

Verdadeiro

Defina algumas variáveis globais.

#Fetch market data
SYMBOL    = "NZDJPY"
TIMEFRAME = mt5.TIMEFRAME_M1

Copie os dados do nosso terminal.

data = pd.DataFrame(mt5.copy_rates_from_pos(SYMBOL,TIMEFRAME,0,300000))

Converta o formato de tempo de segundos.

data["time"]  = pd.to_datetime(data["time"],unit='s')

Calcule o RSI.

data.ta.rsi(length=20,append=True)

Defina até que ponto no futuro devemos fazer a previsão.

#Define the look ahead
look_ahead = 20

Rotule os dados.

#Label the data
data["Target"] = np.nan

data.loc[data["close"] > data["close"].shift(-20),"Target"] = -1
data.loc[data["close"] < data["close"].shift(-20),"Target"] = 1

Remova todas as linhas com valores ausentes dos dados.

data.dropna(inplace=True)
data.reset_index(inplace=True,drop=True)

Crie um vetor para representar os 10 grupos de valores do RSI.

#Create a dataframe 
rsi_matrix = pd.DataFrame(columns=["0-10","11-20","21-30","31-40","41-50","51-60","61-70","71-80","81-90","91-100"],index=[0])

É assim que nossos dados estão até o momento.

dados

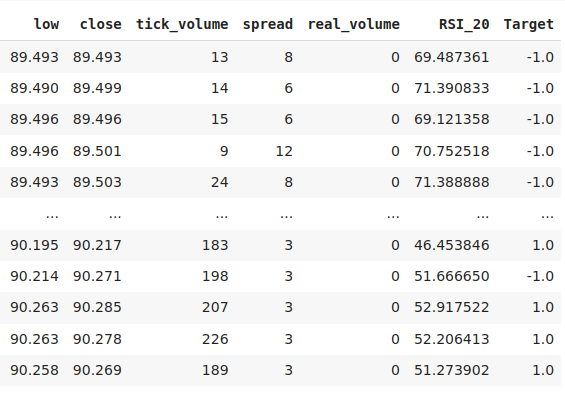
Fig 2: Algumas das colunas no nosso data-frame.

Inicialize a matriz do RSI com todos os valores 0.

#Initialize the rsi matrix to 0
for i in np.arange(0,9):
    rsi_matrix.iloc[0,i] = 0

Particione os dados.

#Split the data into train and test sets
train = data.loc[:(data.shape[0]//2),:]
test  = data.loc[(data.shape[0]//2):,:]

Agora, vamos percorrer o conjunto de treino e observar cada leitura do RSI e a respectiva variação futura nos níveis de preço. Se a leitura do RSI foi 11 e os níveis de preço se valorizaram 20 passos no futuro, incrementaremos em um o valor correspondente à coluna 11-20 na nossa matriz do RSI. Além disso, cada vez que os níveis de preço caírem, penalizaremos a coluna, decrementando seu valor em um. De forma intuitiva, percebemos rapidamente que, ao final, qualquer coluna com valor positivo corresponde a um nível de RSI que apresentou tendência de preceder aumentos nos preços; o oposto é verdadeiro para colunas com valores negativos.

for i in np.arange(0,train.shape[0]):
    #Fill in the rsi matrix, what happened in the future when we saw RSI readings below 10?
    if((train.loc[i,"RSI_20"] <= 10)):
        rsi_matrix.iloc[0,0] = rsi_matrix.iloc[0,0] + train.loc[i,"Target"]
    #What tends to happen in the future, after seeing RSI readings between 11 and 20?
    if((train.loc[i,"RSI_20"] > 10) & (train.loc[i,"RSI_20"] <= 20)):
        rsi_matrix.iloc[0,1] = rsi_matrix.iloc[0,1] + train.loc[i,"Target"]
    #What tends to happen in the future, after seeing RSI readings between 21 and 30?
    if((train.loc[i,"RSI_20"] > 20) & (train.loc[i,"RSI_20"] <= 30)):
        rsi_matrix.iloc[0,2] = rsi_matrix.iloc[0,2] + train.loc[i,"Target"]
    #What tends to happen in the future, after seeing RSI readings between 31 and 40?
    if((train.loc[i,"RSI_20"] > 30) & (train.loc[i,"RSI_20"] <= 40)):
        rsi_matrix.iloc[0,3] = rsi_matrix.iloc[0,3] + train.loc[i,"Target"]
    #What tends to happen in the future, after seeing RSI readings between 41 and 50?
    if((train.loc[i,"RSI_20"] > 40) & (train.loc[i,"RSI_20"] <= 50)):
        rsi_matrix.iloc[0,4] = rsi_matrix.iloc[0,4] + train.loc[i,"Target"]
    #What tends to happen in the future, after seeing RSI readings between 51 and 60?
    if((train.loc[i,"RSI_20"] > 50) & (train.loc[i,"RSI_20"] <= 60)):
        rsi_matrix.iloc[0,5] = rsi_matrix.iloc[0,5] + train.loc[i,"Target"]
    #What tends to happen in the future, after seeing RSI readings between 61 and 70?
    if((train.loc[i,"RSI_20"] > 60) & (train.loc[i,"RSI_20"] <= 70)):
        rsi_matrix.iloc[0,6] = rsi_matrix.iloc[0,6] + train.loc[i,"Target"]
    #What tends to happen in the future, after seeing RSI readings between 71 and 80?
    if((train.loc[i,"RSI_20"] > 70) & (train.loc[i,"RSI_20"] <= 80)):
        rsi_matrix.iloc[0,7] = rsi_matrix.iloc[0,7] + train.loc[i,"Target"]
    #What tends to happen in the future, after seeing RSI readings between 81 and 90?
    if((train.loc[i,"RSI_20"] > 80) & (train.loc[i,"RSI_20"] <= 90)):
        rsi_matrix.iloc[0,8] = rsi_matrix.iloc[0,8] + train.loc[i,"Target"]
    #What tends to happen in the future, after seeing RSI readings between 91 and 100?
    if((train.loc[i,"RSI_20"] > 90) & (train.loc[i,"RSI_20"] <= 100)):
        rsi_matrix.iloc[0,9] = rsi_matrix.iloc[0,9] + train.loc[i,"Target"]

Esta é a distribuição de contagens no conjunto de treino. Chegamos ao nosso primeiro problema: não houve observações de treino na zona 91-100. Portanto, decidi assumir que, como as zonas vizinhas resultaram em quedas nos preços, atribuiríamos a essa zona um valor negativo arbitrário.

rsi_matrix

0-10	11-20	21-30	31-40	41-50	51-60	61-70	71-80	81-90	91-100
4.0	47.0	221.0	1171.0	3786.0	945.0	-1159.0	-35.0	-3.0	NaN

Podemos visualizar essa distribuição. Parece que o preço passa a maior parte do tempo na zona 31-70. Isso corresponde à parte intermediária do RSI. Como mencionamos anteriormente, o preço mostrou-se muito altista na região 41-50 e baixista na região 61-70. No entanto, isso pareceu ser apenas um artefato dos dados de treino, já que essa relação não se confirmou nos dados de validação.

sns.barplot(rsi_matrix)

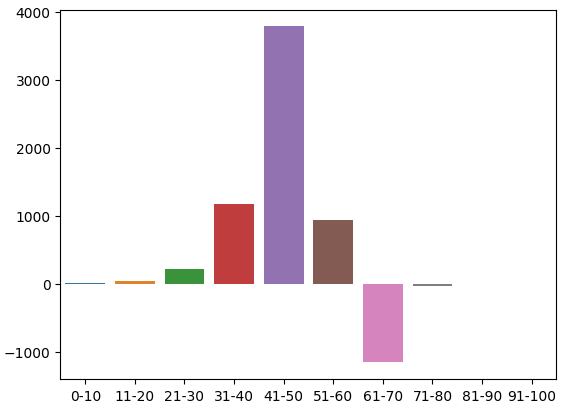
Fig 3: A distribuição dos efeitos observados das zonas do RSI.

Fig 4: Representação visual das transformações realizadas até agora.

Agora vamos avaliar a acurácia do nosso modelo nos dados de validação. Primeiro, redefina o índice dos dados de treino.

test.reset_index(inplace=True,drop=True)

Crie uma coluna para as previsões do nosso modelo.

test["Predictions"]  = np.nan

Preencha as previsões do nosso modelo.

for i in np.arange(0,test.shape[0]):
    #Fill in the predictions
    if((test.loc[i,"RSI_20"] <= 10)):
        test.loc[i,"Predictions"] = 1
    
    if((test.loc[i,"RSI_20"] > 10) & (test.loc[i,"RSI_20"] <= 20)):
        test.loc[i,"Predictions"] = 1
    
    if((test.loc[i,"RSI_20"] > 20) & (test.loc[i,"RSI_20"] <= 30)):
        test.loc[i,"Predictions"] = 1
        
    if((test.loc[i,"RSI_20"] > 30) & (test.loc[i,"RSI_20"] <= 40)):
        test.loc[i,"Predictions"] = 1

    if((test.loc[i,"RSI_20"] > 40) & (test.loc[i,"RSI_20"] <= 50)):
        test.loc[i,"Predictions"] = 1

    if((test.loc[i,"RSI_20"] > 50) & (test.loc[i,"RSI_20"] <= 60)):
        test.loc[i,"Predictions"] = 1

    if((test.loc[i,"RSI_20"] > 60) & (test.loc[i,"RSI_20"] <= 70)):
        test.loc[i,"Predictions"] = -1

    if((test.loc[i,"RSI_20"] > 70) & (test.loc[i,"RSI_20"] <= 80)):
        test.loc[i,"Predictions"] = -1

    if((test.loc[i,"RSI_20"] > 80) & (test.loc[i,"RSI_20"] <= 90)):
        test.loc[i,"Predictions"] = -1

    if((test.loc[i,"RSI_20"] > 90) & (test.loc[i,"RSI_20"] <= 100)):
        test.loc[i,"Predictions"] = -1

Valide se não temos valores nulos.

test.loc[:,"Predictions"].isna().any()

Falso

Vamos descrever a relação entre as previsões do nosso modelo e o alvo, usando pandas. A entrada mais comum é True, o que é um bom indicativo.

(test["Target"] == test["Predictions"]).describe()

count     148636
unique         2
top         True
freq       77409
dtype: object

Vamos estimar o quão preciso está o nosso modelo.

#Our estimation of the model's accuracy
((test["Target"] == test["Predictions"]).describe().freq / (test["Target"] == test["Predictions"]).shape[0])

0.5207957695309346

Estamos interessados na acurácia de cada uma das 10 zonas do RSI.

val_err = []

Registre nossa acurácia em cada zona.

val_err.append(test.loc[(test["RSI_20"] < 10) & (test["Predictions"] == test["Target"])].shape[0] / test.loc[test["RSI_20"] < 10].shape[0])
val_err.append(test.loc[((test["RSI_20"] <= 20) & (test["RSI_20"] > 10)) & (test["Predictions"] == test["Target"])].shape[0] / test.loc[((test["RSI_20"] <= 20) & (test["RSI_20"] > 10))].shape[0])
val_err.append(test.loc[((test["RSI_20"] <= 30) & (test["RSI_20"] > 20)) & (test["Predictions"] == test["Target"])].shape[0] / test.loc[((test["RSI_20"] <= 30) & (test["RSI_20"] > 20))].shape[0])
val_err.append(test.loc[((test["RSI_20"] <= 40) & (test["RSI_20"] > 30)) & (test["Predictions"] == test["Target"])].shape[0] / test.loc[((test["RSI_20"] <= 40) & (test["RSI_20"] > 30))].shape[0])
val_err.append(test.loc[((test["RSI_20"] <= 50) & (test["RSI_20"] > 40)) & (test["Predictions"] == test["Target"])].shape[0] / test.loc[((test["RSI_20"] <= 50) & (test["RSI_20"] > 40))].shape[0])
val_err.append(test.loc[((test["RSI_20"] <= 60) & (test["RSI_20"] > 50)) & (test["Predictions"] == test["Target"])].shape[0] / test.loc[((test["RSI_20"] <= 60) & (test["RSI_20"] > 50))].shape[0])
val_err.append(test.loc[((test["RSI_20"] <= 70) & (test["RSI_20"] > 60)) & (test["Predictions"] == test["Target"])].shape[0] / test.loc[((test["RSI_20"] <= 70) & (test["RSI_20"] > 60))].shape[0])
val_err.append(test.loc[((test["RSI_20"] <= 80) & (test["RSI_20"] > 70)) & (test["Predictions"] == test["Target"])].shape[0] / test.loc[((test["RSI_20"] <= 80) & (test["RSI_20"] > 70))].shape[0])
val_err.append(test.loc[((test["RSI_20"] <= 90) & (test["RSI_20"] > 80)) & (test["Predictions"] == test["Target"])].shape[0] / test.loc[((test["RSI_20"] <= 90) & (test["RSI_20"] > 80))].shape[0])
val_err.append(test.loc[((test["RSI_20"] <= 100) & (test["RSI_20"] > 90)) & (test["Predictions"] == test["Target"])].shape[0] / test.loc[((test["RSI_20"] <= 100) & (test["RSI_20"] > 90))].shape[0])

Plotando nossa acurácia. A linha vermelha é nosso ponto de corte de 50%; qualquer zona de RSI abaixo dessa linha pode não ser confiável. Podemos observar claramente que a última zona tem pontuação perfeita de 1. Entretanto, lembre-se de que isso corresponde à zona 91-100 ausente, que não ocorreu uma única vez em mais de 100.000 minutos de dados de treino que possuíamos. Portanto, essa zona provavelmente é rara e não é ideal para nossa necessidade de trading. A zona 11-20 tem níveis de acurácia de 75%, a mais alta entre as zonas altistas. O mesmo vale para a zona 71-80, que apresentou a maior acurácia entre todas as zonas baixistas.

plt.plot(val_err)
plt.plot(fifty,'r')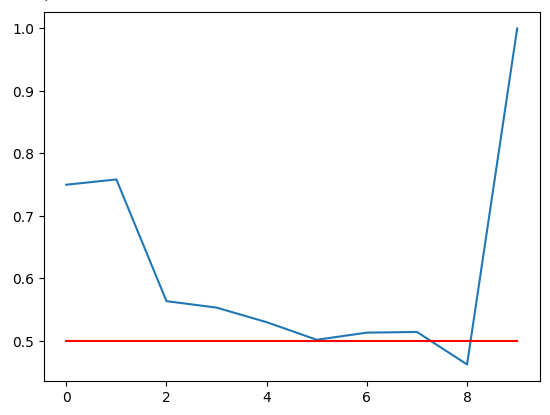

Fig 5: Visualizando nossa acurácia de validação

Nossa acurácia de validação ao longo das diferentes zonas do RSI. Note que obtivemos 100% de acurácia na faixa 91-100. Lembre-se de que nosso conjunto de treino tinha aproximadamente 100.000 linhas, mas não observamos leituras de RSI nessa faixa. Assim, podemos concluir que o preço raramente atinge esses extremos; portanto, esse resultado pode não ser uma decisão ideal para nós.

0-10	11-20	21-30	31-40	41-50	51-60	61-70	71-80	81-90	91-100
0.75	0.75	0.56	0.55	0.53	0.50	0.51	0.51	0.46	1.0

Construindo Nosso Modelo de Markov Profundo

Até agora, construímos apenas um modelo que aprende com a distribuição passada dos dados. Seria possível aprimorar essa estratégia empilhando um aprendiz mais flexível, para descobrir uma estratégia ótima de uso do nosso Modelo de Markov? Vamos treinar uma rede neural profunda e fornecer a ela as previsões feitas pelo Modelo de Markov como entradas; as mudanças observadas nos níveis de preço serão o alvo. Para realizar essa tarefa de forma eficaz, precisaremos subdividir nosso conjunto de treino em 2 metades. Ajustaremos nosso novo Modelo de Markov usando apenas a primeira metade do conjunto de treino. Nossa rede neural será ajustada nas previsões do Modelo de Markov sobre a primeira metade do treino e nas mudanças correspondentes dos níveis de preço.

Observamos que tanto nossa rede neural quanto nosso modelo simples de Markov superaram uma rede neural idêntica tentando aprender diretamente as variações dos níveis de preço a partir das cotações OHLC. Essas conclusões foram extraídas do nosso conjunto de teste, que não foi usado no procedimento de treinamento. Surpreendentemente, nossa rede neural profunda e nosso Modelo de Markov simples tiveram desempenho equivalente. Portanto, isso pode ser visto como um chamado para um esforço maior, a fim de superar o benchmark estabelecido pelo Modelo de Markov.

Vamos começar importando as bibliotecas de que precisamos.

#Let us now try find a machine learning model to learn how to optimally use our transition matrix
from sklearn.neural_network import MLPClassifier
from sklearn.metrics import accuracy_score
from sklearn.model_selection import train_test_split,TimeSeriesSplit

Agora, precisamos realizar um train-test split em nossos dados de treino.

#Now let us partition our train set into 2 halves 
train , train_val = train_test_split(train,shuffle=False,test_size=0.5)

Ajuste o modelo de Markov no novo conjunto de treino.

#Now let us recalculate our transition matrix, based on the first half of the training set
rsi_matrix.iloc[0,0] = train.loc[(train["RSI_20"] < 10) & (train["Target"] == 1)].shape[0] / train.loc[(train["RSI_20"] < 10)].shape[0]
rsi_matrix.iloc[0,1] = train.loc[((train["RSI_20"] > 10) & (train["RSI_20"] <=20)) & (train["Target"] == 1)].shape[0] / train.loc[((train["RSI_20"] > 10) & (train["RSI_20"] <=20))].shape[0]
rsi_matrix.iloc[0,2] = train.loc[((train["RSI_20"] > 20) & (train["RSI_20"] <=30)) & (train["Target"] == 1)].shape[0] / train.loc[((train["RSI_20"] > 20) & (train["RSI_20"] <=30))].shape[0]
rsi_matrix.iloc[0,3] = train.loc[((train["RSI_20"] > 30) & (train["RSI_20"] <=40)) & (train["Target"] == 1)].shape[0] / train.loc[((train["RSI_20"] > 30) & (train["RSI_20"] <=40))].shape[0]
rsi_matrix.iloc[0,4] = train.loc[((train["RSI_20"] > 40) & (train["RSI_20"] <=50)) & (train["Target"] == 1)].shape[0] / train.loc[((train["RSI_20"] > 40) & (train["RSI_20"] <=50))].shape[0]
rsi_matrix.iloc[0,5] = train.loc[((train["RSI_20"] > 50) & (train["RSI_20"] <=60)) & (train["Target"] == 1)].shape[0] / train.loc[((train["RSI_20"] > 50) & (train["RSI_20"] <=60))].shape[0]
rsi_matrix.iloc[0,6] = train.loc[((train["RSI_20"] > 60) & (train["RSI_20"] <=70)) & (train["Target"] == 1)].shape[0] / train.loc[((train["RSI_20"] > 60) & (train["RSI_20"] <=70))].shape[0]
rsi_matrix.iloc[0,7] = train.loc[((train["RSI_20"] > 70) & (train["RSI_20"] <=80)) & (train["Target"] == 1)].shape[0] / train.loc[((train["RSI_20"] > 70) & (train["RSI_20"] <=80))].shape[0]
rsi_matrix.iloc[0,8] = train.loc[((train["RSI_20"] > 80) & (train["RSI_20"] <=90)) & (train["Target"] == 1)].shape[0] / train.loc[((train["RSI_20"] > 80) & (train["RSI_20"] <=90))].shape[0]

rsi_matrix

0-10	11-20	21-30	31-40	41-50	51-60	61-70	71-80	81-90	91-100
1.0	0.655172	0.541701	0.536398	0.53243	0.516551	0.460306	0.491154	0.395349	0

Podemos visualizar essa distribuição de probabilidades. Lembre-se de que essas quantidades representam a probabilidade de os níveis de preço subirem 20 minutos à frente, depois que o preço tiver passado por cada uma das 10 zonas do RSI. A linha vermelha representa o nível de 50%. Todas as zonas acima de 50% são altistas; todas as zonas abaixo são baixistas. Isto é o que podemos assumir como verdadeiro, dada a primeira metade dos dados de treino.

#From the training set, it appears that RSI readings above 61 are bearish and RSI readings below 61 are bullish
plt.plot(rsi_matrix.iloc[0,:])
plt.plot(fifty,'r')

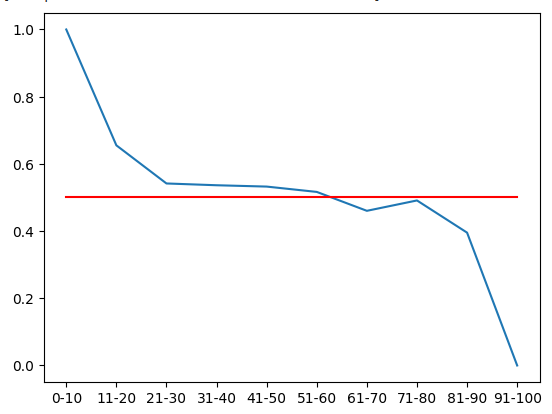
Fig 6: Pela primeira metade do conjunto de treino, parece que todas as zonas abaixo de 61 são altistas e acima de 61 são baixistas.

Registrando as novas previsões feitas pelo modelo de Markov.

#Let's now store our model's predictions
train["Predictions"] = -1
train.loc[train["RSI_20"] < 61,"Predictions"] = 1

train_val["Predictions"] = -1
train_val.loc[train_val["RSI_20"] < 61,"Predictions"] = 1

test["Predictions"] = -1
test.loc[test["RSI_20"] < 61,"Predictions"] = 1

Antes de começarmos a usar redes neurais, como regra geral, padronizar e escalar ajuda. Além disso, nosso RSI está em uma escala fixa de 0–100, enquanto nossas leituras de preço não têm limites. Nesses casos, a padronização é necessária.

#Let's Standardize and scale our data
from sklearn.preprocessing import RobustScaler

Defina nossas entradas e o alvo.

ohlc_predictors = ["open","high","low","close","tick_volume","spread","RSI_20"]
transition_matrix = ["Predictions"]
all_predictors = ohlc_predictors + transition_matrix
target = ["Target"]

Escalar os dados.

scaler = RobustScaler()
scaler =  scaler.fit(train.loc[:,predictors])
train_scaled = pd.DataFrame(scaler.transform(train.loc[:,predictors]),columns=predictors)
train_val_scaled = pd.DataFrame(scaler.transform(train_val.loc[:,predictors]),columns=predictors)
test_scaled = pd.DataFrame(scaler.transform(test.loc[:,predictors]),columns=predictors)

Crie dataframes para armazenar nossa acurácia.

#Create a dataframe to store our cv error on the training set, validation training set and the test set
train_err     = pd.DataFrame(columns=["Transition Matrix","Deep Markov Model","OHLC Model","All Model"],index=np.arange(0,5)) 
train_val_err = pd.DataFrame(columns=["Transition Matrix","Deep Markov Model","OHLC Model","All Model"],index=[0]) 
test_err      = pd.DataFrame(columns=["Transition Matrix","Deep Markov Model","OHLC Model","All Model"],index=[0])

Defina o objeto de divisão de série temporal (time-series split).

#Create a time series split object
tscv = TimeSeriesSplit(n_splits = 5,gap=look_ahead)

Faça a validação cruzada dos modelos.

model = MLPClassifier(hidden_layer_sizes=(20,10))
for i , (train_index,test_index) in enumerate(tscv.split(train_scaled)):
    #Fit the model
    model.fit(train.loc[train_index,transition_matrix],train.loc[train_index,"Target"])
    #Record its accuracy
    train_err.iloc[i,1] = accuracy_score(train.loc[test_index,"Target"],model.predict(train.loc[test_index,transition_matrix]))

#Record our accuracy levels on the validation training set
train_val_err.iloc[0,1] = accuracy_score(train_val.loc[:,"Target"],model.predict(train_val.loc[:,transition_matrix]))

#Record our accuracy levels on the test set
test_err.iloc[0,1] = accuracy_score(test.loc[:,"Target"],model.predict(test.loc[:,transition_matrix]))

#Our accuracy levels on the training set
train_err

Agora, vamos observar a acurácia do nosso modelo na metade de validação do conjunto de treino.

train_val_err.iloc[0,0] = train_val.loc[train_val["Predictions"] == train_val["Target"]].shape[0] / train_val.shape[0]
train_val_err

Matriz de Transição	Modelo de Markov Profundo	Modelo OHLC	Modelo Todos os Dados
0.52309	0.52309	0.507306	0.517291

Agora, mais importante, vamos ver nossa acurácia no conjunto de teste. Como podemos ver nas duas tabelas, nosso modelo híbrido de Markov Profundo não conseguiu superar o nosso modelo simples de Markov. Na minha opinião, isso foi surpreendente. Isso pode indicar que nosso procedimento para treinar a rede neural profunda não foi o ideal; alternativamente, podemos buscar em um conjunto mais amplo de modelos candidatos de machine learning. Outro ponto interessante dos nossos resultados é que o modelo que usou todos os dados não foi o que apresentou o melhor desempenho.

A boa notícia é que conseguimos superar o benchmark definido pela tentativa de prever o preço diretamente das cotações de mercado. Parece que as heurísticas simples do Modelo de Markov ajudam a rede neural a aprender rapidamente a estrutura de mercado em um nível mais básico.

test_err.iloc[0,0] = test.loc[test["Predictions"] == test["Target"]].shape[0] / test.shape[0]
test_err

Matriz de Transição	Modelo de Markov Profundo	Modelo OHLC	Modelo Todos os Dados
0.519322	0.519322	0.497127	0.496724

Implementando em MQL5

Para implementar nosso Expert Advisor baseado no RSI, começaremos importando as bibliotecas necessárias.

//+------------------------------------------------------------------+
//|                                                     Auto RSI.mq5 |
//|                                        Gamuchirai Zororo Ndawana |
//|                          https://www.mql5.com/en/gamuchiraindawa |
//+------------------------------------------------------------------+
#property copyright "Gamuchirai Zororo Ndawana"
#property link      "https://www.mql5.com/en/gamuchiraindawa"
#property version   "1.00"

//+------------------------------------------------------------------+
//| Libraries                                                        |
//+------------------------------------------------------------------+
#include <Trade\Trade.mqh>
CTrade Trade;

Agora, vamos definir nossas variáveis globais.

//+------------------------------------------------------------------+
//| Global variables                                                 |
//+------------------------------------------------------------------+
int rsi_handler;
double rsi_buffer[];
int ma_handler;
int system_state;
double ma_buffer[];
double bid,ask;

//--- Custom enumeration
enum close_conditions
  {
   MA_Close  = 0,
   RSI_Close
  };

Precisamos obter entradas do usuário.

//+------------------------------------------------------------------+
//| Inputs                                                           |
//+------------------------------------------------------------------+
input group "Technical Indicators"
input int rsi_period = 20; //RSI Period
input int ma_period = 20; //MA Period

input group "Money Management"
input double trading_volume = 0.3; //Lot size

input group "Trading Rules"
input close_conditions user_close = RSI_Close; //How should we close the positions?

Sempre que nosso Expert Advisor for carregado pela primeira vez, vamos carregar os indicadores e validá-los.

//+------------------------------------------------------------------+
//| Expert initialization function                                   |
//+------------------------------------------------------------------+
int OnInit()
  {
//--- Load the indicator
   rsi_handler = iRSI(_Symbol,PERIOD_M1,rsi_period,PRICE_CLOSE);
   ma_handler = iMA(_Symbol,PERIOD_M1,ma_period,0,MODE_EMA,PRICE_CLOSE);

//--- Validate our technical indicators
   if(rsi_handler == INVALID_HANDLE || ma_handler == INVALID_HANDLE)
     {
      //--- We failed to load the rsi
      Comment("Failed to load the RSI Indicator");
      return(INIT_FAILED);
     }

//---
   return(INIT_SUCCEEDED);
  }

Se nosso aplicativo não estiver em uso, libere os indicadores.

//+------------------------------------------------------------------+
//| Expert deinitialization function                                 |
//+------------------------------------------------------------------+
void OnDeinit(const int reason)
  {
//--- Release our technical indicators
   IndicatorRelease(rsi_handler);
   IndicatorRelease(ma_handler);
  }

Finalmente, se não houver posições abertas, siga as regras de negociação do nosso modelo. Caso contrário, se houver uma posição aberta, siga as instruções do usuário sobre como fechar as negociações.

//+------------------------------------------------------------------+
//| Expert tick function                                             |
//+------------------------------------------------------------------+
void OnTick()
  {
//--- Update market and technical data
   update();

//--- Check if we have any open positions
   if(PositionsTotal() == 0)
     {
      check_setup();
     }

   if(PositionsTotal() > 0)
     {
      manage_setup();
     }
  }
//+------------------------------------------------------------------+

A função a seguir fechará nossas posições dependendo se o usuário quer que usemos as regras de negociação aprendidas pelo RSI ou pela média móvel simples. Se o usuário quiser que usemos a média móvel, simplesmente fecharemos nossas posições sempre que o preço cruzar a média móvel.

//+------------------------------------------------------------------+
//| Manage our open setups                                           |
//+------------------------------------------------------------------+
void manage_setup(void)
  {
   if(user_close == RSI_Close)
     {
      if((system_state == 1) && ((rsi_buffer[0] > 71) && (rsi_buffer[80] <= 80)))
        {
         PositionSelect(Symbol());
         Trade.PositionClose(PositionGetTicket(0));
         return;
        }

      if((system_state == -1) && ((rsi_buffer[0] > 11) && (rsi_buffer[80] <= 20)))
        {
         PositionSelect(Symbol());
         Trade.PositionClose(PositionGetTicket(0));
         return;
        }
     }


   else
      if(user_close == MA_Close)
        {
         if((iClose(_Symbol,PERIOD_CURRENT,0) > ma_buffer[0]) && (system_state == -1))
           {
            PositionSelect(Symbol());
            Trade.PositionClose(PositionGetTicket(0));
            return;
           }

         if((iClose(_Symbol,PERIOD_CURRENT,0) < ma_buffer[0]) && (system_state == 1))
           {
            PositionSelect(Symbol());
            Trade.PositionClose(PositionGetTicket(0));
            return;
           }
        }
  }

A função a seguir verificará se temos setups válidos. Ou seja, se o preço entrou em alguma de nossas zonas lucrativas. Além disso, se o usuário tiver especificado que devemos usar a média móvel para encerrar as posições, então aguardaremos que o preço esteja do lado certo da média móvel antes de decidir abrir uma posição.

//+------------------------------------------------------------------+
//| Find if we have any setups to trade                              |
//+------------------------------------------------------------------+
void check_setup(void)
  {

   if(user_close == RSI_Close)
     {
      if((rsi_buffer[0] > 71) && (rsi_buffer[0] <= 80))
        {
         Trade.Sell(trading_volume,_Symbol,bid,0,0,"Auto RSI");
         system_state = -1;
        }

      if((rsi_buffer[0] > 11) && (rsi_buffer[0] <= 20))
        {
         Trade.Buy(trading_volume,_Symbol,ask,0,0,"Auto RSI");
         system_state = 1;
        }
     }

   if(user_close == MA_Close)
     {
      if(((rsi_buffer[0] > 71) && (rsi_buffer[0] <= 80)) && (iClose(_Symbol,PERIOD_CURRENT,0) < ma_buffer[0]))
        {
         Trade.Sell(trading_volume,_Symbol,bid,0,0,"Auto RSI");
         system_state = -1;
        }

      if(((rsi_buffer[0] > 11) && (rsi_buffer[0] <= 20)) && (iClose(_Symbol,PERIOD_CURRENT,0) > ma_buffer[0]))
        {
         Trade.Buy(trading_volume,_Symbol,ask,0,0,"Auto RSI");
         system_state = 1;
        }
     }
  }

Esta função atualizará nossos dados técnicos e de mercado.

//+------------------------------------------------------------------+
//| Fetch market quotes and technical data                           |
//+------------------------------------------------------------------+
void update(void)
  {
   bid = SymbolInfoDouble(_Symbol,SYMBOL_BID);
   ask = SymbolInfoDouble(_Symbol,SYMBOL_ASK);

   CopyBuffer(rsi_handler,0,0,1,rsi_buffer);
   CopyBuffer(ma_handler,0,0,1,ma_buffer);
  }
//+------------------------------------------------------------------+

Fig 7: Nosso Expert Advisor

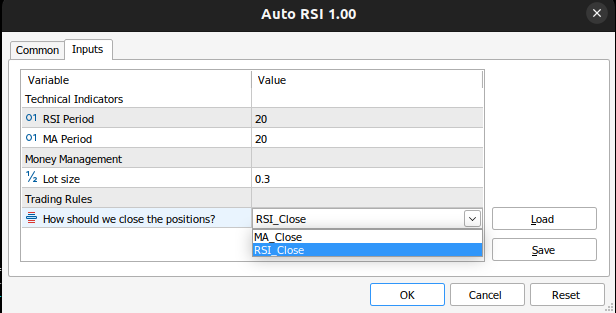
Fig 8: Nosso Aplicativo Expert Advisor

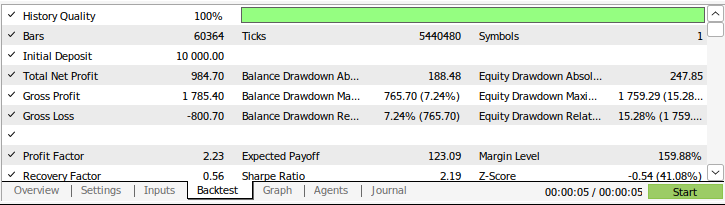
Fig 9: Os resultados do back-testing da nossa estratégia

Conclusão

Neste artigo, demonstramos o poder de modelos probabilísticos simples. Para nossa surpresa, não conseguimos superar o modelo simples de Markov tentando aprender com seus erros. No entanto, se você vem acompanhando esta série de artigos, provavelmente compartilha da minha visão de que estamos no caminho certo. Estamos acumulando, aos poucos, um conjunto de algoritmos que são mais fáceis de modelar do que o próprio preço, mantendo o mesmo nível de informação. Junte-se a nós nas próximas discussões, quando tentaremos entender o que será necessário para superar o modelo simples de Markov.

Traduzido do Inglês pela MetaQuotes Ltd.
Artigo original: https://www.mql5.com/en/articles/16030

Arquivos anexados |

Baixar como ZIP

RSI_Self_Optimizer.ipynb (131.78 KB)

Auto_RSI.mq5 (6.11 KB)

Aviso: Todos os direitos sobre esses materiais pertencem à MetaQuotes Ltd. É proibida a reimpressão total ou parcial.

This article was written by a user of the site and reflects their personal views. MetaQuotes Ltd is not responsible for the accuracy of the information presented, nor for any consequences resulting from the use of the solutions, strategies or recommendations described.

Outros artigos do autor

Últimos Comentários | Ir para discussão (2)

linfo2 | 8 out. 2024 em 20:51

Obrigado por seu esforço, é útil ter o vídeo também. Observe que seu link para o artigo anterior aparece com um erro 404 para mim

Gamuchirai Zororo Ndawana | 9 out. 2024 em 09:18

linfo2 #:
Obrigado por seu esforço, é útil ter o vídeo também. Observe que o link para o artigo anterior aparece com um erro 404 para mim

Olá, Neil, fico feliz que o vídeo tenha sido útil. Farei o possível para continuar anexando vídeos.

Desculpe pelo link inativo, ele passou despercebido, foi um erro meu.

Reimaginando Estratégias Clássicas (Parte IX): Análise de Múltiplos Time-Frames (II)

Na discussão de hoje, examinamos a estratégia de análise de múltiplos time-frames para descobrir em qual time-frame nosso modelo de IA apresenta melhor desempenho. Nossa análise nos levou a concluir que os time-frames Mensal e de 1 Hora produzem modelos com taxas de erro relativamente baixas no par EURUSD. Usamos isso a nosso favor e criamos um algoritmo de negociação que faz previsões de IA no time-frame Mensal e executa suas negociações no time-frame de 1 Hora.

De Iniciante a Especialista: Depuração Colaborativa em MQL5

A resolução de problemas pode estabelecer uma rotina concisa para dominar habilidades complexas, como programar em MQL5. Essa abordagem permite que você se concentre na resolução de problemas enquanto desenvolve suas habilidades ao mesmo tempo. Quanto mais problemas você resolver, mais conhecimento avançado será transferido para o seu cérebro. Pessoalmente, acredito que a depuração é a forma mais eficaz de dominar a programação. Hoje, vamos percorrer o processo de limpeza de código e discutir as melhores técnicas para transformar um programa desorganizado em um funcional e limpo. Leia este artigo e descubra insights valiosos.

Criando um EA em MQL5 com base na estratégia de Rompimento do Intervalo Diário (Daily Range Breakout)

Neste artigo, criamos um EA em MQL5 com base na estratégia de Rompimento do Intervalo Diário (Daily Range Breakout). Vamos abordar os conceitos-chave da estratégia, desenvolver o esquema do EA e implementar a lógica de rompimento em MQL5. Por fim, estudamos os métodos de backtest e otimização do EA para maximizar sua eficiência.

Simplificando a negociação com base em notícias (Parte 4): Aumentando o desempenho

Neste artigo, serão apresentados métodos para melhorar o desempenho do EA no testador de estratégias, além da implementação de um código para dividir o horário dos eventos de notícias em categorias por hora. O acesso a esses eventos será permitido apenas no horário especificado para cada um. Isso permite que o EA gerencie operações de maneira eficiente com base nos eventos, tanto em condições de alta quanto de baixa volatilidade.