Del básico al intermedio: Recursividad

Introducción

El contenido expuesto aquí tiene un propósito puramente didáctico. En ningún caso debe considerarse una aplicación final, cuyo objetivo no sea el estudio de los conceptos mostrados aquí.

En el artículo anterior Del básico al intermedio: Unión (II), se explicó cómo podríamos utilizar uniones para conseguir resolver un problema del cual muchos dicen que no es posible de hacer, o incluso de resolver, utilizando para ello MQL5 puro y simple.

Aunque muchos de ustedes, queridos lectores, piensen que ese tipo de cosas solo las puede hacer un programador extremadamente experimentado, en mi opinión, y según mi manera de entender las cosas, ese tipo de material es algo básico que puede crear cualquier estudiante de programación con unos conocimientos básicos.

Estamos en un momento en que las cosas empiezan a explotar, ofreciéndonos diversas posibilidades de uso y de cosas que podemos hacer, aunque gran parte de la gente todavía no se siente lo suficientemente segura para aventurarse en una programación que puede parecer un poco atrevida. Con base en lo que ya se ha mostrado, de hecho, es posible programar diversas cosas, siempre que no hagamos uso de eventos, ya que aún no se ha explicado cómo trabajar y utilizar los eventos de manera adecuada.

Recuerden, una vez más, que MetaTrader 5 es, sí, un programa basado en eventos, y las aplicaciones que se ejecutan en él también están basadas en eventos, salvo dos tipos que no utilizan eventos de manera general. Uno son los scripts, que se han ido incluyendo en los anexos. El otro son los servicios. En el caso de este último, lo trataremos en un momento más oportuno, ya que manipular y programar servicios implica conocer en detalle cómo funciona MetaTrader 5. De hecho, los servicios son un tipo de aplicación que, en mi opinión, es lo más avanzado que podemos crear orientado al uso de MetaTrader 5.

Aunque, al igual que estos dos, todavía disponemos de los indicadores y del Asesor Experto. Ambos están orientados a la programación basada en eventos y, en este momento, todavía no es adecuado hablar de ellos. Sin embargo, todavía quedan otros temas por explicar y estos siguen formando parte de lo que considero la base para la formación de un buen profesional orientado al mercado de la programación.

Digo esto porque muchos creen estar listos para entrar en este mercado, pero cuando se les pone a prueba, fallan estrepitosamente y a menudo piensan que el mundo ha sido injusto con ellos. Pero la verdad es que no estaban preparados para enfrentar los desafíos que un buen programador maneja de manera simple, rápida y eficiente.

Un bucle especial

Vale, en algunos artículos expliqué comandos orientados a trabajar con bucles. Básicamente, en MQL5, al igual que en otros muchos lenguajes, tenemos tres. Los primeros, y, en mi opinión, más simples, son los comandos while y do while. Además de estos dos, tenemos también el comando for. Sin embargo, existe una cuarta forma de crear bucles, disponible en casi todos los lenguajes de programación. Al menos, recuerdo que el único lenguaje que no permite utilizar esta cuarta forma es BASIC. Esto se debe a que BASIC no es un lenguaje estructurado, orientado a trabajar con funciones y procedimientos. Pero esto no nos importa ni nos interesa aquí, ya que estamos trabajando con MQL5, un lenguaje estructurado que nos permite utilizar funciones y procedimientos, y por tanto, la cuarta forma de crear un bucle.

Normalmente, los bucles se crean de dos maneras: mediante los comandos orientados para ello o mediante una función o procedimiento. Sí, mi querido lector, puede parecer una locura usar una función o procedimiento para crear un bucle, pero, por increíble que parezca, es mucho más común de lo que imaginas.

Cuando usamos un comando orientado a crear interacciones con el fin de obtener un bucle, decimos que estamos utilizando un modo interactivo de efectuar las interacciones. Y, cuando usamos funciones o procedimientos para el mismo objetivo, decimos que estamos utilizando un modo recursivo. Saber y entender cómo crear esta recursividad es algo que todo principiante debería aprender, ya que un bucle recursivo es considerablemente más sencillo de entender que un bucle interactivo.

Aunque entonces, ¿por qué estoy hablando de esto solo ahora? El motivo es que, para entender cómo crear y utilizar este recurso, es decir, la recursividad en tus códigos, se necesita un buen dominio de ciertas cosas, como la utilización del comando if, así como un buen entendimiento sobre variables y constantes, tiempo de vida, transferencia de valores, pero, principalmente, un buen dominio sobre los tipos de datos y sus limitaciones. Dependiendo de lo que se vaya a hacer, es necesario elegir el tipo más adecuado en cada caso. Esto es para evitar ambigüedades que puedan llegar a perjudicar la interacción recursiva.

Observa lo siguiente, mi querido lector: a diferencia de un bucle interactivo, donde todo se hace cerca del código que estamos utilizando, un bucle recursivo puede tener su punto clave en un procedimiento o función muy distante de donde realmente estamos mirando en el código. Y, si ocurre algún tipo de error o fallo, muchas veces tendrás que navegar por todo el código hasta llegar al punto donde todo comenzará a retornar. Y no siempre es una tarea que los principiantes puedan resolver, ya que se debe a la propia naturaleza de la recursividad, que no parece ser lo que realmente es. Es decir, un bucle, pero de tipo especial.

Para empezar a entenderlo mejor, veamos un ejemplo. Pero, antes de hacerlo, un último aviso: todo bucle interactivo puede rehacerse como un bucle recursivo, y todo bucle recursivo puede hacerse como un bucle interactivo. Aunque el nivel de dificultad de la conversión depende de la propia naturaleza del bucle. En general, los bucles interactivos son más rápidos durante la fase de ejecución del código. Sin embargo, los bucles recursivos son más sencillos de programar. Entonces, una cosa compensa la otra. El tiempo que se tarda en transformar un bucle recursivo en uno interactivo puede no compensar la ganancia en términos de rendimiento de la aplicación. En general, la regla del sentido común y del menor coste posible es la que debe aplicarse. Dicho esto, podemos comenzar.

Y vamos a empezar con un ejemplo bien simple, para que sea fácil de entender cómo sucede la cosa en la práctica. Este se muestra justo abajo.

01. //+------------------------------------------------------------------+
02. #property copyright "Daniel Jose"
03. //+------------------------------------------------------------------+
04. void OnStart(void)
05. {
06.     Recursive(5);
07. }
08. //+------------------------------------------------------------------+
09. void Recursive(uchar arg)
10. {
11.     Print(__FUNCTION__, " ", __LINE__, "  :: ", arg);
12.     arg--;
13.     if (arg > 0)
14.         Recursive(arg);
15.     Print(__FUNCTION__, " ", __LINE__, "  :: ", arg);
16. }
17. //+------------------------------------------------------------------+

Código 01

Cuando se ejecuta, este código 01 generará lo que puedes observar en la imagen que se muestra abajo.

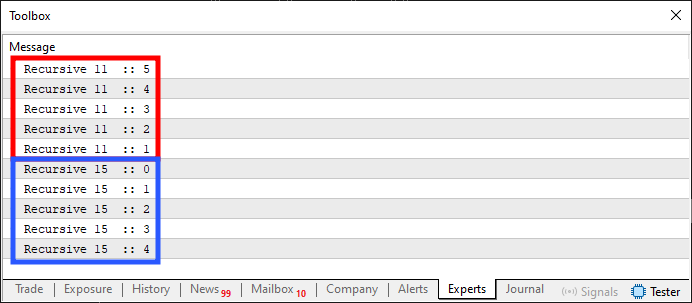
Imagen 01

Aunque, ¿qué locura fue esta? Bien, mi querido lector, esto es, de hecho, lo que hace una rutina recursiva. Parece una locura, pero muchas veces es precisamente lo que queremos y buscamos hacer. Observa que este mismo resultado que se muestra en la imagen 01 podría haberse conseguido utilizando bucles, pero se logró usando precisamente la recursividad. Es decir, cuando una función o procedimiento se llama a sí misma o a otra con el objetivo de crear un bucle entre ellas. Muchos consideran la recursividad como algo inherente solo a una función o procedimiento, aunque no necesariamente está ligada a esto. El único criterio que se debe cumplir es que exista un bucle, sin necesidad de utilizar un comando orientado a crear un bucle. Otro ejemplo de recursividad interesante se muestra justo debajo.

01. //+------------------------------------------------------------------+
02. #property copyright "Daniel Jose"
03. //+------------------------------------------------------------------+
04. void OnStart(void)
05. {
06.     Print("Result: ", Fibonacci(7));
07. }
08. //+------------------------------------------------------------------+
09. uint Fibonacci(uint arg)
10. {
11.     if (arg <= 1)
12.         return arg;
13. 
14.     Print(__FUNCTION__, " ", __LINE__, "  :: ", arg);
15. 
16.     return Fibonacci(arg - 1) + Fibonacci(arg - 2);
17. }
18. //+------------------------------------------------------------------+

Código 02

Este es quizá el ejemplo más típico de recursividad. Esto es así porque este código 02 ejemplifica muy bien lo que sería la recursividad. Al ejecutarlo, se obtiene el resultado que se muestra justo debajo.

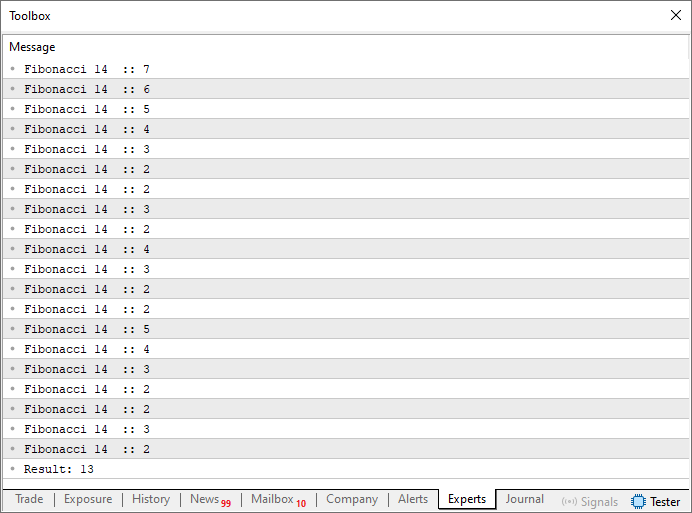
Imagen 02

Es decir, el séptimo valor de la secuencia de Fibonacci es el trece. Y, de hecho, si conoces la secuencia, sabes que este es realmente el séptimo valor. Pero ¿cómo consiguió este código calcular el séptimo valor? La verdad es que no consigo entender cómo fue posible. Bien, mi querido lector, el motivo es que, en la línea 16, tenemos la factorización mínima que se debe hacer para calcular el valor de Fibonacci. Si buscas la expresión matemática que permite calcular el valor de Fibonacci, verás algo similar a lo que se muestra a continuación.

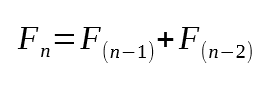
Imagen 03

Ahora, vuelve a mirar la línea 16. ¿Consigues notar alguna semejanza entre la expresión matemática de la imagen 03 y esta línea 16? Esto es lo que usamos para crear una rutina recursiva. Es decir, reducimos el trabajo hasta encontrar un punto en el que la respuesta converge hacia un valor mínimo. ¿Y cuál es este valor mínimo? Bien, mi querido lector, en el caso de la secuencia de Fibonacci, este valor puede ser cero o uno. Y esto es lo que estamos comprobando en la línea 11.

Observa el siguiente hecho: de la misma manera que en el código 01 hicimos una cuenta, primero regresiva y luego aparentemente progresiva, lo mismo sucede aquí en el código 02, solo que en dos etapas. La primera etapa es cuando calculamos el valor de arg menos uno. Para ello, hacemos una serie de llamadas hasta que se ejecute la línea 12. En cada llamada, se ejecuta la línea 14, que nos muestra cuál es el valor en arg. Por esta razón, tenemos una secuencia regresiva en una unidad. Luego, todo esto volverá y tendremos la llamada siguiendo una reducción en dos unidades. Sé que puede parecer complicado, así que cambiaré algunos puntos del código 02 para que sea más fácil entender cómo este código consigue hacer que el cálculo se realice correctamente. Para ello, usaremos el código que se muestra a continuación.

01. //+------------------------------------------------------------------+
02. #property copyright "Daniel Jose"
03. //+------------------------------------------------------------------+
04. void OnStart(void)
05. {
06.     Print("Result: ", Fibonacci(5, 0, 0));
07. }
08. //+------------------------------------------------------------------+
09. uint Fibonacci(uint arg, uint call, int who)
10. {
11.     uint value = 0;
12. 
13.     Print(__FUNCTION__, " ", __LINE__, " Entry point [ ", call," ]  ARG: ", arg, " WHO: ", who);
14. 
15.     if (arg <= 1)
16.     {
17.         Print(__FUNCTION__, " ", __LINE__, " Number Callback [ ", call," ]  ARG: ", arg, " WHO: ", who);
18. 
19.         return arg;
20.     }
21. 
22.     value += Fibonacci(arg - 1, call + 1, 1);
23. 
24.     Print(__FUNCTION__, " ", __LINE__, " Value = ", value, "  >> New call with arg: ", arg);
25. 
26.     value += Fibonacci(arg - 2, call + 1, 2);
27. 
28.     Print(__FUNCTION__, " ", __LINE__, " General Return = ", value);
29. 
30.     return value;
31. }
32. //+------------------------------------------------------------------+

Código 03

En este momento, les pido disculpas a todos, pero lamentablemente no hay otra manera de explicar y mostrar de forma más sencilla lo que está ocurriendo aquí. La imagen de la ejecución de este código 03 se muestra justo abajo.

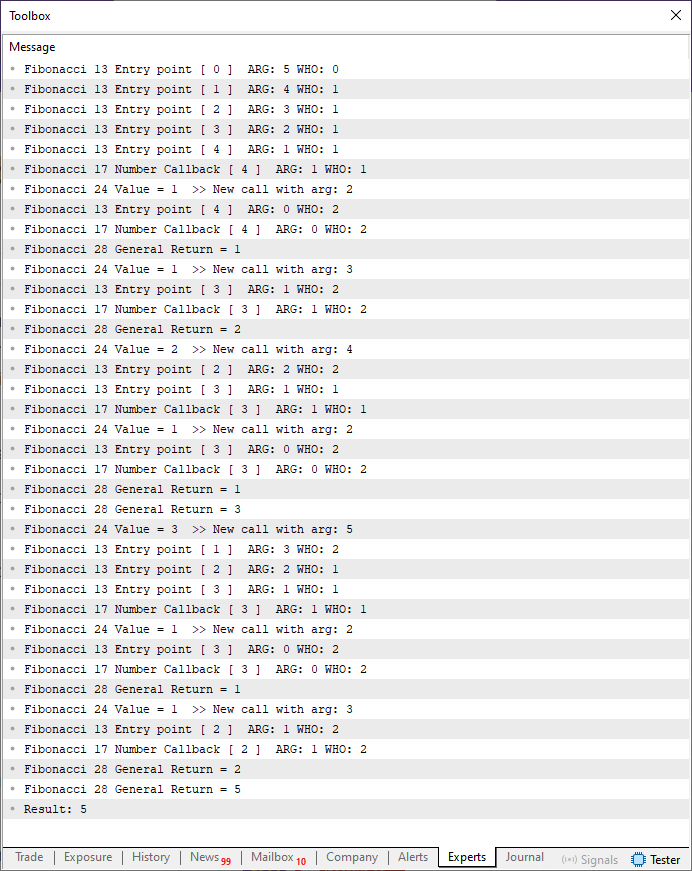
Imagen 04

Sé que la imagen 04 es algo extensa, aunque es necesario señalar que cambié la ejecución de siete a cinco elementos, lo que puede no parecer mucho, pero reduce bastante la cantidad de cosas que deben observarse aquí. Pero, aun así, necesitas entender lo siguiente, mi querido lector: cada vez que se ejecuta la línea 13, significa que estamos entrando en la función, y que podemos tener un retorno inmediato o una nueva llamada. Sin embargo, algo que puede parecer extraño en un primer momento es precisamente el valor de la línea 11. Muchos pueden imaginar que esto interferirá en el resultado final. Sin embargo, si piensas así, es porque no tienes claro qué hace la recursividad con la función o el procedimiento donde se aplica.

Precisamente por esta razón, en la imagen 04 muestro con todo detalle lo que está ocurriendo, hasta el punto de hacer que el código 02 logre calcular el valor correcto.

Vale, como es necesario prestar atención a lo que se explicará a continuación, te pido, mi querido y estimado lector, que elimines cualquier tipo de distracción que pueda distraerte durante esta explicación. Esto se debe a que las funciones o procedimientos recursivos pueden resultar confusos desde el primer contacto con este tipo de programación.

Entonces, con base en la imagen 04, vamos a entender lo que de hecho está ocurriendo aquí. Primero, cuando la línea seis es ejecutada, estaremos llamando a la función Fibonacci como si esta fuera, de hecho, un bucle. No un bucle interactivo, sino un bucle recursivo. Este es el primer punto que necesitas, de hecho, comprender.

El siguiente paso es entender que necesitamos una condición limitadora, así como ocurrió en el código 01, todo bucle que pretenda utilizar la recursividad necesita una condición límite. En este caso, la condición límite es la que se está definiendo en la línea 15. Aunque se dijo que la recursividad necesita reducirse a una expresión simple, quien de hecho evita que un bucle recursivo llegue a convertirse en un bucle infinito es la condición límite. Son conceptos diferentes. Cuidado con no utilizar los conceptos de manera equivocada. Entonces, nuevamente: 

Quien genera la recursividad es la implementación de una expresión matemática mínima. Pero quien limita la recursividad es la condición que evita la aparición del bucle infinito.

Así, quien limita la recursividad en el código 04 es la línea 15. Quien crea la recursividad son las líneas 22 y 26. Ya en el código 02, la limitación sería la línea 11, y quien estaría creando la recursividad sería la línea 16.

Vale, entonces veamos cómo funciona en realidad. Como nuestro argumento inicial es igual a cinco, se ejecutará la línea 13 y, justo después, la línea 22. Al hacer esto, la línea 22 llamará nuevamente a la línea 9, creando así un bucle. Pero presta atención a que, durante la llamada a la línea 22, estaremos reduciendo el argumento en una unidad. Entonces, nuestra pila empezará a construirse, llamada tras llamada hasta que, en algún momento, la línea 15 se vuelva verdadera.

En ese momento, ocurre algo interesante: estamos ejecutando la cuarta llamada y apilando valores cada vez menores en el argumento. Entonces, cuando la línea 15 sea verdadera, se ejecutará la línea 17, que nos mostrará cuál es el valor actual del argumento, así como cuál es el número de llamadas en ese momento. Como el valor es uno, le devolvemos este valor al autor de la llamada, pero el autor de la llamada no es la línea seis, sino la veintidós. Recuerda que estamos apilando una serie de llamadas. Ahora empezamos a desapilar las llamadas. Con esto, el primer valor devuelto es uno, que se suma a la variable value, y esta variable no perderá su valor entre las llamadas, sino que irá construyendo un nuevo valor en cada nueva llamada. Para entender esto mejor, sería necesario explicar cómo funciona una pila, pero, en mi opinión, este tipo de cosas es algo un poco más avanzado. Aunque esto no te impedirá entender cómo funciona la recursividad. Solo tienes que prestar atención.

Vale, entonces ya calculamos cuál sería el primer valor. Sin embargo, debido a la expresión mostrada en la imagen 03, debemos calcular nuevamente la función de la línea 9. Por esta razón, se produce una nueva llamada en la línea 26. Ahora, presta mucha atención, de verdad, si no será imposible entender la recursividad de las funciones compuestas, como esta que calcula Fibonacci.

La llamada de la línea 22 fue reduciendo uno el valor de arg cada vez. Aunque, cuando arg fue igual a uno, en la llamada siguiente, el valor de arg presente en la línea 22, es decir, en la llamada anterior, seguía siendo igual a dos. Así, cuando se ejecute la línea 24, debido a que arg era igual a uno en la llamada de la línea 22, no estaremos tratando con arg en la línea 24 igual a uno, sino igual a dos.

Este tipo de cosas, la primera vez que se oyen, resultan muy confusas. Lo sé, y precisamente por esta razón estoy usando la recursividad más simple que existe, como mostré en el código 01, donde primero se ejecuta una cuenta regresiva y después una cuenta progresiva. Sin embargo, la cuenta progresiva solo surgió debido a que habíamos apilado valores. Así, cuando empezamos a desapilar estos mismos valores, tuvimos la ilusión de que se había producido una cuenta progresiva, cuando en realidad no se había implementado. Todo se debe a una condición propia del uso de llamadas recursivas.

Muy bien, entonces, tomémonos un momento para calmarse. En este preciso momento, en la llamada a la línea 26, arg es igual a dos. Sin embargo, como estamos reduciendo arg dos unidades antes de volver a llamar a la función, cuando se ejecute la línea 13, el valor será cero. En este caso, la línea 15 será verdadera y la función devolverá. Por tanto, la línea 28 imprimirá un valor igual a uno. Es decir, calculamos el Fibonacci del primer elemento de la secuencia.

Ahora recuerda: hemos apilado cinco llamadas y solo hemos devuelto la primera. Así, ahora, en la línea 22, el valor será igual a uno. Pero espera, ¿no era ya igual a uno? No, querido lector, la variable value era igual a uno en la llamada que acabamos de finalizar. Como la función devolvió, volvemos a la línea 22, y antes de eso, value era igual a cero. Ahora es igual a uno. Al ejecutar la línea 24, y como desapilamos una llamada, arg es igual a dos. Esto ocurre en la línea 24. No pierdas el hilo. Bien, como arg es igual a dos, y necesitamos ejecutar la línea 26, donde restaremos dos unidades de este argumento, ahora la función recibirá arg igual a cero, pero WHO igual a dos, esto se debe a que estamos haciendo la llamada desde la línea 26.

Como arg es igual a cero, entonces la línea 15 es verdadera y devolvemos el valor cero en la línea 19. Ahora, como volvemos a la línea 26, sumamos el valor uno calculado anteriormente con el nuevo valor cero. De este modo, obtenemos el valor igual a uno. Es decir, acabamos de calcular el segundo elemento de la secuencia de Fibonacci.

Y volvemos a la línea 22, ya que desapilamos solo dos valores, por lo que necesitamos desapilar cinco, y el valor uno se asigna a la variable value. Sin embargo, arg ahora es igual a tres. Esta es la parte realmente interesante, esto se debe a que, como arg es igual a tres, al restar dos en la línea 26, la función recibirá el valor uno, y, como esto hace verdadera la línea 15, devolveremos uno en la línea 19. Así, la variable value ahora es igual a dos.

De esta forma, conseguimos calcular el tercer elemento de la secuencia. Faltan desapilar otros dos elementos. De nuevo, volvemos a la línea 22, donde esta variable value es igual a dos, y arg es igual a cuatro. Bien, ¿qué pasará cuando se ejecute la línea 26? ¿Adivinas? Se llamará nuevamente a la función Fibonacci, pero ahora con arg igual a dos. Recuerda que restamos dos en la línea 26 antes de llamar a la función.

Vale, como arg en este momento es igual a dos, la línea 15 fallará, y se ejecutará una vez más la línea 22. Solo que, en este punto, la variable value es igual a cero, y no a dos. Este otro valor se almacenó en la pila. Muy bien, como arg es igual a dos, y necesitamos restar uno antes de efectuar la llamada, en la línea 15 arg será igual a uno, y se devolverá uno. Ahora, en la línea 22, value es uno, por lo que se ejecutará la línea 26. En este punto, al restar dos a arg, la función se llama y se restan dos. Como ya se sabe, esto devolverá cero. Y la línea 30 devolverá el valor uno. ¿Pero a dónde lo devolverá? Bueno, querido lector, se le devolverá a la línea 26, que hizo la llamada. Recuerda que, en este momento, value es igual a dos. Como el retorno fue uno, ahora value es igual a tres. Con esto, acabamos de calcular el cuarto elemento de la secuencia. Falta uno. (RISOS)

Creo que tu cerebro se está enredando con estos retornos y llamadas, pero en este último elemento lo haremos de forma diferente, ya que todo será una repetición inmensa de los pasos. Esto se debe a que, ahora, en la línea 26, el valor de arg es igual a cinco y el de value es igual a tres. Como arg necesitará ser restado en dos, se producirá una nueva serie de llamadas. Creo que ya se explicó todo lo que necesitas entender.

Aunque, como pudiste notar, existe una cuestión que se mencionó al principio del artículo: que la recursividad es sencilla de programar, aunque es más lenta de ejecutar. Sin embargo, podemos generar un código equivalente que usa la interactividad en lugar de la recursividad. Con esto, ganamos en velocidad, aunque el código es un poco más complejo.

Para comprobarlo, veamos cómo se haría este tipo de código, cuyo propósito es calcular la secuencia de Fibonacci. Existen diversas formas de hacerlo, pero justo abajo puedes ver una de ellas.

01. //+------------------------------------------------------------------+
02. #property copyright "Daniel Jose"
03. //+------------------------------------------------------------------+
04. void OnStart(void)
05. {
06.     const uchar who = 6;
07. 
08.     Print("Result: ", Fibonacci_Recursive(who));
09.     Print("Result: ", Fibonacci_Interactive(who));
10. }
11. //+------------------------------------------------------------------+
12. uint Fibonacci_Recursive(uint arg)
13. {
14.     if (arg <= 1)
15.         return arg;
16. 
17.     return Fibonacci_Recursive(arg - 1) +  Fibonacci_Recursive(arg - 2);
18. }
19. //+------------------------------------------------------------------+
20. uint Fibonacci_Interactive(uint arg)
21. {
22.     uint v, i, c;
23. 
24.     for (c = 0, i = 0, v = 1; c < arg; i += v, c += 2)
25.         v += i;
26. 
27.     return (c == arg ? i : v);
28. }
29. //+------------------------------------------------------------------+

Código 04

Nota que aquí estamos trabajando con ambas maneras de trabajar con bucles. La primera es mediante la recursividad, y la segunda, mediante la interactividad. Pregunto: ¿cuál crees que es más fácil de entender? Dada esta respuesta, ¿cuál crees que es más rápida en términos de tiempo de ejecución? Teniendo en cuenta lo que ya sabes sobre ambos métodos para hacer el mismo tipo de cálculo.

Como sé que esta función interactiva, que se está implementando en la línea 20, puede resultarles extraña a algunos, voy a dar una breve explicación sobre ella.

En la línea 22 declaramos las variables que necesitaremos. Ya en la línea 24, iniciamos el bucle principal de cálculo. Esta es la parte divertida. Observa que iniciamos los valores antes de efectuar cualquier cálculo. Ahora, observa el siguiente hecho: cuando el elemento que se busca es impar (el primer, tercer, quinto, séptimo elemento, etc.), la variable v apunta al valor correcto. Sin embargo, cuando los elementos que se buscan son pares, el valor de i apunta al resultado correcto. ¿Pero por qué?

El motivo es que la variable c se incrementará dos unidades cada vez, para que no sobrepasemos el resultado correcto. Pero, como en cada interacción tendremos que sumar el valor anterior con un nuevo valor, y no estamos intercambiando los valores de i y v, tenemos este pequeño detalle en esta función interactiva. Existen formas de implementar la misma sin que tal cuestión llegue a surgir, aunque creo innecesario hacer esto, ya que la interacción del bucle me indica cuál será el próximo valor y el valor actual. Así pues, todo lo que necesito hacer es usar un operador ternario para devolver el resultado correcto. Sin este pequeño ajuste, podríamos estar mirando el próximo elemento de la secuencia o el antiguo elemento de la secuencia, todo dependería de si el argumento, o elemento buscado, sería par o impar, y de si usaríamos el valor de i o de v.

Como prueba de que este código 04 funciona, a continuación se muestra la respuesta de su ejecución. Para obtener otros valores y probar ambas formas de calcular la serie de Fibonacci, basta con cambiar el valor de la constante de la línea seis. Pero recuerda que la serie de Fibonacci crece muy rápido, y, como existen limitaciones debido a los tipos utilizados, ten cuidado de no exagerar y tratar de ver un elemento muy distante, pues acabarás generando problemas en el resultado final.

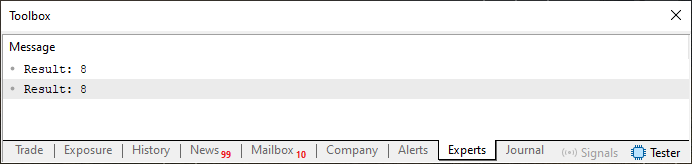
Imagen 05

Existen formas y maneras de corregir esto, y mostrar cualquier valor numérico posible de ser almacenado en la memoria de un ordenador. Aunque, como este es un tema un poco más avanzado, lo dejaré para mostrarlo en otro momento más oportuno. Pero, solo para despertar tu curiosidad sobre el tema, ¿cómo creen que los programadores consiguen calcular el valor de π y otras constantes irracionales con miles de decimales, si no tienen en sus programas los tipos que normalmente se usan en los ordenadores? No tenemos forma de lograr ese objetivo.

Como dije, este tipo de cosas es un poco más avanzada, y necesitas entender ciertos conceptos que aún no han sido explicados. No porque, con los conocimientos ya mostrados, esto no sea posible, si esto fuera así, sería una gran mentira, ya que sí, es posible hacer esto con los conceptos ya mostrados hasta ahora, entre ellos, el uso de la recursividad. Aunque el trabajo de implementar el código sería mucho mayor, ya que sería necesario adaptar ciertas cosas a un formato que no resulta muy fácil de entender desde el principio.

Consideraciones finales

Este artículo tuvo como objetivo presentar un concepto de programación muy interesante y divertido, aunque debe tratarse con extremo respeto, ya que un mal uso o una mala interpretación de lo mostrado aquí convierte programas relativamente simples en algo innecesariamente complicado. Sin embargo, si se utiliza correctamente y se adapta a situaciones apropiadas, la recursividad se convierte en un gran aliado para resolver cuestiones que, de otra manera, serían mucho más laboriosas y tardadas.

Como regla general, usa la recursividad siempre que sea posible, o cuando tengas una expresión matemática que no logres reescribir de forma interactiva. Pero recuerda que la gran cantidad de llamadas entre cada factorización que se necesita efectuar puede hacer que tu código sea más lento de lo normal. Cuando esto ocurra, procura transformar la recursividad en un bucle interactivo, que, aunque sea más complicado de crear al principio, es considerablemente más rápido durante la ejecución del código, sobre todo cuando se deben calcular o ajustar series de datos muy grandes de una determinada manera.