Ferramentas econométricas para previsão de volatilidade: Modelo GARCH

Introdução

A volatilidade é um indicador importante para avaliar a flutuação dos preços dos ativos financeiros. Na análise das cotações, há muito tempo que se observou, que grandes mudanças de preços levam frequentemente a mudanças ainda maiores, especialmente em períodos de crise financeira. Por outro lado, pequenas mudanças nos preços são geralmente seguidas por outras pequenas mudanças. Assim, períodos de relativa estabilidade são alternados com períodos de volatilidade.

O primeiro modelo a tentar explicar esse fenômeno foi o modelo ARCH,desenvolvido por Engle), — que considera a heteroscedasticidade condicional autorregressiva (não uniformidade). Além de explicar o efeito de agrupamento (concentração de retornos em valores altos e baixos), esse modelo também explicava a ocorrência de caudas pesadas e excesso positivo, características de todas as distribuições de incrementos de preços. O sucesso do modelo ARCH condicionalmente gaussiano levou ao surgimento de uma série de generalizações, cujo objetivo era explicar outros fenômenos observados na análise de séries temporais financeiras. Historicamente, uma das primeiras generalizações do modelo ARCH foi o modelo GARCH (Generalized ARCH).

A principal vantagem do GARCH em relação ao ARCH é que ele é mais econômico e não exige uma estrutura de longos atrasos na adequação dos dados amostrais. Neste artigo, pretendo descrever o que é o modelo GARCH, e, mais importante, propor uma ferramenta pronta para a previsão de volatilidade com base nele, já que a previsão — é um dos principais objetivos na análise de dados financeiros.

Abordagem não paramétrica para estimar a volatilidade

O uso da volatilidade para avaliação de riscos é um tema bastante popular entre os traders. A forma mais comum de estimar a volatilidade — simplesmente calcular o desvio padrão em um determinado período.

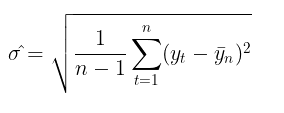
Essa é a abordagem não paramétrica para estimar a volatilidade. A volatilidade calculada dessa forma é denominada volatilidade histórica ou empírica. No modelo gaussiano de caminhada aleatória, essa é a principal medida de incerteza e variação, pois se supõe que a volatilidade é constante no tempo.

Abordagem paramétrica para estimar a volatilidade

No modelo GARCH, por sua vez, supõe-se que a volatilidade seja uma variável aleatória (a volatilidade em si é volátil). Isso está mais próximo da realidade. O processo GARCH é definido pelas seguintes equações:

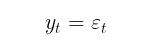
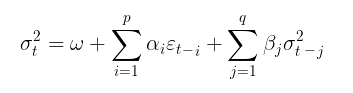
onde:

• Yt – incrementos logarítmicos dos preços,
• ε t – resíduos do modelo,
• σt^² – variância condicional,
• zt = i.i.d. N(0,1) – distribuição gaussiana padrão,
• zt = i.i.d. t-Student(v) – distribuição t de Student padrão com v graus de liberdade,
• (omega, alpha, beta, v) – parâmetros do modelo que devem ser estimados a partir da amostra de dados.

Os parâmetros do modelo estão sujeitos às seguintes restrições:

• omega > 0, condição de positividade da variância,
• alpha ≥ 0,
• beta ≥ 0,
• ∑alpha_i + ∑beta_j < 1, condição de estacionariedade,
• v > 2.

Se beta = 0, então o modelo GARCH se reduz ao modelo ARCH.

Normalmente, o modelo GARCH é complementado por algum-modelo de média condicional ou incondicional. Como modelo de média condicional, pode-se usar, por exemplo, um processo autorregressivo de primeira ordem AR(1):

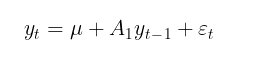
onde:

• u – parâmetro de interceptação,
• A1 – parâmetro do modelo autorregressivo.

O objetivo de modelar a média condicional é determinar uma série de quadrados dos resíduos (εt^²), que será utilizada para calcular a variância condicional. Caso não haja evidência de autocorrelação nos retornos, o que geralmente ocorre, pode-se passar para um modelo de média incondicional:

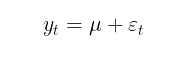
Neste artigo, para simplificar os cálculos, usarei um modelo sem avaliação da autocorrelação dos retornos. Assim, a tarefa de estimar a volatilidade no modelo GARCH se reduz a um problema paramétrico de encontrar os coeficientes do modelo (μ, ω, alpha, beta, v).

Estimação dos parâmetros do modelo GARCH pelo método da máxima verossimilhança

Para estimar os parâmetros desconhecidos, geralmente é utilizado o método da máxima verossimilhança. Sob a suposição de distribuição gaussiana dos resíduos εt a função de log-verossimilhança é dada por:

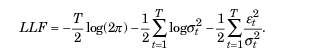
Caso sejam detectados desvios da normalidade, a distribuição t de Student padronizada pode ser usada como uma alternativa apropriada. Para valores pequenos do parâmetro v (graus de liberdade), essa distribuição apresenta um excesso positivo e caudas mais pesadas do que a distribuição normal. Nesse caso, a função de verossimilhança é representada por:

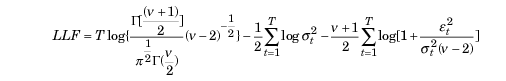
onde ε,

• Г — função gama,
• T – tamanho da amostra de dados.

Otimizador ALGLIB MinBLEIC

Para encontrar os valores dos parâmetros do modelo GARCH, é necessário maximizar a função de verossimilhança. Para isso, utilizam-se métodos de otimização. Nesse contexto, a biblioteca de análise numérica ALGLIB é útil. Para maximizar a função objetivo, escolhi o algoritmo MinBLEIC(Bound Linear Equality Inequality Constraints).

//+------------------------------------------------------------------+
//|  Objective Function: Gaussian loglikelihood                      |
//+------------------------------------------------------------------+
void CNDimensional_GaussianFunc::Func(CRowDouble &x,double &func,CObject &obj)
  {
//x[0] - mu;
//x[1] - omega;
//x[2] - alpha;
//x[3] - beta;
   double returns[];
   ArrayResize(returns,N1);
   for(int i=0;i<N1;i++)
     {
      returns[i] = MathLog(close[i+1]/close[i]);
     }

   double residuals[];
   ArrayResize(residuals,N1);
   for(int i = 0; i<N1; i++)
     {
      residuals[i] = (returns[i] - x[0]);
     }

   double condVar[];
   ArrayResize(condVar,N1);
   condVar[0] = x[1]/(1-x[2]-x[3]);  // Unconditional Variance

   for(int i=1; i<N1; i++)
     {
      condVar[i] = x[1] + x[2]*MathPow(residuals[i-1],2) + x[3]*condVar[i-1]; // Conditional Variance
     }

   double LLF[],a[],b[];
   ArrayResize(LLF,N1);
   ArrayResize(a,N1);
   ArrayResize(b,N1);
   for(int i=0; i<N1; i++)
     {

      a[i]= 1/sqrt(2*M_PI*condVar[i]);
      if(!MathIsValidNumber(a[i]))
        {
         break;
        }

      b[i]= MathExp(- MathPow(residuals[i],2)/(2 * condVar[i]));
      if(!MathIsValidNumber(b[i]))
        {
         break;
        }

      LLF[i]=MathLog(a[i]*b[i]);
      if(!MathIsValidNumber(LLF[i]))
        {
         break;
        }
     }

   func = -MathSum(LLF); // Loglikelihood
  }

Na função GARCH, que interage diretamente com a função objetivo para encontrar os valores ótimos dos parâmetros, é necessário:

• definir os valores iniciais dos parâmetros,
• ajustar a escala dos dados (um aspecto crucial para o sucesso da otimização),
• especificar os limites dentro dos quais os parâmetros podem variar,
• declarar restrições lineares de desigualdade (no caso, apenas a de estacionaridade, α+β<1),
• determinar os critérios de parada para o algoritmo de otimização,
• definir o passo de diferenciação.

//+------------------------------------------------------------------+
//|  Function GARCH  Gaussian                                        |
//+------------------------------------------------------------------+
vector GARCH()
  {
   double              x[],s[];
   int                 ct[];
   CMatrixDouble       c;
   CObject Obj;
   CNDimensional_GaussianFunc ffunc;
   CNDimensional_Rep frep;

   double returns[];
   ArrayResize(returns,N1);
   for(int i=0;i<N1;i++)
     {
      returns[i] = MathLog(close[i+1]/close[i]);
     }
   double returns_mean  = MathMean(returns);
   double returns_var = MathVariance(returns);
   double KurtosisReturns = MathKurtosis(returns);
// Print("KurtosisReturns= ",KurtosisReturns);

// Initial parameters ---------------------------
   ArrayResize(x,4);
   x[0]=returns_mean;  //  Mu
   x[1]=returns_var;  // Omega
   x[2]=0.0;         // alpha
   x[3]=0.0;        // beta
//------------------------------------------------------------
   double mu;
   if(NormalizeDouble(returns_mean,10)==0)
     {
      mu = 0.0000001;
     }
   else
      mu = NormalizeDouble(returns_mean,10);
// Set Scale-----------------------------------------------
   ArrayResize(s,4);
   s[0] = NormalizeDouble(returns_mean,10);  //  Mu
   s[1] = NormalizeDouble(returns_var,10); // omega
   s[2] =1;
   s[3] =1;
//---------------------------------------------------------------
// Linearly inequality constrained: --------------------------------
   c.Resize(1,5);
   c.Set(0,0,0);
   c.Set(0,1,0);
   c.Set(0,2,1);
   c.Set(0,3,1);
   c.Set(0,4,0.999); // alpha + beta <= 0.999
   ArrayResize(ct,1);
   ct[0]=-1; // {-1:<=},{+1:>=},{0:=}
//--------------------------------------------------------------
// Box constraints ------------------------------------------------
   double bndl[4];
   double bndu[4];

   bndl[0] = -0.01;  // mu
   bndl[1] = NormalizeDouble(returns_var/20,10);  // omega
   bndl[2] = 0.0;  // alpha
   bndl[3] = 0.0;  // beta

   bndu[0] = 0.01;  // mu
   bndu[1] = NormalizeDouble(returns_var,10);  // omega
   bndu[2] = 0.999;  // alpha
   bndu[3] = 0.999;  // beta
//--------------------------------------------------------------
   CMinBLEICStateShell state;
   CMinBLEICReportShell rep;
   double epsg=0;
   double epsf=0;
   double epsx=0.00001;
   double diffstep=0.0001;
//--- These variables define stopping conditions for the outer iterations:
//--- * epso controls convergence of outer iterations;algorithm will stop
//---   when difference between solutions of subsequent unconstrained problems
//---   will be less than 0.0001
//--- * epsi controls amount of infeasibility allowed in the final solution
   double epso=0.00001;
   double epsi=0.00001;

   CAlglib::MinBLEICCreateF(x,diffstep,state); //---  create optimizer
   CAlglib::MinBLEICSetBC(state,bndl,bndu);  //--- add boundary constraints
   CAlglib::MinBLEICSetLC(state,c,ct);
   CAlglib::MinBLEICSetScale(state,s);
   CAlglib::MinBLEICSetPrecScale(state); // Preconditioner
   CAlglib::MinBLEICSetInnerCond(state,epsg,epsf,epsx);
   CAlglib::MinBLEICSetOuterCond(state,epso,epsi);
   CAlglib::MinBLEICOptimize(state,ffunc,frep,0,Obj);
   CAlglib::MinBLEICResults(state,x,rep);   // Get parameters
//---------------------------------------------------------

   double residuals[],resSquared[],Realised[];
   ArrayResize(residuals,N1);
   for(int i = 0; i<N1; i++)
     {
      residuals[i] = (returns[i] - x[0]);
     }

   MathPow(residuals,2,resSquared);
   ArrayCopy(resSquared_,resSquared,0,0,WHOLE_ARRAY);
   MathSqrt(resSquared,Realised);

   double condVar[],condStDev[];
   double ForecastCondVar,PriceConf_Upper,PriceConf_Lower;
   ArrayResize(condVar,N1);
   condVar[0] = x[1]/(1-x[2]-x[3]);
   for(int i = 1; i<N1; i++)
     {
      condVar[i] = x[1] + x[2]*MathPow(residuals[i-1],2) + x[3]*condVar[i-1];
     }

   double PlotUncondStDev[];
   ArrayResize(PlotUncondStDev,N1);
   ArrayFill(PlotUncondStDev,0,N1,sqrt(condVar[0])); // for Plot
   ArrayCopy(PlotUncondStDev_,PlotUncondStDev,0,0,WHOLE_ARRAY);
   MathSqrt(condVar,condStDev);
// Print("мат ожидание условного ст отклонения = "," ",MathMean(condStDev));

   ArrayCopy(Real,Realised,0,0,WHOLE_ARRAY);
   ArrayCopy(GARCH_,condStDev,0,0,WHOLE_ARRAY);

   vector v_Realised, v_condStDev;
   v_Realised.Assign(Realised);
   v_condStDev.Assign(condStDev);
   double MSE=v_condStDev.Loss(v_Realised,LOSS_MSE); // Mean Squared Error
//-----------------------------------------------------------------------------
//-------- Standardize Residuals--------------------------------------
   double z[];
   ArrayResize(z,N1);
   for(int i = 0; i<N1; i++)
     {
      z[i] = residuals[i]/sqrt(condVar[i]);
     }
   ArrayCopy(Z,z,0,0,WHOLE_ARRAY);
//----------------------------------------------------------------------------------

//-------------- JarqueBeraTest for Normality  ----------------------------------
   double pValueJB;
   int JBTestH;
   CAlglib::JarqueBeraTest(z,N1,pValueJB);
   if(pValueJB <0.05)
      JBTestH =1;
   else
      JBTestH=0; // H=0 - data Normal, H=1 data are not Normal
   double Kurtosis = MathKurtosis(z); // Kurosis = 0 for Normal distribution
//---------------------------------------------------------------------------------

//-------------------------------------------------------------------------------------
//-------- Forecast Conditional Variance for m bars
   double FCV[];
   ArrayResize(FCV,forecast_m);
   for(int i = 0; i<forecast_m; i++)
     {
      FCV[i] = sqrt(x[1]*((1-MathPow(x[2]+x[3],i+1))/(1-x[2]-x[3])) + MathPow(x[2]+x[3],i)*(x[2]*MathPow(residuals[N1-1],2) + x[3]*condVar[N1-1])) ;
     }
   ArrayCopy(FCV_,FCV,0,0,WHOLE_ARRAY);
//-----------------------------------------------------------------------------------
   double LLF[];
   double Loglikelihood;
   ArrayResize(LLF,N1);
   for(int i = 0; i<N1; i++)
     {
      LLF[i] = MathLog(1/sqrt(2*M_PI*condVar[i])*MathExp(- MathPow(residuals[i],2)/(2*condVar[i])));
     }
   Loglikelihood = MathSum(LLF);
//--------------------------------------------------------------------------

   ForecastCondVar= x[1] + x[2]*MathPow(residuals[N1-1],2) + x[3]*condVar[N1-1];
   int err1;
   PriceConf_Lower = close[N1]*MathExp(-MathAbs(MathQuantileNormal((1-pci)/2,0,1,err1))*sqrt(x[1] + x[2]*MathPow(residuals[N1-1],2) + x[3]*condVar[N1-1])); // confidence interval pci%
   PriceConf_Upper = close[N1]*MathExp(MathAbs(MathQuantileNormal((1-pci)/2,0,1,err1))*sqrt(x[1] + x[2]*MathPow(residuals[N1-1],2) + x[3]*condVar[N1-1]));  // confidence interval pci%

//--------------------------------------------------------------------------------------
   vector result= {x[0],x[1],x[2],x[3],rep.GetTerminationType(),ForecastCondVar,PriceConf_Lower,PriceConf_Upper,MSE,Loglikelihood,condVar[0],returns_var,JBTestH,Kurtosis};
   return (result);
  }
//+------------------------------------------------------------------+

Previsão de Volatilidade com o Modelo GARCH(1,1)

Previsão Pontual de Volatilidade

Após a determinação dos parâmetros do modelo, pode-se avançar para o objetivo principal: a previsão de volatilidade. A previsão de volatilidade para o modelo GARCH(1,1) em m passos à frente é calculada pela fórmula:

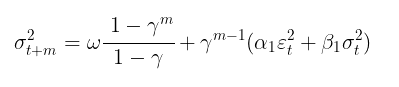
onde:

• γ=α1+β1.

Essa previsão, quando m→∞ converge para a variância incondicional teórica do GARCH (sob a condição de estacionaridade α1+β1<1).

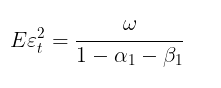
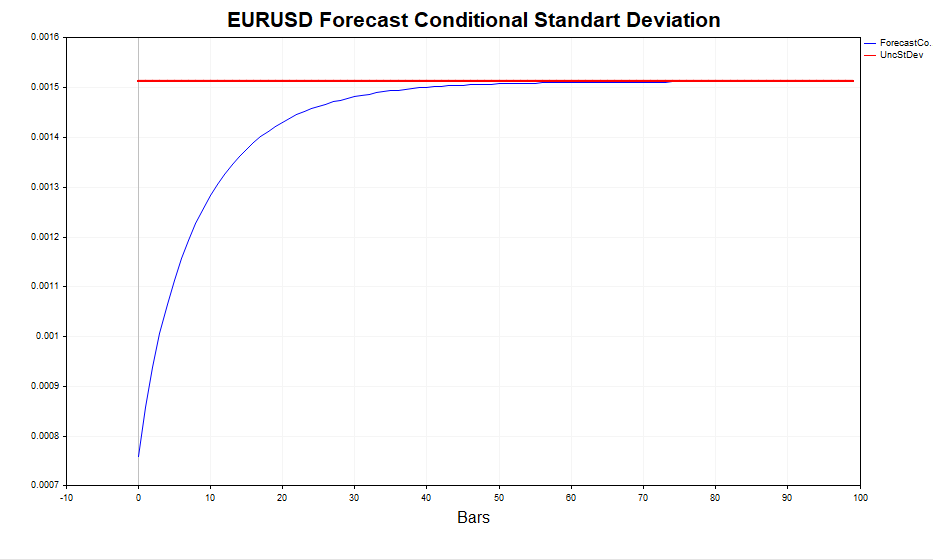
Em outras palavras, quanto mais distante o horizonte da previsão — mais próximo seu valor estará da variância incondicional estacionária. O script GARCH permite calcular a previsão de volatilidade em m passos à frente e comparar esses valores com Eεt ², confirmando empiricamente que o comportamento é como esperado.

Previsão Intervalar

Embora a previsão pontual de volatilidade seja útil, é ainda mais importante obter uma avaliação probabilística dos limites em que os futuros incrementos de preços se encontrarão, isto é, determinar intervalos de confiança com um nível de significância específico.

Sob a suposição de normalidade z t= i.i.d. N(0,1) os intervalos de confiança são calculados pela fórmula:

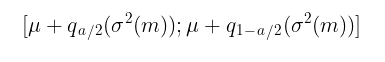
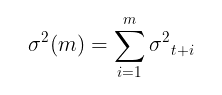
onde:

• q – quantil da distribuição normal padrão

Por exemplo, para um intervalo de confiança com nível de confiança de 90% (α=1−0,9), o intervalo será:

[u−1,65σ; u+1,65σ]

O caso se torna mais desafiador quando se assume que zt= i.i.d. t-Student(v). Nesse caso, não há uma fórmula analítica para a função inversa da distribuição. Assim, para construir intervalos de confiança, é necessário recorrer à simulação pelo método de Monte Carlo.

//+-------------------------------------------------------------------------+
//|Function calculate Forecast Confidence intervals using Monte-Carlo method|
//+-------------------------------------------------------------------------+
bool MCForecastStandardized_t(const double DoF,const double CondStDevForecast,const double prob, double & F_lower[],double & F_upper[])
  {

   double alpha = 1-prob;
   double qlower[1] = {alpha/2};       // q (a/2)
   double qupper[1] = {1-alpha/2};  // q (1-a/2)

   int N = 10000; //number Monte-Carlo simulates
   double h_St[];
   ArrayResize(h_St,N);
   for(int i=0;i<N;i++)
     {
      h_St[i] = CondStDevForecast * Standardized_t(DoF);   // GARCH-Student(1,1)
     }
   MathQuantile(h_St,qlower,F_lower);
   MathQuantile(h_St,qupper,F_upper);
   return(true);
  }

//+--------------------------------------------------------------------------+
//| Function calculate i.i.d. standardized t-distributed variable            |                              |
//+--------------------------------------------------------------------------+
double  Standardized_t(const double DoF)
  {
   double randStandStudent;
   int err;
   randStandStudent = MathRandomNormal(0,1,err) * sqrt(DoF/((MathRandomGamma(DoF/2.0,1)*2.0)));
   randStandStudent = randStandStudent/sqrt(DoF/(DoF-2.0));
   return(randStandStudent);
  }
//+------------------------------------------------------------------+

É evidente que quanto maior o número de simulações (o padrão é 10.000), maior a precisão da previsão, mas isso também aumenta o tempo necessário para os cálculos. Um número aceitável é 100.000, pois os intervalos de confiança tornam-se mais simétricos.

Verificação da Adequação do Modelo GARCH Condicionalmente Gaussiano

Para avaliar o quão bem o modelo GARCH capturou a heteroscedasticidade da volatilidade, é necessário verificar os resíduos padronizados quanto à presença de autocorrelação e sua conformidade com a distribuição normal padrão. Os resíduos padronizados —são simplesmente os incrementos de preços menos a média condicional (ou incondicional), divididos pelo desvio padrão condicional calculado pelo modelo GARCH.

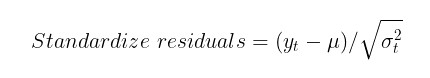Resíduos PadronizadostitlealtResíduos Padronizadosalt

Se o modelo GARCH é adequado aos dados reais, então os resíduos padronizados serão independentes e identicamente distribuídos como variáveis padrão normais.

Como exemplo de análise de resíduos, utilizemos os dados diários do par EURUSD dos últimos quatro anos e calculemos os parâmetros do modelo.

Vamos verificar a autocorrelação nos quadrados dos resíduos.

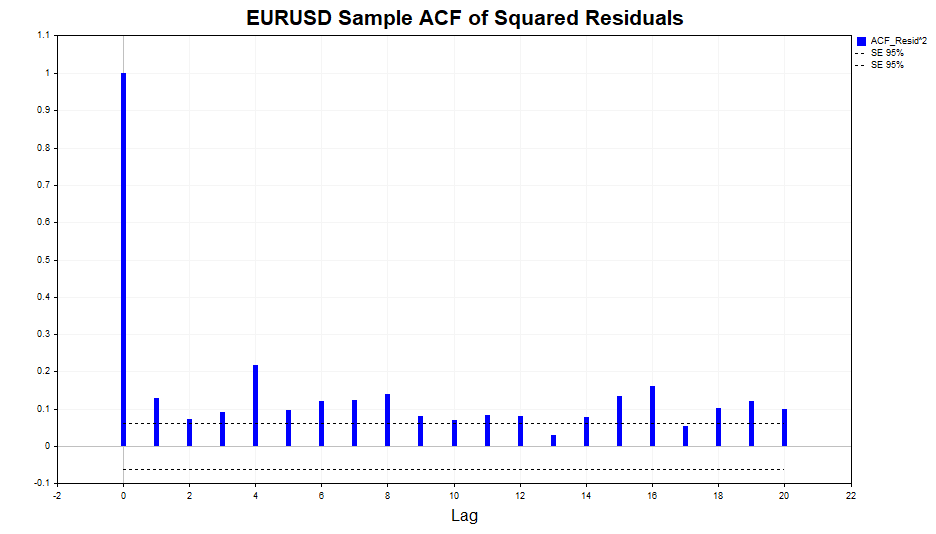
Como podemos observar, há uma leve dependência nos dados, que se estende até o lag 20, inclusive. Agora, verificaremos a autocorrelação nos quadrados dos resíduos padronizados para determinar se o modelo GARCH(1,1) conseguiu descrever adequadamente essa dependência.

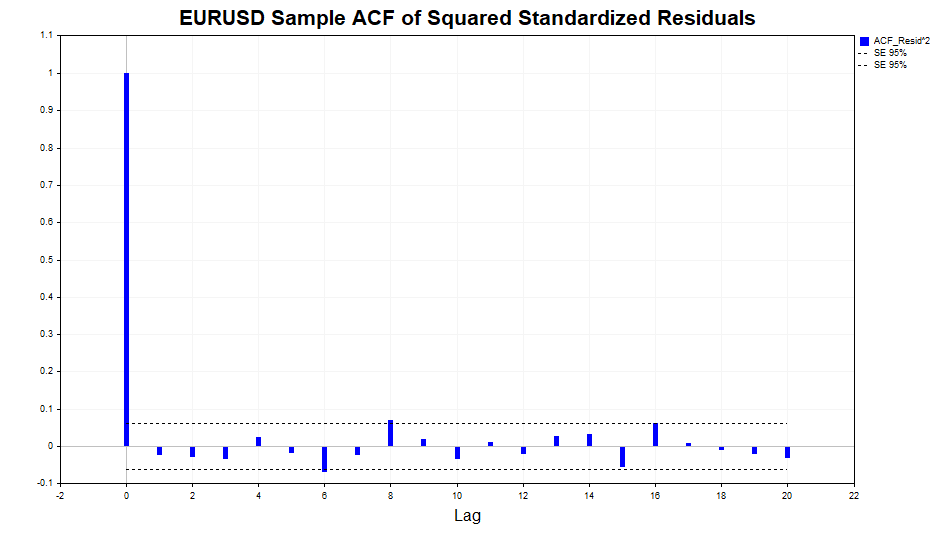
Os resultados mostram que o modelo lidou de forma excelente, pois não há correlação significativa nos dados.

Avaliamos a volatilidade realizada calculada (quadrado dos incrementos logarítmicos dos preços) e o desvio padrão condicional (GARCH). Modelo responde de maneira eficiente às mudanças na volatilidade. O desvio padrão incondicional atua como uma média em torno da qual oscila a GARCH-volatilidade.

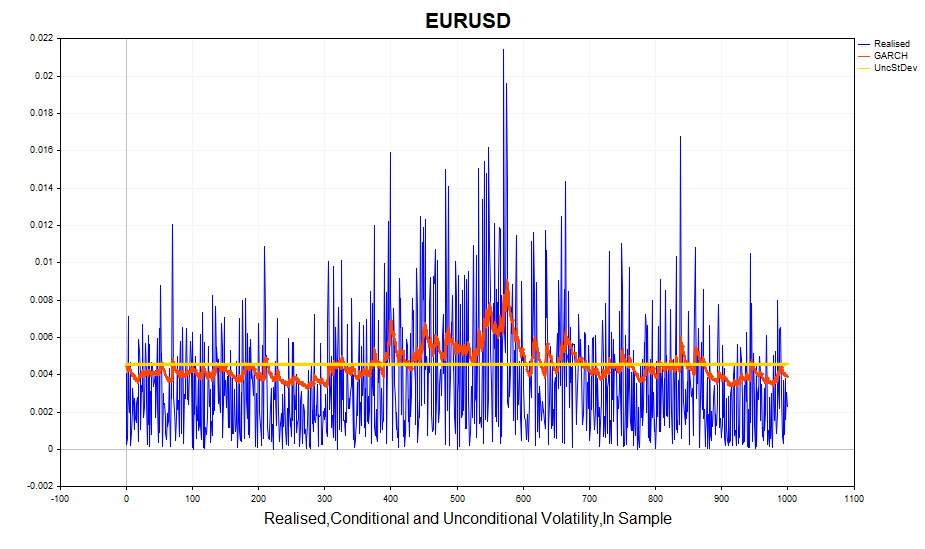
Vamos agora avaliar a normalidade dos resíduos padronizados.

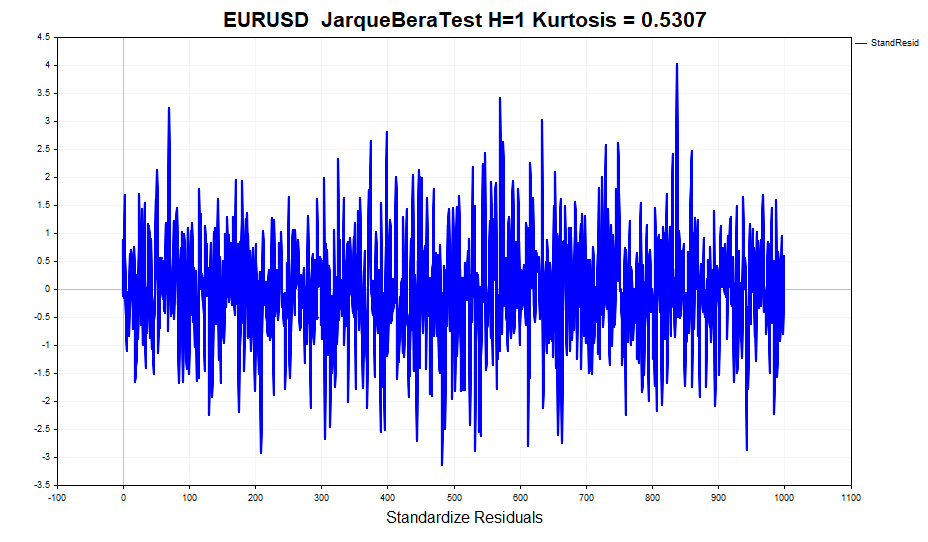
À primeira vista, os dados aparentam ser normais, sem a presença de caudas pesadas. No entanto, testes formais de normalidade, como o Teste Jarque-Bera, rejeitam a hipótese nula de normalidade. A causa disso é o excesso (0,5307), que apresenta um pequeno desvio em relação ao esperado em uma distribuição normal. Para comparação, o excesso das séries de retornos é de 1,2904. Isso indica que o modelo GARCH conseguiu capturar parcialmente o efeito de curtose elevada, embora não completamente. Lembre-se de que a distribuição incondicional do processo GARCH- tem caudas pesadas, porque uma mistura de distribuições gaussianas com diferentes variâncias resulta em uma distribuição com caudas mais pesadas e excesso positivo.

Consequentemente, uma das suposições do modelo GARCH — de que os resíduos padronizados seguem uma distribuição normal condicional — é violada. Isso implica que as estimativas dos parâmetros do modelo, obtidas pelo método da máxima verossimilhança, perdem algumas propriedades desejáveis, como a eficiência assintótica (em outras palavras, para grandes amostras seria possível encontrar estimativas mais precisas dos parâmetros).

Nesse contexto, como alternativa à distribuição normal, pode-se adotar a distribuição t de Student. Com poucos graus de liberdade, essa distribuição apresenta excesso positivo e caudas pesadas. Nesse caso, o número de graus de liberdade torna-se um parâmetro adicional a ser estimado a partir da amostra.

Todas as ações relacionadas à visualização da variada gama de estatísticas discutidas anteriormente foram consolidadas no script GARCH para facilitar a análise.

• Distribution – distribuição normal padrão ou distribuição t de Student padrão.
• Data window – janela de dados para calcular os parâmetros do modelo.
• Shift – deslocamento da janela de dados (1 – penúltima barra no gráfico).
• Confidence interval – nível de significância do intervalo de confiança (quanto maior o nível de significância, mais amplo será o intervalo de confiança).
• Forecast horizon – previsão de volatilidade para um número específico de barras à frente.
• Plot – exibe no gráfico: previsão de volatilidade, resíduos padronizados, comparação entre a volatilidade realizada e GARCH-volatilidade, função de autocorrelação dos quadrados dos resíduos, função de autocorrelação dos quadrados padronizados dos resíduos.

Indicador iGARCH

Para obter uma visão inicial do modelo e dos dados em que desejamos aplicá-lo, o script GARCH. No entanto, para estimar e prever a volatilidade em tempo real, é desejável um algoritmo que recalibre os parâmetros do modelo a cada nova barra, ajustando-se rapidamente ao mercado em constante mudança. O indicador adaptativo iGARCH foi desenvolvido para atender a essa necessidade.

• Plot indicator – número de barras para as quais o cálculo do indicador será realizado.

O indicador prevê a volatilidade (desvio padrão condicional) e os intervalos de confiança para futuros incrementos de preço com um certo nível de confiabilidade um passo à frente. A previsão é exibida na barra zero, e os dados para calcular os parâmetros (Data window) começam a partir da primeira barra. Como os parâmetros do modelo são otimizados a cada nova barra, não é recomendável configurar valores muito altos para o Plot indicator (Bars), pois isso pode aumentar significativamente o tempo de cálculo (especialmente no caso de modelos com a distribuição t de Student).

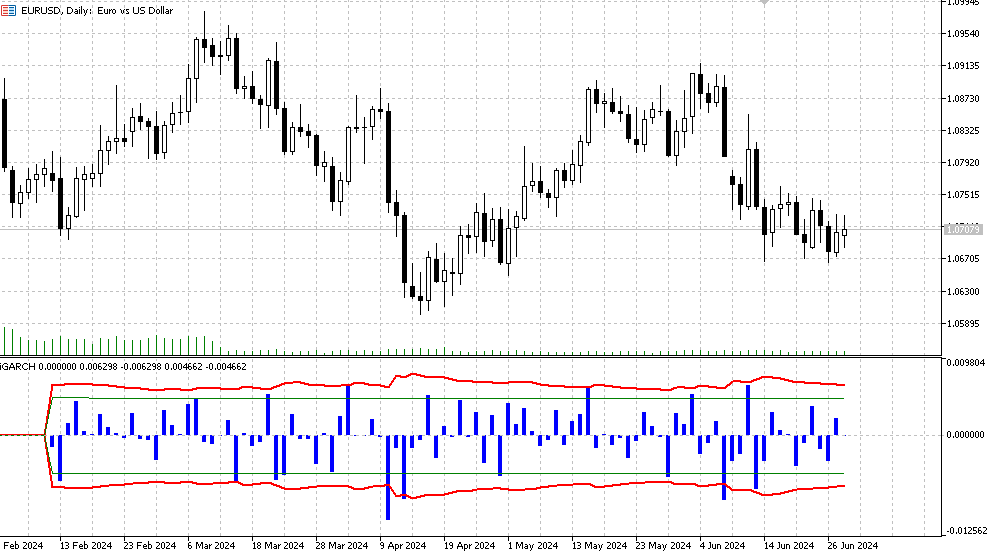
• Histograma – valores do retorno logarítmico LN(Yt/Yt-1).
• Linha vermelha – limites superior e inferior da previsão do desvio padrão condicional, determinados para o nível de significância do confidence interval (padrão, 90%). Isso significa que aproximadamente 90% dos incrementos logarítmicos dos preços estarão dentro desses limites,
• Linhas verdes – representam a volatilidade histórica usual, com seus limites inferior e superior, respectivamente.

Além disso, as seguintes informações são exibidas no log, sendo atualizadas a cada nova barra:

• Os valores mais recentes dos parâmetros otimizados (μ, ω, α, β, v),
• Os valores da função de verossimilhança (LLF),
• Os níveis de preços previstos para o nível de significância escolhido,
• Relatório de conclusão bem-sucedida da otimização,
• Valores previstos do desvio padrão condicional,
• Valores do desvio padrão incondicional teórico do GARCH,
• Valores do desvio padrão histórico.

Considerações finais

Neste trabalho, analisamos um dos modelos de heteroscedasticidade condicional mais populares: o modelo GARCH. Constatamos que os métodos padrão de estimativa de volatilidade, que assumem sua constância ao longo do tempo, não refletem adequadamente a realidade. Em contraste, o modelo GARCH considera a variabilidade da volatilidade ao longo do tempo, tornando-se mais apropriado para a análise das condições de mercado.

Com base no modelo GARCH(1,1), foi desenvolvido um indicador adaptativo que permite prever a volatilidade e os intervalos de confiança para os incrementos logarítmicos dos preços com antecedência. Isso possibilita uma avaliação probabilística das mudanças futuras nos preços, proporcionando uma gestão mais eficiente dos riscos associados às posições abertas.

Este indicador oferece a flexibilidade de utilizar tanto o modelo clássico de resíduos gaussianos quanto o modelo que assume que os resíduos seguem uma distribuição t de Student. Além disso, a otimização dos parâmetros do modelo é realizada a cada nova barra, permitindo uma rápida adaptação às condições atuais do mercado.

Para a estimativa dos parâmetros do modelo pelo método da máxima verossimilhança, utilizou-se o algoritmo de otimização MinBLEIC da biblioteca de análise numérica ALGLIB. O script GARCH calcula todas as estatísticas relevantes associadas ao modelo e fornece ferramentas visuais para a avaliação das dependências nos dados.

Assim, a aplicação do modelo GARCH em pesquisas econométricas e na análise financeira permite obter previsões mais precisas de volatilidade, o que melhora significativamente a gestão de riscos e a tomada de decisões de investimento.