От начального до среднего уровня: Рекурсивность

Введение

Представленные здесь материалы предназначены только для изучения. Ни в коем случае нельзя рассматривать это приложение как окончательное, цели которого будут иные, кроме изучения представленных концепций.

В предыдущей статье От начального до среднего уровня: объединение (II), было рассказано, как с помощью объединений можно решить проблему, которую, по мнению многих, невозможно устранить даже с помощью простого MQL5.

Хотя многие из вас могут подумать, что подобные вещи под силу только очень опытному программисту, на мой взгляд, данный материал - это нечто базовое и это может создать любой студент, изучающий программирование и обладающий базовыми знаниями.

Мы живем в такие времена, когда всё вокруг развивается стремительно, раскрывая нам разнообразные возможности, хотя многие люди всё еще не чувствуют себя достаточно уверенно, чтобы решиться приступить к программированию, которое может показаться немного смелым. Основываясь на том, что уже было показано, можно программировать различные вещи, но только не использовать события, поскольку пока мы не объяснили, как правильно работать и применять события.

Еще раз напомним, что MetaTrader 5 - это программа, ориентированная на события, и работающие на ней приложения тоже событийно-ориентированные, за исключением двух типов, которые не используют события в общем виде. Первое из них - скрипты, которые включены в приложения. Второе - сервисы. Что касается последнего приложения, мы рассмотрим его в более подходящий момент, поскольку манипулирование и программирование сервисов подразумевает детальное знание принципов работы MetaTrader 5. Фактически, сервисы - это (на мой взгляд) самый продвинутый тип приложения, который мы можем сориентировать на использование в MetaTrader 5.

Хотя, как и случается с этими двумя упомянутыми видами приложений, в нашем распоряжении у нас еще имеются индикаторы и советники. Оба они ориентированы на событийно-управляемое программирование, и на данном этапе говорить о них пока нецелесообразно. Однако есть и другие темы, которые необходимо объяснить, и они по-прежнему являются частью того, что я считаю основой для подготовки хорошего программиста, ориентированного на рынок.

Я говорю так, потому что многие считают, что они готовы выйти на этот рынок, но перед сложным испытанием, они с треском проваливают часто думают, что мир был к ним несправедлив. Но правда заключается в том, что они не были готовы к решению тех задач, с которыми хороший программист справляется просто, быстро и эффективно.

Специальный цикл

Итак, в некоторых статьях я рассказывал об операторах, ориентированных на работу с циклами. В принципе, в MQL5, как и во многих других языках, их три вида. Первые, и, на мой взгляд, самые простые, - это операторы while и do while. В дополнение к этим двум операторам у нас также есть оператор for. Однако существует и четвертый способ создания циклов, доступный практически во всех языках программирования. По крайней мере, я помню, что единственный язык, который не допускает этой четвертой формы, - BASIC. Это связано с тем, что BASIC не является структурированным языком, ориентированным на работу с функциями и процедурами. Но это не имеет значения для нас, поскольку мы работаем со структурированным языком MQL5, позволяющим использовать функции и процедуры, а значит, и четвертый способ создания цикла.

Обычно циклы создаются двумя способами: с помощью предназначенных для этого операторов или с помощью функции или процедуры. Да, использование функции или процедуры для создания цикла может показаться безумием, но, как бы невероятно это ни звучало, такое встречается гораздо чаще, чем вы думаете.

Когда мы используем оператор, направленный на создание взаимодействий с целью получения цикла, мы говорим, что используем интерактивный способ выполнения взаимодействий. А когда мы используем функции или процедуры для той же цели, мы говорим, что используем рекурсивный режим. Каждый новичок должен знать и понимать, как создавать рекурсию, ведь рекурсивный цикл значительно проще для понимания, чем интерактивный.

Почему я говорю об этом только сейчас? Для того, чтобы понять, как создать и использовать в своих кодах этот ресурс, то есть рекурсию, нам нужно хорошо знать некоторые моменты, такие как использование оператора if, а также хорошо понимать переменные и константы, время жизни, передачу значений, но в основном хорошо владеть типами данных и их ограничениями. В зависимости от того, что будет происходить, необходимо выбрать наиболее подходящий тип для каждого конкретного случая. Это нужно для того, чтобы избежать двусмысленности, которая может нарушить рекурсивное взаимодействие.

Обратите внимание на следующее: в отличие от интерактивного цикла, где всё организуется вокруг кода, который мы используем, в рекурсивном цикле ключевая точка может находиться в процедуре или функции далеко от того места, который мы смотрим в коде. А если возникнет какая-нибудь ошибка или баг, нам часто придется пробираться через весь код, пока не доберемся до той точки, где всё нужно вернуть на свои места. И эта задача не всегда под силу новичкам, поскольку это связано с самой природой рекурсии, которая совсем не то, чем кажется на первый взгляд. Другими словами, это цикл, но особого рода.

Для лучшего понимания, давайте рассмотрим пример. Но перед этим нужно предупредить в последний раз: каждый интерактивный цикл может быть переделан в рекурсивный, а каждый рекурсивный - в интерактивный. Хотя уровень сложности преобразования зависит от характера самого цикла, в целом интерактивные циклы работают быстрее на этапе выполнения кода. Однако рекурсивные циклы более просты для программирования. Поэтому одно компенсирует другое. Время, необходимое для преобразования рекурсивного цикла в интерактивный, может не компенсировать выгоду в производительности приложения. В целом, следует руководствоваться здравым смыслом и минимальной возможной стоимостью. Итак, теперь можем начинать.

И начнем мы с очень простого примера, чтобы было легче понять, как это происходит на практике. Ниже можно увидеть пример.

01. //+------------------------------------------------------------------+
02. #property copyright "Daniel Jose"
03. //+------------------------------------------------------------------+
04. void OnStart(void)
05. {
06.     Recursive(5);
07. }
08. //+------------------------------------------------------------------+
09. void Recursive(uchar arg)
10. {
11.     Print(__FUNCTION__, " ", __LINE__, "  :: ", arg);
12.     arg--;
13.     if (arg > 0)
14.         Recursive(arg);
15.     Print(__FUNCTION__, " ", __LINE__, "  :: ", arg);
16. }
17. //+------------------------------------------------------------------+

Код 01

После его выполнения код 01 сгенерирует то, что вы видите на изображении ниже:

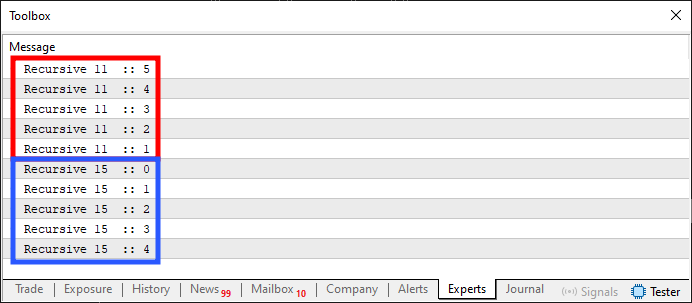
Рисунок 01

Но что это за безумие? Что ж, именно это, по сути, и делает рекурсивная подпрограммы. Звучит безумно, но зачастую это именно то, к чему мы стремимся. Обратите внимание, что результат, показанный на изображении 01, можно было бы получить с помощью циклов, но его получили с помощью рекурсии. Иными словами, когда функция или процедура вызывает саму себя или другую процедуру с целью создания цикла между ними. Многие программисты считают, что рекурсия присуща только функции или процедуре, хотя она не обязательно связана с этим. Единственный критерий, который мы должны соблюсти, - это наличие цикла без необходимости использовать оператора, направленного на создание цикла. Еще один интересный пример рекурсии можно увидеть ниже:

01. //+------------------------------------------------------------------+
02. #property copyright "Daniel Jose"
03. //+------------------------------------------------------------------+
04. void OnStart(void)
05. {
06.     Print("Result: ", Fibonacci(7));
07. }
08. //+------------------------------------------------------------------+
09. uint Fibonacci(uint arg)
10. {
11.     if (arg <= 1)
12.         return arg;
13. 
14.     Print(__FUNCTION__, " ", __LINE__, "  :: ", arg);
15. 
16.     return Fibonacci(arg - 1) + Fibonacci(arg - 2);
17. }
18. //+------------------------------------------------------------------+

Код 02

Это, пожалуй, самый типичный пример рекурсии; код 02 очень хорошо иллюстрирует рекурсию. Запустив его, мы получим результат, показанный ниже:

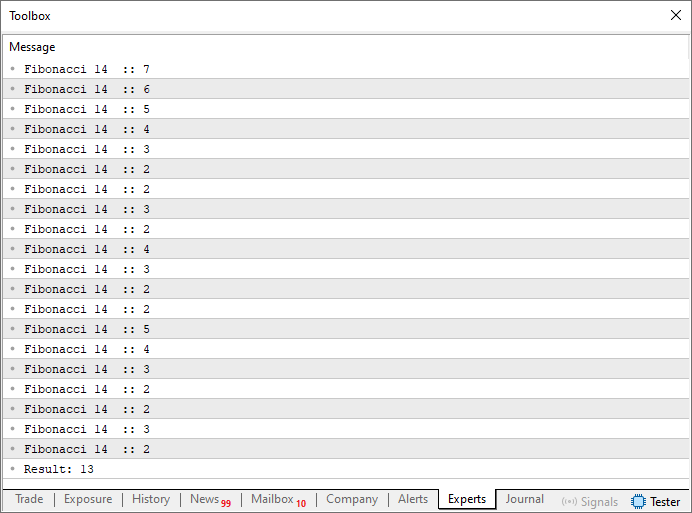
Рисунок 02

Итак, седьмое значение последовательности Фибоначчи равно 13. И если вы знаете последовательность, то понимаете, что это седьмое значение. "Но как этот код смог вычислить седьмое значение? Я действительно не понимаю, как это было возможно". Что ж, причина в том, что в строке 16 мы имеем минимальную факторизацию, которую необходимо выполнить для вычисления значения Фибоначчи. Если мы найдем математическое выражение, позволяющее вычислить значение Фибоначчи, то увидим нечто похожее на то, что показано ниже:

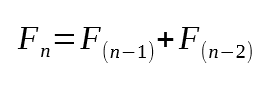
Рисунок 03

Теперь снова посмотрите на строку 16. Можете ли вы увидеть какие-либо сходства между математическим выражением на рисунке 03 и этой строкой 16? Это то, что мы используем для создания рекурсивной подпрограммы. Другими словами, мы уменьшаем объем работы до тех пор, пока не найдем точку, в которой ответ сходится к минимальному значению. И что же это за минимальное значение? Так вот, в случае с последовательностью Фибоначчи это значение может быть нулем или единицей. Вот что мы проверяем в строке 11.

Обратите внимание на следующее: точно так же, как в коде 01 мы провели сначала регрессивный подсчет, а затем, очевидно, прогрессивный, то же самое происходит и в коде 02, только в два этапа. На первом мы вычисляем значение arg минус один. Для этого мы выполняем серию вызовов до тех пор, пока не будет выполнена строка 12. В каждом вызове выполняется строка 14, которая показывает нам какое значение в arg. Поэтому у нас регрессивная последовательность в одном блоке. Затем всё это возвращается, и мы получаем вызов о снижении на две единицы. Я знаю, что это может показаться сложным, поэтому мы изменим несколько пунктов в коде 02, чтобы было проще понять, как данный код справляется с вычислением. Для этого мы используем приведенный ниже код:

01. //+------------------------------------------------------------------+
02. #property copyright "Daniel Jose"
03. //+------------------------------------------------------------------+
04. void OnStart(void)
05. {
06.     Print("Result: ", Fibonacci(5, 0, 0));
07. }
08. //+------------------------------------------------------------------+
09. uint Fibonacci(uint arg, uint call, int who)
10. {
11.     uint value = 0;
12. 
13.     Print(__FUNCTION__, " ", __LINE__, " Entry point [ ", call," ]  ARG: ", arg, " WHO: ", who);
14. 
15.     if (arg <= 1)
16.     {
17.         Print(__FUNCTION__, " ", __LINE__, " Number Callback [ ", call," ]  ARG: ", arg, " WHO: ", who);
18. 
19.         return arg;
20.     }
21. 
22.     value += Fibonacci(arg - 1, call + 1, 1);
23. 
24.     Print(__FUNCTION__, " ", __LINE__, " Value = ", value, "  >> New call with arg: ", arg);
25. 
26.     value += Fibonacci(arg - 2, call + 1, 2);
27. 
28.     Print(__FUNCTION__, " ", __LINE__, " General Return = ", value);
29. 
30.     return value;
31. }
32. //+------------------------------------------------------------------+

Код 03

Теперь я хочу извиниться перед всеми, но, к сожалению, нет другого способа объяснить проще происходящее здесь. Изображение с выполнением данного кода 03 показано ниже:

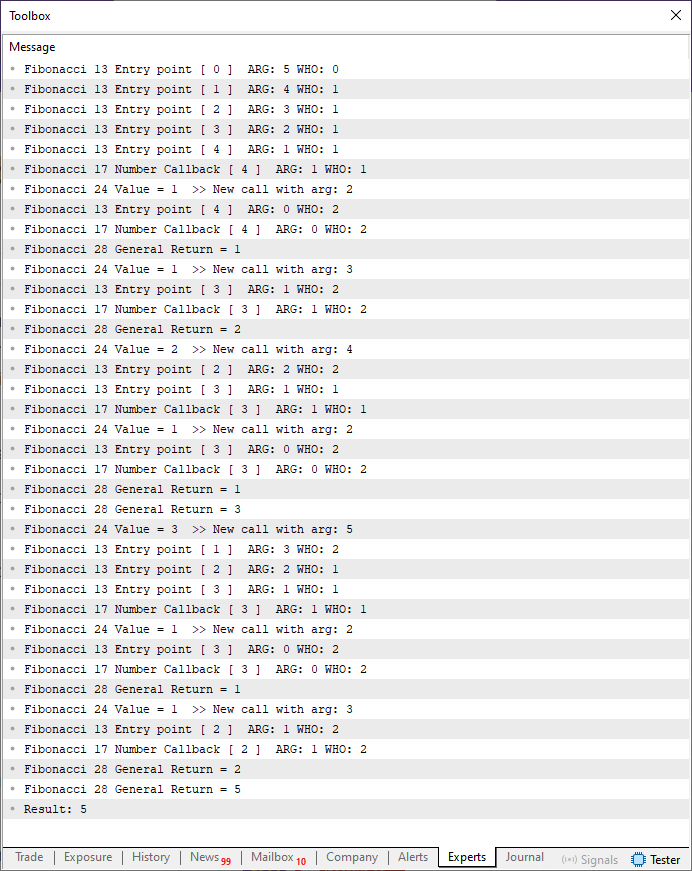
Рисунок 04

Изображение 04 длинновато, но стоит отметить, что мы изменили исполнение с семи до пяти элементов, и может показаться, что это не очень много, но так значительно сокращается количество элементов, на которые нужно обратить внимание. Но всё же вы должны понять следующее: каждый раз, когда выполняется строка 13, значит, мы входим в функцию, и у нас может быть либо немедленное возвращение, либо новый вызов. Однако то, что может показаться странным на первый взгляд - это именно значение строки 11. Многие могут подумать, что это помешает при получении окончательного результата. Но так можно подумать только потому, что вы не понимаете, что делает рекурсия с функцией или процедурой, в которой она применяется.

Именно поэтому на изображении 04 мы подробно показываем, что происходит, вплоть до того момента, когда коду 02 удается вычислить правильное значение.

Поскольку необходимо внимательно отнестись к тому, что будет объяснено ниже, я прошу вас убрать всё, что может отвлечь вас во время этого объяснения. Дело в том, что рекурсивные функции или процедуры могут сбить с толку при первом знакомстве с этим видом программирования.

Основываясь на изображении 04, давайте разберемся, что здесь происходит на самом деле. Во-первых, при выполнении строки 6 мы будем вызывать функцию Фибоначчи так, как если бы это был цикл. Не интерактивный, а рекурсивный. Это первый момент, который необходимо понять.

Следующий шаг - понять, что нам нужно ограничивающее условие. Как и в коде 01, любой цикл, в котором предполагается использовать рекурсию, нуждается в ограничивающем условии. В данном случае ограничивающим является условие, заданное в строке 15. Хотя уже было сказано, что рекурсию нужно свести к простому выражению, на самом деле то, что предотвращает превращение рекурсивного цикла в бесконечный - это ограничивающее условие. Это разные понятия. Прошу вас не использовать понятия не по назначению, это очень важно. Но опять же: 

То, что порождает рекурсию - это реализация минимального математического выражения. Но то, что именно ограничивает рекурсию - это условие, которое позволяет избежать появления бесконечного цикла.

Таким образом, именно строка 15 ограничивает рекурсию в коде 04. Рекурсия создается в строках 22 и 26. Уже в коде 02 ограничение будет в строке 11, а создание рекурсии - в 16.

Давайте теперь посмотрим, как это работает на самом деле. Поскольку наш начальный аргумент равен 5, выполним строку 13, а затем строку 22. При этом строка 22 снова вызовет строку 9, создавая тем самым цикл. Но обратите внимание на то, что во время вызова строки 22 мы уменьшаем аргумент на одну единицу. Затем наш стек начнет строиться, вызов за вызовом, пока в какой-то момент строка 15 не станет истинной.

В этот момент происходит нечто интересное: мы выполняем четвертый вызов и складываем в аргумент всё меньшие и меньшие значения. Затем, когда строка 15 станет true, будет выполнена строка 17, которая покажет нам текущее значение аргумента, а также текущее количество вызовов. Поскольку значение равно единице, мы возвращаем данное значение инициатору вызова, но инициатором вызова является не строка 6, а строка 22. Помните, что мы складываем серию вызовов. Теперь мы начинаем снимать вызовы со стека. При этом первым возвращаемым значением будет единица, которая добавляется к значению переменной, и данная переменная не будет терять свое значение между вызовами, а будет создавать новое значение при каждом новом вызове. Чтобы вам было легче понять, необходимо объяснить, как работает стек, но, на мой взгляд, это более продвинутый уровень. Хотя это не помешает вам понять, как работает рекурсия. Просто надо быть внимательным.

Мы уже вычислили, каким будет первое значение. Однако из-за выражения на рисунке 03, мы должны пересчитать функцию в строке 9. По этой причине в строке 26 мы делаем новый вызов. Будьте внимательны, иначе невозможно будет понять рекурсию составных функций, таких как та, которая вычисляет Фибоначчи.

Вызов в строке 22 каждый раз уменьшал значение arg на единицу. Когда arg был равен единице, при следующем вызове значение arg, присутствующее в строке 22 (т. е. в предыдущем вызове), всё еще было равно двум. Итак, при выполнении строки 24 из-за того, что в вызове строки 22 arg был равен единице, в строке 24 мы будем иметь дело не с arg, равным единице, а с arg, равным двум.

Подобные вещи, когда мы слышим их впервые, очень смущают. Я знаю, и именно по этой причине я использую простейшую рекурсию, как было показано в коде 01, где сначала выполняется регрессивный отсчет, а затем прогрессивный. Однако прогрессивный отсчет возник только потому, что мы складывали значения. Таким образом, когда мы начали снимать со стека эти же значения, у нас возникла иллюзия, что был создан прогрессивный счет, в то время как на самом деле он не был реализован. Всё это связано с условием, присущим использованию рекурсивных вызовов.

Хорошо, давайте успокоимся на секунду. В этот самый момент, при вызове строки 26, arg равен двум. Однако, поскольку перед повторным вызовом функции мы уменьшаем arg на две единицы, при выполнении строки 13 значение будет уже равно нулю. В этом случае строка 15 будет true, и функция вернется. Поэтому в строке 28 будет выведено значение, равное единице. То есть мы вычисляем Фибоначчи первого элемента последовательности.

Вспомните: мы сделали пять вызовов и вернули только первый. Так что теперь в строке 22 значение будет равно единице. "Но подождите, разве оно уже не равно единице?" Нет, уважаемый читатель, значение переменной было равно единице в вызове, который мы только что завершили. Когда функция вернулась, то мы вернулись к строке 22, а до этого значение было равно нулю. Теперь оно равно единице. При выполнении строки 24 и снятии со стека одного вызова, arg становится равным двум. Данный момент происходит в строке 24. Не упускайте последовательность. Так как arg равен двум, а нам нужно выполнить строку 26, где мы вычтем из этого аргумента две единицы, то теперь функция получит arg равный нулю, а WHO равным 2, это происходит так, потому что мы осуществляем вызов из строки 26.

Так как arg равен нулю, то строка 15 равна true, и мы возвращаем значение ноль в строке 19. Теперь, возвращаясь к строке 26, мы прибавляем ранее вычисленное значение единицы к новому значению нуля. Таким образом, мы получаем значение, равное единице, то есть мы только что вычислили второй элемент последовательности Фибоначчи.

И мы возвращаемся в строку 22, поскольку мы сняли со стека только два значения, поэтому нам нужно снять пять, и значение один присваивается переменной value. Однако теперь arg равен 3. Это действительно интересная часть, ведь из-за того, что arg равен 3, при вычитании двух в строке 26, то функция получит значение один, и, поскольку это делает строку 15 равной true, мы вернем единицу в строке 19. Таким образом, значение переменной теперь равно 2.

Таким образом, нам удается вычислить третий элемент последовательности. Осталось снять со стека еще два элемента. Снова возвращаемся к строке 22, где значение данной переменной равно 2, а arg - 4. А что произойдет, когда будет выполнена строка 26? Угадали? Функция Фибоначчи будет вызвана снова, но теперь с arg, равным 2. Помните, что перед вызовом функции мы вычитаем 2 в строке 26.

Итак, поскольку arg в этот момент равен 2, строка 15 завершится неудачей, и строка 22 будет выполнена еще раз. Только в этот момент переменная значения равна нулю, а не 2. Это другое значение было сохранено в стеке. Хорошо, поскольку arg равен 2, а нам нужно вычесть единицу перед вызовом, в строке 15 arg будет равен единице, и вернется единица. Теперь в строке 22 значение равно единице, поэтому будет выполнена строка 26. В этот момент при вычитании 2 из arg вызывается функция и происходит вычитание 2. Как вы знаете, это вернет ноль. А строка 30 вернет значение 1, но куда оно вернется? Что ж, вы будете возвращены на 26-ю строку, которая и сделала этот вызов. Помните, что в данный момент значение равно 2. Поскольку возврат был один, теперь значение равно 3. Таким образом, мы только что вычислили четвертый элемент последовательности. Одного не хватает. (СМЕХ)

Думаю, ваш мозг уже запутался в этих возвратах и вызовах, но в этом последнем элементе мы будем действовать по-другому, поскольку всё это станет огромным повторением шагов. Это происходит так, потому что теперь, в строке 26, значение arg равно 5, а value равно 3. Так как arg нужно будет вычесть пополам, будет произведена новая серия вызовов. Думаю, всё, что вам нужно понять, мы уже объяснили.

Хотя, как вы могли заметить, существует проблема, о которой говорилось в начале статьи: рекурсию легко запрограммировать, но выполняется она медленнее. Однако мы можем сгенерировать эквивалентный код, который использует интерактивность вместо рекурсии. Благодаря этому мы выигрываем в скорости, хотя код будет немного сложнее.

Чтобы проверить это, давайте посмотрим, как будет выполняться подобный код, целью которого является вычисление последовательности Фибоначчи. Существует несколько способов сделать это, но чуть ниже можно увидеть один из них:

01. //+------------------------------------------------------------------+
02. #property copyright "Daniel Jose"
03. //+------------------------------------------------------------------+
04. void OnStart(void)
05. {
06.     const uchar who = 6;
07. 
08.     Print("Result: ", Fibonacci_Recursive(who));
09.     Print("Result: ", Fibonacci_Interactive(who));
10. }
11. //+------------------------------------------------------------------+
12. uint Fibonacci_Recursive(uint arg)
13. {
14.     if (arg <= 1)
15.         return arg;
16. 
17.     return Fibonacci_Recursive(arg - 1) +  Fibonacci_Recursive(arg - 2);
18. }
19. //+------------------------------------------------------------------+
20. uint Fibonacci_Interactive(uint arg)
21. {
22.     uint v, i, c;
23. 
24.     for (c = 0, i = 0, v = 1; c < arg; i += v, c += 2)
25.         v += i;
26. 
27.     return (c == arg ? i : v);
28. }
29. //+------------------------------------------------------------------+

Код 04

Обратите внимание, что здесь мы действуем с обоими способами работы с циклами. Первый - через рекурсию, второй - через интерактивность. Я спрашиваю: как вы думаете, что легче для понимания? Учитывая данный ответ, как вы думаете, какой вариант быстрее с точки зрения времени выполнения? Учитывая то, что вы уже знаете об обоих методах, можно выполнить одно и то же вычисление.

Поскольку я знаю, что эта интерактивная функция, реализуемая в строке 20, может показаться кому-то странной, давайте дадим краткое пояснение.

В строке 22 мы объявляем нужные переменные. Уже в строке 24 мы запускаем основной цикл вычислений. Это самое интересное. Обратите внимание, что мы инициализируем значения перед выполнением вычислений. Кроме того, когда искомый элемент нечетный (первый, третий, пятый, седьмой и т. д.), переменная v указывает на правильное значение. Однако, когда искомые элементы являются четными, значение i указывает на правильный результат. Но почему?

Причина в том, что переменная c будет каждый раз увеличиваться на две единицы, чтобы мы не превысили правильный результат. Но поскольку при каждом взаимодействии нам придется добавлять предыдущее значение к новому, а мы не обмениваемся значениями i и v, то в данной интерактивной функции есть такая маленькая деталь. Есть способы реализовать это без подобных проблем, хотя я считаю, что в этом нет необходимости, поскольку взаимодействие цикла сообщает нам, какими будут следующее и текущее значения. Таким образом, всё, что нам нужно сделать - это использовать тернарный оператор, чтобы вернуть правильный результат. Без этой небольшой поправки мы могли бы просматривать следующий элемент последовательности или старый элемент последовательности в зависимости от того, будет ли искомый аргумент или элемент нечетным или четным, а также от того, используем ли мы значение i или v.

В качестве доказательства того, что код 04 работает, ниже приведен ответ на его выполнение. Чтобы получить другие значения и проверить оба способа вычисления последовательности Фибоначчи, просто измените значение константы в строке 6. Но помните, что ряд Фибоначчи растет очень быстро, и, поскольку существуют ограничения, связанные с используемыми типами, будьте осторожны, не переусердствуйте в попытках увидеть очень далекий элемент, так как в итоге вы создадите проблемы в конечном результате.

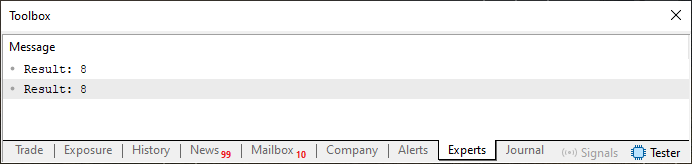
Рисунок 05

Существуют способы и средства, позволяющие исправить ситуацию и вывести на экран любое числовое значение, которое только может храниться в памяти компьютера. Однако, поскольку это несколько более сложная тема, я оставлю ее для более подходящего случая. Но, чтобы разбудить ваше любопытство, задам вам вопрос: как, по-вашему, программисты умудряются вычислять значение π и других иррациональных констант с тысячами знаков после запятой, если в их программах нет типов, которые обычно используются в компьютерах? У нас нет способов для достижения этой цели.

Как уже было сказано, это более сложная задача, и вам нужно понять некоторые концепции, которые еще не были объяснены. Но это связано не с тем, что с уже показанными знаниями это было бы невозможно (если бы это было так, то это было бы большой ложью), ведь действительно это возможно сделать с концепциями, которые уже были изучены к настоящему моменту, среди которых использование рекурсии. Однако работа по внедрению кода будет намного сложнее, так как придется адаптировать некоторые элементы к формату, который не очень легко понять с самого начала.

Заключительные идеи

Эта статья была написана с целью представить очень интересную концепцию программирования, однако к ней следует относиться с большим предостережением, поскольку неправильное использование или неверная интерпретация того, что здесь показано, превращает относительно простые программы в нечто неоправданно сложное. Однако при правильном использовании и адаптации к соответствующим ситуациям рекурсия становится отличным помощником в решении задач, которые в противном случае были бы гораздо более трудоемкими и сложными.

Возьмите за правило использовать рекурсию всегда, когда это возможно, или когда у вас будет математическое выражение, которое вы не можете переписать интерактивно. Но помните, что большое количество вызовов между каждой факторизацией может сделать ваш код медленнее обычного. В этом случае попробуйте преобразовать рекурсию в интерактивный цикл, который, хотя и сложнее создать в начале, значительно ускоряет выполнение кода, особенно когда необходимо вычислить или скорректировать определенным образом очень большие массивы данных.