Teoria do caos no trading (Parte 1): Introdução, aplicação nos mercados financeiros e o indicador de Lyapunov

Introdução à teoria do caos e sua conexão com os mercados financeiros

O que é a teoria do caos e como pode ser aplicada nos mercados financeiros? Vamos explorar essa questão hoje.

Está planejado um ciclo de artigos que responderá às perguntas: o que é a teoria do caos? Como o conceito de caos no mercado, proposto por Bill Williams, difere da teoria clássica, cientificamente fundamentada? Como essa teoria descreve o mercado? Como pode ser aplicada e em quais áreas do trading? 

Vamos abordar tanto a base teórica quanto criar uma série de ferramentas que podem ajudar os traders em suas operações.

Conceitos principais da teoria do caos: atratores, fractais e o efeito borboleta

A teoria do caos é uma área interessante da matemática e da física que nos ajuda a compreender melhor sistemas complexos, como os mercados financeiros. Vamos analisar três ideias principais dessa teoria:

1. Atratores: são como ímãs para os estados do sistema, para os quais o sistema tende ao longo do tempo. Nos mercados financeiros, esses atratores podem ser preços específicos ou padrões recorrentes que o mercado revisita continuamente. Os atratores estranhos, especialmente encontrados em sistemas caóticos, são particularmente interessantes. Eles parecem complexos e podem revelar uma ordem oculta no comportamento aparentemente aleatório do mercado.

2. Fractais: são figuras geométricas que se apresentam da mesma forma em qualquer nível de ampliação. Nos mercados financeiros, os fractais podem ser observados nos gráficos de preços, pois o mesmo padrão pode ser identificado tanto em intervalos de tempo curtos quanto longos. Isso permite que os mesmos métodos de análise sejam aplicados em diferentes escalas temporais, auxiliando na avaliação de riscos e na análise de mudanças nos preços.

3. Efeito borboleta: esse efeito demonstra que até mesmo pequenas mudanças no início podem levar a consequências grandes e inesperadas. No mundo financeiro, isso significa que pequenas alterações nos dados ou no modelo podem modificar significativamente as previsões. Isso torna o prognóstico de longo prazo nos mercados financeiros desafiador e ressalta a importância de atualizar e adaptar constantemente nossos modelos às novas condições.

Compreender essas ideias oferece aos analistas e traders uma nova perspectiva sobre os mercados, ajudando-os a identificar padrões ocultos e possíveis pontos de entrada ou saída de negociações. A teoria do caos proporciona uma nova abordagem para análise e previsão, superando os modelos convencionais.

Sistemas caóticos no contexto dos mercados financeiros

Os mercados financeiros possuem características de sistemas caóticos, algo fundamental para sua análise e previsão.

• Não linearidade: pequenas mudanças provocam oscilações desproporcionais.
• Sensibilidade às condições iniciais: eventos pequenos podem gerar movimentos significativos.
• Autorganização: formação de tendências e padrões sem controle externo.
• Estrutura fractal: gráficos de preços exibem propriedades fractais.
• Previsibilidade limitada: a precisão das previsões diminui com o aumento do horizonte temporal.
• Atratores estranhos: oscilações em torno de determinados níveis ou estados.
• Transições entre estados: mudanças súbitas de estabilidade para volatilidade.

Compreender isso ajuda no desenvolvimento de métodos avançados de análise, gerenciamento de riscos e algoritmos de trading.

Volatilidade no trading

A volatilidade é um conceito fundamental no trading e nas finanças, estando diretamente ligada à teoria do caos. Ela mede a intensidade das variações no preço de um ativo em determinado período. No trading, a volatilidade é usada para avaliar riscos, precificar opções e desenvolver estratégias de negociação.

Os mercados financeiros frequentemente se comportam como sistemas caóticos. Eles podem reagir de maneira inesperada a pequenas alterações, de forma similar ao efeito borboleta. Além disso, os mercados têm a capacidade de se autorganizar, criando tendências e padrões sem intervenção externa. Gráficos de preços apresentam semelhança em diferentes escalas de tempo, o que caracteriza as propriedades fractais.

A teoria do caos oferece ferramentas exclusivas para a análise da volatilidade, como a reconstrução do espaço de fase e o índice de Lyapunov, que ajudam a identificar padrões ocultos e a avaliar a previsibilidade. Esses modelos caóticos podem complementar métodos tradicionais, como os modelos GARCH, principalmente na determinação de regimes de mercado e na previsão de mudanças bruscas na volatilidade.

Compreender a natureza caótica da volatilidade possibilita uma análise mais precisa e previsões mais confiáveis da dinâmica dos mercados, permitindo o desenvolvimento de estratégias de negociação eficazes e métodos avançados de gerenciamento de riscos.

Teoria clássica do caos e abordagem de Bill Williams

A teoria clássica do caos e o conceito de "caos" de Bill Williams diferem significativamente. A teoria clássica do caos baseia-se em princípios matemáticos rigorosos e emprega ferramentas complexas para análise de sistemas. Por outro lado, Williams adota uma abordagem intuitiva e utiliza indicadores técnicos, como Alligator e Fractals, que não estão diretamente relacionados à teoria matemática do caos.

A teoria clássica do caos é fundamentada em princípios matemáticos precisos e em pesquisas científicas sobre dinâmica não linear. Ela considera o caos um comportamento determinístico, porém imprevisível, analisado por meio de métodos matemáticos exatos. Já Williams utiliza o termo "caos" de maneira mais ampla, referindo-se à imprevisibilidade geral dos mercados. Seus métodos são voltados para a aplicação prática no trading, explorando a natureza caótica dos mercados apenas de maneira superficial.

Embora Williams tenha adaptado alguns termos da teoria do caos, sua abordagem está mais alinhada ao uso de análise técnica e à interpretação pessoal dos movimentos do mercado. Especialistas em teoria do caos têm criticado o uso do termo "caos" nesse contexto, considerando-o potencialmente enganoso.

Teoria do caos na análise dos mercados

A teoria do caos oferece uma nova perspectiva para a análise da dinâmica de mercado, reconhecendo sua complexidade e imprevisibilidade. Ao contrário dos métodos tradicionais, ela incorpora a não linearidade e a complexidade dos processos de mercado.

Esse enfoque ajuda a explicar por que eventos pequenos podem gerar movimentos significativos nos mercados e por que as previsões de longo prazo muitas vezes são imprecisas. A teoria do caos permite analisar fenômenos como quebras de mercado e bolhas financeiras, oferecendo novas ferramentas para uma avaliação de mercado mais precisa e adaptativa.

Indicador de Lyapunov e sua aplicação na análise de séries temporais financeiras

O indicador de Lyapunov é uma ferramenta da teoria do caos que ajuda a compreender a sensibilidade de um sistema às condições iniciais. Nos mercados financeiros, isso é particularmente importante, pois permite avaliar o impacto de pequenas alterações nas condições do mercado sobre os preços.

Se o indicador de Lyapunov for positivo, isso indica que o sistema se comporta de maneira caótica, de modo que pequenas mudanças podem resultar em grandes oscilações no futuro. Se o indicador for negativo, o sistema é mais estável, e as variações de preço serão menores.

Com esse indicador, é possível identificar quando o mercado se torna mais instável ou previsível. Valores altos podem sinalizar mudanças bruscas nos preços, o que é útil para avaliar riscos e ajustar estratégias de negociação.

Para calcular o indicador de Lyapunov em dados financeiros, é necessário reconstruir o espaço de fase e analisar como pontos próximos nesse espaço divergem. Esse processo exige a escolha de parâmetros adequados, como dimensionalidade e atraso temporal.

Um aspecto importante do uso do indicador de Lyapunov é avaliar por quanto tempo as previsões permanecem precisas. Quanto maior o valor do indicador, menor o período em que os prognósticos são confiáveis. Isso é especialmente relevante para o trading de curto prazo e o gerenciamento de riscos.

Agora podemos avançar para a implementação do indicador de Lyapunov em MQL5.

Implementação do indicador de Lyapunov com MQL5

Este indicador implementa o cálculo do indicador de Lyapunov para análise de séries temporais financeiras. Ele permite avaliar o grau de caoticidade do mercado e a previsibilidade potencial dos movimentos de preço.

Parâmetros de entrada:

input int    InpTimeLag = 1;       // Time lag
input int    InpEmbedDim = 2;      // Embedding dimension
input int    InpDataLength = 1000; // Data length for calculation

• InpTimeLag: define o atraso temporal para reconstrução do espaço de fase.
• InpEmbedDim: especifica a dimensionalidade da incorporação para a reconstrução do espaço de fase.
• InpDataLength: define o número de velas usadas no cálculo do indicador.

Há uma variável global:

double LyapunovBuffer[];

Inicialização:

int OnInit()
{
   SetIndexBuffer(0, LyapunovBuffer, INDICATOR_DATA);
   IndicatorSetInteger(INDICATOR_DIGITS, 5);
   IndicatorSetString(INDICATOR_SHORTNAME, "Lyapunov Exponent");
   return(INIT_SUCCEEDED);
}

Na função OnInit(), configuramos o buffer do indicador, definimos a precisão de exibição para 5 casas decimais e atribuímos um nome curto ao indicador.

int OnCalculate(const int rates_total,
                const int prev_calculated,
                const datetime &time[],
                const double &open[],
                const double &high[],
                const double &low[],
                const double &close[],
                const long &tick_volume[],
                const long &volume[],
                const int &spread[])
{
   int start;
   if(prev_calculated == 0)
      start = InpDataLength;
   else
      start = prev_calculated - 1;
   
   for(int i = start; i < rates_total; i++)
   {
      LyapunovBuffer[i] = CalculateLyapunovExponent(close, i);
   }
   
   return(rates_total);
}

A função OnCalculate() é chamada a cada tick e realiza o cálculo do indicador de Lyapunov para cada vela, a partir do valor definido em InpDataLength.

Cálculo do indicador de Lyapunov:

double CalculateLyapunovExponent(const double &price[], int index)
{
   if(index < InpDataLength)
      return 0;
   
   double sum = 0;
   int count = 0;
   
   for(int i = 0; i < InpDataLength - (InpEmbedDim - 1) * InpTimeLag; i++)
   {
      int nearestNeighbor = FindNearestNeighbor(price, index - InpDataLength + i, index);
      if(nearestNeighbor != -1)
      {
         double initialDistance = MathAbs(price[index - InpDataLength + i] - price[nearestNeighbor]);
         double finalDistance = MathAbs(price[index - InpDataLength + i + InpTimeLag] - price[nearestNeighbor + InpTimeLag]);
         
         if(initialDistance > 0 && finalDistance > 0)
         {
            sum += MathLog(finalDistance / initialDistance);
            count++;
         }
      }
   }
   
   if(count > 0)
      return sum / (count * InpTimeLag);
   else
      return 0;
}

A função CalculateLyapunovExponent() implementa o algoritmo para calcular o indicador local de Lyapunov. Ela utiliza o método dos vizinhos mais próximos para estimar a divergência de trajetórias no espaço de fase reconstruído.

Busca pelo vizinho mais próximo:

int FindNearestNeighbor(const double &price[], int startIndex, int endIndex)
{
   double minDistance = DBL_MAX;
   int nearestIndex = -1;
   
   for(int i = startIndex; i < endIndex - (InpEmbedDim - 1) * InpTimeLag; i++)
   {
      if(MathAbs(i - startIndex) > InpTimeLag)
      {
         double distance = 0;
         for(int j = 0; j < InpEmbedDim; j++)
         {
            distance += MathPow(price[startIndex + j * InpTimeLag] - price[i + j * InpTimeLag], 2);
         }
         distance = MathSqrt(distance);
         
         if(distance < minDistance)
         {
            minDistance = distance;
            nearestIndex = i;
         }
      }
   }
   
   return nearestIndex;
}

A função FindNearestNeighbor() encontra o ponto mais próximo no espaço de fase reconstruído, usando a distância euclidiana.

Interpretação dos resultados

• Valores positivos do indicador apontam para a presença de comportamento caótico no mercado.
• Valores negativos indicam uma dinâmica de preços mais estável e potencialmente mais previsível.
• Quanto maior o valor absoluto do indicador, mais intensamente a característica correspondente (caoticidade ou estabilidade) se manifesta.

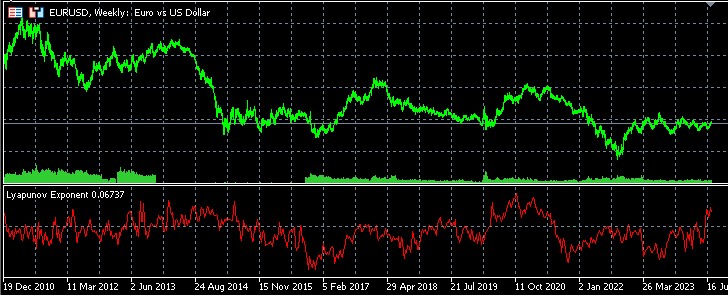
Análise estatística de reversões e continuidades de tendência com o uso do indicador de Lyapunov

Para aprofundar o estudo da relação entre o indicador de Lyapunov e a dinâmica dos mercados financeiros, desenvolvemos um script especializado em MQL5. Este instrumento realiza uma análise estatística detalhada das reversões e continuidades de tendência, considerando os valores do indicador de Lyapunov, fornecendo informações valiosas sobre o comportamento do mercado para traders e analistas.

O script trabalha com dados históricos do instrumento financeiro selecionado e analisa um número predefinido de barras. Para cada barra, o indicador de Lyapunov local é calculado utilizando o método de reconstrução do espaço de fase e a busca pelos vizinhos mais próximos. Essa abordagem permite avaliar o grau de caoticidade do sistema em cada ponto específico do tempo.

Paralelamente ao cálculo do indicador de Lyapunov, o script analisa a dinâmica de preços, identificando reversões e continuidades de tendência. Uma reversão é definida como uma situação em que o preço de fechamento atual está acima do anterior, mas o seguinte está abaixo do atual (ou vice-versa). Todos os demais casos são considerados como continuidade de tendência.

Uma característica central do script é sua capacidade de correlacionar os momentos de reversão e continuidade da tendência com os valores do indicador de Lyapunov. Isso possibilita identificar padrões estatísticos entre o comportamento caótico do mercado e sua dinâmica de preços. O script contabiliza o número de reversões e continuidades de tendência ocorridas em períodos de valores positivos e negativos do indicador de Lyapunov.

Ao finalizar a análise, o script apresenta estatísticas detalhadas, incluindo valores absolutos e percentuais de reversões e continuidades de tendência associados a valores positivos e negativos do indicador de Lyapunov. Essas informações ajudam os traders a avaliar a frequência com que reversões de tendência coincidem com períodos de maior caoticidade no mercado e, inversamente, a frequência com que continuidades de tendência ocorrem em períodos mais estáveis.

Interpretação dos resultados da análise estatística

Os resultados obtidos da análise estatística das reversões e continuidades de tendência utilizando o indicador de Lyapunov fornecem insights interessantes sobre a dinâmica do mercado EURUSD no timeframe de uma hora.

Um ponto notável é a distribuição quase equilibrada de eventos entre valores positivos e negativos do indicador de Lyapunov. Tanto as reversões quanto as continuidades de tendência ocorrem em aproximadamente metade dos casos, com o indicador Lyapunov apresentando valores positivos ou negativos. Isso pode indicar que o mercado EURUSD no gráfico de uma hora apresenta um equilíbrio entre períodos de relativa estabilidade e caoticidade.

Os valores positivos do indicador de Lyapunov, frequentemente associados a comportamentos mais caóticos e imprevisíveis, foram observados em pouco mais da metade dos casos (50,61% para reversões e 51,09% para continuidades). Esse dado pode sugerir uma leve predominância de períodos de maior volatilidade ou incerteza no mercado.

Os valores negativos do indicador de Lyapunov, geralmente interpretados como um sinal de comportamento mais ordenado e menos caótico do sistema, foram observados em 49,39% dos casos de reversão e 48,91% dos casos de continuidade de tendência. Esses períodos podem ser caracterizados por movimentos de preços mais previsíveis, que seguem padrões mais definidos.

É interessante observar que a proporção percentual de reversões e continuidades de tendência é praticamente idêntica tanto para valores positivos quanto negativos do indicador de Lyapunov. A diferença é inferior a 0,5% em ambos os casos. Isso sugere que o indicador de Lyapunov, por si só, não é um fator determinante para prever reversões ou continuidades de tendência.

Essa distribuição uniforme de eventos entre valores positivos e negativos de Lyapunov pode indicar a natureza complexa do mercado do par EURUSD, no qual períodos de estabilidade e caoticidade se alternam com uma frequência aproximadamente igual. 

Considerações finais

A teoria do caos oferece uma abordagem inovadora para a análise dos mercados financeiros, proporcionando uma compreensão mais profunda de sua natureza complexa e não linear. Neste artigo, exploramos os principais conceitos da teoria do caos — atratores, fractais e o efeito borboleta — e sua aplicação às séries temporais financeiras. Demos destaque especial ao indicador de Lyapunov, apresentando-o como uma ferramenta para avaliar o grau de caoticidade na dinâmica do mercado.