Возможности Мастера MQL5, которые вам нужно знать (Часть 29): Темпы обучения и многослойные перцептроны

Введение

Мы завершаем наш обзор различных форматов темпа обучения применительно к производительности советника рассмотрением адаптивного темпа обучения и темпа обучения одного цикла. Формат этой статьи будет соответствовать подходу, который мы использовали в предыдущей статье - отчеты тестирования будут располагаться отдельно по разделам, посвященным разным форматам, а не в конце статьи.

Прежде чем перейти к делу, я хотел бы упомянуть некоторые другие важные аспекты машинного обучения, которые могут существенно повлиять на эффективность модели. Одним из них является пакетная нормализация входных данных. Я уже касался этого в предыдущих статьях, объясняя, почему это важно, однако в нашей следующей статье мы подробно рассмотрим этот вопрос. Однако на данный момент при проектировании режима и формата сети пакетная нормализация рассматривается совместно с алгоритмами активации, которые будут использоваться моделью или сетью. До сих пор мы использовали активацию soft plus, которая имеет тенденцию давать несвязанные результаты, то есть в отличие от активаций TANH или Sigmoid, которые дают результаты в диапазонах от -1,0 до +1,0 и от 0,0 до 1,0 соответственно, soft plus может довольно часто выдавать результаты, которые не проходят проверку на корректность действительного числа и, таким образом, делают процесс обучения и прогнозирования недействительным.

Поэтому в качестве подготовки к следующей статье мы вносим некоторые изменения не только в алгоритмы активации, используемые нашими сетями, но и в тестируемый форекс-символ. Мы используем алгоритм активации с выходной привязкой Sigmoid для всех активаций слоев. Более того, наша тестовая пара форекс-символов будет иметь свои входные данные (которые в нашем случае по-прежнему являются необработанными ценами, поскольку мы не выполняем пакетную нормализацию) в диапазоне от 0,0 до 1,0. Существует не так много валютных пар, цены на которые в течение нашего тестового периода (2023 год) находились бы в этом диапазоне, однако пара NZDUSD находится в этом диапазоне, поэтому мы будем использовать ее.

Это делает сравнение результатов производительности с результатами, приведенными в предыдущей статье, нецелесообразным, поскольку основа изменилась. Однако с этой новой сетью, алгоритмом активации и валютной парой форматы темпа обучения, рассмотренные в предыдущей статье, по-прежнему могут быть протестированы читателем, чтобы получить сопоставимое сравнение, при поиске своего метода темпа обучения. Кроме того, результаты тестов, представленные здесь, а часто и в этих статьях в целом, получены не в самых лучших условиях, что вполне ожидаемо. Они показаны только в ознакомительных целях, поэтому задача читателя — точно настроить входные данные советника для достижения оптимального результата не только с использованием высококачественных исторических данных, но и, желательно, в ходе форвард-тестирования после периода тестирования стратегии на демо-счетах.

Итак, в статье показан только потенциал. Темп обучения является очень чувствительным показателем производительности, как это очевидно из расхождений в результатах тестов, которые мы получили в предыдущей статье. Адаптируемый темп обучения призван решить проблему слишком большого количества параметров, определяющих идеальный темп обучения модели. Напомним, что темп обучения сам по себе является всего лишь средством для получения идеальных весов и смещений сети, поэтому при использовании этих методов следует избегать использования дополнительных параметров, таких как степень полинома, которую мы рассматривали в предыдущей статье, или минимальный темп обучения. Чтобы минимизировать параметризацию, адаптируемое обучение генерирует темп обучения для каждого параметра слоя, основываясь на его градиенте обучения. В результате возникает ситуация, когда почти все параметры имеют собственный темп обучения, однако необходимые входные данные минимальны. Распространены четыре формата адаптируемых темпов обучения, а именно: адаптивный градиент, адаптивное среднеквадратичное значение, адаптивное среднеэкспоненциальное значение и адаптивная дельта. Рассмотрим каждый из них по отдельности.

Адаптивный градиент

Это, вероятно, самый простой формат среди адаптируемых темпов обучения, однако он по-прежнему придерживается настраиваемого темпа обучения для каждого параметра во всех слоях, несмотря на наличие одного входного сигнала — начального темпа обучения. Реализация темпа обучения на основе параметров требует настроек, которые распространяются на наш родительский класс Expert за пределами класса пользовательского сигнала, как это было в предыдущей статье о темпах обучения. Это связано с тем, что градиенты обучения, которые служат входными данными, определяющими темп обучения, доступны только из интерфейса класса родительской сети. Мы можем вносить изменения в класс и делать их общедоступными, но, учитывая необходимость дополнительной настройки (где потенциально каждый вес и смещение слоя могут иметь свой собственный темп обучения), вызов обратного распространения может потерять необходимую эффективность. Благодаря расчету каждого отдельного темпа обучения в процессе обучения сеть настраивается на работу почти так же эффективно, как при использовании единого темпа обучения для всех параметров, поскольку вычисленный темп обучения применяется немедленно к конкретному параметру, вместо того, чтобы сначала разрабатывать специальную структуру для размещения новых темпов обучения для всех параметров, потом выполнять итеративный процесс вычисления каждого темпа обучения по отдельности, а затем применить каждый индивидуальный темп обучения. В последнем случае код не стал бы более громоздким, но потребовались бы более интенсивные вычисления. Однако сначала мы вносим изменения в родительский сетевой класс, вводя два параметра векторного массива adaptive_gradients и adaptive_deltas, как показано в новом интерфейсе класса ниже:

//+------------------------------------------------------------------+
//|                                                                  |
//+------------------------------------------------------------------+
enum ENUM_ADAPTIVE
{  ADAPTIVE_NONE = -1,
   ADAPTIVE_GRAD = 0,
   ADAPTIVE_RMS = 1,
   ADAPTIVE_ME = 2,
   ADAPTIVE_DELTA = 3,
};
//+------------------------------------------------------------------+
//|                                                                  |
//+------------------------------------------------------------------+
class Cmlp
{
protected:
   matrix            weights[];
   vector            biases[];
   
   vector            adaptive_gradients[];
   vector            adaptive_deltas[];
   
....

   bool              validated;
   
   void              AdaptiveGradientUpdate(double LearningRate, int LayerIndex, vector &Gradients, vector &Outputs);
   void              AdaptiveRMSUpdate(double DecayRate, double LearningRate, int LayerIndex, vector &Gradients, vector &Outputs);
   void              AdaptiveMEUpdate(double DecayRate, double LearningRate, int LayerIndex, vector &Gradients, vector &Outputs);
   void              AdaptiveDeltaUpdate(double DecayRate, double LearningRate, int LayerIndex, vector &Gradients, vector &Outputs);
   
public:
   
...

   void              Forward();
   void              Backward(double LearningRate = 0.1, ENUM_ADAPTIVE AdaptiveType = ADAPTIVE_NONE, double DecayRate = 0.9);

....

   void              ~Cmlp(void) { };
};

После необходимых объявлений в интерфейсе класса, нам необходимо внести существенные изменения в функцию обратного распространения Backward. В первую очередь изменения касаются добавления входных параметров и их проверки для определения подходящего типа темпа обучения. Добавляем только два параметра в функцию Backward - AdaptiveType и DecayRate. AdaptiveType является одним из четырех типов адаптируемого темпа обучения. Наша сеть по-прежнему оставляет возможность не использовать адаптируемые темпы обучения, поэтому параметру присвоено значение по умолчанию ADAPTIVE_NONE. Кроме того, следующие три формата адаптируемого темпа обучения, которые мы рассмотрим ниже, требуют темпа затухания, поэтому третьим и конечным входным параметром нашей функции обратного распространения будет это значение, и поскольку предыдущим двум параметрам присвоены значения по умолчанию, этому параметру также будет присвоено значение.

В этой функции основные изменения происходят в двух "точках обучения", то есть там, где мы обновляем выходные веса и смещения, а также в масштабируемой части, где мы обновляем скрытые веса и скрытые смещения каждого скрытого слоя, если они есть в сети. Эти части являются отдельными, поскольку включение скрытых слоев опционально и не является обязательным при построении сети. Сеть масштабируема, поскольку будет обновлять все скрытые слои одновременно, если они присутствуют, независимо от их количества. Таким образом, изменения, внесенные в обратное распространение предыдущей сети призваны проверить, используется ли адаптивное обучение в каждой из этих точек. У нас есть 4 типа адаптируемого темпа обучения, и все они представлены ниже для полноты картины. Наш первый пункт теперь будет выглядеть следующим образом:

//+------------------------------------------------------------------+
//| Backward pass through the neural network to update weights       |
//| and biases using gradient descent                                |
//+------------------------------------------------------------------+
void Cmlp::Backward(double LearningRate = 0.1, ENUM_ADAPTIVE AdaptiveType = ADAPTIVE_NONE, double DecayRate = 0.9)
{  if(!validated)
   {  printf(__FUNCSIG__ + " invalid network settings! ");
      return;
   }
// Calculate output layer gradients
   vector _output_error = target - output;
   vector _output_gradients;
   _output_gradients.Init(output.Size());
   for (int i = 0; i < int(output.Size()); i++)
   {  _output_gradients[i] = _output_error[i] * ActivationDerivative(output[i]);
   }
// Update output layer weights and biases
   if(AdaptiveType == ADAPTIVE_NONE)
   {  for (int i = 0; i < int(output.Size()); i++)
      {  for (int j = 0; j < int(weights[hidden_layers].Cols()); j++)
         {  weights[hidden_layers][i][j] += LearningRate * _output_gradients[i] * hidden_outputs[hidden_layers - 1][j];
         }
         biases[hidden_layers][i] += LearningRate * _output_gradients[i];
      }
   }
// Adaptive updates
   else if(AdaptiveType != ADAPTIVE_NONE)
   {  if(AdaptiveType == ADAPTIVE_GRAD)
      {  AdaptiveGradientUpdate(LearningRate, hidden_layers, _output_gradients, hidden_outputs[hidden_layers - 1]);
      }
      else if(AdaptiveType == ADAPTIVE_RMS)
      {  AdaptiveRMSUpdate(DecayRate, LearningRate, hidden_layers, _output_gradients, hidden_outputs[hidden_layers - 1]);
      }
      else if(AdaptiveType == ADAPTIVE_ME)
      {  AdaptiveMEUpdate(DecayRate, LearningRate, hidden_layers, _output_gradients, hidden_outputs[hidden_layers - 1]);
      }
      else if(AdaptiveType == ADAPTIVE_DELTA)
      {  AdaptiveDeltaUpdate(DecayRate, LearningRate, hidden_layers, _output_gradients, hidden_outputs[hidden_layers - 1]);
      }
   }
// Calculate hidden layer gradients
   
...

}

Аналогично, изменения в обновлениях скрытых весов и смещений следующие:

//+------------------------------------------------------------------+
//| Backward pass through the neural network to update weights       |
//| and biases using gradient descent                                |
//+------------------------------------------------------------------+
void Cmlp::Backward(double LearningRate = 0.1, ENUM_ADAPTIVE AdaptiveType = ADAPTIVE_NONE, double DecayRate = 0.9)
{  if(!validated)
   {  printf(__FUNCSIG__ + " invalid network settings! ");
      return;
   }
// Calculate output layer gradients
   
...

// Calculate hidden layer gradients
   vector _hidden_gradients[];
   ArrayResize(_hidden_gradients, hidden_layers);
   for(int h = hidden_layers - 1; h >= 0;  h--)
   {  vector _hidden_target;
      _hidden_target.Init(hidden_outputs[h].Size());
      _hidden_target.Fill(0.0);
      _hidden_gradients[h].Init(hidden_outputs[h].Size());
      if(h == hidden_layers - 1)
      {  for(int j = 0; j < int(hidden_outputs[h].Size()); j++)
         {  double _sum = 0.0;
            for(int i = 0; i < int(target.Size()); i++)
            {  if(weights[h + 1][i][j] != 0.0)
               {  _sum += (target[i] / weights[h + 1][i][j]);
               }
            }
            _hidden_target[j] = ActivationDerivative(_sum - biases[h][j]);
         }
      }
      else if(h < hidden_layers - 1)
      {  for(int j = 0; j < int(hidden_outputs[h].Size()); j++)
         {  double _sum = 0.0;
            for(int i = 0; i < int(hidden_outputs[h + 1].Size()); i++)
            {  if(weights[h][i][j] != 0.0)
               {  _sum += (hidden_outputs[h + 1][i] / weights[h][i][j]);
               }
            }
            _hidden_target[j] = ActivationDerivative(_sum - biases[h][j]);
         }
      }
      vector _hidden_error = _hidden_target - hidden_outputs[h];
      for (int i = 0; i < int(_hidden_target.Size()); i++)
      {  _hidden_gradients[h][i] = _hidden_error[i] * ActivationDerivative(hidden_outputs[h][i]);
      }
   }
// Adaptive updates
   if(AdaptiveType != ADAPTIVE_NONE)
   {  for(int h = hidden_layers - 1; h >= 0;  h--)
      {  vector _outputs = inputs;
         if(h > 0)
         {  _outputs = hidden_outputs[h - 1];
         }
         if(AdaptiveType == ADAPTIVE_GRAD)
         {  AdaptiveGradientUpdate(LearningRate, h, _hidden_gradients[h], _outputs);
         }
         else if(AdaptiveType == ADAPTIVE_RMS)
         {  AdaptiveRMSUpdate(DecayRate, LearningRate, h, _hidden_gradients[h], _outputs);
         }
         else if(AdaptiveType == ADAPTIVE_ME)
         {  AdaptiveMEUpdate(DecayRate, LearningRate, h, _hidden_gradients[h], _outputs);
         }
         else if(AdaptiveType == ADAPTIVE_DELTA)
         {  AdaptiveDeltaUpdate(DecayRate, LearningRate, h, _hidden_gradients[h], _outputs);
         }
      }
   }
// Update hidden layer weights and biases
   else if(AdaptiveType == ADAPTIVE_NONE)
   {  for(int h = hidden_layers - 1; h >= 0;  h--)
      {  for (int i = 0; i < int(weights[h].Rows()); i++)
         {  for (int j = 0; j < int(weights[h].Cols()); j++)
            {  if(h == 0)
               {  weights[h][i][j] += LearningRate * _hidden_gradients[h][i] * inputs[j];
               }
               else if(h > 0)
               {  weights[h][i][j] += LearningRate * _hidden_gradients[h][i] * hidden_outputs[h - 1][j];
               }
            }
            biases[h][i] += LearningRate * _hidden_gradients[h][i];
         }
      }
   }
}

Все функции, упомянутые выше в этих изменениях, будут выделены в соответствующих разделах. Реализация функции обновления адаптивного градиента выглядит так:

//+------------------------------------------------------------------+
// Adaptive Gradient Update function
//+------------------------------------------------------------------+
void Cmlp::AdaptiveGradientUpdate(double LearningRate, int LayerIndex, vector &Gradients, vector &Outputs)
{  for (int i = 0; i < int(weights[LayerIndex].Rows()); i++)
   {  adaptive_gradients[LayerIndex][i] += (Gradients[i] * Gradients[i]);
      double _learning_rate = LearningRate / (MathSqrt(adaptive_gradients[LayerIndex][i]) + __NON_ZERO);
      for (int j = 0; j < int(weights[LayerIndex].Cols()); j++)
      {  weights[LayerIndex][i][j] -= (_learning_rate * Gradients[i] * Outputs[j]);
      }
      //
      biases[LayerIndex][i] -= _learning_rate * Gradients[i];
   }
}

Добавленный векторный массив адаптивных градиентов накапливает квадраты значений градиентов для каждого параметра на каждом слое. Эти квадратичные значения, специфичные для каждого параметра, затем снижают темп обучения в разной степени в зависимости от задействованного параметра и истории его градиентов на протяжении всего процесса обучения. Сумма квадратов градиентов выступает в качестве знаменателя темпа обучения, поэтому чем больше градиенты, тем меньше темп обучения.

Мы проводим несколько тестовых запусков с адаптивными градиентными темпами обучения, и вот некоторые из наших результатов:

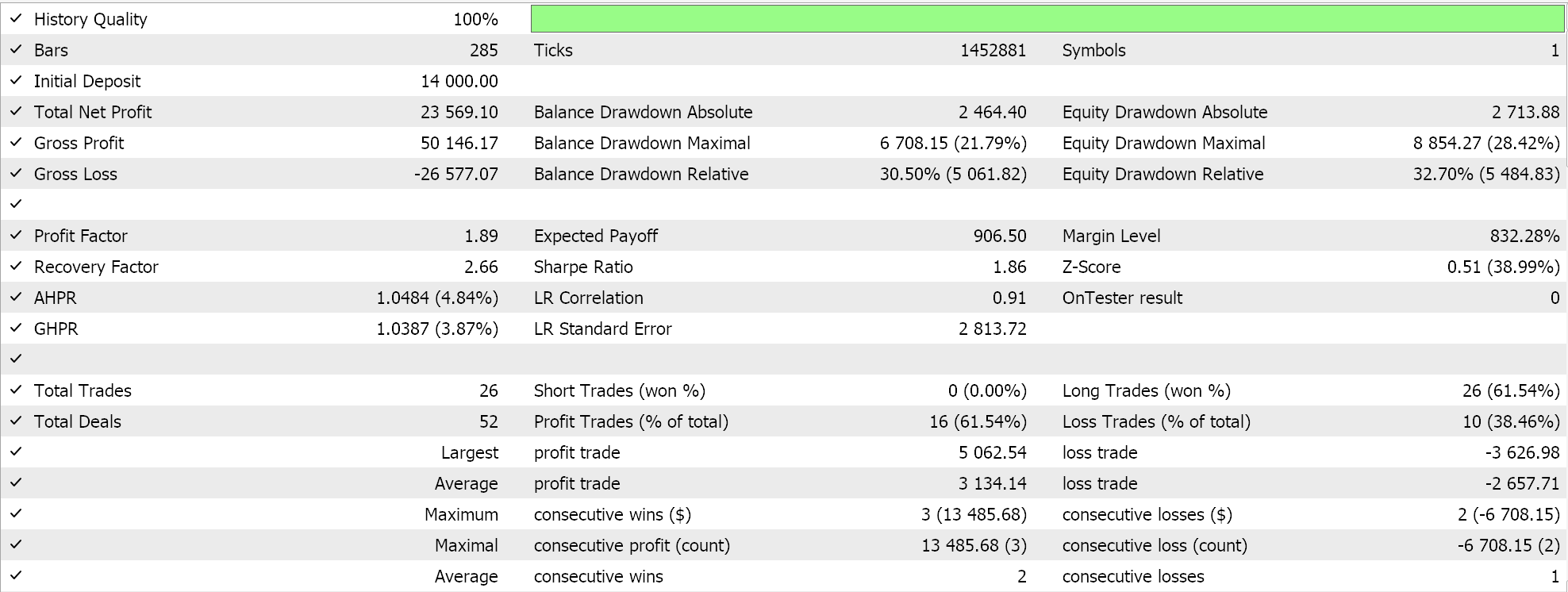
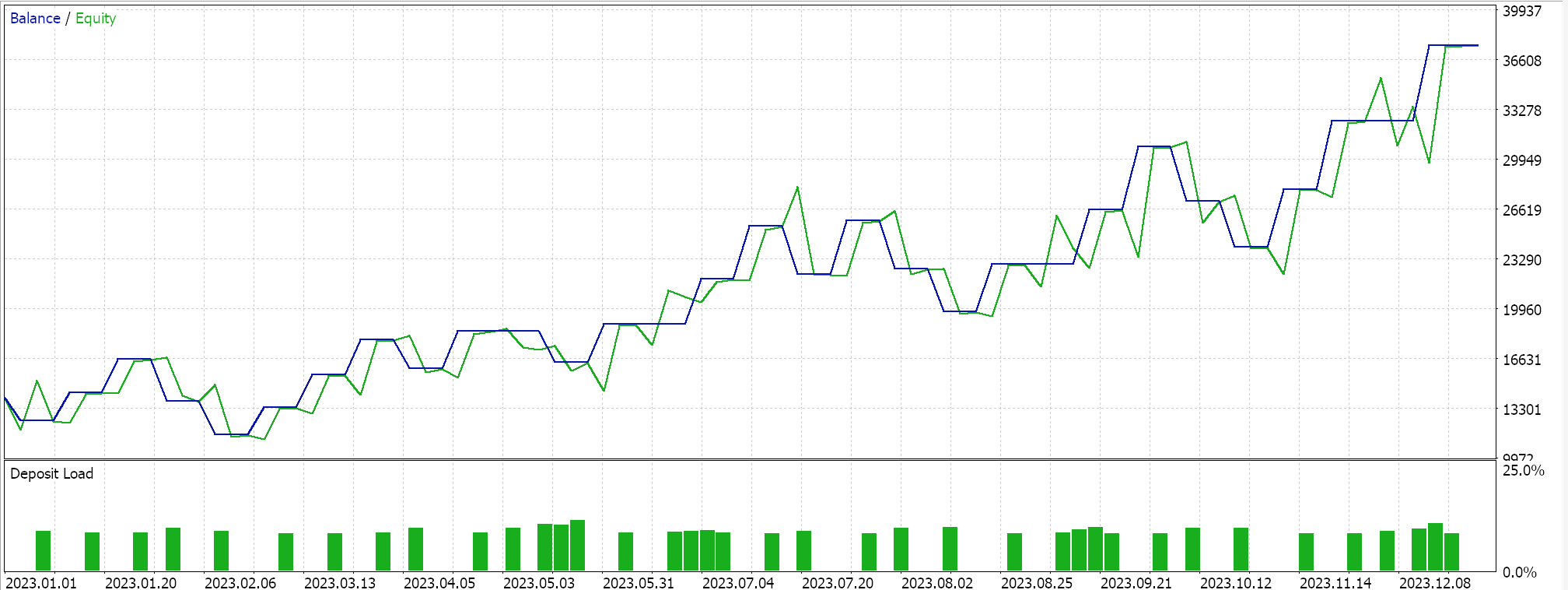
Эти тестовые прогоны выполнены для 2023 года на дневном таймфрейме для валютной пары NZDUSD. Использование NZDUSD необходимо для пакетной нормализации, о чем я более подробно расскажу в следующей статье. На данный момент, как упоминалось выше, мы используем активацию Sigmoid, которая сохраняет свои выходные данные в диапазоне от 0,0 до 1,0. Это хорошо подходит для целей тестирования при изучении идеальных темпов обучения. Как только каждый параметр имеет собственный темп обучения, веса и смещения обновляются с помощью функции обновления адаптивного градиента, листинг которого уже приведен выше.

Поскольку наши входные данные, представляющие собой необработанные цены, находятся в диапазоне от 0,0 до 1,0, а мы активируем Sigmoid, наши сетевые выходные данные также должны находиться в диапазоне от 0,0 до 1,0. Мы имеем дело с необработанными ценами, и поскольку мы снабжаем нашу сеть историческими ценовыми данными и обучаем ее на последовательных ценовых данных, мы можем ожидать, что наша сеть спрогнозирует следующую цену закрытия. Мы делаем все это без пакетной нормализации, что очень рискованно, поскольку даже если выходной сигнал будет находиться в желаемом диапазоне от 0,0 до 1,0, он может легко оказаться выше текущей цены спроса (или ниже ее), что даст постоянные сигналы на покупку или продажу. Это уже очевидно из наших "идеальных" результатов тестов, приведенных выше. Я действительно проводил прогоны, в ходе которых открывались как длинные, так и короткие позиции, но отсутствие пакетной нормализации вызывает опасения. Чтобы генерировать значения сигналов или условий из наших функций условий покупки и продажи в пользовательском классе сигналов, нам необходимо нормализовать прогнозируемую цену так, чтобы она находилась в целочисленном диапазоне от 0 до 100.

Как всегда, существует множество способов добиться этого, однако в нашем случае мы просто сравниваем прогнозируемую цену с массивом входных цен и получаем процентильное double-значение. Мы преобразуем это процентильное значение в целое число в диапазоне от 0 до 100 и получаем выходное условие. Такая нормализация выполняется только в каждой из длинных и коротких условных функций, если прогнозируемая цена сети выше или ниже текущей цены bid соответственно. Исходный код представлен ниже:

//+------------------------------------------------------------------+
//| "Voting" that price will grow.                                   |
//+------------------------------------------------------------------+
int CSignalCMLP::LongCondition(void)
{  int result = 0;
   double _mlp_output = 0.0;
   GetOutput(_mlp_output);
   m_symbol.Refresh();
   m_symbol.RefreshRates();
   if(_mlp_output > m_symbol.Bid())
   {  vector _scale;
      _scale.CopyRates(m_symbol.Name(), m_period, 8, 0, __MLP_INPUTS);
      result = int(round(100.0 * (fmin(_mlp_output, _scale.Max()) - _scale.Min()) / fmax(m_symbol.Point(), _scale.Max() - _scale.Min())));
   }
//printf(__FUNCSIG__ + " output is: %.5f, change is: %.5f, and result is: %i", _mlp_output, m_symbol.Bid()-_mlp_output, result);return(0);
   return(result);
}
//+------------------------------------------------------------------+
//| "Voting" that price will fall.                                   |
//+------------------------------------------------------------------+
int CSignalCMLP::ShortCondition(void)
{  int result = 0;
   double _mlp_output = 0.0;
   GetOutput(_mlp_output);
   m_symbol.Refresh();
   m_symbol.RefreshRates();
   if(_mlp_output < m_symbol.Bid())
   {  vector _scale;
      _scale.CopyRates(m_symbol.Name(), m_period, 8, 0, __MLP_INPUTS);
      result = int(round(100.0 * (fmin(_mlp_output, _scale.Max()) - _scale.Min()) / fmax(m_symbol.Point(), _scale.Max() - _scale.Min())));
   }
//printf(__FUNCSIG__ + " output is: %.5f, change is: %.5f, and result is: %i", _mlp_output, m_symbol.Bid()-_mlp_output, result);return(0);
   return(result);
}

Использование этого кода, прикрепленного в конце статьи, осуществляется путем сборки советника с помощью Мастера MQL5. Необходимые руководства можно найти здесь и здесь.

Адаптивное среднеквадратическое значение

Этот формат темпа обучения вводит дополнительный параметр для управления быстрым падением темпа обучения, которое часто происходит при столкновении с большими градиентами, поскольку они накапливаются в течение всего процесса обучения. Этот параметр представляет собой темп затухания, который мы уже ввели выше как один из новых дополнительных входных параметров для модифицированной функции обратного распространения. Однако в предыдущей статье мы использовали темп затухания в темпе обучения с пошаговым затуханием, с экспоненциальным затуханием и обратным временным затуханием с почти аналогичной целью. В нашем классе пользовательских сигналов есть отдельный входной параметр под названием "темп затухания" (decay rate), который служит всем этим целям, поскольку в любом сеансе обучения можно выбрать только один формат темпа обучения. Таким образом, темп затухания будет соответствовать выбранному типу темпа обучения.

Однако, продолжая тему адаптируемых темпов обучения, среднеквадратическое распространение корня (RMS-prop) ограничивает накопление исторических градиентов, что может стать проблемой для адаптивных градиентов, поскольку они значительно замедляют обучение до такой степени, что оно фактически останавливается. Это происходит из-за обратной зависимости между историческими градиентами и темпом обучения, о которой уже упоминалось выше. Инновация RMS prop заключается в эффективном замедлении падения темпа обучения благодаря фактору затухания. Это достигается следующим образом:

//+------------------------------------------------------------------+
// Adaptive RMS Update function
//+------------------------------------------------------------------+
void Cmlp::AdaptiveRMSUpdate(double DecayRate, double LearningRate, int LayerIndex, vector &Gradients, vector &Outputs)
{  for (int i = 0; i < int(weights[LayerIndex].Rows()); i++)
   {  adaptive_gradients[LayerIndex][i] += (DecayRate * adaptive_gradients[LayerIndex][i]) + ((1.0 - DecayRate)*(Gradients[i] * Gradients[i]));
      double _learning_rate = LearningRate / (MathSqrt(adaptive_gradients[LayerIndex][i]) + __NON_ZERO);
      for (int j = 0; j < int(weights[LayerIndex].Cols()); j++)
      {  weights[LayerIndex][i][j] -= (_learning_rate * Gradients[i] * Outputs[j]);
      }
      biases[LayerIndex][i] -= _learning_rate * Gradients[i];
   }
}

Другая проблема с адаптивным градиентом заключается в том, что при работе с нестационарными данными базовое распределение и характеристики данных со временем меняются, и, таким образом, даже при использовании обучающего набора накопленные градиенты могут устареть и стать менее релевантными, что приведет к неоптимальным темпам обучения. RMS prop следит за тем, чтобы в дело вступали более поздние градиенты, оказывающие большее влияние на темп обучения. Это делает процесс обучения более адаптируемым и, возможно, более полезным в сценариях, особенно актуальных для трейдеров, таких как прогнозирование временных рядов.

Кроме того, в случаях, когда обучение проводится на разреженных наборах данных, например, за пределами нашей основной компетенции в торговле, включая обработку естественного языка или системы рекомендаций, адаптивные градиенты могут чрезмерно снижать градиенты при считывании редко используемых функций или точек данных. Таким образом, RMS prop позволяет сделать процесс обучения более сбалансированным, поддерживая темп обучения на относительно высоком уровне в течение более длительных периодов, благодаря чему эти сети (которые остаются полезными для трейдеров в определенных ситуациях) могут иметь более оптимальные веса и смещения.

Наконец, адаптивные градиенты очень восприимчивы и чувствительны к зашумленным данным, поскольку по сути градиент положительно коррелирует с шумом. Таким образом, в ситуациях, когда обучающие данные не отфильтрованы должным образом для выявления этих выбросов, быстрое снижение темпа обучения по сути будет означать, что сеть будет больше обучаться на выбросах и шуме, чем на основных или идеальных данных. Сглаживающий эффект RMS prop с коэффициентом затухания означает, что скорость обучения может "пережить" резкие выбросы и по-прежнему эффективно влиять на веса и смещения сети, когда основные или идеальные данные в конечном итоге встречаются в обучающем наборе.

Проведем несколько тестовых запусков с адаптивным обучением RMS prop. Ниже приведен пример результатов наших тестов:

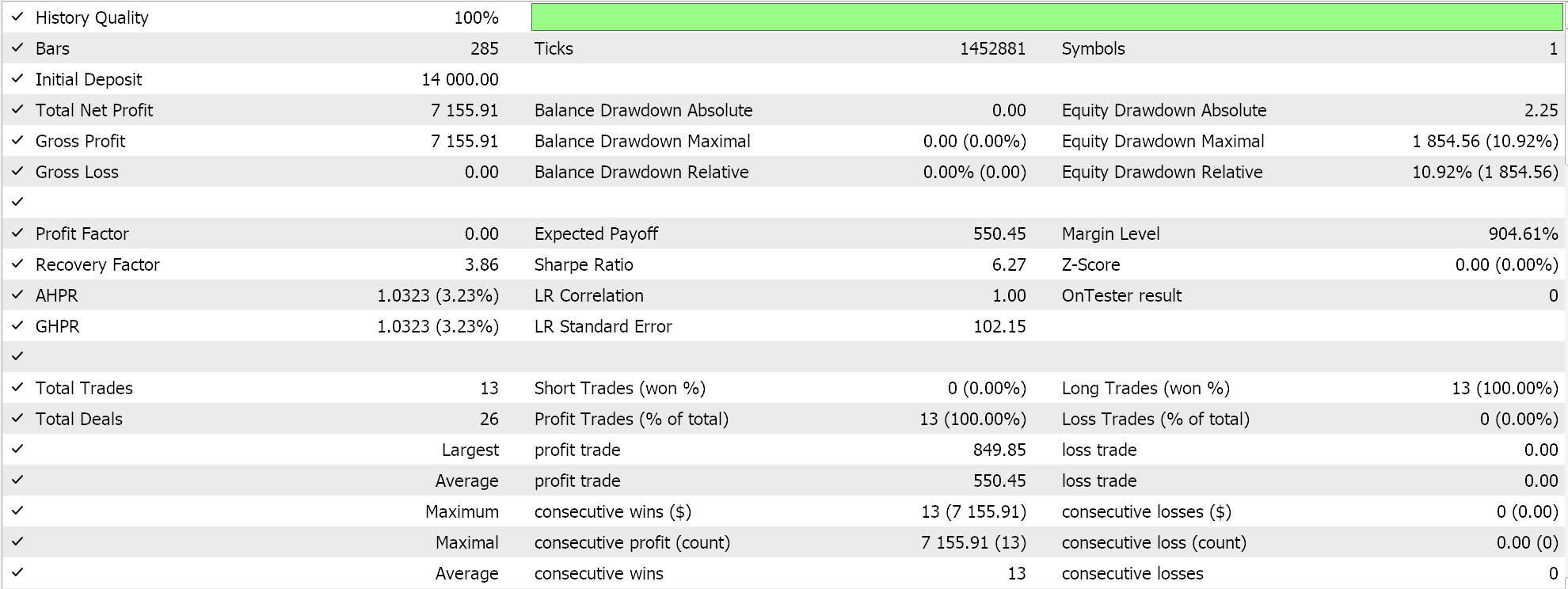
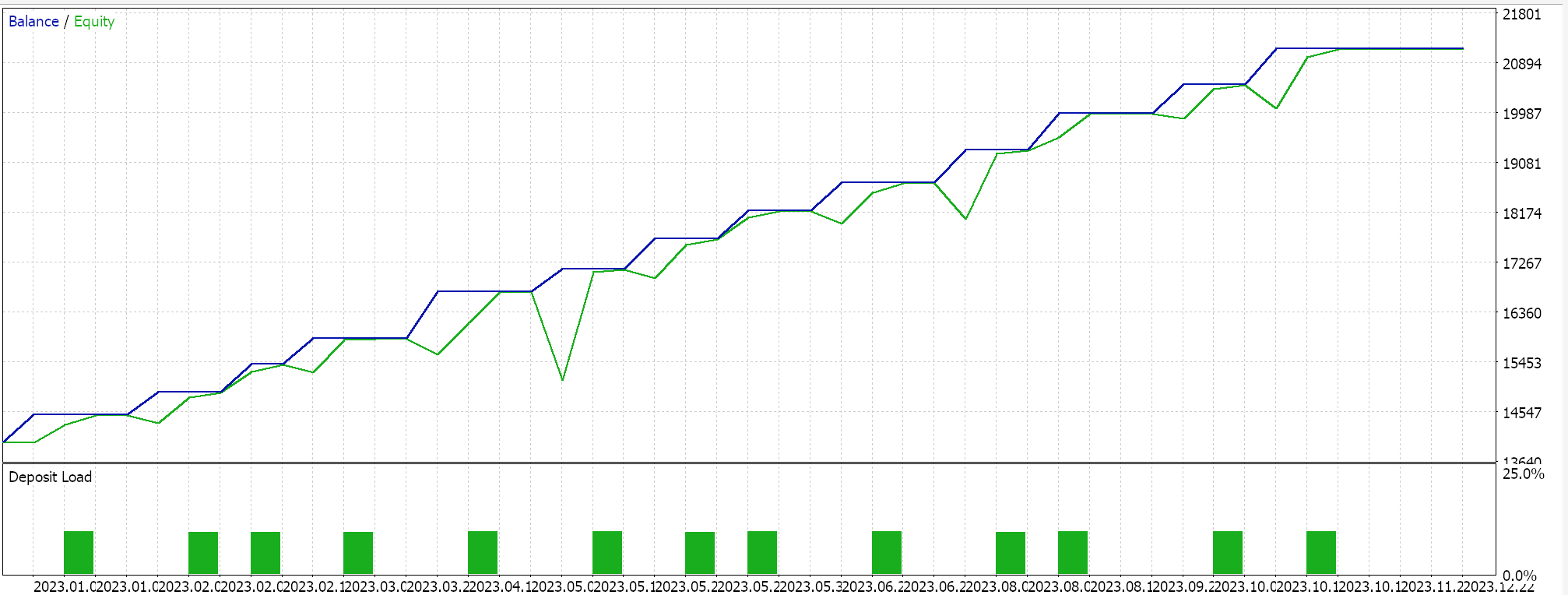
Поскольку входные данные нашей сети не нормализованы пакетно в соответствии с выбором функции активации для этой сети (мы используем Sigmoid вместо Soft Max), наши результаты тестирования искажены и приводят только к размещению длинных сделок, поскольку прогнозируемая цена на выходе всегда была выше текущей цены bid. Могут существовать способы нормализации выходной цены для обеспечения баланса между длинными и короткими позициями, которые наш подход не учитывает, но я бы предпочел, чтобы мы начали с надлежащей пакетной нормализации входных данных, прежде чем рассматривать такие подходы. Как уже упоминалось выше, этот вопрос будет рассмотрен в следующей статье.

Адаптивная оценка моментов (или средняя экспоненциальная)

Адаптивная оценка моментов (Adaptive Moment Estimation, ADAM) — еще один вариант адаптивных темпов обучения, который направлен на то, чтобы сделать такие подходы, как RMS, описанные выше, еще более плавными за счет двухстороннего рассмотрения как среднего градиента, так и дисперсии градиента (импульса). В MQL5 это реализовано следующим образом:

//+------------------------------------------------------------------+
// Adaptive Mean Exponential(ME) Update function
//+------------------------------------------------------------------+
void Cmlp::AdaptiveMEUpdate(double DecayRate, double LearningRate, int LayerIndex, vector &Gradients, vector &Outputs)
{  for (int i = 0; i < int(weights[LayerIndex].Rows()); i++)
   {  adaptive_gradients[LayerIndex][i] = (DecayRate * adaptive_gradients[LayerIndex][i]) + ((1.0 - DecayRate)*(Gradients[i] * Gradients[i]));
      double _learning_rate = LearningRate / (fabs(adaptive_gradients[LayerIndex][i]) + __NON_ZERO);
      for (int j = 0; j < int(weights[LayerIndex].Cols()); j++)
      {  weights[LayerIndex][i][j] -= (_learning_rate * Gradients[i] * Outputs[j]);
      }
      //
      biases[LayerIndex][i] -= _learning_rate * Gradients[i];
   }
}

Мы только что увидели выше, что темпы обучения RMS prop являются шагом вперед по сравнению с темпами градиентов в том смысле, что они замедляют снижение темпа обучения, и это может обеспечить ряд преимуществ, некоторые из которых были описаны выше. ADAM продолжает двигаться в этом направлении, особенно когда сталкивается с данными большой размерности. По мере увеличения размеров обрабатываемых наборов данных увеличивается и количество параметров в массиве градиента. В таких ситуациях, как распознавание изображений и речи, учет импульса в дополнение к среднему значению помогает более чутко адаптировать темп обучения к набору данных, чем если бы учитывалось только среднее значение. В зависимости от конструкции сети такой сценарий высокой размерности может встречаться при прогнозировании финансовых временных рядов.

Относительно нестабильная и медленная сходимость при использовании только среднего квадрата градиентов делает RMS prop менее надежным в зашумленных данных, чем ADAM. Сочетание как квадрата среднего, так и дисперсии обеспечивает более плавную, надежную, стабильную и быструю обработку сходимости. Разреженные градиенты в системах обработки естественного языка и рекомендаций лучше обрабатываются RMS prop, чем адаптивным градиентом. Но еще лучше они обрабатываются с помощью ADAM благодаря взвешиванию импульса в темпе обучения. Кроме того, в ситуациях, когда параметры часто меняются, например, когда новая сеть инициализируется со случайными весами и смещениями, ориентация RMS prop на недавнюю историю градиентов может привести к чрезмерно консервативным обновлениям, тогда как учет импульса в ADAM позволяет ему по-прежнему лучше реагировать даже в таких ситуациях.

Наконец, при работе с нестационарными целями, где целевая функция меняется со временем, RMS prop, хотя и с помощью среднего значения, все равно может не адаптироваться так же хорошо, как ADAM. В качестве примера рассмотрим ситуацию, когда ваша сеть смоделирована для прогнозирования цен на недвижимость, и она обрабатывает входные данные или характеристики, такие как размер дома, количество жилых комнат и местоположение. Целевая функция, которую мы используем для нашей сети многослойного перцептрона (MLP network) во время обратного распространения, — это просто векторная разность между целью и прогнозом, но обычно эта цель может принимать различные формы, такие как среднеквадратическая ошибка, где в этой ситуации у нас будет следующая формула:

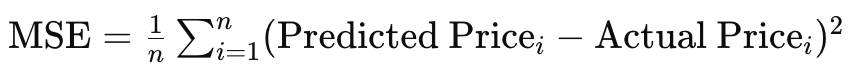
где:

• n - количество домов в выборке данных
• MSE - среднеквадратическая ошибка

Это будет функция ошибки обратного распространения, результат которой со временем уменьшается по мере того, как сеть обучается, соответствующим образом обновляя свои веса и смещения, при этом более низкие значения MSE указывают на улучшение производительности сети. Теперь предположим, что изучаемый рынок недвижимости кардинально меняется, так что существенно меняется соотношение между сетевыми характеристиками (входными данными) и прогнозируемыми ценами, например, когда в регионе, где находится изучаемая недвижимость, появляется станция метро. Это, безусловно, изменило бы модель ценообразования на недвижимость в этом районе, и это сделало бы целевую функцию менее полезной для адаптации к этим изменениям. Пересмотр сети путем добавления более релевантных признаков (входных полей) может привести к более оптимальному результату, поскольку веса и смещения будут обновлены. ADAM лучше справляется с этим переходом к пересмотру и обновлению сетевой модели за счет добавления новых функций, поскольку процесс обновления веса учитывает импульс.

Результаты тестирования с помощью ADAM дают нам следующий отчет:

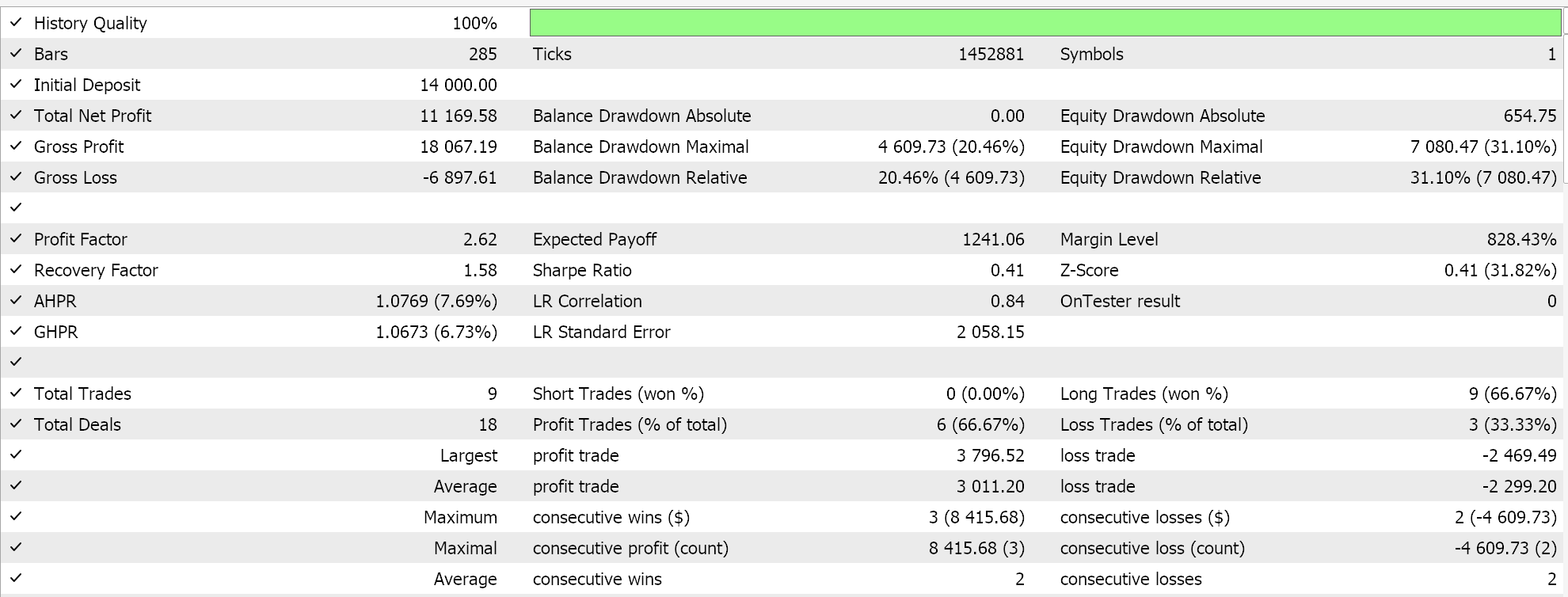
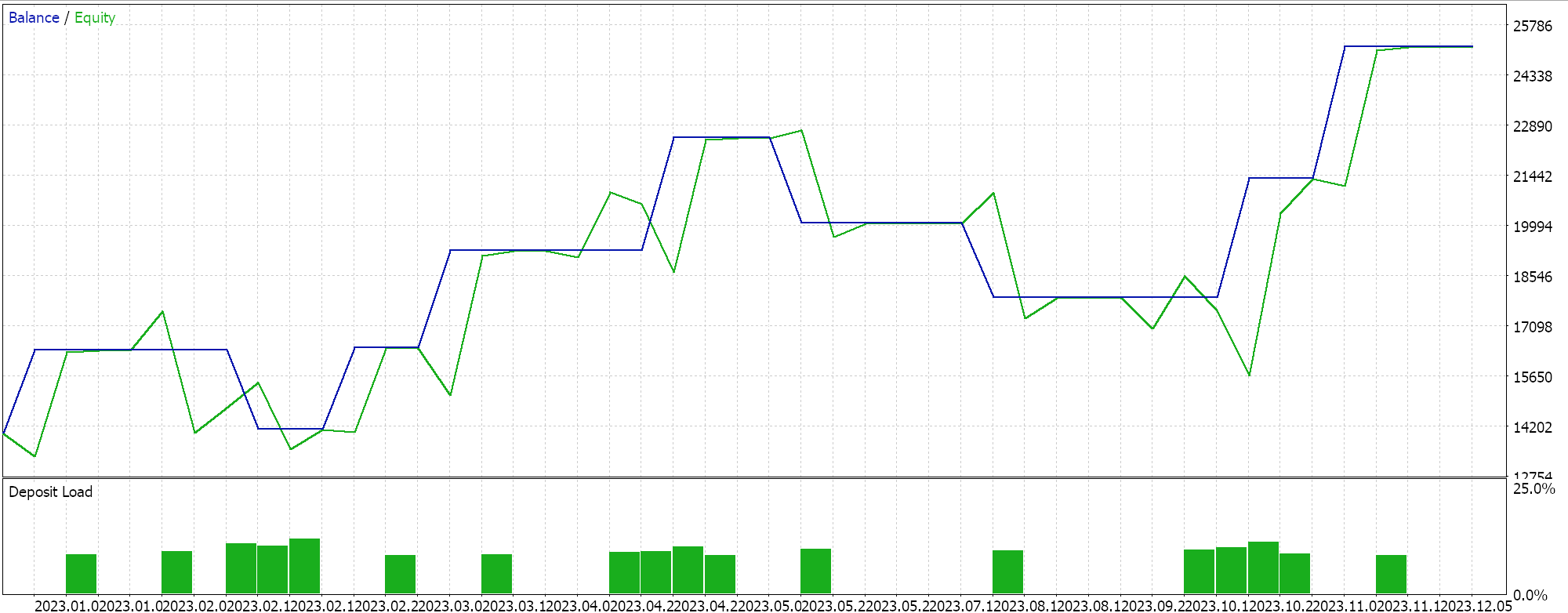
Это не самые лучшие и не идеальные настройки, но они лишь демонстрируют, как темп обучения ADAM применяется в сети MLP. В предыдущей статье мы использовали пару сетей GAN, а здесь мы используем нечто более элементарное, но все же интуитивно понятное — многослойный перцептрон всего с тремя слоями в конфигурации 5-8-1.

Адаптивная дельта

Наш окончательный адаптивный темп обучения — это ADADELTA, и хотя он не принимает никаких новых входных параметров, он способствует оптимальной настройке темпа обучения во время тренировки. Его формула относительно сложна, но в принципе, помимо учета затухающего накопления градиентов, также учитывается затухающее накопление весов. В MQL5 это реализовано следующим образом:

//+------------------------------------------------------------------+
// Adaptive Delta Update function
//+------------------------------------------------------------------+
void Cmlp::AdaptiveDeltaUpdate(double DecayRate, double LearningRate, int LayerIndex, vector &Gradients, vector &Outputs)
{  for (int i = 0; i < int(weights[LayerIndex].Rows()); i++)
   {  adaptive_gradients[LayerIndex][i] = (DecayRate * adaptive_gradients[LayerIndex][i]) + ((1.0 - DecayRate)*(Gradients[i] * Gradients[i]));
      double _delta = (MathSqrt(adaptive_deltas[LayerIndex][i] + __NON_ZERO) / MathSqrt(adaptive_gradients[LayerIndex][i] + __NON_ZERO)) * Gradients[i];
      adaptive_deltas[LayerIndex][i] = (DecayRate * adaptive_deltas[LayerIndex][i]) + ((1.0 - DecayRate) * _delta * _delta);
      for (int j = 0; j < int(weights[LayerIndex].Cols()); j++)
      {  weights[LayerIndex][i][j] -= (_delta * Outputs[j]);
      }
      // Bias update with AdaDelta
      biases[LayerIndex][i] -= _delta;
   }
}

Большинство преимуществ менее быстрого снижения темпа обучения, упомянутых выше для RMS prop и ADAM, применимы и к ADADELTA. Здесь стоит упомянуть преимущества дополнительного буфера адаптивных дельт, который ADADELTA вводит при оценке темпа обучения.

ADAM использует скользящие средние квадрата среднего градиента и дисперсии для адаптации темпов обучения для каждого параметра. Хотя это и является эффективным улучшением по сравнению с RMS prop, существуют случаи, когда сосредоточение на исторических градиентах приводит к выходу за пределы минимумов, что приводит к нестабильности при обучении, особенно при обработке зашумленных данных. Включение буфера квадратичных обновлений, который называется "адаптивными дельтами". Такое накопление помогает лучше сбалансировать обновления темпа обучения, так как оно основано как на величине последних градиентов, так и на эффективности последних дельта-обновлений.

Отслеживая квадратичные обновления, ADADELTA может динамически корректировать размеры шагов, учитывая недавнюю эффективность этих обновлений. Это полезно для процесса обучения, так как не дает ему стать чрезмерно консервативным, что может произойти, если величины градиентов значительно уменьшатся. Кроме того, дополнительное накопление обновлений веса обеспечивает механизм нормализации обновлений с использованием шкалы последних обновлений, улучшая способность оптимизатора адаптироваться к изменениям в градиентном ландшафте. Это имеет решающее значение в сценариях с нестационарными распределениями наборов данных или сильно изменчивыми градиентами.

Другими нововведениями ADADELTA являются снижение чувствительности гиперпараметров и предотвращение снижения скорости обучения. Тесты с темпом обучения ADADELTA на символах, периодах тестирования и таймфреймах, аналогичных тем, что указаны выше, показывают различные прибыльные результаты. Ниже представлен один из отчетов:

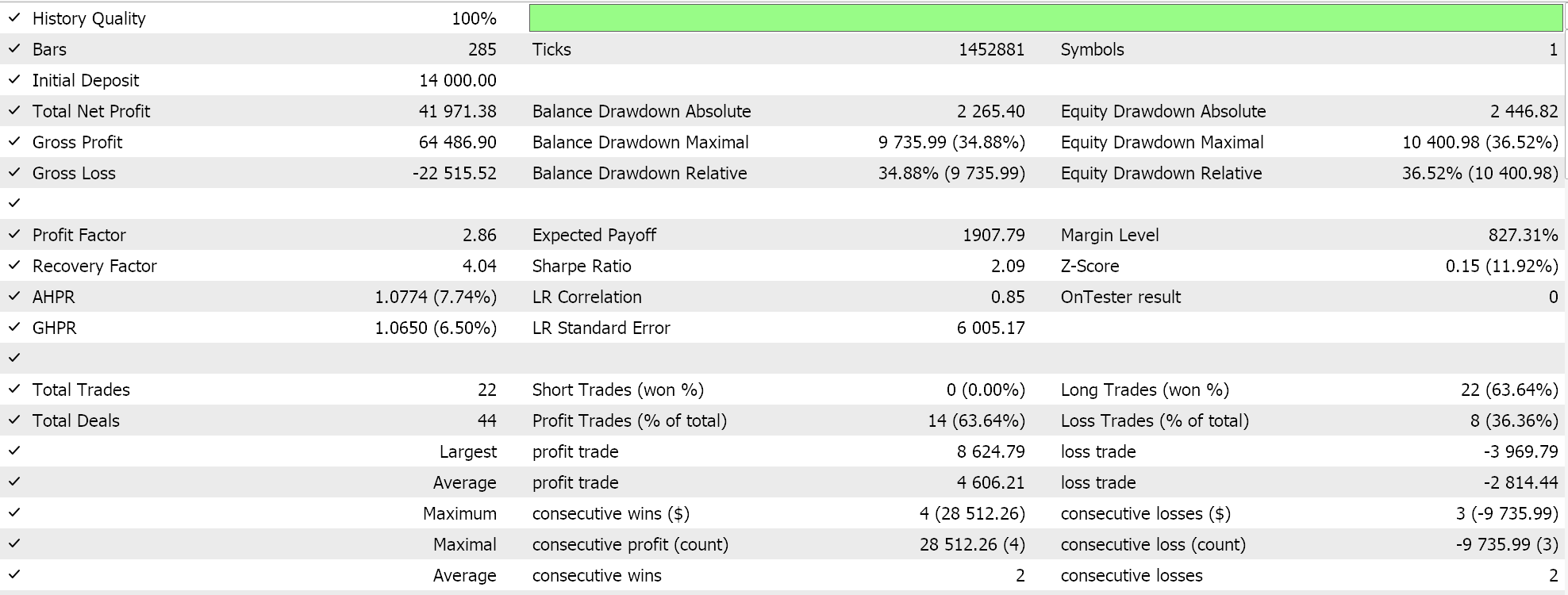
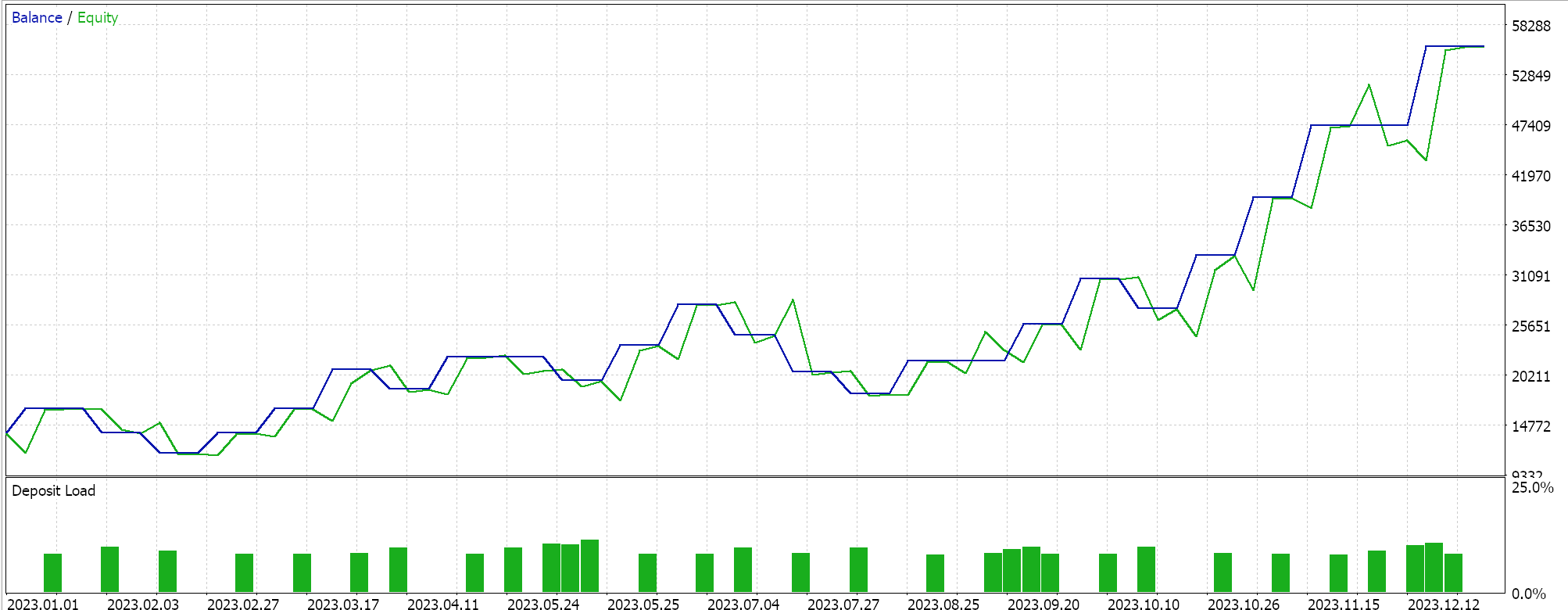
Один цикл

Этот подход к корректировке темпа обучения лишен сложности методов адаптивного темпа обучения и больше похож на формат косинусного отжига, который мы рассматривали в предыдущей статье. Однако он немного проще, чем косинусный отжиг, в том смысле, что темп обучения сначала увеличивается, а затем уменьшается к концу сеанса обучения. Реализовано это следующим образом:

      else if(m_learning_type == LEARNING_ONE_CYCLE)
      {  double _cycle_position = (double)((m_epochs - i) % (2 * m_epochs)) / (2.0 * m_epochs);
         if (_cycle_position <= 0.5)
         {  _learning_rate = m_min_learning_rate + (2.0 * _cycle_position * (m_learning_rate - m_min_learning_rate));
         }
         else
         {  _learning_rate = m_learning_rate - (2.0 * (_cycle_position - 0.5) * (m_learning_rate - m_min_learning_rate));
         }
      }

Таким образом, в отличие от относительно сложных подходов, которые мы рассмотрели в этой статье, в одном цикле темп обучения изначально просто увеличивается в так называемой фазе разминки, затем он достигает пика, после чего снижается в фазе охлаждения, которая является последней частью процесса обучения. За исключением косинусного отжига, большинство подходов к темпу обучения стремятся начать с большого темпа обучения и затем уменьшать его по мере обработки большего количества данных.

Темп обучения в одном цикле делает нечто противоположное: он стартует с минимального значения. Минимальный и максимальный темпы обучения являются предопределенными входными параметрами, а путь или скорость изменения темпа обучения зависят от количества эпох или продолжительности сеанса обучения. Проведем тестирование одного цикла. Один из отчетов представлен ниже:

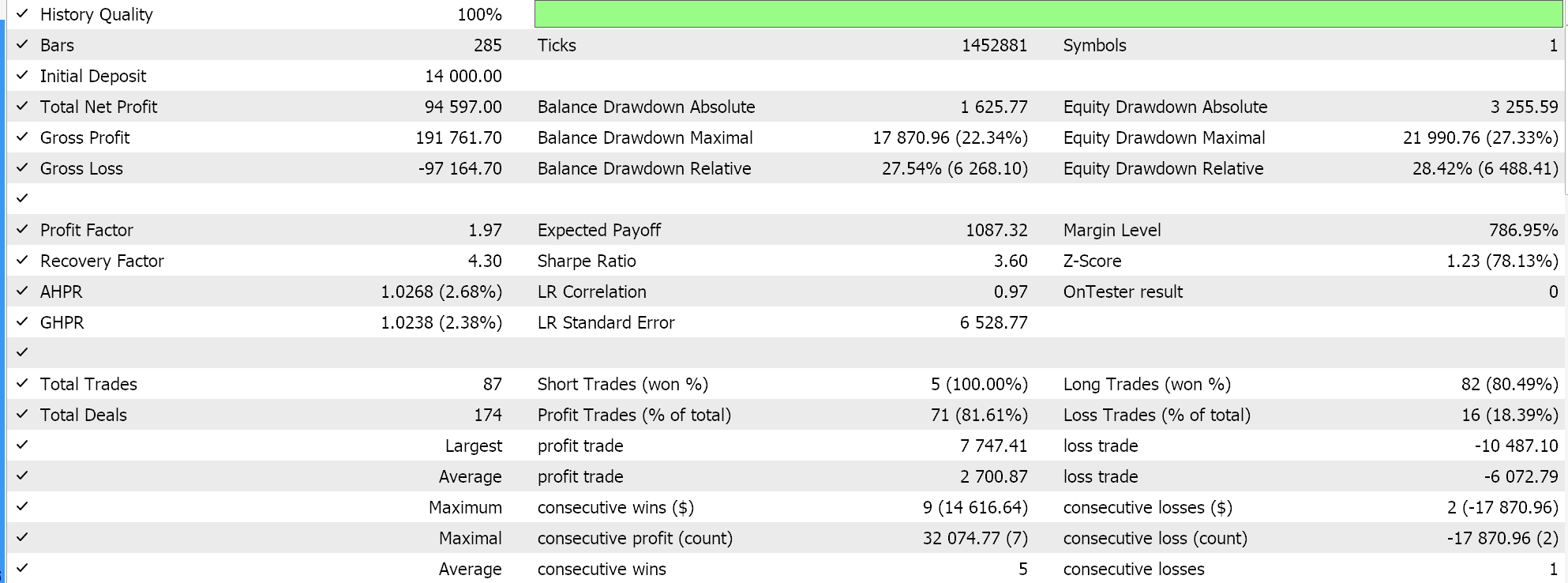
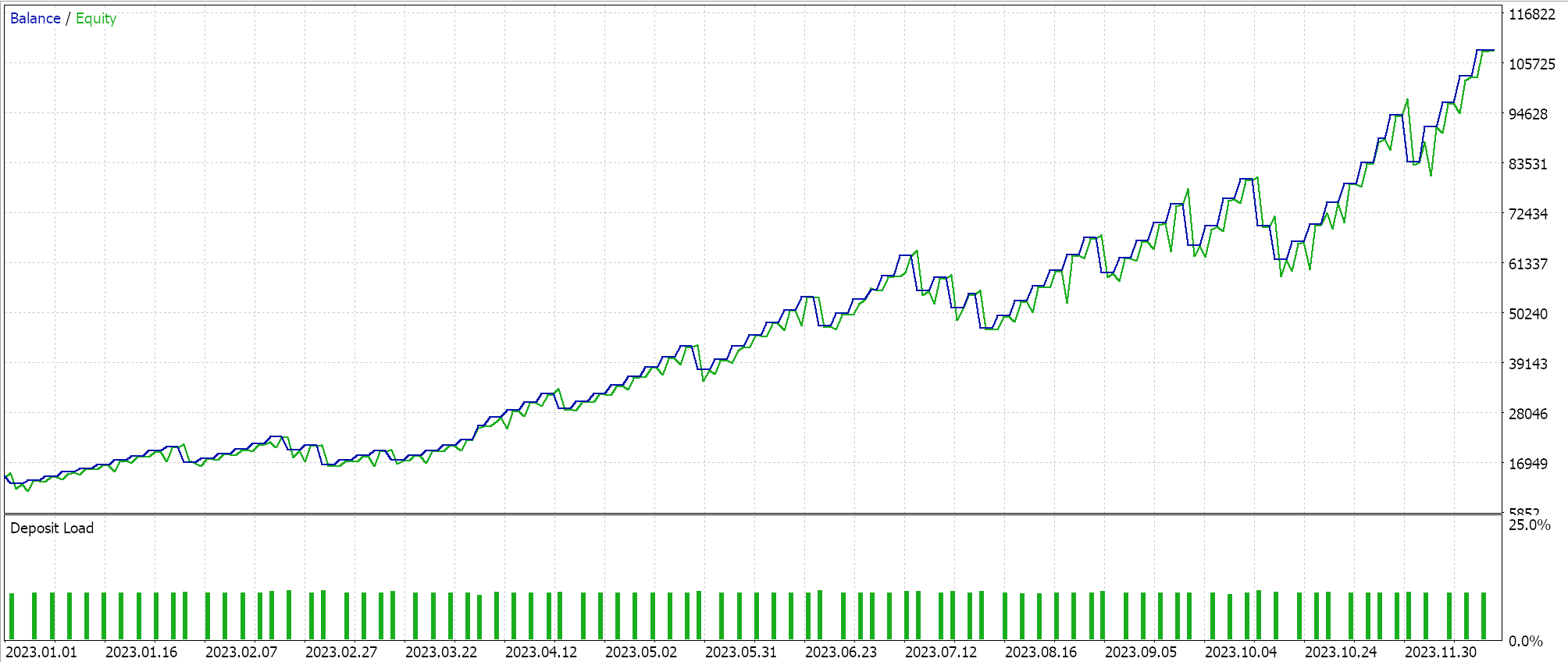
Из приведенных выше результатов следует, что, несмотря на отсутствие надлежащей пакетной нормализации, всего лишь изменив темп обучения, мы наконец-то смогли открыть несколько коротких сделок. Это происходит при прогнозировании необработанных цен символов (без пакетной нормализации) и нормализации условий на покупку и продажу таким же образом, как мы делали при тестировании методов адаптивного темпа обучения. Это еще раз демонстрирует, насколько подход к использованию и настройке темпа обучения чувствителен к производительности нейронной сети.

Заключение

Подводя итог, можно сказать, что темп обучения является важнейшим и очень чувствительным аспектом алгоритмов машинного обучения. Мы рассмотрели варианты внедрения различных форматов, сосредоточившись на последовательных инновациях в каждом из них, поскольку большинство подходов к темпу обучения были разработаны для улучшения более ранних методов и подходов. Такой подход к улучшению темпов обучения, безусловно, требует дальнейшего развития, однако не следует пренебрегать и более простыми подходами, такими как темп обучения за один цикл, поскольку они могут быть весьма эффективными, как мы увидели из некоторых результатов наших тестов.