
您应当知道的 MQL5 向导技术(第 29 部分):继续学习率与 MLP
概述
我们通过验证自适应学习率和一个轮转学习率,重新审视、并总结不同格式的学习率对智能系统的性能影响。至于本文,该格式将遵循我们在上一篇文章中采用的方式,即在每个学习率格式小节就提供测试报告,而非堆积在文章末尾。
我们跃进之前,我们要提一些其它重要的机器学习设计注意事项,这些可能会极大地影响模型的性能。其中之一是导入数据的批量归一化。我在之前的文章中已触及为什么它如此显要,不过我们的下一篇文章将正视这一点。然而,就目前,在设计网络的模式和格式时,批量归一化要与模型或网络采用的激活算法通盘考虑。迄今为止,我们一直在使用 Softplus 激活,其具有产生无定数结果的倾向,即,不像 TANH 或 Sigmoid 激活,分别产生 -1.0 到 +1.0 和 0.0 到 1.0 范围内的输出,Softplus 激活的生成结果经常无法通过有效测试,且因此致训练和预测过程无效。
因此,作为下一篇文章的预运行,我们正在进行一些改变,不仅是网络所用的激活算法,还有所测试的外汇品种。我们在所有层上使用输出绑定激活算法 Sigmoid 作为激活,但比之更要紧的是,我们测试外汇品种对的输入(在我们的例子中,它仍然是原始价格,未执行批量归一化)在 0.0 到 1.0 范围。在我们的测试区间,即 2023 年,价格在这个范围内的外汇对并不太多;不过,NZDUSD 正好,故我们就选用它。
比之上一篇文章的性能结果,这已变得不切实际,因为基础已改变。然而,配以新的网络和激活算法、以及外汇对,读者仍可测试上一篇文章中探讨的学习率格式,以便获得如同收窄偏好学习率方法时的同比。还有,此处和这些文章中经常呈现的测试结果,并非来自最佳设定,也非它们有意为之。展示它们仅出于探索目的,故读者的工作始终是为优化智能系统而微调输入,不仅要配合高品质的历史数据,而且在部署之前,最好在模拟账户上,自策略测试器区间之后进行前向测试。
故此,所呈现的只是潜力。毕竟,学习率已展现出是一个非常敏感的性能衡量度,从我们在上一篇文章中得到的测试结果差异,就显而易见。自适应学习率意在解决判定模型理想学习率时参数过多的问题。回想一下,学习率本身只是取得理想网络权重和乖离的一种手段,故配以这些方法可避免用到额外参数,就像我们在上一篇文章中所见的多项式幂、或最小学习率。为了参数最小化,原则上,自适应学习依据其训练梯度,为每个层生成学习率参数。这种情形的影响是,其中几乎所有参数都有自己的学习率,但为达成这一点所提供的输入却最少。自适应学习率有四种常见格式,即:自适应梯度、自适应 RMS、自适应均值指数、和自适应增量。我们每次研究一个。
自适应梯度学习率
这大概是自适应学习率中最简单的格式,不过尽管具有单一输入,即初始学习率,但它仍遵循在所有层上自定义学习率参数的制度。在每个参数基础上实现自定义学习率的需求,这要扩展我们的智能系统父类,超越自定义信号类,就像我们在上一篇文章讲述学习率时所做。这是因为判定学习率时,作为输入的训练梯度,仅能从父网络类接口内访问。我们可以修改类,并将它们公开,但给定的额外自定义所涉及的反向传播调用(其中每层的权重和偏差可能都有自己的学习率)也许不会像应有的那般有效。在训练过程中计算出的每个单独学习率,当所有参数都采用单一学习率时,筹备的网络几乎可以同样高效地运行,因为计算出的学习率会立即应用于特定参数,而非先开发一个自定义结构来容纳所有参数的新学习率,然后遍历迭代过程,计算每个单独的学习率,之后在另一个迭代过程中应用每个单独学习率,至此完毕。这显然不会让代码更臃肿,但计算肯定会更加密集。然而,我们先修改父网络类,引入 'adaptive_gradients' 和 'adaptive_deltas' 两个向量数组参数,如下所示的新类接口:
//+------------------------------------------------------------------+ //| | //+------------------------------------------------------------------+ enum ENUM_ADAPTIVE { ADAPTIVE_NONE = -1, ADAPTIVE_GRAD = 0, ADAPTIVE_RMS = 1, ADAPTIVE_ME = 2, ADAPTIVE_DELTA = 3, }; //+------------------------------------------------------------------+ //| | //+------------------------------------------------------------------+ class Cmlp { protected: matrix weights[]; vector biases[]; vector adaptive_gradients[]; vector adaptive_deltas[]; .... bool validated; void AdaptiveGradientUpdate(double LearningRate, int LayerIndex, vector &Gradients, vector &Outputs); void AdaptiveRMSUpdate(double DecayRate, double LearningRate, int LayerIndex, vector &Gradients, vector &Outputs); void AdaptiveMEUpdate(double DecayRate, double LearningRate, int LayerIndex, vector &Gradients, vector &Outputs); void AdaptiveDeltaUpdate(double DecayRate, double LearningRate, int LayerIndex, vector &Gradients, vector &Outputs); public: ... void Forward(); void Backward(double LearningRate = 0.1, ENUM_ADAPTIVE AdaptiveType = ADAPTIVE_NONE, double DecayRate = 0.9); .... void ~Cmlp(void) { }; };
在类接口内声明之后,我们必须针对反向传播函数进行重大修改,我们将其命名为 'Backward'。这些修改主要涉及添加输入,并检查这些输入,以便判定所要用到的相应学习率类型。我们仅往 'Backward' 函数里添加两个参数,即 'AdaptiveType' 和 'DecayRate'。自适应类型,顾名思义,若要用到自适应学习率,则将提供四种自适应学习率类型之一。我们的网络仍保留了不使用自适应学习率的选项,这就是为什么该参数的默认值为 'ADAPTIVE_NONE' 的原因,其含义如标签所示。此外,我们将在下面考察自适应学习率的接下来三种格式,都需要衰减率,故反向传播函数的第 3 个、也是最后一个输入参数就是该值,并且由于前 2 个参数都赋予了默认值,该参数也随即被赋予了一个数值。
在该函数内,主要的变化是在两个 “学习点”,即我们更新输出权重和乖离之所在,以及可扩展部分,其中我们更新每个隐藏层的隐藏权重和隐藏乖离(如果网络有这些)。这些更新部分都是分开的,因为在构早该网络时,包含隐藏层是一个选项,且非强制性。它具有可扩展性,即它一趟更新所有隐藏层(如果存在),无关它们的数量。故此,自旧网络的反向传播所做的修改,只是检查在每个点是否用到了自适应学习率。我们有 4 种自适应学习率类型,出于完整性,它们都在下面呈现,如此就不必在之后文章中重复。我们的第一点现在看上去如下:
//+------------------------------------------------------------------+ //| Backward pass through the neural network to update weights | //| and biases using gradient descent | //+------------------------------------------------------------------+ void Cmlp::Backward(double LearningRate = 0.1, ENUM_ADAPTIVE AdaptiveType = ADAPTIVE_NONE, double DecayRate = 0.9) { if(!validated) { printf(__FUNCSIG__ + " invalid network settings! "); return; } // Calculate output layer gradients vector _output_error = target - output; vector _output_gradients; _output_gradients.Init(output.Size()); for (int i = 0; i < int(output.Size()); i++) { _output_gradients[i] = _output_error[i] * ActivationDerivative(output[i]); } // Update output layer weights and biases if(AdaptiveType == ADAPTIVE_NONE) { for (int i = 0; i < int(output.Size()); i++) { for (int j = 0; j < int(weights[hidden_layers].Cols()); j++) { weights[hidden_layers][i][j] += LearningRate * _output_gradients[i] * hidden_outputs[hidden_layers - 1][j]; } biases[hidden_layers][i] += LearningRate * _output_gradients[i]; } } // Adaptive updates else if(AdaptiveType != ADAPTIVE_NONE) { if(AdaptiveType == ADAPTIVE_GRAD) { AdaptiveGradientUpdate(LearningRate, hidden_layers, _output_gradients, hidden_outputs[hidden_layers - 1]); } else if(AdaptiveType == ADAPTIVE_RMS) { AdaptiveRMSUpdate(DecayRate, LearningRate, hidden_layers, _output_gradients, hidden_outputs[hidden_layers - 1]); } else if(AdaptiveType == ADAPTIVE_ME) { AdaptiveMEUpdate(DecayRate, LearningRate, hidden_layers, _output_gradients, hidden_outputs[hidden_layers - 1]); } else if(AdaptiveType == ADAPTIVE_DELTA) { AdaptiveDeltaUpdate(DecayRate, LearningRate, hidden_layers, _output_gradients, hidden_outputs[hidden_layers - 1]); } } // Calculate hidden layer gradients ... }
类似地,更新隐藏权重和乖离的修改如下:
//+------------------------------------------------------------------+ //| Backward pass through the neural network to update weights | //| and biases using gradient descent | //+------------------------------------------------------------------+ void Cmlp::Backward(double LearningRate = 0.1, ENUM_ADAPTIVE AdaptiveType = ADAPTIVE_NONE, double DecayRate = 0.9) { if(!validated) { printf(__FUNCSIG__ + " invalid network settings! "); return; } // Calculate output layer gradients ... // Calculate hidden layer gradients vector _hidden_gradients[]; ArrayResize(_hidden_gradients, hidden_layers); for(int h = hidden_layers - 1; h >= 0; h--) { vector _hidden_target; _hidden_target.Init(hidden_outputs[h].Size()); _hidden_target.Fill(0.0); _hidden_gradients[h].Init(hidden_outputs[h].Size()); if(h == hidden_layers - 1) { for(int j = 0; j < int(hidden_outputs[h].Size()); j++) { double _sum = 0.0; for(int i = 0; i < int(target.Size()); i++) { if(weights[h + 1][i][j] != 0.0) { _sum += (target[i] / weights[h + 1][i][j]); } } _hidden_target[j] = ActivationDerivative(_sum - biases[h][j]); } } else if(h < hidden_layers - 1) { for(int j = 0; j < int(hidden_outputs[h].Size()); j++) { double _sum = 0.0; for(int i = 0; i < int(hidden_outputs[h + 1].Size()); i++) { if(weights[h][i][j] != 0.0) { _sum += (hidden_outputs[h + 1][i] / weights[h][i][j]); } } _hidden_target[j] = ActivationDerivative(_sum - biases[h][j]); } } vector _hidden_error = _hidden_target - hidden_outputs[h]; for (int i = 0; i < int(_hidden_target.Size()); i++) { _hidden_gradients[h][i] = _hidden_error[i] * ActivationDerivative(hidden_outputs[h][i]); } } // Adaptive updates if(AdaptiveType != ADAPTIVE_NONE) { for(int h = hidden_layers - 1; h >= 0; h--) { vector _outputs = inputs; if(h > 0) { _outputs = hidden_outputs[h - 1]; } if(AdaptiveType == ADAPTIVE_GRAD) { AdaptiveGradientUpdate(LearningRate, h, _hidden_gradients[h], _outputs); } else if(AdaptiveType == ADAPTIVE_RMS) { AdaptiveRMSUpdate(DecayRate, LearningRate, h, _hidden_gradients[h], _outputs); } else if(AdaptiveType == ADAPTIVE_ME) { AdaptiveMEUpdate(DecayRate, LearningRate, h, _hidden_gradients[h], _outputs); } else if(AdaptiveType == ADAPTIVE_DELTA) { AdaptiveDeltaUpdate(DecayRate, LearningRate, h, _hidden_gradients[h], _outputs); } } } // Update hidden layer weights and biases else if(AdaptiveType == ADAPTIVE_NONE) { for(int h = hidden_layers - 1; h >= 0; h--) { for (int i = 0; i < int(weights[h].Rows()); i++) { for (int j = 0; j < int(weights[h].Cols()); j++) { if(h == 0) { weights[h][i][j] += LearningRate * _hidden_gradients[h][i] * inputs[j]; } else if(h > 0) { weights[h][i][j] += LearningRate * _hidden_gradients[h][i] * hidden_outputs[h - 1][j]; } } biases[h][i] += LearningRate * _hidden_gradients[h][i]; } } } }
上述修改,在所有涉及函数中,会分别在各自部分高亮显示。对于自适应梯度更新函数,我们的实现如下:
//+------------------------------------------------------------------+ // Adaptive Gradient Update function //+------------------------------------------------------------------+ void Cmlp::AdaptiveGradientUpdate(double LearningRate, int LayerIndex, vector &Gradients, vector &Outputs) { for (int i = 0; i < int(weights[LayerIndex].Rows()); i++) { adaptive_gradients[LayerIndex][i] += (Gradients[i] * Gradients[i]); double _learning_rate = LearningRate / (MathSqrt(adaptive_gradients[LayerIndex][i]) + __NON_ZERO); for (int j = 0; j < int(weights[LayerIndex].Cols()); j++) { weights[LayerIndex][i][j] -= (_learning_rate * Gradients[i] * Outputs[j]); } // biases[LayerIndex][i] -= _learning_rate * Gradients[i]; } }
添加的自适应梯度矢量数组累积每层的每个参数的梯度平方值。这些特定于每个参数的平方值,随后根据所涉及的参数、及其在整个训练过程中的梯度历史记录,按照不同额度降低学习率。平方梯度合计充当学习率的分母,故可理解为梯度越大,学习率越小。
我们依照自适应梯度学习率执行了一些测试运行,我们的一些测试结果如下:
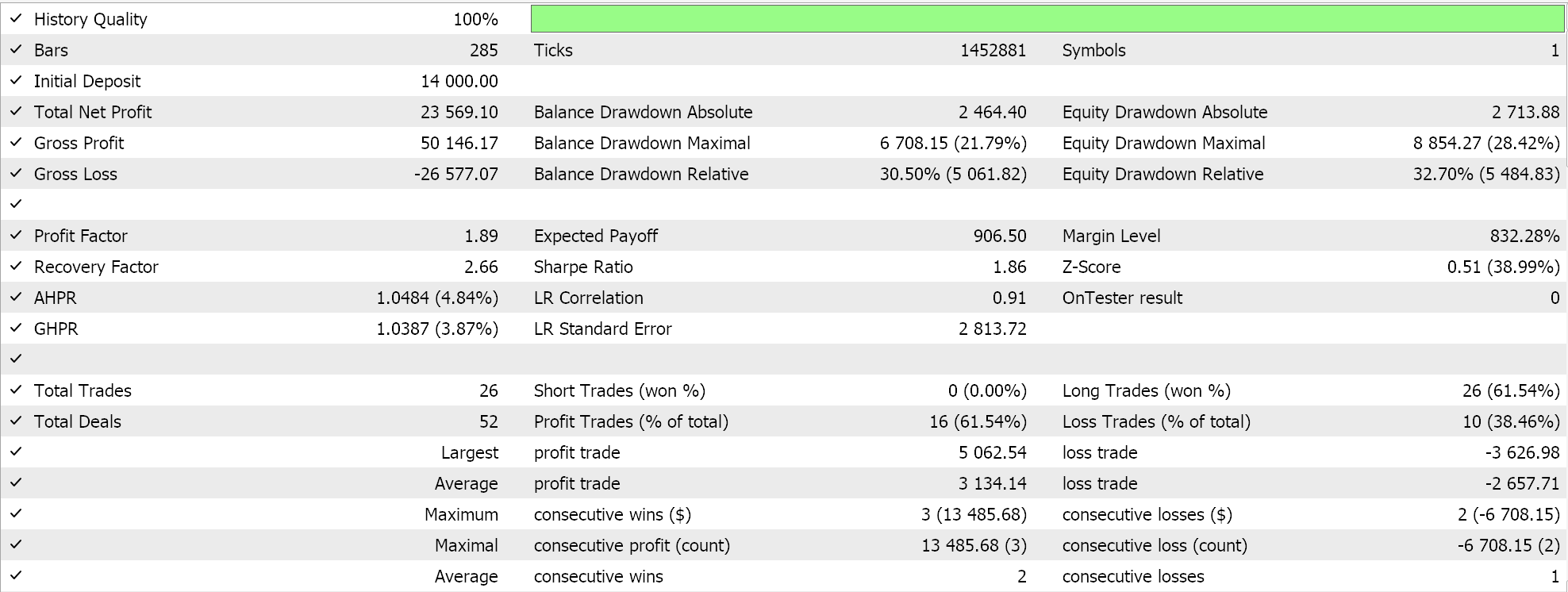

这些测试运行都是依据外汇对 NZDUSD 的 2023 年日线时间帧进行的。采用 NZDUSD 是出于批量归一化目的,我们将在下一篇文章中涵盖更多细节。不过就目前而言,如上所述,我们正用 Sigmoid 激活,将其输出保持在 0.0 到 1.0 范围,对于探索理想学习率的测试目的,这是个很好的预兆。一旦每个参数都有了自己的学习率,权重和乖离就会由自适应梯度更新函数更新,其清单已分享如上。
由于我们的原生价格输入数据在 0.0 到 1.0 范围内,且我们是由 Sigmoid 激活的,故我们的网络输出也应在 0.0 到 1.0 范围。我们正在与原生价格打交道,鉴于我们正在为我们的网络投喂历史价格数据,并在连续价格数据上训练它,故我们能够期待我们的网络会预测下一个收盘价。我们在没有批量归一化的情况下完成这一切,这是非常冒险的,因为即使输出可能在所需的 0.0 到 1.0 范围,它给出的价格很容易偏离当前出价(或高或低),这将发出永久买入或卖出信号。在我们上面的 “理想 ”测试结果中已经有所显现。现在,我运行了几次,其中多头和空头均有开仓,但缺乏批量归一化需要警惕。为了能在自定义信号类中,自我们做多和做空条件函数里生成信号或条件值,我们需要将预测价格归一化为 0 到 100 的整数范围。
如常,有大量方式可达成这一点,不过在我们的例子中,我们只需拿预测价格与输入价格数组进行比较,然后得出一个百分位数的双精度值。我们将该百分位数值转换为预期 0 到 100 之间的整数,如此我们得到一个输出条件。仅当网络的预测价格分别高于或低于当前出价时,才会在每个多头和空头条件函数中完成这种归一化。源代码分享如下:
//+------------------------------------------------------------------+ //| "Voting" that price will grow. | //+------------------------------------------------------------------+ int CSignalCMLP::LongCondition(void) { int result = 0; double _mlp_output = 0.0; GetOutput(_mlp_output); m_symbol.Refresh(); m_symbol.RefreshRates(); if(_mlp_output > m_symbol.Bid()) { vector _scale; _scale.CopyRates(m_symbol.Name(), m_period, 8, 0, __MLP_INPUTS); result = int(round(100.0 * (fmin(_mlp_output, _scale.Max()) - _scale.Min()) / fmax(m_symbol.Point(), _scale.Max() - _scale.Min()))); } //printf(__FUNCSIG__ + " output is: %.5f, change is: %.5f, and result is: %i", _mlp_output, m_symbol.Bid()-_mlp_output, result);return(0); return(result); } //+------------------------------------------------------------------+ //| "Voting" that price will fall. | //+------------------------------------------------------------------+ int CSignalCMLP::ShortCondition(void) { int result = 0; double _mlp_output = 0.0; GetOutput(_mlp_output); m_symbol.Refresh(); m_symbol.RefreshRates(); if(_mlp_output < m_symbol.Bid()) { vector _scale; _scale.CopyRates(m_symbol.Name(), m_period, 8, 0, __MLP_INPUTS); result = int(round(100.0 * (fmin(_mlp_output, _scale.Max()) - _scale.Min()) / fmax(m_symbol.Point(), _scale.Max() - _scale.Min()))); } //printf(__FUNCSIG__ + " output is: %.5f, change is: %.5f, and result is: %i", _mlp_output, m_symbol.Bid()-_mlp_output, result);return(0); return(result); }
由 MQL5 向导组装智能系统时所用代码均附于本文底部。有关行事的指南,可于此处和此处找到。
自适应 RMS 学习率
RMS prop 自适应学习率引入了一个额外的参数,管控学习率的急速跌落,当面对较大的训练梯度时,就会大量发生,因为这些累积贯穿整个训练过程。该参数是衰减率,我们已在上面引入,作为修改后的反向传播函数新的额外输入参数之一。在上一篇文章中,我们在步进衰减学习率、指数衰减学习率、和逆时衰减学习率中都用到一个衰减率,其目的大致相似。自我们的自定义信号类,我们有一个名为 DecayRate 的双精度输入参数,其可充当所有这些目的,因为在任何训练期间都只能选择一种学习率格式。故此,衰减率将作用于选定的学习率类型。
为了继续使用自适应学习率,尽管 RMS-prop 限制了历史梯度的累积,这可能是与自适应梯度配合的问题,因为学习会明显降速,至某点实际上就停止了。这是因为历史梯度与上面已经提到的学习率之间存在反比关系。多亏衰减因子,RMS prop 的创新有效地减缓学习率的跌落,具体实现如下:
//+------------------------------------------------------------------+ // Adaptive RMS Update function //+------------------------------------------------------------------+ void Cmlp::AdaptiveRMSUpdate(double DecayRate, double LearningRate, int LayerIndex, vector &Gradients, vector &Outputs) { for (int i = 0; i < int(weights[LayerIndex].Rows()); i++) { adaptive_gradients[LayerIndex][i] += (DecayRate * adaptive_gradients[LayerIndex][i]) + ((1.0 - DecayRate)*(Gradients[i] * Gradients[i])); double _learning_rate = LearningRate / (MathSqrt(adaptive_gradients[LayerIndex][i]) + __NON_ZERO); for (int j = 0; j < int(weights[LayerIndex].Cols()); j++) { weights[LayerIndex][i][j] -= (_learning_rate * Gradients[i] * Outputs[j]); } biases[LayerIndex][i] -= _learning_rate * Gradients[i]; } }
自适应梯度的另一个问题是,当处置非稳态数据时,且数据底层分布和特征会随时间推移变化,因此即使遍历了训练集,累积的梯度也会变得过时,且相关性降低,从而导致学习率欠佳。RMS prop 从另一方面看到,是最近的梯度在起作用,因此对学习率的影响更大。这令学习过程更具适应性,按理说在与交易者更直接相关的场景中更实用,例如时间序列预测。
此外,在稀疏数据集上进行训练的情况下,譬如在我们的交易核心能力之外的数据集,像是在自然语言处理、或推荐系统中,自适应梯度在读取不常用特征、或数据点时会过度减少梯度。因此,RMS prop 通过将学习率长时间保持在相对较高的水平,来做到更平衡的训练过程,如此令这些网络(交易者在某些状况下仍会发现这很实用)可以具有更优权重和乖离。
最后,自适应梯度对噪声数据非常易感和敏锐,因为从本质上讲,梯度与噪声呈正相关。故此,在训练数据没有针对这些异常值进行相应筛选的状况下,学习率的急速降低本质上意味着,网络从异常值和噪声中所学,比之核心或理想数据更多。RMS prop 对衰减因子的平滑效果意味着学习率能就杂乱的异常值“生存”,且在训练集中核心或理想数据最终满意时,仍然继续有效地促进网络权重和乖离。
我们配合 RMS prop 自适应学习执行了一些测试运行,以下是我们的测试结果示例:
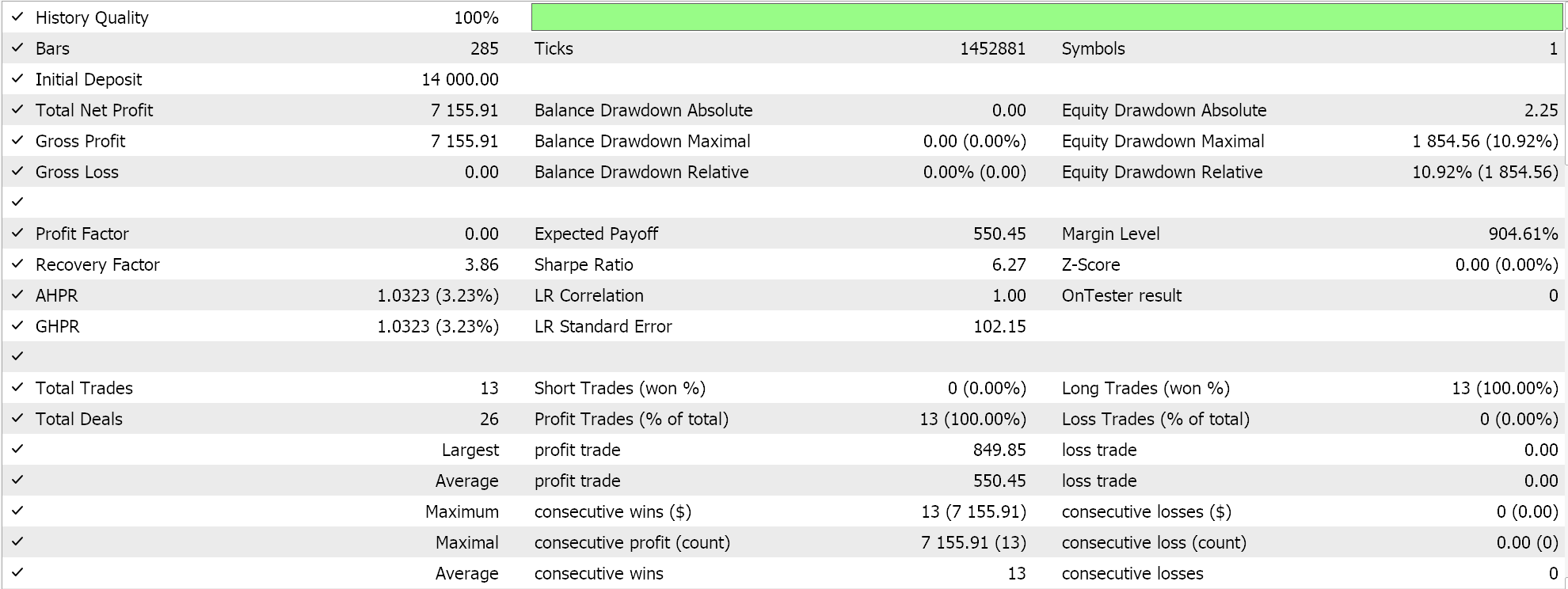
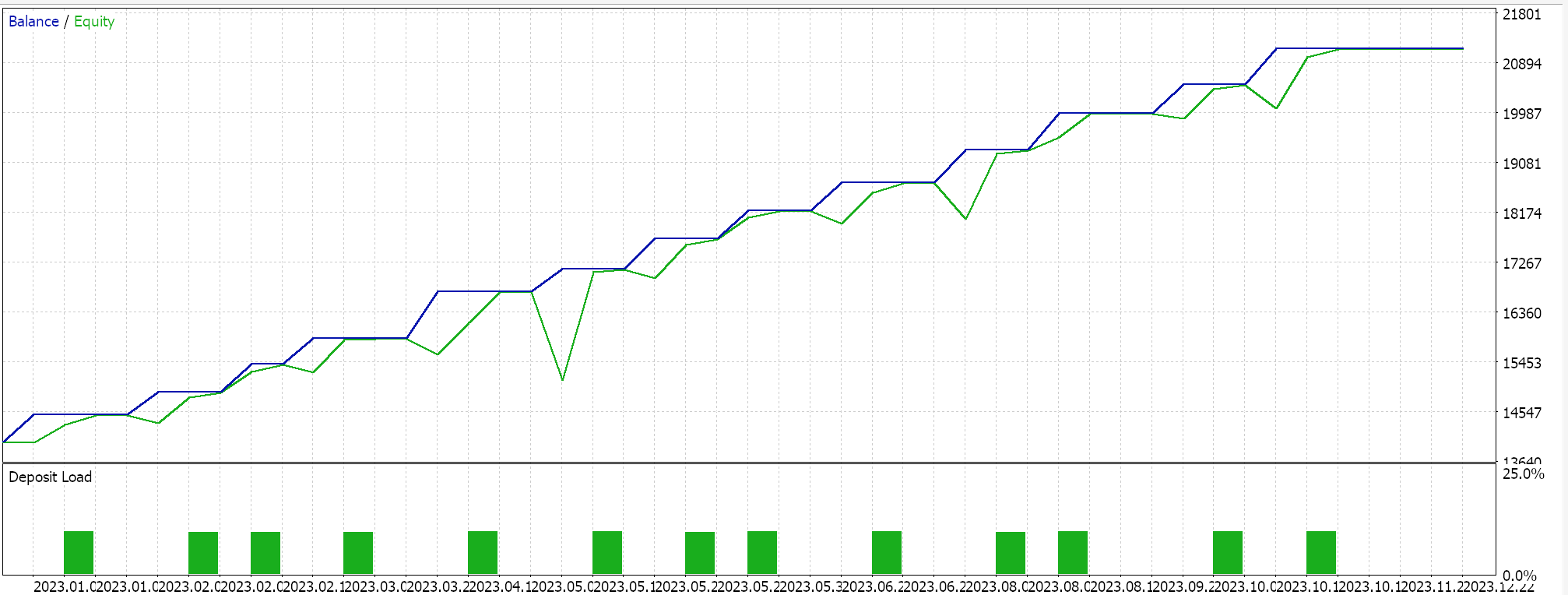
因为我们的网络输入没有针对该网络选定的激活函数进行批量归一化(我们正在用 Sigmoid 与 Soft Max),故我们的测试结果往做多交易倾斜,因为输出预测价格始终高于当前出价。可能有一些归一化方式,给出的输出价格能在做多和做空之间取得平衡,此处我们的方式并未深思,但我更愿意在研究这些方式之前,先对输入数据进行适当的批量归一化。因此就该问题,我们将在下篇文章中更有效地跟踪,如上所述。
自适应动量评估(或均值指数)学习率
自适应动量评估(又名 ADAM)是自适应学习率的另一种变体,旨在通过梯度均值和梯度方差(动量),双管齐下令上述 RMS 等方式更加平滑。MQL5 实现如下:
//+------------------------------------------------------------------+ // Adaptive Mean Exponential(ME) Update function //+------------------------------------------------------------------+ void Cmlp::AdaptiveMEUpdate(double DecayRate, double LearningRate, int LayerIndex, vector &Gradients, vector &Outputs) { for (int i = 0; i < int(weights[LayerIndex].Rows()); i++) { adaptive_gradients[LayerIndex][i] = (DecayRate * adaptive_gradients[LayerIndex][i]) + ((1.0 - DecayRate)*(Gradients[i] * Gradients[i])); double _learning_rate = LearningRate / (fabs(adaptive_gradients[LayerIndex][i]) + __NON_ZERO); for (int j = 0; j < int(weights[LayerIndex].Cols()); j++) { weights[LayerIndex][i][j] -= (_learning_rate * Gradients[i] * Outputs[j]); } // biases[LayerIndex][i] -= _learning_rate * Gradients[i]; } }
我们刚在上面看到了 RMS prop 学习率是如何比梯度率高出一个台阶的,即它们减慢了学习率的降速,这样就提供了许多优势,其中一些已在上面分享。是的,ADAM 继续沿此方向,尤其是在面对高维数据的状况下。随着已处理数据集的维度增加,故梯度数组中的参数量也会增加。如这般状况下,这可能是图像和语音识别,比之仅参考均值,额外参考动量有助于学习率更敏感地适配数据集。根据某个网络设计,这样的高维场景肯定会在金融时间序列预测中遇到。
当仅用梯度平方平均值时,相对不稳定、且收敛缓慢,这令 RMS prop 在嘈杂数据中的可靠性低于 ADAM。平方均值和方差的组合则提供了更平滑、更稳健、稳定和快速的收敛处理。此外,自然语言处理和推荐系统中的稀疏梯度,虽然由 RMS prop 处理比之自适应梯度更好,但多谢学习率中的动量加权,搭配 ADAM 管理甚至更佳。甚至,在参数频繁变化的状况下,譬如当采用随机权重和乖离初始化新网络时,RMS prop 关注最近梯度历史可能会导致过于保守的更新,而 ADAM 的动量参考令其即使处于这些状况,也能更好地响应。
最后,在处置目标函数随时间变化的非稳态目标时,RMS prop 虽然有均值的辅助,但仍可能无法像 ADAM 那样适配。如该例,研究这样一种状况:您的建模网络是为预测房地产价格,并处理输入或特征,例如房屋大小、卧室数量、和位置。反向传播期间,我们所用的 MLP 网络目标函数,只是目标和预测之间的差值向量,但通常该目标可以取多种形式,诸如均方误差(MSE),在这种状况下,您将有以下公式:
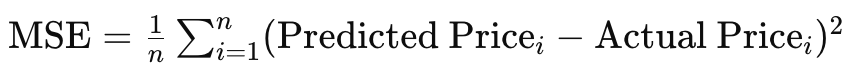
其中:
- n 是数据样本中的房屋数量
- MSE 是均方误差
这将是一个反向传播误差函数,其结果会随时间推移而降低,因为网络学习会相应更新其权重和乖离,MSE 值越低,表示网络性能越好。现在假设所研究的房地产市场发生了巨大变化,以至于网络特征(输入)和预测价格之间的关系发生了变化显著,举例,在考察的房地产所在区域内,引入了一条新的地铁。这肯定会改变该区域房地产的定价模型,这令目标函数在适配这些变化时实用性较低。随着权重和乖离的更新,通过添加更多相关特征(输入字段)来修订网络能带来更优化的成果。ADAM 通过添加新特征,能更好地管理网络模型修定和更新的过渡,因为权重更新过程已含动量因素。
ADAM 的测试结果为我们给出了以下报告:
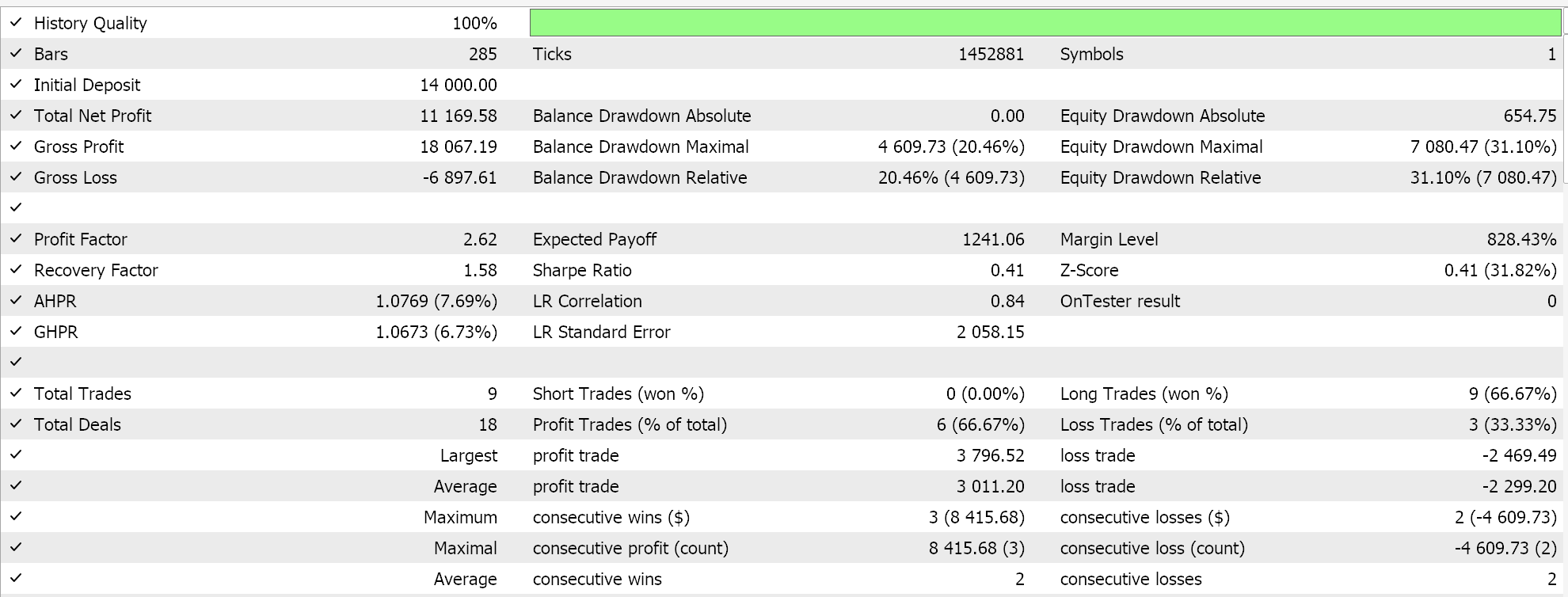
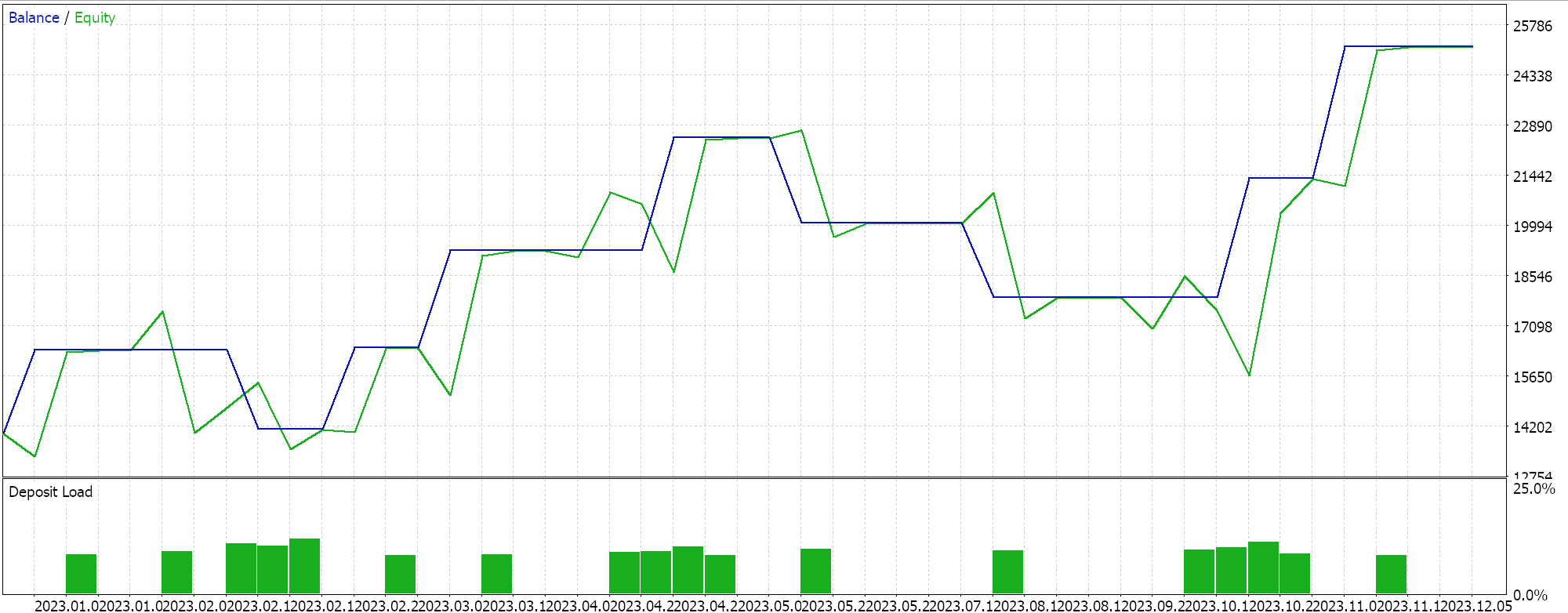
这并非来自最佳或理想的设定,而只是展示 ADAM 学习率如何应用于 MLP 网络。在上一篇文章中,我们用到一对 GAN 网络,而在此我们所用的更基本、但仍直观,即仅有三层的多层感知器,采用 5-8-1 的形式。
自适应增量学习率
我们最后的自适应学习率是 ADADELTA,尽管它没有采用任何新的输入参数,但它在调整学习率的训练时,深化了优化效力。其公式相对复杂,但理论上,除了考虑到梯度衰减累积之外,还参考了权重的衰减累积。MQL5 实现如下:
//+------------------------------------------------------------------+ // Adaptive Delta Update function //+------------------------------------------------------------------+ void Cmlp::AdaptiveDeltaUpdate(double DecayRate, double LearningRate, int LayerIndex, vector &Gradients, vector &Outputs) { for (int i = 0; i < int(weights[LayerIndex].Rows()); i++) { adaptive_gradients[LayerIndex][i] = (DecayRate * adaptive_gradients[LayerIndex][i]) + ((1.0 - DecayRate)*(Gradients[i] * Gradients[i])); double _delta = (MathSqrt(adaptive_deltas[LayerIndex][i] + __NON_ZERO) / MathSqrt(adaptive_gradients[LayerIndex][i] + __NON_ZERO)) * Gradients[i]; adaptive_deltas[LayerIndex][i] = (DecayRate * adaptive_deltas[LayerIndex][i]) + ((1.0 - DecayRate) * _delta * _delta); for (int j = 0; j < int(weights[LayerIndex].Cols()); j++) { weights[LayerIndex][i][j] -= (_delta * Outputs[j]); } // Bias update with AdaDelta biases[LayerIndex][i] -= _delta; } }
上面提到的 RMS prop 和 ADAM 快速拉低学习率较低的大部分优势,也适用于 ADADELTA。现在值得一提的是 ADADELTA 在评估学习率时引入的自适应增量的额外缓冲区的益处。
ADAM 使用平方梯度的均值,和方差的移动平均值来调整每个参数的学习率,虽然对 RMS prop 进行了有效改进,但在某些实例下,专注历史梯度会导致超调最小值,从而在训练时产生不稳定,尤其是在处理嘈杂数据时。包含平方更新的缓冲区,这称为“自适应增量”。这种累积有助于更好地平衡学习率更新,如此它就基于最近梯度的量级、和最近增量更新有效性两者。
通过持续跟踪平方更新,ADADELTA 可以通过参考这些更新的最新有效性,来动态调整步长。这样学习过程更富变化,防止它变得过于保守,若梯度的量级衰退明显,就会发生这种情况。甚至,权重更新的额外累积提供了一种机制,可在使用最近更新尺度的同时,对更新进行归一化,从而提高优化器适配梯度场景变化的能力。这在非稳态数据集分布、或梯度高度可变的状况下至关重要。
ADADELTA 的其它创新是降低超参数敏感性、及避免学习率衰退。我们配以 ADADELTA 学习率运行测试,如上类似的品种、测试周期、和时间帧,并得到各种可盈利结果。以下是其中一份报告:
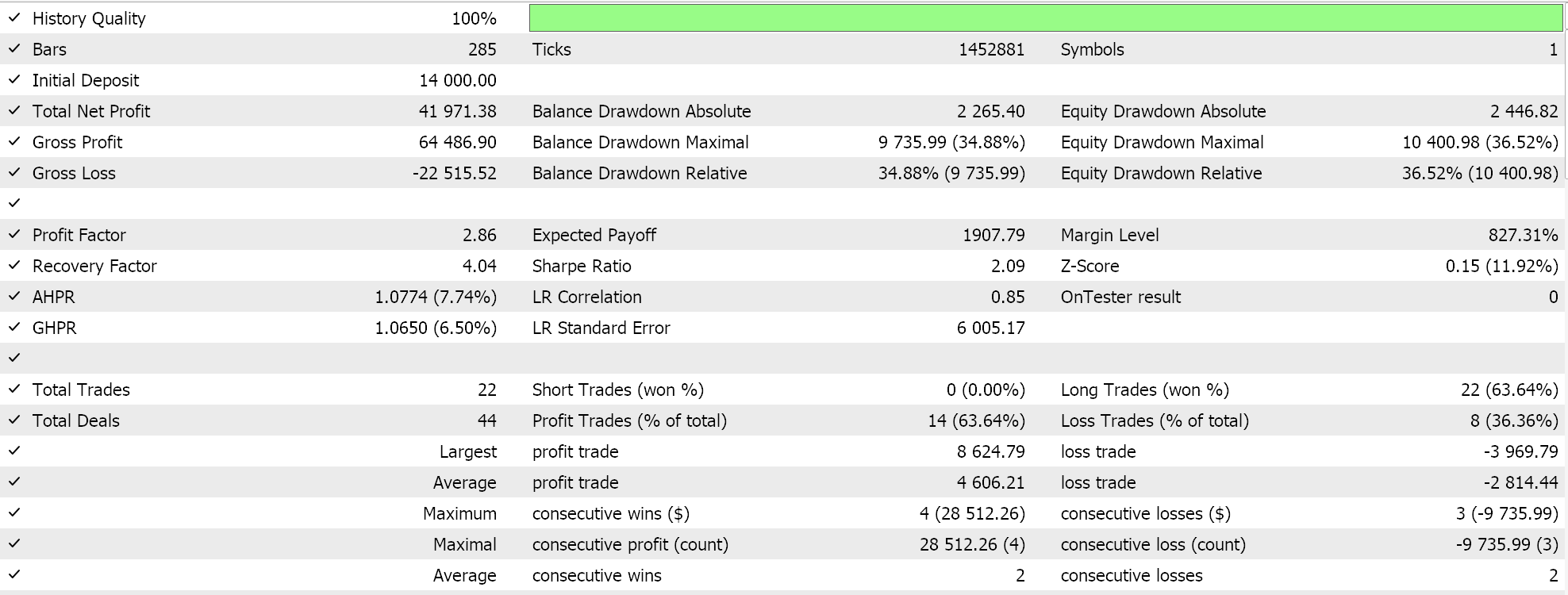
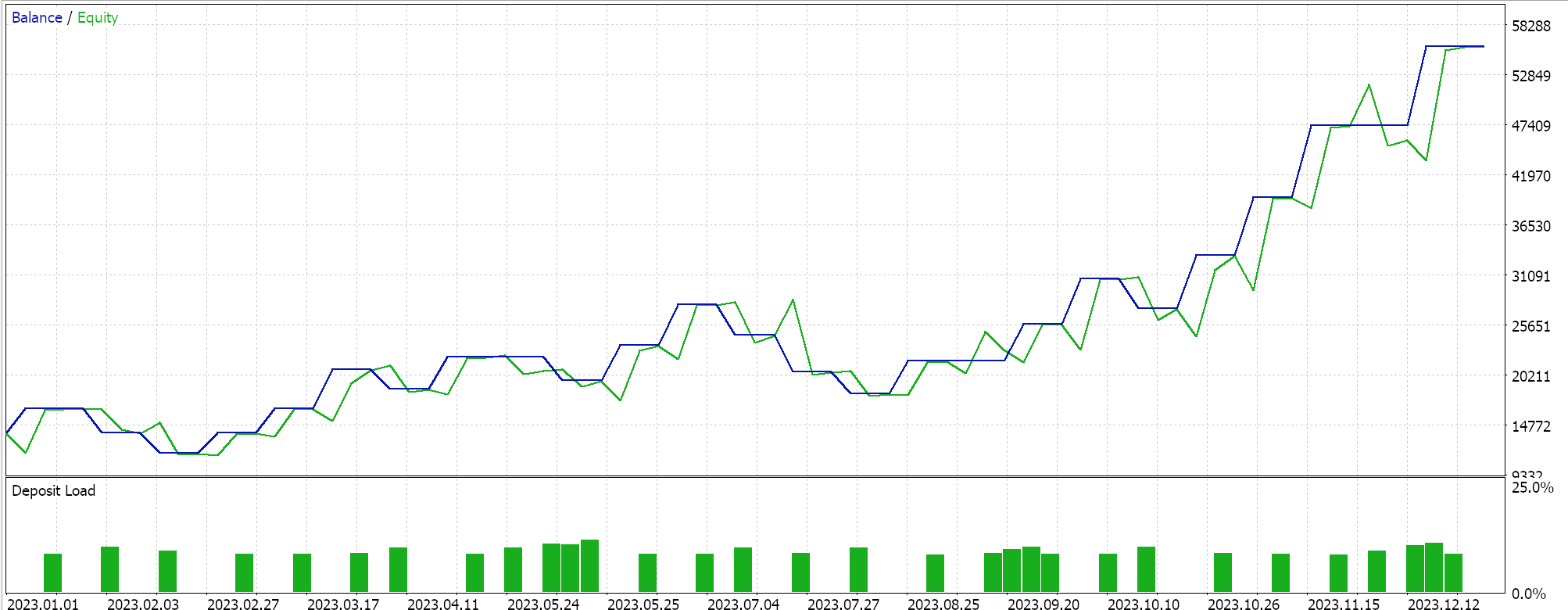
一次轮转的学习率
该学习率调整方式缺乏自适应学习率方法的精密性,更类似于我们在上一篇文章中研究的余弦退火格式。不过,它比余弦退火更简单一些,因为学习率朝向训练结束时会先增加、后降低。实现如下:
else if(m_learning_type == LEARNING_ONE_CYCLE) { double _cycle_position = (double)((m_epochs - i) % (2 * m_epochs)) / (2.0 * m_epochs); if (_cycle_position <= 0.5) { _learning_rate = m_min_learning_rate + (2.0 * _cycle_position * (m_learning_rate - m_min_learning_rate)); } else { _learning_rate = m_learning_rate - (2.0 * (_cycle_position - 0.5) * (m_learning_rate - m_min_learning_rate)); } }
故此,不像我们在本文中研究的调整学习率的相对复杂方式,在一次轮转中,学习率最初只是在所谓的热身阶段增加,然后达到峰值学习率,随后在冷却阶段(训练过程的后半部分)降低。除了余弦退火之外,大多数学习率方式都热衷于从较大的学习率开始,后随处理数据量增加而降低该值。
一次轮转学习率的作用有点相反,因为它从最低学习率开始。最小学习率和最大学习率是预定义的输入参数,学习率的路径、或变化率,受局次数、或训练区间长度的影响。正如我们对自适应学习率所做的那样,我们据一次轮转学习率执行测试运行,我们的一份测试报告如下所示:
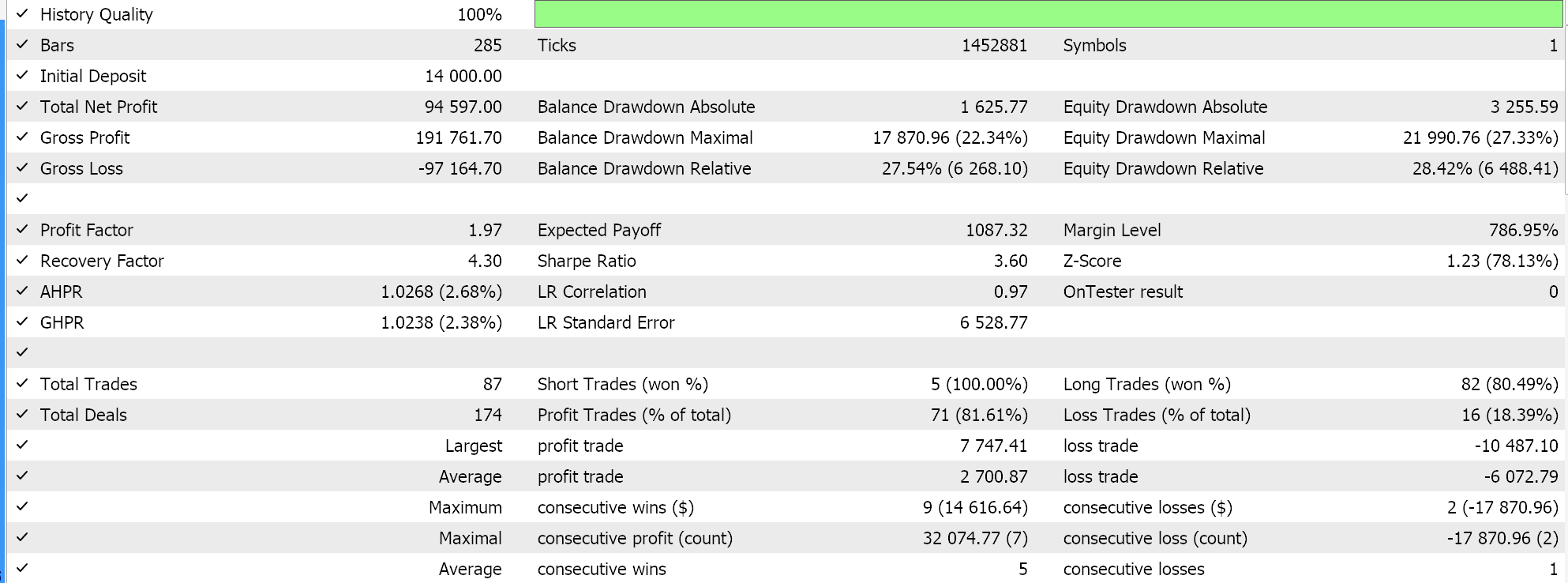
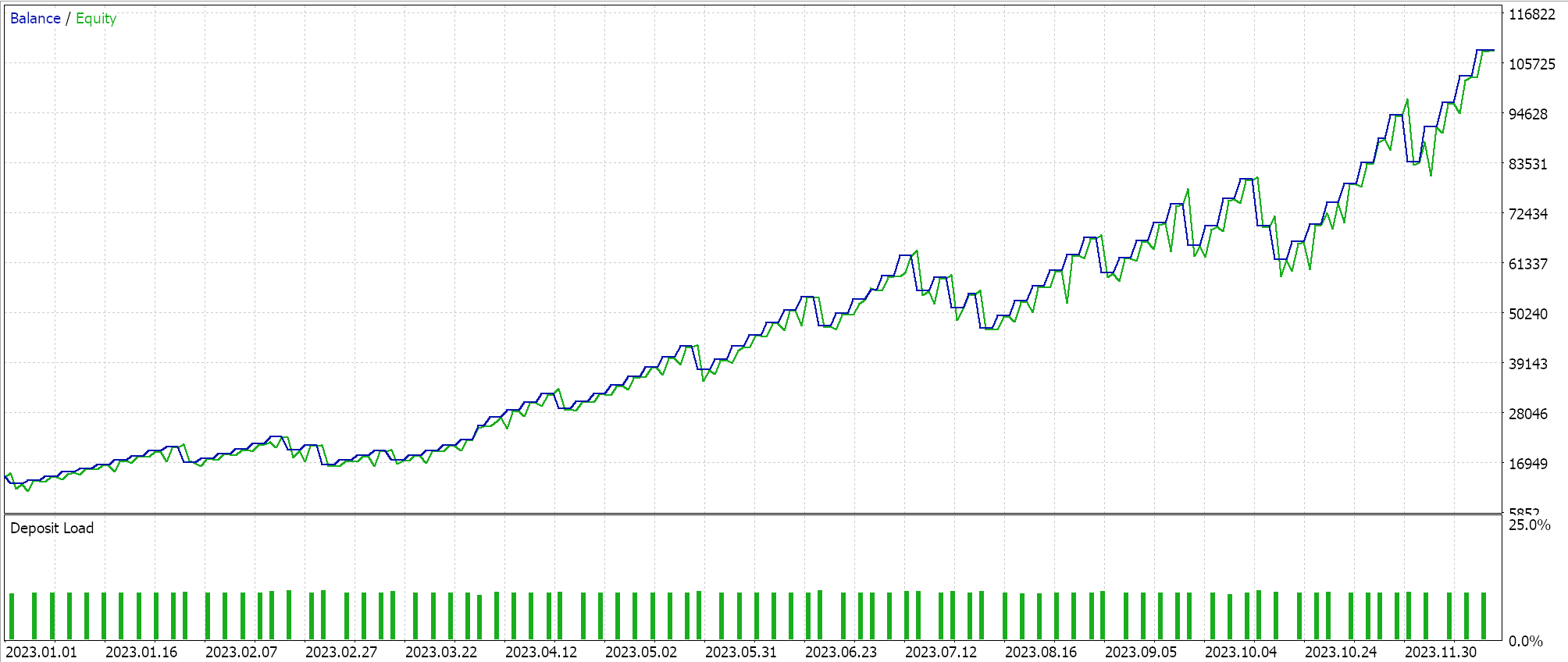
从我们上面的结果来看,尽管缺乏相应的批量归一化,但仅通过调整学习率,我们最终能够开立一些做空交易。这是在预测原生品种价格(无批量归一化),且归一化做多和做空条件,就像我们在测试自适应学习率方法时所做。这再次表明,采取调整学习率的方式对神经网络的性能有多么敏感。
结束语
综上所述,学习率是机器学习算法的一个关键、且非常敏感的层面。我们验证了实现各种格式的变数,同时关注每种格式的顺序创新,因为大多数开发的学习率方式都是为了改进早期的方法和方式。当然,提升这些学习率的旅程仍在迈进中,并会继续,然而,更简单的骨架方式,像是一次轮转学习率,也不应忽视,它们同样可能相当行之有效,正如我们从一些测试结果中所见。
本文由MetaQuotes Ltd译自英文
原文地址: https://www.mql5.com/en/articles/15405
注意: MetaQuotes Ltd.将保留所有关于这些材料的权利。全部或部分复制或者转载这些材料将被禁止。
本文由网站的一位用户撰写,反映了他们的个人观点。MetaQuotes Ltd 不对所提供信息的准确性负责,也不对因使用所述解决方案、策略或建议而产生的任何后果负责。
 在 MQL5 中创建交易管理员面板(第一部分):构建消息接口
在 MQL5 中创建交易管理员面板(第一部分):构建消息接口
 MetaTrader 中的 Multibot(第二部分):改进的动态模板
MetaTrader 中的 Multibot(第二部分):改进的动态模板


亲爱的斯蒂芬,
感谢您分享有关此交易系统的知识和工作!
我饶有兴趣地阅读了您的文章。然而,当我下载您所附的压缩文件时,它只包括:
1. Cmlp_ad.mqh
2.SignalWZ_29.mqh
3. mlp_learn_r.mq5
在mlp_learn_r.mq5 中,它需要以下文件:
1. Expert.mqh
2. TrailingNone.mqh
3.MoneyFixedMargin.mqh
请问如何获得这些文件?
没有这些文件......EA 无法运行。
谢谢!非常感谢!
亲爱的斯蒂芬,
,感谢您分享有关此交易系统的知识和工作!
,我饶有兴趣地阅读了您的文章。然而,当我下载您所附的压缩文件时,它只包括:
1. Cmlp_ad.mqh
2.SignalWZ_29.mqh
3. mlp_learn_r.mq5
在mlp_learn_r.mq5 中,它需要以下文件:
1. Expert.mqh
2. TrailingNone.mqh
3.MoneyFixedMargin.mqh
请问如何获得这些文件?
没有这些文件......EA 无法运行。
谢谢!非常感谢!
它们已经存在于 MQL include 文件夹中,您应该添加一个页眉。