Características del Wizard MQL5 que debe conocer (Parte 29): Continuación sobre las tasas de aprendizaje con MLP

Introducción

Volvemos a examinar y concluimos nuestro análisis del papel que desempeñan los distintos formatos de tasas de aprendizaje en el rendimiento del Asesor Experto examinando las tasas de aprendizaje adaptativo y la tasa de aprendizaje de un ciclo. El formato de este artículo seguirá el enfoque que teníamos en el último artículo al tener informes de pruebas en cada sección de formato de tasa de aprendizaje en lugar de al final del artículo.

Antes de entrar en materia, nos gustaría mencionar otras consideraciones críticas sobre el diseño del aprendizaje automático que pueden influir enormemente en el rendimiento de un modelo. Una de ellas es la normalización por lotes de los datos de entrada. Ya he mencionado este tema en artículos anteriores sobre por qué es importante, sin embargo, nuestro próximo artículo se centrará directamente en este tema. Por ahora, sin embargo, al diseñar el modo y formato de una red, la normalización por lotes se considera junto con los algoritmos de activación que empleará el modelo o la red. Por ejemplo, a diferencia de las activaciones TANH o sigmoidea, que producen resultados en los rangos de -1,0 a +1,0 y de 0,0 a 1,0 respectivamente, la activación suave puede producir a menudo resultados que no superen la prueba de validez y, por tanto, invalidar el proceso de formación y previsión.

Como adelanto del próximo artículo, estamos realizando algunos cambios no sólo en los algoritmos de activación utilizados por nuestras redes sino también en el símbolo de Forex probado. Estamos utilizando el algoritmo de activación de salida sigmoide para todas las activaciones de capa, pero además, nuestro par de símbolos de Forex de prueba tendrá sus entradas (que en nuestro caso siguen siendo precios brutos, ya que no estamos realizando la normalización por lotes) en el rango de 0,0 a 1,0. No hay muchos pares de divisas que para nuestro período de prueba, que es el año 2023, tengan sus precios en este rango; sin embargo, el NZDUSD sí, y por eso lo utilizaremos.

Esto hace que comparar los resultados de rendimiento de los resultados en el artículo anterior sea poco práctico, ya que la base ha cambiado. Sin embargo, con esta nueva red, algoritmo de activación y par de divisas, el lector puede seguir probando los formatos de tasa de aprendizaje explorados en el último artículo para obtener una comparación similar a medida que se reduce el método de tasa de aprendizaje preferido. Además, los resultados de las pruebas presentados aquí y a menudo en estos artículos en general no proceden de las mejores configuraciones, ni pretenden serlo. Se muestran sólo con fines exploratorios, por lo que siempre es trabajo del lector afinar las entradas del Asesor Experto para su óptimo, no sólo con datos históricos de alta calidad, sino también preferiblemente en pruebas a futuro después del período de prueba de la estrategia en cuentas demo antes de su despliegue.

Por tanto, lo que se presenta es sólo el potencial. Y para ello, la tasa de aprendizaje ha demostrado ser una métrica muy sensible sobre el rendimiento, como se desprende de la disparidad de los resultados de las pruebas que obtuvimos en el último artículo. La tasa de aprendizaje adaptativa pretende resolver el problema de que demasiados parámetros determinen la tasa de aprendizaje ideal para un modelo. Recordemos que la tasa de aprendizaje en sí es simplemente un medio para llegar a los pesos y sesgos ideales de la red, por lo que el uso de parámetros adicionales como la potencia polinómica que vimos en el último artículo, o la tasa de aprendizaje mínima se pretende evitar con estos métodos. Para minimizar la parametrización, en principio, el aprendizaje adaptativo genera la tasa de aprendizaje para cada parámetro de capa basándose en su gradiente de entrenamiento. El resultado es una situación en la que casi todos los parámetros tienen su propio ritmo de aprendizaje y, sin embargo, las aportaciones para conseguirlo son mínimas. Son comunes cuatro formatos de tasas de aprendizaje adaptativo, a saber: gradiente adaptativo, RMS adaptativo, exponencial medio adaptativo y delta adaptativo. Lo consideraremos de uno en uno.

Tasa de aprendizaje de gradiente adaptativo

Este es probablemente el formato más simple entre las tasas de aprendizaje adaptativo, sin embargo, aún se adhiere al régimen de tasa de aprendizaje personalizada por parámetro en todas las capas a pesar de tener una sola entrada, la tasa de aprendizaje inicial. La implementación de la tasa de aprendizaje por parámetro requiere personalizaciones que se extienden a nuestra clase principal Expert más allá de la clase de señal personalizada, como hicimos en las tasas de aprendizaje del artículo anterior. Esto se debe a que solo se puede acceder a los gradientes de entrenamiento que sirven como entradas para determinar la tasa de aprendizaje desde la interfaz de la clase de red principal. Podemos realizar cambios en la clase y hacerlos públicos, pero dada la personalización adicional involucrada (donde potencialmente cada peso y sesgo de capa podría tener su propia tasa de aprendizaje) llamar a la retropropagación puede dejar de ser tan eficiente como debería ser. Al calcular cada tasa de aprendizaje individual durante el proceso de entrenamiento, la red se prepara para funcionar casi con la misma eficiencia cuando se utiliza una única tasa de aprendizaje en todos los parámetros, porque la tasa de aprendizaje calculada se aplica inmediatamente al parámetro específico en lugar de desarrollar primero una estructura personalizada para albergar las nuevas tasas de aprendizaje para todos los parámetros, luego pasar por el proceso iterativo de calcular cada tasa de aprendizaje por separado y luego concluir con otro proceso iterativo de aplicación de cada tasa de aprendizaje individual. Está claro que esto no sería más complicado de codificar, pero seguramente requeriría un mayor esfuerzo computacional. Sin embargo, estamos haciendo cambios en la clase de red padre en primer lugar mediante la introducción de dos parámetros de matriz de vectores de 'adaptive_gradients' y 'adaptive_deltas' como se muestra en la nueva interfaz de clase a continuación:

//+------------------------------------------------------------------+
//|                                                                  |
//+------------------------------------------------------------------+
enum ENUM_ADAPTIVE
{  ADAPTIVE_NONE = -1,
   ADAPTIVE_GRAD = 0,
   ADAPTIVE_RMS = 1,
   ADAPTIVE_ME = 2,
   ADAPTIVE_DELTA = 3,
};
//+------------------------------------------------------------------+
//|                                                                  |
//+------------------------------------------------------------------+
class Cmlp
{
protected:
   matrix            weights[];
   vector            biases[];
   
   vector            adaptive_gradients[];
   vector            adaptive_deltas[];
   
....

   bool              validated;
   
   void              AdaptiveGradientUpdate(double LearningRate, int LayerIndex, vector &Gradients, vector &Outputs);
   void              AdaptiveRMSUpdate(double DecayRate, double LearningRate, int LayerIndex, vector &Gradients, vector &Outputs);
   void              AdaptiveMEUpdate(double DecayRate, double LearningRate, int LayerIndex, vector &Gradients, vector &Outputs);
   void              AdaptiveDeltaUpdate(double DecayRate, double LearningRate, int LayerIndex, vector &Gradients, vector &Outputs);
   
public:
   
...

   void              Forward();
   void              Backward(double LearningRate = 0.1, ENUM_ADAPTIVE AdaptiveType = ADAPTIVE_NONE, double DecayRate = 0.9);

....

   void              ~Cmlp(void) { };
};

Con estos declarados dentro de la interfaz de la clase, entonces tenemos que hacer cambios significativos a la función de retropropagación, que hemos llamado 'Backward'. Principalmente, los cambios implican agregar entradas y verificar dichas entradas para determinar el tipo de tasa de aprendizaje apropiado a utilizar. Solo agregamos dos parámetros a la función 'Backward', es decir, 'AdaptiveType' y 'DecayRate'. El tipo adaptativo, como sugiere su nombre, es uno de los cuatro tipos de tasa de aprendizaje adaptativo que se proporcionarían si se fueran a utilizar las tasas de aprendizaje adaptativo. Nuestra red aún deja abierta la opción de no utilizar tasas de aprendizaje adaptativas, por lo que este parámetro tiene un valor por defecto asignado de 'ADAPTIVE_NONE' que implica lo que sugiere su etiqueta. Además, los próximos tres formatos de la tasa de aprendizaje adaptativo que vamos a ver a continuación sí requieren una tasa de decaimiento por lo que el 3^er y último parámetro de entrada a nuestra función de retropropagación será este valor y dado que los 2 parámetros anteriores tienen todos valores por defecto asignados, se deduce que a éste también se le asigna un valor.

Dentro de esta función, los cambios principales están en los dos "puntos de aprendizaje", es decir, donde actualizamos los pesos y sesgos de salida, así como la parte escalable donde actualizamos los pesos ocultos y los sesgos ocultos de cada capa oculta si la red los tiene. Estas partes de actualización están separadas porque la inclusión de capas ocultas es una opción y no obligatoria al construir esta red. Es escalable ya que actualizará todas las capas ocultas a la vez si están presentes, independientemente de su número. Por lo tanto, los cambios realizados a partir de la antigua propagación hacia atrás de la red simplemente verifican si se está utilizando el aprendizaje adaptativo en cada uno de estos puntos. Tenemos 4 tipos de tasa de aprendizaje adaptativo y todos se presentan a continuación para que estén completos y no se repitan en el artículo posterior. Nuestro primer punto ahora se verá así:

//+------------------------------------------------------------------+
//| Backward pass through the neural network to update weights       |
//| and biases using gradient descent                                |
//+------------------------------------------------------------------+
void Cmlp::Backward(double LearningRate = 0.1, ENUM_ADAPTIVE AdaptiveType = ADAPTIVE_NONE, double DecayRate = 0.9)
{  if(!validated)
   {  printf(__FUNCSIG__ + " invalid network settings! ");
      return;
   }
// Calculate output layer gradients
   vector _output_error = target - output;
   vector _output_gradients;
   _output_gradients.Init(output.Size());
   for (int i = 0; i < int(output.Size()); i++)
   {  _output_gradients[i] = _output_error[i] * ActivationDerivative(output[i]);
   }
// Update output layer weights and biases
   if(AdaptiveType == ADAPTIVE_NONE)
   {  for (int i = 0; i < int(output.Size()); i++)
      {  for (int j = 0; j < int(weights[hidden_layers].Cols()); j++)
         {  weights[hidden_layers][i][j] += LearningRate * _output_gradients[i] * hidden_outputs[hidden_layers - 1][j];
         }
         biases[hidden_layers][i] += LearningRate * _output_gradients[i];
      }
   }
// Adaptive updates
   else if(AdaptiveType != ADAPTIVE_NONE)
   {  if(AdaptiveType == ADAPTIVE_GRAD)
      {  AdaptiveGradientUpdate(LearningRate, hidden_layers, _output_gradients, hidden_outputs[hidden_layers - 1]);
      }
      else if(AdaptiveType == ADAPTIVE_RMS)
      {  AdaptiveRMSUpdate(DecayRate, LearningRate, hidden_layers, _output_gradients, hidden_outputs[hidden_layers - 1]);
      }
      else if(AdaptiveType == ADAPTIVE_ME)
      {  AdaptiveMEUpdate(DecayRate, LearningRate, hidden_layers, _output_gradients, hidden_outputs[hidden_layers - 1]);
      }
      else if(AdaptiveType == ADAPTIVE_DELTA)
      {  AdaptiveDeltaUpdate(DecayRate, LearningRate, hidden_layers, _output_gradients, hidden_outputs[hidden_layers - 1]);
      }
   }
// Calculate hidden layer gradients
   
...

}

De manera similar, los cambios en las actualizaciones de pesos y sesgos ocultos son los siguientes:

//+------------------------------------------------------------------+
//| Backward pass through the neural network to update weights       |
//| and biases using gradient descent                                |
//+------------------------------------------------------------------+
void Cmlp::Backward(double LearningRate = 0.1, ENUM_ADAPTIVE AdaptiveType = ADAPTIVE_NONE, double DecayRate = 0.9)
{  if(!validated)
   {  printf(__FUNCSIG__ + " invalid network settings! ");
      return;
   }
// Calculate output layer gradients
   
...

// Calculate hidden layer gradients
   vector _hidden_gradients[];
   ArrayResize(_hidden_gradients, hidden_layers);
   for(int h = hidden_layers - 1; h >= 0;  h--)
   {  vector _hidden_target;
      _hidden_target.Init(hidden_outputs[h].Size());
      _hidden_target.Fill(0.0);
      _hidden_gradients[h].Init(hidden_outputs[h].Size());
      if(h == hidden_layers - 1)
      {  for(int j = 0; j < int(hidden_outputs[h].Size()); j++)
         {  double _sum = 0.0;
            for(int i = 0; i < int(target.Size()); i++)
            {  if(weights[h + 1][i][j] != 0.0)
               {  _sum += (target[i] / weights[h + 1][i][j]);
               }
            }
            _hidden_target[j] = ActivationDerivative(_sum - biases[h][j]);
         }
      }
      else if(h < hidden_layers - 1)
      {  for(int j = 0; j < int(hidden_outputs[h].Size()); j++)
         {  double _sum = 0.0;
            for(int i = 0; i < int(hidden_outputs[h + 1].Size()); i++)
            {  if(weights[h][i][j] != 0.0)
               {  _sum += (hidden_outputs[h + 1][i] / weights[h][i][j]);
               }
            }
            _hidden_target[j] = ActivationDerivative(_sum - biases[h][j]);
         }
      }
      vector _hidden_error = _hidden_target - hidden_outputs[h];
      for (int i = 0; i < int(_hidden_target.Size()); i++)
      {  _hidden_gradients[h][i] = _hidden_error[i] * ActivationDerivative(hidden_outputs[h][i]);
      }
   }
// Adaptive updates
   if(AdaptiveType != ADAPTIVE_NONE)
   {  for(int h = hidden_layers - 1; h >= 0;  h--)
      {  vector _outputs = inputs;
         if(h > 0)
         {  _outputs = hidden_outputs[h - 1];
         }
         if(AdaptiveType == ADAPTIVE_GRAD)
         {  AdaptiveGradientUpdate(LearningRate, h, _hidden_gradients[h], _outputs);
         }
         else if(AdaptiveType == ADAPTIVE_RMS)
         {  AdaptiveRMSUpdate(DecayRate, LearningRate, h, _hidden_gradients[h], _outputs);
         }
         else if(AdaptiveType == ADAPTIVE_ME)
         {  AdaptiveMEUpdate(DecayRate, LearningRate, h, _hidden_gradients[h], _outputs);
         }
         else if(AdaptiveType == ADAPTIVE_DELTA)
         {  AdaptiveDeltaUpdate(DecayRate, LearningRate, h, _hidden_gradients[h], _outputs);
         }
      }
   }
// Update hidden layer weights and biases
   else if(AdaptiveType == ADAPTIVE_NONE)
   {  for(int h = hidden_layers - 1; h >= 0;  h--)
      {  for (int i = 0; i < int(weights[h].Rows()); i++)
         {  for (int j = 0; j < int(weights[h].Cols()); j++)
            {  if(h == 0)
               {  weights[h][i][j] += LearningRate * _hidden_gradients[h][i] * inputs[j];
               }
               else if(h > 0)
               {  weights[h][i][j] += LearningRate * _hidden_gradients[h][i] * hidden_outputs[h - 1][j];
               }
            }
            biases[h][i] += LearningRate * _hidden_gradients[h][i];
         }
      }
   }
}

Todas las funciones mencionadas anteriormente en estos cambios serán resaltadas en sus respectivas secciones. Para la función de actualización de gradiente adaptativo, nuestra implementación es la siguiente:

//+------------------------------------------------------------------+
// Adaptive Gradient Update function
//+------------------------------------------------------------------+
void Cmlp::AdaptiveGradientUpdate(double LearningRate, int LayerIndex, vector &Gradients, vector &Outputs)
{  for (int i = 0; i < int(weights[LayerIndex].Rows()); i++)
   {  adaptive_gradients[LayerIndex][i] += (Gradients[i] * Gradients[i]);
      double _learning_rate = LearningRate / (MathSqrt(adaptive_gradients[LayerIndex][i]) + __NON_ZERO);
      for (int j = 0; j < int(weights[LayerIndex].Cols()); j++)
      {  weights[LayerIndex][i][j] -= (_learning_rate * Gradients[i] * Outputs[j]);
      }
      //
      biases[LayerIndex][i] -= _learning_rate * Gradients[i];
   }
}

La matriz vectorial agregada de gradientes adaptativos acumula valores cuadrados de gradientes para cada parámetro en cada capa. Estos valores cuadrados, que son específicos de cada parámetro, reducen luego la tasa de aprendizaje en diversas cantidades dependiendo del parámetro involucrado y su historial de gradientes a lo largo del proceso de entrenamiento. La suma de los gradientes al cuadrado actúa como denominador de la tasa de aprendizaje, por lo que se puede entender que cuanto mayores sean los gradientes, menor será la tasa de aprendizaje.

Realizamos algunas pruebas con las tasas de aprendizaje de gradiente adaptativo y algunos de los resultados de nuestras pruebas son los siguientes:

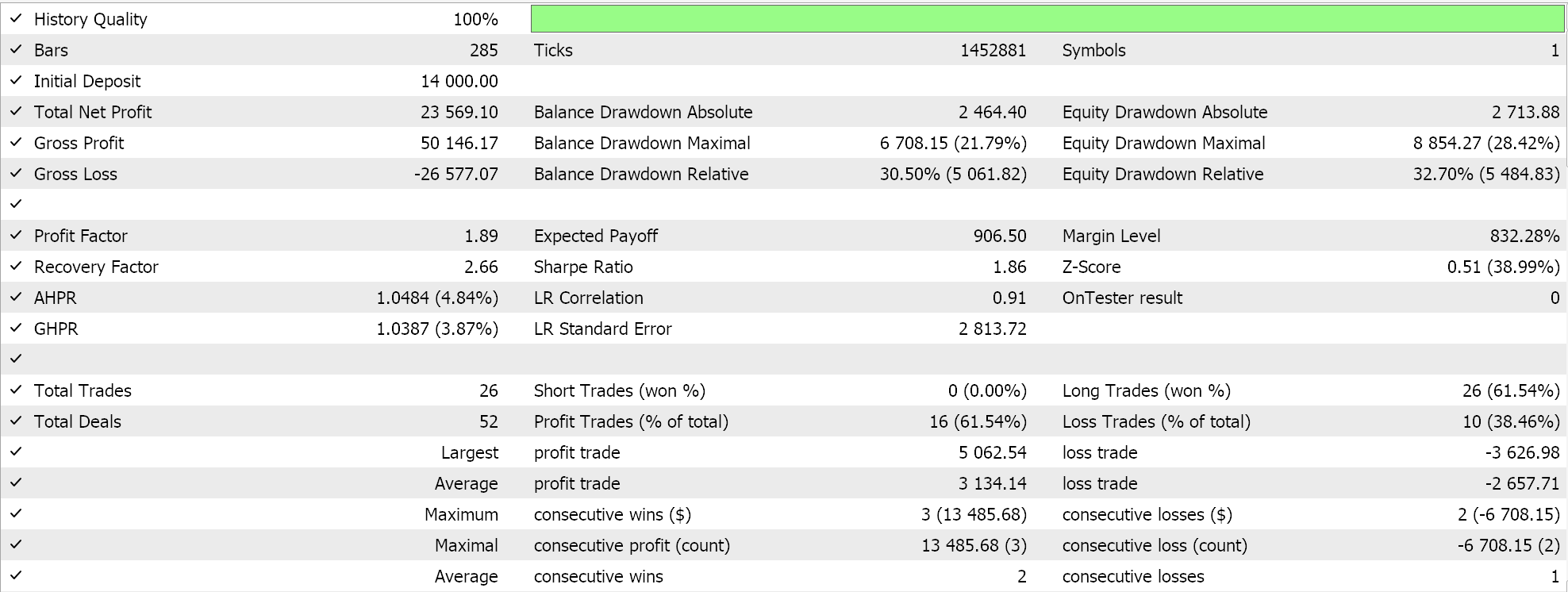
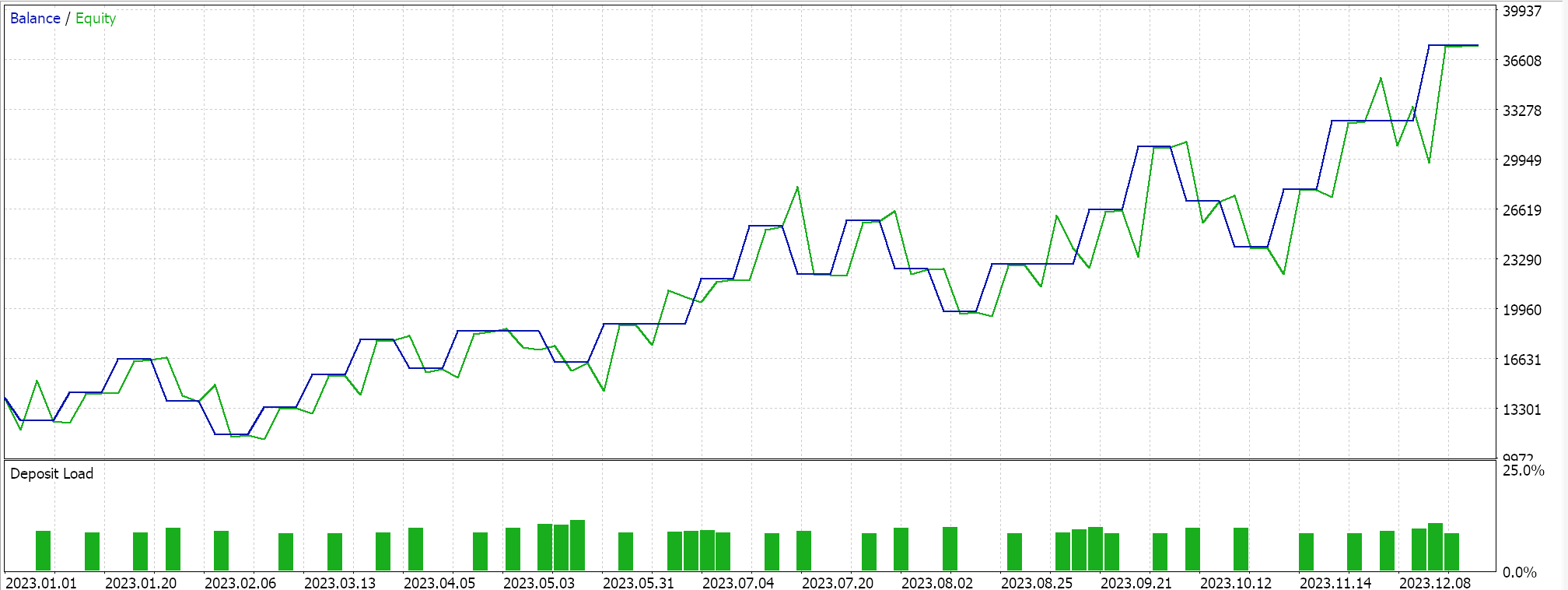
Estas pruebas se realizan para el año 2023 en el marco de tiempo diario para el par de divisas NZDUSD. El uso de NZDUSD es para fines de normalización de lotes que cubriremos con más detalle en el próximo artículo. Por ahora, sin embargo, como se mencionó anteriormente, estamos usando la activación sigmoidea que mantiene sus salidas en el rango de 0.0 a 1.0 y esto es un buen augurio para propósitos de prueba al explorar tasas de aprendizaje ideales. Una vez que cada parámetro tiene su propia tasa de aprendizaje, los pesos y los sesgos se actualizan mediante la función de actualización de gradiente adaptativo, cuyo listado ya se compartió anteriormente.

Dado que nuestros datos de entrada, de precios brutos, están dentro del rango de 0,0 a 1,0, y estamos activando mediante Sigmoide, nuestras salidas de red también deberían estar en el rango de 0,0 a 1,0. Estamos tratando con precios brutos y dado que alimentamos nuestra red con datos de precios históricos y la entrenamos con datos de precios secuenciales, podemos esperar que nuestra red pronostique el próximo precio de cierre. Estamos haciendo todo esto sin normalización de lotes, lo cual es muy riesgoso ya que, si bien la salida podría estar en el rango deseado de 0,0 a 1,0, puede fácilmente sesgarse por encima del precio de oferta actual (o por debajo de este), lo que daría señales de compra o venta permanentes. Esto ya se puede ver en nuestros resultados de prueba "ideales" mostrados anteriormente. Ahora bien, realicé corridas en las que se abrieron posiciones largas y cortas, pero la falta de normalización de lotes es algo a tener en cuenta. Para generar señales o valores de condición a partir de nuestras funciones de condición larga y corta en la clase de señal personalizada, necesitamos normalizar el precio de pronóstico para que esté en el rango de números enteros de 0 a 100.

Como siempre, hay muchas maneras de lograr esto, sin embargo, en nuestro caso simplemente comparamos el precio proyectado con la matriz de precios de entrada y obtenemos un valor doble del percentil. Convertimos este valor de percentil en un número entero en el rango esperado de 0 a 100, y tenemos una condición de salida. Esta normalización solo se realiza en cada una de las funciones de condición larga y corta si el precio de pronóstico de la red está por encima de la oferta actual o por debajo del precio de oferta actual, respectivamente. El código fuente de esto se comparte a continuación:

//+------------------------------------------------------------------+
//| "Voting" that price will grow.                                   |
//+------------------------------------------------------------------+
int CSignalCMLP::LongCondition(void)
{  int result = 0;
   double _mlp_output = 0.0;
   GetOutput(_mlp_output);
   m_symbol.Refresh();
   m_symbol.RefreshRates();
   if(_mlp_output > m_symbol.Bid())
   {  vector _scale;
      _scale.CopyRates(m_symbol.Name(), m_period, 8, 0, __MLP_INPUTS);
      result = int(round(100.0 * (fmin(_mlp_output, _scale.Max()) - _scale.Min()) / fmax(m_symbol.Point(), _scale.Max() - _scale.Min())));
   }
//printf(__FUNCSIG__ + " output is: %.5f, change is: %.5f, and result is: %i", _mlp_output, m_symbol.Bid()-_mlp_output, result);return(0);
   return(result);
}
//+------------------------------------------------------------------+
//| "Voting" that price will fall.                                   |
//+------------------------------------------------------------------+
int CSignalCMLP::ShortCondition(void)
{  int result = 0;
   double _mlp_output = 0.0;
   GetOutput(_mlp_output);
   m_symbol.Refresh();
   m_symbol.RefreshRates();
   if(_mlp_output < m_symbol.Bid())
   {  vector _scale;
      _scale.CopyRates(m_symbol.Name(), m_period, 8, 0, __MLP_INPUTS);
      result = int(round(100.0 * (fmin(_mlp_output, _scale.Max()) - _scale.Min()) / fmax(m_symbol.Point(), _scale.Max() - _scale.Min())));
   }
//printf(__FUNCSIG__ + " output is: %.5f, change is: %.5f, and result is: %i", _mlp_output, m_symbol.Bid()-_mlp_output, result);return(0);
   return(result);
}

El uso de este código que se adjunta al final de este artículo es mediante el ensamblaje de un Asesor Experto a través del asistente MQL5. Se puede encontrar orientación sobre cómo hacerlo aquí y aquí.

Tasa de aprendizaje RMS adaptativa

La tasa de aprendizaje adaptativa RMS introduce un parámetro adicional para gestionar la rápida caída en la tasa de aprendizaje que sucede a menudo cuando se enfrentan grandes gradientes de entrenamiento, ya que estos se acumulan durante todo el proceso de entrenamiento. Este parámetro es la tasa de decaimiento, que ya hemos introducido anteriormente como uno de los nuevos parámetros de entrada adicionales a la función de retropropagación modificada. Sin embargo, en el artículo anterior usamos una tasa de decaimiento en la tasa de aprendizaje de decaimiento escalonado, la tasa de aprendizaje de decaimiento exponencial y la tasa de aprendizaje de decaimiento en tiempo inverso, y cumplió una finalidad casi similar. A partir de nuestra clase de señal personalizada, tenemos un solo parámetro de entrada llamado tasa de caída que cumple todos estos propósitos porque en cualquier sesión de entrenamiento solo se puede seleccionar un formato de tasa de aprendizaje. Por lo tanto, la tasa de decadencia servirá al tipo de tasa de aprendizaje seleccionado.

Sin embargo, para continuar con las tasas de aprendizaje adaptativo, el RMS-prop limita la acumulación de gradientes históricos, lo que puede ser un problema con los gradientes adaptativos ya que ralentizan significativamente el aprendizaje hasta un punto en el que se detiene efectivamente. Esto se debe a la relación inversa entre los gradientes históricos y la tasa de aprendizaje ya mencionada anteriormente. La innovación de RMS-prop, gracias al factor de decaimiento, es ralentizar eficazmente esta caída en la tasa de aprendizaje y esto se consigue de la siguiente manera:

//+------------------------------------------------------------------+
// Adaptive RMS Update function
//+------------------------------------------------------------------+
void Cmlp::AdaptiveRMSUpdate(double DecayRate, double LearningRate, int LayerIndex, vector &Gradients, vector &Outputs)
{  for (int i = 0; i < int(weights[LayerIndex].Rows()); i++)
   {  adaptive_gradients[LayerIndex][i] += (DecayRate * adaptive_gradients[LayerIndex][i]) + ((1.0 - DecayRate)*(Gradients[i] * Gradients[i]));
      double _learning_rate = LearningRate / (MathSqrt(adaptive_gradients[LayerIndex][i]) + __NON_ZERO);
      for (int j = 0; j < int(weights[LayerIndex].Cols()); j++)
      {  weights[LayerIndex][i][j] -= (_learning_rate * Gradients[i] * Outputs[j]);
      }
      biases[LayerIndex][i] -= _learning_rate * Gradients[i];
   }
}

Otro problema con el gradiente adaptativo es que cuando se trata de datos no estacionarios y la distribución y las características subyacentes de los datos cambian con el tiempo, y por lo tanto incluso a través de un conjunto de entrenamiento, los gradientes acumulados pueden volverse obsoletos y menos relevantes, lo que lleva a tasas de aprendizaje subóptimas. Por otro lado, RMS-prop se encarga de que los gradientes más recientes entren en juego y, por lo tanto, tengan mayor influencia en la tasa de aprendizaje. Esto hace que el proceso de aprendizaje sea más adaptable y posiblemente más útil en escenarios más pertinentes para los traders, como el pronóstico de series de tiempo.

Además, en los casos en que el entrenamiento se realiza en conjuntos de datos dispersos, como aquellos fuera de nuestra competencia principal de trading, como en el procesamiento del lenguaje natural o en los sistemas de recomendación, los gradientes adaptativos pueden reducir excesivamente los gradientes al leer características o puntos de datos que se usan con poca frecuencia. Por lo tanto, RMS-prop permite un proceso de entrenamiento más equilibrado al mantener la tasa de aprendizaje en un nivel relativamente más alto durante períodos más largos, de modo que estas redes (que los traders aún podrían encontrar útiles en ciertas situaciones) pueden tener pesos y sesgos más óptimos.

Finalmente, los gradientes adaptativos son muy susceptibles y sensibles a los datos ruidosos ya que en esencia el gradiente se correlaciona positivamente con el ruido. Por lo tanto, en situaciones donde los datos de entrenamiento no se filtran adecuadamente para estos valores atípicos, las reducciones rápidas en la tasa de aprendizaje implicarían esencialmente que la red aprendería más de los valores atípicos y el ruido que de los datos centrales o ideales. El efecto de suavizado de RMS-prop con el factor de decaimiento significa que la tasa de aprendizaje puede "sobrevivir" a los valores atípicos y aún así continuar contribuyendo de manera efectiva a los pesos y sesgos de la red cuando los datos centrales o ideales finalmente se cumplen en el conjunto de entrenamiento.

Realizamos algunas pruebas con el aprendizaje adaptativo de apoyo RMS y a continuación se muestra una muestra de los resultados de nuestras pruebas:

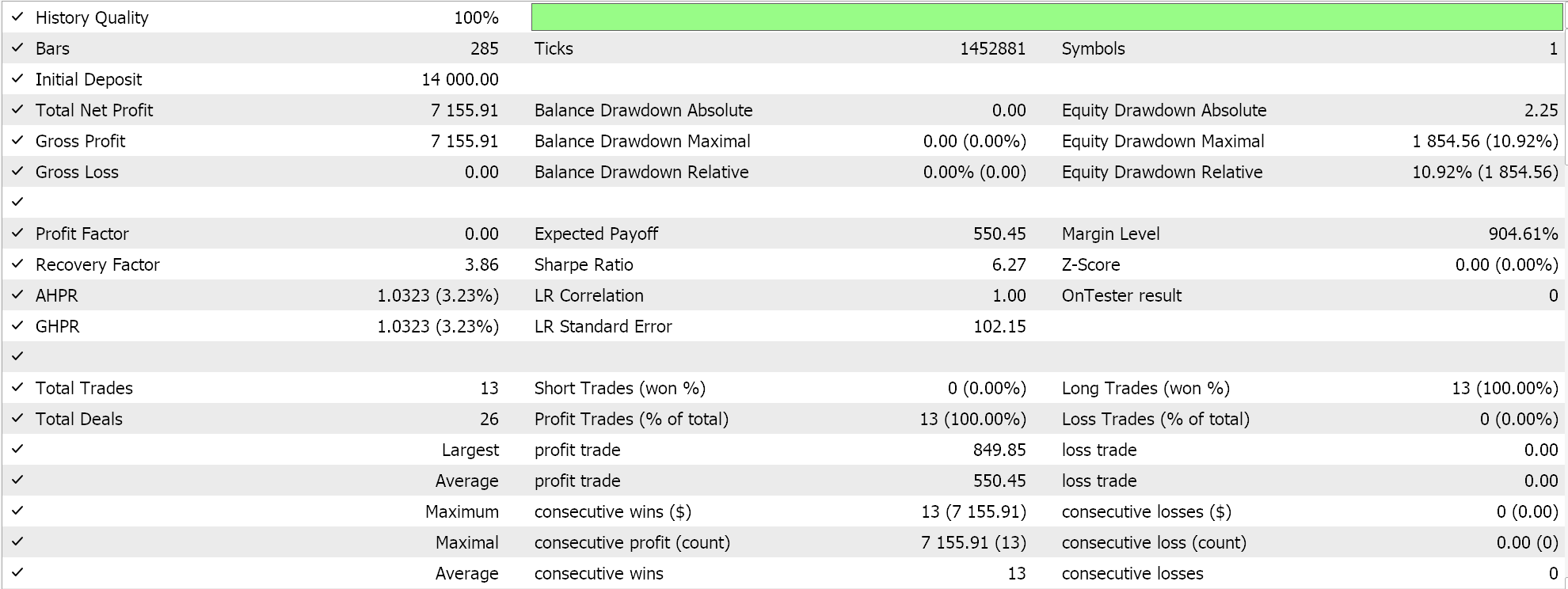
Debido a que las entradas de nuestra red no están normalizadas por lotes de acuerdo con la elección de la función de activación para esta red (estamos utilizando sigmoide frente a suave máximo) nuestros resultados de prueba están sesgados para colocar sólo operaciones largas porque el precio de pronóstico de salida siempre estuvo por encima de la oferta actual. Podría haber formas de normalizar el precio de salida para dar un equilibrio entre posiciones largas y cortas, que nuestro enfoque aquí no ha considerado, pero preferiría que comencemos con una normalización por lotes adecuada de los datos de entrada antes de considerar dichos enfoques. Por lo tanto, este es un problema que abordaremos de forma más efectiva en el artículo en línea, como se mencionó anteriormente.

Estimación de momento adaptativo (o tasa de aprendizaje exponencial media)

La estimación de momento adaptativo (también conocida como ADAM) es otra variante de las tasas de aprendizaje adaptativo que tiene como objetivo hacer que los enfoques como el RMS mencionado anteriormente sean aún más suaves a través de una consideración doble de la media del gradiente y la varianza del gradiente (momentum). Esto se implementa en MQL5 de la siguiente manera:

//+------------------------------------------------------------------+
// Adaptive Mean Exponential(ME) Update function
//+------------------------------------------------------------------+
void Cmlp::AdaptiveMEUpdate(double DecayRate, double LearningRate, int LayerIndex, vector &Gradients, vector &Outputs)
{  for (int i = 0; i < int(weights[LayerIndex].Rows()); i++)
   {  adaptive_gradients[LayerIndex][i] = (DecayRate * adaptive_gradients[LayerIndex][i]) + ((1.0 - DecayRate)*(Gradients[i] * Gradients[i]));
      double _learning_rate = LearningRate / (fabs(adaptive_gradients[LayerIndex][i]) + __NON_ZERO);
      for (int j = 0; j < int(weights[LayerIndex].Cols()); j++)
      {  weights[LayerIndex][i][j] -= (_learning_rate * Gradients[i] * Outputs[j]);
      }
      //
      biases[LayerIndex][i] -= _learning_rate * Gradients[i];
   }
}

Acabamos de ver cómo las tasas de aprendizaje de apoyo RMS son un paso adelante respecto de las tasas de gradientes en el sentido de que reducen la tasa de reducción en la tasa de aprendizaje, y esto puede proporcionar una serie de ventajas, algunas de las cuales se han compartido anteriormente. Pues bien, ADAM continúa en esta dirección especialmente cuando se enfrenta a situaciones de datos de alta dimensión. A medida que aumentan las dimensiones de los conjuntos de datos manejados, también aumenta el número de parámetros en una matriz de gradiente. En situaciones como estas, que podrían ser reconocimiento de imágenes y voz, considerar el momento además de la media ayuda a que la tasa de aprendizaje se adapte de manera más sensible al conjunto de datos que si solo se considerara la media. Dependiendo del diseño de la red, un escenario de tan alta dimensión podría encontrarse en la previsión de series de tiempo financieras.

La convergencia relativamente inestable y lenta cuando se utiliza solo la media de los gradientes al cuadrado hace que RMS-prop sea menos confiable en datos ruidosos que ADAM. La combinación de las medias al cuadrado y la varianza proporciona un manejo más suave, más sólido, más estable y más rápido de la convergencia. Además, los gradientes dispersos en el procesamiento del lenguaje natural y los sistemas de recomendación, aunque se manejan mejor con RMS-prop que en el gradiente adaptativo, se gestionan incluso mejor con ADAM gracias a la ponderación del momento en la tasa de aprendizaje. Además, en situaciones donde los parámetros cambian con frecuencia, como cuando se inicializa una nueva red con pesos y sesgos aleatorios, el enfoque de RMS-prop en el historial de gradiente reciente puede llevar a actualizaciones demasiado conservadoras, mientras que las consideraciones de impulso de ADAM le permiten responder mejor incluso en estas situaciones.

Por último, al tratar con objetivos no estacionarios donde la función objetivo cambia con el tiempo, aunque RMS esté asistido por una media, puede que no se adapte tan bien como ADAM. Como ejemplo de esto, considere una situación en la que su red está modelada para pronosticar precios inmobiliarios y maneja entradas o características como el tamaño de la casa, la cantidad de habitaciones y la ubicación. La función objetivo que estamos usando para nuestra red MLP, durante la retropropagación, es simplemente la diferencia vectorial entre el objetivo y el pronóstico, pero normalmente este objetivo puede tomar muchas formas, como el error cuadrático medio (MSE), donde en esta situación tendría la siguiente fórmula:

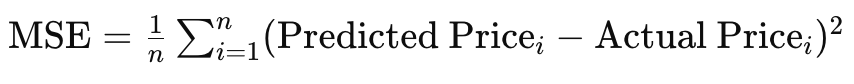
Donde:

• 'n' es el número de casas en la muestra de datos.
• MSE es el error cuadrático medio.

Esta sería una función de error de retropropagación cuyo resultado disminuye con el tiempo a medida que la red aprende actualizando adecuadamente sus pesos y sesgos, donde los valores de MSE más bajos significan un mejor rendimiento de la red. Ahora supongamos que el mercado inmobiliario estudiado cambia drásticamente de tal manera que la relación entre las características de la red (entradas) y los precios previstos cambia significativamente, donde por ejemplo se introduce un nuevo metro en la región ocupada por el inmueble examinado. Esto ciertamente cambiaría el modelo de precios de los bienes inmuebles en esa zona, y haría que la función objetivo fuera menos útil para adaptarse a estos cambios. Revisar la red agregando características más pertinentes (campos de entrada) podría conducir a un resultado más óptimo a medida que se actualizan los pesos y los sesgos. ADAM gestiona mejor esta transición de revisión y actualización de un modelo de red mediante la incorporación de nuevas funciones, ya que el proceso de actualización de peso tiene en cuenta el impulso.

Los resultados de las pruebas con ADAM nos dan el siguiente informe:

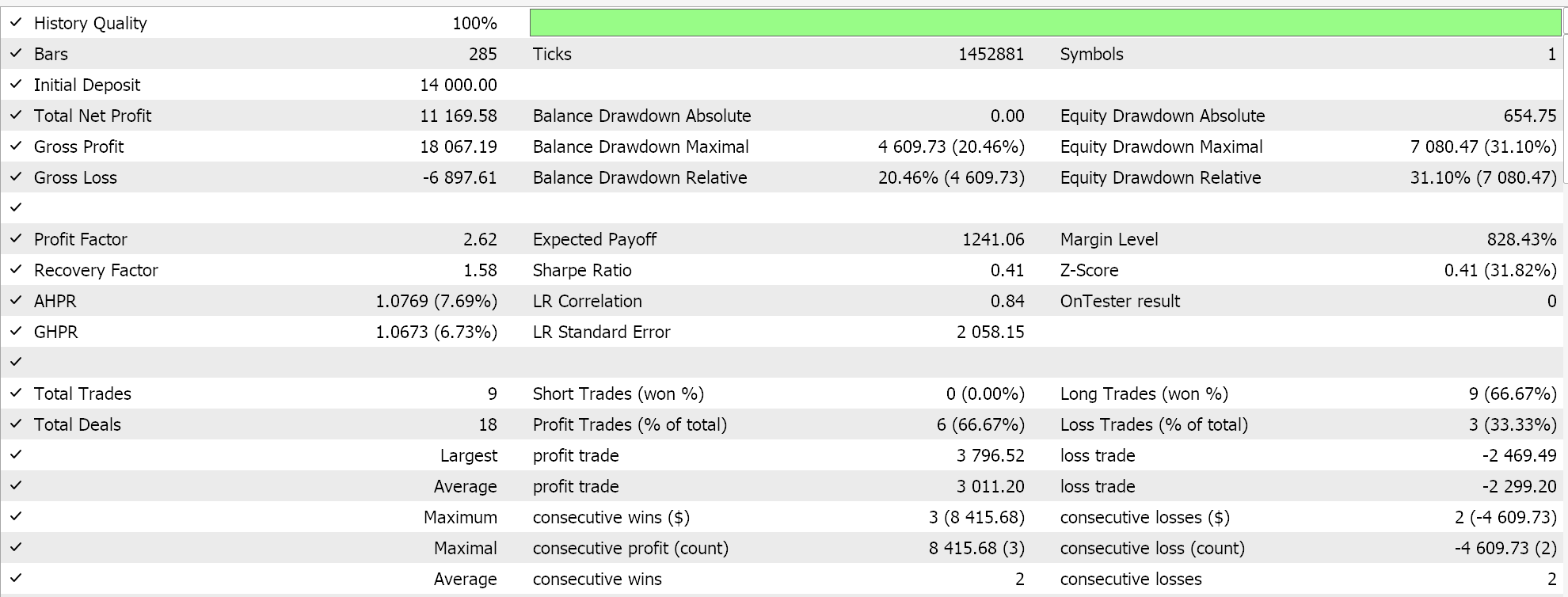
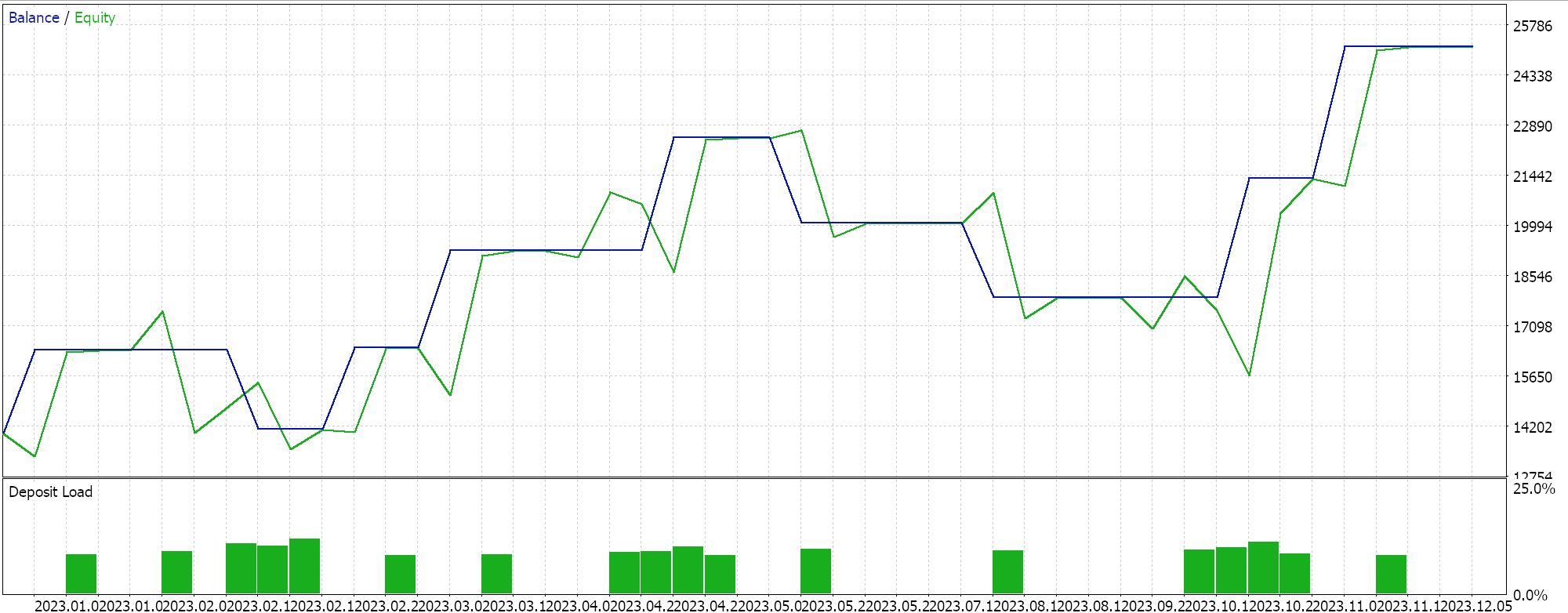
Esta no es la mejor configuración ni la ideal, pero solo muestra cómo se aplica la tasa de aprendizaje de ADAM en una red MLP. En el último artículo usamos un par de redes GAN mientras que aquí estamos usando algo más rudimentario pero aún intuitivo, el Multi-Layer-Perceptron con solo tres capas, en una formación 5-8-1.

Tasa de aprendizaje delta adaptativa

Nuestra tasa de aprendizaje adaptativa final es ADADELTA y aunque no asume ningún parámetro de entrada nuevo, fomenta el esfuerzo de ajustar de manera óptima la tasa de aprendizaje durante el entrenamiento. La fórmula para esto es relativamente complicada, pero en principio, además de tener en cuenta una acumulación decaída de gradientes, también se considera una acumulación decaída de pesos. Esto se realiza en MQL5 de la siguiente manera:

//+------------------------------------------------------------------+
// Adaptive Delta Update function
//+------------------------------------------------------------------+
void Cmlp::AdaptiveDeltaUpdate(double DecayRate, double LearningRate, int LayerIndex, vector &Gradients, vector &Outputs)
{  for (int i = 0; i < int(weights[LayerIndex].Rows()); i++)
   {  adaptive_gradients[LayerIndex][i] = (DecayRate * adaptive_gradients[LayerIndex][i]) + ((1.0 - DecayRate)*(Gradients[i] * Gradients[i]));
      double _delta = (MathSqrt(adaptive_deltas[LayerIndex][i] + __NON_ZERO) / MathSqrt(adaptive_gradients[LayerIndex][i] + __NON_ZERO)) * Gradients[i];
      adaptive_deltas[LayerIndex][i] = (DecayRate * adaptive_deltas[LayerIndex][i]) + ((1.0 - DecayRate) * _delta * _delta);
      for (int j = 0; j < int(weights[LayerIndex].Cols()); j++)
      {  weights[LayerIndex][i][j] -= (_delta * Outputs[j]);
      }
      // Bias update with AdaDelta
      biases[LayerIndex][i] -= _delta;
   }
}

La mayoría de las ventajas de reducir menos rápidamente la tasa de aprendizaje que se han mencionado anteriormente con RMS-prop y ADAM también se aplican a ADADELTA. Lo que valdría la pena mencionar ahora serían los beneficios del buffer adicional de deltas adaptativos que ADADELTA introduce al estimar la tasa de aprendizaje.

ADAM utiliza promedios móviles de la media y la varianza del gradiente al cuadrado para adaptar las tasas de aprendizaje para cada parámetro, mientras que una mejora efectiva sobre RMS-prop. Hay casos en los que un enfoque en los gradientes históricos conduce a sobrepasar los mínimos, lo que genera inestabilidad durante el entrenamiento, especialmente cuando se manejan datos ruidosos. La inclusión de un buffer de actualizaciones al cuadrado, a lo que se denomina "deltas adaptativos". Esta acumulación ayuda a equilibrar mejor las actualizaciones de la tasa de aprendizaje, de modo que se base tanto en la magnitud de los gradientes recientes como en la efectividad de las actualizaciones delta recientes.

Al realizar un seguimiento de las actualizaciones al cuadrado, ADADELTA puede ajustar dinámicamente los tamaños de los pasos teniendo en cuenta la efectividad reciente de estas actualizaciones. Esto es útil para el proceso de aprendizaje, evitando que se vuelva demasiado conservador, lo que puede suceder si las magnitudes de los gradientes disminuyen significativamente. Además, la acumulación adicional de actualizaciones de peso proporciona un mecanismo para normalizar las actualizaciones mientras se utiliza la escala de actualizaciones recientes, lo que mejora la capacidad del optimizador para adaptarse a los cambios en el panorama de gradientes. Esto es vital en escenarios con distribuciones de conjuntos de datos no estacionarios o gradientes altamente variables.

Otras innovaciones de ADADELTA son la reducción de la sensibilidad de los hiperparámetros y la evitación de la disminución de las tasas de aprendizaje. Realizamos pruebas con una tasa de aprendizaje ADADELTA en símbolos, períodos de prueba y marcos de tiempo similares a los mencionados anteriormente y obtenemos una variedad de resultados rentables. A continuación se muestra uno de los informes:

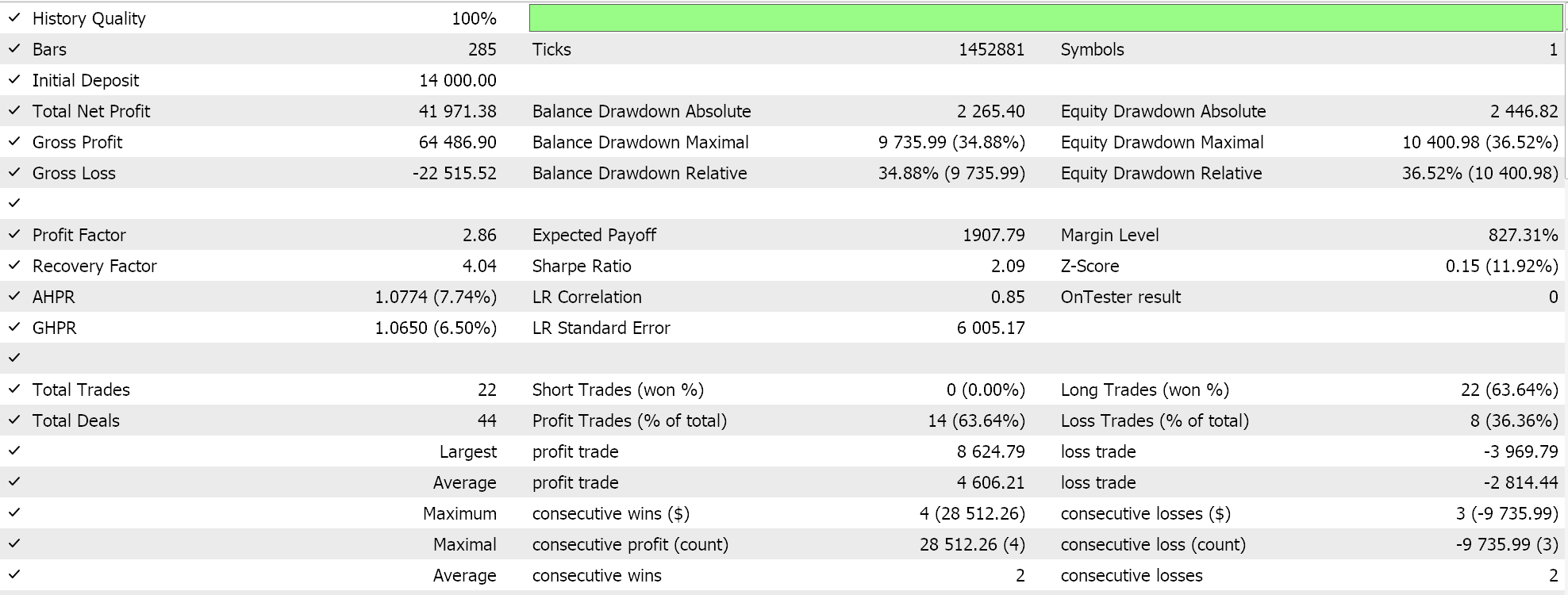
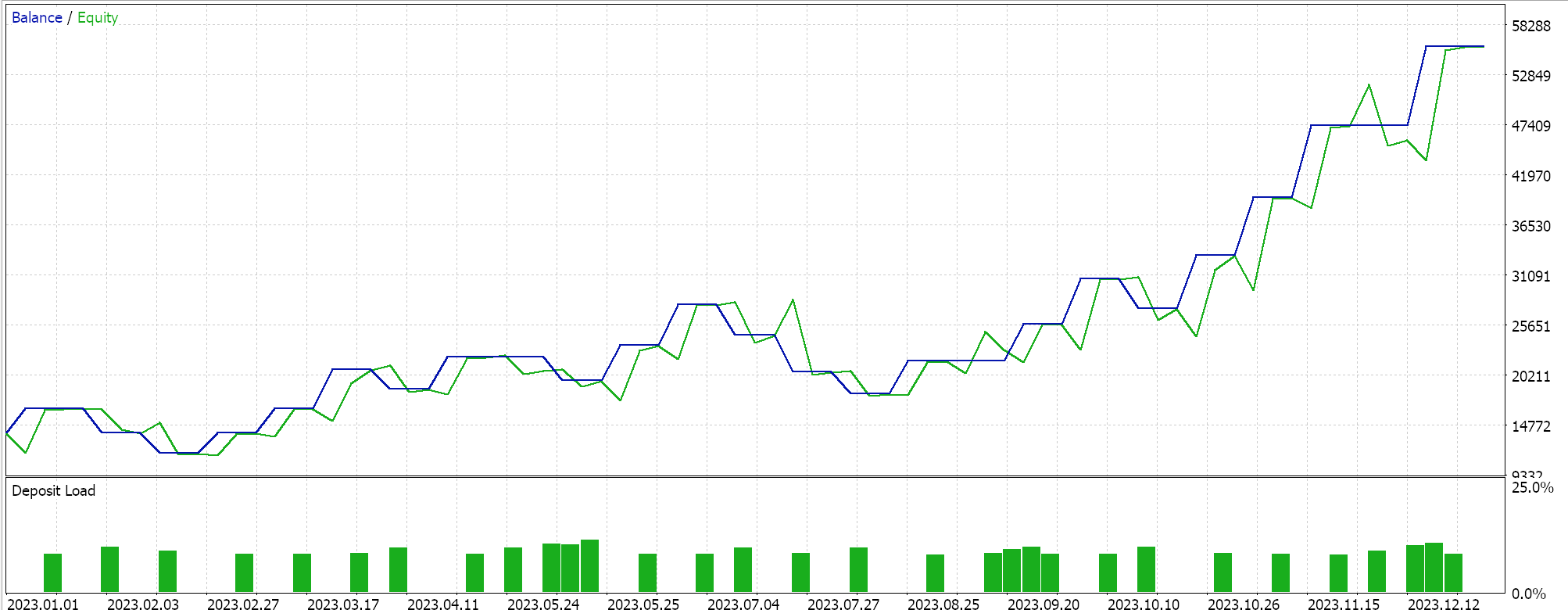
Tasa de aprendizaje de un ciclo

Este enfoque de ajuste de la tasa de aprendizaje carece de la sofisticación de los métodos de tasa de aprendizaje adaptativo y es más parecido al formato de recocido de coseno que consideramos en el último artículo. Sin embargo, es un poco más simple que el recocido coseno, ya que la tasa de aprendizaje aumenta y luego se reduce hacia el final de la sesión de entrenamiento. Esto se implementa de la siguiente manera:

      else if(m_learning_type == LEARNING_ONE_CYCLE)
      {  double _cycle_position = (double)((m_epochs - i) % (2 * m_epochs)) / (2.0 * m_epochs);
         if (_cycle_position <= 0.5)
         {  _learning_rate = m_min_learning_rate + (2.0 * _cycle_position * (m_learning_rate - m_min_learning_rate));
         }
         else
         {  _learning_rate = m_learning_rate - (2.0 * (_cycle_position - 0.5) * (m_learning_rate - m_min_learning_rate));
         }
      }

Entonces, a diferencia de los enfoques relativamente complejos que hemos examinado para este artículo para ajustar la tasa de aprendizaje, para un ciclo la tasa de aprendizaje simplemente se incrementa inicialmente en lo que se conoce como fase de calentamiento, luego llega a la tasa de aprendizaje máxima después de la cual se reduce en la fase de enfriamiento, que es la última parte del proceso de entrenamiento. Con la excepción del recocido de coseno, la mayoría de los enfoques de tasa de aprendizaje se inclinan a comenzar con una tasa de aprendizaje grande y luego reducir este valor a medida que se procesan más datos.

Una tasa de aprendizaje de ciclo hace algo un poco a la inversa, ya que comienza en la tasa de aprendizaje mínima. La tasa de aprendizaje mínima y la tasa de aprendizaje máxima son parámetros de entrada predefinidos, y la ruta o tasa de cambio de la tasa de aprendizaje está influenciada por la cantidad de épocas o la duración de la sesión de entrenamiento. Al igual que lo hemos hecho con las tasas de aprendizaje adaptativo, realizamos pruebas con la tasa de aprendizaje de un ciclo y uno de nuestros informes de pruebas se presenta a continuación:

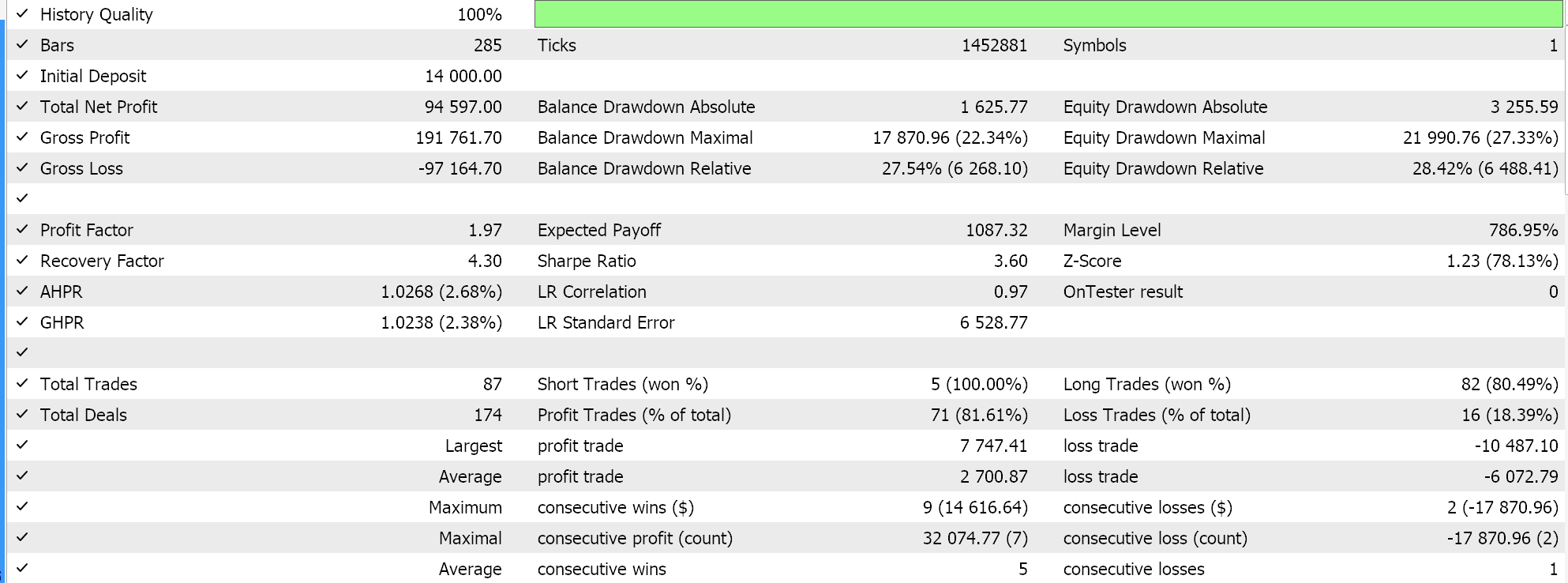
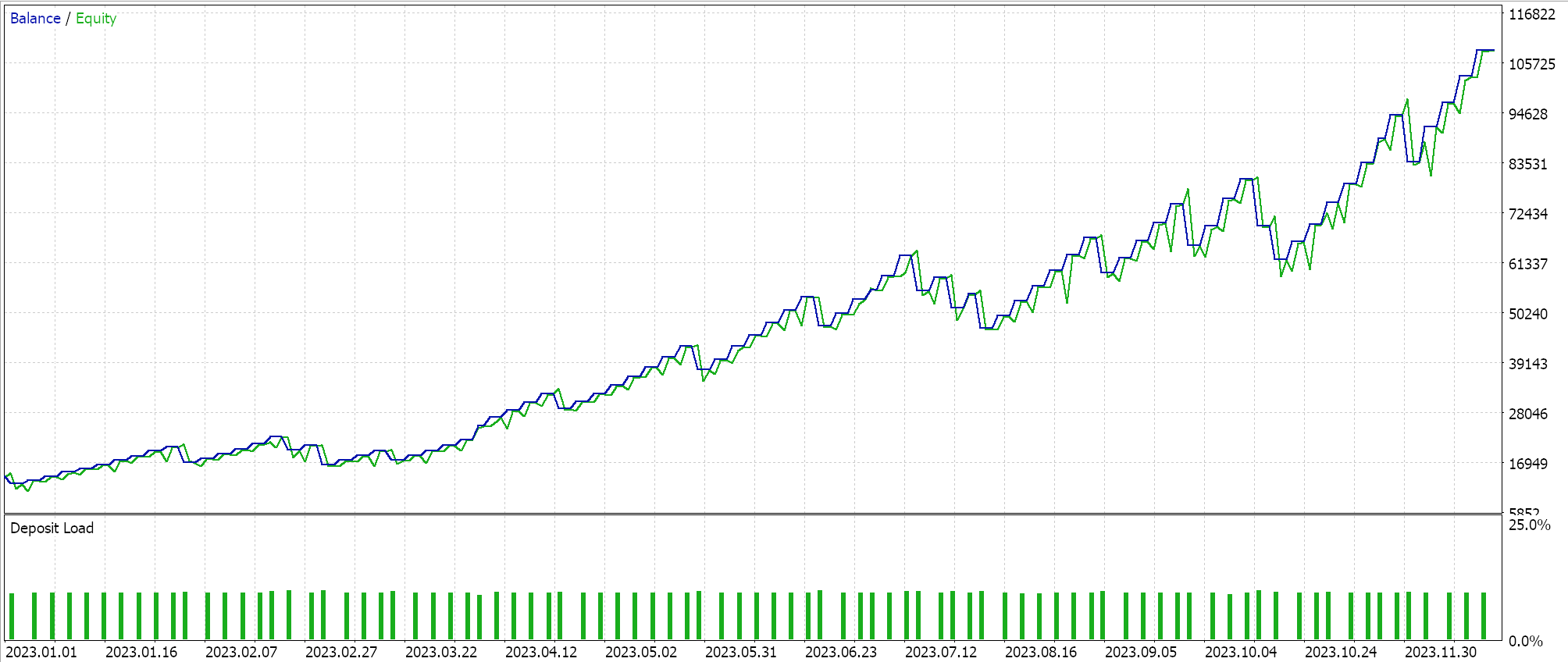
A partir de nuestros resultados anteriores, a pesar de la falta de una normalización de lotes adecuada, con solo ajustar la tasa de aprendizaje finalmente podemos abrir algunas operaciones cortas. Esto es cuando se pronostican precios de símbolos brutos (sin normalización de lotes) y se normalizan las condiciones largas y cortas de la misma manera que lo hicimos al probar los métodos de tasa de aprendizaje adaptativo. Esto demuestra una vez más cuán sensible es el enfoque adoptado para utilizar y ajustar la tasa de aprendizaje con respecto al rendimiento de una red neuronal.

Conclusión

En resumen, las tasas de aprendizaje son un aspecto crucial y muy sensible de los algoritmos de aprendizaje automático. Hemos examinado las variaciones en la implementación de los distintos formatos, centrándonos en las innovaciones secuenciales de cada uno, porque la mayoría de los enfoques de tasa de aprendizaje se desarrollaron para mejorar los métodos y enfoques anteriores. Este viaje para mejorar estas tasas de aprendizaje ciertamente aún está en marcha y continúa, sin embargo, los enfoques más simples como la tasa de aprendizaje de un ciclo tampoco deben descuidarse, ya que pueden ser bastante impactantes, como hemos visto en algunos de los resultados de nuestras pruebas.