Gerenciamento de capital de Vince. Realização como módulo de Assistente MQL5

Introdução

Ao trabalhar nos mercados financeiros, estamos constantemente envolvidos na busca de um sistema lucrativo. Ao mesmo tempo, queremos que ele seja estável e tenha um risco mínimo, quanto possível. E, para conseguir isso, seu desenvolvimento é focado em encontrar pontos de entrada/saída ideais; são criados indicadores técnicos e sinais de negociação que indicam quando comprar/vender; é desenvolvido todo um sistema de modelos de preços (formas) para a análise técnica. No entanto, como mostrado no trabalho "The Mathematics of Money Management" de Ralph Vince, a quantidade de capital utilizado para realizar transações não é menos importante. Para otimizar os lucros e preservar o depósito, é necessário determinar o tamanho do lote que queremos operar.

No seu trabalho, Vince refuta falsos conceitos que são muito comuns. Por exemplo, a um desses conceitos é relacionada a bem conhecida regra "quanto maior o risco, maior o lucro":

O lucro potencial é uma função linear do risco potencial. Não é assim!

O seguinte falso conceito é a diversificação reduz as perdas. Mas, isso também não é assim. De acordo com Vince:

A diversificação pode fazê-lo, mas só até certo ponto, isto é, muito menos do que a maioria dos trader acha.

Fundamentos

Para maior clareza, consideraremos as idéias básicas e usaremos exemplos. Suponhamos que temos um sistema de duas transações. A primeira transação ganha 50%, enquanto a segunda perde 40%. Se não reinvestimos, ganhamos 10%, e se reinvestimos, essa mesma sequência de transações dá uma perda de 10%. (P&L=Profit or Loss).

Número de transações	P&L sem reinvestimento	Capital total		P&L com reinvestimento	Capital total
		100			100
1	+50	150		+50	150
2	-40	110		-60	90

Ao reinvestir, os lucros de um sistema vencedor se transformaram num perdedor. Vê-se facilmente que a ordem das transações não importa. Este exemplo mostra que, ao reinvestir o capital, não podemos agir da mesma maneira como quando operamos com lote fixo. Justamente, a base do método de Vince para gerenciar o capital consiste na busca do tamanho ideal de lote ao reinvestir.

Vamos partir do simples para o complexo, ou seja, comecemos com o lançamento de uma moeda. Suponhamos que no caso de uma vitória, ficamos com US$ 2, caso contrário, perdemos US$ 1. A probabilidade de perder ou ganhar é 1/2. Digamos que temos US$ 100. Então, se apostamos todos os US$ 100, nosso lucro potencial é de US$ 200. Porém, se não ganhamos, perdemos o valor total e não podemos continuar o jogo. Se o jogo não tivesse fim, seria garantido que perdemos.

Se nós colocamos apenas uma parte dos US$ 100, por exemplo, US$ 20, no caso de perda, temos dinheiro para continuar o jogo. Consideremos a sequência de possíveis transações com várias porções do capital numa transação. O capital inicial é de US$ 100, em todos os lugares.

Operação	P&L quando К=0.1	Capital		P&L quando К=0.2	Capital		P&L quando К=0.5	Capital		P&L quando К=0.7	Capital		P&L quando К=1	Capital
		100			100			100			100			100
+2	20	120		40	140		100	200		140	240		200	300
-1	-12	108		-28	112		-100	100		-168	72		-300	0
+2	21.6	129.6		44.8	156.8		100	200		100.8	172.8		0	0
-1	-12.96	116.64		-31.36	125.44		-100	100		-120.96	51.84		0	0
+2	23.33	139.97		50.18	175.62		100	200		72.58	124.42		0	0
-1	-14	125.97		-35.12	140.5		-100	100		-87.09	37.32		0	0
Total		126			141			100			37			0

Como observado acima, o lucro/prejuízo não depende da seqüência de transações. Portanto, é correto termos transações rentáveis ​​alternadas com não lucrativas. 

Claramente, há um certo coeficiente ideal (divisor) em que o lucro é máximo. Para casos simples, quando a probabilidade de ganhar e a relação entre o lucro/perda é constante, esse coeficiente é dado pela fórmula de Kelly:

f=((B+1)*P-1)/B

f - proporção fixa ideal que vamos procurar;

P - probabilidade de ganhar;

B - relação ganho/perda.

Por conveniência, passaremos a chamar a f de coeficiente.

É claro que, na prática, o tamanho e a probabilidade de ganhar mudam constantemente e a fórmula de Kelly não é aplicável. Portanto, para dados empíricos, o coeficiente f é encontrado por meio de métodos numéricos. Vamos otimizar a rentabilidade do sistema de acordo com o fluxo arbitrário de transações. Vince usa o termo HPR para o lucro por transação (holding period returns, ou lucro durante o período de retenção da posição). Se a transação trouxer um lucro de 10%, então HPR =1+0.1=1.1. Por conseguinte, para uma transação HPR =1+f*Lucro/(Perda máxima possível), onde o lucro é tomado com um mais ou um menos, dependendo do facto de levar ganhos ou receber perdas. O coeficiente real f é o coeficiente do máximo rebaixamento possível. Para encontrar o f ideal, precisamos encontrar o máximo do produto de todas as transações max(HPR1 * HPR2 * ... *HPRn).

Escrevemos o programa para encontrar o f para uma matriz de dados arbitrária.

Programa 1. Busca do f ideal.

double PL[]={9,18,7,1,10,-5,-3,-17,-7};  // Matriz de lucros/perdas do livro
double Arr[]={2,-1};

void OnStart()
{
SearchMaxFactor(Arr);                   //Ou PL e outra matriz

}

void SearchMaxFactor(double &arr[])
{
double MaxProfit=0,K=0;                  // Lucro máximo
                                         // e coeficiente em conformidade com ela
for(int i=1;i<=100;i++)
{
   double k,profit,min;
   min =MathAbs(arr[ArrayMinimum(arr)]); // encontramos a perda máxima na matriz
   k =i*0.01;                            
   profit =1;
// Encontramos o rendimento para dado coeficiente
      for(int j=0;j<ArraySize(arr);j++)
      {
         profit =profit*(1+k*arr[j]/min);
      }
// Comparamos com o rendimento máximo
   if(profit>MaxProfit)
   {
   MaxProfit =profit;
   K=k;
   }
}
Print("Optimal K  ",K," Profit   ",NormalizeDouble(MaxProfit,2));

}

Pode ser visto que, para o caso +2,-1,+2,-1, etc. f será o mesmo que o obtido pela fórmula de Kelly.

Tenha em mente que a otimização faz sentido só para sistemas rentáveis ​​unicamente, ou seja, sistemas para os quais o valor esperado (lucro médio) é positivo. Para sistemas desfavoráveis, o f ideal = 0. Gestão do lote não faz com que um sistema desfavorável se torne rentável. Pelo contrário, se, no fluxo não houver perdas, isto é, se todos os P&L>0, a otimização também não faz sentido, f=1, e é necessário operar com o lote máximo.

Nós podemos, usando as capacidades gráficas da MQL5, encontrar não só o valor máximo de f, mas também ver toda a curva de distribuição de lucro, dependendo de f. Abaixo está um programa que desenha o gráfico de lucro dependendo do coeficiente f.

Programa 2. Gráfico de lucro dependendo de f.

//+------------------------------------------------------------------+
//|                                                      Graphic.mq5 |
//|                                                       Orangetree |
//|                                             https://www.mql5.com |
//+------------------------------------------------------------------+
#property copyright "Orangetree"
#property link      "https://www.mql5.com"
#property version   "1.00"

#include<Graphics\Graphic.mqh>
//+------------------------------------------------------------------+
//| Script program start function                                    |
//+------------------------------------------------------------------+
//double PL[]={9,18,7,1,10,-5,-3,-17,-7};             // Matriz de lucros/perdas do livro
double PL[]={2,-1};

void OnStart()
  {
double X[100]={0};
for(int i=1;i<=100;i++)
   X[i-1]=i*0.01;
double Y[100];
                                      
double min =PL[ArrayMinimum(PL)];                   

if(min>=0){Comment("f=1");return;}
min =MathAbs(min);

int n = ArraySize(X);
double maxX[1]= {0};
double maxY[1] ={0};

for(int j=0;j<n;j++)
{
   double k =X[j];
   double profit =1;
   for(int i=0;i<ArraySize(PL);i++)
   {
     profit =profit*(1+k*PL[i]/min);
   }
   Y[j] =profit;
   if(maxY[0]<profit)
   {
      maxY[0] =profit;
      maxX[0] =k;
   }
}  
CGraphic Graphic;
Graphic.Create(0,"Graphic",0,30,30,630,330);
CCurve *Curve=Graphic.CurveAdd(X,Y,ColorToARGB(clrBlue,255),CURVE_LINES,"Profit");
Curve.LinesStyle(STYLE_DOT);

//Se desejar, pode suavizar o gráfico
/*Curve.LinesSmooth(true);
Curve.LinesSmoothTension(0.8);
Curve.LinesSmoothStep(0.2);*/


CCurve *MAX =Graphic.CurveAdd(maxX,maxY,ColorToARGB(clrBlue,255),CURVE_POINTS,"Maximum");
MAX.PointsSize(8);
MAX.PointsFill(true);
MAX.PointsColor(ColorToARGB(clrRed,255));
Graphic.XAxis().MaxLabels(100);
Graphic.TextAdd(30,30,"Text",255);  
Graphic.CurvePlotAll();
Graphic.Update(); 
Print("Max factor f =   ", maxX[0]);  
  }

Gráfico para {+2,-1} tem a forma:

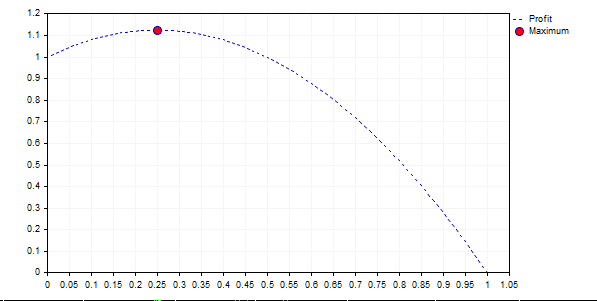
A partir deste gráfico, é claro que a regra "quanto maior o risco, maior o lucro" é errada. Em todos os casos, quando a curva é inferior a 1 (f>0.5), nós, no final das contas, obtemos uma perda, enquanto, ao jogar infinitamente, temos 0 na conta.

Aqui há uma contradição interessante. Quanto maior o valor esperado e mais estável o sistema, maior é o coeficiente f. Por exemplo, para o fluxo {-1,1,1,1,1,1,1,1,1,1}, o coeficiente é igual a 0.8, ou seja, parece que só podemos sonhar com um sistema desse tipo. No entanto, o coeficiente 0.8 significa que a perda máxima admissível é igual a 80%, e um dia você vai perder 80% da conta! Sim, do ponto de vista da estatística matemática, isso é o tamanho ideal do lote para maximizar o saldo, mas você está pronto para tais perdas?

Um pouco sobre a diversificação

Suponhamos que temos duas estratégias de negociação A e B com a mesma distribuição de lucros/perdas, por exemplo, as mesmas (+ 2, -1). Para estes sistemas, o f ideal é igual a 0,25. Consideremos o caso em que os sistemas têm uma correlação de 1,0 e -1. Vamos simplesmente dividir igualmente o saldo da conta entre esses sistemas.

Correlação 1, f=0.25

Sistema А	Transação P&L		Sistema B	Transação P&L		Pontuação combinada
	50			50		100
2	25		2	25		150
-1	-18.75		-1	-18.75		112.5
2	28.13		2	28.13		168.75
-1	-21.09		-1	-21.09		126.56
						lucro 26.56

Como seria de esperar, esta variante não é diferente de operar todo o capital numa estratégia. Agora pegamos o caso em que a correlação é 0.

Correlação 0, f=0.25

Sistema А	Transação P&L	Sistema B	Transação P&L	Pontuação combinada
	50		50	100
2	25	2	25	150
2	37.5	-1	-18.75	168.75
-1	-21.1	2	42.19	189.85
-1	-23.73	-1	-23.73	142.39
				Lucro 42.39

O lucro é muito maior. E, finalmente, no caso da correlação -1.

Correlação -1, f=0.25

Sistema А	Transação P&L	Sistema B	Transação P&L	Pontuação combinada
	50		50	100
2	25	-1	-12.5	112.5
-1	-14.08	2	28.12	126.56
2	31.64	-1	-15	142.38
-1	17.8	2	35.59	160.18
				Lucro 60.18

Neste caso, o lucro é máximo. Nestes e em exemplos semelhantes, pode ser visto que, ao reinvestir o lucro, a diversificação dá os melhores resultados. Além disso, também é fácil ver que o reinvestimento não evita que aconteça o pior caso (no nosso exemplo, a maior perda é f= 0,25 sobre o valor do saldo) excepto a variante quando os sistemas têm uma correlação de -1. Na prática, não existem sistemas com uma correlação de exatamente -1. Isto é semelhante ao caso da abertura de posições no mesmo instrumento em sentidos opostos. Com base em raciocínios desse tipo, Vince chega à seguinte conclusão. Aqui está uma citação do livro.

A moral é que, quando se realiza corretamente, a diversificação é um método que aumenta os lucros. Isso não significa necessariamente reduzir as perdas no pior caso, o que é absolutamente contrário da crença popular.

Correlação e outras estatísticas

Antes de iniciar o assunto dos métodos paramétricos para encontrar o coeficiente f, consideremos mais algumas caraterísticas do fluxo de lucros. Pode acontecer que recebemos uma série de resultados interligados. Transações favoráveis são seguidas de outras favoráveis, enquanto transações desfavoráveis são seguidas de outras desfavoráveis. Para identificar essas dependências, consideremos dois métodos: a permanência da autocorrelação e teste serial.

O teste serial consiste em calcular o índice (cálculo de Z). O conteúdo do "Z-score" é o número de desvios padrão em que os dados distam da média de uma distribuição normal. Um valor negativo de Z indica que a faixa (de séries contínuas de lucros/perdas) é mais pequena do que a distribuição normal, e, portanto, é provável que o lucro seja seguido de uma perda, e vice-versa. Fórmula para o cálculo de Z:

Z=(N(R-0.5)-Х)/((Х(Х-N))/(N-1))^(1/2) 

ou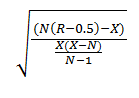

Onde:

• N - número total de transações;
• R - número total de séries;
• X=2*W*L, onde
• W = número total de transações vencedoras consecutivas;
• L = número total de transações perdedoras consecutivas.

Programa 3. Cálculo de Z.

double Z(double &arr[])
{
int n =ArraySize(arr);
int W,L,X,R=1;
   if(arr[0]>0)
   {
      W=1;
      L=0;
   }
   else
   {
      W=0;
      L=1;
   }

   for(int i=1;i<n;i++)
   {
    if(arr[i]>0)
      {
      W++;
      if(arr[i-1]<=0){R++;}
      }
    else
      {
      L++;
      if(arr[i-1]>0){R++;}
      }    
   }
 X =2*W*L;
 double x=(n*(R-0.5)-X);
 double y =X*(X-n);
 y=y/(n-1);
 double Z=(n*(R-0.5)-X)/pow(y,0.5);  
Print(Z);
return Z;
}

O "Z-score" é calculado pelo testador de estratégias, onde o relatório (Backtest) é chamado de "Z-score".

A autocorrelação é a relação estática entre as sequências de valores de uma série, sequências essas tomada com deslocamento. Para a série {1,2,3,4,5,6,7,8,9,10}, trata-se da correlação entre as séries {1,2,3,4,5,6,7,8,9} e {2,3,4,5,6,7,8,9,10}. Abaixo é considerado um programa para encontrar a autocorrelação.

Programa 4. Autocorrelação.

double AutoCorr(double &arr[])
{
   int n =ArraySize(arr);
   
   double avr0 =0;
   for(int i=0;i<n-1;i++)
   {
   avr0=avr0+arr[i];
   }
   avr0=avr0/(n-1);
   
   double avr1 =0;
   
   for(int i=1;i<n;i++)
   {
   avr1=avr1+arr[i];
   }
   avr1=avr1/(n-1);
   
   double D0 =0;
   double sum =0.0;
   
   for(int i=0;i<n-1;i++)
   {
   sum =sum+(arr[i]-avr0)*(arr[i]-avr0);
   }
   D0 =MathSqrt(sum);
   
   double D1 =0;
   sum =0.0;
   for(int i=1;i<n;i++)
   {
   sum =sum+(arr[i]-avr1)*(arr[i]-avr1);
   }
   D1 =MathSqrt(sum);
   
   sum =0.0;
   for(int i=0;i<n-1;i++)
   {
   sum =sum +(arr[i]-avr0)*(arr[i+1]-avr1);
   }
   if(D0==0||D1==0) return 1;
   double k=sum/(D0*D1);
return k;
}

Se os resultados das transações estão relacionados entre si, faz sentido ajustar a estratégia de negociação. Os melhores resultados são obtidos se usarmos dois coeficientes diferentes - f1 e f2 - para lucros e perdas. Para este caso, será escrito um módulo separado de gerenciamento de capital em MQL5.

Métodos paramétricos

Ao otimizar os parâmetros do sistema, podemos usar duas abordagens. A primeira é empírica e baseada diretamente em dados experimentais, quando optimizamos os parâmetros de acordo com resultados específicos. E a segunda é paramétrica e com base nas dependências quer funcionais quer estáticas. Um exemplo de método paramétrico é encontrar o coeficiente ideal da fórmula de Kelly. 

Para encontrar o melhor coeficiente, Vince propõe a utilização da distribuição dos lucros obtidos. Primeiro, ele examina a distribuição normal, como a mais estudada e difundida, em seguida, constrói uma distribuição generalizada.

A tarefa é formulada como se segue. Suponhamos que nossos ganhos/perdas são distribuídos de acordo com uma distribuição normal (ou, em geral, com qualquer outra). Encontramos o coeficiente ideal f para esta distribuição. Em caso de distribuição normal, dos dados experimentais apenas precisamos encontrar o valor médio do fluxo de PL (lucro/prejuízo) e o desvio padrão. Estes dois parâmetros caracterizam completamente a distribuição normal.

Lembre a fórmula a densidade da distribuição normal:

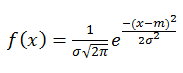
Onde

• σ -desvio padrão
• m - valor esperado (valor médio).

Eu gostei da idéia em si, quer dizer, encontrar o caráter da distribuição de lucros/perdas, usando dados empíricos. E é segundo esta função encontrar o parâmetro f, evitando assim a influência dos valores aleatórios. Infelizmente, as coisas não são tão simples na prática. Mas uma coisa de cada vez. Primeiro, falemos sobre o método em si.

 

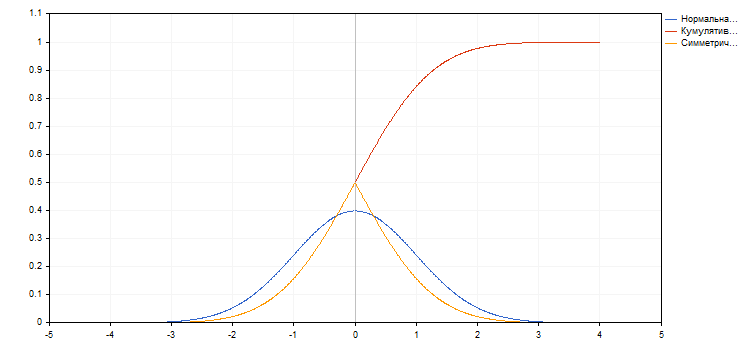
No gráfico, a cor azul, é apresentada a densidade da distribuição normal, onde o valor médio é igual a zero e o desvio padrão - unidade. A vermelho, é mostrada a integral desta função. Esta é a probabilidade cumulativa, ou seja, a probabilidade de que o valor seja menor ou igual ao X definido. Ela é frequentemente designada F(x). O gráfico laranja é a probabilidade de que o valor é menor ou igual a x para x<0 e esse valor é maior ou igual a x para х>0 (F(x)' =1-F(x), para х>0. Todas estas funções são bem conhecidas e seus valores fáceis de obter.

Precisamos encontrar a maior média geométrica das transações distribuídas de acordo com esta regra. Para fazer isso, Vince oferece os seguintes passos.

Primeiro, encontramos as características de distribuição, isto é, o valor médio e o desvio padrão. Em seguida, selecionamos o "intervalo de confiança" ou largura de corte, que é expressa em desvios padrão. Normalmente, é selecionado o intervalo 3σ. Valores maiores que 3σ são cortados. Depois, o intervalo é dividido em segmentos, e são procurados os "valores associados" de ganhos/perdas (PL). Por exemplo, para σ=1 e m=0, os valores associados de PL nas bordas do intervalo serão m +- 3σ = +3 e -3. Se dividimos o intervalo em trechos de 0.1σ de comprimento, os valores associados de PL serão -3, -2.9, -2.8 ... 0 ... 2.8, 2,9, 3. E é para esse fluxo PL que encontramos o f ideal.

Como valores diferentes de PL têm uma probabilidade diferente, para cada valor é encontrada sua "probabilidade associada" P. Depois destas conversões, é procurado o máximo dos produtos:

HPR=(1+PL*f/maxLoss)^P, onde maxLoss é a perda máxima (em valor absoluto).

Aqui, Vince propõe, como probabilidade associada, tomar a probabilidade cumulativa, que temos no gráfico, a laranja, F'(x).

Seria lógico que a probabilidade cumulativa fosse tomada apenas para os valores extremos, enquanto para os valores restantes P=F'(x)-F'(y), onde х e у são valores de F(x) nas bordas do intervalos.

 

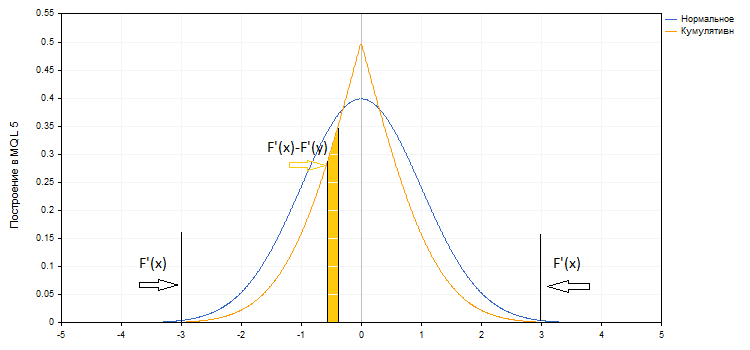
Então, o multiplicador HPR=(1+PL*f/maxLoss)^P seria um tipo de "valor ponderado". A probabilidade total desses valores, como esperado, seria igual a um. No livro, Vince admite que os resultados obtidos desta forma não coincidem com os resultados obtidos com base em dados reais. Ele atribui isso à restrição da amostra e à diferença entre a distribuição real e a normal. Ao aumentar o número de elementos e distribuições, confirmar-se que os valores paramétricos e reais do coeficiente ideal f convergem.

Curiosamente, no exemplo examinado segundo seu método, à probabilidade total é igual a 7,9. Para encontrar a média geométrica, ele apenas remove do resultado a raiz de potência 7,9. Aparentemente, essa abordagem tem uma base matemática rigorosa.

Nós, tendo à nossa disposição uma ferramenta como a MQL5, podemos verificar tudo isso facilmente. Para fazer isso, temos a biblioteca Normal.mqh, localizada em <Math\Stat\Normal.mqh>.

Para os experimentos, fiz duas versões: como Vince e como descrito acima. Para encontrar as "probabilidades associadas", usa-se função de biblioteca MathCumulativeDistributionNormal(PL,mean,stand,ProbCum).

 Programa 5. Pesquisa do f ideal numa distribuição normal (segundo Vince).

//+------------------------------------------------------------------+
//|                                                         Vince.mq5 |
//|                        Copyright 2017, MetaQuotes Software Corp. |
//|                                             https://www.mql5.com |
//+------------------------------------------------------------------+
#property copyright "Copyright 2017, MetaQuotes Software Corp."
#property link      "https://www.mql5.com"
#property version   "1.00"

#include<Math\Stat\Math.mqh>
#include<Math\Stat\Normal.mqh>

input double N=3;                      // intervalo limiar nos desvios padrão
input int M=60;                        // número de divisões
//+------------------------------------------------------------------+
//| Script program start function                                    |
//+------------------------------------------------------------------+
void OnStart()
  {
double arr[10000];  
bool ch =MathRandomNormal(1,8,10000,arr);
double mean =MathMean(arr);
double stand =MathStandardDeviation(arr);

double PL[];                      // matriz de "lucros associados"
ArrayResize(PL,M+1);
                                  // Preenchimento da matriz
for(int i=0;i<M+1;i++)
   {
   double nn =-N+2.0*i*N/M;
   PL[i] =stand*nn+mean;
   }
//............................. matriz de "probabilidades associadas"
double ProbCum[];
ArrayResize(ProbCum,M+1);
//............................. Preenchimento da matriz ..................
ch =MathCumulativeDistributionNormal(PL,mean,stand,ProbCum);
//F'(x)= 1-F(x) quando х>0

for(int i=0,j=0;i<M+1;i++)
{
if(i<=M/2)continue;
else j=M-i;
ProbCum[i] =ProbCum[j];
}

double SumProb=0;
for(int i=0;i<M+1;i++)
{
SumProb =SumProb+ProbCum[i];
}
Print("SumProb ",SumProb);
double MinPL =PL[ArrayMinimum(PL)];
double min =arr[ArrayMinimum(arr)];

double f=0.01,HPR=1,profit=1; 
double MaxProfit=1,MaxF=0;


for(int k=0;k<1000;k++)
   {
   f=k*0.001;
   profit =1;  
      for(int i=0;i<M+1;i++)
      {
      HPR=pow((1-PL[i]/MinPL*f),ProbCum[i]);
      profit =HPR*profit;
      }
   if(MaxProfit<profit)
     {
     MaxF =f;
     MaxProfit =profit;
     } 
   }
Print("Profit Vince");   
Print(MaxF,"   ",pow(MaxProfit,1/SumProb),"  ",Profit(MaxF,min,arr));
//... Para comparação, encontramos o lucro máximo de acordo com os dados reais
MaxF =0;
MaxProfit =1;

for(int k=0;k<1000;k++)
   {
   f=k*0.001;
   profit =Profit(f,min,arr);  

   if(MaxProfit<profit)
     {
     MaxF =f;
     MaxProfit =profit;
     } 
   }
Print("------MaxProfit-------");   
Print(MaxF,"   ",MaxProfit);

  }

//   Programa para encontrar o lucro de acordo com os dados reais
//   matriz arr[] com valor mínimo min
//   e valor de f definido

double Profit(double f,double min, double &arr[])
{
if(min>=0)
{
   return 1.0;
   Alert("min>=0");
}

double profit =1;
int n =ArraySize(arr);
   for(int i=0;i<n;i++)
   {
   profit =profit*(1-arr[i]*f/min);
   }
return profit;
}

O código do programa se encontra no arquivo Vince.mq5

Neste programa, encontra-se o coeficiente da distribuição normal e, depois, o usado para a comparação em dados reais. A segunda versão difere apenas na matriz de "probabilidades associadas" e PL.

Programa 6. 

.............................................
double ProbDiff[];
ArrayResize(ProbDiff,M+2);
double PLMean[];
ArrayResize(PLMean,M+2);

ProbDiff[0]=ProbCum[0];
ProbDiff[M+1]=ProbCum[M];
PLMean[0]=PL[0];
PLMean[M+1]=PL[M];

for(int i=1;i<M+1;i++)
{
ProbDiff[i] =MathAbs(ProbCum[i]-ProbCum[i-1]);
PLMean[i] =(PL[i]+PL[i-1])/2;
}
..............................................

O código do programa se encontra no arquivo Vince_2.mq5

Aqui, PLMean[i] =(PL[i]+PL[i-1])/2; é o valor médio de PL no segmento de divisão, enquanto ProbDiff[] são os valores da probabilidade de o valor estar dentro de um intervalo predeterminado. Ao longo das bordas, os valores são cortados (possivelmente pelo stop-loss ou take-profit), portanto, nas bordas, a probabilidade é apenas igual à probabilidade cumulativa.

Ambos os programas funcionam mais ou menos igual e dão aproximadamente os mesmos resultados. Verificou-se que a resposta é fortemente dependente de N, isto é, a largura de corte ( "intervalo de confiança"). Sendo que, o mais triste disto tudo é que, quando aumenta N, o coeficiente de f, resultante da distribuição normal, tende a 1. Teoricamente, quanto maior o intervalo de "corte", mais preciso é obtido o resultado. Na prática, não é bem assim.

Pode acontecer assim devido aos erros acumulados. A função exponencial decresce rapidamente, e nós temos de lidar com valores bastante pequenos, isto é, HPR=pow((1-PL[i]/MinPL*f),ProbCum[i]). É possível que, em algum lugar, o próprio método tenha um erro. Mas para a aplicação prática não importa. Em qualquer caso, para trabalhar corretamente, precisamos de alguma forma "encaixar" o parâmetro N, que influencia fortemente o resultado.

É claro que o fluxo de PL real difere de uma distribuição normal. A este respeito, Vince cria uma distribuição generalizada com parâmetros simulando as características de qualquer distribuição arbitrária. São adicionados parâmetros que especificam diferentes momentos da distribuição (média, curtose, largura, assimetria). Em seguida, através de métodos numéricos, devem-se encontrar estes parâmetros para os dados empíricos e construir função de distribuição do fluxo de PL.

Como não gostei dos resultados dos experimentos com a distribuição normal, decidi não prosseguir na realização dos cálculos numéricos com a distribuição generalizada. Agora argumento em favor de minhas dúvidas. 

Vince afirma que os métodos paramétricos são muito mais poderosos. Pois, com o aumento no número de experimentos, os dados tendem para os resultados teóricos, uma vez que o coeficiente obtido na amostra é impreciso devido à amostragem limitada. Mas, no caso da distribuição normal (valor médio e desvio padrão), obtemos os parâmetros a partir desta amostra limitada. A imprecisão do cálculo das características da distribuição é exatamente a mesma. Em seguida, essa imprecisão só aumenta devido a erros acumulados em cálculos crescentes. Neste caso, como se vê, na aplicação prática, os resultados ainda dependem da largura do corte. Como, na prática, a distribuição não é normal, acrescentamos mais um elemento, isto é, a busca da função de distribuição, novamente com base nos mesmos dados empíricos finais. Elementos adicionais implicam erros computacionais adicionais.

Expresso a minha humilde opinião. A abordagem paramétrica é uma ilustração do fato de uma bela idéia na teoria nem sempre ser tão bonita e prática.

Uma visão geral do livro de Vince

É hora de resumir o "The Mathematics of Money Management” de Vince. O livro é uma mistura de métodos estatísticos com diferentes métodos para encontrar o coeficiente f ideal. Nele, é examinado um conjunto bastante amplo de temas: modelo de Markowitz de gerenciamento de carteiras, o teste de Kolmogorov-Smirnov para distribuições, modelo de avaliação de opções de ações de Black-Scholes e até mesmo métodos para resolver sistemas de equações. Tudo isso vai muito além de um único artigo. Mas o mais importante é todos estes métodos serem discutidos no contexto da busca do coeficiente ideal f. Por isso, em vez de me debruçar sobre eles, decidi passar para a aplicação prática deste método. A implementação será na forma de módulos para o assistente MQL5.

Módulo do assistente MQL5

Em geral, a realização do módulo é semelhante à do módulo padrão já existente MoneyFixedRisk. Neste caso, o tamanho do lote é definido por um stop loss. Para maior clareza, deixamos o stop loss independente e definimos o coeficiente f e a perda máxima de forma explícita através dos parâmetros de entrada. 

Primeiro, criamos no diretório Include/Expert uma nova pasta para os módulos, por exemplo, MyMoney. Nela, criamos o arquivo MoneyF1.mql.

Todos os módulos de negociação consistem num conjunto de peças padrão: classe do módulo de negociação e sua descrição especial (descritor de classe). 

A classe contém normalmente:

• construtor;
• destruidor;
• função a definição de parâmetros de entrada;
  
• função de verificação de valores inseridos de parâmetros ValidationSettings (void);
• métodos de definição do volume da posição CheckOpenLong(double price,double sl) e CheckOpenShort(double price,double sl).

Chamamos nossa classe CMoneyFactor

class CMoneyFactor : public CExpertMoney
  {
protected:
   //--- input parameters
   double            m_factor;          // coeficiente de perda máxima f
   double            m_max_loss;        // perda máxima em pontos

public:
                     CMoneyFactor(void);
                    ~CMoneyFactor(void);
   //---
   void              Factor(double f)       { m_factor=f;}       
   void              MaxLoss(double point)  { m_max_loss=point;}         
   virtual bool      ValidationSettings(void);
   //---
   virtual double    CheckOpenLong(double price,double sl);               
   virtual double    CheckOpenShort(double price,double sl);
  };
//+------------------------------------------------------------------+
//| Constructor                                                      |
//+------------------------------------------------------------------+
void CMoneyFactor::CMoneyFactor(void) : m_factor(0.1),
                                        m_max_loss(100)
  {
  }
//+------------------------------------------------------------------+
//| Destructor                                                       |
//+------------------------------------------------------------------+
void CMoneyFactor::~CMoneyFactor(void)
  {
  }

A perda máxima em pontos é definida pelo tipo double para estar em conformidade com os módulos padrão. Isto é devido ao fato de, em outros módulos que vêm com a distribuição, o stop-loss e take-profit serem especificados em pontos definidas na classe base ExpertBase.mqh

   ExpertBase.mqh
   int digits_adjust=(m_symbol.Digits()==3 || m_symbol.Digits()==5) ? 10 : 1;
   m_adjusted_point=m_symbol.Point()*digits_adjust;

Ou seja, para cotações com cinco e três casas decimais um ponto é igual a 10*Point(). Em Point() 105 pontos são iguais a 10.5 pontos nos módulos padrão para MQL5.

As funções Factor(double f) e MaxLoss(double point) estabelecem os parâmetros de entrada e devem ser chamadas da mesma forma como será descrito mais tarde no descritor de módulo.

Função para verificar que os parâmetros sejam inseridos corretamente:

bool CMoneyFactor::ValidationSettings(void)
  {
   if(!CExpertMoney::ValidationSettings())
   return(false);
//--- initial data checks  
   if(m_factor<0||m_factor>1)
   {
   Print(__FUNCTION__+"O tamanho do coeficiente dever estar na faixa de 0 a 1");
   return false;   
   }
 
  return true;
  }

Aqui nós verificamos que o valor do coeficiente seja entre 0 e 1.

Finalmente, as próprias funções para determinar o volume da posição. Para abrir em "Long":

double CMoneyFactor::CheckOpenLong(double price,double sl)
{
   if(m_symbol==NULL)
      return(0.0);
//--- Definição do tamanho do lote
   double lot;
   
/*   
      ExpertBase.mqh
      int digits_adjust=(m_symbol.Digits()==3 || m_symbol.Digits()==5) ? 10 : 1;
      m_adjusted_point=m_symbol.Point()*digits_adjust;
*/
    double loss;
    if(price==0.0)price =m_symbol.Ask();
    loss=-m_account.OrderProfitCheck(m_symbol.Name(),ORDER_TYPE_BUY,1.0,price,price - m_max_loss*m_adjusted_point);
    double stepvol=m_symbol.LotsStep();
    lot=MathFloor(m_account.Balance()*m_factor/loss/stepvol)*stepvol;
   
   double minvol=m_symbol.LotsMin();
//---verificação do lote mínimo
   if(lot<minvol)
      lot=minvol;
//---verificação do lote máximo
   double maxvol=m_symbol.LotsMax();
   if(lot>maxvol)
      lot=maxvol;
//--- return trading volume
   return(lot);

}

Aqui, a perda máxima é encontrada usando o método de biblioteca da classe CAccountInf, isto é, OrderProfitCheck(). Em seguida, é adicionada a verificação de se o lote cumpre os limites permitidos, isto é, mínimo e máximo.

No início de cada módulo, há uma descrição (descritor) necessária para o compilador reconhecê-la.

// wizard description start
//+------------------------------------------------------------------+
//| Description of the class                                         |
//| Title=Negociação com coeficiente f ideal                     |
//| Type=Money                                                       |
//| Name=FixedPart                                                   |
//| Class=CMoneyFactor                                               |
//| Page= ?                                                          |
//| Parameter=Factor,double,0.1,Proporção fixa ideal       |
//| Parameter=MaxLoss,double,50,Perda máxima em pontos        |
//+------------------------------------------------------------------+
// wizard description end

Para os experimentos, este módulo pode ser compilado módulo com quaisquer módulos de sinais de negociação disponíveis. O módulo selecionado de sinais de negociação pode ser previamente compilado com o módulo de gerenciamento de capital com um lote fixo. Usamos os resultados obtidos para encontrar a perda máxima e o fluxo de PL. Em seguida, de acordo com estes resultados, encontramos fator ideal f com ajuda do Programa 1. Assim, é possível, usando os dados experimentais, encontrar o f ideal. Outra forma consiste em encontrar o f ideal diretamente a partir do EA com base em nosso módulo através de sua optimização. Meus resultados diferem em apenas +/- 0.01. Isto é devido a um erro de cálculo, por exemplo, devido a arredondamentos.

O código do módulo está no arquivo MoneyF1.mqh.

Pode acontecer que o fluxo de nossos lucros/perdas tenha uma autocorrelação significativa. Isso pode ser descoberto com a ajuda dos programas de "cálculo Z" e autocorrelação, apresentados anteriormente. Então faz sentido definir dois fatores - f1 e f2. O primeiro é implementado após transações favoráveis, o segundo - após as desfavoráveis. Para dada estratégia, escrevemos o segundo módulo de gerenciamento de capital. Os coeficientes podem ser encontrados com a ajuda de otimização, mas você pode fazê-lo diretamente de acordo com o fluxo de lucros/perdas para a mesma estratégia com um lote fixo.

Programa 7. Definição de f1 e f2 ideais segundo o fluxo de lucros/perdas.

void OptimumF1F2(double &arr[])
{
double f1,f2;
double profit=1;
double MaxProfit =0;
double MaxF1 =0,MaxF2 =0;
double min =MathAbs(arr[ArrayMinimum(arr)]);

   for(int i=1;i<=100;i++)
   {
   f1 =i*0.01;
      for(int j=1;j<=100;i++)
      {
         f2 =j*0.01;
         profit =profit*(1+f1*arr[0]/min);
            for(int n=1;n<ArraySize(arr);n++)
            {
            if(arr[n-1]>0){profit =profit*(1+f1*arr[n]/min);}
            else{profit =profit*(1+f2*arr[n]/min);}
            }
         if(MaxProfit<profit)
         {
         MaxProfit=profit;
         MaxF1 =i;MaxF2 =j;
         }   
      }
   }

Assim, para o assistente MQL5, é necessário alterar as funções básicas do módulo de gerenciamento de capital. Em primeiro lugar, adicionamos uma outro parâmetro - F2 - e sua verificação. Em segundo lugar, refazemos as funções CheckOpenLong() e  CheckOpenShort(). Para definir o resultado financeiro da anterior transação, adicionaremos a função CheckLoss().

//+------------------------------------------------------------------+
//| Verifica o resultado da anterior transação                       |
//+------------------------------------------------------------------+
double CMoneyTwoFact:: CheckLoss()
  {
double lot=0.0;
HistorySelect(0,TimeCurrent());

int deals=HistoryDealsTotal();           // número de transações no histórico
CDealInfo deal;
//--- busca da transação anterior
if(deals==1) return 1;
   for(int i=deals-1;i>=0;i--)
   {
   if(!deal.SelectByIndex(i))
      {
      printf(__FUNCTION__+": erro ao selecionar a transação segundo o índice");
      break;
      }
//--- seleção de transações segundo o símbolo ou outro
      if(deal.Symbol()!=m_symbol.Name()) continue;
//--- retornamos o resultado da transação
    lot=deal.Profit();
    break;
   }

   return(lot);
  }

Funções CheckOpenLong() e CheckOpenShort():

double CMoneyTwoFact::CheckOpenLong(double price,double sl)
  {
   double lot=0.0;
   double p=CheckLoss();
   
/*   
      ExpertBase.mqh
      int digits_adjust=(m_symbol.Digits()==3 || m_symbol.Digits()==5) ? 10 : 1;
      m_adjusted_point=m_symbol.Point()*digits_adjust;
*/
   
   double loss;
   
   if(price==0.0)price =m_symbol.Ask();   
   if(p>0)
      {
      loss=-m_account.OrderProfitCheck(m_symbol.Name(),ORDER_TYPE_BUY,1.0,price,price - m_max_loss*m_adjusted_point);
      double stepvol=m_symbol.LotsStep();
      lot=MathFloor(m_account.Balance()*m_factor1/loss/stepvol)*stepvol;
      }  
   if(p<0)
      { 
      loss=-m_account.OrderProfitCheck(m_symbol.Name(),ORDER_TYPE_BUY,1.0,price,price - m_max_loss*m_adjusted_point);
      double stepvol=m_symbol.LotsStep();
      lot=MathFloor(m_account.Balance()*m_factor2/loss/stepvol)*stepvol;
      }
 

  return(lot);   
  }
//+------------------------------------------------------------------+

double CMoneyTwoFact::CheckOpenShort(double price,double sl)
  {
  double lot=0.0;
  double p=CheckLoss();
/*   int digits_adjust=(m_symbol.Digits()==3 || m_symbol.Digits()==5) ? 10 : 1;
   m_adjusted_point=m_symbol.Point()*digits_adjust;*/
   
   double loss;
   
   if(price==0.0)price =m_symbol.Ask();   
   if(p>0)
      {
      loss=-m_account.OrderProfitCheck(m_symbol.Name(),ORDER_TYPE_SELL,1.0,price,price+m_max_loss*m_adjusted_point);
      double stepvol=m_symbol.LotsStep();
      lot=MathFloor(m_account.Balance()*m_factor1/loss/stepvol)*stepvol;
      }  
   if(p<0)
      { 
      loss=-m_account.OrderProfitCheck(m_symbol.Name(),ORDER_TYPE_SELL,1.0,price,price+m_max_loss*m_adjusted_point);
      double stepvol=m_symbol.LotsStep();
      lot=MathFloor(m_account.Balance()*m_factor2/loss/stepvol)*stepvol;
      }
  return(lot);     
  }

O código do módulo está no arquivo MoneyF1F2.mqh.

Como mencionado acima, todo o conceito de gerenciamento do dinheiro de Vince gira em torno do coeficiente ideal f. Portanto, o exemplo pode ser limitado a dois módulos. Embora seja possível inventar algumas variações adicionais. Por exemplo, adicionar elementos de Martingale.

Arquivos anexados

No arquivo Programs.mq5, se encontram os códigos dos programas utilizados no artigo. Aqui também foi adicionado o programa para leitura de dados a partir do arquivo void ReadFile(string file,double &arr[]). Ele é necessário para encontrar os coeficientes f com relação ao fluxo de lucros/perdas do testador de estratégias. Pode-se, naturalmente, abordar o assunto a fundo e escrever uma classe para analisar relatórios, como feito no artigo "Decompondo as entradas em indicadores". Mas, isso é um programa inteiro separado com classes próprias.

Em minha opinião, é mais fácil fazê-lo assim. Realizamos uma estratégia com um lote fixo no testador de estratégias. Salvamos o relatório do teste como Open XML (MS Office Excel). À coluna "Lucro" adicionamos "swap" e "Comissão" - obtemos o fluxo de lucro de PL. Separadamente, armazenamos esta coluna num arquivo de texto ou arquivo csv. Obtemos o conjunto de linhas contendo os resultados individuais de cada transação. A função ReadFile() lê estes resultados na matriz arr[]. Desta forma simples, podemos encontrar o f ideal de qualquer estratégia com um lote fixo.

Nos arquivos Vince.mq5 e Vince_2.mq5, encontram-se as fontes dos métodos paramétricos para encontrar os coeficientes ideias, examinados no artigo.

Os arquivos MoneyF1.mqh e MoneyF1F2.mqh são os códigos-fonte dos módulos de negociação de gerenciamento de capital.

O arquivo ZIP contém todos esses arquivos estruturados de acordo com sua posição no MetaEditor.