Matrizes e vetores em MQL5: funções de ativação

Introdução

Um enorme número de livros e artigos já foi publicado sobre o tema do treinamento de redes neurais. Membros de MQL5.com também já publicaram muitos materiais, incluindo várias séries de artigos.

Aqui, descreveremos apenas um dos aspectos do aprendizado de máquina: as funções de ativação. Vamos mergulhar nos detalhes internos do processo.

Visão geral breve

Em redes neurais artificiais, a função de ativação de neurônio calcula o valor de um sinal de saída com base nos valores de um sinal de entrada ou de um conjunto de sinais de entrada. A função de ativação deve ser diferenciável no conjunto inteiro de valores. Essa condição garante que a retropropagação de erros seja possível ao treinar redes neurais. Para retropropagar o erro, é necessário calcular o gradiente da função de ativação - o vetor de derivadas parciais da função de ativação para cada valor do vetor de sinal de entrada. Acredita-se que funções de ativação não lineares são melhores para o treinamento. Embora a função ReLU completamente linear tenha demonstrado sua eficácia em muitos modelos.

Ilustrações

Os gráficos da função de ativação e suas derivadas foram preparados em uma sequência monotonamente crescente de -5 a 5 como ilustrações. O script exibindo o gráfico da função no gráfico de preços também foi desenvolvido. A caixa de diálogo de abertura de arquivo é exibida para especificar o nome da imagem salva ao pressionar a tecla Page Down.

A tecla ESC encerra o script. O próprio script está anexado abaixo. Um script similar foi escrito pelo autor do artigo Redes neurais de retropropagação usando matrizes MQL5. Usamos sua ideia para exibir o gráfico dos valores das derivadas da função de ativação correspondente junto com o gráfico da própria função de ativação.

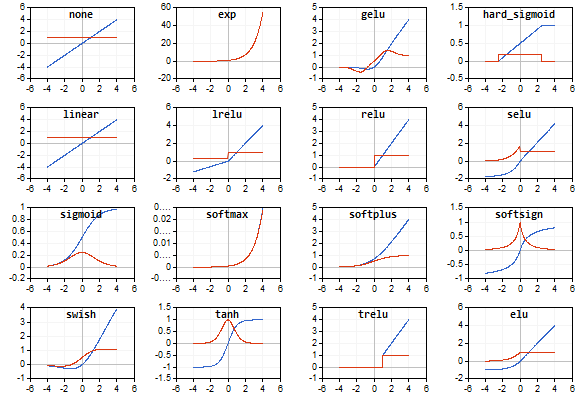
A função de ativação é mostrada em azul, enquanto as derivadas da função são exibidas em vermelho.

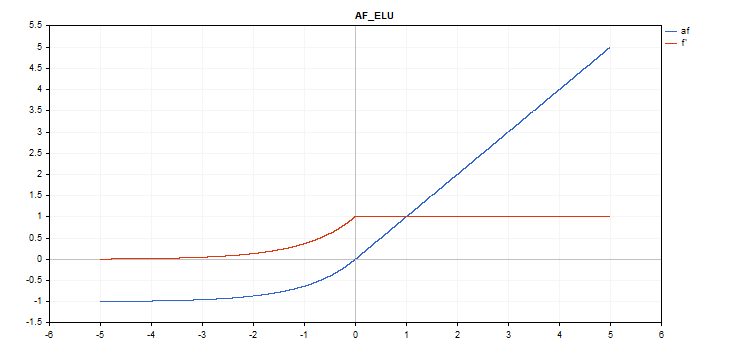
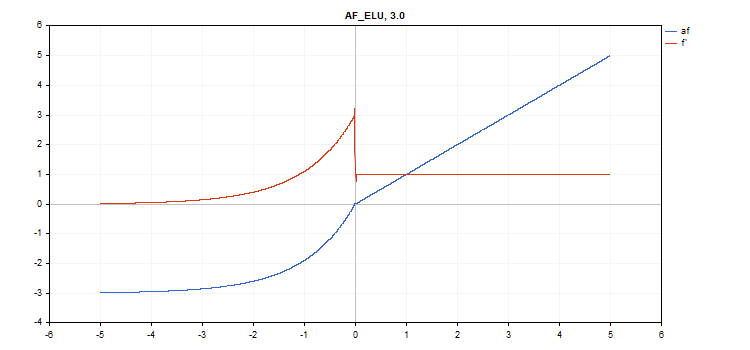
Função de ativação da Unidade Linear Exponencial (ELU)

Cálculo da função

   if(x >= 0)
      f = x;
   else
      f = alpha*(exp(x) - 1);

Cálculo da derivada

   if(x >= 0)
      d = 1;
   else
      d = alpha*exp(x);

Essa função assume um parâmetro adicional alfa. Se não for especificado, então seu valor padrão é 1.

   vector_a.Activation(vector_c,AF_ELU);      // call with the default parameter

   vector_a.Activation(vector_c,AF_ELU,3.0);  // call with alpha=3.0

Função de ativação exponencial

Cálculo da função

   f = exp(x);

A própria função exp serve como derivada da função exp.

Como podemos ver na equação de cálculo, a função de ativação exponencial não possui parâmetros adicionais.

vector_a.Activation(vector_c,AF_EXP);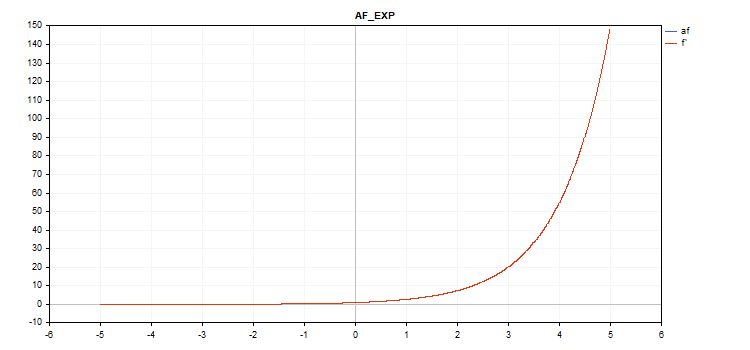

Função de ativação da Unidade Linear de Erro Gaussiano (GELU)

Cálculo da função

   f = 0.5*x*(1 + tanh(sqrt(M_2_PI)*(x+0.044715*pow(x,3)));

Cálculo da derivada

   double x_3 = pow(x,3);
   double tmp = cosh(0.0356074*x + 0.797885*x);
   d = 0.5*tanh(0.0356774*x_3 + 0.398942*x)+(0.535161*x_3 + 0.398942*x)/(tmp*tmp) + 0.5;

Sem parâmetros adicionais.

vector_a.Activation(vector_c,AF_GELU);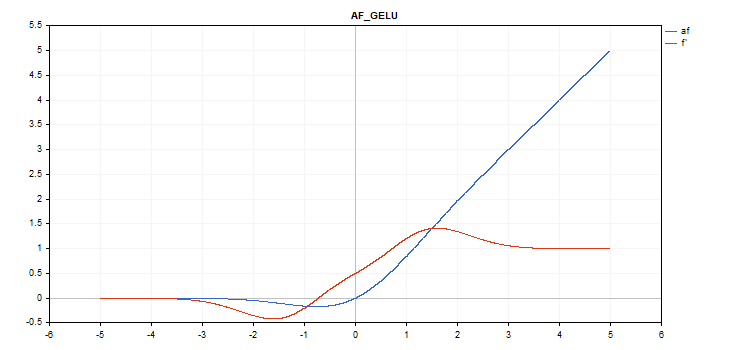

Função de ativação Hard Sigmoid

Cálculo da função

   if(x < -2.5)
      f = 0;
   else
     {
      if(x > 2.5)
         f = 1;
      else
         f = 0.2*x + 0.5;
     }

Cálculo da derivada

   if(x < -2.5)
      d = 0;
   else
     {
      if(x > 2.5)
         d = 0;
      else
         d = 0.2;
     }

Sem parâmetros adicionais.

vector_a.Activation(vector_c,AF_HARD_SIGMOID);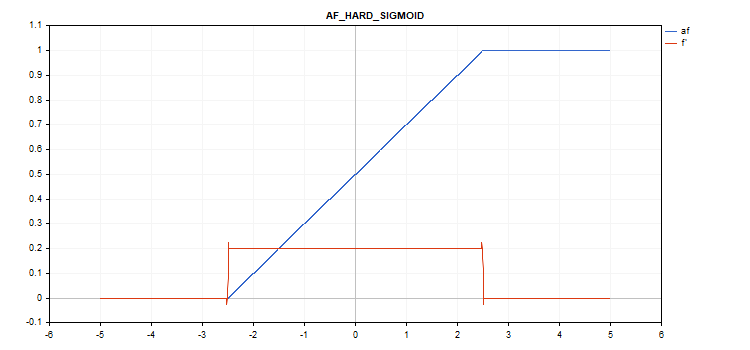

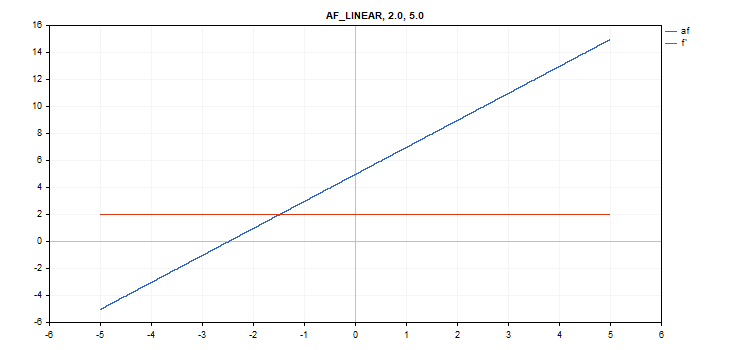
Função de ativação linear

Cálculo da função

   f = alpha*x + beta

Cálculo da derivada

   d = alpha

Parâmetros adicionais alpha = 1.0 e beta = 0.0.

vector_a.Activation(vector_c,AF_LINEAR);         // call with default parameters

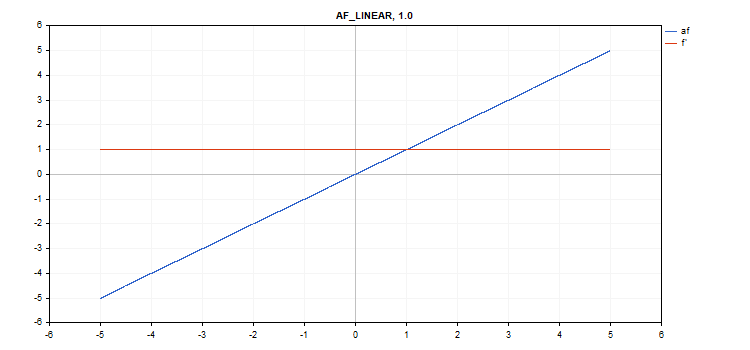
vector_a.Activation(vector_c,AF_LINEAR,2.0,5.0);  // call with alpha=2.0 and beta=5.0

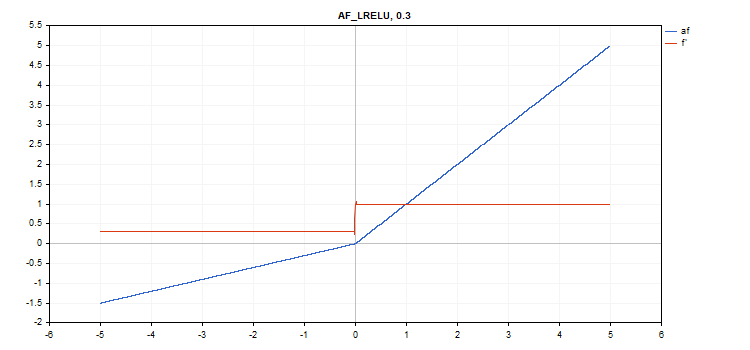
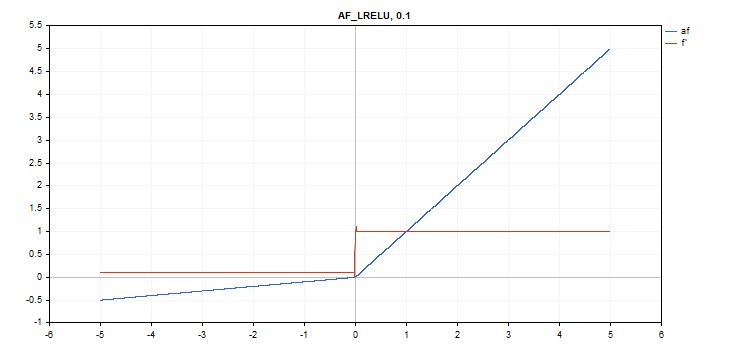
Função de ativação Unidade Linear Retificada com Vazamento (LReLU)

Cálculo da função

   if(x >= 0)
      f = x;
   else
      f = alpha * x;

Cálculo da derivada

   if(x >= 0)
      d = 1;
   else
      d = alpha;

Essa função assume um parâmetro adicional alfa. Se não for especificado, então seu valor padrão é 0,3.

   vector_a.Activation(vector_c,AF_LRELU);      // call with the default parameter

vector_a.Activation(vector_c,AF_LRELU,0.1);  // call with alpha=0.1

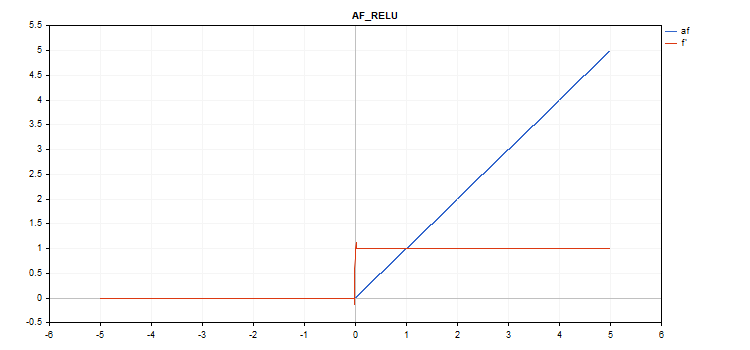
Função de ativação da Unidade Linear Retificada (ReLU)

Cálculo da função

   if(alpha==0)
     {
      if(x > 0)
         f = x;
      else
         f = 0;
     }
   else
     {
      if(x >= max_value)
         f = x;
      else
         f = alpha * (x - treshold);
     }

Cálculo da derivada

   if(alpha==0)
     {
      if(x > 0)
         d = 1;
      else
         d = 0;
     }
   else
     {
      if(x >= max_value)
         d = 1;
      else
         d = alpha;
     }

Parâmetros adicionais alpha=0, max_value=0 e treshold=0.

vector_a.Activation(vector_c,AF_RELU);         // call with default parameters

vector_a.Activation(vector_c,AF_RELU,2.0,0.5);      // call with alpha=2.0 and max_value=0.5

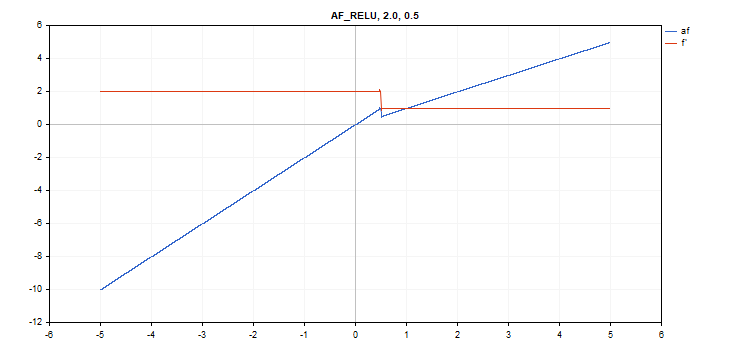
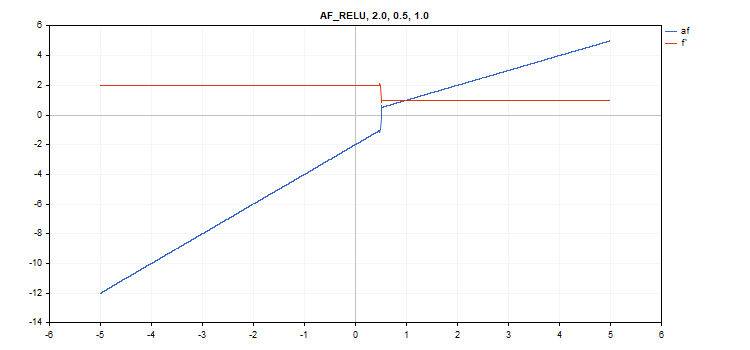
vector_a.Activation(vector_c,AF_RELU,2.0,0.5,1.0);  // call with alpha=2.0, max_value=0.5 and treshold=1.0

Função de ativação da Unidade Linear Exponencial Escalada (SELU)

Cálculo da função

   if(x >= 0)
      f = scale * x;
   else
      f = scale * alpha * (exp(x) - 1);

где scale = 1.05070098, alpha = 1.67326324

Cálculo da derivada

   if(x >= 0)
      d = scale;
   else
      d = scale * alpha * exp(x);

Sem parâmetros adicionais.

vector_a.Activation(vector_c,AF_SELU);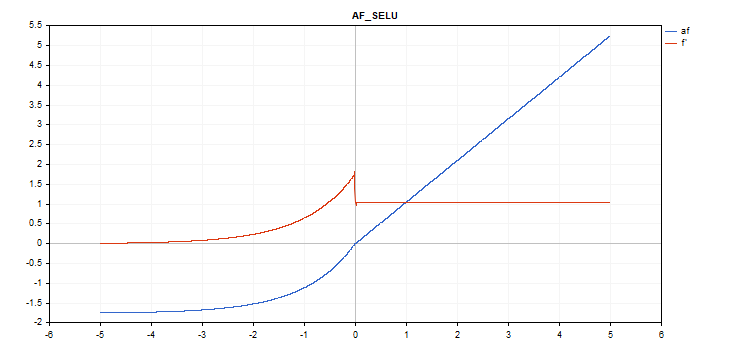

Função de ativação sigmoide

Cálculo da função

   f = 1 / (1 + exp(-x));

Cálculo da derivada

   d = exp(x) / pow(exp(x) + 1, 2);

Sem parâmetros adicionais.

vector_a.Activation(vector_c,AF_SIGMOID);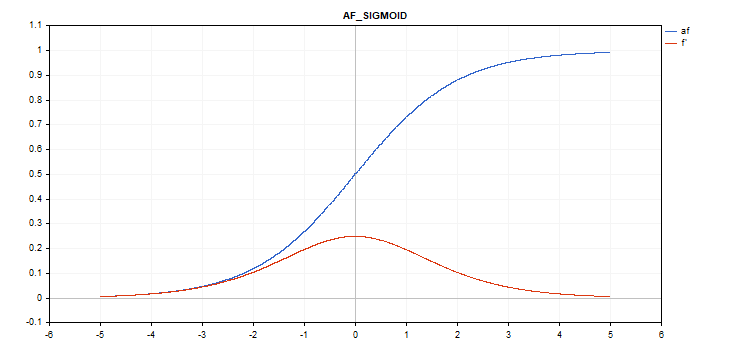

Função de ativação Softplus

Cálculo da função

   f = log(exp(x) + 1);

Cálculo da derivada

   d = exp(x) / (exp(x) + 1);

Sem parâmetros adicionais.

vector_a.Activation(vector_c,AF_SOFTPLUS);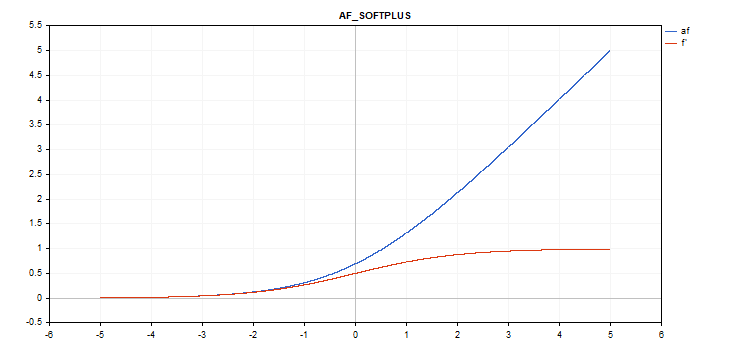

Função de ativação Softsign

Cálculo da função

   f = x / (|x| + 1)

Cálculo da derivada

   d = 1 / (|x| + 1)^2

Sem parâmetros adicionais.

vector_a.Activation(vector_c,AF_SOFTSIGN);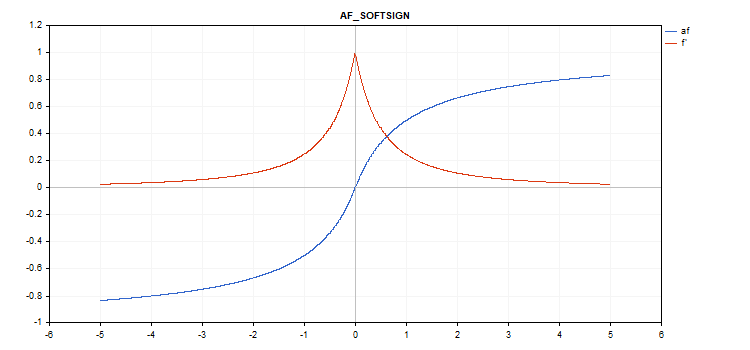

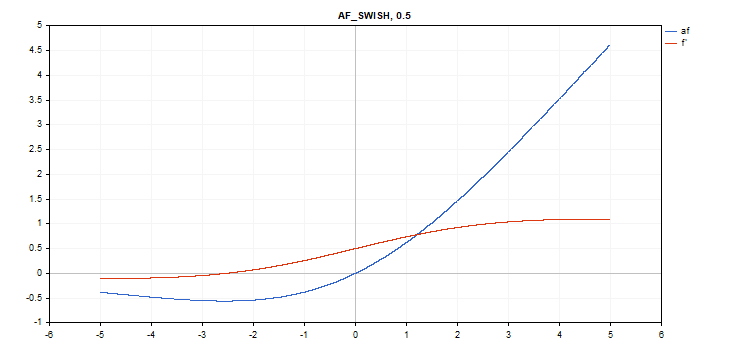
Função de ativação Swish

Cálculo da função

   f = x / (1 + exp(-x*beta));

Cálculo da derivada

   double tmp = exp(beta*x);
   d = tmp*(beta*x + tmp + 1) / pow(tmp+1, 2);

Parâmetro adicional beta = 1

vector_a.Activation(vector_c,AF_SWISH);         // call with the default parameter

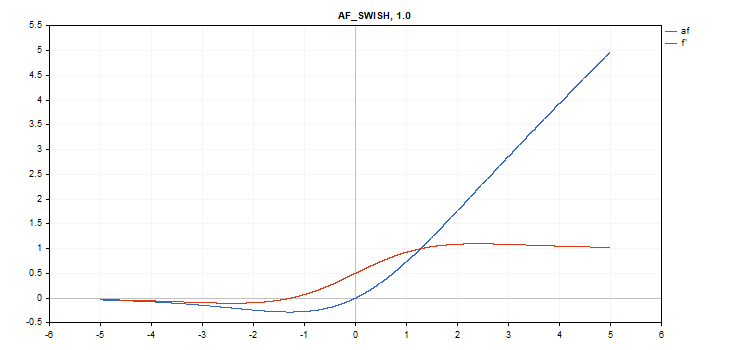
vector_a.Activation(vector_c,AF_SWISH,2.0);     // call with beta = 2.0

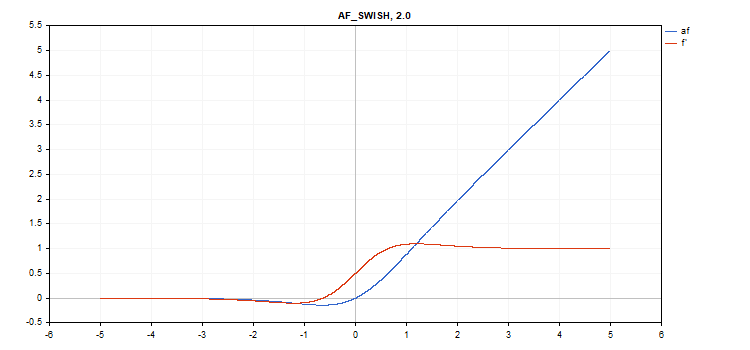
vector_a.Activation(vector_c,AF_SWISH,0.5);   // call with beta=0.5

Função de ativação Tangente Hiperbólica (TanH)

Cálculo da função

   f = tanh(x);

Cálculo da derivada

   d = 1 / pow(cosh(x),2);

Sem parâmetros adicionais.

vector_a.Activation(vector_c,AF_TANH);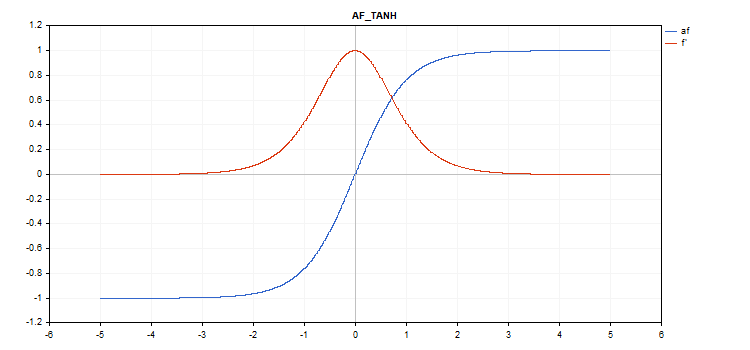

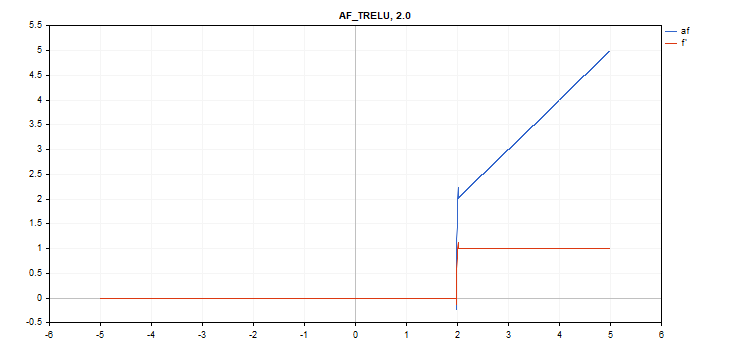
Função de ativação da Unidade Linear Retificada com Limite (TReLU)

Cálculo da função

   if(x > theta)
      f = x;
   else
      f = 0;

Cálculo da derivada

   if(x > theta)
      d = 1;
   else
      d = 0;

Parâmetro adicional theta = 1

vector_a.Activation(vector_c,AF_TRELU);         // call with default parameter

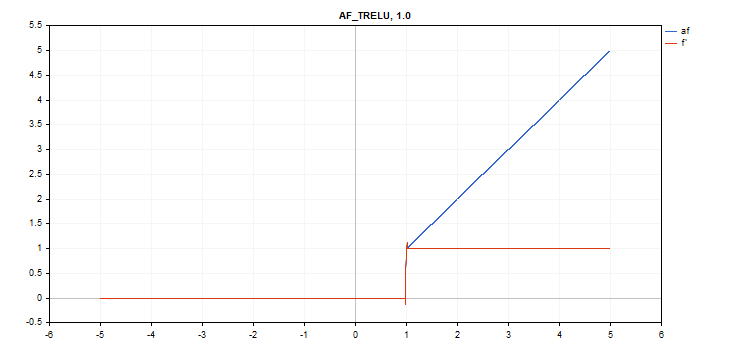
vector_a.Activation(vector_c,AF_TRELU,0.0);     // call with theta = 0.0

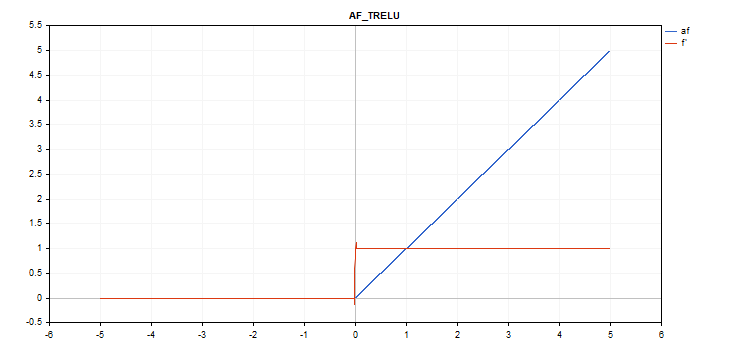
vector_a.Activation(vector_c,AF_TRELU,2.0);      // call with theta = 2.0

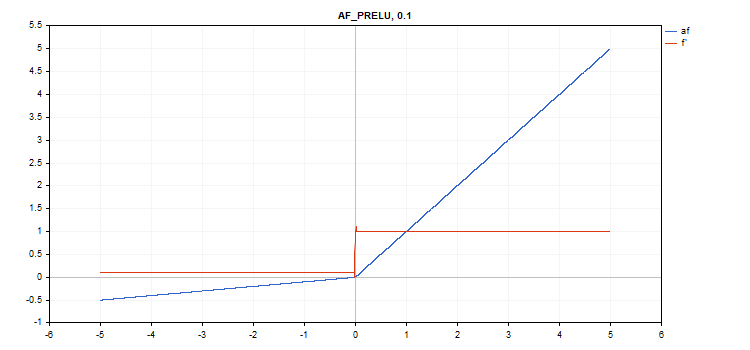
Função de ativação da Unidade Linear Retificada Paramétrica (PReLU)

Cálculo da função

   if(x[i] >= 0)
      f[i] = x[i];
   else
      f[i] = alpha[i]*x[i];

Cálculo da derivada

   if(x[i] >= 0)
      d[i] = 1;
   else
      d[i] = alpha[i];

Parâmetro adicional - vetor de coeficientes alpha.

vector alpha=vector::Full(vector_a.Size(),0.1);
vector_a.Activation(vector_c,AF_PRELU,alpha);

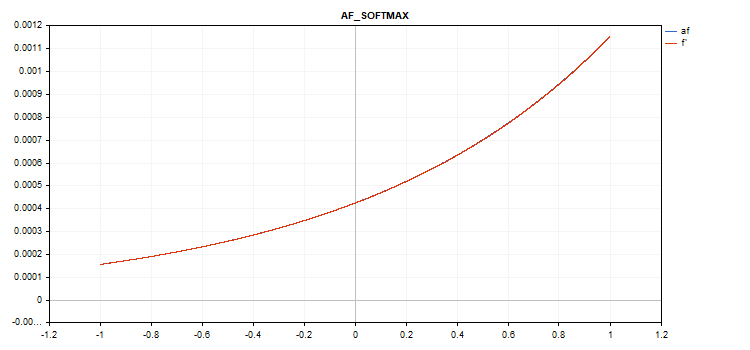
Função Softmax especial

O resultado do cálculo da função de ativação Softmax depende não apenas de um valor específico, mas também de todos os valores do vetor.

   sum_exp = Sum(exp(vector_a))
   f = exp(x) / sum_exp

Cálculo da derivada

   d = f*(1 - f)

Assim, a soma de todos os valores do vetor ativado é 1. Portanto, a função de ativação Softmax é muito frequentemente usada para a última camada de modelos de classificação.

Gráfico da função de ativação do vetor com valores de -5 a 5

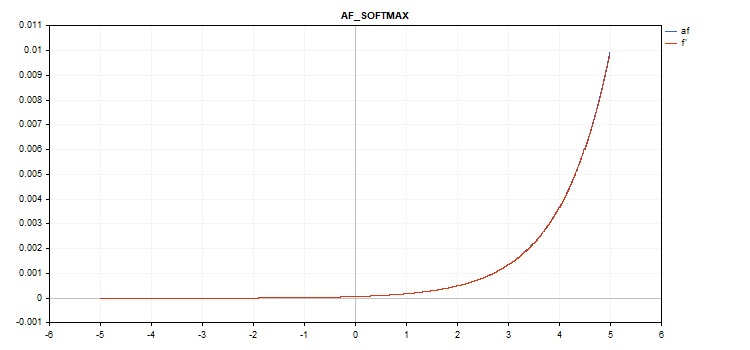
Gráfico da função de ativação do vetor com valores de -1 a 1

Se não houver função de ativação (AF_NONE)

Se não houver função de ativação, então os valores do vetor de entrada são transferidos para o vetor de saída sem quaisquer transformações. Na verdade, esta é a função de ativação Linear com alpha = 1 e beta = 0.

Considerações finais

Por fim, sugerimos que você leia o código-fonte das funções de ativação e derivadas, que estão no arquivo anexo ActivationFunction.mqh.