MQL5 中的矩阵和向量：激活函数

概述

关于训练神经网络这一主题已有大量书籍和文章发表。 MQL5.com 成员还发表了许多素材，包括若干个系列文章。

此处，我们只讲述机器学习的一个方面 — 激活函数。 我们将深入研究该过程的内部运作。

简要概览

在人工神经网络中，神经元激活函数会根据一个或一组输入信号的数值，计算输出信号值。 激活函数必须在整个数值集合上是可微分的。 这种情况在训练神经网络时提供了反向传播误差的可能性。 为了反向传播误差，必须计算激活函数的梯度 — 输入信号向量的每个值的激活函数的偏导数向量。 人们认为非线性激活函数更适合进行训练。 尽管完全线性的 ReLU 函数在许多模型中都显示出其有效性。

描图

激活函数及其导数的图形基于从 -5 到 5 的单调递增序列来描图。 在价格图表上显示函数图的脚本也已开发完毕。 显示打开文件对话框，可通过按 “下一页（Page Down）”键来指定保存图像的文件名称。

ESC 键终止脚本。 脚本本身附在下面。 类似的脚本是由利用 MQL5 矩阵的反向传播神经网络一文的作者编写。 我们延用他的思路，将相应激活函数导数的数值图形与激活函数本身的图形一并显示。

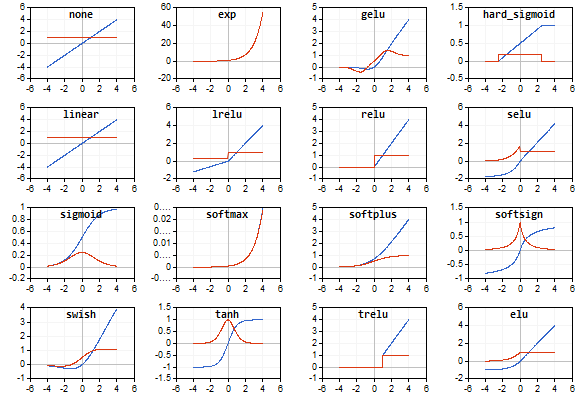
激活函数以蓝色显示，而函数导数则以红色显示。

指数线性单元（ELU）激活函数

函数计算

   if(x >= 0)
      f = x;
   else
      f = alpha*(exp(x) - 1);

导数计算

   if(x >= 0)
      d = 1;
   else
      d = alpha*exp(x);

该函数取额外的 “alpha” 参数。 如果未指定，则其默认值为 1。

   vector_a.Activation(vector_c,AF_ELU);      // call with the default parameter

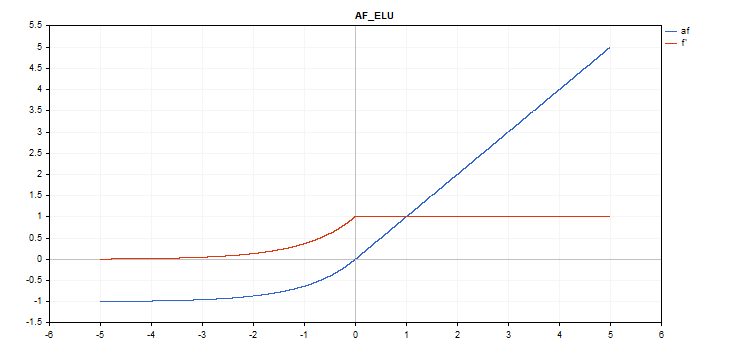
   vector_a.Activation(vector_c,AF_ELU,3.0);  // call with alpha=3.0

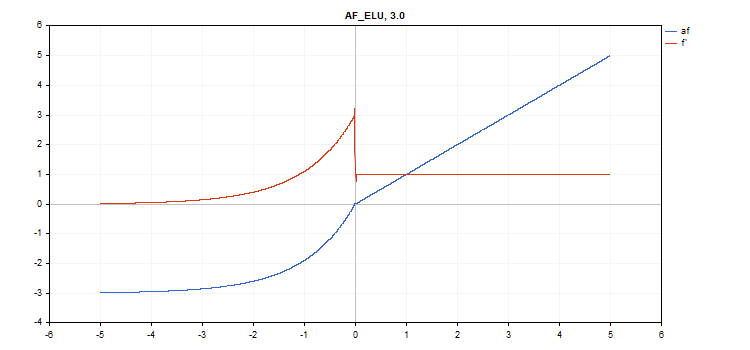
指数激活函数

函数计算

   f = exp(x);

相同的 exp 函数用作 exp 函数的导数。

正如我们在计算方程中所见，指数激活函数没有额外的参数。

vector_a.Activation(vector_c,AF_EXP);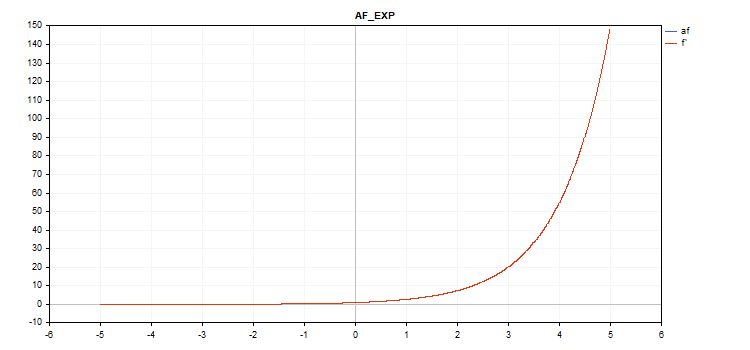

高斯误差线性单元（GELU）激活函数

函数计算

   f = 0.5*x*(1 + tanh(sqrt(M_2_PI)*(x+0.044715*pow(x,3)));

导数计算

   double x_3 = pow(x,3);
   double tmp = cosh(0.0356074*x + 0.797885*x);
   d = 0.5*tanh(0.0356774*x_3 + 0.398942*x)+(0.535161*x_3 + 0.398942*x)/(tmp*tmp) + 0.5;

没有额外参数。

vector_a.Activation(vector_c,AF_GELU);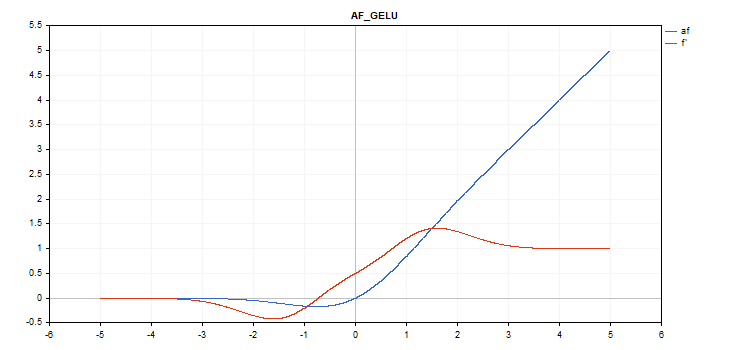

硬希格玛（Sigmoid）激活函数

函数计算

   if(x < -2.5)
      f = 0;
   else
     {
      if(x > 2.5)
         f = 1;
      else
         f = 0.2*x + 0.5;
     }

导数计算

   if(x < -2.5)
      d = 0;
   else
     {
      if(x > 2.5)
         d = 0;
      else
         d = 0.2;
     }

没有额外参数。

vector_a.Activation(vector_c,AF_HARD_SIGMOID);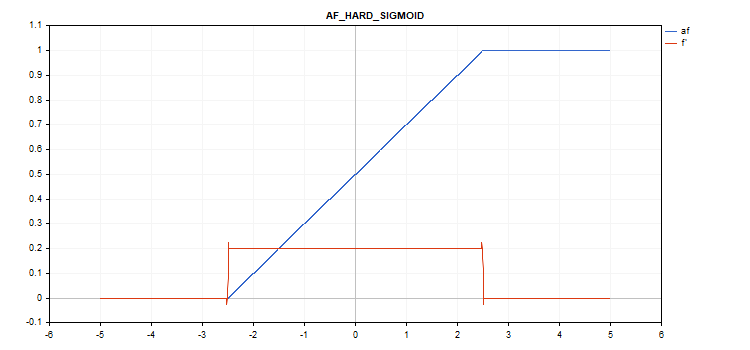

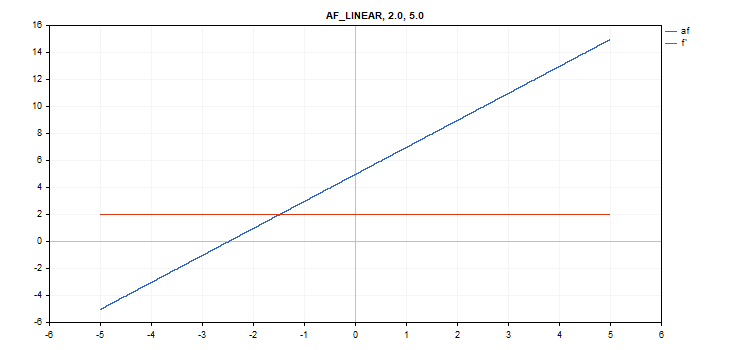
线性激活函数

函数计算

   f = alpha*x + beta

导数计算

   d = alpha

额外参数 alpha = 1.0，且 beta = 0.0

vector_a.Activation(vector_c,AF_LINEAR);         // call with default parameters

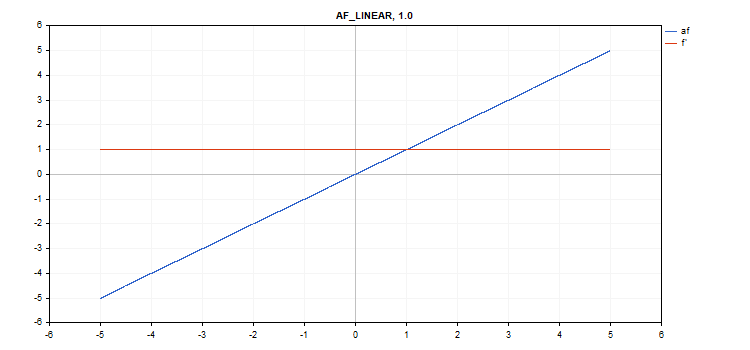
vector_a.Activation(vector_c,AF_LINEAR,2.0,5.0);  // call with alpha=2.0 and beta=5.0

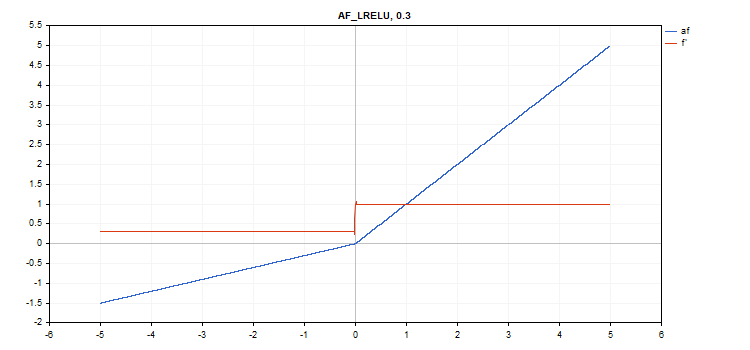
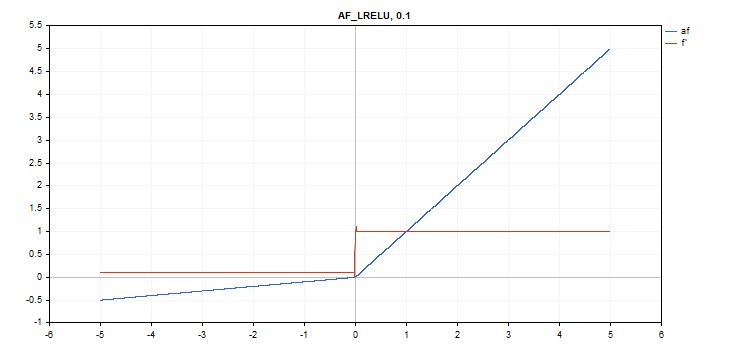
泄露修整线性单元（LReLU）激活函数

函数计算

   if(x >= 0)
      f = x;
   else
      f = alpha * x;

导数计算

   if(x >= 0)
      d = 1;
   else
      d = alpha;

该函数取额外的 “alpha” 参数。 如果未指定，则其默认值为 0. 3

   vector_a.Activation(vector_c,AF_LRELU);      // call with the default parameter

vector_a.Activation(vector_c,AF_LRELU,0.1);  // call with alpha=0.1

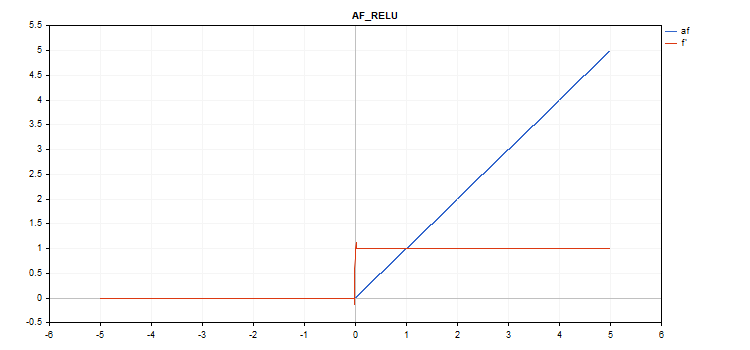
修整线性单元（ReLU）激活函数

函数计算

   if(alpha==0)
     {
      if(x > 0)
         f = x;
      else
         f = 0;
     }
   else
     {
      if(x >= max_value)
         f = x;
      else
         f = alpha * (x - treshold);
     }

导数计算

   if(alpha==0)
     {
      if(x > 0)
         d = 1;
      else
         d = 0;
     }
   else
     {
      if(x >= max_value)
         d = 1;
      else
         d = alpha;
     }

额外参数 alpha = 0，max_value=0，且 treshold=0。

vector_a.Activation(vector_c,AF_RELU);         // call with default parameters

vector_a.Activation(vector_c,AF_RELU,2.0,0.5);      // call with alpha=2.0 and max_value=0.5

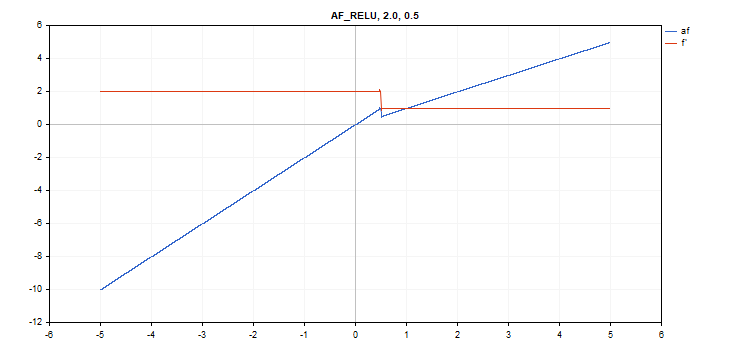
vector_a.Activation(vector_c,AF_RELU,2.0,0.5,1.0);  // call with alpha=2.0, max_value=0.5 and treshold=1.0

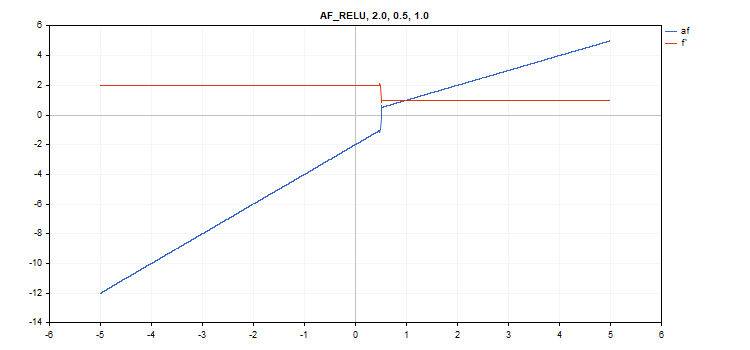
伸缩指数线性单元（SELU）激活函数

函数计算

   其中 scale = 1.05070098，alpha = 1.67326324

导数计算

   if(x >= 0)
      d = scale;
   else
      d = scale * alpha * exp(x);

没有额外参数。

vector_a.Activation(vector_c,AF_SELU);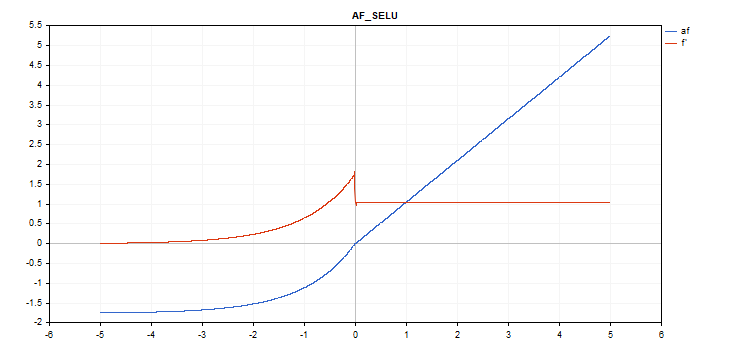

希格玛（Sigmoid）激活函数

函数计算

   f = 1 / (1 + exp(-x));

导数计算

   d = exp(x) / pow(exp(x) + 1, 2);

没有额外参数。

vector_a.Activation(vector_c,AF_SIGMOID);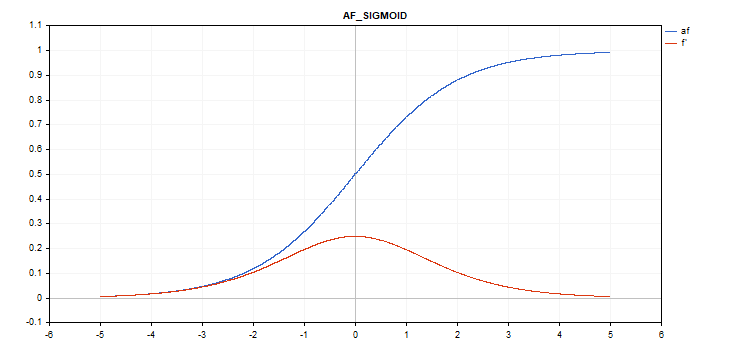

Softplus 激活函数

函数计算

   f = log(exp(x) + 1);

导数计算

   d = exp(x) / (exp(x) + 1);

没有额外参数。

vector_a.Activation(vector_c,AF_SOFTPLUS);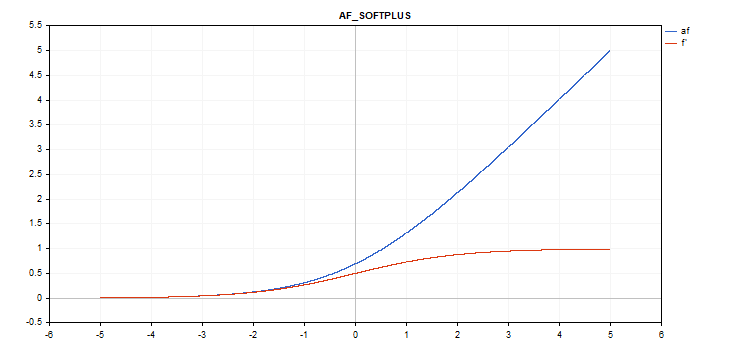

Softsign 激活函数

函数计算

   f = x / (|x| + 1)

导数计算

   d = 1 / (|x| + 1)^2

没有额外参数。

vector_a.Activation(vector_c,AF_SOFTSIGN);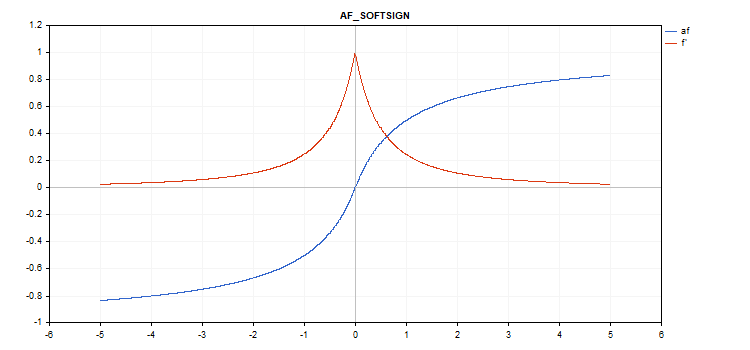

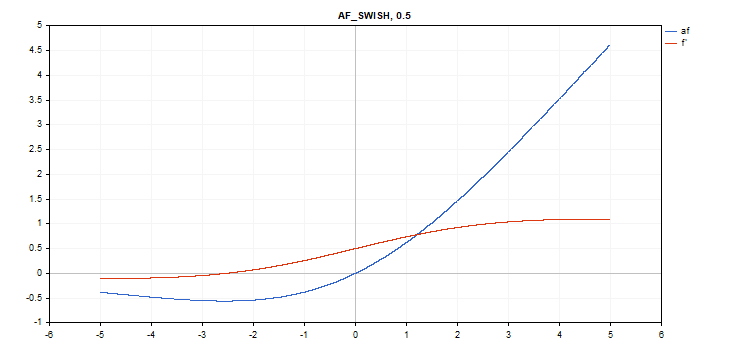
Swish 激活函数

函数计算

   f = x / (1 + exp(-x*beta));

导数计算

   double tmp = exp(beta*x);
   d = tmp*(beta*x + tmp + 1) / pow(tmp+1, 2);

额外参数 beta = 1

vector_a.Activation(vector_c,AF_SWISH);         // call with the default parameter

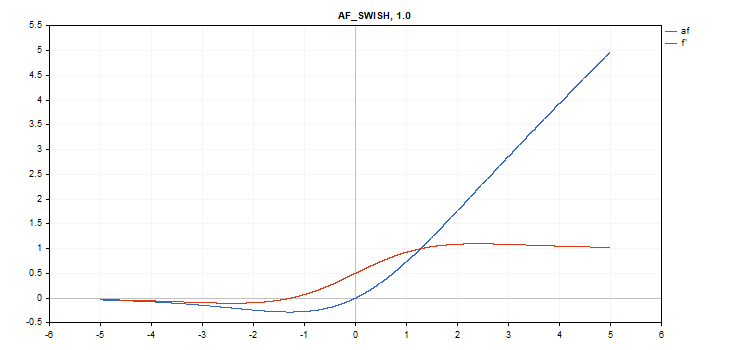
vector_a.Activation(vector_c,AF_SWISH,2.0);     // call with beta = 2.0

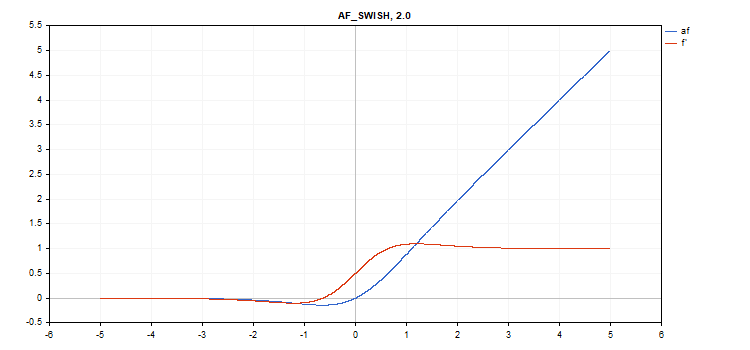
vector_a.Activation(vector_c,AF_SWISH,0.5);   // call with beta=0.5

双曲正切（TanH）激活函数

函数计算

   f = tanh(x);

导数计算

   d = 1 / pow(cosh(x),2);

没有额外参数。

vector_a.Activation(vector_c,AF_TANH);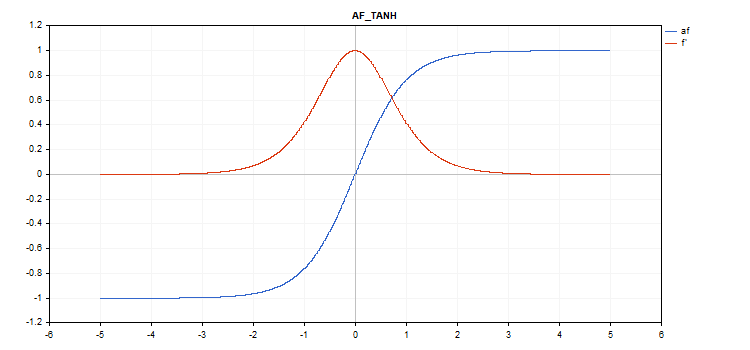

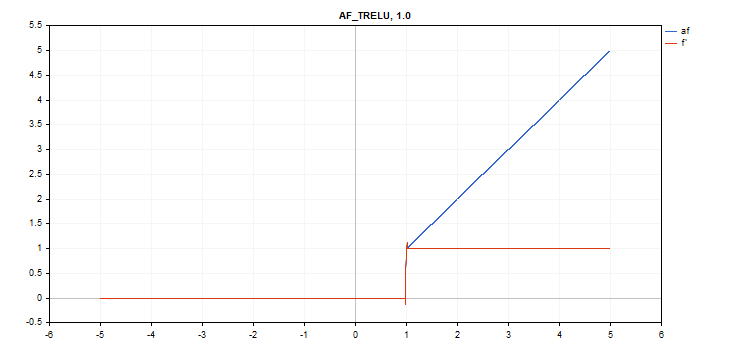
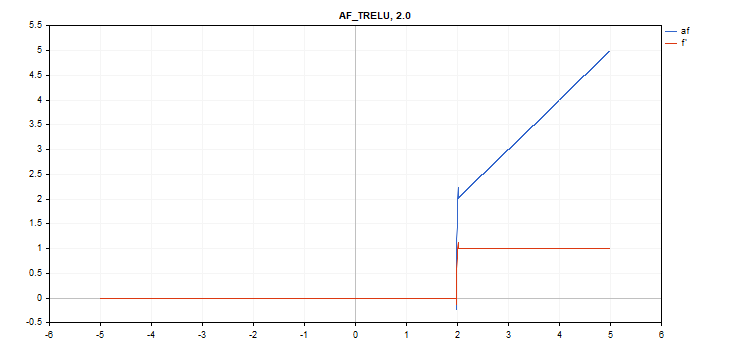
阈值修整线性单元（TReLU）激活函数

函数计算

   if(x > theta)
      f = x;
   else
      f = 0;

导数计算

   if(x > theta)
      d = 1;
   else
      d = 0;

额外参数 theta = 1

vector_a.Activation(vector_c,AF_TRELU);         // call with default parameter

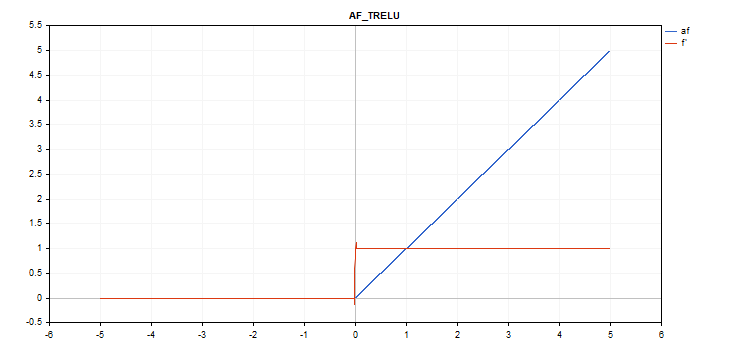
vector_a.Activation(vector_c,AF_TRELU,0.0);     // call with theta = 0.0

vector_a.Activation(vector_c,AF_TRELU,2.0);      // call with theta = 2.0

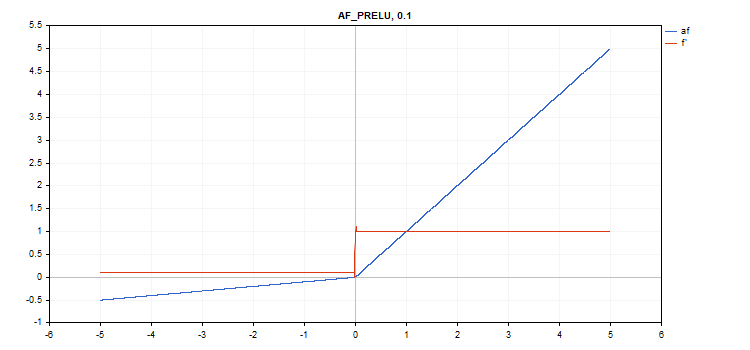
参数化修整线性单元（PReLU）激活函数

函数计算

   if(x[i] >= 0)
      f[i] = x[i];
   else
      f[i] = alpha[i]*x[i];

导数计算

   if(x[i] >= 0)
      d[i] = 1;
   else
      d[i] = alpha[i];

额外参数 — 'alpha' 系数向量。

vector alpha=vector::Full(vector_a.Size(),0.1);
vector_a.Activation(vector_c,AF_PRELU,alpha);

特殊的 Softmax 函数

计算 Softmax 激活函数的结果不仅取决于特定值，还取决于所有向量值。

   sum_exp = Sum(exp(vector_a))
   f = exp(x) / sum_exp

导数计算

   d = f*(1 - f)

因此，所有激活的向量值的总和为 1。 如此，Softmax 激活函数经常用在分类模型的最后一层。

数值从 -5 到 5 的向量激活函数图形

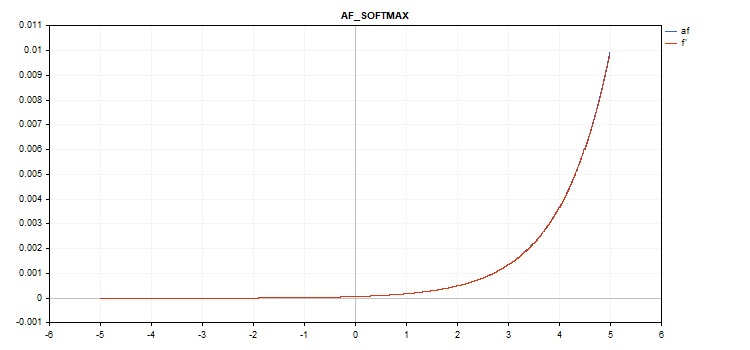
数值从 -1 到 1 的向量激活函数图形

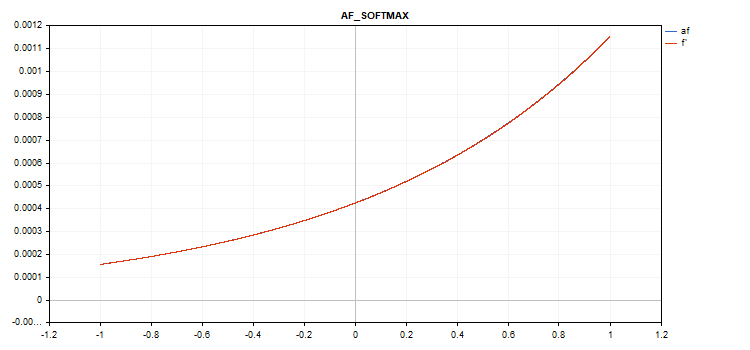
如果没有激活函数（AF_NONE）

如果没有激活函数，则输入向量中的数值将直接传输到输出向量，无需任何转换。 事实上，这是 alpha = 1 且 beta = 0 的线性激活函数。

结束语

请您自行从文后所附的 ActivationFunction.mqh 文件中随意掌握激活函数和衍生函数的源代码。