Matrizen und Vektoren in MQL5: Die Aktivierungsfunktionen

Einführung

Zum Thema Training neuronaler Netze ist bereits eine Vielzahl von Büchern und Artikeln veröffentlicht worden. Die Mitglieder von MQL5.com haben auch eine Menge Material veröffentlicht, darunter mehrere Artikelserien.

Hier wird nur einer der Aspekte des maschinellen Lernens beschrieben — die Aktivierungsfunktionen. Wir werden uns mit den inneren Abläufen des Prozesses befassen.

Kurzer Überblick

In künstlichen neuronalen Netzen berechnet eine Neuronenaktivierungsfunktion einen Ausgangssignalwert auf der Grundlage der Werte eines Eingangssignals oder eines Satzes von Eingangssignalen. Die Aktivierungsfunktion muss auf der gesamten Menge der Werte differenzierbar sein. Diese Bedingung bietet die Möglichkeit der Backpropagation von Fehlern beim Training neuronaler Netze. Um den Fehler rückwärts zu propagieren, muss der Gradient der Aktivierungsfunktion berechnet werden — der Vektor der partiellen Ableitungen der Aktivierungsfunktion für jeden Wert des Eingangssignalvektors. Es wird davon ausgegangen, dass sich nichtlineare Aktivierungsfunktionen besser für das Training eignen. Obwohl sich die vollständig lineare ReLU-Funktion in vielen Modellen bewährt hat.

Illustrationen

Die Graphen der Aktivierungsfunktion und ihrer Ableitungen wurden zur Veranschaulichung in einer monoton ansteigenden Folge von -5 bis 5 erstellt. Das Skript, das den Funktionsgraphen auf dem Preisdiagramm anzeigt, wurde ebenfalls entwickelt. Das Dialogfeld zum Öffnen der Datei wird angezeigt, in dem Sie den Namen des gespeicherten Bildes angeben können, indem Sie die Bild-herunter-Taste drücken.

Mit der ESC-Taste wird das Skript beendet. Das Skript selbst ist unten beigefügt. Ein ähnliches Skript wurde vom Autor des Artikels Backpropagation von Neuronalen Netze mit MQL5-Matrizen geschrieben. Wir haben seine Idee aufgegriffen, um den Graphen der Werte der entsprechenden Ableitungen der Aktivierungsfunktion zusammen mit dem Graphen der Aktivierungsfunktion selbst anzuzeigen.

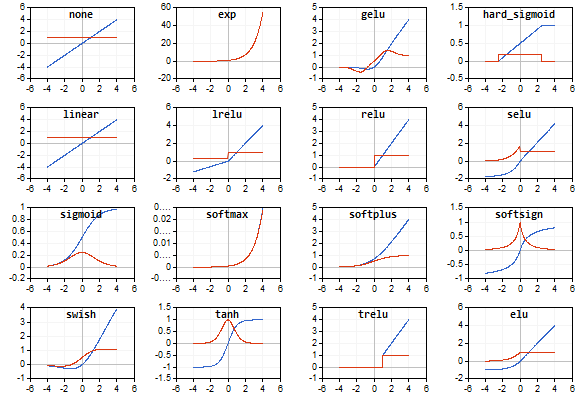
Die Aktivierungsfunktion ist blau dargestellt, während die Ableitungen der Funktion rot angezeigt werden.

Exponential Linear Unit (ELU) Aktivierungsfunktion

Berechnung der Funktion

   if(x >= 0)
      f = x;
   else
      f = alpha*(exp(x) - 1);

Berechnung der Ableitung

   if(x >= 0)
      d = 1;
   else
      d = alpha*exp(x);

Diese Funktion hat einen zusätzlichen 'alpha'-Parameter. Wird er nicht angegeben, ist sein (Standard-) Wert 1.

   vector_a.Activation(vector_c,AF_ELU);      // call with the default parameter

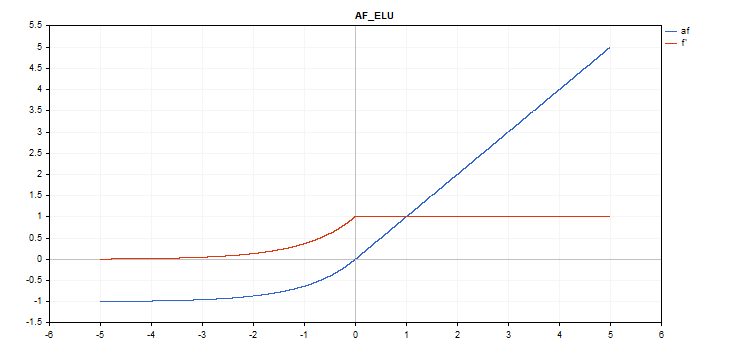
   vector_a.Activation(vector_c,AF_ELU,3.0);  // call with alpha=3.0

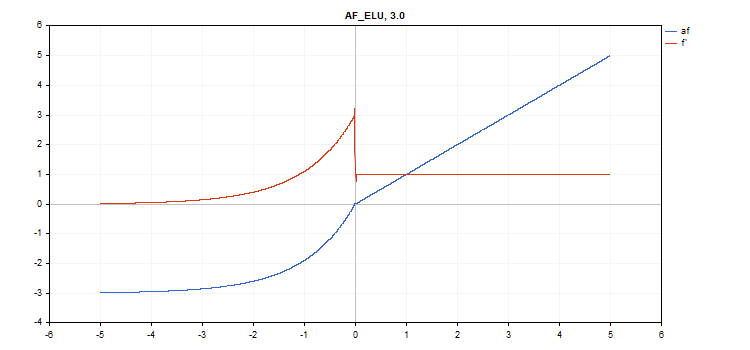
Exponentiale Aktivierungsfunktion

Berechnung der Funktion

   f = exp(x);

Die gleiche exp-Funktion dient als Ableitung der exp-Funktion.

Wie wir in der Berechnungsgleichung sehen können, hat die Exponentialaktivierungsfunktion keine zusätzlichen Parameter

vector_a.Activation(vector_c,AF_EXP);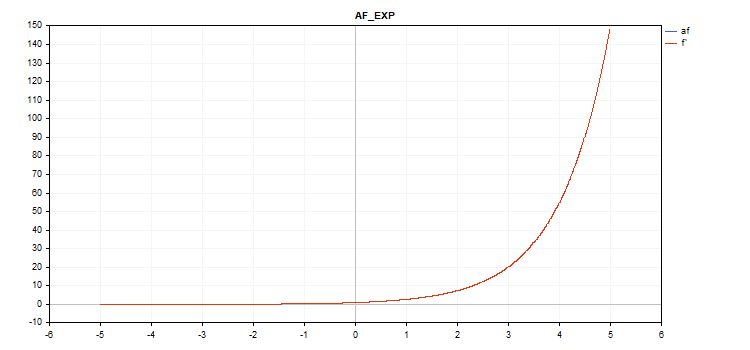

Die Aktivierungsfunktion Gaussian Error Linear Unit (GELU)

Berechnung der Funktion

   f = 0.5*x*(1 + tanh(sqrt(M_2_PI)*(x+0.044715*pow(x,3)));

Berechnung der Ableitung

   double x_3 = pow(x,3);
   double tmp = cosh(0.0356074*x + 0.797885*x);
   d = 0.5*tanh(0.0356774*x_3 + 0.398942*x)+(0.535161*x_3 + 0.398942*x)/(tmp*tmp) + 0.5;

Keine zusätzlichen Parameter.

vector_a.Activation(vector_c,AF_GELU);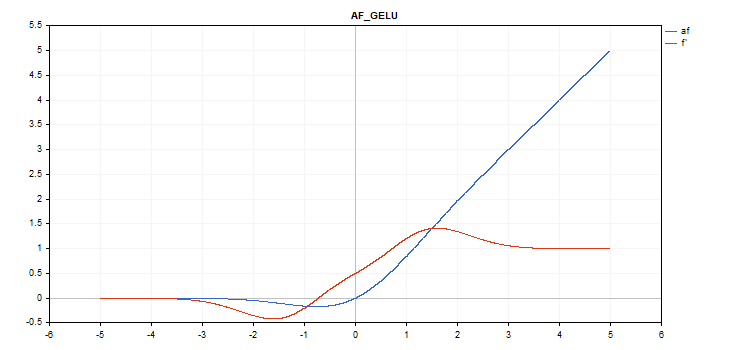

Harte Sigmoid-Aktivierungsfunktion

Berechnung der Funktion

   if(x < -2.5)
      f = 0;
   else
     {
      if(x > 2.5)
         f = 1;
      else
         f = 0.2*x + 0.5;
     }

Berechnung der Ableitung

   if(x < -2.5)
      d = 0;
   else
     {
      if(x > 2.5)
         d = 0;
      else
         d = 0.2;
     }

Keine zusätzlichen Parameter.

vector_a.Activation(vector_c,AF_HARD_SIGMOID);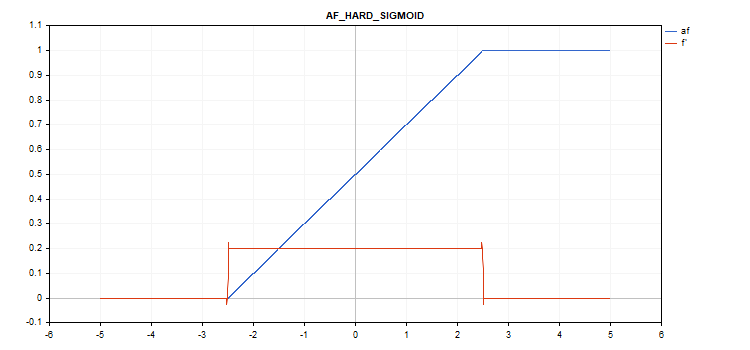

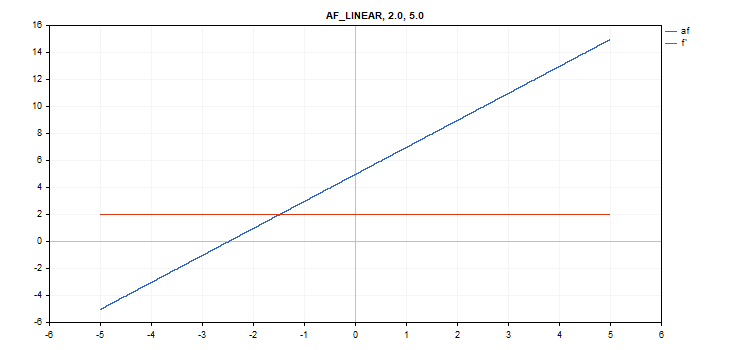
Lineare Aktivierungsfunktion

Berechnung der Funktion

   f = alpha*x + beta

Berechnung der Ableitung

   d = alpha

Zusätzliche Parameter alpha = 1,0 und beta = 0,0

vector_a.Activation(vector_c,AF_LINEAR);         // call with default parameters

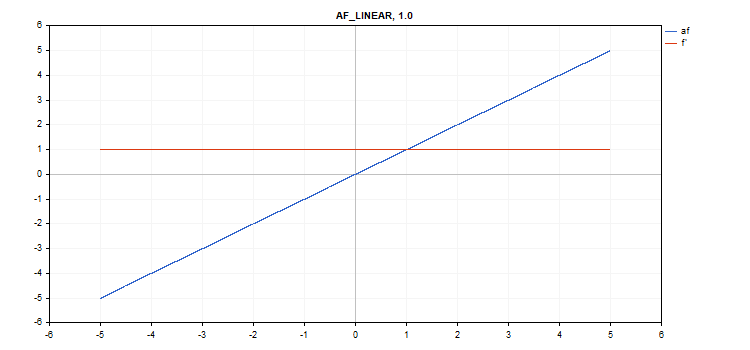
vector_a.Activation(vector_c,AF_LINEAR,2.0,5.0);  // call with alpha=2.0 and beta=5.0

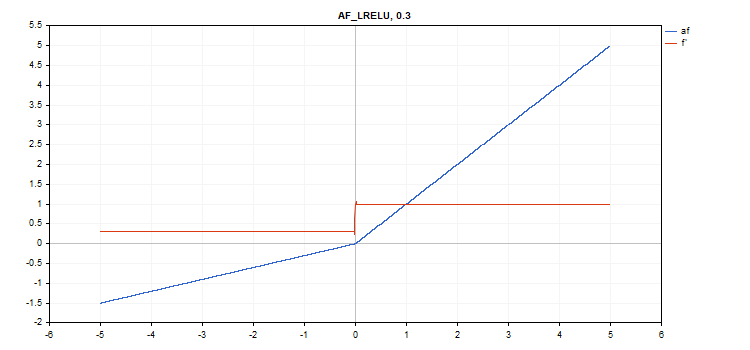
Die Aktivierungsfunktion Leaky Rectified Linear Unit (LReLU)

Berechnung der Funktion

   if(x >= 0)
      f = x;
   else
      f = alpha * x;

Berechnung der Ableitung

   if(x >= 0)
      d = 1;
   else
      d = alpha;

Diese Funktion hat einen zusätzlichen 'alpha'-Parameter. Wird er nicht angegeben, so ist der Standardwert 0. 3

   vector_a.Activation(vector_c,AF_LRELU);      // call with the default parameter

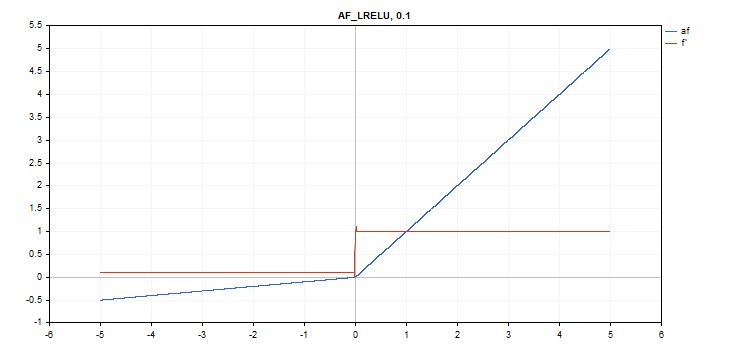
vector_a.Activation(vector_c,AF_LRELU,0.1);  // call with alpha=0.1

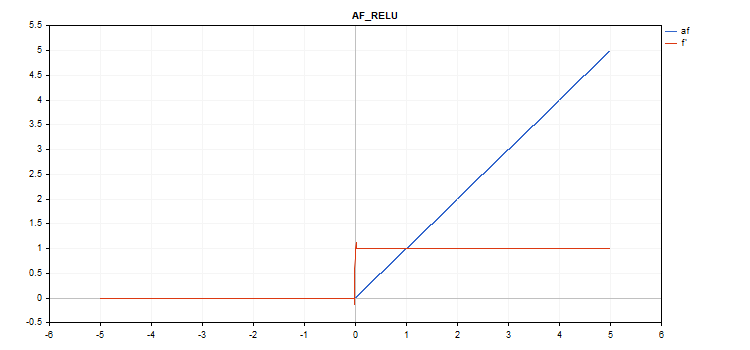
Rectified Linear Unit (ReLU) Aktivierungsfunktion

Berechnung der Funktion

   if(alpha==0)
     {
      if(x > 0)
         f = x;
      else
         f = 0;
     }
   else
     {
      if(x >= max_value)
         f = x;
      else
         f = alpha * (x - treshold);
     }

Berechnung der Ableitung

   if(alpha==0)
     {
      if(x > 0)
         d = 1;
      else
         d = 0;
     }
   else
     {
      if(x >= max_value)
         d = 1;
      else
         d = alpha;
     }

Zusätzliche Parameter alpha=0, max_value=0 und treshold=0.

vector_a.Activation(vector_c,AF_RELU);         // call with default parameters

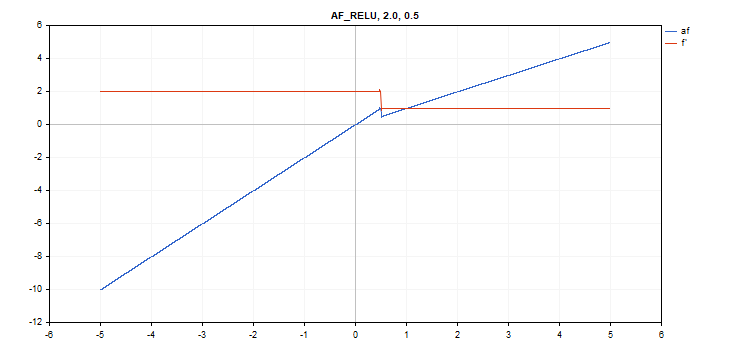
vector_a.Activation(vector_c,AF_RELU,2.0,0.5);      // call with alpha=2.0 and max_value=0.5

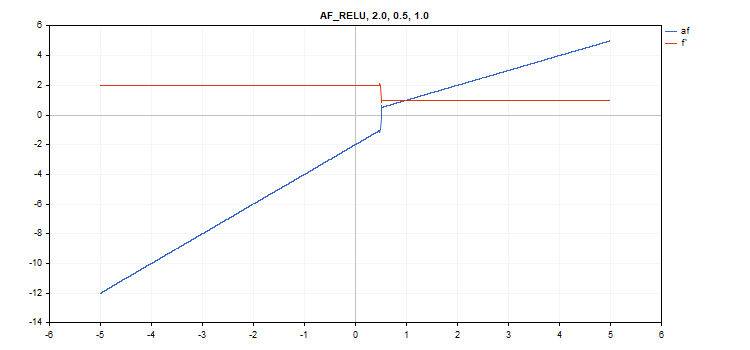
vector_a.Activation(vector_c,AF_RELU,2.0,0.5,1.0);  // call with alpha=2.0, max_value=0.5 and treshold=1.0

Skalierte Exponential-Linear-Einheit (SELU) Aktivierungsfunktion

Berechnung der Funktion

   if(x >= 0)
      f = scale * x;
   else
      f = scale * alpha * (exp(x) - 1);

where scale = 1.05070098, alpha = 1.67326324

Berechnung der Ableitung

   if(x >= 0)
      d = scale;
   else
      d = scale * alpha * exp(x);

Keine zusätzlichen Parameter.

vector_a.Activation(vector_c,AF_SELU);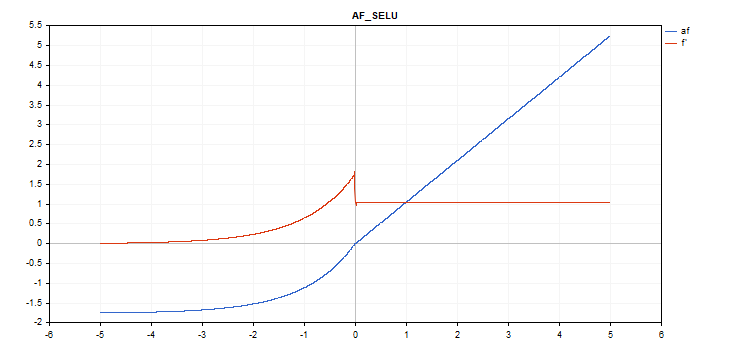

Die Aktivierungsfunktion Sigmoid

Berechnung der Funktion

   f = 1 / (1 + exp(-x));

Berechnung der Ableitung

   d = exp(x) / pow(exp(x) + 1, 2);

Keine zusätzlichen Parameter.

vector_a.Activation(vector_c,AF_SIGMOID);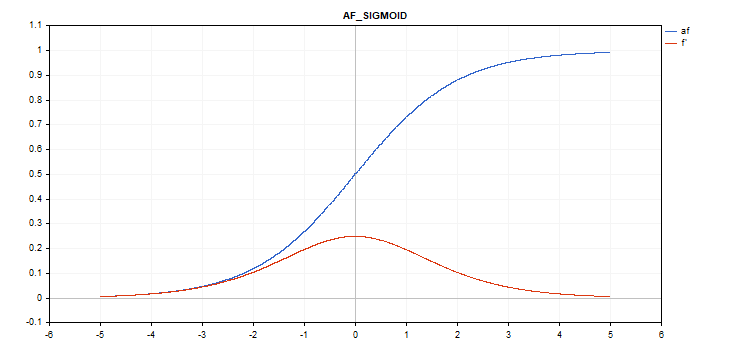

Die Aktivierungsfunktion Softplus

Berechnung der Funktion

   f = log(exp(x) + 1);

Berechnung der Ableitung

   d = exp(x) / (exp(x) + 1);

Keine zusätzlichen Parameter.

vector_a.Activation(vector_c,AF_SOFTPLUS);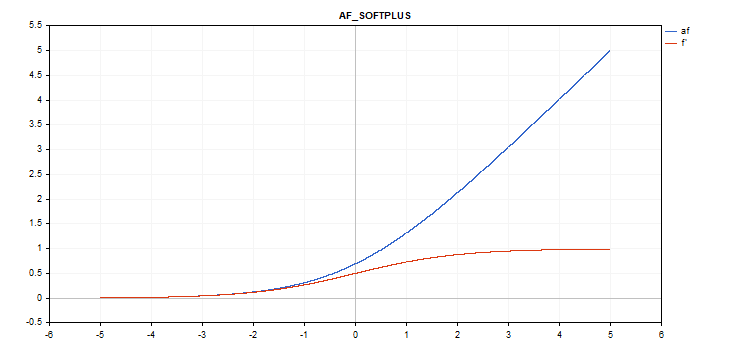

Die Aktivierungsfunktion Softsign

Berechnung der Funktion

   f = x / (|x| + 1)

Berechnung der Ableitung

   d = 1 / (|x| + 1)^2

Keine zusätzlichen Parameter.

vector_a.Activation(vector_c,AF_SOFTSIGN);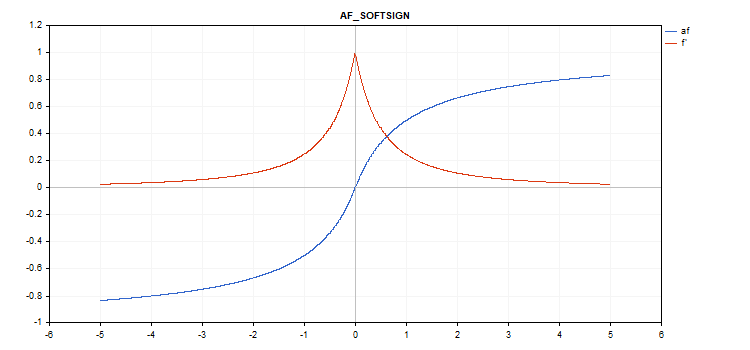

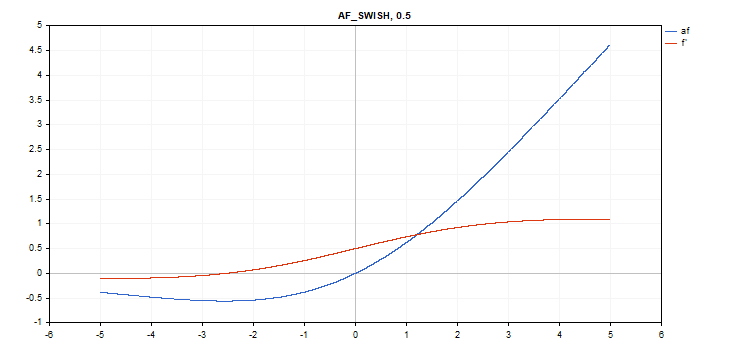
Die Aktivierungsfunktion Swish

Berechnung der Funktion

   f = x / (1 + exp(-x*beta));

Berechnung der Ableitung

   double tmp = exp(beta*x);
   d = tmp*(beta*x + tmp + 1) / pow(tmp+1, 2);

Zusätzlicher Parameter beta = 1

vector_a.Activation(vector_c,AF_SWISH);         // call with the default parameter

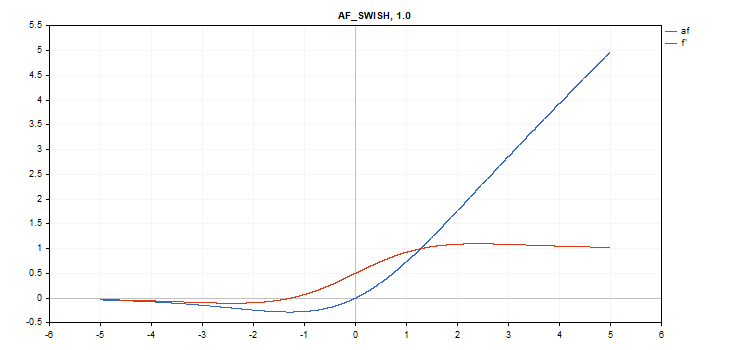
vector_a.Activation(vector_c,AF_SWISH,2.0);     // call with beta = 2.0

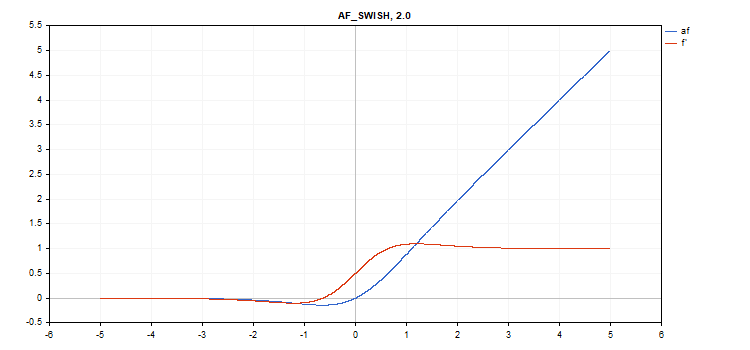
vector_a.Activation(vector_c,AF_SWISH,0.5);   // call with beta=0.5

Die Aktivierungsfunktion Tangens Hyperbolicus(TanH)

Berechnung der Funktion

   f = tanh(x);

Berechnung der Ableitung

   d = 1 / pow(cosh(x),2);

Keine zusätzlichen Parameter.

vector_a.Activation(vector_c,AF_TANH);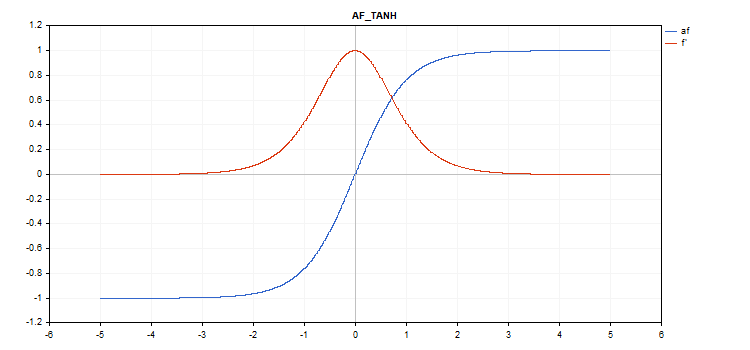

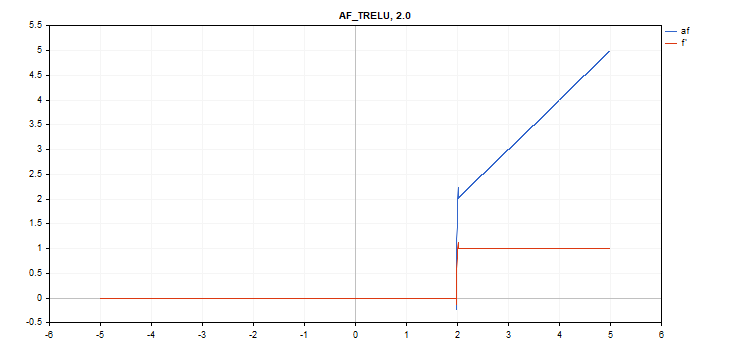
Die Aktivierungsfunktion Thresholded Rectifiedl Linear Unit (TReLU)

Berechnung der Funktion

   if(x > theta)
      f = x;
   else
      f = 0;

Berechnung der Ableitung

   if(x > theta)
      d = 1;
   else
      d = 0;

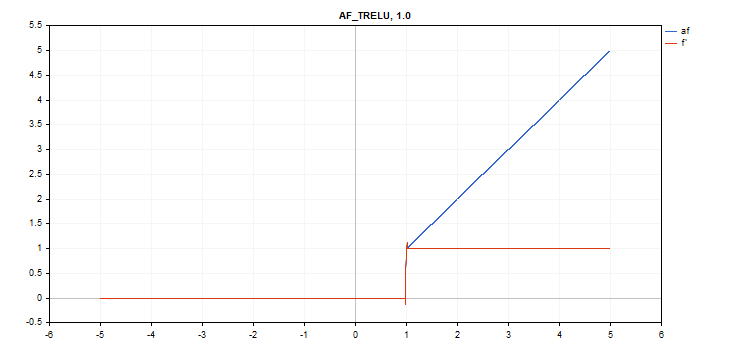
Zusätzlicher Parameter theta = 1

vector_a.Activation(vector_c,AF_TRELU);         // call with default parameter

vector_a.Activation(vector_c,AF_TRELU,0.0);     // call with theta = 0.0

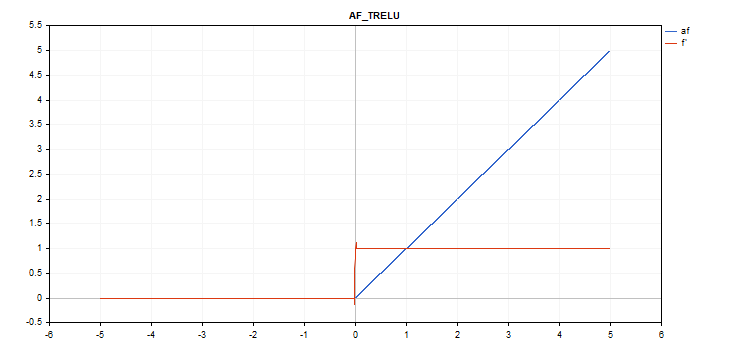
vector_a.Activation(vector_c,AF_TRELU,2.0);      // call with theta = 2.0

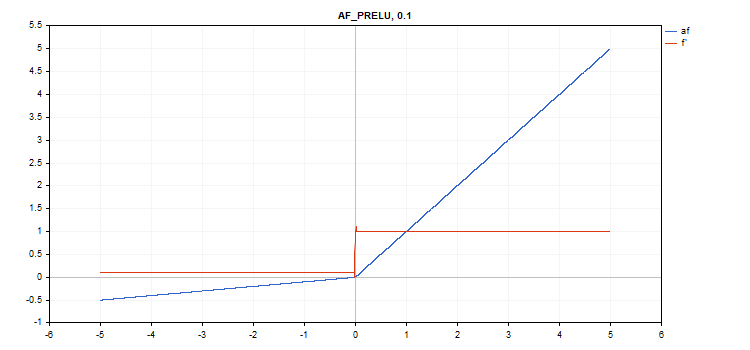
Die Aktivierungsfunktion Parametric Rectified Linear Unit (PReLU)

Berechnung der Funktion

   if(x[i] >= 0)
      f[i] = x[i];
   else
      f[i] = alpha[i]*x[i];

Berechnung der Ableitung

   if(x[i] >= 0)
      d[i] = 1;
   else
      d[i] = alpha[i];

Zusätzlicher Parameter — Koeffizientenvektor „alpha“.

vector alpha=vector::Full(vector_a.Size(),0.1);
vector_a.Activation(vector_c,AF_PRELU,alpha);

Die spezielle Softmax-Funktion

Das Ergebnis der Berechnung der Softmax-Aktivierungsfunktion hängt nicht nur von einem bestimmten Wert ab, sondern auch von allen Vektorwerten.

   sum_exp = Sum(exp(vector_a))
   f = exp(x) / sum_exp

Berechnung der Ableitung

   d = f*(1 - f)

Die Summe aller aktivierten Vektorwerte ist also 1. Daher wird die Softmax-Aktivierungsfunktion sehr häufig für die letzte Schicht von Klassifikationsmodellen verwendet.

Graph der Vektoraktivierungsfunktion mit Werten von -5 bis 5

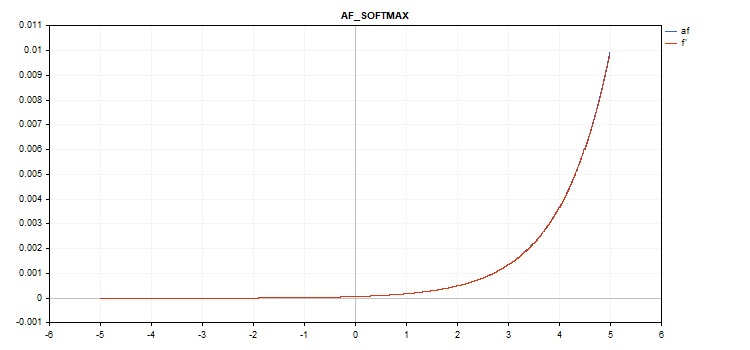
Graph der Vektoraktivierungsfunktion mit Werten von -1 bis 1

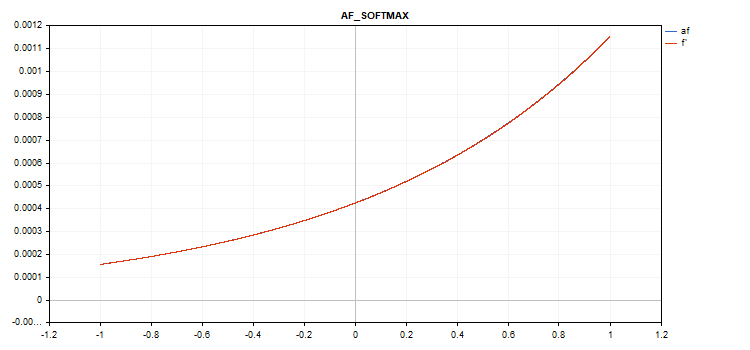
Wenn es keine Aktivierungsfunktion gibt (AF_NONE)

Wenn es keine Aktivierungsfunktion gibt, werden die Werte aus dem Eingangsvektor ohne jegliche Transformation in den Ausgangsvektor übertragen. Es handelt sich um die lineare Aktivierungsfunktion mit Alpha = 1 und Beta = 0.

Schlussfolgerung

Machen Sie sich mit den Quellcodes der Aktivierungsfunktionen und Ableitungen in der unten angehängten Datei ActivationFunction.mqh vertraut.