Matrices y vectores en MQL5: funciones de activación

Introducción

Ya se han publicado muchos libros y artículos sobre el tema del entrenamiento de redes neuronales, y en nuestro recurso MQL5.com, los miembros de la comunidad también han publicado multitud de materiales, incluidas varias series de artículos.

En esta publicación, describiremos solo uno de los aspectos del aprendizaje automático: las funciones de activación. Hoy le mostraremos lo que hay "debajo del capó".

Una breve panorámica

En las redes neuronales artificiales, las funciones de activación de neuronas calculan el valor de la señal de salida en función de los valores de una señal de entrada o un conjunto de señales de entrada. La función de activación debe ser diferenciable en todo el conjunto de valores. Esta condición posibilita la propagación inversa del error al entrenar redes neuronales. Para propagar el error de forma inversa, deberemos calcular el gradiente de la función de activación: el vector de derivadas parciales de la función de activación para cada valor del vector de señal de entrada. Se cree que las funciones de activación no lineales son mejores en el aprendizaje, aunque la función ReLU completamente lineal ha demostrado su eficacia en muchos modelos.

Ilustraciones

Como ilustraciones, hemos preparado gráficos de la función de activación y sus derivados en una secuencia monótonamente creciente de -5 a 5. Hemos preparado un script que muestra el gráfico de la función en el gráfico de precios. Al presionar la tecla Page Down, se mostrará un cuadro de diálogo de apertura de archivo para especificar el nombre de la imagen a guardar.

La tecla ESC finaliza el script. No ofrecemos el texto de este script aquí, lo encontrará adjunto al artículo. Un script similar fue escrito por el autor del artículo Redes neuronales de propagación inversa del error en matrices MQL5; tomamos la idea de él para mostrar, junto con el gráfico de la función de activación, un gráfico con los valores de las derivadas de la función de activación correspondiente.

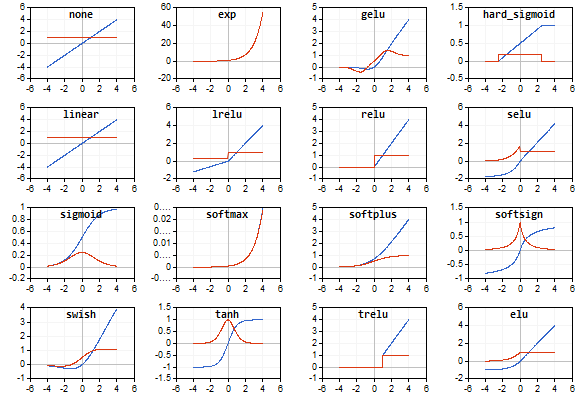
La gráfica de la función de activación se traza con una línea azul; la gráfica de las derivadas de la función se traza en rojo.

Función de activación Exponential Linear Unit (ELU)

Evaluación de la función

   if(x >= 0)
      f = x;
   else
      f = alpha*(exp(x) - 1);

Cálculo de la derivada

   if(x >= 0)
      d = 1;
   else
      d = alpha*exp(x);

Esta función presupone un parámetro adicional alpha. Si no se indica, su valor predeterminado será 1.

   vector_a.Activation(vector_c,AF_ELU);      // call with the default parameter

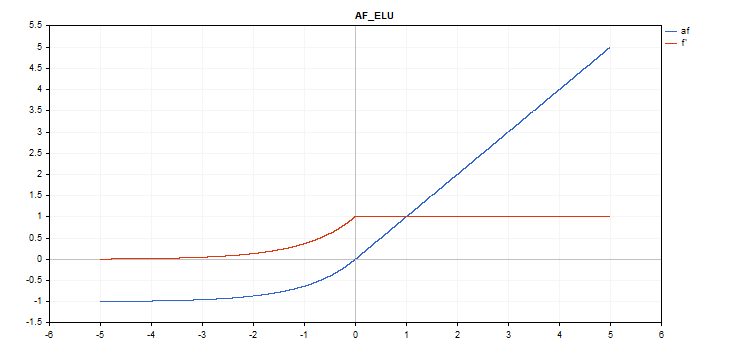
   vector_a.Activation(vector_c,AF_ELU,3.0);  // call with alpha=3.0

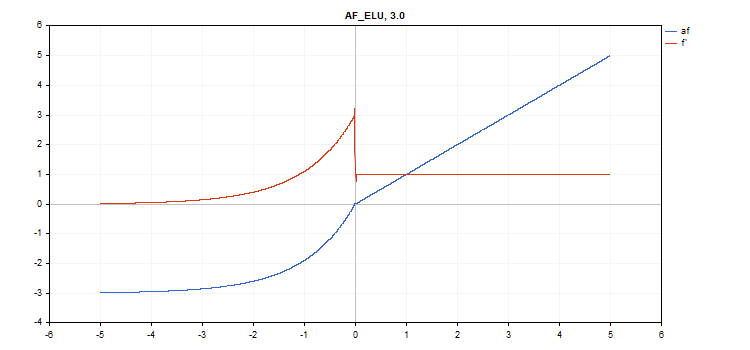
Función de activación Exponential

Evaluación de la función

   f = exp(x);

La derivada de la función exp es la propia función exp.

Como podemos ver en la fórmula de cálculo, la función de activación Exponential no tiene parámetros adicionales

vector_a.Activation(vector_c,AF_EXP);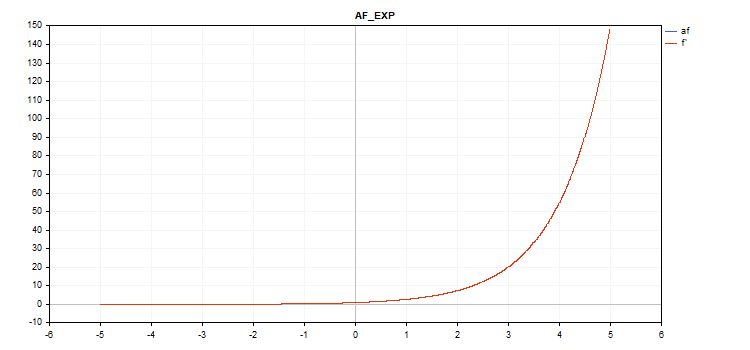

Función de activación Gaussian Error Linear Unit (GELU)

Evaluación de la función

   f = 0.5*x*(1 + tanh(sqrt(M_2_PI)*(x+0.044715*pow(x,3)));

Cálculo de la derivada

   double x_3 = pow(x,3);
   double tmp = cosh(0.0356074*x + 0.797885*x);
   d = 0.5*tanh(0.0356774*x_3 + 0.398942*x)+(0.535161*x_3 + 0.398942*x)/(tmp*tmp) + 0.5;

No hay parámetros adicionales.

vector_a.Activation(vector_c,AF_GELU);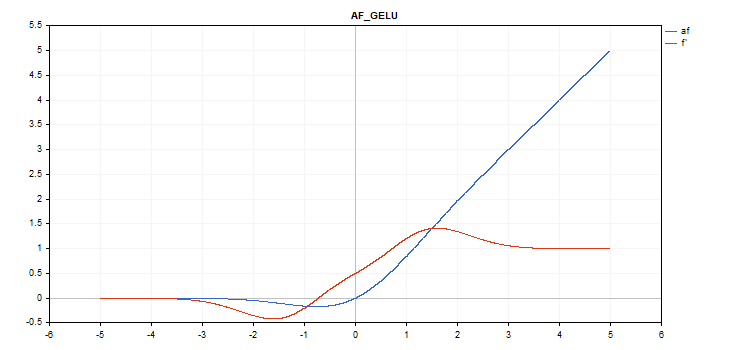

Función de activación Hard Sigmoid

Evaluación de la función

   if(x < -2.5)
      f = 0;
   else
     {
      if(x > 2.5)
         f = 1;
      else
         f = 0.2*x + 0.5;
     }

Cálculo de la derivada

   if(x < -2.5)
      d = 0;
   else
     {
      if(x > 2.5)
         d = 0;
      else
         d = 0.2;
     }

No hay parámetros adicionales.

vector_a.Activation(vector_c,AF_HARD_SIGMOID);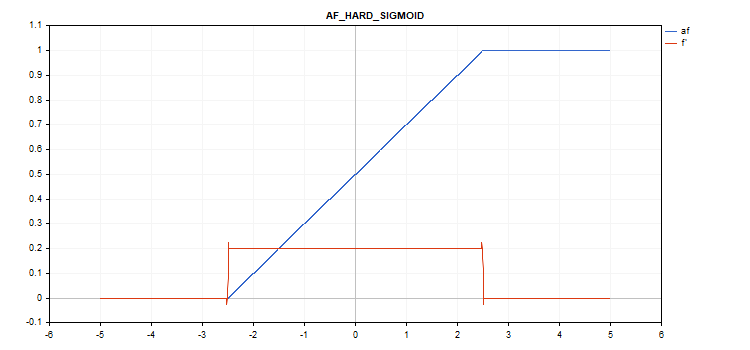

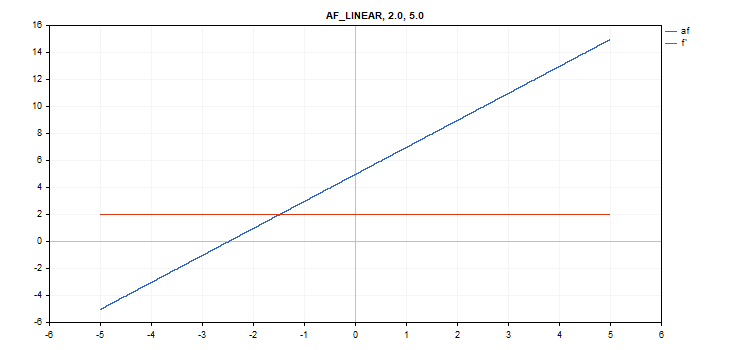
Función de activación Linear

Evaluación de la función

   f = alpha*x + beta

Cálculo de la derivada

   d = alpha

Parámetros adicionales alpha = 1,0 y beta = 0,0

vector_a.Activation(vector_c,AF_LINEAR);         // call with default parameters

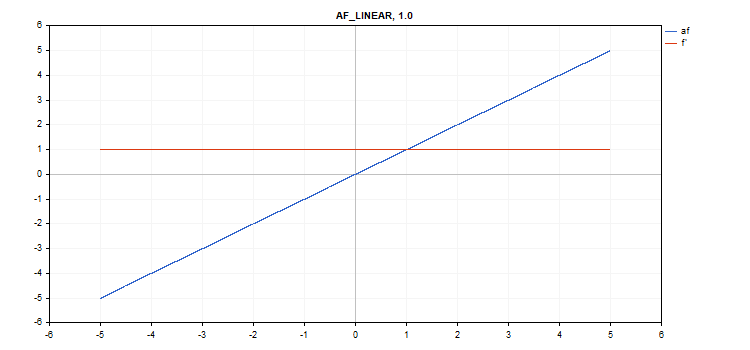
vector_a.Activation(vector_c,AF_LINEAR,2.0,5.0);  // call with alpha=2.0 and beta=5.0

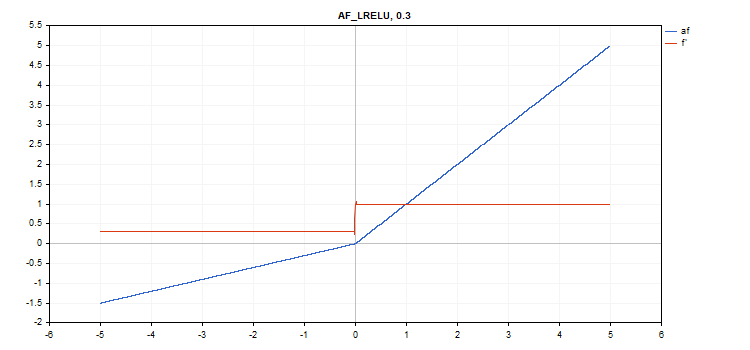
Función de activación Leaky Rectified Linear Unit (LReLU)

Evaluación de la función

   if(x >= 0)
      f = x;
   else
      f = alpha * x;

Cálculo de la derivada

   if(x >= 0)
      d = 1;
   else
      d = alpha;

Esta función presupone un parámetro adicional alpha. Si no se indica, su valor predeterminado será 0. 3

   vector_a.Activation(vector_c,AF_LRELU);      // call with the default parameter

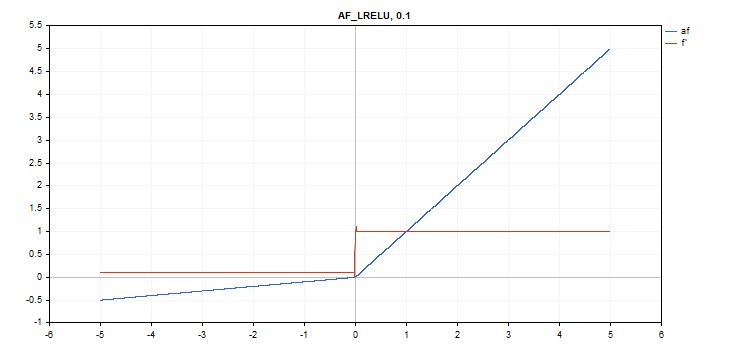
vector_a.Activation(vector_c,AF_LRELU,0.1);  // call with alpha=0.1

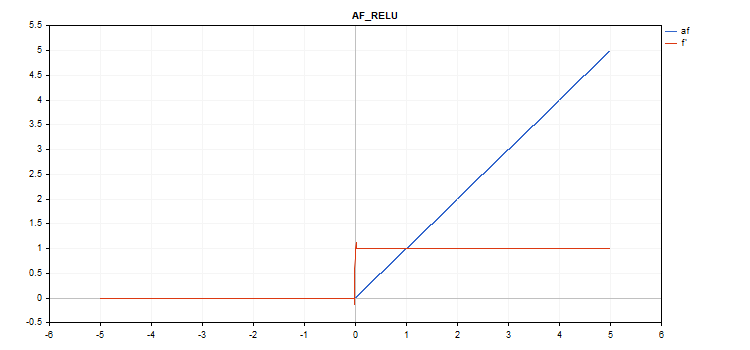
Función de activación Rectified Linear Unit (ReLU)

Evaluación de la función

   if(alpha==0)
     {
      if(x > 0)
         f = x;
      else
         f = 0;
     }
   else
     {
      if(x >= max_value)
         f = x;
      else
         f = alpha * (x - treshold);
     }

Cálculo de la derivada

   if(alpha==0)
     {
      if(x > 0)
         d = 1;
      else
         d = 0;
     }
   else
     {
      if(x >= max_value)
         d = 1;
      else
         d = alpha;
     }

Parámetros adicionales alfa=0, max_value=0 y umbral=0.

vector_a.Activation(vector_c,AF_RELU);         // call with default parameters

vector_a.Activation(vector_c,AF_RELU,2.0,0.5);      // call with alpha=2.0 and max_value=0.5

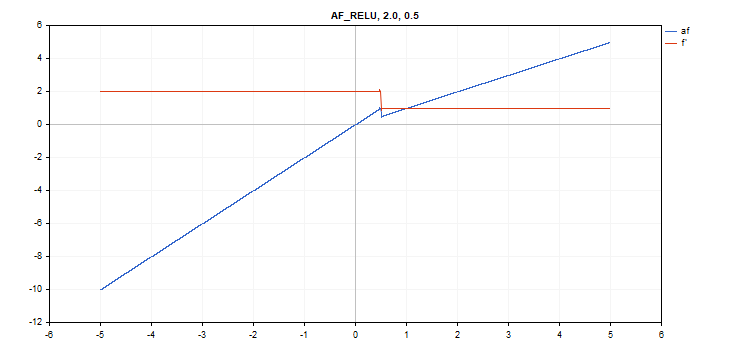
vector_a.Activation(vector_c,AF_RELU,2.0,0.5,1.0);  // call with alpha=2.0, max_value=0.5 and treshold=1.0

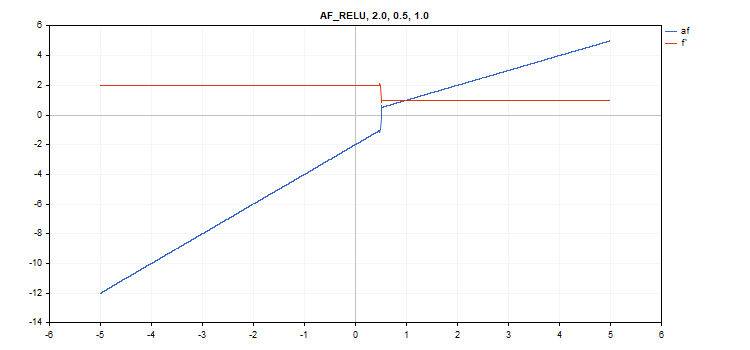
Función de activación Scaled Exponential Linear Unit (SELU)

Evaluación de la función

   if(x >= 0)
      f = scale * x;
   else
      f = scale * alpha * (exp(x) - 1);

where scale = 1.05070098, alpha = 1.67326324

Cálculo de la derivada

   if(x >= 0)
      d = scale;
   else
      d = scale * alpha * exp(x);

No hay parámetros adicionales.

vector_a.Activation(vector_c,AF_SELU);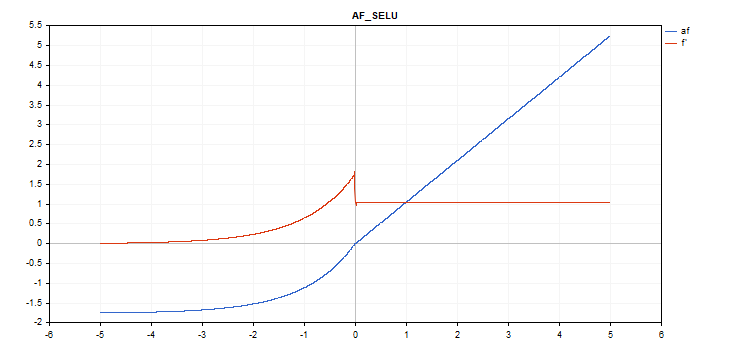

Función de activación Sigmoid

Evaluación de la función

   f = 1 / (1 + exp(-x));

Cálculo de la derivada

   d = exp(x) / pow(exp(x) + 1, 2);

No hay parámetros adicionales.

vector_a.Activation(vector_c,AF_SIGMOID);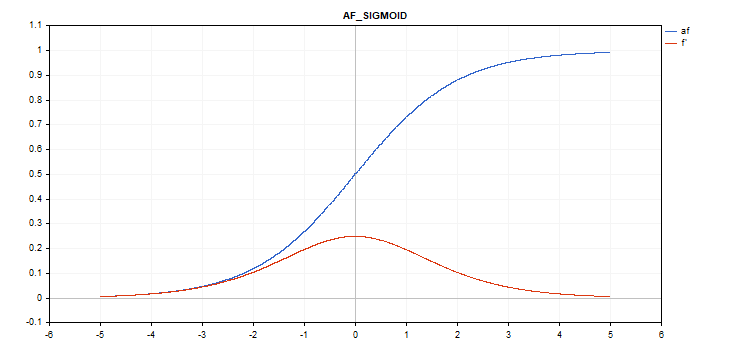

Función de activación Softplus

Evaluación de la función

   f = log(exp(x) + 1);

Cálculo de la derivada

   d = exp(x) / (exp(x) + 1);

No hay parámetros adicionales.

vector_a.Activation(vector_c,AF_SOFTPLUS);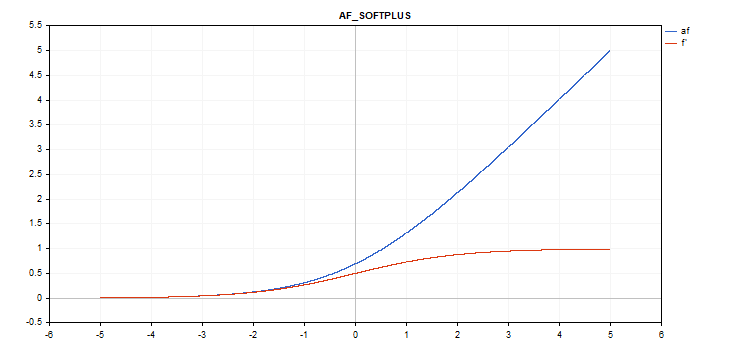

Función de activación Softsign

Evaluación de la función

   f = x / (|x| + 1)

Cálculo de la derivada

   d = 1 / (|x| + 1)^2

No hay parámetros adicionales.

vector_a.Activation(vector_c,AF_SOFTSIGN);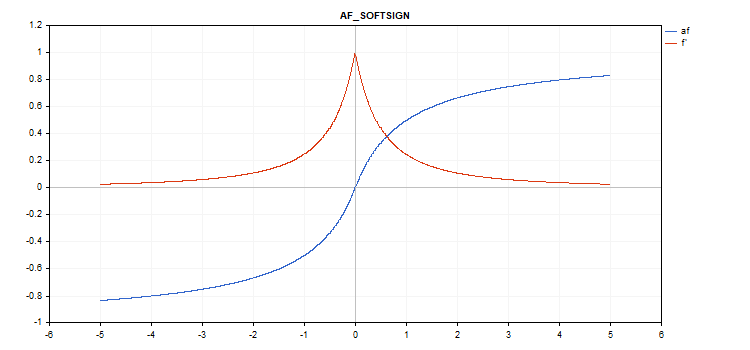

Función de activación Swish

Evaluación de la función

   f = x / (1 + exp(-x*beta));

Cálculo de la derivada

   double tmp = exp(beta*x);
   d = tmp*(beta*x + tmp + 1) / pow(tmp+1, 2);

Parámetro adicional beta = 1

vector_a.Activation(vector_c,AF_SWISH);         // call with the default parameter

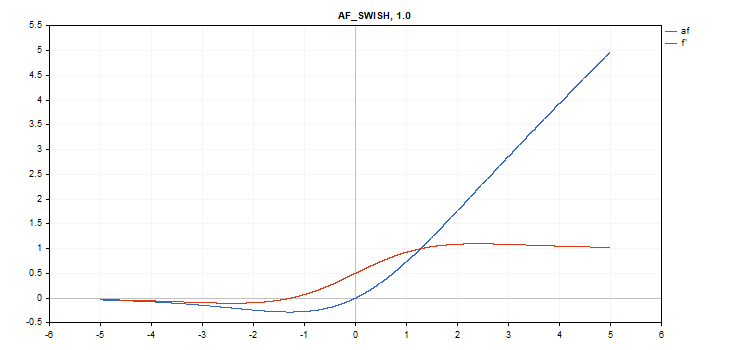
vector_a.Activation(vector_c,AF_SWISH,2.0);     // call with beta = 2.0

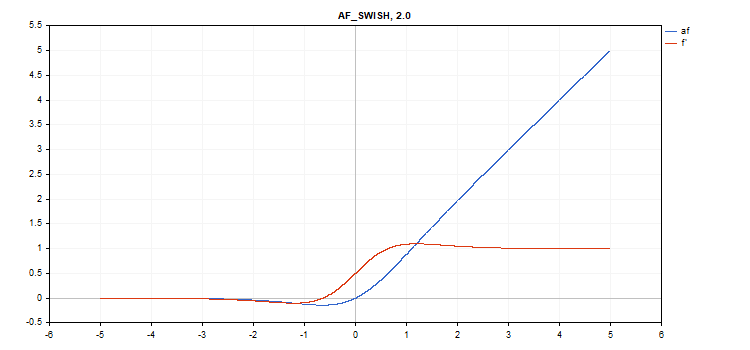
vector_a.Activation(vector_c,AF_SWISH,0.5);   // call with beta=0.5

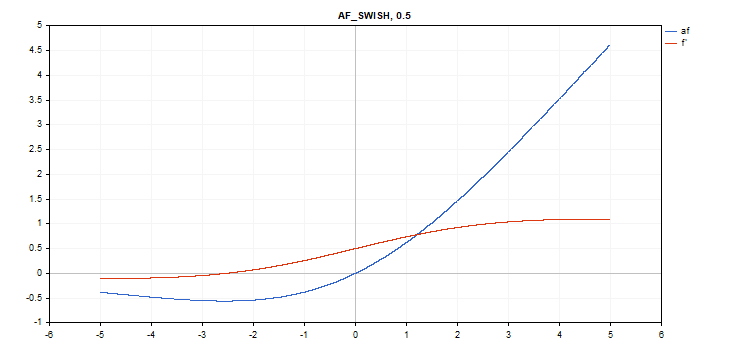
Función de activación Hyperbolic Tangent (TanH)

Evaluación de la función

   f = tanh(x);

Cálculo de la derivada

   d = 1 / pow(cosh(x),2);

No hay parámetros adicionales.

vector_a.Activation(vector_c,AF_TANH);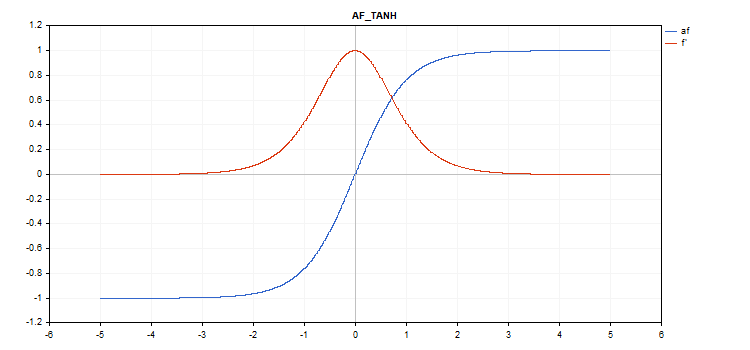

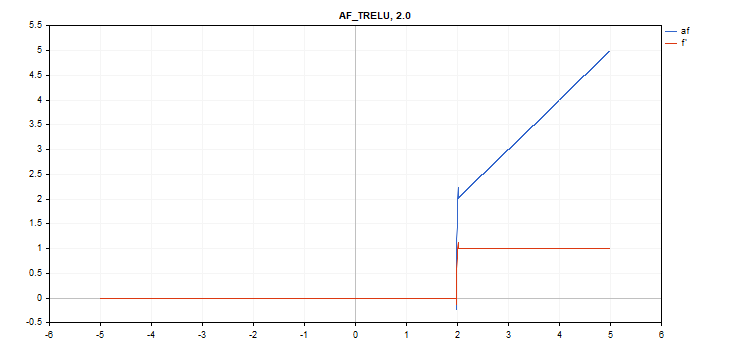
Función de activación Thresholded Rectifiedl Linear Unit (TReLU)

Evaluación de la función

   if(x > theta)
      f = x;
   else
      f = 0;

Cálculo de la derivada

   if(x > theta)
      d = 1;
   else
      d = 0;

Parámetro adicional theta = 1

vector_a.Activation(vector_c,AF_TRELU);         // call with default parameter

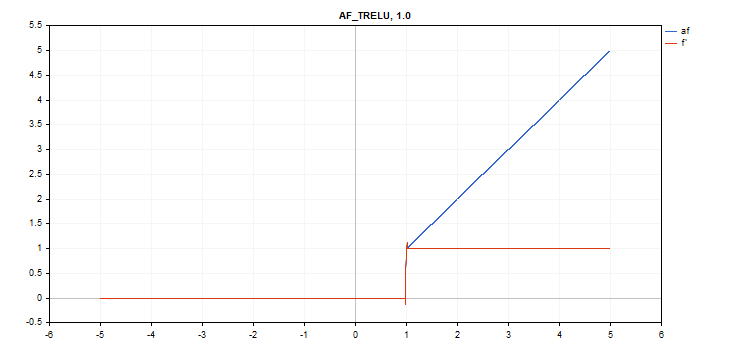
vector_a.Activation(vector_c,AF_TRELU,0.0);     // call with theta = 0.0

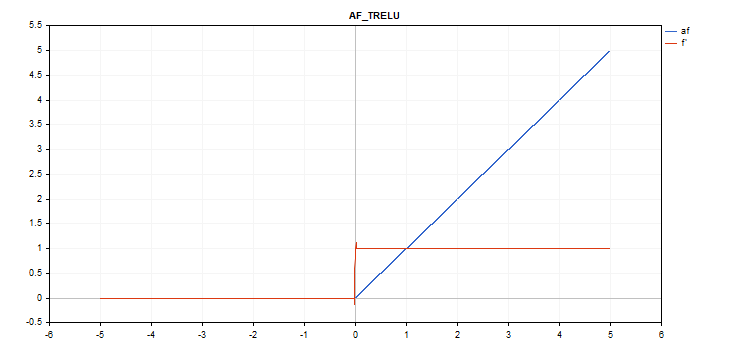
vector_a.Activation(vector_c,AF_TRELU,2.0);      // call with theta = 2.0

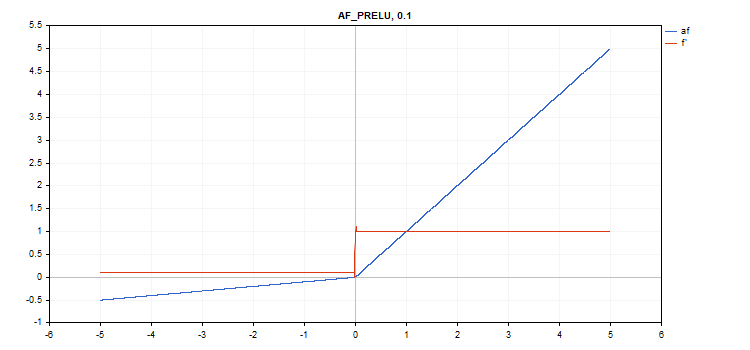
Función de activación Parametric Rectifiedl Linear Unit (PReLU)

Evaluación de la función

   if(x[i] >= 0)
      f[i] = x[i];
   else
      f[i] = alpha[i]*x[i];

Cálculo de la derivada

   if(x[i] >= 0)
      d[i] = 1;
   else
      d[i] = alpha[i];

El parámetro adicional es el vector de coeficientes alpha.

vector alpha=vector::Full(vector_a.Size(),0.1);
vector_a.Activation(vector_c,AF_PRELU,alpha);

Función especial Softmax

El resultado del cálculo de la función de activación Softmax depende no solo de un valor específico, sino también de todos los valores del vector.

   sum_exp = Sum(exp(vector_a))
   f = exp(x) / sum_exp

Cálculo de la derivada

   d = f*(1 - f)

Por consiguiente, la suma de todos los valores del vector activado será 1. Por eso, la función de activación de Softmax se utiliza muy a menudo para la última capa de modelos de clasificación.

Gráfico de la función de activación del vector con valores de -5 a 5

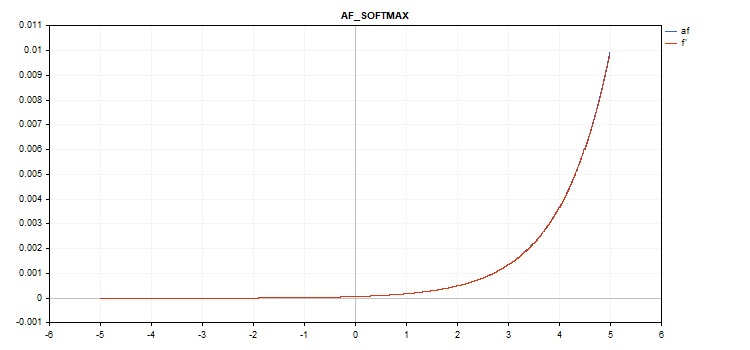
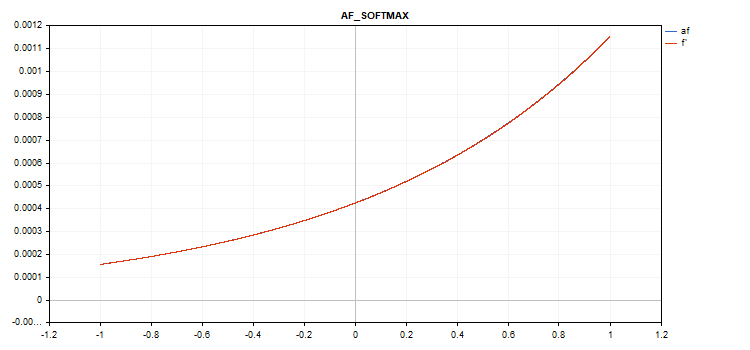
Gráfico de la función de activación del vector con valores de -1 a 1

Si no hay función de activación (AF_NONE)

Si no hay una función de activación, los valores del vector de entrada se transmitirán al vector de salida sin ninguna transformación. En la práctica, esta es una función de activación lineal con parámetros alpha = 1 y beta = 0.

Conclusión

Como conclusión, le sugerimos que se familiarice con los textos originales de las funciones de activación y sus derivadas que se encuentran en el archivo adjunto ActivationFunction.mqh.