Matrices et vecteurs en MQL5 : Fonctions d'activation

Introduction

Un grand nombre d'ouvrages et d'articles ont déjà été publiés sur le thème de l'apprentissage des réseaux neuronaux. Les membres de MQL5.com ont également publié de nombreux documents, dont plusieurs séries d'articles.

Nous ne décrirons ici qu'un seul des aspects de l'apprentissage automatique, à savoir les fonctions d'activation. Nous nous pencherons sur les rouages du processus.

Vue d'ensemble

Dans les réseaux neuronaux artificiels, la fonction d'activation d'un neurone calcule la valeur d'un signal de sortie en fonction des valeurs d'un signal d'entrée ou d'un ensemble de signaux d'entrée. La fonction d'activation doit être différentiable sur l'ensemble des valeurs. Cette condition permet la rétropropagation des erreurs lors de la formation des réseaux neuronaux. Pour rétropropager l'erreur, il faut calculer le gradient de la fonction d'activation : le vecteur des dérivées partielles de la fonction d'activation pour chaque valeur du vecteur du signal d'entrée. On estime que les fonctions d'activation non linéaires sont plus adaptées à la formation. Bien que la fonction ReLU complètement linéaire ait montré son efficacité dans de nombreux modèles.

Illustrations

Les graphiques de la fonction d'activation et leurs dérivés ont été préparés dans une séquence monotone croissante de -5 à 5 à titre d'illustration. Le script affichant le graphique des fonctions sur le graphique des prix a également été développé. La boîte de dialogue d'ouverture de fichier s'affiche pour spécifier le nom de l'image enregistrée en appuyant sur la touche Page suivante.

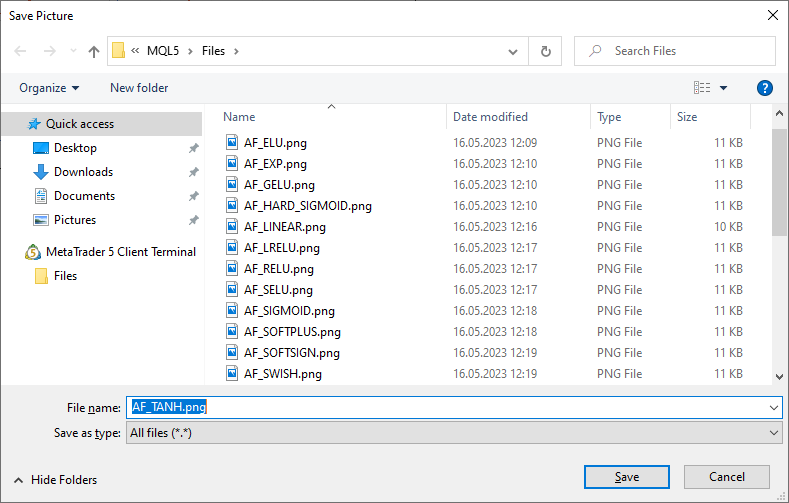
La touche ESC met fin au script. Le script lui-même est attaché ci-dessous. Un script similaire a été écrit par l'auteur de l'article Backpropagation neural networks using MQL5 matrices. Nous avons utilisé son idée pour afficher le graphique des valeurs des dérivés de la fonction d'activation correspondante en même temps que le graphique de la fonction d'activation elle-même.

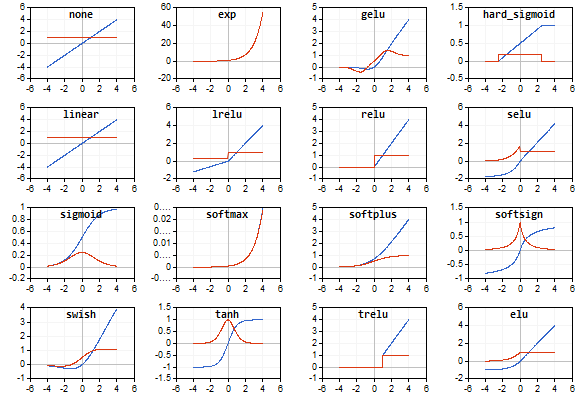
La fonction d'activation est représentée en bleu, et les dérivés de la fonction sont affichés en rouge.

Fonction d'activation de l'unité linéaire exponentielle (ELU)

Calcul de la fonction

   if(x >= 0)
      f = x;
   else
      f = alpha*(exp(x) - 1);

Calcul des dérivés

   if(x >= 0)
      d = 1;
   else
      d = alpha*exp(x);

Cette fonction prend un paramètre supplémentaire "alpha". S'il n'est pas spécifié, sa valeur par défaut est 1.

   vector_a.Activation(vector_c,AF_ELU);      // call with the default parameter

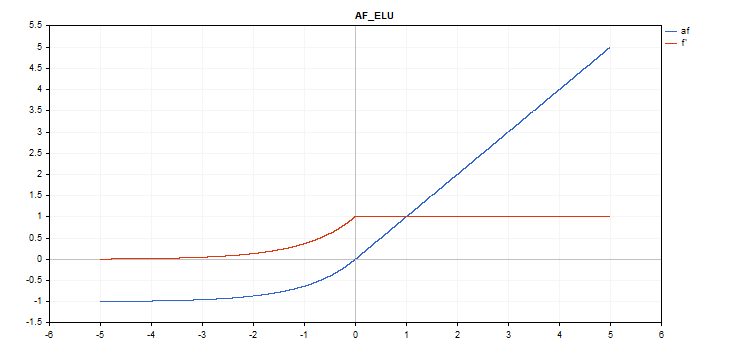
   vector_a.Activation(vector_c,AF_ELU,3.0);  // call with alpha=3.0

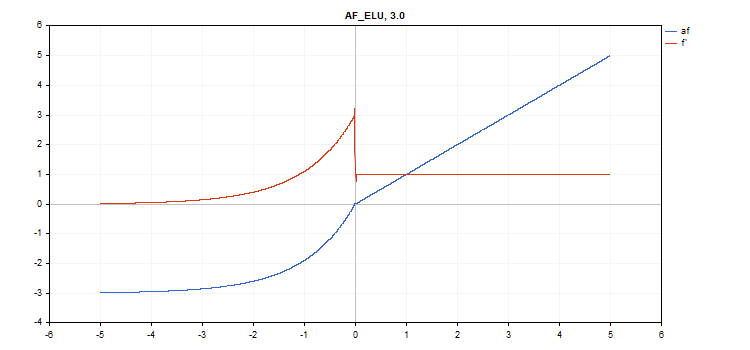
Fonction d'activation exponentielle

Calcul de la fonction

   f = exp(x);

La même fonction exp sert de dérivée à la fonction exp.

Comme nous pouvons le voir dans l'équation de calcul, la fonction d'activation exponentielle n'a pas de paramètres supplémentaires.

vector_a.Activation(vector_c,AF_EXP);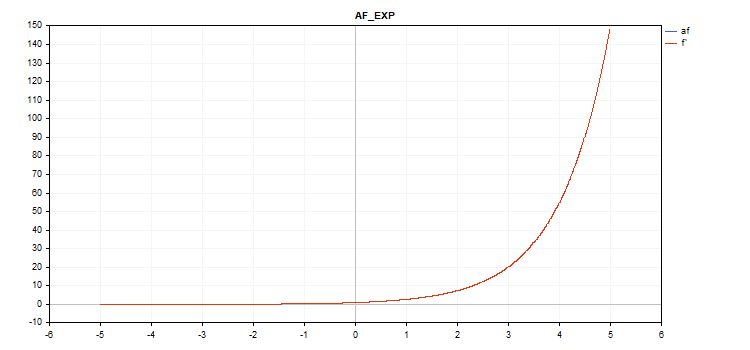

Fonction d'activation GELU (Gaussian Error Linear Unit)

Calcul de la fonction

   f = 0.5*x*(1 + tanh(sqrt(M_2_PI)*(x+0.044715*pow(x,3)));

Calcul des dérivés

   double x_3 = pow(x,3);
   double tmp = cosh(0.0356074*x + 0.797885*x);
   d = 0.5*tanh(0.0356774*x_3 + 0.398942*x)+(0.535161*x_3 + 0.398942*x)/(tmp*tmp) + 0.5;

Pas de paramètres supplémentaires.

vector_a.Activation(vector_c,AF_GELU);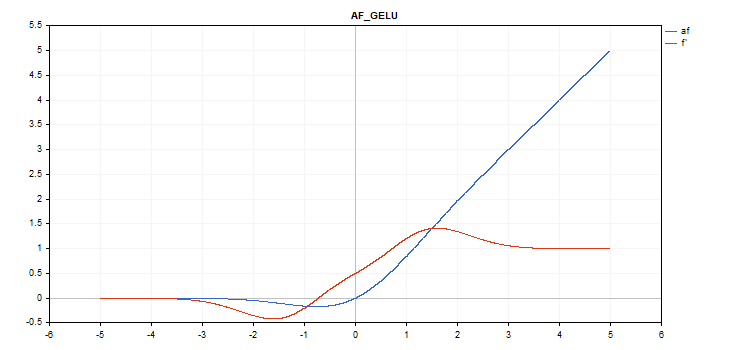

Fonction d'activation sigmoïde dure

Calcul de la fonction

   if(x < -2.5)
      f = 0;
   else
     {
      if(x > 2.5)
         f = 1;
      else
         f = 0.2*x + 0.5;
     }

Calcul des dérivés

   if(x < -2.5)
      d = 0;
   else
     {
      if(x > 2.5)
         d = 0;
      else
         d = 0.2;
     }

Pas de paramètres supplémentaires.

vector_a.Activation(vector_c,AF_HARD_SIGMOID);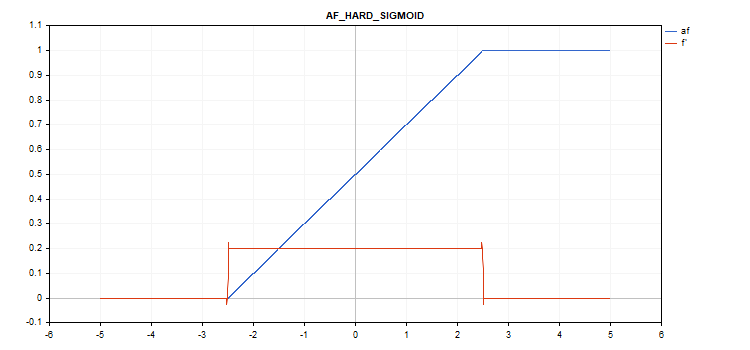

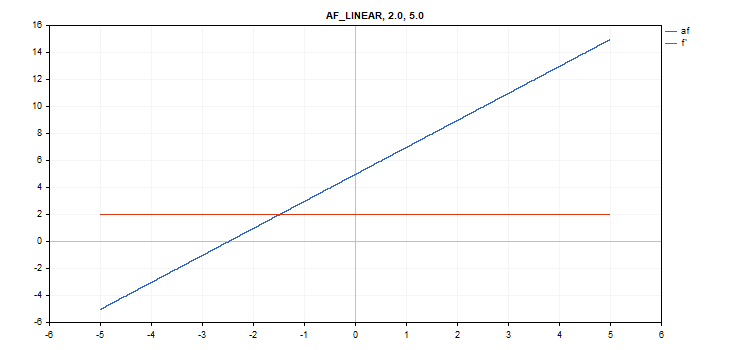
Fonction d'activation linéaire

Calcul de la fonction

   f = alpha*x + beta

Calcul des dérivés

   d = alpha

Paramètres supplémentaires alpha = 1,0 et beta = 0,0

vector_a.Activation(vector_c,AF_LINEAR);         // call with default parameters

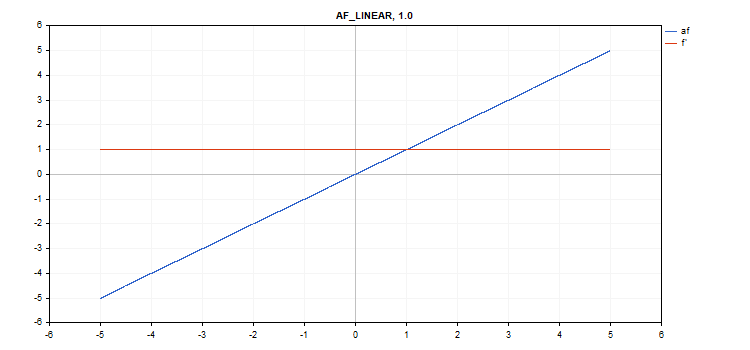
vector_a.Activation(vector_c,AF_LINEAR,2.0,5.0);  // call with alpha=2.0 and beta=5.0

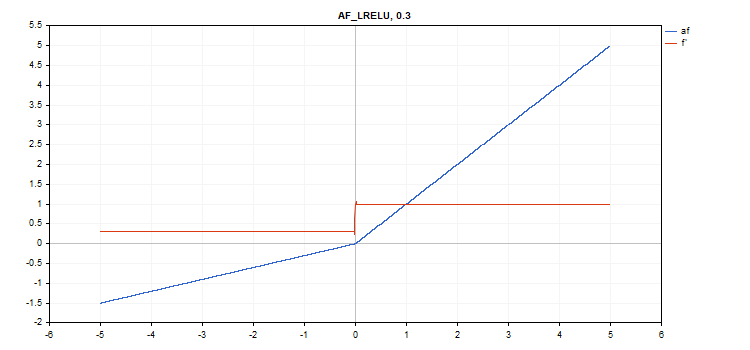
Fonction d'activation LReLU (Leaky Rectified Linear Unit)

Calcul de la fonction

   if(x >= 0)
      f = x;
   else
      f = alpha * x;

Calcul des dérivés

   if(x >= 0)
      d = 1;
   else
      d = alpha;

Cette fonction prend un paramètre supplémentaire "alpha". S'il n'est pas spécifié, sa valeur par défaut est 0. 3

   vector_a.Activation(vector_c,AF_LRELU);      // call with the default parameter

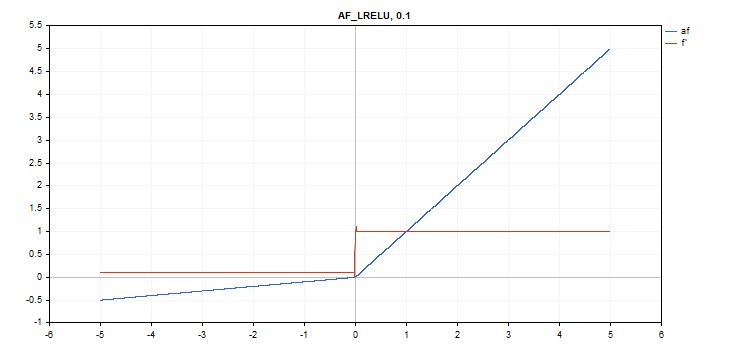
vector_a.Activation(vector_c,AF_LRELU,0.1);  // call with alpha=0.1

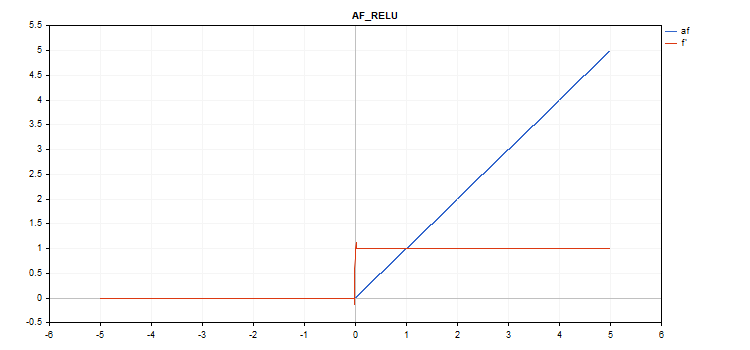
Fonction d'activation de l'unité linéaire rectifiée (ReLU)

Calcul de la fonction

   if(alpha==0)
     {
      if(x > 0)
         f = x;
      else
         f = 0;
     }
   else
     {
      if(x >= max_value)
         f = x;
      else
         f = alpha * (x - treshold);
     }

Calcul des dérivés

   if(alpha==0)
     {
      if(x > 0)
         d = 1;
      else
         d = 0;
     }
   else
     {
      if(x >= max_value)
         d = 1;
      else
         d = alpha;
     }

Paramètres supplémentaires alpha=0, max_value=0 et treshold=0.

vector_a.Activation(vector_c,AF_RELU);         // call with default parameters

vector_a.Activation(vector_c,AF_RELU,2.0,0.5);      // call with alpha=2.0 and max_value=0.5

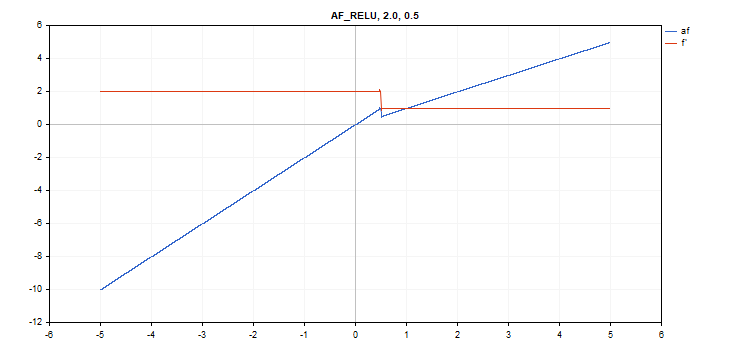
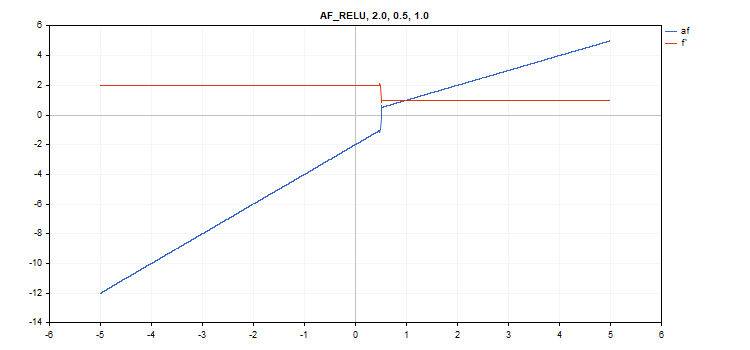
vector_a.Activation(vector_c,AF_RELU,2.0,0.5,1.0);  // call with alpha=2.0, max_value=0.5 and treshold=1.0

Fonction d'activation SELU (Scaled Exponential Linear Unit)

Calcul de la fonction

   if(x >= 0)
      f = scale * x;
   else
      f = scale * alpha * (exp(x) - 1);

where scale = 1.05070098, alpha = 1.67326324

Calcul des dérivés

   if(x >= 0)
      d = scale;
   else
      d = scale * alpha * exp(x);

Pas de paramètres supplémentaires.

vector_a.Activation(vector_c,AF_SELU);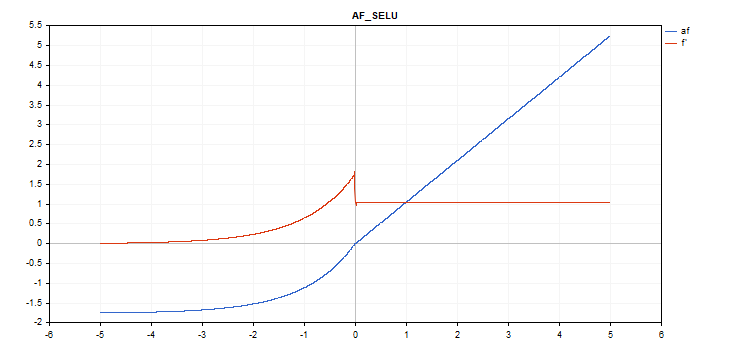

Fonction d'activation sigmoïde

Calcul de la fonction

   f = 1 / (1 + exp(-x));

Calcul des dérivés

   d = exp(x) / pow(exp(x) + 1, 2);

Pas de paramètres supplémentaires.

vector_a.Activation(vector_c,AF_SIGMOID);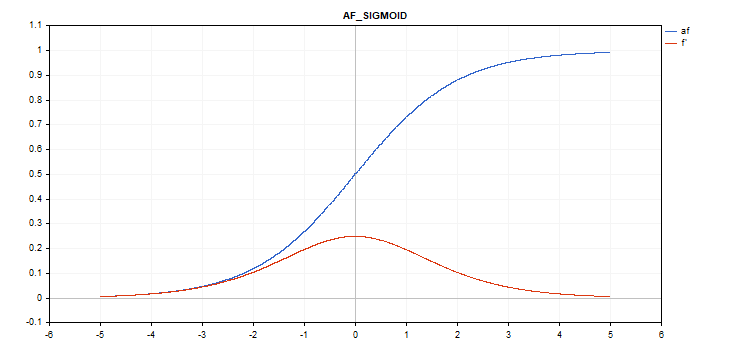

Fonction d'activation Softplus

Calcul de la fonction

   f = log(exp(x) + 1);

Calcul des dérivés

   d = exp(x) / (exp(x) + 1);

Pas de paramètres supplémentaires.

vector_a.Activation(vector_c,AF_SOFTPLUS);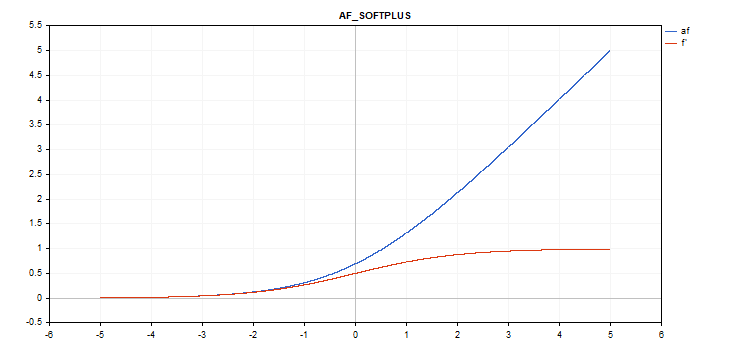

Fonction d'activation Softsign

Calcul de la fonction

   f = x / (|x| + 1)

Calcul des dérivés

   d = 1 / (|x| + 1)^2

Pas de paramètres supplémentaires.

vector_a.Activation(vector_c,AF_SOFTSIGN);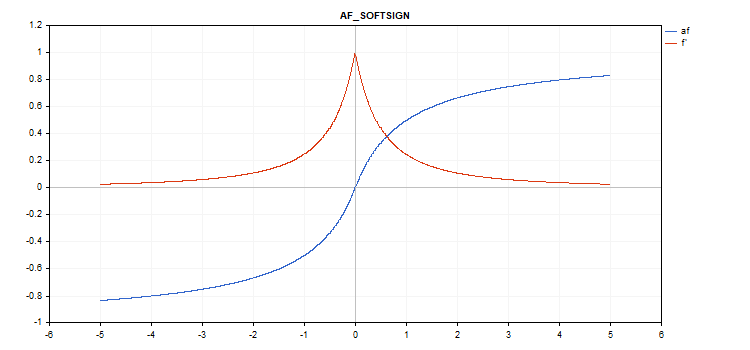

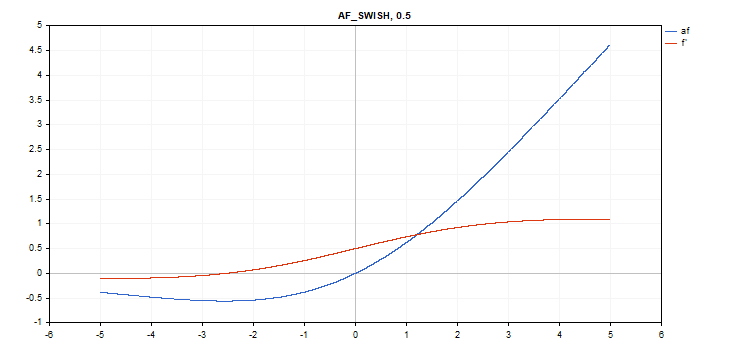
Fonction d'activation Swish

Calcul de la fonction

   f = x / (1 + exp(-x*beta));

Calcul des dérivés

   double tmp = exp(beta*x);
   d = tmp*(beta*x + tmp + 1) / pow(tmp+1, 2);

Paramètre supplémentaire beta = 1

vector_a.Activation(vector_c,AF_SWISH);         // call with the default parameter

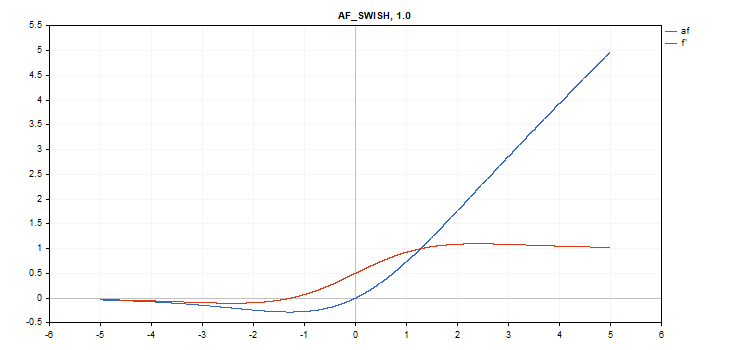
vector_a.Activation(vector_c,AF_SWISH,2.0);     // call with beta = 2.0

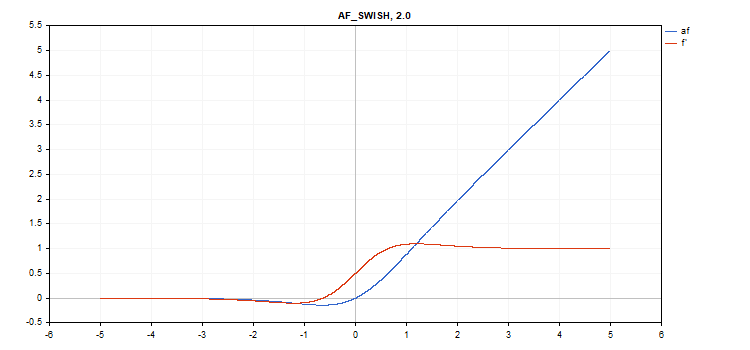
vector_a.Activation(vector_c,AF_SWISH,0.5);   // call with beta=0.5

Fonction d'activation tangente hyperbolique (TanH)

Calcul de la fonction

   f = tanh(x);

Calcul des dérivés

   d = 1 / pow(cosh(x),2);

Pas de paramètres supplémentaires.

vector_a.Activation(vector_c,AF_TANH);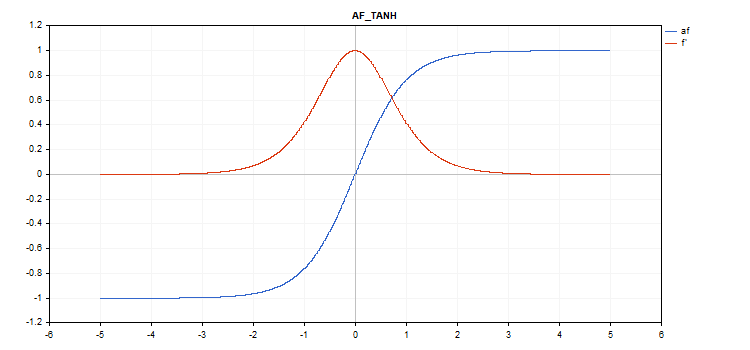

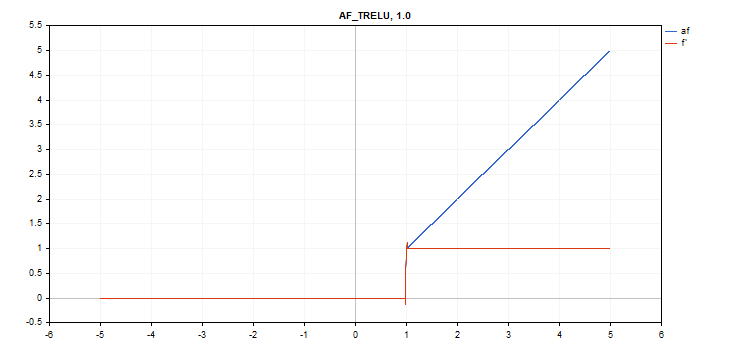
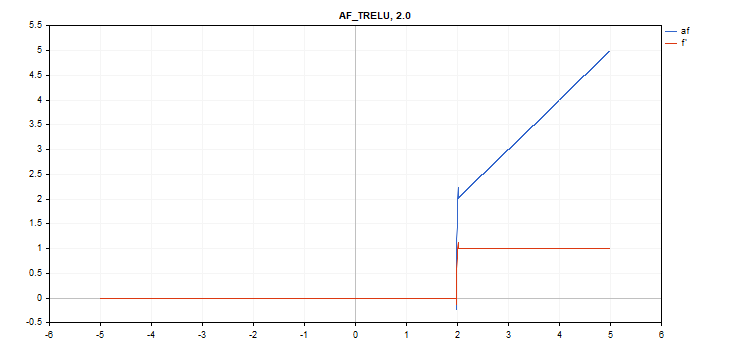
Fonction d'activation TReLU (Thresholded Rectifiedl Linear Unit)

Calcul de la fonction

   if(x > theta)
      f = x;
   else
      f = 0;

Calcul des dérivés

   if(x > theta)
      d = 1;
   else
      d = 0;

Paramètre supplémentaire thêta = 1

vector_a.Activation(vector_c,AF_TRELU);         // call with default parameter

vector_a.Activation(vector_c,AF_TRELU,0.0);     // call with theta = 0.0

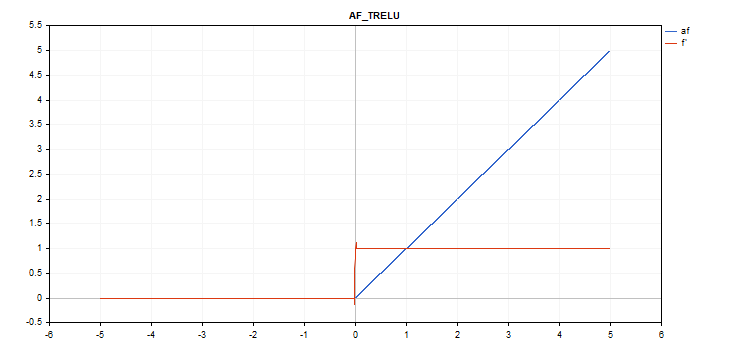
vector_a.Activation(vector_c,AF_TRELU,2.0);      // call with theta = 2.0

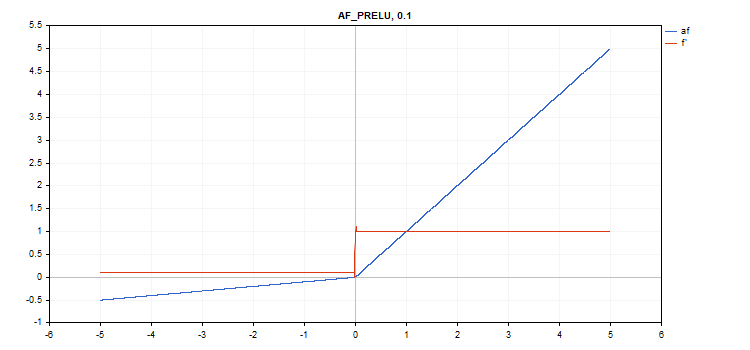
Fonction d'activation PReLU (Parametric Rectifiedl Linear Unit)

Calcul de la fonction

   if(x[i] >= 0)
      f[i] = x[i];
   else
      f[i] = alpha[i]*x[i];

Calcul des dérivés

   if(x[i] >= 0)
      d[i] = 1;
   else
      d[i] = alpha[i];

Paramètre supplémentaire : vecteur de coefficient "alpha".

vector alpha=vector::Full(vector_a.Size(),0.1);
vector_a.Activation(vector_c,AF_PRELU,alpha);

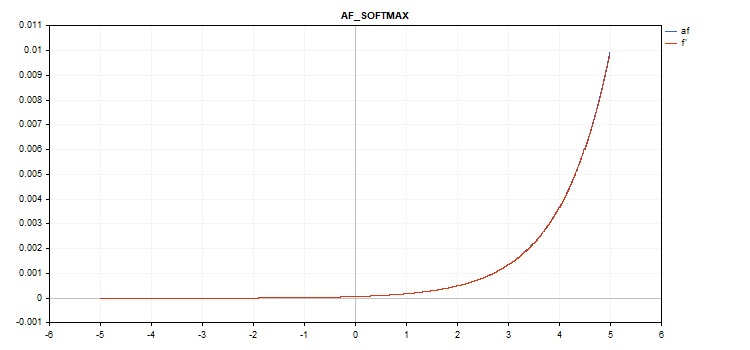
Fonction spéciale Softmax

Le résultat du calcul de la fonction d'activation Softmax dépend non seulement d'une valeur spécifique, mais aussi de toutes les valeurs du vecteur.

   sum_exp = Sum(exp(vector_a))
   f = exp(x) / sum_exp

Calcul des dérivés

   d = f*(1 - f)

Ainsi, la somme de toutes les valeurs des vecteurs activés est de 1. C'est pourquoi la fonction d'activation Softmax est très souvent utilisée pour la dernière couche des modèles de classification.

Graphique de la fonction d'activation vectorielle avec des valeurs comprises entre -5 et 5

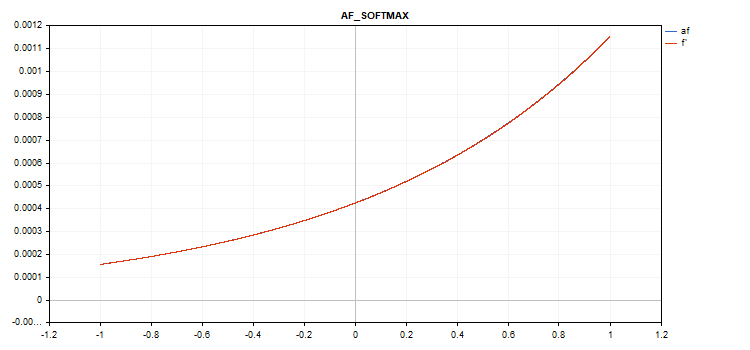
Graphique de la fonction d'activation vectorielle avec des valeurs de -1 à 1

S'il n'y a pas de fonction d'activation (AF_NONE)

S'il n'y a pas de fonction d'activation, les valeurs du vecteur d'entrée sont transférées au vecteur de sortie sans aucune transformation. En fait, il s'agit de la fonction d'activation linéaire avec alpha = 1 et beta = 0.

Conclusion

N'hésitez pas à vous familiariser avec les codes sources des fonctions d'activation et des dérivés dans le fichier ActivationFunction.mqh attaché ci-dessous.